Mathematics as a Conduit for Translational Research in Post-Traumatic Osteoarthritis

Abstract

Biomathematical models offer a powerful method of clarifying complex temporal interactions and the relationships among multiple variables in a system. We present a coupled in silico biomathematical model of articular cartilage degeneration in response to impact and/or aberrant loading such as would be associated with injury to an articular joint. The model incorporates fundamental biological and mechanical information obtained from explant and small animal studies to predict post-traumatic osteoarthritis (PTOA) progression, with an eye toward eventual application in human patients. In this sense, we refer to the mathematics as a “conduit of translation”. The new in silico framework presented in this paper involves a biomathematical model for the cellular and biochemical response to strains computed using finite element analysis. The model predicts qualitative responses presently, utilizing system parameter values largely taken from the literature. To contribute to accurate predictions, models need to be accurately parameterized with values that are based on solid science. We discuss a parameter identification protocol that will enable us to make increasingly accurate predictions of PTOA progression using additional data from smaller scale explant and small animal assays as they become available. By distilling the data from the explant and animal assays into parameters for biomathematical models, mathematics can translate experimental data to clinically relevant knowledge.

Introduction

“We are buried beneath the weight of information, which is being confused with knowledge” – Tom Waits

The generation of massive amounts of data, in orthopaedic research as in any field of inquiry, brings into contrast the distinction between information and knowledge. In the case of post-traumatic osteoarthritis (PTOA), a wealth of valuable data comes from smaller-scale in vitro assays and small animal models^1–7; however, the challenge is to translate this information into clinically relevant knowledge. Chu and Andriacchi have called for a systems-level approach to this challenge⁸. We argue here that new mathematical descriptions of the cellular and biochemical processes, added to the existing body of biomechanical models, is the answer to this call. Here, we present some specifics of a mathematical and computational approach designed to translate information gained from cell biology and animal modeling into strategies for the treatment and prevention of PTOA. In addition to its role in translation, in silico models have the added benefits of lower expense, greater diversity of models, and shorter times to results, when compared to experimental studies.

Our group’s focus to date has been on modeling the balancing act between pro- and anti-inflammatory cytokines in injured articular cartilage, an approach based on a wound healing perspective⁹. Thus far we have modeled single mechanical insults such as occur in articular fractures and other joint injuries. Here we incorporate the contributions of chronic insults, which can occur with residual incongruity, a common sequela of joint fracture. Biomechanical models and computational simulations have a long, rich history in helping to understand the mechanics of bone and cartilage^10–16. Incorporation of cell biology and biochemistry into these rigorous systems requires what we refer to as “biomathematical” models and simulations that are just beginning to be developed for PTOA^17–21. Here, we propose that the chain of events leading from acute joint injury to PTOA, including mechanical stress and specific cellular pathways, can ultimately be described in sets of equations that represent known biomechanics and cellular responses to mechanical stress. Defining such multiscale relationships may help to predict thresholds for induction of disease after injury or the effectiveness of drugs and other treatments under real-world conditions.

Our specific approach to providing a “conduit for translation” relies upon calibration of in silico mathematical models by smaller-scale in vitro assays and the animal model data available. The preclinical information therein can thus be converted into predictions of human disease. These models, and hence the relevance of smaller-scale assays, can then be validated by large mammal or human data, allowing iterative refinement of the models themselves. By continuing to incorporate an ever increasing understanding of constituent processes, these mechanistic models bypass the need to infer outcomes from data often obtained in a somewhat different setting. For example, the ability to predict the weather worldwide with ever increasing accuracy, but not earthquakes, may be due to the relatively greater foundational understanding of the underlying physics of weather patterns in the context of topography, seasons, jet stream, etc., encapsulated in mechanistic mathematical models not available for earthquakes²².

Thus, as an example of this conduit of translation we have built a mathematical model for cartilage response to injury from overloading. Here, as in our group’s prior work^17–21, cartilage cell populations are separated into three model compartments, based on cells being “healthy”, “sick”, or “dead”. Within these compartments, cells are further subdivided based on signaling state or being necrotic or apoptotic. This approach originally relied upon delay differential equations, and later a mathematical construct called “age structure”, to represent the delays in the various signaling processes over time. Going forward, instead of representing the role of mechanical stress implicitly through certain functional forms in our biomathematical model, we are using finite element analysis (FEA) to incorporate biomechanical criteria explicitly²¹. The project presented here was designed to qualitatively predict the cartilage tissue’s reaction to systemic overload, in the context of inflammation and oxidative stress, with our simulations covering a period of 14 days post-injury. We showed previously that impact injuries to osteochondral explants cause chondrocyte necrosis and alarmin release, which provokes a local pro-inflammatory response^23,24. This was mimicked in cell culture experiments using freeze-thawed chondrocyte lysates. We have shown in animal models that impact injuries to joint surfaces lead reliably to OA^5,7.

Methods

The model in this paper belongs to a lineage of increasingly faithful representations of the underlying biological mechanisms, and increasingly rigorous calibrations to data. By translating explant and other small-scale assays to clinically relevant understanding, we have undertaken a mechanistic, rather than phenomenological, approach. Thus, the terms in the model equations represent specific mechanisms (e.g., the diffusion or production of a certain cytokine), and the parameters in the model have concrete meaning and units (e.g., a specific diffusion coefficient or production rate constant). This is in contrast to phenomenological models, where terms represent interactions between model components (e.g., the influence of one cell type on another), and the parameters have a more abstract meaning and are usually dimensionless (e.g., the basic reproductive number, R₀, in epidemiology models). Parameterization (i.e., the calibration of the model by determining the parameters) is often the deciding factor in which kind of model to choose. Phenomenological models can be useful when detailed measurements of the underlying mechanisms are not available or of interest. However, in this case we have chosen to take advantage of a wealth of data from the research laboratories of the University of Iowa Department of Orthopedics and Rehabilitation to begin to construct mechanistic mathematic models of joint injury.

We recognize that the current state of knowledge does not allow a fully mechanistic determination of all the parameters in our model. To help us move towards a truly mechanistic model, in this paper we introduce a tiered classification scheme for our parameters. Tier I parameters must be estimated to match the desired output and are in greatest need of empirical determination. To partially address this weakness, we have examined the sensitivity of the simulation results to changes in Tier I parameters to rule out significant qualitative changes in the results from these parameters. Tier II parameters come from assays where the measurements are indirectly related to the mechanism the parameter represents. Tier III parameters are determined from direct assays of the mechanism the parameter represents. Tier IV parameters differ from Tier III parameters only in that their determination assays have been reproduced and as a result there is enough reliable data to produce a probability distribution of the parameter value. Our long term goal is to have all parameters reach Tier IV. The process of reaching this goal, iterating between experiment and simulation, is one means in which we view mathematics as a conduit of translation.

Model Equations

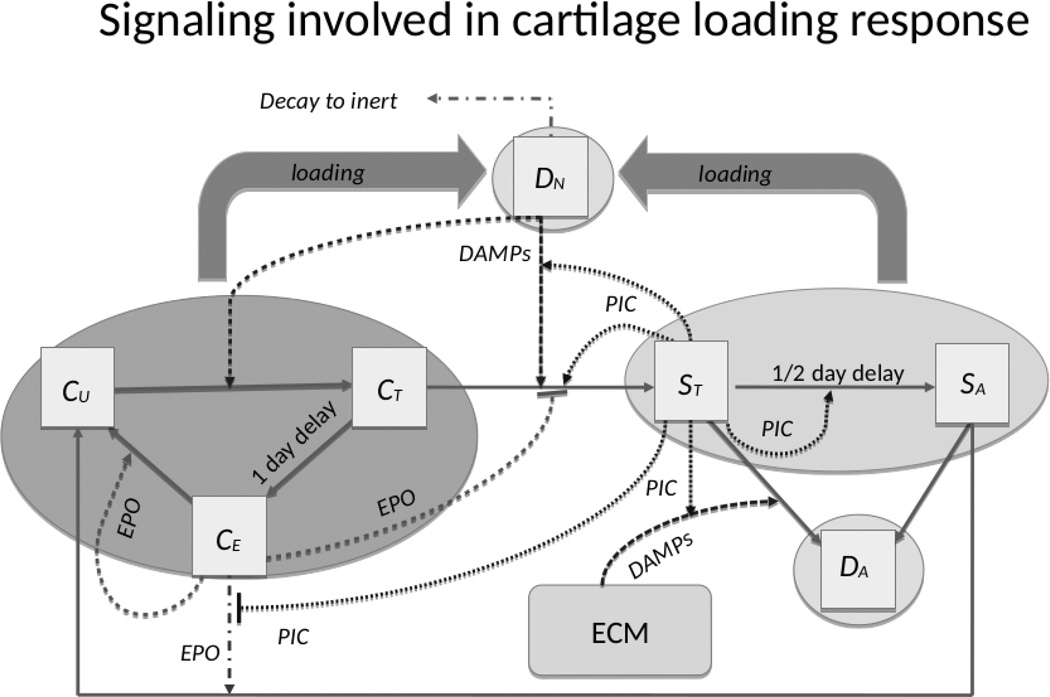
The model equations are based on the schematic in Figure 1. The model consists broadly of three populations of chondrocyte states: healthy, sick, and dead. We also track the extracellular matrix density. We consider three broad classes of cytokines: pro-inflammatory cytokines such as TNF-α and IL-6; anti-inflammatory cytokines such as erythropoietin (EPO); and damage-associated molecular patterns (DAMPs). For the cytokines, we represent the broader class of pro-inflammatory cytokines (PIC) by the variable F, the anti-inflammatory cytokines by the variable P, and the concentration of DAMPs by the variable M. The equations for the chondrocyte state variables, as well as the concentration of extracellular matrix, U, are shown in Figure S-1. The model is based on conventional wound healing scenarios where expression of TNF-α and IL-6 is the initial response, which is followed by EPO. This sequence was confirmed in the osteochondral explant impact model^19,20. Both TNF-α and IL-6 are well-known to be involved in the development of PTOA²⁵.

Figure 1. Schematic of the mathematical model.

The boxes indicate chondrocyte states, solid arrows indicate cell state transitions, dashed arrows indicate promotion of a transition, and dashed barriers indicate suppression of a transition. The affecting cytokine is indicated along the arrow. The variables C_U, C_T, and C_E denote the three healthy-cell populations, resp.: those not yet signaled by DAMPs, those signaled by DAMPS and in the process of becoming catabolic, and those starting to produce EPO. The variables S_T and S_A denote the two sick-cell populations, resp.: “catabolic” cells that synthesize inflammatory cytokines and ROS, and EPOR-active cells that express a receptor for EPO and can switch back to the healthy state C_U when signaled by EPO. Apoptotic and necrotic cell populations are denoted by D_A and D_N, resp.

For the cell state variables, within the healthy state we subdivide chondrocytes into those not yet signaled by DAMPs, those signaled by DAMPs and in the process of becoming catabolic, and those starting to produce EPO, denoted by C_U, C_T, and C_E, respectively. Equations for the healthy cell populations are shown in Figure S-1. The state variables C_U, C_T, and C_E use functional forms with specific meaning and importance. Equation (4) in Figure S-3 is the means by which we are able to use age-structure to model delays. Equation (5) in Figure S-3 links aspects of the biomechanics (strain) to the biomathematical model for the cytokine dynamics and cellular responses. The sick cell populations are divided into “catabolic” cells that synthesize inflammatory cytokines, and erythropoietin receptor (EPOR)-active cells that express a receptor for EPO and can switch back to the healthy state C_U when signaled by EPO. These are denoted by the variables S_T and S_A, respectively. The equations for the sick cell populations are shown in Figure S-4. The dead cells are divided into apoptotic and necrotic cell populations, denoted by D_A and D_N, respectively. Among the dead cells, we only track D_N explicitly. Apoptotic cells are assumed to be removed from the system. The equations governing D_N are shown in Figure S-5.

The model equations are solved numerically on a computer. We use Abaqus FEA software (Dassault Systèmes, Paris, France) to simulate the external loading on an articular cartilage explant. As with the biomathematical model, we assume radial symmetry of the cylindrical explant (radius = 2.5 cm, height = 1 cm), so that the axisymmetric computational domain is a rectangle. A pressure of 0.4 MPa is applied on top of the rectangle to simulate constant external loading from a cylindrical indenter (radius = 5.5 mm). The resulting vertical displacements are computed at over 250,000 nodes, with the axial strains calculated and entered into the model as the parameter ε in function Γ (see Eqn. 5 in Figure S-2). Once we have the steady-state strain computations from Abaqus, we solve the age- and space-structured equations using our own software and methods. The methods have a rigorous mathematical foundation^26–29, and have been used in a range of applications such as Proteus mirabilis swarm colony formation^30–32, avascular tumor invasion³³, biofilm growth and senescence^34,35, dormancy in bacteria^36,37, and articular cartilage lesion formation related to the work in this manuscript^19–21.

All parameters and their chosen default values are shown in Table S-1. Several of the parameters were estimated from the literature^4,17–20,38. Thirteen of the model parameters were estimated from previous computational work and were perturbed as part of a sensitivity analysis. The parameters and the ranges over which they were perturbed are shown in Table S-2. The way the sensitivity analysis was done was by changing the desired parameter, keeping all other parameters at their default values, running the software, and recording the resulting variable values. The relative difference between the variable values of the changed parameter run versus the default parameter run was calculated using the formula: relative difference = (perturbed parameter value – default value)/default value. The “values” were the average variable value over all spatial points at the final time step, integrating over age for the age-dependent variables.

Convergence Analysis

The default parameter run was compared to three refined discretization runs to verify the adequacy of our spatial mesh resolution, the age intervals, and the time steps. The first refinement successively halved the spatial intervals, the second successively halved the age intervals, and the third successively halved the time tolerance (essentially halving the time step interval). The relative errors for the variables C_U, S_T, and P (EPO) (cellular densities and chemical concentrations) were estimated by the formula: Relative error = (refined value − default value)/default value, where “value” was the value for the given variable at each spatial points at the final time step (14 days). For the age-dependent variable S_T, we integrated over the age interval. For the time step and age interval refinement runs, the maximum relative errors were 0.0002 and 0.0005, respectively. For the spatial interval refinement run, the highest relative error was 0.007.

Results

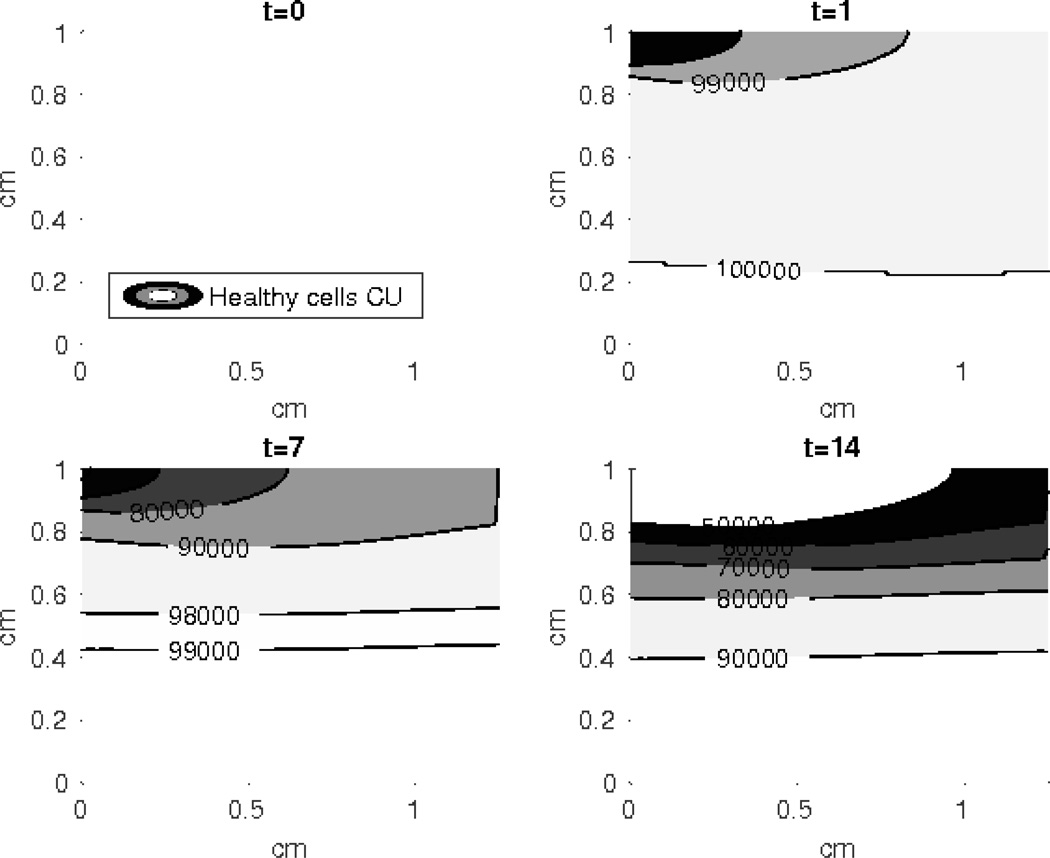
At the current stage of parameterization, our predictions are qualitative and meant to match a generic response to modest overloading, as seen in Figure 2 and in more detail in Figures S-6 to S-11. As the parameterizations become more exact, we anticipate more exact simulation results. At this stage, the more significant results are in the sensitivity of model output to changes in a parameter. Sensitivity to a parameter either identifies an area for model refinement (if the sensitivity is an artifact of the mathematics), or an area for therapeutic intervention (if the sensitivity observed is due to an underlying biological, biomechanical, or biochemical mechanism).

Figure 2. Contour plot of the healthy unsignaled cells (C_U).

The density of the C_U cells reduces more rapidly at the top of the simulated cartilage explant and the effect of the external loading diminishes at the bottom layers. The horizontal axis is radius of the cylindrical explant, and the vertical axis is depth.

Sensitivity Analysis

A study of the response of the system to changes in the parameters has the potential to provide a sense of the reasonableness of the parameter choices, especially for our Tier I (estimated) parameters; and using parameter sensitivity, due to underlying physiological processes, to identify potential areas of therapeutic intervention. Sensitivity analysis of our parameters, in their current state of determination, mainly gives us the former: a check on the reasonableness of our estimations. As more and more parameters become determined experimentally, and the sensitivity of a given parameter is observed both in silico and in vitro, sensitivity analyses would increasingly gain value in how they help translate the results of the small scale assays to identify targets for therapeutic intervention. Sensitivity analyses, and Uncertainty Quantification (UQ) more generally, are the rough analogs, for modeling and simulation, of statistical analyses for experimental assays³⁹.

The results of the sensitivity analysis can be seen in Table 1. The most sensitive parameters (within the range of the chosen values) were β₁₃ and λ_M, where β₁₃ determines the rate at which unsignaled cells (C_U) become pre-catabolic cells (C_T) and λ_M controls the effect of DAMPs on that transition. The importance of these two parameters for the behavior of the system, especially in the initial stages, is evident. Several parameters changed the system behavior significantly at certain values: λ_F = 0.1 (controls the impact of PIC on the system), β₁₁ = 50 (controls the rate at which pre-catabolic C_T cells transition to catabolic S_T cells), κ₁ = 0.037, and κ₂ = 1. The parameters κ₁ and κ₂ define the rate of transitions of C_E to C_T and S_T to S_A cell states, respectively. Since low λ_F increases the impact of PIC on the system, the resulting large increase in “sick” cells and harmful chemicals is not surprising. Lowering β₁₁ leads to fewer catabolic cells, hence lower concentrations of PIC. Lower values for κ₁ and κ₂ decrease the rate of cellular recovery (“sick” to unsignaled), hence the higher values for “sick” cells and harmful chemicals, as seen in Table 1. Table 1 does not include sensitivity of C_U and D_N cells. The ECM is not included either because most parameter perturbations did not lead to significant ECM damage. The only parameter values that resulted in damage to the ECM were λ_M = 0.1 and λ_F = 0.1, the relative decrease in ECM density being 0.2%.

Table 1.

The relative effect of the perturbed parameters on the variable values

Variable	Mod. Pos.	High Pos.	Extr. Pos.	Mod. Neg.	High Neg.
CT	β13 = 15; κ1 = 1	β13 = 20		λF = 0.1 λM = 0.9	β13 = 1, 5 λM = 0.1
CE	β13 = 15	β13 = 20		β13 = 5 κ1 = 5 λF = 0.1	β13 = 1 κ1 = 1 λM = 0.1
ST	κ1 = 1 κ2 = 5	β13 = 15	β13 = 20 κ2 = 1 λF = 0.1 λM = 0.3	β11 = 50 β13 = 5 κ2 = 20 λM = 0.7	β13 = 1 λM = 0.1, 0.9
SA	β11 = 150	β13 = 15 κ1 = 1 λF = 0.3	β13 = 20 λF = 0.1 λM = 0.1, 0.3	λF = 0.9	β11 = 50 β13 = 1, 5 κ2 = 1 λM = 0.7, 0.9
M	β13 = 15 κ2 = 1	β13 = 20 λF = 0.3	λF = 0.1 λM = 0.1, 0.3	β13 = 5 λM = 0.9	β13 = 1
F	β11 = 150 κ1 = 1 κ2 = 5	β13 = 15	β13 = 20 κ2 = 1 λF = 0.1 λM = 0.1, 0.3	β11 = 50 λM = 0.7	β13 = 1, 5 λM = 0.9
P	β13 = 15	β13 = 20		β13 = 5 κ1 = 5 λF = 0.1	β13 = 1 κ1 = 1 λM = 0.1

Mod. Pos. = moderately positive (30 – 50% relative increase), High Pos. = highly positive (50 – 100% relative increase), Extr. Pos = extremely positive (>100% relative increase), Mod. Neg. = moderately negative (30–50% relative decrease), High Neg. = highly negative (50–100% relative decrease). The table includes the parameter and the value at which the difference can be observed in the model outcome.

Discussion

While the behavior of our model is heuristically reasonable in that model predictions qualitatively match observations in larger animal models and humans, a rigorous validation of these results is not yet possible. When we have a higher fidelity parameter set, we will move ahead with the challenge of validation. Once the biomathematical model is validated, we can move on to our ultimate goal of patient-specific treatment and prevention. The mechanistic models, calibrated by the smaller-scale assays, will need to be augmented with patient-specific information such as injury severity, time since injury, the age of the patient, the presence of diabetes or other relevant comorbidities, and the specific joint in question.

A more extensive exploration of the computational results against clinical results, an important eventual milestone, will require additional complementary data. In this regard, we note that future model predictions of chondrocyte health following an intra-articular fracture (IAF) will be informed by evidence we have gathered in clinical studies over the past decade^{1,6,15,40–45}. Results from those studies have clarified the pathomechanical etiology of PTOA using patent-specific computational modeling methods. This has led to a better understanding of the role of both the acute fracture severity and the chronic contact stress exposure following surgical fracture reduction in determining the fate of the joint tissues.

Complementary explant and animal studies have clarified the direct influence of these mechanical factors on chondrocyte health and survival^3,5,46. Strong evidence also indicates preferential chondrocyte death associated with IAF along fracture edges at the articular surface⁴⁷. The acute fracture metrics can be calculated from pre-op CT scan data using methods developed in the UI Orthopedic Biomechanics Laboratory^1,43,44. Fracture mechanics theory is used to compute the fracture energy by appropriately weighting fracture-liberated (inter-fragmentary) surface area by local bone density information, available from the CT Hounsfield Unit intensities. The articular fracture edge length can be computed once inter-fragmentary surfaces have been identified in the CT data, by classifying different surfaces of bone fragments involving the articular surface to define the articular fracture edge as the boundary between the subchondral bone “surface” and inter-fragmentary surfaces⁴⁵. Patient-specific computational stress analysis methods provide a direct measure of the chronic contact stress exposures^6,41.

One of the greatest challenges for continuation of this project is applying this mathematic approach in space at each scale. Advancing and refining the FEA computations will allow for more accurate descriptions of the mechanical environment a given cell might be under; however, the architecture of cartilage including tissue zones and chondrocyte groupings must also be replicated within the model. These additions are challenging, but possible. We have also refined our understanding of redox processes in this context to the point where we consider them to only be an intracellular player, given the distances between individual chondrocytes. While nitric oxide may diffuse between cells, it seems highly unlikely other ROS can make the trip.

As presented, the greatest strength of our model system has been positing a time course for cytokine release and cell responses. Our data suggest that after 14 days, the tissue response appears to be largely determined and the damage to the ECM is irreversible. Therefore, the time frame for successful treatment approaches is short and injuries that may have induced cartilage surface incongruities have to be examined as early as possible, at most within a week. Observing this trend through subsequent iterations of our model may suggest improvements that can be made to current surgical techniques or, particularly, drug development and the timeliness of drug application.