Population structure reduces benefits from partner choice in mutualistic symbiosis

Abstract

Mutualistic symbioses are key drivers of evolutionary and ecological processes. Understanding how different species can evolve to interact in mutually beneficial ways is an important goal of evolutionary theory, especially when the benefits require costly investments by the partners. For such costly investments to evolve, some sort of fitness feedback mechanism must exist that more than recoups the direct costs. Several such feedback mechanisms have been explored both theoretically and empirically, yet we know relatively little of how they might act together, as they probably do in nature. In this paper, I model the joint action of three of the main mechanisms that can maintain interspecific cooperation in symbioses: partner choice by hosts, population structure amongst symbionts and undirected rewards from hosts to symbionts. The model shows that population structure reduces the benefit from partner choice to hosts. It may help or hinder beneficial symbionts and create positive or negative frequency dependence depending on the nature of host rewards to the symbiont. Strong population structure also makes it less likely that host choosiness and symbiont cooperation will be jointly maintained in a population. The intuition behind these results is that all else being equal, population structure reduces local variation available to the host to choose from. Thus, population structure is not always beneficial for the evolution of cooperation between species. These results also underscore the need to do full analyses of multiple mechanisms of social evolution to uncover the interactions between them.

1. Introduction

Mutualisms are crucial mediators of important ecological and evolutionary processes, including ecosystem functions [1], disease dynamics in the wild and in humans [2], biodiversity [3,4] and responses of ecosystems to changing environments [5]. Mutualistic interactions can arise simply as by-products of adaptations in one species benefiting others [6], but many do involve traits that impose a direct cost on their bearers and directly benefit only other species. Such traits create a trade-off or conflict between the partners, because increasing a partner's benefit (all else being equal) means decreasing one's own [7–11]. This conflict is in tension with the opportunity for mutual benefit, and a large body of theoretical (reviewed in [8,9,12]) and empirical work (e.g. [13–22]) focuses on elucidating mechanisms that can resolve this tension and enable the evolutionary maintenance of mutual benefit in nature.

In general, mutualisms with costly investments can be evolutionarily stable if some mechanism creates a fitness feedback to a focal individual from investments that directly benefits the partner [12]. The most straightforward type of feedback is the direct coupling of partners' fitnesses by vertical transmission of symbionts [23]. In the absence of such coupling, several other mechanisms exist that can generate fitness feedback favouring cooperative investments. These mechanisms include non-random association between cooperative partners through population structure [24] or through active partner choice [8,25], and phenotypically plastic investments (termed phenotypic feedback [12]) that respond to benefits provided by a partner to create a return to cooperative investments. Phenotypic feedback can be specifically directed towards more cooperative partners [26,27], or undirected, accruing to all partners, but according to the total benefit received by the focal individual. Each of these mechanisms of fitness feedback have been extensively studied theoretically and empirically, but largely in isolation from each other, or under the assumption that they act additively [28]. As a result, we know relatively little about how multiple mechanisms of fitness feedback interact with each other, and whether such interactions should change our understanding of mutualism evolution.

Past theoretical work indicates that interactions between multiple types of feedback can be decisive for whether cooperation between species can evolve. Akçay & Simms [29] showed in the legume-rhizobium mutualism that both directed feedback (as produced by a negotiation process) and undirected ones are needed to maintain cooperation in rhizobia. Similarly, Van Cleve & Akçay [30] showed that phenotypic feedback and population structure within and between species reinforce each other's effect, consistent with results from within-species social evolution theory [7,31,32]. Here, I focus on three major types of fitness feedback in the context of mutualistic symbioses: partner choice, population structure and different kinds of phenotypic feedback from the host.

Partner choice, i.e. hosts preferentially associating and rewarding more beneficial symbionts [8,25], has long been recognized as a mechanism that can select for cooperation. Empirical work further shows that there is usually variation in host expression of partner choice [e.g. [16,33,34]], and recent work has started to quantify more precisely the variation across [21,35] and within species [36]. Recent theoretical work has also suggested that discriminating genotypes of hosts might coexist with non-discriminating ones [37,38], which can explain how symbiont variability is maintained within populations. The latter is both an empirically observed phenomenon in need of an explanation [39], and a theoretical requirement for the maintenance of costly partner choice mechanisms [40].

In parallel, theory shows that when hosts reward their symbionts according to the benefits received, population structure among symbionts can favour cooperative investments because cooperative symbionts benefit from feedback induced by other cooperative neighbours that they tend to co-occur with [24,41,42]. However, the effects of partner choice in structured populations remains underexplored, except for a couple of recent studies by Bever et al. [43] and Verbruggen et al. [17] that show the role of within-host population structure in facilitating or hindering host plant partner choice of mycorrhizae. No previous study, to my knowledge, has formally considered how population-scale genetic structure of symbionts affects the evolutionary consequences of partner choice combined with phenotypic feedback.

Intuitively, a host can only exercise partner choice among symbionts available to it locally, and therefore effective partner choice requires local variation within the symbiont population. However, for a given overall level of genetic variation, stronger genetic structure (e.g. owing to limited dispersal) will diminish local genetic variation. Therefore, we might expect partner choice in structured populations to be less effective than in well-mixed populations. On the other hand, as mentioned above, population structure can favour cooperation through kin-selected effects.

To explore how these potentially conflicting effects play out, I develop a general model of a choosy host interacting with a patch structured population of symbionts. My results show that population structure does reduce the benefit to the host from partner choice. On the symbiont side, the effect of population structure on the selection for symbiont cooperation depends on the nature of the rewards from the host. When symbionts receive a fixed reward from the host per infection, population structure disfavours the cooperative symbiont, whereas when rewards are feedback-dependent (i.e. they are tied to the host benefit), population structure tends to favour symbiont cooperation. Furthermore, depending on the type of rewards and host benefits, both positive and negative frequency dependence might occur at different combinations of choosiness and population structure. Finally, population structure in a coevolutionary model of host choosiness and symbiont benefits tends to make the maintenance of cooperative symbionts and choosy hosts less likely. Overall, my results show that in contrast with its generally positive role in promoting cooperation in social evolution, population structure is not always good news for mutualisms with partner choice.

2. Model

I consider a well-mixed population of hosts that interacts with a subdivided population of two strains of symbionts, strains A and B. Each host individual encounters a local population in which strain A is at frequency q, whereas the overall frequency of strain A in the population is denoted by p. Population structure determines the distribution of this local frequency q given p, or f(q|p). For example, in a well-mixed population, f(q|p) would be binomially distributed. In structured populations, the distribution of q will be wider, so that a host will experience a wider range of local frequencies of the two strains. In particular, I assume that the symbiont population is patch structured, and with non-overlapping generations. This allows me to use well-known results from island-structured populations, in particular, the fact that the distribution of local frequencies of the two strains (corresponding to alleles) over patches is given by a beta distribution (see the electronic supplementary material, equation (SI-9) [44,45]).

(a). Partner choice

By convention, I assume strain A is preferred by the host and also provides more benefit, so I refer to it as the ‘beneficial strain,’ though both strains might be giving some benefits to the host. I model partner choice as follows: the host samples symbionts randomly from the environment but ‘rejects’ each infection by strain B with probability s(0 ≤ s ≤ 1), whereas infections from strain A are always accepted. The variable s therefore measures the choosiness of the host. I assume that the host has a fixed target number of symbionts, and keeps sampling (and rejecting as appropriate) symbionts until it reaches that number. This assumption corresponds to a biological scenario where hosts have control over the total number of symbionts they interact with, and have a target number determined by ecological factors (e.g. nutrient availability) other than symbiont frequency. I assume the target number to be large, and thus ignore sampling variance [46]. Under these assumptions, the new frequency of strain A after partner choice, q_c, is given by

2.1

Figure 1 depicts the effect of partner choice in increasing the post-choice frequency of the beneficial symbiont.

Figure 1.

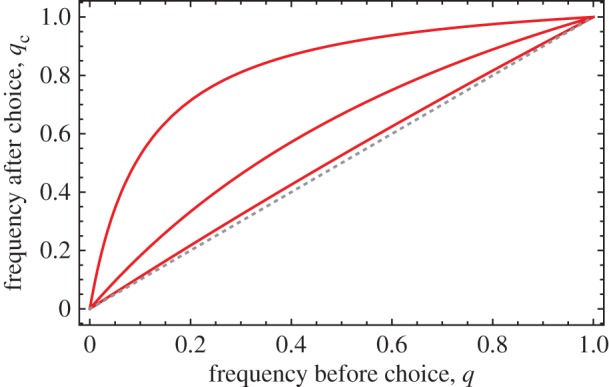
The frequency of strain A (the ‘beneficial symbiont’) after choice, q_c, as a function of its local frequency before choice, q. The dotted grey line is q_c = q, whereas the solid red curves depict q_c as given by equation (2.1) with (from top to bottom) s = 0.9, s = 0.5 and s = 0.1. Note that the enrichment of the beneficial symbiont (distance between the solid and dashed lines) is greatest at intermediate local frequencies. (Online version in colour.)

(b). Host fitness

I assume that the host fitness, denoted by w_H, is a benefit b(q_c) obtained as a function of q_c minus some cost of partner choice, c(s):

2.2

where I assume that b(q_c) is an increasing function. This expression assumes that the cost of partner choice and benefit from the interaction are additively separable. The expected fitness of the host is then given by

2.3

An approximation of the expected host fitness can be written by writing the host fitness in a Taylor series, and discarding terms of cubic order and higher:

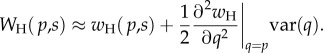2.4

This approximation is particularly useful for our purposes because it decomposes the expected fitness into the fitness at the average symbiont frequency plus a term dependent on the variance of the local frequencies. This variance is directly related to the classical measure of population structure, Wright's F_st, which is defined as var(q)/(p(1−p)) (see also the electronic supplementary material, section SI-1). Thus, for a given overall frequency p, highly structured populations will have higher var(q), because local patches will be more likely to be enriched in one strain or the other. Thus, the coefficient of var(q), the second derivative of w_H in q gives us the effects of increased population structure on the host fitness. This approximation is valid either when the host fitness w_H is a linear or quadratic function of q, or when the population is not too strongly structured (i.e. when higher-order moments of q are small).

(c). Symbiont fitness

I assume that symbiont fitness is derived from their interaction with the host through two potential reward mechanisms: fixed and feedback-dependent. In fixed rewards, all symbionts that are not rejected by the host receive a fixed fitness increment from the host, denoted by h₀ ≥ 0, independent of the strain identity, the performance of the host or the symbiont frequency on the host. By contrast, the feedback-dependent reward results from the host providing rewards that are proportional to the benefits it receives, i.e. h₁b(q_c), where h₁ ≥ 0 is a constant. I assume both strains experience the same rewards after the partner choice stage. Thus, a symbiont that survived partner choice gets benefit

2.5

The beneficial strain, in consequence of providing more benefits to the host, incurs a cost k that the non-beneficial strain does not incur. Finally, I assume that symbionts which do not infect the host do not gain any rewards or pay costs. Thus, the per-infection fitness of the beneficial strain A in a local population with frequency q is

2.6

Likewise, for the non-beneficial strain B, we have

2.7

In equations (2.6) and (2.7), the fractions on the right-hand side account for the fact that partner choice enriches the beneficial strain on the host relative to the non-beneficial strain, and hence increases the relative per capita fitness of the beneficial strain. The expected per capita fitness of the strains are given by

2.8

and

2.9

The sign of the difference W_A(p, s)−W_B(p, s) tells us whether symbiont A or B is favoured by selection. Assuming selection is weak so that f(q|p) is given by a beta distribution [44,45], the integrals (2.8) and (2.9) can be evaluated analytically, but the expressions are too cumbersome to reproduce here. Note that taking the expectation of the difference of individual fitnesses of both strains is equivalent to calculating the inclusive fitness effect that is widely used to measure selection in structured populations [47–49]. For the presentation of the results, I use Wright's F_st = var(q)/p(1−p) as the measure of population structure. In the infinite island model with haploid individuals and no mutation, F_st = 1/(1+2nm), where n is the deme size, and m the migration rate between demes (this is also equal to the regression definition of relatedness in this model [50]; see also the electronic supplementary material, SI-1).

3. Effect of population structure on host fitness

As a baseline, we first compute the effect of population structure on a non-choosy host (with s = 0, i.e. always accepts all strains). As explained above, the coefficient of the variance term in the Taylor expansion of expected host fitness gives the effect of population structure in the weak structure limit. In the absence of partner choice, this coefficient evaluates to

3.1

In other words, the variance term has the same sign as the second derivative of the host benefit function b(p). Therefore, stronger symbiont population structure will increase a non-choosy host's expected fitness if the benefit function b(p) is accelerating (b″(p) > 0), and decrease if the benefit function is decelerating (b″(p) < 0), in q. If host benefits are linear in q, the expected fitness of a non-choosy host is independent of population structure.

When the host is choosy, i.e. s > 0, the coefficient of var(q) in equation (2.4) becomes

3.2

The denominator of this term is always positive, while in the numerator, the second term in the square brackets is always negative (because b′(·) > 0 by assumption). Thus, the sign of the variance term in host fitness again depends on b″(·), the shape of the host benefits as a function of q. With linear host fitness in q(b″(·) = 0), expression (3.2) is negative, meaning that host fitness decreases with population structure (increased var(q). More generally, a sufficient condition for symbiont population structure to decrease host fitness is that b(q) is concave, i.e. the host's benefit is a decelerating function of the frequency of the beneficial symbiont. Conversely, a necessary (but not sufficient) condition for population structure to increase a choosy host's fitness is that the benefit from the beneficial symbiont is accelerating (b″(·) > 0). These results indicate that partner choice tends to interact negatively with population structure in the expected host fitness, as the region where the host fitness increases with population structure is diminished with choice.

We can confirm these results by directly evaluating the expected host fitness in equation (2.3) for particular host benefit functions. Figure 2 shows that, consistent with the analytical approximation, population structure tends to decrease the expected benefits to choosy hosts, except for low choosiness and accelerating benefits from the beneficial symbiont. This shows that for a given cost of choosiness, selection for host partner choice would be weaker or absent when symbiont populations are more strongly structured.

Figure 2.

Increased population structure tends to decrease the expected benefit to choosy hosts. Here, I depict the host benefit as a function of host choosiness and the relatedness among symbionts as a measure of population structure, for three types of host benefit functions: linear (panel (a) b(q_c) = q_c), diminishing returns (panel (b) b(q_c) = q_c−q_c²/2), and accelerating returns (panel (c) b(q_c) = q_c+q_c²/2). Lighter shading indicates higher expected host benefit. For a given level of choosiness, increasing population structure (increasing relatedness) decreases host fitness when host benefits are linear or diminishing returns. For accelerating returns host benefits, increased population structure increases expected host benefit for low choosiness, but decreases for high choosiness. In all panels the patch size for symbionts, n = 100 and the overall frequency of the beneficial strain, p = 0.5.

4. Effect of population structure on symbiont fitness

(a). Fixed rewards: population structure hurts the beneficial symbiont

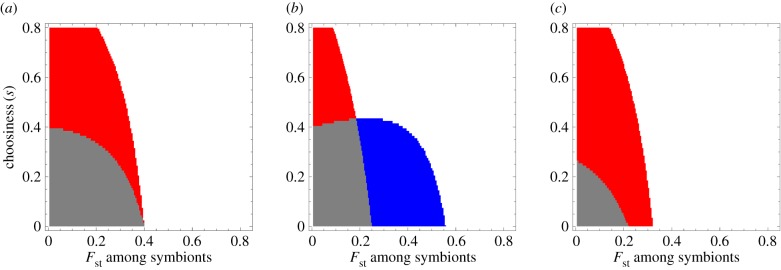
First, we consider the case where the reward to each selected symbiont is fixed; in other words, we set the feedback coefficient h₁ = 0 in equation (2.5), while h₀ > 0. By computing the expected fitness difference W_A(s)−W_B(s) using equations (2.8) and (2.9) at p ≈ 0 and p ≈ 1, we determine the invasion and fixation of the beneficial symbiont (Mathematica code included in the electronic supplementary material). Figure 3 shows the representative result: with increasing population structure, the beneficial symbiont becomes less likely to be able to invade and fix in a population of the non-beneficial symbiont. Figure 3 also shows that there exist combinations of choosiness and symbiont relatedness that create positive frequency dependence, where the beneficial symbiont cannot increase when rare but can go to fixation if it is common.

Figure 3.

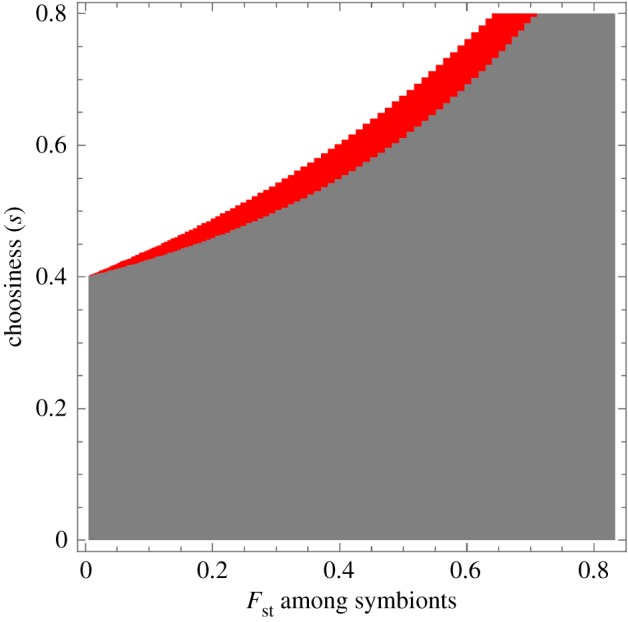
Increasing population structure hurts the beneficial strain under fixed rewards from the host. The plot gives the combinations of host choosiness and relatedness between the symbionts that allow the beneficial symbiont to invade when rare and go to fixation when common in the population. Grey, beneficial symbiont can neither fix nor invade; red, beneficial symbiont can fix but cannot invade; white, beneficial symbiont can both invade and fix. For a given choosiness (going along a horizontal line), increasing relatedness between symbionts only makes the invasion and fixation conditions harder to satisfy. For all values depicted here, the selection differential changes sign at most once. Parameter values are: h₀=1, h₁=0, k = 0.4, n = 100.

(b). Feedback-dependent rewards: population structure helps the beneficial symbiont

Next, we consider the case when the reward to the symbiont is entirely feedback-dependent, i.e. when h₀ = 0 while h₁ > 0. In particular, we set h₁ = 1 and consider host benefit functions that exhibit constant, diminishing, or accelerating returns to the frequency of the beneficial symbiont (i.e. linear, concave or convex functions of q_c). As above, we compute the expected fitness difference of the two strains using equations (2.8) and (2.9) at invasion and fixation of the beneficial strain. Figure 4 shows that unlike the fixed-rewards case (figure 4a), population structure with feedback-dependent rewards tends to favour the beneficial symbiont. In the linear host benefit case without partner choice (s = 0), the beneficial symbiont goes from being selected against at both invasion and fixation to selected for at a threshold F_st value. With partner choice (s > 0), the threshold relatedness for which the symbiont can both invade and fix goes down. Moreover, a region appears when the beneficial symbiont is favoured when common but disfavoured when rare, leading to positive frequency dependence. A similar pattern is observed for accelerating host benefits (figure 4c).

Figure 4.

With feedback-dependent rewards, increasing population structure tends to help the beneficial symbiont. Panel (a) depicts the case where the host fitness is a linear function of the frequency of the beneficial symbiont after choice (specifically, b(q_c) = q_c; panel (b) a concave function (diminishing returns, b(q_c) = q_c−1/2 q_c²); and panel (c) a convex function (accelerating returns, b(q_c) = q_c−1/2 q_c²). Colour scheme as in figure 3: grey, beneficial symbiont can neither fix nor invade; red, beneficial symbiont can fix but cannot invade; white, beneficial symbiont can both invade and fix; blue, beneficial symbiont can invade but cannot fix. In all three panels, for a given choosiness (going along a horizontal line), increasing relatedness between symbionts tends to make the invasion and fixation conditions easier to satisfy. In all cases, high choosiness and low population structure tends to generate positive frequency dependence; with diminishing return benefits to the host, low choosiness and high relatedness can also result in negative frequency dependency (in blue in the panel (b)). In all panels, the selection differential changes sign at most once. Parameter values for all panels are: h₀=0, h₁=1, n = 100. In panels (a,c) k = 0.4; in (b), k = 0.2.

In the diminishing return case, a slightly different outcome obtains: at low choosiness, as population structure gets strong, the population transitions from one where the beneficial symbiont is selected against to one with negative frequency dependence where the beneficial symbiont is favoured to invade but not fix (figure 4b). At high choosiness, we again have a region of positive frequency dependence. At intermediate choosiness, there can also be a small region where increased relatedness hurts the beneficial symbiont, taking away the advantage it has when common.

Intuitively, these results can be understood by noting that the host benefit acts as a public good through the rewards feeding back. In public goods dilemmas, increased relatedness tends to favour increased cooperation. Public goods with diminishing returns tend to produce negative frequency dependence, whereas those with accelerating returns generate positive dependence [51], consistent with our findings. Independently of this, as demonstrated by the fixed-rewards case, partner choice by itself tends to generate positive frequency dependence to the basic public goods selection patterns. Thus, depending on the combination of host choosiness, population structure and host benefits, either kind of frequency dependence can obtain.

(c). Local competition

The above analyses for selection on symbionts are based on the effect of the interaction on symbiont reproduction only. However, it is well known that factors such as local dispersal which create population structure can also create local competition between related individuals, which can cancel out the effects of population structure on fertility [52]. The presence, direction and magnitude of this effect depends on the exact mode of population regulation and scale of competition [53]. In the electronic supplementary material, SI-2, I consider the full life cycle of one of the simplest models where hosts and symbionts live in island structured models, and compete locally with conspecifics after dispersal (electronic supplementary material, figure S1). This model is a good approximation to many plant or microbial populations where seeds (or spores) form a global migrant pool and compete for establishment after dispersal. When local competition is taken into account, the effect of population structure disappears with fixed rewards (owing to the cancellation effect mentioned above). With feedback-dependent rewards, population structure hurts the beneficial symbiont at low to moderate host choosiness, but helps it at high host choosiness, regardless of the shape of the benefit curve.

5. Coevolution of host choosiness and symbiont cooperation

(a). Weak selection

The above results all focus on the effect of symbiont population structure because they are derived for the case where the host population is fixed for a given level of choosiness, where host population structure by definition will have no effect. In this section, I present results from a coevolutionary model with both choosy and non-choosy hosts, where the former has choosiness s and pays a cost c(s) = χs with χa constant (see the electronic supplementary material, section SI-3, for model construction). I assume both hosts and symbionts share an island-structured population, and vary both symbiont and host population structure (modulated by the migration rates, m and m_h, respectively). This subsection presents results under weak selection; the next one deals with strong selection. The weak selection assumption allows us to use the neutral local frequency distributions of both hosts and symbionts. A corollary of this assumption is that we can neglect the build-up of covariances between symbiont and host genotypes, and because hosts and symbionts disperse independently, the stationary distributions of host and symbiont frequencies will be independent from each other, as confirmed by simulations with weak selection (not shown). Therefore, we use the product of the host and symbiont distributions to model the joint local frequency distribution.

Figure 6 depicts the basic pattern when the host is well mixed. A population without the beneficial strain and non-choosy host is always a stable equilibrium. In addition to this equilibrium, the coevolutionary dynamics may also exhibit one of the following: a stable internal equilibrium where a polymorphism of both the symbiont and host are maintained by selection, an unstable internal equilibrium, and a stable limit cycle.

Figure 6.

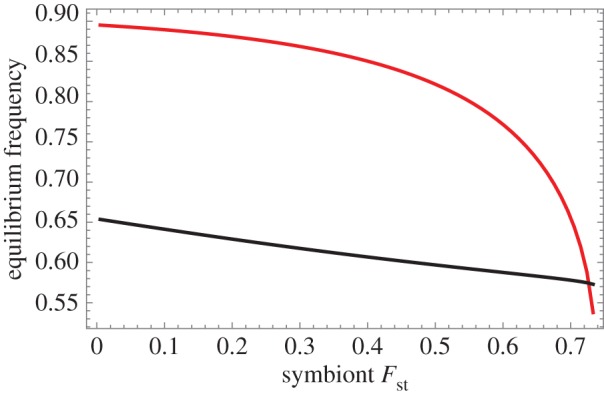
Population structure reduces the equilibrium frequencies of the beneficial symbiont and choosy host. This figure depicts the location of the stable equilibrium (red curve: symbiont frequency, black: host) for linear host benefits and fixed symbiont rewards (h₀ = 1, h₁ = 0). The equilibrium stays stable throughout, however, it disappears completely at very strong population structure. Parameters same as in figure 5. (Online version in colour.)

A stable internal equilibrium exists with both fixed and feedback-dependent symbiont rewards, when host fitness is a linear or concave (diminishing returns) function of the frequency of the beneficial symbiont (figure 5; electronic supplementary material, figure S4). It requires that s is higher than a threshold (determined by the cost of symbiont cooperation) and the cost of host choosiness is not too high. The first ensures that for some frequency of choosy hosts beneficial symbionts can be maintained in the population, while the second for some frequency of the beneficial symbionts, choosy hosts can be maintained. The convergence to this internal equilibrium is always oscillatory. Even when a stable internal equilibrium exists, however, it is never globally stable: there always exists a region from which the population converges to the no-cooperation/no-choosiness equilibrium.

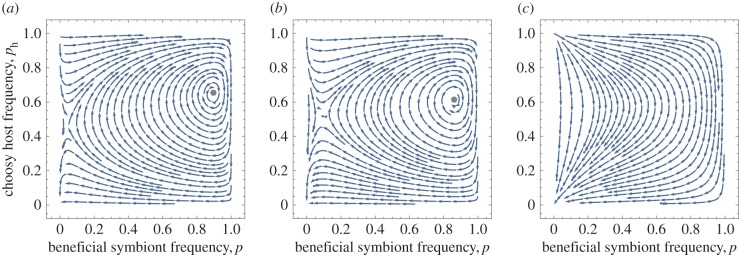
Figure 5.

Coevolutionary dynamics of choosiness and symbiont cooperation show stable polymorphisms in both. The curved arrows depict the direction of frequency changes given by the electronic supplementary material, equations (SI-17) and (SI-23). The black circles depict the location of the stable internal equilibrium when it exists. In all three panels, symbionts have fixed rewards and host benefit is linear (b(q_c) = q_c). In panel (a), the symbiont population is well-mixed (m = 1); panel (b) depicts the case with relatively strong population structure (m = 0.01); while panel (c) is with very strong population structure (m = 0.001). Stronger symbiont population structure somewhat shrinks the basin of attraction of the stable polymorphism while also shifting it slightly downwards and left, before removing the internal equilibrium entirely; in other words, decreasing the expected cooperation maintained in the population. Parameters: χ = 0.1, s = 0.6, h₀ = 1, h₁ = 0, b(q_c) = q_c, n_h = n = 100, m_h = 1. (Online version in colour.)

The effect of symbiont population structure is to: (i) decrease the stable frequency of the beneficial strain (figure 6, though for diminishing returns to host, this frequency might initially increase; see the electronic supplementary material, figure S3), (ii) to make the basin of attraction for this equilibrium smaller (figure 5b), and (iii) when very strong, to make the internal equilibrium disappear entirely, leaving only the no-cooperation/no-choosiness equilibrium (figure 5c).

Host population structure under weak selection does not affect this progression qualitatively, but tends to also work against the maintenance of cooperation and choosiness. For well-mixed symbiont populations, host population structure has no effect on the existence, stability and basin of attraction of the internal equilibrium (top rows of the electronic supplementary material, figures S5 and S6). With structured symbiont populations, when a stable internal equilibrium exists, host population structure makes its basin of attraction smaller (middle rows of the electronic supplementary material, figures S5 and S6). When the internal equilibrium does not exist, host population structure does not bring it back (bottom rows of the electronic supplementary material, figures S5 and S6). These results can be understood by noting that selection on symbionts is independent of host population structure under weak selection (electronic supplementary material, equation (SI-23)), while the effect of population structure on hosts is of opposite sign to the expected fitness differential between choosy and non-choosy hosts (electronic supplementary material, equation (SI-17)). The latter means that increased host population structure tends to work against the choosy hosts when they are favoured, and for them when they are not favoured.

(b). Strong selection

When selection is strong, there can be significant build-up of correlation between host and symbiont frequencies, in which case, host population structure can have an effect on dynamics and might interact with symbiont population structure in different ways. Simulations of the island model with strong selection (code included in the electronic supplementary material) show that the effect of symbiont population structure survives in the strong selection case: strong symbiont population structure tends to reduce the basin of attraction of the stable equilibrium and eventually destabilizes it. On the other hand, the effect of host population structure is inconsistent across contexts: for fixed rewards, host population structure tends to increase the basin of attraction of the internal stable equilibrium, and also increase the equilibrium frequencies of beneficial symbionts and choosy hosts (electronic supplementary material, figure S9). However, host population structure can also destabilize the internal equilibrium (e.g. for diminishing returns to the host; electronic supplementary material, figure S7). For feedback-dependent rewards, the internal equilibrium tends to be unstable, but strong host population structure can stabilize it under some parameter values (e.g. with linear or diminishing returns and weak symbiont population structure; electronic supplementary material, figure S8). On the other hand, with accelerating host rewards, host population structure shrinks the basin of attraction of the stable equilibrium (electronic supplementary material, figure S9).

Overall, the coevolutionary model shows that depending on the type of benefit to the host and symbiont, polymorphisms of costly choosiness and symbiont cooperation can stably exist owing to selection even without further (either through mutation or migration) input of variation into the population. Stronger population structure makes the maintenance of cooperation and choosiness less likely. On the other hand, host population structure under strong selection can help or hinder the maintenance of cooperation and choosiness, depending on context.

6. Discussion

The basic question of this paper is how different mechanisms that generate fitness feedback interact with each other to promote or hinder the maintenance of cooperation in symbioses. In particular, I considered partner choice in conjunction with population structure and different kinds of rewards (fixed versus feedback-dependent). The main results of the model are the following: (i) for hosts, the benefit of partner choice is diminishing with increased population structure, except for fast enough accelerating benefits; for symbionts, (iia) when rewards from the interaction are fixed, population structure disfavours the beneficial strain; however, (iib) when rewards are feedback-dependent, population structure tends to generally favour the beneficial strain with potential for positive or negative density dependence, depending on the shape of the host benefit curve; (iic) accounting for local competition removes the fixed reward effect of population structure, and while the beneficial effect with feedback-dependent rewards is conditional on high host choosiness; and (iii) when host choosiness and symbiont cooperation coevolve, a stable polymorphism in both can be sustained by selection, but population structure in both hosts and symbionts tends to shrink the basin of attraction of this equilibrium and eventually destroy it. Therefore, population structure under weak selection makes the maintenance of cooperation less likely. When selection is strong, symbiont population structure still has the same effect, but the build-up of associations between choosy hosts and beneficial symbionts can in some cases favour cooperation. Taken together, these results paint a complex pattern of interaction between these mechanisms commonly invoked to explain mutualism maintenance.

The main implication of the results for host evolution is that partner choice is less beneficial to hosts when symbiont populations are more strongly structured. This effect follows directly from the logic of how partner choice works (that it requires local variation). Importantly, this effect is a direct one, i.e. independent of any changes in overall symbiont frequencies resulting from population structure. We do know that in many horizontally acquired symbioses, local pools of symbionts will vary between hosts owing to population viscosity (as shown in, for example, rhizobia [54,55] and mycorrhizae [56]). Such population viscosity is expected to drive local populations of symbionts to extreme frequencies, restricting the effectiveness of partner choice mechanisms. The results from the coevolutionary model confirm this intuition: stronger partner choice tends to make it less likely that equilibria where choice and beneficial symbionts are maintained are attained. This is because both the range of symbiont frequencies at which choice is worthwhile (for a given cost) diminishes and the threshold frequency of hosts required to favour the beneficial symbiont increases with increased population structure.

For the symbionts, the model reveals that population structure can hinder or promote selection for beneficial symbionts through partner choice, depending on what happens after choice. When each chosen symbiont gets a fixed fitness increment, population structure works against the beneficial strain. This scenario indicates that the interaction between partner choice and population structure by itself is negative: each reduces the effectiveness of the other. When feedback tied to the host's performance (sometimes termed partner fidelity feedback) are added to the mix, population structure can promote selection for the beneficial strain. This is consistent with the fact that the feedback rewards from the host are effectively public goods for the symbiont, and increased relatedness favours production of public goods [41,42].

The intuition that population structure might reduce local variation available to partner choice has been pointed out by Verbruggen et al. [17], but their treatment focused on within-host genetic structure of the symbiont, as opposed to population-level structure that this paper treats. Another difference between the current work and Verbruggen et al. lies in the fact that this work derives the fitness consequences of partner choice in structured population from a simple but generally applicable model of partner choice in structured population, rather than assuming functional forms of relative fitness, as Verbruggen et al. do. These differences notwithstanding, the current model is closest to the ‘coarse control’ model of Verbruggen et al., because it assumes that hosts (after choice) reward each symbiont partner equally (whether through fixed- or feedback-dependent rewards). It will be interesting how these results might change when hosts can provide directed or negotiated [29,57] rewards to only beneficial symbionts after choice. In both cases, there is potential for negative interaction between population structure and directed rewards after choice [29,42].

Kiers et al. [58] discuss the importance of spatial structure in maintaining cooperation in the agriculturally (in addition to ecologically) important plant–soil symbioses. They mainly focus on the conflicting effects of relatedness and local competition in promoting and opposing cooperation, indicating that the overall effects of agricultural practices like tilling that reduce population structure can be theoretically ambiguous. The results presented here (figure 2) suggest that increased population structure (e.g. a no-till agricultural strategy) will directly reduce average plant performance (before any changes in symbiont frequencies), but if symbiont fitness is mainly driven by feedback-dependent rewards, this direct effect can be offset by an increase in the frequency of beneficial strains. The evidence reviewed by Kiers et al. mostly indicates higher mutualistic benefits from more structured soil populations, but no direct study exist to my knowledge that attempts to tease apart the direct effects of population structure from the effects of subsequent symbiont evolution.

The results in this paper also have implications for how variation in mutualisms can be maintained in the face of mechanisms that favour more cooperative partners. This problem has recently come to the forefront of theoretical and empirical research [37,39,40,46]. The model I present provides three qualitatively different scenarios in which variation in the symbiont can be maintained. First, feedback-dependent rewards and diminishing returns benefits to the host can generate negative frequency dependence (figure 4b), in accordance with public goods games theory [51]. Second, both fixed and feedback-dependent rewards can result in positive frequency dependence, and therefore bistability (figures 3 and 4; electronic supplementary material, figure S1). Such bistability can lead to a geographical mosaic of coexistence over larger spatial scales [59,60]. Third, when host choosiness is coevolving at the same time-scale as symbiont frequencies, there can be stable polymorphisms in both hosts and symbionts. Under weak selection, stronger population structure in both hosts and symbionts tends to make all three scenarios less likely by favouring one or the other strain unconditionally, or by removing polymorphic coevolutionary equilibria. The effect of symbiont population structure stays the same with strong selection. By contrast, I find that host population structure can have contrasting effects depending on context. In all cases, I find that beneficial symbionts and choosy hosts face a catch-22: one cannot invade the population unless the other is already at relatively high frequency. This suggests that for the initial evolution of choosiness, other mechanisms that lead to the build-up of associations between choosy hosts and beneficial symbionts are likely to be important [61].

In conclusion, these results show that multiple mechanisms of fitness feedback can interact in complex ways in selecting for or against cooperation between species and variation thereof. Understanding these interactions will lead to a more complete picture of the evolutionary and ecological dynamics of mutualisms.

Competing interests

I have no competing interests.

Funding

This work was funded by the University of Pennsylvania.