An Efficient Basket Trial Design

Abstract

The landscape for early phase cancer clinical trials is changing dramatically due to the advent of targeted therapy. Increasingly, new drugs are designed to work against a target such as the presence of a specific tumor mutation. Since typically only a small proportion of cancer patients will possess the mutational target, but the mutation is present in many different cancers, a new class of basket trials is emerging, whereby the drug is tested simultaneously in different baskets, i.e., sub-groups of different tumor types. Investigators not only desire to test whether the drug works, but also to determine which types of tumors are sensitive to the drug. A natural strategy is to conduct parallel trials, with the drug’s effectiveness being tested separately, using for example, the popular Simon two-stage design independently in each basket. The work presented is motivated by the premise that the efficiency of this strategy can be improved by assessing the homogeneity of the baskets’ response rates at an interim analysis and aggregating the baskets in the second stage if the results suggest the drug might be effective in all or most baskets. Via simulations we assess the relative efficiencies of the two strategies. Since the operating characteristics depend on how many tumor types are sensitive to the drug, there is no uniformly efficient strategy. However, our investigation demonstrates substantial efficiencies are possible if the drug works in most or all baskets, at the cost of modest losses of power if the drug works in only a single basket.

1. Introduction

Historically, cancer is a disease that has been organized and investigated separately based on the anatomic location of the primary tumor. Thus, we have breast cancer, lung cancer and so forth. This applies not only to the reporting of the disease in cancer registries, but also to the way it is treated, both surgically and medically. In fact, new drugs are usually tested and approved by the U.S. Food and Drug Administration (FDA) for use in specific disease sites, with prescription for other types of cancer considered “off-label”. However, the current drug development landscape is dominated by efforts to develop and test drugs that are designed to work against tumors that possess specific somatic mutations. Since these specific mutational targets typically occur in only a small proportion of tumors but also tend to be present in many tumor types, investigators increasingly are interested in evaluating the efficacy of the new drug in different groups of patients whose tumors possess the mutation. However, they simultaneously need to collect evidence about whether the drug is efficacious across all or only in some tumor sites. This has led to a new type of early phase clinical trial, variously termed “basket” trial or “bucket” trial, whereby the drug is tested simultaneously in the different baskets. The term “basket” trial has been used to refer to different contexts, depending on the drug’s mechanism of action and the molecular selection of patients [1]. For our paper when refering to a “basket” trial, we consider one target mutation and one drug targeting that mutation being tested in several tumor types. Here, investigators wish to know, not only if the drug is active, but also the specific tumor sites in which it is active. Due to the complex nature of these trials and the small sample sizes, these trials are considered discovery trials and promising efficacious results should be further evaluated in subsequent trials if possible.

There are two very prominent examples of such basket trials. In 2006, imatinib mesylate (Novartis) was approved by the FDA for 5 different types of cancer on the basis of a single phase II trial. In this study, 186 patients with 40 different non-gastrointestinal stromal tumor malignancies with KIT mutations were evaluated. The number of different malignancies, or baskets, and the number of patients per basket were not pre-specified, as this study was intended to be a proof-of-concept about the activity of imatinib to warrant future trials. Consequently, no inferential methods were used and power analyses did not contribute to sample size considerations. Each basket was permitted to enroll up to 10 patients, with the possibility of enrolling additional patients in baskets suggesting clinical efficacy [2]. While this study showed promising activity of imatinib in 6 malignancies, 40 different tumor subtypes were included and 24 indications (subgroups) were evaluated. There was no control of the false positive error rate, since no hypothesis testing was performed (or planned).

More recently, vemurafenib has been approved for patients with BRAF V600 positive-mutations in two types of nonmelanoma cancers, based on an on-going phase II trial. In this study, investigators defined 6 disease-specific baskets and an all-others basket, enrolling patients with any BRAF V600 mutation-positive, non-melanoma cancer. A total of 122 patients were enrolled with 27 patients with colorectal cancer receiving combination therapy, after observing futile results using monotherapy of vemurafenib. An adaptive two-stage design was planned for each disease-specific basket [3]. The all-others basket was purely exploratory with no inferential methods planned; however, investigators added the flexibility to create a disease-specific basket, should enrollment be large enough [4]. This trial explicitly stated response rate thresholds for what is considered promising and not promising and the design quantified the false positive error rate and power within each basket.

Conventional testing of a new drug addresses one question of overriding interest. Does the drug work? In the setting of testing targeted agents, investigators also need to know whether the drug works uniformly in all cancer sites with the mutation of interest or whether the activity is site-dependent. The basket design, in which patients are recruited purposefully to gain knowledge of the drug’s efficacy in distinct cancer sites, or baskets, is a natural design strategy to address these questions. A logical analytic strategy is to regard each basket as a separate, independent study of the drug’s efficacy. Thus one can, for example, perform separate two-stage study designs in each basket. Indeed this strategy of parallel, independent designs has been performed in at least one prominent trial [4], as well as in some other categories of basket trials [5, 6]. Such an approach can, of course, lead to a substantially inflated false positive error rate in the context of the question “does the drug work?” but this can be easily remedied by adjusting the significance levels in the individual trials to account for multiple comparisons.

There are numerous statistical methods for phase II trials with multiple strata proposed in the literature. Several methods have been developed specifically to identify promising biomarkers and are not easily generalizable to other settings [7, 8, 9]. Some of the proposals in the literature originally developed for phase II trials with multiple subtypes are candidates for use in basket trials [10, 11, 12]. The design by London and Chang [11] is primarily concerned with obtaining stratified estimates and tests, and does not address the question of “does the drug work?”. The design of Thall et al. [10] is more applicable but requires accepting hierarchical modeling and is more computationally demanding. The design of Leblanc et al. [12] is the closest to a basket trial among the three, evaluating individual and overall response rates simultaneously, however it does not offer protection against FWER. To the best of our knowledge, very few alternative designs appropriate for addressing the primary goals of basket trials, while controlling the false positive error rate, have been proposed in the literature. Berry et al. used Bayesian hierarchical modeling to evaluate the overall and basket-specific response rates, while sharing information across baskets to improve power [13]. More recently, Simon et al. used Bayesian model averaging to simulataneously model the baskets as homogeneous and heterogeneous, with an additional model parameter to represent the homogeneity of treatment effects across baskets [14]. Neuenschwander et al. used Bayesian hierarchical modeling and proposed an exchangeability-nonexchangeability approach to improve robustness for more heterogeneous populations [15]. A common theme among the basket trial designs proposed so far is the use of a Bayesian framework.

In this article we explore whether we can modify the approach of using independent Simon designs for each basket to improve the efficiency of the trial overall. Our fundamental premise is that efficiencies are possible by aggregating the information from separate baskets for which we believe, based on an interim analysis, the drug has similar efficacy. This potential aggregation allows us, in the second stage of the trial, to employ a much smaller sample size to obtain the necessary power to demonstrate clinical efficacy overall. However the relative trade-offs are complex, since such aggregation diminishes the power of the study to distinguish effects in different baskets. Furthermore, the relative efficiencies and classification accuracies depend on the true configuration of effects, i.e. the actual number of baskets in which the drug is efficacious. As a result there is no uniformly most powerful design strategy. Nonetheless we endeavor to demonstrate that our aggregation strategy has a large payoff in efficiency when the drug is effective in all or most baskets, at the cost of modestly reduced power when the efficacy of the drug is limited to a single or very few baskets.

2. Methods

2.1. Study Design Overview

We evaluate an adaptive study design that makes use of an interim assessment of the heterogeneity of treatment effects across baskets. We assume that the first stage of the study is similar to a parallel, independent two-stage Simon design, which is used for our reference design further detailed in Section 2.5. After the first stage when each basket has accrued a modest number of participants we evaluate the heterogeneity of response rates across baskets. On the basis of this, we make several key decisions. First, we determine whether the results support the premise that the drug’s effect is similar across baskets. If the answer to this question is yes, then we either terminate the trial for futility if the overall response rate is low or continue to the second stage, in which patients are accrued from all baskets and analyzed for a unitary effectiveness at the end of the trial. If, on the other hand, the evidence suggests heterogeneity of efficacy across baskets, then we continue the trial only for baskets with interim evidence of efficacy and analyze these continuing baskets separately at the end of the trial. The decision points are outlined schematically in Figure 1.

Figure 1.

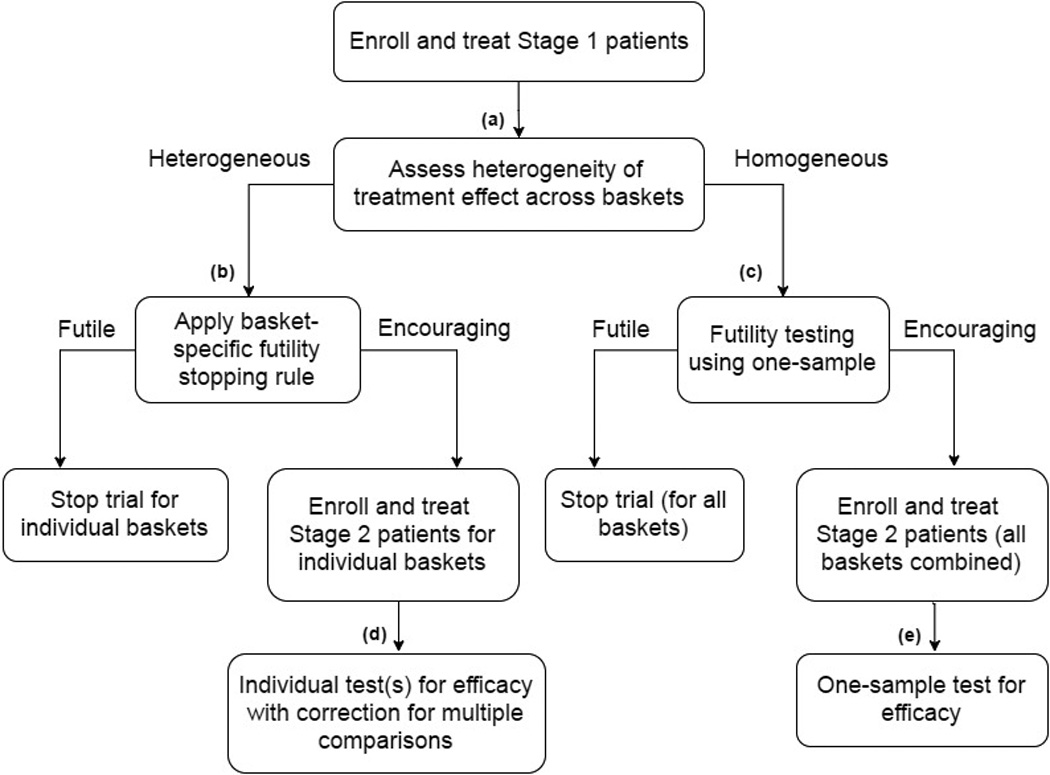
Flow chart of proposed design. See Section 2.2 for specific details.

2.2. Decision Rules and Design Parameters

We assume that there are K baskets under consideration and that in each basket the true response rate θ_k for k = 1, …, K is either at a null value θ₀ or at an effective value θ_a. The decision nodes in all admissible designs are created (via a computational search) to possess an overall false positive rate of ε. That is ε represents the probability that at least one basket will be declared effective when in fact the drug possesses no efficacy for any of the baskets considered, i.e., θ_k = θ₀ ∀k. For our notation, we use an upper case N to refer to the total number of patients across all baskets and we use a lower case n to refer to the number of patients in an individual basket. We define N₁ to be the total number of patients across all baskets in stage 1 and we define n_1k to be the stage 1 sample size for basket k, so that $N_1={\sum }_{k=1}^K{n}_{1k}$. Similarly, we define N₂ to be the total number of patients across all baskets in stage 2 in the homogeneous track and define n_2k to be the stage 2 sample size for basket k in the heterogeneous track.

The first decision node we reach in our design is the interim assessment of heterogeneity, depicted as (a) in Figure 1. Here, based on our assessment we will select a design path that treats baskets as either homogeneous or heterogeneous. The design parameter used to select the most appropriate path is the critical value for an exact test of a K × 2 contingency table. We define the design parameter for decision node (a) as γ and explore our design for γ on the domain of (0,1). Here, γ essentially functions as a tuning parameter optimized over its domain to achieve desired operating characteristics, further discussed in the Supplementary Materials. We note that for larger values of γ our design is more likely to pursue the heterogeneous design path. We also note that we do not interpret this as a stand-alone test of homogeneity, but rather we see it as a tool to better inform the decision regarding which design path to select based on the current data.

Within the homogeneous and heterogeneous design paths, there are two more decision nodes. For the heterogeneous design path, the next decision node we encounter is the basket-specific stopping rule for futility, depicted as (b) in Figure 1. In this design path, we have determined the response rates between baskets are different enough that we should evaluate baskets independently. For each individual basket, we decide if we should stop the trial for that basket due to lack of responsiveness to the drug or continue to stage 2. The design parameter necessary for decision node (b) is r_S, defining the minimum number of responses (in a single basket) needed in stage 1 to warrant enrolling additional patients in stage 2. Let us define K* as the subset of baskets continuing to stage 2. For baskets that display encouraging response rates, we enroll and treat n_2k patients in stage 2, for all k ∈ K*. At study completion, we have our final decision node to evaluate the drug’s activity for each remaining basket, depicted as (d) in Figure 1. We evaluate the remaining baskets’ response rates separately using one-sided Binomial exact tests, with a correction for multiple comparisons. At node (d), our design parameter is the significance level for each individual test, defined as α_S/K*.

For the homogeneous design path, the decision node following our heterogeneity assessment (a) is again a futility rule. However, this rule applies to all baskets collectively, depicted as (c) in Figure 1. Our design parameter for decision node (c) is the critical value for the one-sided Binomial exact test, defined as r_C (i.e., the minimum number of responses needed across all baskets combined in stage 1 to warrant enrolling additional patients in stage 2 to all baskets). We select r_C based on the stage 1 sample size N₁ and the null response rate θ₀, further detailed in Section 3.1. If we determine that stage 1 results appear futile, we stop the trial in all baskets and the study is complete. However, if we determine that stage 1 results appear encouraging, we enroll and treat an additional total of N₂ patients sampled from all baskets. At study completion, we have our final decision node to evaluate the drug’s activity overall, depicted as (e) in Figure 1. We evaluate the overall response rate using a one-sided Binomial exact test and all available data. At node (e), our design parameter is the significance level for the one-sample test for efficacy using all combined baskets, defined as α_C. Note that in this path we either declare that the drug is active in all baskets or that it is active in none. We provide a glossary of all of the described design parameters for quick reference in Table 1.

Table 1.

Glossary of Terms

Notation	Definition
θ0	Null response rate
θa	Alternative response rate
K	Total number of baskets
A	Number of truly active baskets
ε	Target family wise error rate when A = 0
(1 − β)	Target marginal power when A = 2 (or 3 depending on K)
(1 − β)min	Minimum acceptable power when A = 1
n1k	Stage 1 sample size for basket k
N1	Total stage 1 sample size
n2k	Stage 2 sample size for basket k, given heterogeneous design path
N2	Total stage 2 sample size, given homogeneous design path
γ	Assessment of heterogeneity tuning parameter
rS	Minimum required number of responses in stage 1 for an individual basket to continue to stage 2, given heterogeneous design path
rC	Minimum required number of responses in stage 1 across all baskets to continue all baskets to stage 2, given homogeneous design path
αS	Significance level for final separate analyses (before correction for multiple comparisons), given heterogeneous design path
αC	Significance level for final combined analysis, given homogeneous design path
FWER	Empirical family wise error rate
Pk	Empirical marginal power (%) for basket k = 1, …, K
EN	Expected trial sample size
ET	Expected trial duration (months)

2.3. Operating Characteristics

In the setting of multiple baskets there is no clear analog of the conventional type 1 and type 2 error rates. We can consider the null scenario as being the case when the drug does not work in any of the baskets. However, there is a composite of alternative scenarios that must be considered simultaneously, such as that the drug may only work in 1 basket, or that it works in 2 baskets, and so on. The following three metrics are used to construct our proposed design and evaluate its performance under various scenarios: family wise error rate (FWER), marginal power (P_k), and expected trial sample size (EN). The family wise error rate (FWER) is defined as the probability of incorrectly declaring activity in one or more baskets when in fact the drug does not work in any basket, previously defined as ε. The marginal power (P_k) for basket k is defined as the probability of correctly declaring activity in basket k when in fact the drug works in basket k. The marginal power differs depending on the true alternative, i.e. the number of baskets in which the drug actually works. Our approach involves first electing all candidate designs for which both the FWER and the marginal power for a specific alternative conform to desired levels, then choosing from these candidates the design that optimizes a utility function that trades off power and expected sample size across all alternative hypotheses (see Supplementary Material for more details). In evaluating operating characteristics, we examine marginal power and expected sample size for each possible alternative, and compare these with a reference design that employs independent Simon designs in each basket. Other metrics we consider for comparing the operating characteristics are the expected trial duration (ET) and average trial sensitivity and specificity, defined as the sensitivity and specificity of the K decisions made for all baskets in a trial, averaged over all simulations.

2.4. Optimization

In our proposed design, there are 8 unknown design parameters: N₁, n_2k, N₂, γ, r_S, r_C, α_S, α_C that are selected to optimize the utility function based on marginal power and expected sample size. Due to computational issues and practical limits on design parameters, we elected to fix four of the design parameters: N₁, N₂, r_S, r_C, using logical arguments and preliminary simulations. For example, r_S (the number of responders in an individual basket needed in stage 1 to continue to stage 2) must be defined on the space [0,n_1k]. We explore the sensitivity of these design parameters in the Supplementary Materials.

We chose a modest value for N₁, the total number of patients in stage 1, to best reflect common practice. We fix N₂, the total number of stage 2 patients for the homogeneous design track, to be smaller than ∑_k∈K* n_2k for K* containing more than 1 basket, since the homogeneous design track uses a pooled analysis and thus can achieve higher power using fewer patients per basket. We further reduce the dimensionality of the design parameters by fixing the heterogeneous and homogeneous design tracks’ stopping rules. These stopping rules satisfy clinical investigators’ desire to both avoid erroneously missing an active basket while at the same time minimizing patients exposure to an ineffective drug. In the heterogeneous design track we opted for a rule in which a basket should continue to stage 2 if there is any evidence of response (r_S ≥ 1) in the first n_1k patients for each basket k = 1, …, K. We thus declare futility for individual baskets with no responders in stage 1. Similarly, we fix the homogeneous design path’s stopping rule to be r_C = K, which equivalently requires around 1 responder per basket in order to continue all baskets to stage 2. After fixing these four design parameters, we determine the remaining four design parameters that optimize the power and sample size and declare the corresponding design as optimal. This optimization is restricted to designs that are calibrated to achieve the same FWER (i.e., ε) as the reference design when the drug is active in A = 0 baskets (see Section 2.5 below) and the same power (i.e., 1 − β) when the drug is active specifically in A = 2 baskets, while ensuring that the power achieves a minimum target level when the drug is active in only a single basket (A = 1), where A is the number of baskets in which the drug truly works. These restrictions are suitable when there are K = 5 baskets. Other calibration strategies are more suitable for trials with larger numbers of baskets. Further details describing the optimization of the remaining four design parameters can be found in the Supplementary Materials. We can potentially increase the number of optimal parameters, while reducing the computational time by considering simulated annealing with a well-constructed objective function. This is of interest for future work.

We calculate the expected trial sample size (EN) as:

$$\begin{gathered} EN=\sum _{k=1}^K{n}_{1k}+\sum _{k\in K^{*}}{n}_{2k}\text{Pr}(r_{Sk}\ge 1|\text{heterogeneous})\text{ Pr}(\text{heterogeneous}) \\ +N_2\text{Pr}(r_C\ge 5|\text{homogeneous})\text{ Pr}(\text{homogeneous}) \end{gathered}$$

To account for different accrual rates across baskets in practice, we assume patients from basket k enter the trial according to a Poisson distribution with rate parameter λ_k, so that the inter-patient arrival times in basket k follow an exponential distribution with rate parameter 1/λ_k. Define T to be the trial duration (in months) for a single trial, calculated as:

$$T={\mathit{\text{max}}}_{k\in K}\{\text{stage }1\text{ trial time for basket }k\}+{\mathit{\text{max}}}_{k\in K}\{\text{stage }2\text{trial time for basket }k\}$$

The expected trial duration ET is then the average trial duration over all simulated trials.

2.5. Reference Design

For our reference design, we assume parallel, independent optimal Simon two-stage designs are planned and carried out for each basket [16]. For each individual basket, we assume a type 1 error rate of α = ε/K, so that the FWER is controlled at ε for K baskets; we assume a type 2 error rate of β, so that the desired (marginal) power per basket is 1 − β. With these specifications, each basket will enroll and treat n_1R patients in stage 1 and if r_1k responders are observed, enroll and treat n_2R patients in stage 2.We declare the drug works in basket k if there are at least r_k responders in the k^th basket. Specific details can be found in Section 3.1. We use the function ph2simon from the R package clinfun to calculate the appropriate design parameters [17].

3. Simulation Study

In the following, we compare the operating characteristics of the proposed design with the reference design, based on the setting in which there are K = 5 baskets.

3.1. Trial Details

In our simulation study, we used parameter values that are informed by the discussions we had with investigators during the course of designing similar trials. We also made an effort to make our specific example to resemble the Hyman et al. basket trial, discussed in Section 1. We provide in Section 4 general suggestions for choosing parameters for those who want to use our software to design a basket trial. We assume that in each basket the true response rate θ_k for k = 1, …, K is either at a null value θ₀ = 0.15 or at an effective value θ_a = 0.45 and we focus on the setting where K = 5. Consequently, we set the total stage 1 sample size to be N₁ = 35 patients, so that with equal accrual rates each basket should accrue on average n_1k = 7 patients in the first stage, for k = 1, …, K. Furthermore, we set the total stage 2 sample size for the homogeneous design path to be N₂ = 20 patients, so that with equal accrual rates each basket should accrue on average 4 patients in the second stage. With these specifications, the minimum required number of responders in stage 1 for the homogeneous design path, in order to continue all baskets to stage 2 is set to be r_C ≥ K(= 5) patients. For the heterogeneous design path, the minimum required number of responders in stage 1 in order to continue an individual basket to stage 2 is set to be r_S ≥ 1 responders in the first n_1k = 7 patients. In simulation studies, we explored using n_1k = 6, 7, 8, 9 patients per basket (or N₁ = 30, 35, 40, 45) and N₂ = 20, 25, 30 but we elected to use n_1k = 7 and N₂ = 20.We note that increases in N₂ display larger increases in the expected trial sample size (EN) with negligible gains in marginal power (P_k), where P_k is the power to detect activity in the k^th basket, and where lower numbered baskets are the active ones. Thus when A = 1, basket k = 1 is active and baskets k = 2, …, 5 are inactive; when A = 2, baskets k = 1, 2 are active and baskets k = 3, 4, 5 are inactive; etc.

For the reference design, assuming α = 1% and β = 20% correspond to requiring r_1k ≥ 3 responders in the first n_1R = 9 patients to continue to stage 2; and requiring r_k ≥ 9 responders over all 27 patients, to declare the drug works in the k^th basket at study completion. We assume α = 1% in order to control the FWER at ε = 5%. We calibrate our proposed design against the reference design such that ε = 5% in both when there are A = 0 baskets in which the drug is truly active and the power is 1 − β = 80% in both the reference and proposed design when there are A = 2 baskets in which the drug is truly active. We note the two designs were not calibrated to have comparable trial durations.

We explored calibrating our design for other values of A, such as A = 1 or 3 truly active baskets, but found that calibrating under the A = 2 active setting produced desirable and robust operating characteristics for the other alternative scenarios. Due to the pooling in our proposed design, the marginal power is an increasing function of the number of baskets in which the drug is truly active, with the maximum power achieved when A = 5. Since we calibrate to achieve 1 − β power for the setting of A = 2, the marginal power is less than 1 − β when the drug is active in only one basket (A = 1). To address this issue we use the concept of minimum acceptable (marginal) power: (1 − β)_min and restrict candidate designs to those for which the marginal power is ≥ (1 − β)_min, for the case when the drug only works in a single basket (A = 1). We have assumed that (1 − β)_min = 70% marginal power is acceptable when A = 1. To construct and calibrate our design, we assume equal accrual rates for all baskets, i.e., λ_k = 2 for k = 1, …, K, corresponding to an average enrollment of 2 patients per month for each basket.

Frequently investigators can expect unequal accrual rates across baskets. This is especially important to consider in our design at the interim assessment of heterogeneity. Stopping and waiting for all baskets to accrue an equal number of patients in stage 1 is not ideal and can be impractical if the mutation is rare in some diseases. Therefore, we propose guidelines to avoid such pitfalls. We assumed that the heterogeneity assessment is completed after N₁ patients have been treated with a minimum of 3 patients per basket. With the small sample sizes in stage 1, the heterogeneity assessment can be sensitive to the response rates of baskets with larger sample sizes. Therefore, we suggest a maximum sample size per basket as well. For K = 5 baskets with N₁ = 35 patients over all baskets, we assume a maximum of 10 patients in any individual basket in stage 1. Similarly, for the homogeneous design track, we suggest the one-sample test for efficacy should be performed after N₂ = 20 patients have been treated and a minimum of 1 patient per basket; we assumed a maximum of 6 patients per basket to avoid a single basket dominating the overall response rate. These minimum and maximum patient requirements can be tailored in consideration of the numbers of patients in stage 1 and 2 and expected accrual rates.

We used 1000 simulated trials both to construct our design and also to evaluate and compare the optimal and reference designs’ operating characteristics. With the preceding requirements and using the approach detailed in the Supplementary Materials, we found the optimal design in the setting of 5 baskets with null and active response rates of 15% and 45%, respectively, leads to n_2k = 15 patients, γ = 0.52, α_S = 0.07, and α_C = 0.05. Thus, the optimal design sets the following parameters: N₁ = 35, γ = 0.52, n_2k = 15, r_S = 1, α_S = 0.07, r_C = 5, N₂ = 20, and α_C = 0.05. In the next section, we compare the operating characteristics of the reference and proposed designs.

We acknowledge the first stage of the reference design is larger than the first stage of our proposed design, however, this is because we calibrate the two designs to have comparable FWER when A = 0 and power when A = 2 in order to evaluate the efficiencies gained in the total sample size.

3.2. Results

We present 6 scenarios: the null scenario in which the drug does not work (15% response rate) in any basket, i.e., “0 Active” (A = 0), and five alternative scenarios, i.e., “1 Active”, …, “5 Active”, where without loss of generality Basket 1 is the active basket (45% response rate) when A = 1, Baskets 1 and 2 are the active baskets when A = 2, and so forth. The A = 0 and A = 5 scenarios capture the homogeneous design configuration; and the A = 1, 2, 3, and 4 scenarios capture the heterogeneous design configuration. Our proposed design controls the FWER weakly. That is, FWER ≤ ε = 5% under the null scenario, i.e., no active baskets (A = 0).

3.2.1. Equal Accrual Rates

Initially, we assume equal accrual rates, i.e., λ_k = 2, for k = 1, …, K. This specification of λ corresponds to an average accrual of 2 patients per month for each basket. The corresponding results for the proposed and reference designs are displayed in Table 2. In Table 2, under the null scenario when the drug does not work in any of the baskets, we see our empirical family wise error rate is controlled at the nominal level, ε = 5%. In this scenario, our proposed design requires an average of 58 patients and 7.0 months to complete (last two columns). For the reference design under the null scenario in Table 2, we see the empirical family wise error rate is also controlled at the nominal level, ε = 5%. Under the null scenario, the reference design requires an average of 58 patients and 10.4 months to complete. We see the reference design’s false positive rates in each basket are controlled at 1% (the nominal ε/K level). For our proposed design, the false positive rates in each basket are slightly higher (2%) when the drug is inactive (A = 0).

Table 2.

Power and Expected Sample Size: Equal Accrual

Design	Scenario (A)	FWER	Marginal Power*					EN	ET
			P1	P2	P3	P4	P5
Proposed	0 Active	5	2	2	2	2	2	58	7.0
	1 Active		70	7	7	7	7	74	9.5
	2 Active		80	80	11	11	11	83	10.4
	3 Active		84	85	85	17	17	86	10.5
	4 Active		86	85	86	86	23	88	10.2
	5 Active		88	90	88	88	88	78	8.3
Reference	0 Active	5	1	1	1	1	1	58	10.4
	1 Active		79	1	2	1	2	69	13.3
	2 Active		81	82	1	1	1	83	14.8
	3 Active		80	82	81	1	1	96	15.4
	4 Active		82	84	80	80	1	108	15.9
	5 Active		82	81	80	80	82	121	16.3

^*Marginal error rates for inactive baskets

For the setting in which the drug works in only one basket, i.e., A = 1, we see our empirical marginal power in Basket 1 (P₁ = 70%) achieves the nominal minimum power level 70%. In this scenario, our proposed design requires an average 74 patients and 9.5 months to complete. Alternatively, for the reference design, we see its empirical marginal power for Basket 1 is 80% and the design would require an average 69 patients and 13.3 months to complete. This is a difficult scenario for any design that considers aggregating baskets, since a majority of the baskets display homogeneous futile results. Our ideal design path for this scenario is to use separate analyses. Next in Table 2, we see our proposed design is properly calibrated under the A = 2 active scenario, displaying 80% marginal power for Baskets 1 and 2. In this scenario, our proposed design requires an average of 83 patients and 10.4 months to complete. The reference design displays 81–82% marginal power for Baskets 1 and 2 and requires an average of 83 patients and 14.8 months to complete. When the drug truly works in 3 baskets, i.e., A = 3, we see a 3–4% increase in marginal power (across all active baskets: Baskets 1, 2, and 3) using 10% fewer patients in our proposed design compared to the reference design. When A = 4, we see a 1–6% increase in marginal power (across all active baskets) using 19% fewer patients in our proposed design compared to the reference design. Lastly, when the drug truly works in all 5 baskets, we see a 6–9% increase in marginal power (across all baskets) using 36% fewer patients in our proposed design compared to the reference design. While the reference design’s marginal power is set to be 80%, we note the empirical power varies between 79–84% due to simulated variability.

Table 3 displays the sensitivities and specificities characterizing the accuracies of classifying active versus inactive baskets in a trial. The reference design maintains 99% specificity and around 80% sensitivity over all scenarios. For our proposed design, we see comparable specificity under the null (98%). However, our specificity decreases as the number of active baskets increases, due to the possibility that active and inactive baskets are pooled. Conversely, we see the sensitivity of our proposed design increases as the number of baskets increases.

Table 3.

Active/Inactive Basket Accuracy: Equal Accrual

Design	Scenario (A)	TP	FP	FN	TN	Specificity	Sensitivity	EN	ET
Proposed	0 Active		2		98	98		58	7.0
	1 Active	14	6	6	74	93	70	74	9.5
	2 Active	32	7	8	53	89	80	83	10.4
	3 Active	51	7	9	33	83	84	86	10.5
	4 Active	69	5	11	15	77	86	88	10.2
	5 Active	88		12			88	78	8.3
Reference	0 Active		1		99	99		58	10.4
	1 Active	16	1	4	79	99	79	69	13.3
	2 Active	33	1	7	59	99	82	83	14.8
	3 Active	48	0	12	40	99	81	96	15.4
	4 Active	65	0	15	20	99	81	108	15.9
	5 Active	81		19			81	121	16.3

TP: true positive rate; FP: false positive rate; FN: false negative rate; TN: true negative rate

Due to the pooling in our proposed design, as the number of baskets in which the drug is truly active increases we see an increase in our ability to correctly identify these baskets at reduced sample sizes. Conversely, we see an increase in the number of false positives occurring in the few baskets where the drug does not work. We believe that these false positives would be identifiable in a secondary analysis. Furthermore, we believe this is concordant with our perception that the primary objective of investigators is to avoid missing active baskets. We note that an additional input parameter could be incorporated that defines the maximum false positive rate, i.e., α_max. Then, our design would be controlled strongly at α_max. Here, we would control the number of false positives at α_max when A = 4, since this is the scenario we are most likely to make false positive errors due to pooling.

3.2.2. Different Accrual Rates

A challenge to our proposed design is the adverse consequences of unequal accrual rates to baskets. To address this concern, we vary the accrual rates across baskets. We considered two extremes: (i) the setting when the inactive basket(s) have the fastest accrual rate(s), and conversely, (ii) the setting when the active basket(s) have the fastest accrual rate(s). For (i) we assume the following accrual rates: λ₁ = 1, λ₂ = 1, λ₃ = 1, λ₄ = 2, λ₅ = 3, for basket k = 1, 2, 3, 4, 5, respectively. For (ii) we assume: λ₁ = 3, λ₂ = 2, λ₃ = 1, λ₄ = 1, λ₅ = 1, for basket k = 1, 2, 3, 4, 5, respectively. Results are displayed in Tables 4 and 5.

Table 4.

Power and Expected Sample Size: Varying Accrual

Accrual Rates	Scenario (A)	FWER	Marginal Power*					EN	ET	ENRef	ETRef
			P1	P2	P3	P4	P5
(i) (1,1,1,2,3)	0 Active	6	1	2	2	2	2	60	12.2	58	17.7
	1 Active		68	6	6	6	6	75	16.5	69	25.6
	2 Active		76	78	9	8	9	84	18.5	83	29.1
	3 Active		80	81	79	13	13	90	19.1	96	30.4
	4 Active		83	83	81	88	20	90	18.1	108	30.6
	5 Active		87	87	87	90	91	76	13.6	121	30.7
(ii) (3,2,1,1,1)	0 Active	5	3	2	2	2	2	60	11.7	58	17.7
	1 Active		79	8	8	8	8	75	16.2	69	17.5
	2 Active		86	85	16	15	16	79	16.6	83	18.5
	3 Active		88	87	82	19	18	84	17.5	96	25.9
	4 Active		87	89	84	83	27	84	16.7	108	28.8
	5 Active		90	90	85	88	87	75	13.3	121	30.6

^*Marginal error rates for inactive baskets

Table 5.

Active/Inactive Basket Accuracy: Varying Accrual

Accrual Rates	Scenario (A)	TP	FP	FN	TN	Specificity	Sensitivity	EN	ET
(i) (1,1,1,2,3)	0 Active		2		98	98		60	12.2
	1 Active	14	5	6	75	94	68	75	16.5
	2 Active	31	5	9	55	91	77	84	18.5
	3 Active	48	5	12	35	87	80	90	19.1
	4 Active	67	4	13	16	80	84	90	18.1
	5 Active	89		11			89	76	13.6
(ii) (3,2,1,1,1)	0 Active		2		98	98		60	11.7
	1 Active	16	7	4	73	92	79	75	16.2
	2 Active	34	9	6	51	85	86	79	16.6
	3 Active	51	8	9	32	81	86	84	17.5
	4 Active	69	5	11	15	73	86	84	16.7
	5 Active	88		12			88	75	13.3

TP: true positive rate; FP: false positive rate; FN: false negative rate; TN: true negative rate

The most noticeable effect of variable accrual rates is a substantial increase in the trial duration. This occurs for both the proposed and reference design. However, the other trends are largely preserved. The proposed design continues to deliver increased power with a reduced trial duration when A ≥ 3 at the expense of reduced power when A = 1. These trends are somewhat stronger when the fast accruing baskets are the ones in which the drug is active, i.e., setting (i) versus setting (ii).

4. Software and Implementation

We have developed and are making available R code to facilitate the calculation of optimal design parameters (currently available at https://www.mskcc.org/departments/epidemiology-biostatistics/biostatistics/basket-trials). The input specifications are the number of baskets (K), the specified response rates representing absence of activity (θ₀) and presence of activity (θ_a), the accrual rate(s) (we suggest using the minimum or average accrual rate across baskets), the family wise error rate (ε), the target power (1 − β), and the minimum acceptable power (1 − β)_min. The code allows users to change the fixed design parameters: the stage 1 sample size for each basket (n₁), the combined stage 2 sample size for the homogeneous track (N₂), and the futility stopping rules (r_S, r_C); but will use the default arguments if not otherwise specified.

On the basis of these inputs the program will calculate the remaining parameters that define the optimal study design, namely the stage 2 sample size for the heterogeneous baskets that survive futility testing (n_2k), the tuning parameter for the heterogeneity assessment (γ), and the critical values for the decision regarding efficacy for the single baskets (α_S) and the combined baskets (α_C). It will also provide projections of false positive and false negative error rates per basket and the expected sample size.

4.1. Choosing N₁, N₂, r_S and r_C

Our design has eight parameters. In principle, one can find an optimal design by maximizing all of these parameters over their permissible ranges. In practice, this is a daunting computational task. For this reason we chose to fix the values of N₁, N₂, r_S and r_C and optimize the remaining parameters. This has the disadvantage of requiring users to provide values for N₁, N₂, r_S and r_C to be used as input. We recommend choosing N₁ first, the total number of stage 1 cases. We expect that this parameter will typically be limited by available resources to a narrow range. For example, funding agencies or sponsors may specify an amount of time for first-stage results to be available or an initial budget to be used in the first-stage of the trial. In the absence of any such restriction, a reasonable starting choice for N₁ would be simply the first stage sample size of the reference design (n₁) multiplied by the number of baskets, K. After N₁ is chosen, r_S and r_C, the stopping criteria, can be selected with relative ease since the value of n₁ limits considerably permissible values of r_S. We believe that in most contemporary settings the observation of a single response in a modest first stage sample size will be sufficient for investigators to want to continue accrual to a basket, i.e., r_S = 1. However, in general r_S will be a very small integer. It seems reasonable to us to choose r_C to be close to the selected value of r_S multiplied by the number of baskets. N₂, the second stage sample size in the aggregated setting, needs to be selected to deliver good power. However, in this path we will already have accrued a substantial aggregated stage 1 sample size, so N₂ does not need to be especially large, and indeed should typically be smaller than N₁. In the aggregated arm, N₂ should be in the range of second stage sample size of the corresponding Simon optimal design. We expect users to choose a few values for each of these parameters and explore the resulting options informally. In the Supplementary Materials (Section 3) we describe the preceding thought process using a worked example.

4.2. Calibrating Trials for Larger K

In our simulations, we focused on the case of K = 5 baskets. In this setting, we found that calibrating the design parameters such that the power is specified for the case where the drug is active in 2 baskets leads to a strategy that overall has much better properties than the reference design. If on the other hand one wishes to design a trial with, say, K = 10 baskets, our preliminary simulations (data not shown) indicated that calibration of the design for the setting in which the drug is active in 3 baskets is best suited. In short, the calibration strategy needs to be tuned to the total number of baskets in the trial. In the software this is controlled by a simple indicator variable, which will calibrate the design to achieve target power when either A = 2 or A = 3.

5. Discussion

The advent of targeted therapies in response to rapid developments of knowledge about the genomics of tumors has led to reconsideration of the design of early stage clinical trials. The merits of the old paradigm of testing new drugs separately in different tumor sites has been replaced by an impetus to test targeted agents in patients whose tumors possess the genomic target. Since typically the target is present in relatively small proportions of patients across multiple tumor sites, interest in using clinical trials that encompass patients with tumors in different sites has emerged, where the goal is both to test the efficacy of the drug and at the same time garner evidence about whether it works across the board or only in specific types of tumors. Early basket trials of this nature have striven to test the effect of the drug by testing efficacy in separate baskets, with the underlying assumption that proven efficacy in at least one basket is sufficient to demonstrate success. Our research was motivated by the premise that it is possible to answer the overall question “does the drug work?” more efficiently, using a design where an interim analysis informs us whether the drug effect appears to be homogeneous across baskets. If so, we continue the trial if we determine there is encouraging evidence that a subsequent aggregate analysis will demonstrate efficacy convincingly with a much smaller overall sample size. We believe that our simulations demonstrate that the power to address this question can be increased while at the same time the duration of the trial can be shortened considerably when the drug is either uniformly ineffective or effective in all or most of the baskets.

There are, of course, trade-offs. Our design is less accurate in answering the inevitably important secondary questions regarding the effectiveness of the drug in separate baskets. Essentially this is because the algorithm has the possibility of aggregating effective baskets with ineffective baskets. Despite this, we believe that the large potential gains in power for answering the primary question with substantially fewer patients makes this still an attractive design strategy in this complex clinical setting.

We recognize that the design strategy we have advocated may not even be the most optimal one, in that we did not optimize across all design parameters. Because of the challenging computational problems of optimizing 8 decision criteria while simultaneously calibrating both power and family-wise error rates with the reference design we opted to fix a number of key design parameters and optimize the design over the remaining ones. For example, we arbitrarily selected both futility decision rules, largely based on our sense of what would be logically acceptable to investigators conducting these trials. It is entirely possible that a more expansive optimization might lead to even greater efficiencies. Also, our overall strategy is a strict frequentist one in which the parameter values in each basket are assumed to be either at the specified null value or at the pre-specified alternative, with corresponding statistical tests, false positive and false negative rates. In practice one could approach the problem in a more flexible random effects framework to make inferences about the individual effects in each basket. The trade-offs of such an approach are topics for further research. Nonetheless we believe that the current proposed design and analysis strategy represents a practical one that could be implemented immediately, and it is for this reason that we have made the software available.

In summary, we believe that considerable efficiencies are possible in the design of clinical trials in this new era of precision medicine. Our proposed design offers the possibility of faster drug evaluation and approval.