Abstract
Propensity score methods are an important tool to help reduce confounding in non-experimental studies and produce more accurate causal effect estimates. Most propensity score methods assume that covariates are measured without error. However, covariates are often measured with error. Recent work has shown that ignoring such error could lead to bias in treatment effect estimates. In this paper, we consider an additional complication: that of differential measurement error across treatment groups, such as can occur if a covariate is measured differently in the treatment and control groups. We propose two flexible Bayesian approaches for handling differential measurement error when estimating average causal effects using propensity score methods. We consider three scenarios: systematic (i.e., a location shift), heteroscedastic (i.e., different variances), and mixed (both systematic and heteroscedastic) measurement error. We also explore various prior choices (i.e., weakly-informative or point mass) on the sensitivity parameters related to the differential measurement error. We present results from simulation studies evaluating the performance of the proposed methods and apply these approaches to an example estimating the effect of neighborhood disadvantage on adolescent drug use disorders.
Keywords: Bayesian hierarchical model, Differential measurement error, Inverse probability of treatment weighting, Propensity score
1 Introduction
In psychology, education, and the behavioral sciences more generally, researchers using non-experimental designs need to control for all potential confounders in order to draw accurate causal inferences regarding clinical or scientific questions. Most statistical methods for doing so, such as propensity scores, assume that the covariates are measured without error. However, covariate measurement error is inevitable and potentially problematic as it could lead to biased results (Steiner, Cook, and Shadish, 2011). An unbiased treatment effect estimate is obtained when treatment and control groups are balanced with respect to all covariates affecting both treatment assignment and outcomes (i.e., confounders), as is obtained in a randomized experiment. Propensity score methods strive to create balance between groups on the observed covariates. However, if a covariate is measured with error, we cannot directly balance the two groups (at least not just using the observed, mismeasured covariate), resulting in potentially biased estimates of treatment effects.
Covariate measurement error exists in many applications. For example, depression or school test scores may not reflect the true underlying psychometric profile or intellectual ability of subjects, a large-scale survey may have only self-reported and not actual income or education level, and health care claims data may only have diagnoses without clinical measures of health status (such as cholesterol level). Furthermore, the degree of measurement error can differ by exposure or treatment status, a type of differential measurement error. For example, when combining multiple data sources or comparing a study sample to another dataset such as a nationally representative survey, different measurement (e.g., depression) scales may be used for the treated and control groups. This type of measurement error is more complex than the typically considered classical measurement error and adds challenges when aiming to estimate a causal effect.
Propensity scores, defined as the probability of treatment assignment given observed covariates, are widely used in non-experimental study designs to balance observed covariates between treated and control groups (Rosenbaum and Rubin, 1983). Generally, we first estimate propensity scores for each subject without using outcomes, and this step is called the propensity score stage. This stage is considered part of the study design because the outcome information is not incorporated. Then we estimate an average treatment effect by comparing outcomes between treated and control groups after weighting, matching, or stratifying based on the estimated propensity scores, called the outcome stage (Stuart, 2010). Numerous propensity score methods have been developed under a frequentist framework (Rosenbaum and Rubin, 1983; Rosenbaum, 2002; Stuart, 2010). Recently, Bayesian counterparts have been actively investigated (McCandless, Gustafson, and Austin, 2009; An, 2010; Kaplan and Chen, 2012).
Although most existing propensity score approaches assume no measurement error, some can handle classical (non-differential) measurement error, where error-prone covariates are noisy, unbiased versions of true covariates. These include propensity score calibration (Stürmer and others, 2005) and corrected propensity score weighting (McCaffrey, Lockwood, and Setodji, 2013). In addition, various methods have been developed including multiple imputation (Cole, Chu, and Greenland, 2006), simulation-extrapolation (Lockwood and McCaffrey, 2014), latent variable methods (Raykov, 2012), and Bayesian approaches (Gössl and Kuechenhoff, 2001; Gustafson, 2003). As far as we know, no methods are targeted to the case with differential measurement error in covariates.
In this paper, we consider Bayesian propensity score approaches to model differential covariate measurement error in observational study settings where the true value of the covariate is associated with both treatment status and outcome. This may be particularly relevant for many settings in psychology and education where individuals self-select their own “treatments” rather than having decisions made for them by physicians or researchers. (In the latter case the decisions may in fact be made based on the observed, mis-measured covariates, which is not the scenario of interest in this work). We are concerned with settings where the true underlying covariates are the ones that influence treatment selection and outcomes, which can make causal inference difficult in settings with measurement error.
The remainder of the paper is structured as follows. First, Section 2 overviews a general causal framework, propensity scores, causal effect estimation, and Bayesian propensity score methods. Then, we introduce three possible differential measurement error scenarios where the measurement error differs between treatment groups: systematic, heteroscedastic, and mixed measurement error. Section 3 proposes two Bayesian hierarchical modeling approaches accounting for differential covariate measurement error. We show extensive simulation studies in Section 4 to assess and validate our models. In Section 5, we apply the Bayesian approaches to a real data analysis. Finally, Section 6 discusses our work, its limitations, and needed future methodological developments.
2 Background and setting
In this paper, we consider a binary treatment indicator A, a continuous outcome Y, and two continuous confounders X and Z. Here, Z is observed and correctly measured while X is not observed but instead we observe W which is the mismeasurement of X. Note that X and Z could be sets of confounders instead of scalars.
2.1 Causal inference framework
Our research question of interest is to estimate an effect of a treatment on a certain outcome. For the ith subject, the binary treatment indicator is Ai = 0 or 1 for untreated or treated, respectively. Following the Rubin causal model (Rubin, 1974), Yi(Ai = a) is the potential outcome for individual i when the individual is assigned to the treatment (a = 1) or control (a = 0). However, it is not feasible to observe both potential outcomes for an individual. Our estimand of interest is the average treatment effect (ATE), defined as E(Y (1) − Y (0)), where the expectation taken over some population of interest. This paper is interested in non-experimental studies, where we simply observe that some people received the treatment and others received the control condition (in contrast to randomized studies, where treatment conditions are assigned to individuals randomly).
In non-experimental studies where all variables are correctly measured, given an observed confounder (or a set of observed confounders) Xi, the identification of the estimand relies on the following assumptions: no unmeasured confounders (or called ignorability), Yi(a)⫫Ai | Xi; consistency, Yi(a) = (Yi | Ai = a) for subject i; and positivity, 0 < P (Ai = a | Xi) < 1 for all Xi. An additional assumption is the stable unit treatment value assumption (SUTVA) meaning that one person’s treatment assignment does not influence another person’s potential outcomes and there is only one version of each treatment (Rubin, 1980).
The non-random treatment assignment in non-experimental studies results in various sources of bias (i.e., selection bias). Since the treatment assignment may depend on sample characteristics, treated and untreated groups can differ in the distribution of confounders, obscuring the true treatment effect. To estimate an unbiased causal effect, both treated and untreated groups should be exchangeable across confounding variables.
2.2 Propensity scores and inverse probability of treatment weighting method
A particularly useful tool in non-experimental studies is that of propensity scores, proposed by Rosenbaum and Rubin (1983), defined as ei(Xi) = P (Ai = 1 | Xi) for subject i. Propensity scores are usually estimated by fitting a logistic (or probit) regression model, and have two important properties. First, propensity scores balance the treated and control groups in terms of the distribution of all observed covariates, Xi⫫Ai | ei(Xi). The second property is that if ignorability holds given the full set of covariates then it also holds given the propensity score, that is if Yi(a)⫫Ai | Xi then Yi(a)⫫Ai | ei(Xi). Thus, propensity scores behave as a summary of all observed confounders so that we can use them to equate the treatment and comparison groups using matching, weighting, or subclassification instead of the full set of covariates.
In this paper, we use a propensity score approach known as inverse probability of treatment weighting (IPTW). In the outcome analysis, those who are actually treated are weighted by w1i =1/ei and those who are not have weights w0i = 1/(1−ei). The ATE is estimated by
| (1) |
where is an estimate of the ATE. Although we only consider a simple difference in means, more complex doubly robust approaches could be used as well (Robins and others, 2007).
The underlying assumption for estimating unbiased ATE is that all observed confounders are measured without error. Suppose that X is not correctly measured, but instead we observe W, which is a mismeasurement of X. That is, W is an error-prone confounder. To obtain an unbiased estimate of the ATE using IPTW, we should use the “true” confounder X to balance treated and control groups. If we use W instead of X to balance the two groups, we would expect a biased IPTW estimate because balancing on W will not imply balance on X. Note that this is only true when X is a confounder (i.e., when ignorability requires conditioning on X, not W). If W (not X) is related to the treatment assignment then the measurement error on X might not be influential at all in terms of estimating the ATE, because ignorability would hold given W (i.e., Y (a)⫫A | W. In this case, W would be the confounder, not X.
2.3 Bayesian propensity score methods
A Bayesian model provides flexibility given appropriate prior distributions, incorporates all parameter uncertainties, and offers probability-based interpretations. Under a Bayesian framework, we can account for the uncertainty of estimated propensity scores via Markov chain Monte Carlo (MCMC) algorithms, instead of considering the estimated propensity scores as fixed. In addition, we can easily calculate 95% credible intervals for parameters from their posterior distributions (Carlin and Louis, 2009).
McCandless, Gustafson, and Austin (2009) and An (2010) propose practical Bayesian propensity score methods that estimate a causal effect by modeling the propensity score and outcome stages jointly. Kaplan and Chen (2012) propose other Bayesian propensity score methods, which retain the separation of design and analysis inherent in the two-step propensity score approaches of design and outcome analysis. Although both approaches account for uncertainties of estimated propensity scores when estimating a causal effect, there is a thorny issue about combining propensity score and outcome models in the joint model approach. In conventional propensity score methods, the propensity score model should not depend on the information about outcome values (due to a desire to separate the design of the study from the outcome analysis), while the Bayesian joint model does not provide this separation. On the other hand, Little (2004) suggests that combining both propensity score and outcome models can produce estimates with good frequentist properties. Given the pros and cons in both approaches, the purpose of our paper is not validating which approach is better, but proposing the use of the two Bayesian propensity score approaches when existing differential covariate measurement error.
2.4 Differential covariate measurement error scenarios
Figure 1 depicts the data generating mechanism under differential covariate measurement error. Since we assume that the measurement error of X is differential by treatment status, the arrow from A to W exists, while this arrow would be removed under the classical measurement error case. Corresponding models can be written as
Figure 1.
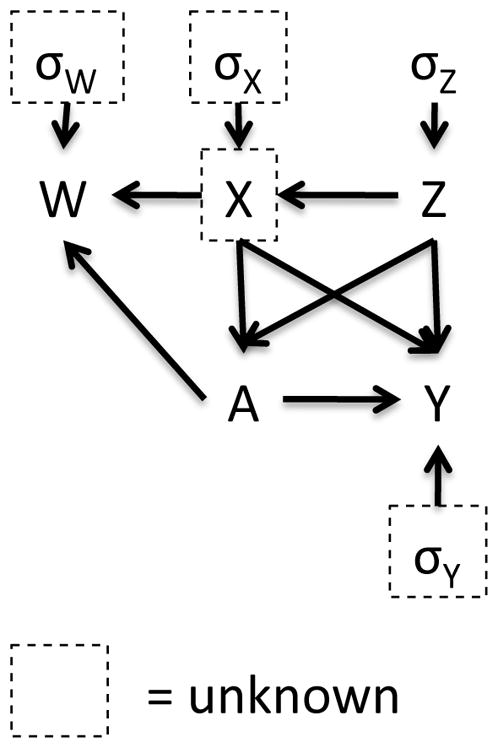
Data generating mechanism
| (2) |
| (3) |
| (4) |
| (5) |
Here, we assume that P(W | X, A, Z) = P(W | X, A) and P(Y | X, A, Z, W) = P(Y | X, A, Z). In (2), we assume X and Z are correlated. The treatment assignment A depends on these two covariates as shown in (3). For differential measurement error, (4) shows that W relies on the treatment assignment with a location shift parameter γ and scale parameter δ. Note that (4) reflects a classical measurement error case when γ and δ equal 0. In (5), the conditional mean of the outcome Y is a linear combination of treatment and confounding effects.
Based on γ and δ settings in (4), we can define three measurement error scenarios. Section 5 provides examples of these types of measurement error.
Systematic measurement error
The measurement error means differ by treatment status, when γ ≠ 0 and δ = 0. That is, the mean of W is shifted by γ from X only for the treated group, though the variance of W is the same for both groups.
Heteroscedastic measurement error
The measurement error variances differ by treatment status, but the mean of W in both groups is X when γ = 0 and δ ≠ 0. The variance in (4) assumes that the distribution of W for the treated group is noisier than that for the control group. When the opposite is assumed, we can simply switch the labels of treatment and control groups, or the variance needs to be replaced with .
Mixed measurement error
This case corresponds to one where γ ≠ 0 and δ ≠ 0, that is both the mean and variance of W differ by treatment status. The distribution of W for the treated group is shifted by γ from X and more variable than that for the control group.
In this paper, we choose the IPTW estimator in (1) as the estimator of our estimand ATE because using IPTW can help prevent reliance on a particular outcome model assumption. In the outcome model (5), ψ2 could be an alternative estimator of the ATE. However, if the outcome model is misspecified, ψ2 could not correctly account for the covariate balance between treated and untreated groups because we do not directly incorporate the propensity score weights into the outcome model (i.e., we do not use a weighted regression model). As such, we use the IPTW estimator for inference.
3 Bayesian hierarchical modeling for differential covariate measurement error
In this section, we introduce Bayesian hierarchical models to estimate causal effects when some covariates are measured with error, particularly where the magnitude of measurement error is different by treatment status. As we described in Section 2.4 we consider three differential measurement error structures: systematic, heteroscedastic and mixed measurement error. Under a Bayesian framework, we model differential measurement error structures in addition to the propensity score and outcome models, and consider the unobserved X to be an unknown variable. We apply two types of Bayesian propensity score methods: joint and separate modeling of propensity score and outcome stages. Our models assume that there is no internal or external validation data providing information about the relationship between X and W. In addition, we assume that investigators have some baseline knowledge about the extent of differential measurement error (e.g., measurement in the treated group is shifted less than some number of standard deviation units, relative to the shift in the control group), and this prior knowledge can be used when specifying prior distributions.
3.1 Joint model of propensity score and outcome stages
The first approach we consider models the propensity score, measurement error, and outcome stages jointly by fully incorporating all known information. Given our data framework in Section 2.4, we model equations (2) to (5), where (3), (4), and (5) represent propensity score, measurement error, and outcome stages, respectively. Recall that we assume that Z is observed and measured without error and X is an unknown variable to be estimated. The likelihood of the observed data is written as
where α = (α0, α1, α2), ψ = (ψ0, ψ1, ψ2, ψ3), and ξ = (σw |x,a, σy |x,a,z). The full conditional posterior distribution is derived in the supplementary material.
The relationship of X and Z in (2) can be used as a prior distribution for X, such as . We assign normal priors to α, ψ, and β, where β = (β0, β1) and uniform priors to σy |x,a,z and σx|z. Informative priors can be applied when strong prior information is available. In addition, we assign prior distributions to the parameters related to the measurement error as follows:
Systematic measurement error
For the location parameter γ, we consider 1) a normal prior, but with a reasonably small variance for better model convergence and 2) point mass priors for conducting sensitivity analyses. We assign a uniform prior to σw | x.
Heteroscedastic measurement error
Similarly, we assign 1) two separate uniform priors to the standard deviations of two treatment groups, σw | x,a=0 and σw | x,a=1, where δ can be calculated by solving the equation , and 2) point mass priors to δ for conducting sensitivity analyses with a uniform prior to σw | x,a=0.
Mixed measurement error
Under the mixed measurement error scenario, a combination of those two prior options for γ and δ, a total of four prior setups, are used. We will discuss the impact of prior choices for γ and δ in Sections 4 and 5.
In our setting with no validation data, the choice of hyperparameters of priors for γ, σw | x,a=0 and σw | x,a=1 in measurement error models is important because we have limited information about the relationship between X and W. As we assume that the scientific knowledge about the extent of differential measurement error is available this information will help us assign somewhat informative priors. For example, we might know that the mean of the covariate is shifted less in the treated group than in the untreated group (e.g., the shift in the treated group is less than 1 unit than the shift in the control group). Using this information we would assign γ a normal prior with mean zero and a fairly small variance instead of a large variance. Similarly, the treated group might be more variable (but less than 2 times, for example) than the untreated group, and we could assign σw | x,a=0 and σw | x,a=1 a uniform prior having a reasonably narrow range instead of a wide range.
3.2 Two-step approach with multiple imputation
Our second approach models the propensity score and outcome stages separately. That is, in the first step (i.e., study design step), we sample X by fitting propensity score and measurement error models under a Bayesian framework. In the second step, we apply the multiple imputation approach proposed by Rubin (1987) using the posterior samples of X obtained in the first step.
In the first step, we model equations (2) to (4) with similar prior distributions we used for joint models. We save M samples of Xi from their posterior distributions and denote them , where m = 1, …, M. As a result, we have M complete datasets, (Y, A, X(m), Z). When we impute Xi in this step, we do not borrow any information from the outcome. That is, the relationship of X on Y has nothing to do with the posterior distribution of Xi.
In the second step, we regard those M complete datasets as a product of multiple imputation. For each complete dataset, we estimate propensity scores using Zi and by fitting a frequentist logistic regression. Then, we calculate weights and and estimate the treatment effect, , and its standard error, , by fitting a weighted regression model of Y on A. By applying Rubin’s rule (Rubin, 1987), the ATE and its standard error are calculated by
where and representing within-imputation and between-imputation variances, respectively. Note that we do not implement a Bayesian model in the second step because running M separate Bayesian models is computationally expensive, and for a simple regression the Bayesian models with vague priors would provide results similar to those under frequentist models.
4 Simulation studies
4.1 Settings for simulated data
In this simulation study, we investigate the performance of our joint and two-step Bayesian models in terms of estimating the ATE. In addition, we study the impact of various prior choices and model misspecification on performance. Furthermore, we explore how well the approach works across a range of X-Y association scenarios. Bias, mean squared error (MSE), the average width of 95% credible intervals of estimates, and coverage probabilities, one of the frequentist properties, are used as measures of performance. We generate 1000 datasets using equations (2) to (5) and each simulated dataset has 1000 subjects. True parameters are set up as follows.
True covariates
In (2), we set (μx, μz) = (1, 1), (σx, σz) = (1, 1), and ρ = 0.5.
Treatment assignment
Ai for subject i is drawn from a Bernoulli distribution with probability of being treated expit(α0 + α1Xi + α2Zi) in (3). We consider two sets of α: (−1, 0.5, 0.5) and (−2, 1, 1), where the standardized mean differences of X, defined by {E(X | A = 1) − E(X | A = 0)}/σx | a=0 are around 0.7 and 1, thus the imbalance of X between treated and untreated groups are regarded as moderate and high, respectively. In both settings, about half of the subjects are treated.
Outcome
Given X, Z, and A, we simulate the outcome Y using the linear regression model in (5). We consider two cases regarding the strength of association between X and Y. We set the intercept and coefficients for A, X, and Z of the linear model for Y to be 1) ψ = (0, 2, 0.5, 0.5) for low X-Y association and 2) ψ = (0, 2, 2, 2) for high X-Y association. The true ATE is 2 in both cases. The conditional variance of Y, , is 1.
Differential measurement error
We specify the location shift parameter γ and the scale parameter δ to generate the error-prone covariate W given the true covariate X and the treatment status A. Table 1 summarizes the parameter setups under three measurement error scenarios. We choose (γ, δ) in (4) to be (1, 0), (0, 0.5), and (1, 0.5) for systematic, heteroscedastic, and mixed measurement error cases, respectively. We set to imply a reliability of 0.7 in the control group. The choice of γ does not affect reliability in the treated group while a large δ value results in low reliability in the treated group.
Table 1.
Parameter setup of measurement error for simulation study
| Control group | Treated group | |||
|---|---|---|---|---|
| W | X, A = 0 | Reliability | W | X, A = 1 | Reliability | |
| Systematic | N(X, 0.43) | 0.7 | N(X + 1, 0.43) | 0.7 |
| Heteroscedastic | N(X, 0.43) | 0.7 | N(X, 0.43(1.5)2) | 0.4 |
| Mixed | N(X, 0.43) | 0.7 | N(X + 1, 0.43(1.5)2) | 0.4 |
4.2 Settings for fitted models
Across all three measurement error scenarios, we begin with fitting two Bayesian models not accounting for the measurement error. We estimate propensity score ei by fitting a logistic regression model for treatment assignment with covariates Zi and Xi, denoted as the “True” model, and with covariates Zi and the error-prone Wi, denoted as the “Naïve” model.
To account for measurement error, we fit our proposed joint and two-step models, and Table 2 summarizes model names and corresponding prior options. We denote the joint Bayesian models as “Joint” and the two-step models as “TS”.
Table 2.
Fitted models and prior setup for simulation study
| Model | Prior for γ | Prior for δ | |
|---|---|---|---|
| Systematic | Joint_inf | γ~N(0, 3) | |
| Joint_PM | γ ≡ 1 | ||
| TS_PM | γ ≡ 1 | ||
|
| |||
| Heteroscedastic | Joint_inf | σw | x,a=0, σw | x,a=1~Uniform(0.01, 3) | |
| Joint_PM | δ ≡ 0.5 | ||
| TS_PM | δ ≡ 0.5 | ||
|
| |||
| Mixed | Joint_inf | γ ~ N(0, 3) | σw | x,a=0, σw | x,a=1~Uniform(0.01, 3) |
| Joint_S | γ ≡ 1 | σw | x,a=0, σw | x,a=1~Uniform(0.01, 3) | |
| Joint_H | γ ~ N(0, 3) | δ ≡ 0.5 | |
| Joint_SH | γ ≡ 1 | δ ≡ 0.5 | |
| TS_SH | γ ≡ 1 | δ ≡ 0.5 | |
Systematic measurement error
Joint models adopt an informative prior for γ, namely N(0, 3), and a point mass prior where we choose γ to be the true value 1. These two models are denoted by “Joint_inf” and “Joint_PM”, respectively. We apply the same point mass prior for the two-step model, denoted by “TS_PM”, and compare the results with Joint_PM.
Heteroscedastic measurement error
Similar prior settings were utilized for the heteroscedastic scenario. A uniform(0.01, 3) prior distribution is used for the standard deviations of W of the joint model, and δ is set to 0.5 as the point mass prior option for both joint and two-step models.
Mixed measurement error
With regard to the mixed measurement error scenario, four different prior options are applied to the joint model: 1) informative priors on both γ and δ (denoted Joint_inf); 2) a point mass prior to γ but an informative prior to δ (Joint_S); 3) a point mass prior to δ but an informative prior to γ (Joint_H); 4) and point mass priors to both γ and δ (Joint_SH). We only consider the fourth prior for the two-step model, denoted by “TS_SH”, because the main findings when comparing joint and two-step models are similar under other prior options.
All other regression coefficients and standard deviations have N(0, 3) and Uniform(0.01, 3) priors, respectively. Here, we use somewhat informative priors on these parameters to guarantee model convergence. For two-step models, we set M = 100.
In addition, we investigate performance under outcome and propensity score model misspecification. For the outcome model misspecification setting, we simulate a dataset using (2) – (4) and we add a quadratic term for X in (5), such as E(Y | X, A, Z) = ψ0 + ψ1A + ψ2X +ψ3Z +0.25 ψ2X2. Then, we fit the same joint and two-step models ignoring the quadratic effect of X on outcome. Similarly, for the propensity score misspecification setting, we simulate a dataset using a true propensity score model that has an added quadratic term for X, such as A | X, Z~Ber(logit−1(α0 + α1X + α2Z + 0.25α1X2)), and then fit the same joint and two-step models ignoring the quadratic effect of X on treatment assignment.
For all models, the ATE is estimated using the IPTW estimator in (1). We performed simulation studies in R using the R2jags package (Su and Yajima, 2014). For each Bayesian model parameter, a single chain was run and 20000 samples were obtained after discarding the first 20000 samples as a burn-in.
4.3 Results
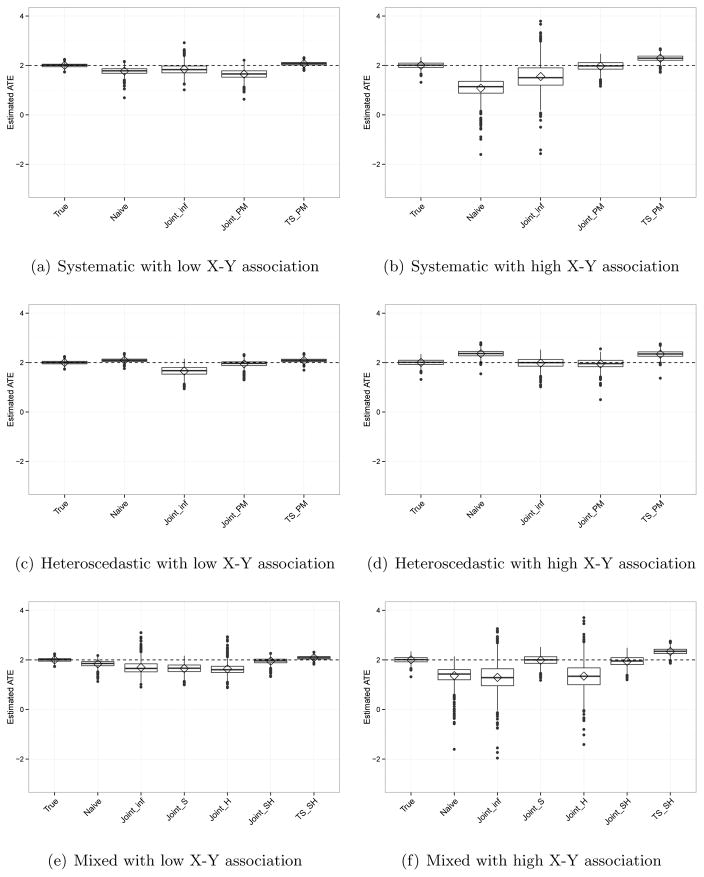
Table 3 displays bias, MSE, coverage probability, and the average width of 95% credible intervals of estimates and Figure 2 exhibits box plots of the ATE estimates under six different settings: the three measurement error scenarios for each of the low and high X-Y associations. Here, the average width shows uncertainty of estimates. Again, the true ATE is 2. We show results for α = (−1, 0.5, 0.5), which indicates moderate imbalance on X between the treated and control groups. The results for the higher imbalance setting (α = (−2, 1, 1)) are in the supplementary material. We first explain findings under each measurement error structure, followed by more comprehensive results across all measurement error structures.
Table 3.
Bias, MSE, coverage probabilities, and average width of 95% credible intervals (95% CI width) of ATE in the simulation study.
| X-Y association | Model | Bias | MSE | Coverage probability | 95% CI width |
|---|---|---|---|---|---|
| Systematic measurement error | |||||
|
| |||||
| Low | True | 0.001 | 0.006 | 0.911 | 0.269 |
| Naïve | −0.231 | 0.075 | 0.268 | 0.363 | |
| Joint_inf | −0.153 | 0.076 | 0.969 | 1.516 | |
| Joint_PM | −0.353 | 0.164 | 0.640 | 0.928 | |
| TS_PM | 0.071 | 0.011 | 0.985 | 0.539 | |
|
|
|||||
| High | True | 0.004 | 0.017 | 1.000 | 1.076 |
| Naïve | −0.928 | 1.050 | 0.138 | 1.450 | |
| Joint_inf | −0.459 | 0.618 | 0.906 | 2.978 | |
| Joint_PM | −0.030 | 0.040 | 0.999 | 1.283 | |
| TS_PM | 0.289 | 0.102 | 0.996 | 1.630 | |
|
| |||||
| Heteroscedastic measurement error | |||||
|
| |||||
| Low | True | 0.001 | 0.006 | 0.911 | 0.269 |
| Naïve | 0.089 | 0.013 | 0.677 | 0.241 | |
| Joint_inf | −0.341 | 0.157 | 0.691 | 0.944 | |
| Joint_PM | −0.055 | 0.019 | 0.915 | 0.486 | |
| TS_PM | 0.084 | 0.013 | 0.945 | 0.454 | |
|
|
|||||
| High | True | 0.004 | 0.017 | 1.000 | 1.076 |
| Naïve | 0.359 | 0.147 | 0.818 | 0.963 | |
| Joint_inf | −0.022 | 0.046 | 0.998 | 1.323 | |
| Joint_PM | −0.053 | 0.044 | 0.997 | 1.253 | |
| TS_PM | 0.339 | 0.134 | 0.949 | 1.338 | |
|
| |||||
| Mixed measurement error | |||||
|
| |||||
| Low | True | 0.001 | 0.006 | 0.911 | 0.269 |
| Naïve | −0.158 | 0.042 | 0.488 | 0.332 | |
| Joint_inf | −0.309 | 0.164 | 0.909 | 1.740 | |
| Joint_S | −0.345 | 0.154 | 0.676 | 0.946 | |
| Joint_H | −0.367 | 0.191 | 0.763 | 1.760 | |
| Joint_SH | −0.051 | 0.017 | 0.922 | 0.483 | |
| TS_SH | 0.085 | 0.013 | 0.929 | 0.448 | |
|
|
|||||
| High | True | 0.004 | 0.017 | 1.000 | 1.076 |
| Naïve | −0.636 | 0.542 | 0.489 | 1.323 | |
| Joint_inf | −0.708 | 0.919 | 0.853 | 3.401 | |
| Joint_S | −0.017 | 0.044 | 0.998 | 1.321 | |
| Joint_H | −0.650 | 0.734 | 0.896 | 3.378 | |
| Joint_SH | −0.058 | 0.045 | 0.999 | 1.255 | |
| TS_SH | 0.340 | 0.134 | 0.952 | 1.320 | |
Figure 2.
Estimated ATE from simulation under various differential measurement error scenarios with low or high level of X-Y association.
Systematic measurement error
When the X-Y association is low, in Panel (a) of Figure 2, the Joint_inf model performs better than the Naïve model in terms of bias and coverage probability while the Joint_PM model provides slightly larger bias and MSE than the Naïve model. Comparing joint and two-step models with point mass priors, the two-step model yields a less biased ATE with smaller MSE and better coverage. However, these findings differ when the X-Y association is large (Panel (b)). In this setting, the Joint_inf, Joint_PM, and TS_PM models perform better than the Naïve model, and using a point mass prior reduces bias and MSE more than using an informative non-point mass prior when using the joint model approach. Joint_inf always provides the largest variability resulting in the widest 95% credible intervals. In addition, the TS_PM model yields larger bias and MSE than Joint_PM. The same trend is observed when we compare joint and two-step models using informative non-point mass priors (results not shown).
Heteroscedastic measurement error
When X is not a strong predictor of outcome in Panel (c), the Joint_PM model results in a less biased ATE than the Naïve model. The TS_PM model yields slightly larger bias but smaller MSE than Joint_PM. With a strong X-Y association (Panel (d)), ATE estimates under Joint_inf show dramatic improvement in bias, MSE, and coverage probability, and the bias is smaller than that under Joint_PM. Again, the two-step model produces larger bias and MSE than Joint_PM.
Mixed measurement error
In Panel (e), with a low X-Y association, the Joint_SH and TS_SH models perform better than the Naïve model. Joint_inf, Joint_S, and Joint_H provide similar bias and MSE, though Joint_inf yields the largest coverage probability. Note that this large coverage probability in Joint_inf is due to the large uncertainty of estimates resulting in wide 95% credible intervals. When the X-Y association is large (Panel (f)), we observe that prior choices affect the estimates. The Joint_S and Joint_SH models result in much smaller bias and MSE with slightly better coverage than Joint_inf and Joint_H. This shows that adopting a point mass prior on the shift parameter γ is more beneficial to have an unbiased and precise ATE estimate than using a point mass prior on the scale parameter δ. The TS_SH model provides larger bias and MSE than Joint_SH.
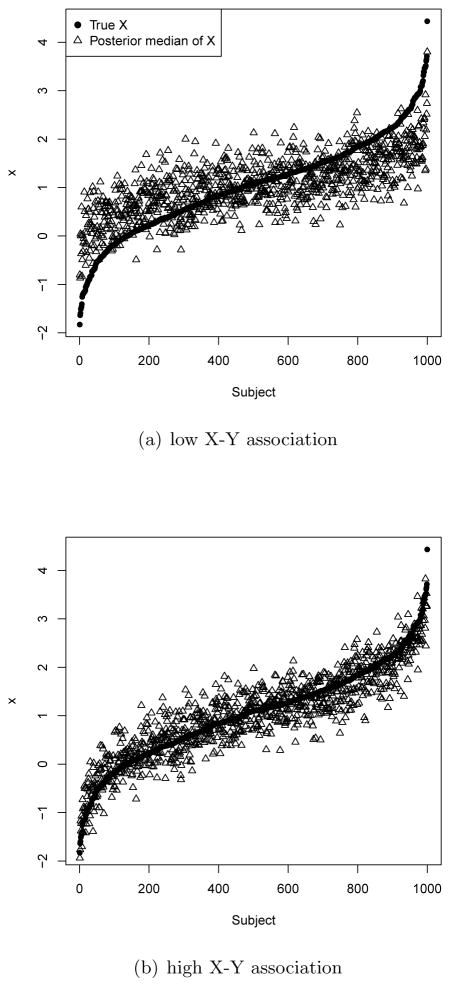
In general, the magnitude of the association between the true covariate X and the outcome is related to the methods’ performance; this can be explained by the performance of posterior samples of Xi. As a model imputes Xi better, propensity scores control for Xi better, so we can estimate a more accurate treatment effect. To illustrate, Figure 3 plots the true Xi and posterior medians of imputed Xi from a single simulated dataset under the Joint_PM model with systematic measurement error. In Panel (b), the setting where X is a strong predictor of outcome, the imputed Xi are closer to the true values than in Panel (a). Specifically, the imputed values are more centered towards the mean of Xi with a low X-Y association. This is because there is relatively little information on Xi in Yi so their posterior samples shrink towards their mean.
Figure 3.
True Xi and posterior median of imputed Xi under the Joint_PM model from a case study with systematic measurement error.
In addition, the performance of two-step models is related to the magnitude of the X-Y association. The two-step models consistently result in larger bias and MSE (though the coverage probabilities are acceptable) than the joint models using the same point mass priors when X is a strong predictor of Y. As the two-step models ignore the X-Y association when imputing X, they can yield a biased and imprecise estimate when a strong predictor of outcome is mis-measured.
Furthermore, the joint models are more sensitive to the prior choice for γ than to the prior choice for δ. For example, in the systematic measurement error scenario with a large X-Y association, the bias of the ATE under Joint_PM is much smaller than that under Joint_inf (−0.030 versus −0.459), whereas in the heteroscedastic measurement error scenario, the bias under Joint_PM is relatively similar to the bias under Joint_inf (−0.053 vs. −0.022). Moreover, in the mixed measurement error scenario, compared to Joint_inf, Joint_S decreases the bias by 98% (from −0.708 to −0.017) while Joint_H decreases the bias by 8% (from −0.708 to −0.650). That is, using a point mass prior on γ is more helpful to reduce bias than using a point mass prior on δ. In the supplementary material, we compare prior and posterior distributions of the parameters in the measurement error models to show how different prior choices affect the estimation of these parameters.
We also investigate covariate balance using the standardized mean difference (SMD) to examine how similar the treatment and control groups are after weighting in terms of the imputed X and the true X in the mixed measurement error scenario with the high X-Y association. The SMD of X is 0.7 before applying our methods. Joint_inf and Joint_SH give the SMDs for the imputed X (on which propensity scores directly balance the two groups) 0.007 and 0.001, respectively, showing that the two groups are well-balanced on the imputed X. However, the SMDs for the true X are −0.244 and 0.053 under Joint_inf and Joint_SH, respectively, showing that the balance between two groups on the true X is not as good as the balance on the imputed X. Note that as the SMD of the true X is smaller, the ATE estimate tends to be less biased (the bias values under Joint_inf and Joint_SH are −0.708 and −0.058, respectively).
The results of misspecification of the outcome and propensity score models under the mixed measurement error scenario are in the supplementary material. The results under outcome model misspecification show the similar trend to panels (e) and (f) of Figure 2, but the bias and MSE are much larger in Joint_inf and Joint_H with a large X-Y association (see Web Figure 1 of the supplementary material). The results under propensity score model misspecification show that propensity score model misspecification affects bias and MSE less than does outcome model misspecification, as previously shown by Drake (1993).
5 Illustrative data example
5.1 NCS-A data
We apply our Bayesian approaches to data from a representative survey of U.S. adolescents, the National Comorbidity Survey Replication Adolescent Supplement (NCS-A). The NCS-A has been described elsewhere (Merikangas and others, 2009; Kessler and others, 2009a). The Human Subjects Committees of Harvard Medical School and the University of Michigan approved recruitment and consent/assent procedures.
Our goal is to estimate the association between living in a disadvantaged neighborhood and past-year drug abuse or dependence (using Diagnostic Statistical Manual IV diagnoses (Kessler and others, 2009b)). Neighborhood disadvantage was operationalized using an established scale (Roux and others, 2001) that has been used with the NCS-A data (Rudolph and others, 2004). Neighborhoods in the lowest tertile of scale scores were considered disadvantaged.
Maternal age at the birth reflects family socioeconomic status (SES) (lower SES families have children at younger ages, on average, than higher SES families), and is a confounder in analyses of neighborhood and mental health (Leventhal and Brooks-Gunn, 2000). In the NCS-A, maternal age at birth was reported by the adolescent. For a subset of adolescents, maternal age at birth was also reported by the mother. We consider the mother’s report to be the true confounder, X, and the adolescent’s report to be a mismeasurement of X, W. For this illustrative example, we examine the subset of adolescents who have both X and W (n=4,792) to compare estimates using our Bayesian approaches to the “true” estimate made using X. Due to confidentiality issues, our dataset cannot be uploaded to high-performance computing clusters and thus our models have to be run on a desktop computer that has limited computing capacity. As a result, we further restrict to a random sample of 1,000 participants to alleviate memory and computation issues. Our models would be feasible to run with larger datasets on a high performance cluster.
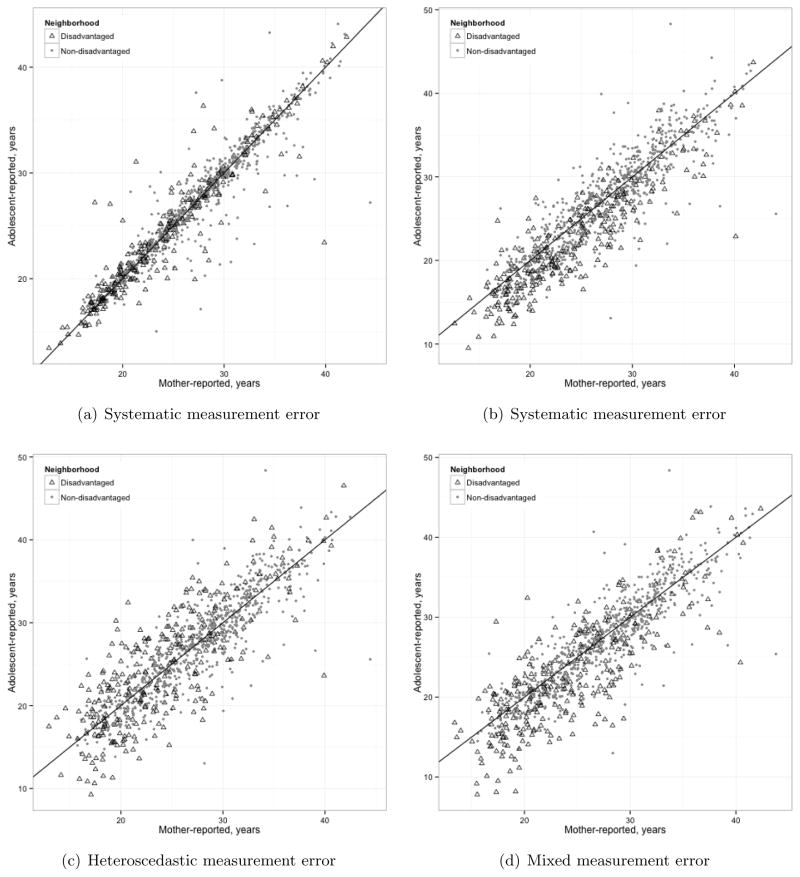
Figure 4 (a) shows the correlation between maternal-reported and adolescent-reported maternal age at birth. This example is appropriate to our objective of correcting for differential measurement error. Adolescents in disadvantaged neighborhoods are slightly more likely to overestimate the age of their mother than adolescents in nondisadvantaged neighborhoods (i.e., the “treatment” shifts the measurement error mean away from zero by a constant), and less reliable in reporting their mother’s age (i.e., the measurement error variance exhibits heteroscedasticity by “treatment” status). In general though, the adolescent’s report correlates very highly with the mother’s report, correlation=0.95. Because of the little difference between the adolescent’s and mother’s report, for illustration purpose, we simulated additional systematic, heteroscedastic, and mixed measurement error as shown in Figure 4 (b), (c), and (d), respectively.
Figure 4.
Scatter plots of mother-reported age and adolescent-reported age with a 45 degree dotted line under differential covariate measurement error scenarios: (a) no additional measurement error added, (b) systematic measurement error added, (c) heteroscedastic measurement error added, and (d) both systematic and heteroscedastic measurement error added. N=4,792.
Suppose Wobs denotes the observed W. Since the reliability between X and Wobs is close to 1, to decrease reliability we add pure noise to Wobs, namely N (0, 4). We call the noisy version of W Wnoise and the reliability between X and Wnoise becomes 0.87. Based on Wnoise, we simulate additional differential measurement errors for the treated group as follows:
| (6) |
| (7) |
| (8) |
where Wsys, Whet, and Wmix denote the simulated W under each scenario, and are plotted in Figure 4 (b), (c), and (d), respectively. Note that Wsys, Whet, and Wmix equal Wnoise for the untreated group. Finally, we standardize Wsys, Whet, and Wmix for all analyses to improve convergence and computation time. In both heteroscedastic and mixed cases, the 9.3 variance of additional error results in δ = 0.5 and 0.73 reliability in the treated group. The reliability in the untreated group is 0.84.
The propensity for living in a disadvantaged neighborhood is estimated as a function of adolescent gender, age, race/ethnicity, maternal age at birth, family income, and region of the country and urbanicity status of the adolescent’s residence. We estimate the ATE, the average effect of living in a disadvantaged neighborhood on probability of having a drug use or dependence disorder. We control for confounding using IPTW.
We use STAN (Stan Development Team, 2014) for the data analysis because it handles categorical variables better than JAGS. We use 100,000 iterations, the first 50,000 of which were the burn-in period, and 2 chains. Convergence is assessed with visual checks for adequate mixing using trace plots and by the R̂ statistic.
We compare the ATE estimated using various methods: 1) using the mother-reported age, X, “Truth”; 2) simply using the adolescent-reported age, W, “Naïve”; 3) using W in the Bayesian joint modeling approach with informative priors for γ~N(−2/sd(W), 3) and δ~Uniform(0.05, 3), “Joint_inf”; 4) using W in the Bayesian joint modeling approach with an informative prior for δ~Uniform(0.05, 3) and different point mass prior values for γ: −3/sd(W), −2.5/sd(W), −2/sd(W), −1.5/sd(W), −1/sd(W) = −0.46, −0.38, −0.31, −0.23, −0.15 for “Joint_S1”, “Joint_S2”, “Joint_S3”, “Joint_S4”, and “Joint_S5”, respectively; 5) using W in the Bayesian joint model modeling approach with an informative prior for γ~N(−2/sd(W), 3) and different point mass prior values for δ: = 0, 0.25, 0.5, 0.75, 1 for “Joint_H1”, “Joint_H2”, “Joint_H3”, “Joint_H4”, and “Joint_H5”, respectively; 6) using W in the Bayesian joint modeling approach with point mass priors for γ = −0.31 and δ = 0.5, “Joint_SH”; and 7) using W in the Bayesian two-step modeling approach with point mass priors for γ =−0.31 and δ = 0.5, “TS_SH”. All other regression coefficients have a N(0, 100) prior. We use M = 1000 for our data analysis.
5.2 Results
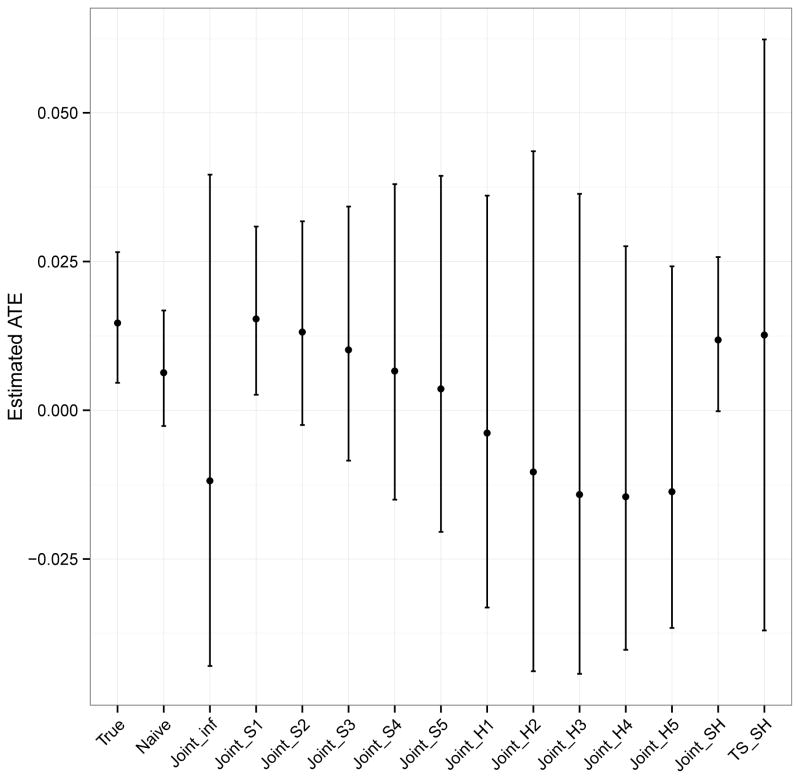
Figure 5 shows the ATE estimates for each method using Wmix. The pattern of results is similar for Wsys and Whet, and these results are given in the supplementary material. Using mother-reported age, X, as the truth, the mean posterior ATE is 0.014, 95% CI: 0.005, 0.027. This suggests that living in a disadvantaged neighborhood is associated with a slightly higher and statistically significant probability of having a drug use or dependence disorder in the past 12 months. The naïve approach, using adolescent-reported age, W, as if it were the truth also results in a mean posterior ATE of 0.006 but this association is no longer statistically significant as the 95% CI now crosses zero: −0.003, 0.017. Although statistical significance changes depending on whether X or W is used, the naïve approach actually results in very little bias. This is because maternal age at birth is a weak confounder in these data.
Figure 5.
Estimated ATE and 95% CI by method in the illustrative example using Wmix. The ATE is the average effect of living in a disadvantaged neighborhood on probability of past-year drug abuse or dependence. N=1,000.
Using correctly specified point mass priors in the joint Bayesian model (Joint_SH) results in a similar estimate and statistically significant inference as obtained using the true X. In contrast, using informative non-point mass priors for either or both γ and δ results in more variable estimates, rendering the association no longer significant. Results are more sensitive to using a non-point mass prior for γ than δ, as was seen in the simulation. When an informative non-point mass prior is used for γ (Joint_H) bias and variance are much larger than when an informative non-point mass prior is used for δ (Joint_S). The two-step model using correctly specified point mass priors (TS_SH) produces wider confidence intervals than any other method.
6 Discussion
In this paper, we consider a scenario of covariate measurement error that is differential by treatment status. We implement joint and two-step Bayesian models that address this measurement error in the context of a propensity score approach. We propose and evaluate their performance via simulation and a data example. The results show that using a Bayesian framework provides flexible approaches for addressing measurement error but prior distributions should be carefully specified. Our proposed approaches can straightforwardly handle complex measurement error models such as when measurement error is differential across treatment groups.
In the simulation study, when a strong predictor of outcome X is mismeasured, the Bayesian joint model works best while the two-step model performs poorly because the posterior distribution of X does not incorporate information from the relationship between X and the outcome. When X is a weak predictor of the outcome, fitting our Bayesian models does not improve the bias and MSE of ATE estimates much compared to the naïve model (though always improves coverage probability). Webb-Vargas and others (2015) show similar results that when X is strongly related to the outcome, using the outcome in the imputation with external calibration data to handle classical measurement error makes propensity score approaches work better. However, when X is only weakly related to the outcome using such an approach does not change inferences. In addition, we found that checking balance on the imputed X can be misleading because the balance on the imputed X may or may not reflect the balance on the true X. However, checking balance on the true X might not be possible in real data examples as the true X is usually not available, and a diagnostic tool should be developed for future work.
Considering the data analysis, we find little difference between the naïve and true models in estimating the average effect of living in a disadvantaged neighborhood of drug abuse or dependence disorder, although the statistical inference is changed. This is likely due to maternal age at birth being weakly related to the outcome, conditional on the other confounding variables. Thus, this data example is most similar to the low X-Y association scenario considered in the simulation. We recommend that, in low X-Y association scenarios, using the joint Bayesian approach as a sensitivity analysis by comparing estimates specifying various plausible point mass priors for γ and δ may be the most informative strategy. Specifying point mass priors for γ and δ can be informed by referring to external validation data that contain W, X, and treatment status. To use such external validation data, we need to assume transportability between the study data and validation data, meaning that the measurement error model estimated from the external validation data generalizes to the study data (Pearl and Bareinboim, 2011).
When estimating propensity score weights, extreme weights can be a problem in some situations. In our data analyses and our simulation studies with moderate imbalance on X between treated and control groups, we do not have extreme weights. In practice, one common approach to handle extreme propensity score weights is trimming large weights downward and this approach performs well with misspecified propensity score models (Lee, Lessler, and Stuart, 2011). Although not needed in the analyses in this paper that approach could also be considered in the context of differential covariate measurement error.
Our Bayesian models use a “subjective” Bayes approach, where the prior quantifies what is known by the investigators before the data is collected especially for parameters in the measurement error model. Other alternatives include “empirical” Bayes where the prior is estimated from the data itself, and “objective” Bayes where the choice of prior is based on certain mathematical properties (Carlin and Louis, 2009). However, our Bayesian models do not perform well with non-point mass priors on measurement error parameters because those parameters are hard to identify with limited information (i.e., absence of validation data) and present challenges in approximating a posterior distribution. To resolve this issue, we have some parametric assumptions such as specifying a structure of measurement error. Another possible solution is to have internal validation data (although it is rarely available). Our next research topic is to investigate the impact of using internal validation data on controlling for differential measurement error. In addition, Gustafson and others (2010) provide several recommendations to deal with nonidentified models: limit the number of hyperparameters and priors to be specified, or redefine unobserved parameters to update parameters involved in the likelihood separately from those not involved in the MCMC algorithm.
A limitation of the Bayesian joint model is that the outcome model must be combined with the propensity score model to consistently estimate the ATE. Our joint models allow “model feedback” between the outcome and propensity score models. That is, the outcome values are indirectly used to impute the true covariate and then the imputed true covariate contributes information to the propensity score model. This negates an advantage of propensity scores, which is that propensity score model fit is typically optimized without looking at the outcome–thus reflecting their role in the design stage of the study and preventing researchers from modifying their analysis to get desired results in terms of the effect estimates (Stuart, 2010). Recently, Zigler and others (2013) point out that the propensity score adjustment approach can result in model feedback that biases ATE estimates. Our joint models use a propensity score weighting approach and perform better in imputing the true covariate than two-step models. However, we do not rigorously assess the potential negative impact of model feedback when using IPTW and this is beyond the scope of this paper.
In this paper, we did not consider the case where measurement error is differential across groups given by a binary covariate, not the treatment assignment. We think that our proposed models can be applied to such a case, but we expect that differential measurement error across groups given by a covariate would cause less bias when estimating the ATE than does differential measurement error across treatment groups. In addition, measurement error in outcomes is another related and interesting topic, but it is beyond the scope of this paper (Yanez, Kronmal, and Shemanski, 1988).
In summary, we propose Bayesian approaches to estimate treatment effects when a single covariate is mis-measured and the measurement error is differential by treatment assignment. More methods need to be developed to handle differential measurement error on multiple covariates and researchers should further study which approaches work best under what scenarios.
Supplementary Material
Acknowledgments
This work was supported in part by the National Institute of Mental Health (R01MH099010; PI: Stuart). KER’s time was supported by the Drug Dependence Epidemiology Training program, (T32DA007292-21; PI: Deborah Furr-Holden) and the Robert Wood Johnson Foundation Health & Society Scholars program. The National Comorbidity Survey Replication Adolescent Supplement (NCS-A) and the larger program of related National Comorbidity Surveys are supported by the National Institute of Mental Health (ZIA MH002808). The views and opinions expressed in this article are those of the authors and should not be construed to represent the views of any of the sponsoring organizations, agencies, or U.S. Government. The authors claim no conflicts of interest. The authors wish to thank Kathleen Merikangas for support in providing the NCS-A data.
References
- An W. Bayesian propensity score estimators: incorporating uncertainties in propensity scores into causal inference. Sociological Methodology. 2010;40:151–189. [Google Scholar]
- Carlin BP, Louis TA. Bayesian Methods for Data Analysis. 3. Boca Raton, FL: Chapman & Hall/CRC; 2009. [Google Scholar]
- Cole SR, Chu H, Greenland S. Multiple-imputation for measurement-error correction. International Journal of Epidemiology. 2006;35:1074–1081. doi: 10.1093/ije/dyl097. [DOI] [PubMed] [Google Scholar]
- Drake C. Effects of misspecification of the propensity score on estimators of treatment effect. Biometrics. 1993;49:1231–1236. [Google Scholar]
- Gössl C, Kuechenhoff H. Bayesian analysis of logistic regression with an unknown change point and covariate measurement error. Stat Med. 2001;20:3109–3121. doi: 10.1002/sim.928. [DOI] [PubMed] [Google Scholar]
- Gustafson P. Measurement error and misclassification in statistics and epidemiology: impacts and Bayesian adjustments. Boca Raton, FL: Chapman & Hall/CRC; 2003. [Google Scholar]
- Gustafson P, McCandless LC, Levy AR, Richardson S. Simplified Bayesian Sensitivity analysis for mismeasured and unobserved confounders. Biometrics. 2010;66:1129–1137. doi: 10.1111/j.1541-0420.2009.01377.x. [DOI] [PubMed] [Google Scholar]
- Kaplan D, Chen J. A two-step Bayesian approach for propensity score analysis: Simulations and case study. Psychometrika. 2012;77:581–609. doi: 10.1007/s11336-012-9262-8. [DOI] [PubMed] [Google Scholar]
- Kessler RC, Avenevoli S, Costello EJ, Green JG, Gruber MJ, Heeringa S, Merikangas KR, Pennell BE, Sampson NA, Zaslavsky AM. National comorbidity survey replication adolescent supplement (NCS-A): II. Overview and design. J Am Acad Child Adolesc Psychiatry. 2009a;48:380–385. doi: 10.1097/CHI.0b013e3181999705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessler RC, Avenevoli S, Green J, Gruber MJ, Guyer M, He Y, Jin R, Kaufman J, Sampson NA, Zaslavsky AM, et al. National comorbidity survey replication adolescent supplement (NCS-A): III. Concordance of DSM-IV/CIDI diagnoses with clinical reassessments. J Am Acad Child Adolesc Psychiatry. 2009b;48:386–399. doi: 10.1097/CHI.0b013e31819a1cbc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee BK, Lessler J, Stuart EA. Weight trimming and propensity score weighting. PloS one. 2011;6:e18174. doi: 10.1371/journal.pone.0018174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leventhal T, Brooks-Gunn J. The neighborhoods they live in: the effects of neighborhood residence on child and adolescent outcomes. Psychological bulletin. 2000;126:309. doi: 10.1037/0033-2909.126.2.309. [DOI] [PubMed] [Google Scholar]
- Little RJA. To model or not to model? Competing modes of inference for finite population sampling. Journal of the American Statistical Association. 2004;99:546–556. [Google Scholar]
- Lockwood JR, McCaffrey DF. Correcting for test score measurement error in ANCOVA models for estimating treatment effects. J Educ Behav Stat. 2014;39:22–52. [Google Scholar]
- McCaffrey DF, Lockwood JR, Setodji CM. Inverse probability weighting with error-prone covariates. Biometrika. 2013:ast022. doi: 10.1093/biomet/ast022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCandless LC, Gustafson P, Austin PC. Bayesian propensity score analysis for observational data. Statistics in Medicine. 2009;28:94–112. doi: 10.1002/sim.3460. [DOI] [PubMed] [Google Scholar]
- Merikangas KR, Avenevoli S, Costello EJ, Koretz D, Kessler RC. National comorbidity survey replication adolescent supplement (NCS-A): I. Background and measures. J Am Acad Child Adolesc Psychiatry. 2009;48:367–379. doi: 10.1097/CHI.0b013e31819996f1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J, Bareinboim E. Transportability of causal and statistical relations: A formal approach. In Data Mining Workshops (ICDMW), 2011 IEEE 11th International Conference on; IEEE; 2011. pp. 540–547. [Google Scholar]
- Raykov T. Propensity Score Analysis With Fallible Covariates A Note on a Latent Variable Modeling Approach. Educational and Psychological Measurement. 2012;72:715–733. [Google Scholar]
- Robins J, Sued M, Lei-Gomez Q, Rotnitzky A. Comment: Performance of double-robust estimators when “inverse probability” weights are highly variable. Statistical Science. 2007;22:544–559. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Rosenbaum PR. Observational Studies. 2. Springer; New York: 2002. [Google Scholar]
- Roux AVD, Kiefe CI, Jacobs DR, Haan M, Jackson SA, Nieto FJ, Paton CC, Schulz R. Area characteristics and individual-level socioeconomic position indicators in three population-based epidemiologic studies. Ann Epidemiol. 2001;11:395–405. doi: 10.1016/s1047-2797(01)00221-6. [DOI] [PubMed] [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of educational Psychology. 1974;66:688. [Google Scholar]
- Rubin DB. Randomization analysis of experimental data: the Fisher randomization test comment. Journal of the American Statistical Association. 1980;75:591–593. [Google Scholar]
- Rubin DB. Multiple imputation for nonresponse in surveys. J. Wiley & Sons; New York, NY: 1987. [Google Scholar]
- Rudolph KE, Stuart EA, Glass TA, Merikangas KR. Neighborhood disadvantage in context: the influence of urbanicity on the association between neighborhood disadvantage and adolescent emotional disorders. Social psychiatry and psychiatric epidemiology. 2004;49:467–475. doi: 10.1007/s00127-013-0725-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stan Development Team. RStan: the R interface to Stan, Version 2.5.0. 2014 http://mc-stan.org/rstan.html.
- Steiner PM, Cook TD, Shadish WR. On the importance of reliable covariate measurement in selection bias adjustments using propensity scores. Journal of Educational and Behavioral Statistics. 2011;36:213–236. [Google Scholar]
- Stuart EA. Matching methods for causal inference: A review and a look forward. Statistical science. 2010;25:1. doi: 10.1214/09-STS313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stürmer T, Schneeweiss S, Avorn J, Glynn RJ. Adjusting effect estimates for unmeasured confounding with validation data using propensity score calibration. American journal of epidemiology. 2005;162:279–289. doi: 10.1093/aje/kwi192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Y, Yajima M. R2jags: A Package for Running jags from R. R package version 0.04-03. 2014 http://CRAN.R-project.org/package=R2jags.
- Webb-Vargas Y, Rudolph KE, Lenis D, Murakami P, Stuart EA. Applying multiple imputation for external calibration to propensity score analysis. Statistical Methods in Medical Research. 2015 doi: 10.1177/0962280215588771. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanez ND, Kronmal RA, Shemanski LR. The effects of measurement error in response variables and tests of association of explanatory variables in change models. Statistics in medicine. 1988;17:2597–2606. doi: 10.1002/(sici)1097-0258(19981130)17:22<2597::aid-sim940>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- Zigler CM, Watts K, Yeh RW, Wang Y, Coull BA, Dominici F. Model feedback in bayesian propensity score estimation. Biometrics. 2013;69:263–273. doi: 10.1111/j.1541-0420.2012.01830.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.