Understanding in-line probing experiments by modeling cleavage of nonreactive RNA nucleotides

Abstract

Ribonucleic acid (RNA) is involved in many regulatory and catalytic processes in the cell. The function of any RNA molecule is intimately related with its structure. In-line probing experiments provide valuable structural data sets for a variety of RNAs and are used to characterize conformational changes in riboswitches. However, the structural determinants that lead to differential reactivities in unpaired nucleotides have not been investigated yet. In this work, we used a combination of theoretical approaches, i.e., classical molecular dynamics simulations, multiscale quantum mechanical/molecular mechanical calculations, and enhanced sampling techniques in order to compute and interpret the differential reactivity of individual residues in several RNA motifs, including members of the most important GNRA and UNCG tetraloop families. Simulations on the multinanosecond timescale are required to converge the related free-energy landscapes. The results for uGAAAg and cUUCGg tetraloops and double helices are compared with available data from in-line probing experiments and show that the introduced technique is able to distinguish between nucleotides of the uGAAAg tetraloop based on their structural predispositions toward phosphodiester backbone cleavage. For the cUUCGg tetraloop, more advanced ab initio calculations would be required. This study is the first attempt to computationally classify chemical probing experiments and paves the way for an identification of tertiary structures based on the measured reactivity of nonreactive nucleotides.

INTRODUCTION

Ribonucleic acid (RNA) participates in several kinds of cellular processes, which involve the transmission of genetic information, the synthesis of proteins, cellular differentiation and development, the regulation of gene expression, and enzyme-like catalysis (Strulson et al. 2012; Kung et al. 2013; Sarkies and Miska 2014). Detailed information about RNA secondary structures is a preliminary step required for tertiary structure determination and, ultimately, for understanding RNA function (Walter 2009). Identification of specific small RNA motifs, like RNA tetraloops, is particularly important as they stabilize larger RNA structures and can be involved in RNA–RNA or RNA–protein interactions (Hall 2015). Indirect information about RNA secondary structure is usually obtained by chemical probing experiments (Xu and Culver 2009; Weeks 2010; Kubota et al. 2015). Among those, selective 2′-hydroxyl (2′-OH) acylation characterized by primer extension (SHAPE) (Merino et al. 2005) and in-line probing (Soukup and Breaker 1999) experiments provide sequence independent structural information on RNA at single-nucleotide resolution (Weeks 2010).

In-line probing characterizes backbone mobility by structural-dependent phosphodiester cleavage, which breaks RNA molecules into segments at distinct positions (Soukup and Breaker 1999). Unpaired nucleotides within single-stranded RNA regions are often unstable and degrade over time (Reynolds et al. 1996; Welch et al. 1997). The chemical reaction, termed as an internal transesterification, starts with a 2′-OH attack of neighboring phosphate moiety and results with 2′,3′-cyclic phosphate and 5′-hydroxyl termini (Soukup and Breaker 1999; Lilley 2003). The same RNA backbone cleavage (or RNA degradation) is performed by self-catalytic systems called RNA enzymes (ribozymes) (Doudna and Cech 2002; Scott 2007; Lilley and Eckstein 2008) and by ribonuclease A (RNase A) (Raines 1998), although in these cases with significantly higher rate constants. By comparing nucleotides from various RNA motifs, Soukup and Breaker (1999) observed a relation between the cleavage rate constant and the in-line attack angle of the scissile phosphate, i.e., the angle between O2′ oxygen, the adjacent phosphorus, and O5′ oxygen. Later, they defined the ability to bring the active site toward the in-line attack conformation (the in-line attack angle close to 180°) as one of the catalytic strategies for the phosphodiester backbone cleavage used by ribozymes (Breaker et al. 2003; Emilsson et al. 2003). Since then, in-line probing is routinely used in studies of riboswitches, where the binding of a small molecule (ligand) results in a conformational change of the whole RNA molecule (Mandal and Breaker 2004; Montange and Batey 2008; Regulski and Breaker 2008; Garst et al. 2011). In general, chemical probing experiments are typically used to identify unpaired and flexible nucleotides, allowing one to choose among different predicted secondary structures. However, it must be noted that not all the unpaired nucleotides are usually reactive. The reactivity pattern of unpaired nucleotides could in principle provide a wealth of information that is usually discarded. To the best of our knowledge, the pattern of reactivity of specific motifs has never been analyzed in detail.

Computational techniques are an established tool for the investigation of structural and dynamical properties of RNA at an atomistic level (Schlick 2010; Cheatham and Case 2013; Šponer et al. 2013) and could in principle allow for an investigation and interpretation of reactivity patterns in RNA. In particular, quantum mechanical/molecular mechanical (QM/MM) (Warshel and Levitt 1976) approaches, where only the reactive portion of the system is described at the QM level, have been used to characterize cleavage reactions within catalytic RNA systems (Banáš et al. 2008; Lee et al. 2008; Nam et al. 2008a,b; Mlýnský et al. 2011, 2015; Rosta et al. 2011; Xu et al. 2012; Gu et al. 2013; Ganguly et al. 2014; Dubecký et al. 2015; Thaplyal et al. 2015; Zhang et al. 2015; Casalino et al. 2016). Single-point QM/MM calculations evaluate potential energy surfaces neglecting entropic contributions. The reconstruction of free-energy surfaces (FES) along the reaction pathway requires a combination of QM/MM calculations with molecular dynamics (MD) simulations and enhanced sampling techniques (Palermo et al. 2015). In this context, semi-empirical (SE) methods allow for a reasonable compromise between accuracy and efficiency (Christensen et al. 2016), allowing statistically converged FES to be computed. Two SE methods have been carefully parameterized for reactions involving the phosphate moiety (Nam et al. 2007; Yang et al. 2008).

In this article, we combine QM/MM calculations and enhanced sampling methods to model phosphodiester backbone cleavage of nucleotides from three model systems: one tetraloop from each of the GNRA and UNCG families (R = purine and N = any nucleotide) and a double-stranded RNA (dsRNA). Regions undergoing the cleavage reaction were described by a DFTB3 SE method, which allowed us to perform simulations on tens-of-ns timescales and obtain converged free-energy landscapes. Our calculations required us to design a putative reaction pathway with a number of restraints in order to overcome persisting shortcomings within parameterization of the DFTB3. However, we were able to differentiate among nucleotides within simple motifs by comparing their activation free-energy barriers. Computational results were validated against available experimental data from in-line probing measurements. To our knowledge, this represents the first attempt to design computations in order to understand and mimic in-line probing experiments and, more generally, to investigate the phosphodiester backbone cleavage within nonreactive RNA nucleotides, i.e., not considering the active centers of RNA catalytic motifs.

RESULTS

We performed combined QM/MM-MetaD simulations (see Materials and Methods) and reconstructed FES relative to the phosphodiester cleavage reaction for nucleotides within three simple RNA motifs: uGAAAg tetraloop, dsRNA (GC-duplex), and cUUCGg tetraloop. For the tetraloops, we computed the reactivity for the unpaired residues and for the closing base pairs. For the duplex, we chose three consecutive nonterminal residues from each strand (Supplemental Fig. S1). We thus analyzed relative differences in reactivities among 6 nt for each system by comparing ΔG^‡ cleavage barriers along reaction pathways designed to be equivalent for all nucleotides from different RNA motifs. Since our intention was not to give insight into the mechanism of phosphodiester backbone cleavage, possible involvement of other RNA groups, water molecules, and ions was omitted and any mechanistic interpretation deliberately neglected.

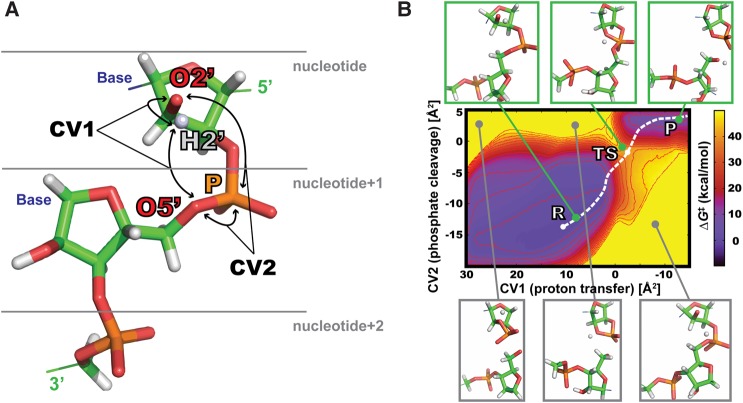
The computed FES profiles mapped ΔG changes along two tracked distance-based collective variables (CVs) (Fig. 1A) to describe the proton transfer and the phosphodiester cleavage. The most relevant information that we want to extract is the ΔG^‡ cleavage barrier, which was estimated as explained in Materials and Methods. The FES displays two energy minima containing reactant (R) and product (P) state geometries (Fig. 1B). The R state minimum is very broad because the simulation is allowed to sample all the possible geometries, including different orientations of the active 2′-OH group. This is necessary for the accurate estimation of ΔG^‡ barriers. On the contrary, we restrained the extensive separation of the RNA molecule after the cleavage reaction, leading to a narrower free-energy minimum associated to P state. The complete exploration of P state geometries would make convergence very difficult and is irrelevant for a proper estimation of the cleavage barrier.

FIGURE 1.

(A) Selection of QM region and definition of collective variables (CVs). QM region for a particular nucleotide contained ribose ring (reactive 2′-OH group), phosphate with ribose ring of nucleotide+1, and phosphate moiety of nucleotide+2. Bases were described at MM level of theory (AMBER ff14). FES of phosphate cleavage reaction was defined by two CVs. CV1 described the proton transfer (difference of squared [O5′…H2′] and [O2′…H2′] distances), and CV2 described the phosphate cleavage (difference of squared [O5′…P] and [O2′…P] distances). (B) FES of phosphodiester backbone cleavage for G4 nucleotide from uGAAAg tetraloop. Snapshots in boxes show different conformation and reaction states of QM atoms defined by specific values of CVs. The proton from 2′-OH is represented as unbound to be clearly visible. Green boxes show geometries close to R, TS, and P states, whereas gray boxes display structures energetically penalized by restraints (see Supplemental Material for details). The white dashed line marks the estimated reaction coordinate.

The FES profiles for nucleotides within three different RNA motifs (uGAAAg and cUUCGg tetraloops, GC-duplex) are qualitatively very similar among each other (see Supplemental Fig. S2 for all computed FES). The R and transition (TS) states have slightly different locations for particular nucleotides within each RNA motif, but no relevant correlations. For instance, purine/pyrimidine or tetraloop/duplex differences were not detected. The computed ΔG^‡ barriers after 40-nsec-long QM/MM-MetaD simulations were in the range between 40.0 and 44.5 kcal/mol. Note that the reaction coordinates are affected by the applied restraints and approximations, which forced the proton from the 2′-OH to be kept around the direct pathway (Fig. 1). Furthermore, the reported cleavage barriers are expected to be overestimated due to the complete exclusion of scenarios involving proton transfer through nonbridging oxygens (nbO) of the adjacent phosphate and/or through other proximal RNA groups. However, this allows for a consistent estimation of ΔG^‡ values and their comparison across nucleotides within different RNA motifs.

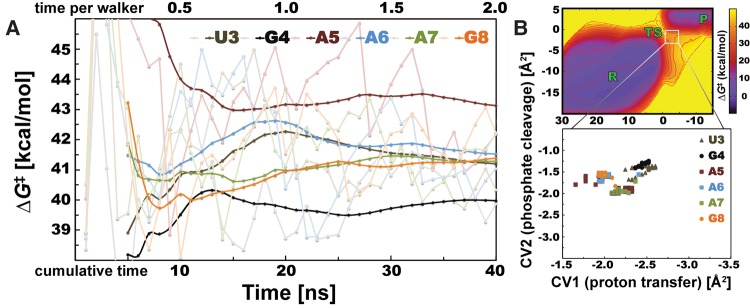
We tested carefully the statistical convergence of computed phosphodiester cleavage barriers. The analysis showed that ΔG^‡ barriers of six investigated nucleotides within the uGAAAg tetraloop fluctuate within a few kcal/mol over the time of the simulation (shaded lines, Fig. 2A), making it difficult to differentiate among nucleotides. All those barriers were estimated by using the final bias potential. In order to increase the accuracy of the method, we then calculated ΔG^‡ from time-averaged bias potentials. This latter approach gives a smoother convergence, which enables nucleotides to be clearly distinguished. The resulting ΔG^‡ barriers of uGAAAg nucleotides are clearly converged after 40 nsec of cumulative simulated time (Fig. 2A). Note that even initial estimated averages (∼7 nsec of total simulated time) show clear differences within ΔG^‡ among tested nucleotides. The GC-duplex was used as a control simulation because the computed ΔG^‡ barriers are expected to be identical for three equivalent nucleotides. Our approach shows that the computed ΔΔG^‡ differences of equivalent G and C nucleotides are negligible after 40 nsec, i.e., up to 0.4 and 0.5 kcal/mol, respectively (Supplemental Fig. S3A). We also analyzed the location of TS during different stages of the simulations because the estimation of ΔG^‡ depends on the position of TS and R states on the FES. The TS positions of all nucleotides within the uGAAAg tetraloop are located within a small region in the CV space (Fig. 2B). The variance in positions of R states was even smaller (data not shown). The same trend was observed for the nucleotides within the GC-duplex (Supplemental Fig. S3B), whereas differences in TS positions on FES were slightly larger for nucleotides within the cUUCGg tetraloop (Supplemental Fig. S4B).

FIGURE 2.

Convergence of cleavage barriers and distribution of TS positions of nucleotides from uGAAAg tetraloop. (A) Instantaneous estimates of ΔG^‡ barrier (shaded lines) fluctuate, whereas barriers calculated from time-averaged bias potentials (see Materials and Methods) are converged (bold lines). Each uGAAAg nucleotide is displayed in a specific color with two (shaded and bold) tones. Horizontal axis has two scales, showing timescale of single simulation (one walker, upper scale) or cumulative time considering 20 concurrent QM/MM-MetaD simulations (lower scale). The ΔG^‡ values were analyzed every 1 nsec in total timescale. (B) Position of TS states on FES is not changing significantly during QM/MM-MetaD simulations. TS states of all tested nucleotides from uGAAAg tetraloop are located within the same area with minimal changes of CV2 (describing the proton transfer). Colors for each nucleotide and the interval for analysis correspond with those on panel A.

The phosphodiester backbone cleavage ΔG^‡ barriers are generally between 41 and 42 kcal/mol, but some nucleotides showed intrinsic differences. G4 within the uGAAAg tetraloop revealed the lowest barrier among all the nucleotides (40.0 kcal/mol, Supplemental Fig. S2). The following A5 showed a significantly higher barrier of 43.1 kcal/mol, whereas the ΔG^‡ barriers for the remaining nucleotides were comparable (∼41.5 kcal/mol). All the nucleotides within the GC-duplex revealed comparable barriers between 40.9 and 41.5 kcal/mol. Among cUUCGg nucleotides, U5 showed the lowest barriers (40.6 kcal/mol), whereas U4 and C6 provided significantly higher barriers of 44.5 and 43.5 kcal/mol, respectively (Supplemental Figs. S2, S4A).

We then compared the computed ΔG^‡ barriers against data from the in-line probing measurements. The experimental reactivities (pseudo free energies) were derived from available polyacrylamide gel electrophoresis (PAGE) data sets, quantified and normalized separately according to the scheme described in Materials and Methods. We observed good agreement between computed and experimental reactivities for nucleotides within the uGAAAg tetraloop. Our computations overestimated the ΔG^‡ barriers for U3 and A5 nucleotides, but led to the correct trend overall (Fig. 3A). However, a similar comparison for the nucleotides within the cUUCGg tetraloop revealed some differences. U5, C6, and G7 were identified as reactive nucleotides according to the experiment (Strauss et al. 2012), but the computed ΔG^‡ barrier for C6 was significantly higher, suggesting that the nucleotide is nonreactive (Fig. 3C). Note that the in-line probing data for a uniform GC-duplex are not available, but that reactivity of paired residues is typically lower than reactivity for unpaired residues (Soukup and Breaker 1999; Kulshina et al. 2009; Erion and Strobel 2011; Strauss et al. 2012; Nelson et al. 2013; Hickey and Hammond 2014; Furukawa et al. 2015).

FIGURE 3.

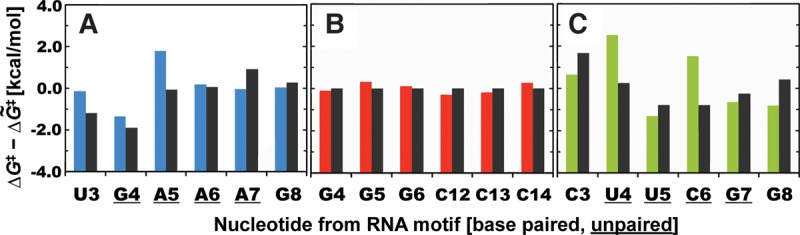
Comparison between computed and experimentally derived cleavage barriers for nucleotides from three different motifs. Correlation between computed ΔG^‡ barriers (with specific color for each motif) and barriers derived from experiments (black, pseudo free energies, see Materials and Methods for details) for nucleotides from uGAAAg tetraloop (A), GC-duplex (B), and cUUCGg tetraloop (C). Both computed and experimentally derived ΔG^‡ barriers are displayed as deviations from the corresponding median value. Note that in-line probing data for a uniform GC-duplex are not available, but equivalent G–C base pairs are expected to have similar ΔG^‡ barriers (deviations from the median are set to zero in the figure). Unpaired nucleotides from tetraloops are underlined (see Supplemental Fig. S1 for nucleotide labeling).

DISCUSSION

In this article, we used QM/MM-MetaD calculations to classify in-line probing experiments characterized by the phosphodiester backbone cleavage reaction. To this aim, we calculated the free-energy profiles modeling the RNA backbone cleavage for 18 nucleotides (nt) within two RNA tetraloops and a dsRNA. The computed ΔG^‡ barrier obtained from the QM/MM-MetaD calculation is expected to be related to the reactivity of the particular nucleotide as observed in in-line probing experiments. The aim of our study was not to predict absolute reactivities but to explain differential reactivities observed among nucleotides within the same or from different RNA motifs. To minimize the error in differential estimates, we forced the system to explore a similar reaction pathway for each nucleotide and prolonged simulations in the tens-of-ns timescale. The approach provides converged and consistent results for all the nucleotides. Results were then assessed by comparing ΔG^‡ barriers of identical nucleotides within a GC-duplex motif and by analyzing reference in-line probing reactivities from PAGE gels.

We included a number of artificial restraints, which were required in order to automatize the computational protocol, i.e., to allow the straightforward comparison of various nucleotides within distinct RNA motifs. Restraints improved stability of the simulations namely by preventing spurious rupture of bonds and by excluding several unphysical geometries detected during phosphodiester cleavage reaction. However, all the backbone dihedrals, sugar puckers, glycosidic bonds, as well as base-pairing and stacking interactions were left free to rearrange. We actually observed significant dynamics during our QM/MM-MetaD simulations. This is important since the essence of in-line probing experiments is to quantify the effects of RNA structural fluctuations on the phosphodiester cleavage rate. The introduction of restraints is nevertheless expected to affect the computed barriers, and thus the respective cleavage rates, in two specific ways. First, restraints forced the cleavage reaction to proceed through the designed reaction pathway that is similar for all nucleotides and likely different from the validated in-line attack reaction pathway. The possible contributions of other reaction pathways, which could be different from one nucleotide to the other, were thus ignored. As a result, the reactivity trends estimated as differences of ΔG^‡ barriers could in principle be compressed. Second, all the computed ΔG^‡ barriers are expected to be overestimated by excluding the scenario where the proton from the 2′-OH group is transferred through nbO atoms. Considering the typical timescale of in-line probing experiments (hours/days), the ΔG^‡ barriers derived from the estimated rate constants using the Eyring equation are expected to be in the range from ∼26 to ∼32 kcal/mol (Soukup and Breaker 1999), i.e., by ∼7 to ∼13 kcal/mol lower than the herein reported ΔG^‡ barriers. Both those issues are very difficult to tackle since they depend on intrinsic deficiencies of the DFTB3 parameterizations. Despite the fact that DFTB and other SE methods improved significantly during the last decade (Huang et al. 2014; Christensen et al. 2016), their general application toward chemical reactions remains challenging. In particular, recent studies carefully assessed the performance and revealed limitations of DFTB methods in description of phosphoranes and phosphoryl transfers (Gaus et al. 2014; Mlýnský et al. 2014; Huang et al. 2015; Lu et al. 2016). In this study, we still opted for the usage of DFTB3 because we did not aim for an accurate description of states along phosphodiester cleavage reaction. We rather focused on relative differences of ΔG^‡ barriers among different nucleotides, forcing the reaction to proceed through the same pathway for all the analyzed nucleotides. We expect such an approach to be more robust and less sensitive to the applied QM method. QM/MM-MetaD simulations, at least on a several-ns timescale, are required to converge these FES computations to a level allowing for the discrimination of reactivity patterns, ruling out more accurate QM methods such as DFT or ab initio.

Here, we ranked different RNA nucleotides, i.e., base paired/unpaired, purine/pyrimidine, from duplex and tetraloops by their tendency to undergo phosphodiester backbone cleavage. Nucleotide reactivities reported by in-line probing experiments were used as a reference. A number of experimental data sets for specific motifs from different RNA systems are available (Supplemental Fig. S5; Soukup and Breaker 1999; Kulshina et al. 2009; Erion and Strobel 2011; Strauss et al. 2012; Furukawa et al. 2015), but their quantitative estimation is often affected by unclear signals (Erion and Strobel 2011; Hickey and Hammond 2014; Furukawa et al. 2015) and/or participation in a tertiary interaction within a complex RNA structure (Soukup and Breaker 1999; Kulshina et al. 2009; Erion and Strobel 2011). Hence, we used a single specific experiment providing distinct signals for all nucleotides as a reference of each of the tetraloop motifs (Strauss et al. 2012; Nelson et al. 2013). We observed that nucleotides within the cUUCGg tetraloop revealed some differences between predicted and calculated reactivities (Fig. 3C). Calculated ΔG^‡ barriers of U4 and C6 nucleotides are significantly overestimated, resulting in a poor correlation between theory and experiment (R = 0.17, Fig. 4A). We notice that (i) the FES profiles for cUUCGg nucleotides are statistically converged (Supplemental Fig. S4A), (ii) experimental reactivities for nucleotides within the cUUCGg motif reveal similar trends among different systems (Supplemental Fig. S5B), and (iii) the procedure of quantification of experimental reactivities, i.e., using digitalized images (see Materials and Methods) provide almost identical profiles against the raw count data (a comparison for the uGAAAg tetraloop is reported, Supplemental Fig. S6). Thus, the poor correlation between computed ΔG^‡ barriers and experimental reactivities for cUUCGg suggests possible limitations of our approach. We carefully inspected the structures along the cleavage reaction and found that the reactive 2′-OH of U5 and, especially U4, established H-bonds with other RNA groups outside the QM region (described by the empirical force field, Supplemental Fig. S7). Such interactions could result in overstabilization of R states, leading to the overestimation of the computed ΔG^‡ barriers by the current approach. Furthermore, the cleavage site of C6 favored rare conformations with high in-line attack angles. Such geometry is not favorable for the mechanism enforced herein and would require us to explore the in-line attack reaction pathway, where nbO atoms (and/or external RNA groups, water molecules) are involved in the proton transfer. This was not possible due to deficiencies within DFTB3 parameterization (see Supplemental Material for details). One possible way to improve the results for cUUCGg would be to increase the number of atoms within the QM region (described by DFTB3). However, we identified that RNA groups forming those interactions are typically belonging to nucleotides located further away along the sugar–phosphate backbone, making those calculations unfeasible.

FIGURE 4.

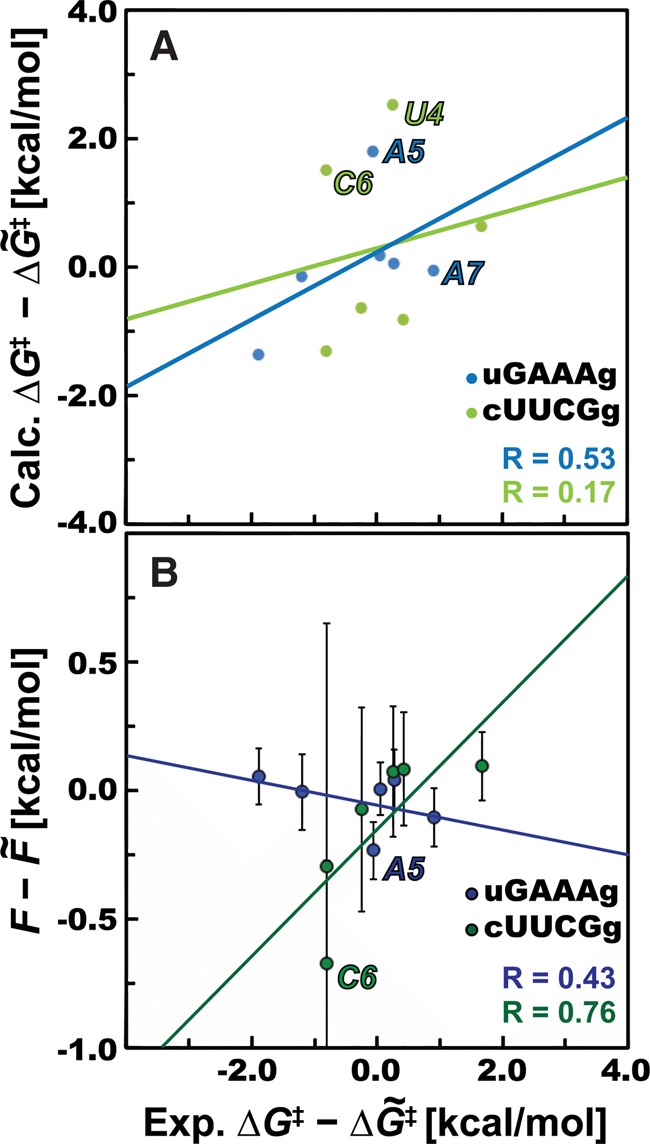
Direct correlation between theory and experiments for nucleotides within two tetraloops. (A) The correlation between calculated ΔG^‡ and barriers derived from experiments for nucleotides within uGAAAg (blue) and cUUCGg (green) tetraloops. Both computed and experimental barriers are displayed as deviations from the corresponding median value. (B) A similar correlation plot obtained using the logarithm of in-line fitness F = −RTln(Fitness) (Soukup and Breaker 1999), instead of the here calculated ΔG^‡. We displayed averaged values of fitness from the set of X-ray structures (considering 41 uGAAAg and 754 cUUCGg tetraloops, respectively) from the PDB database with bars showing their standard deviations. F-values are displayed the same way as ΔG^‡ barriers subtracting medians. Points corresponding to specific residues that are worsening the correlation (outliers) are labeled.

On the other hand, the agreement between theory and experiment is satisfactory for both GC-duplex and uGAAAg tetraloop. In the former case, nucleotides revealed very similar ΔG^‡ barriers, which are expected for three consecutive equivalent G and C within dsRNA. The fact that each of these barriers was obtained with a totally independent simulation further confirms the low statistical error and hence the reproducibility of our computational approach. The possible differences between purine and pyrimidine nucleotides were negligible for this motif (within the error of our approach, Supplemental Fig. S3A). However, we observed that those ΔG^‡ barriers are comparable with cleavage barriers of several unpaired residues within tetraloop motifs. This is unexpected, since the reactivity of paired nucleotides is generally lower (Reynolds et al. 1996; Welch et al. 1997; Soukup and Breaker 1999). We speculate that such behavior is caused by the number of restraints used in our computations, although it could also be linked to the approximations in the DFTB3 method. In the uGAAAg tetraloop, QM/MM-MetaD simulations can clearly predict that the unpaired G4 is significantly more reactive than the other nucleotides. Simulations are long enough to consider this difference statistically significant. Other nucleotides have higher ΔG^‡ barriers, in agreement with the lower reactivity observed in experiments (Fig. 3A). Plotting computational and experimental reactivities against each other revealed that the two unpaired nucleotides (A5 and A7) are worsening the correlation (R = 0.53) due to slightly overestimated (A5) and underestimated (A7) ΔG^‡ barriers (Fig. 4A). It is worth noting that the overall stability and flexibility of the tetraloop motifs can be affected by the nature of the closing base pair (Proctor et al. 2002; Blose et al. 2009). For this reason, we explicitly replaced the G–C base pair observed in the crystal structure with the wobble G–U pair found in the sequence used in the reference in-line probing experiments.

Our results can also be compared against predictions using the approach introduced by Soukup and Breaker (1999), where a correlation between geometrical parameter (in-line fitness) and cleavage rates was proposed. The fitness parameter combines the in-line attack angle and the distance between O2′ and the adjacent phosphorus. Interestingly, the fluctuations of the in-line attack angle were proposed as a proxy for the chemical reactivity of individual nucleotides (Kirmizialtin et al. 2015). We searched among high-resolution X-ray structures (≤3.5 Å) of RNA molecules from the RCSB Protein Data Bank (PDB) (Berman et al. 2000) and used the baRNAba tool (Bottaro et al. 2014) to extract representative uGAAAg tetraloops. The average fitness values for those nucleotides are anti-correlated with the experimental reactivities derived from gels (Fig. 4B), showing that the in-line fitness formula (Soukup and Breaker 1999) derived from static X-ray structures cannot reproduce the experimental reactivity pattern for this motif. This is not surprising, since the in-line fitness was not designed for differentiating among random nucleotides, but rather for the specific identification of highly reactive nucleotides within catalytic centers of ribozymes (see Fig. 8 in the original paper, Soukup and Breaker 1999).

Inspection of the starting structure used for uGAAAg computations (PDB ID 4QLM) (Ren and Patel 2014) revealed accidental syn orientation of the unpaired A5 and A7, which surprisingly improved the correlation between in-line fitness and experimental reactivity (R = 0.85, Supplemental Fig. S8A). We recall that considering the structures extracted from the PDB as well as solution experiments (Heus and Pardi 1991; Jucker et al. 1996; Bottaro et al. 2016), the syn conformation is rare and unexpected for nucleotides within the uGAAAg tetraloop. Since we did not find any apparent crystallographic contact that may invoke those reorientations, it appears likely that the higher flexibility of unpaired bases affected the refinement and resulted in poor electron densities for unpaired nucleotides located away from the important (binding) centers of the ydaO riboswitch. Syn/anti flips of A5, A6, and A7 nucleotides also occurred during classical MD simulation used for the system equilibration. Remarkably, all nucleotides revealed the correct anti conformation after 100 nsec of the simulation time, i.e., in the structure used for subsequent QM/MM-MetaD calculations, indicating that the MM force field used was able to recover the expected native structure. We notice that the syn/anti flips of all unpaired nucleotides from the uGAAAg tetraloop were also occasionally detected during QM/MM-MetaD simulations (in timescale of tens to hundreds of ps), despite the fact that the starting structure contained all bases in correct anti conformation. This may suggest that possible anti/syn reorientation might induce the phosphodiester backbone cleavage by enabling a more favorable ribose pucker state (C2′-endo) for the initial nucleophilic attack and/or different conformations of the adjacent phosphate. Interestingly, functional nucleotides within catalytic centers of RNAs are frequently found in syn conformation (Sokoloski et al. 2011).

In conclusion, we presented an approach to characterize the reactivity in RNA motifs. We used QM/MM calculations with semi-empirical methods, in combination with multiple-walkers metadynamics, to compute the free-energy barriers associated with phosphodiester backbone cleavage in generic, noncatalytic nucleotides. The computational protocol is fast and robust, though limited by the currently available parameters for the DFTB3 method. Remarkably, our procedure was able to reproduce and explain differential reactivities in a common RNA tetraloop (uGAAAg). However, reactivities in another tetraloop (cUUCGg) were more difficult to classify. Our results suggest that better DFTB3 parameters would be required for appropriate modeling of phosphodiester cleavage reactions of this system and our protocol may serve as a benchmark for the further improvements of the semi-empirical method. To the best of our knowledge, this study represents the first computational approach for the interpretation and classification of chemical probing experiments. The introduced procedure could be applied to more complex RNA motifs, providing the initial step for fast and cheap distinguishing among several experimentally suggested RNA structures.

MATERIALS AND METHODS

Initial structures of RNA motifs were taken from crystal structures, i.e., PDB ID 4QLM (uGAAAg tetraloop) (Ren and Patel 2014), 1QCU (dsRNA) (Klosterman et al. 1999), and 4JF2 (cUUCGg tetraloop) (Liberman et al. 2013). Tetraloop motifs contain 10 nt and the dsRNA duplex consists of eight G–C base pairs (see Supplemental Fig. S1 and Supplemental Methods section for structures and details). The QM region included two ribose rings and two phosphates (Fig. 1A). We used the DFTB3 method (Gaus et al. 2011), as implemented in GROMACS 5.0 (Abraham et al. 2015; Kubař et al. 2015), in combination with PLUMED (Tribello et al. 2014). Recent corrections (Huang et al. 2014) that improve the description of ribose rings (sugar-puckers) were additionally applied using PLUMED. Bases were described at the MM level by AMBER ff14 (Cornell et al. 1995; Wang et al. 2000; Pérez et al. 2007; Zgarbová et al. 2011) in order to handle all of them at the same level of theory. We explicitly tested the performance of all available DFTB3 parameter sets, i.e., MIO (Gaus et al. 2011), 3OB (Gaus et al. 2014), and 3OB-OPhyd (Gaus et al. 2014). After accurate validations we opted for the MIO set, and all results reported herein were calculated by that setup. To avoid spurious reactions and unphysical geometries, we had to enforce specific reaction pathways with a number of artificial restraints to disallow the rupture of bonds not involved in the cleavage reaction. These restraints might penalize the reactive in-line attack geometry, and the enforced pathway is likely to be different from the reaction monitored by in-line probing experiments (see Supplemental Material for details).

Well-tempered metadynamics (MetaD) (Laio and Parrinello 2002; Barducci et al. 2008) under the multiple-walker algorithm (Raiteri et al. 2006) was used to accelerate the phosphodiester cleavage and to estimate the associated FES. Two CVs were used (Fig. 1A): one to describe the proton transfer and the other to describe the phosphodiester cleavage. FES was computed either considering the final bias potential or considering time-averages of the bias potential (Micheletti et al. 2004), and convergence was monitored during different stages of the simulation. Further discussion and justification for the time-averaging procedure can be found in the Methods section of the Supplemental Material. The activation free-energy (ΔG^‡) barrier of the phosphodiester backbone cleavage for the particular nucleotide was extracted from computed FES by localizing the saddle point (TS) on the reaction coordinate, i.e., the most convenient path (requiring the lowest energies) connecting two areas with minimal energies on the FES, corresponding to R and P state geometries (Fig. 1).

Experimental reactivities for specific nucleotides within uGAAAg and cUUCGg tetraloops were quantified by analyzing PAGE data. We took digitalized images extracted from the original papers (Strauss et al. 2012; Nelson et al. 2013) and we integrated the color density present in the area of the image corresponding to each nucleotide. Subsequently, pseudo-free-energy reactivities were derived using an approach similar to the one developed for SHAPE experiments (Low and Weeks 2010): ΔG_Exp = −mlns, where s is the signal intensity from gels and m = 2.6 kcal/mol. Intensities were normalized by shifting the medians of experimental reactivities to match those of the calculated barriers for each tetraloop motif. We note that all the considered systems were studied using identical settings and analysis procedures so as to allow for an unbiased comparison.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.