Abstract
Fluorescence recovery after photobleaching (FRAP) is a well-established experimental technique to study binding and diffusion of molecules in cells. Although a large number of analytical and numerical models have been developed to extract binding and diffusion rates from FRAP recovery curves, active transport of molecules is typically not included in the existing models that are used to estimate these rates. Here we present a validated numerical method for estimating diffusion, binding/unbinding rates, and active transport velocities using FRAP data that captures intracellular dynamics through partial differential equation models. We apply these methods to transport and localization of mRNA molecules in Xenopus laevis oocytes, where active transport processes are essential to generate developmental polarity. By providing estimates of the effective velocities and diffusion, as well as expected run times and lengths, this approach can help quantify dynamical properties of localizing and nonlocalizing RNA. Our results confirm the distinct transport dynamics in different regions of the cytoplasm, and suggest that RNA movement in both the animal and vegetal directions may influence the timescale of RNA localization in Xenopus oocytes. We also show that model initial conditions extracted from FRAP postbleach intensities prevent underestimation of diffusion, which can arise from the instantaneous bleaching assumption. The numerical and modeling approach presented here to estimate parameters using FRAP recovery data is a broadly applicable tool for systems where intracellular transport is a key molecular mechanism.
Introduction
Fluorescence recovery after photobleaching (FRAP) is a widely used tool for investigating protein mobility and local molecular transport in living cells (1, 2). Because fluorescence is visualized as diffuse staining, FRAP data cannot be used to distinguish or track individual particles; to make predictions about mobility and local transport, further analysis is needed. A large number of diffusion and reaction-diffusion models have been proposed for the quantitative analysis of FRAP recovery data (reviewed in (1, 2)). Most previous work makes use of linear reaction-diffusion partial differential equation (PDE) models to predict diffusion and binding in cells. Depending on the relative timescales of diffusion and binding, these methods involve estimating diffusion coefficients and binding rates by fitting the fluorescence recovery data to analytical solutions of the equations (3, 4, 5, 6, 7, 8, 9, 10, 11, 12) or by using optimization and numerical solutions of the PDEs for more complex geometries and models (13, 14, 15). FRAP data analysis typically involves modeling two particle states, and making assumptions about diffusion, the number and type of binding interactions, and their respective timescales in cells (6).
In addition to movement by diffusion, macromolecules are actively transported on cytoskeletal networks by molecular motors such as myosin, kinesin, or dynein in many cell types. However, in systems with active movement, FRAP data analysis may overestimate diffusion rates if active transport is not taken into account (1). The goal of this work is to develop an approach for extracting movement information from FRAP data in cells where transport is a key mechanism for the dynamics. To capture active transport, we propose advection-reaction-diffusion PDEs that account for binding, diffusion, and active transport of particles. Parameter estimation is carried out through optimization of numerical solutions of the PDE models considered. We demonstrate that our approach allows efficient extraction of consistent estimates for movement, diffusion, and transition rate parameters from FRAP data using models of two- or four-particle states (see Fig. 1). We note that advection has been included in active transport models to describe spatial localization of RNA in Drosophila oocytes and embryos (16, 17), neurofilament transport along axons in neurons (18, 19), and motor-driven transport along filaments (20, 21). However, to our knowledge, such models were not applied to FRAP experimental data. Here we design general techniques for FRAP parameter estimation using transport PDE modeling frameworks and demonstrate their efficacy.
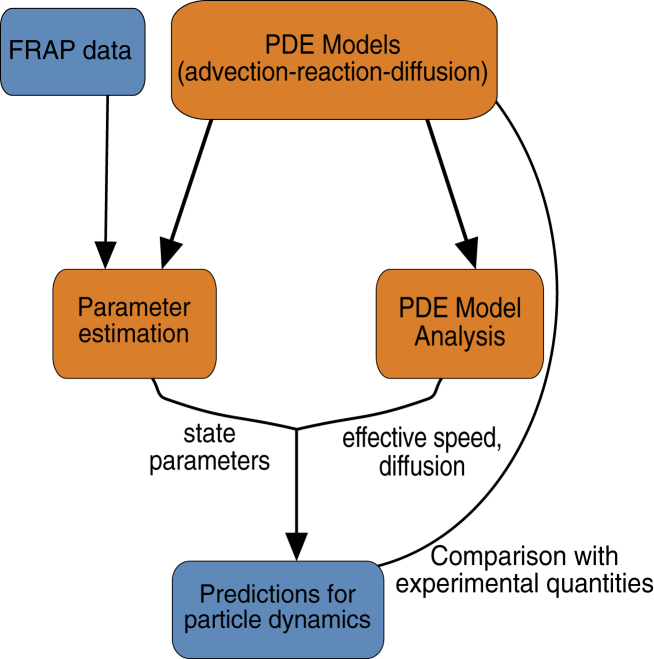
Figure 1.
Cartoon of the proposed approach to drawing predictions for particle dynamics from FRAP data. To see this figure in color, go online.
In addition, given estimates of the coefficients in the transport models considered, we show how these parameters can be used to predict effective velocities and diffusion rates for long-term dynamics (see Fig. 1). Consider, for instance, a system where particles switch between movement and diffusion. In one state, particles move with speed c, and in the other, they diffuse with rate d (see (1a), (1b) for details). Because the particles can switch between states with transition rates β1 and β2, the effective velocity and diffusion of the particles in the long run are different from the individual state parameters. Dynamical systems analysis of general advection-reaction-diffusion models allows us to provide general formulas for these large time quantities that go beyond specific examples (18, 19) and extend the treatment of reaction-hyperbolic systems (20, 22, 23, 24) and of diffusion in one population (21). Mathematical derivations of these large time solutions, as well as calculation of expected run lengths of motor-cargo complexes on microtubules, allow us to compare parameter estimation predictions with experimental observations (see Fig. 1). Our approach is applicable to many systems, and we validate it here through the study of active transport mechanisms including bidirectional transport on microtubules (MTs) for mRNA dynamics in Xenopus oocytes (25, 26).
In oocytes of the frog Xenopus laevis, mRNA transport and localization drive the developmental polarity (27). In particular, restricted expression of Vg1 protein in the vegetal hemisphere of the egg is critical for correct patterning of the embryo (28, 29, 30), making transport of Vg1 mRNA an important model for understanding how maternal molecules are localized to influence pattern and polarity. In other cell types, such as Drosophila oocytes, as well as neurons and yeast cells, the accumulation of mRNAs to specific regions of the cell also ensures asymmetric distributions of mRNAs (31). Transport of Vg1 mRNA to the vegetal cortex of the Xenopus oocyte requires a sequence element in the 3′ untranslated region of Vg1 mRNA termed the “vegetal localization element” (VLE) (32). Because microinjected VLE RNA localizes to the vegetal cortex (32), we refer to it as “localizing RNA”. Vegetal transport of VLE RNA has been shown to rely on both plus-end-directed kinesin and minus-end-directed dynein motors and to incorporate both bidirectional and vegetally directed transport steps (25, 26). However, analysis of transport directionality in vivo has been met with obstacles. Because transport of RNA by molecular motors is shown to occur on the timescales of FRAP experiments, it is necessary to include active transport mechanisms in parameter estimation to fully capture the dynamics of cellular RNA using fluorescence recovery data. Knowledge of parameters such as velocities of motor-RNA complexes, diffusion coefficients of free RNA, and rates of transport between different states are crucial to better understand the timescale of RNA transport and localization. Identifying the mechanisms involved in transport will also be critical to distinguish the activity and regulation of motor proteins such as kinesin and dynein, which move the RNA cargoes in opposite directions along MTs. Importantly, most RNAs do not localize; we refer to RNA that is not actively transported but instead only diffuses as “nonlocalizing RNA”.
Our approach provides insights into the mechanisms of transport for both localizing and nonlocalizing RNA in Xenopus oocytes. Our method shows that RNAs in oocytes treated with nocodazole (which disrupts the cytoskeletal network) may be highly immobile, possibly due to their retention in large granules of RNAs. On the other hand, nonlocalizing β-globin RNAs switch between reaction and diffusion in the cytoplasm. For localizing VLE RNA, we confirm distinct directionality in different regions in the cell as suggested by photoactivation experiments in Gagnon et al. (25). The transport in the vegetal direction is predicted to be faster close to the nucleus, while the effective diffusion is expected to be higher in the lower vegetal cytoplasm. Importantly, our results suggest that some movement in both the animal and vegetal directions occurs throughout the vegetal cytoplasm in Xenopus oocytes. Moreover, moving RNAs are predicted to remain in paused states for extended times, as observed experimentally (33). In addition to intracellular transport in frog oocytes, our techniques for parameter estimation and the calculation of biological quantities apply more generally to understand the contribution of diffusion, active transport, and binding kinetics in various systems.
Materials and Methods
Oocyte microinjection, culture, and FRAP acquisition: RNA synthesis
The tight binding between MS2 bacteriophage coat protein (MCP) and MS2 RNA stem loop (34, 35) allowed us to perform in vivo imaging of RNA transcripts carrying MS2 stem loops that are bound by a chimeric MCP protein fused to a fluorescent mCherry (mCh) protein (36). For this approach, chimeric VLE-MS2 and βG-MS2 RNA transcripts containing MS2 stem loops and either the VLE or nonlocalizing Xenopus β-globin (βG) sequences as well as chimeric mCh-MCP transcripts were synthesized by in vitro transcription, as detailed in Gagnon et al. (25) and Powrie et al. (37). The presence of a nuclear localization signal within the mCh-MCP protein restricts the chimeric protein as in Bertrand et al. (34) to the nucleus, unless bound to RNA molecules carrying MS2 stem loops. Thus, cytoplasmic mCh-MCP is RNA-bound. We note that localizing VLE-MS2 RNA (denoted “VLE RNA”) accumulates at the cortex of Xenopus oocytes (Fig. 2 B; (25)), whereas βG-MS2 RNA (denoted β-globin RNA) and VLE RNA in nocodazole-treated Xenopus oocytes are nonlocalizing because no transport to the cell periphery is observed.
Figure 2.
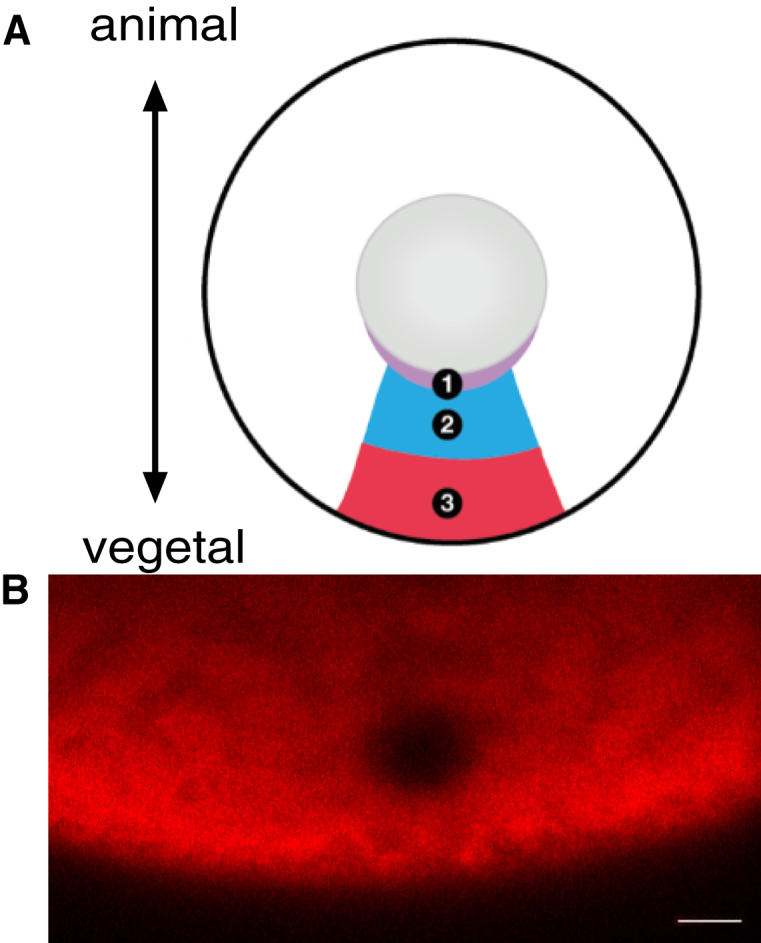
(A) FRAP bleach regions are numbered according to their location: the perinuclear cup (Region 1), the upper vegetal cytoplasm (Region 2), and the lower vegetal cytoplasm (Region 3). (B) Shown is a representative oocyte in which a 5 μm circular ROI of VLE-MS2 RNA bound by MCP-mCh was bleached in the vegetal cytoplasm (Region 3). Scale bars represent 10 μm. To see this figure in color, go online.
Microinjection of Xenopus oocytes
Live stage III albino oocytes were microinjected with 2 nL of 250 nM mCh-MCP RNA and cultured overnight at 18°C to allow expression of chimeric mCh-MCP protein, as described in Gagnon et al. (25) and Powrie et al. (37). Oocytes were next injected with 2 nL of either 250 nM VLE-MS2 and βG-MS2 RNA and after culture for 8 h, oocytes were mounted for imaging as detailed in Powrie et al. (37).
FRAP
FRAP analyses were carried out using an LSM 510 Meta Confocal Laser Scanning Microscope (Carl Zeiss, Oberkochen, Germany) equipped with a 40× water correction C-19 Apochromat objective. Regions for FRAP were identified for each oocyte as follows: Region 1 was 15 μm from the nucleus, Region 2 was 50 μm from the nucleus, Region 3 was 25 μm from the vegetal cortex, and Region 4 was 25 μm from the animal cortex. Within each region, a 5-μm circular region of interest (ROI) was bleached using the 405, 488, 561, and 633 laser lines at 100%. An example of the fluorescence bleach spot for VLE RNA in Region 3 of a wild-type (WT) oocyte is illustrated in Fig. 2 (see Fig. S1 for an example for β-globin RNA). Fluorescence recovery was monitored at 5 s intervals to track VLE-MS2 recovery and 1 s intervals for βG-MS2.
Transport model PDEs
We model the particle dynamics using systems of advection-reaction-diffusion PDEs. In the application to Xenopus RNA dynamics, the variables correspond to concentrations of mRNA and mRNA-motor complexes in different dynamical states. The simplest model we consider assumes that particles can be in one of two states: a population u moving with speed c (e.g., carried by molecular motor proteins to the cell cortex), and a population v diffusing in the cytoplasm with diffusion coefficient d. As in Khuc Trong et al. (16), particles can transition from moving to diffusing, and vice versa, so that the dynamics is described by the PDE system:
| (1a) |
| (1b) |
where β1 is the rate of transition from the moving to the diffusing state, and β2 is the rate of transition from the diffusing to the moving state (see Fig. 3 A). We note that movement is assumed to be one-dimensional (e.g., along a microtubule), while diffusion can occur in two spatial dimensions. We will refer to this model as the “two-state model” from here on. While FRAP experiments do not distinguish between different dynamical states (see Fig. 2 B), our approach allows us to use FRAP recovery curves to estimate transport parameters and rates for each state.
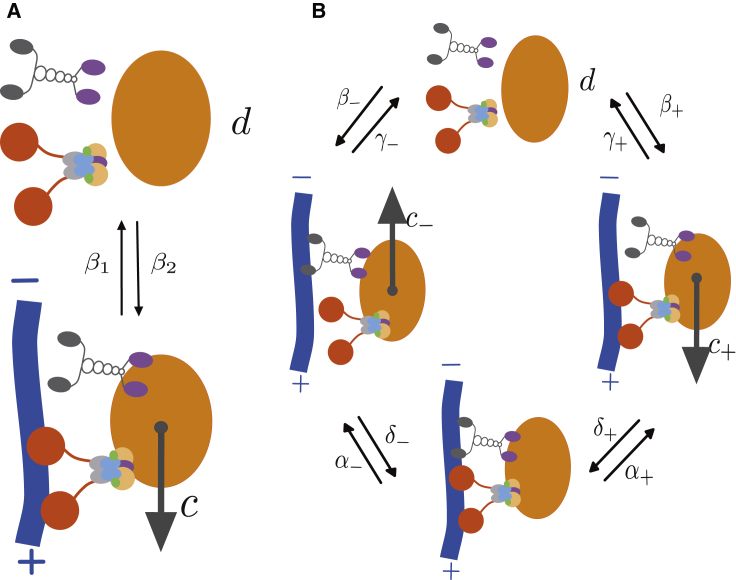
Figure 3.
(A) Cartoon of the two-state model of active transport, consisting of a population of diffusing particles with diffusion coefficient d, and a population of moving particles with velocity c. (B) Cartoon of the four-state model of active transport, consisting of a population of diffusing particles with diffusion coefficient d, a population of particles moving toward the cortex with velocity c+, and one moving toward the nucleus with velocity c−, and a stationary population. To see this figure in color, go online.
To take into account the possibility of bidirectional transport of particles, we also consider a more complex four-state model. In this model, we consider a moving population u+ carried by one type of motor protein (e.g., dynein) to the vegetal cortex, a moving population u− carried by another type of motor protein (e.g., kinesin) to the nucleus, a population v diffusing in the cytoplasm with diffusion coefficient d, and a population w paused on the microtubules. Different mechanisms that may account for the stationary population w are reviewed in Hancock (33). These four states react through binding and unbinding reactions as follows:
| (2a) |
| (2b) |
| (2c) |
| (2d) |
with rates α+, α−, β+, β−, δ+, δ−, γ+, and γ− as in Fig. 3 B. In Xenopus oocytes, assuming that dynein moves the mRNA down toward the cortex and kinesin mostly moves the cargo up to the nucleus (25), the rates β+ and β− can be interpreted as binding rates for dynein and kinesin, respectively, to microtubules, while the rates γ+, and γ− correspond to unbinding rates for dynein and kinesin, respectively, from microtubules (see Table 1).
Table 1.
Fixed Parameters for the Four-State Model, Model 2
| Parameter | Kinesin | Dynein |
|---|---|---|
| Binding rate (s−1) | β− = 5 | β+ = 1.6 |
| Unbinding rate (s−1) | γ− = 1 | γ+ = 0.27 |
To accurately capture the dynamics of particles that are not actively transported (e.g., nonlocalizing β-globin RNA), we also consider the reaction-diffusion system
| (3a) |
| (3b) |
where population u is in the stationary state and population v is diffusing. This model has been previously analyzed in many studies, including Sprague et al. (6).
Postbleach intensity profile approximations
To provide initial conditions for the concentrations of RNA in (1a), (1b)–(3a), (3b), we analyze the FRAP postbleach intensity profiles from Xenopus experiments. The photobleaching process in FRAP is commonly assumed to be an irreversible first-order reaction (1, 3, 5, 10):
where C is the spatial concentration of fluorophores, r denotes the radial position, and α is a bleaching parameter.
The bleaching distribution is assumed to have a Gaussian profile (3):
where re is the effective radius of the distribution. This profile is due to the limitations of bleaching and scanning in FRAP, which lead to what is referred to as a “corona effect” of the bleached region in Weiss (13). The distribution of fluorophore concentration after photobleaching can therefore be described by (1), where K is the bleaching depth parameter.
We focus on the focal plane of the fluorescence distribution in the first frame after photobleach, and fit parameters K, re, and x0 to the initial profile:
| (4) |
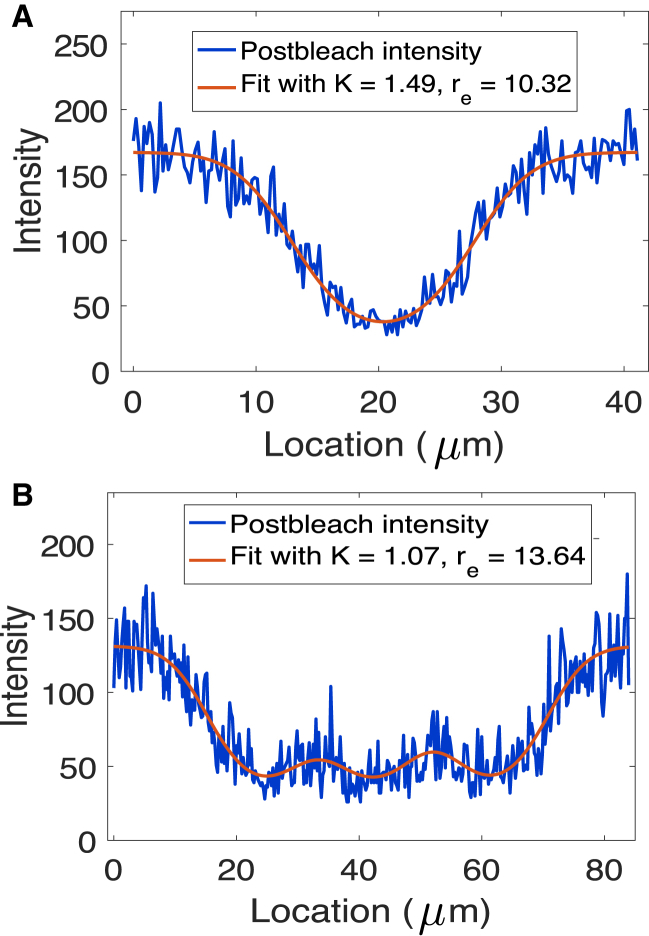
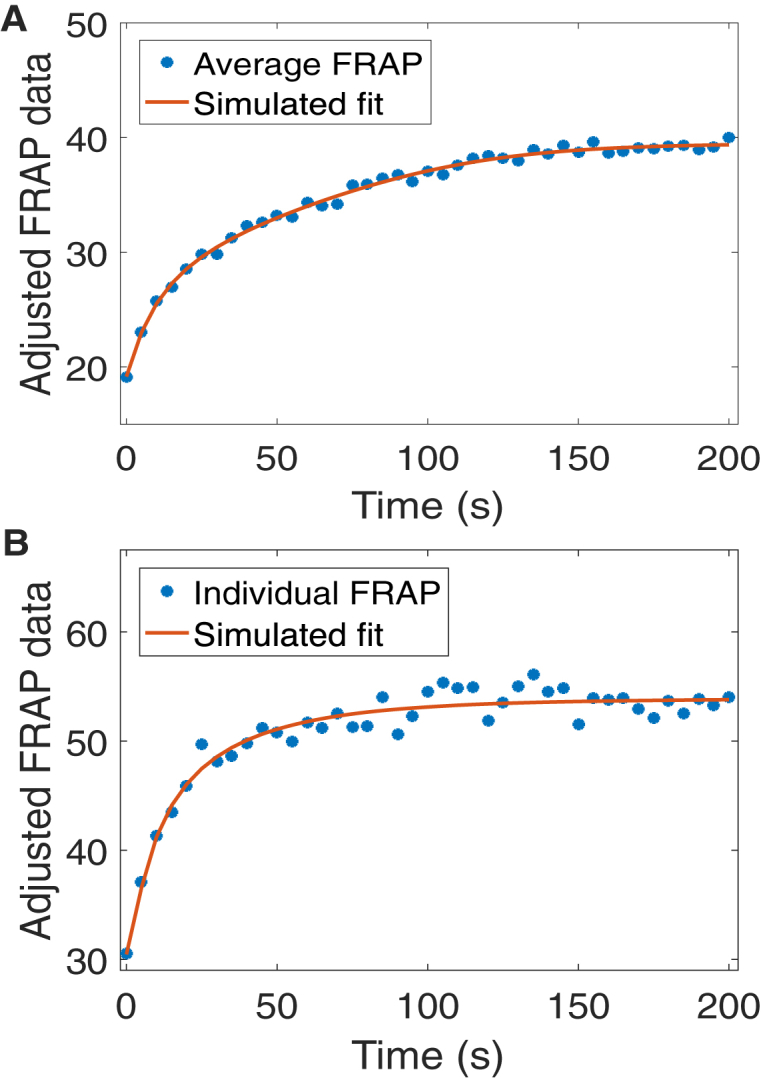
We note that x0 corresponds to the center of the bleach location. Similar to Kang et al. (11), the fit of the postbleach intensity profile to the exponential of a Gaussian is very good, as can be seen in Fig. 4 A.
Figure 4.
Sample fit of FRAP postbleach intensity distribution for VLE RNA (see bleach spot in Fig. 2) with Eq. 4 (A) and for β-globin RNA (see bleach spots in Fig. S1) with Eq. 5 (B). To see this figure in color, go online.
Postbleach profiles indicate that the three bleach spots in the cytoplasm are not clearly separated for FRAP experiments in β-globin RNA oocytes (see Fig. S1). Because parameter estimation is sensitive to the initial condition given by the postbleach profile (see Accounting for the Dynamics during the Photobleach Process is Needed to Estimate the Order of Magnitude of the Diffusion Coefficient), we decided to treat all three spots together in the initial condition to accurately model the photobleach dynamics (see Fig. 4 B). The advantage of the numerical parameter estimation method described in the next section is that it can be applied to experimental data where more than one bleach spot must be considered. The fitting procedure above is repeated for parameters K, re, x0, x1, and x2 using the postbleach distribution model:
| (5) |
An example of a postbleach intensity profile in the nonlocalizing RNA case and the fit to Eq. 5 is provided in Fig. 4 B. The equations for postbleach distribution are modeled in MATLAB (The MathWorks, Natick, MA), and the optimization is carried out using the MATLAB routine nlinfit.
It is worth noting that studies, including Axelrod et al. (3), Braeckmans et al. (5), and Sprague et al. (6), assume uniform and instantaneous photobleaching of the circular area during FRAP. In this uniform disk model, the postbleaching intensity profile is assumed to have a flat circular profile instead of the exponential of a Gaussian in Blonk et al. (4), as this simplifies the analytical calculations in those approaches.
Procedure for FRAP data fitting using transport PDE models
We analyzed the FRAP recovery curves by numerically integrating the model (1a), (1b)–(3a), (3b) using an efficient exponential time-differencing fourth-order Runge-Kutta scheme (38, 39) for time integration coupled with Fourier spectral methods for space discretization (see Supporting Materials and Methods). We assumed a uniform point spread function (1) for detection of fluorescence by the microscope, which means that the observed fluorescence recovery is obtained by integrating the concentrations of particles in all states over the bleach spot. For the two-state model, this implies:
| (6) |
This is a reasonable assumption given that the microscope resolution is much smaller than the radius of the bleach spots in our experiments (8). Because photofading during image acquisition can affect parameter estimation (40), we adjusted the FRAP data by correcting for background fluorescence and dividing the result by the fluorescence intensity of a neighboring ROI at each time point (37, 40) (see details in Supporting Materials and Methods). Parameter estimation was carried out for individual oocyte data or for an average of data from multiple oocytes, as indicated in the text. It is worth noting that the diffuse fluorescence staining in FRAP experiments does not distinguish between different particle populations. The method proposed here provides insight into the contribution of the different dynamical states by fitting the sum of the particle concentrations over the bleach spot to the ensemble FRAP fluorescence.
The model equations and the fit to experimental data were programmed in MATLAB (The MathWorks). The MATLAB routine lsqnonlin was used to perform L2-norm fits of the experimental FRAP data to equations similar to Eq. 6 for the appropriate model. Tests of fitting to FRAP data generated using known parameters for model 1 revealed that the initial guess for the unknown parameters is instrumental in convergence to the true parameter fit. Model fits of the experimental data were therefore preceded by ample parameter sweeps, as in Sprague et al. (6) and Braga et al. (15). For the two-state model, we sampled through values of c, d, β1, and β2 and chose the parameter combinations that yielded the smallest L2-norm difference with the experimental data as initial guesses for the routine lsqnonlin. We used these parameter combinations from all experimental trials for a certain region or type of RNA as initial guesses for multiple starting-point search optimization in MATLAB using MultiStart. This allowed us to reduce the computational cost of the fitting procedure by running the same optimization solver (lsqnonlin) using different initial conditions in parallel on a computer cluster.
The parameter estimation procedure is similar when using the reaction-diffusion model (model 3). For the four-state model (model 2), the estimates for speed c and diffusion coefficient D using model 1 are used as initial guesses for c+ and d in this more complex model. Available parameter values, such as the binding and unbinding rates for kinesin and dynein in Klumpp and Lipowsky (41) and Müller et al. (42), are set constant to further reduce the size of the parameter sweep (see Table 1). Table 1 illustrates a choice of the binding/unbinding rates where dynein moves cargo down to the periphery, and kinesin up to the nucleus, given the evidence for the upper cytoplasm of Xenopus oocytes (25); however, different assumptions on the motors carrying the RNA in either direction do not significantly alter the parameter estimates. Sweeps of the parameter space are then performed for the remaining five model parameters (c−, α+, α−, δ+, and δ−), and then refined in local parameter regions that yield best data fits. This ample parameter sweep provides initial guesses for the optimization; even though different initial conditions may lead to different estimates of the kinetic rates, the parallel computation setup of our optimization allows us to identify multiple initial conditions that lead to the smallest least squares residuals and consistent estimates of velocities and diffusion.
Results and Discussion
The FRAP parameter estimation method is validated by fitting PDE model simulations of synthetic FRAP curves
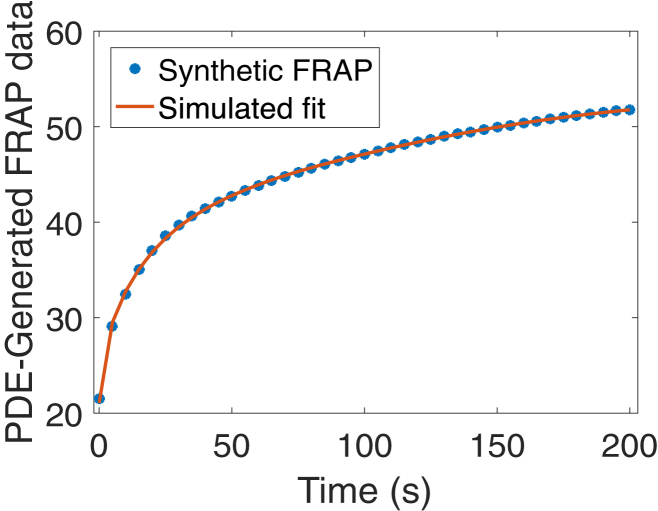
To ensure the accuracy of our parameter estimation procedure, we tested our parameter estimation methods on synthetic FRAP data. Having fixed parameters, (1a), (1b) and (2a), (2b), (2c), (2d) were ran with a uniform disk initial condition to generate synthetic FRAP recovery curves. These curves were then used to estimate parameters using the procedure outlined in Materials and Methods, assuming unknown parameters and using the parameter sweep approach to generate initial guesses. We compared the results with the original fixed parameters, which were taken from a previous experimental run for VLE RNA in Region 1. A fit of the PDE-generated synthetic data with the two-state model (model 1) is illustrated in Fig. 5. Fig. S2 shows that estimates of the speed to cortex c+, diffusion coefficient d, and effective velocity v (see derivation in Supporting Materials and Methods) are almost identical to the originally estimated parameters. This confirms that parameter estimates for velocities and diffusion can be recovered using the proposed parameter sweep and multiple start-point optimization methods. We note that the parameters used in generating synthetic data are different from the ones we report for real FRAP data because we used the uniform disk initial condition for these validation tests.
Figure 5.
Sample synthetic FRAP data generated using (1a), (1b) and parameters c = 0.031 μm/s, d = 0.061 μm2/s, β1 = 4e−13 s−1, and β2 = 0.007 s−1 were fit using our parameter estimation procedure. The recovered parameters are c = 0.029 μm/s, d = 0.06 μm2/s, β1 = 1e−12 s−1, and β2 = 0.007 s−1. To see this figure in color, go online.
Parameter estimates were further validated using recovery curves generated from a continuous-time Markov chain in which the states correspond to the populations in model 2 (see Supporting Materials and Methods). Particles are assumed to switch between states using transition rates as in model 2, and the times spent in each state are assumed to be exponential random variables with rates given by the transition parameters. Instead of adding Gaussian noise to simulated recovery curves as in Braga et al. (7), this stochastic model generates more realistic noisy FRAP recovery curves (see synthetic data and fits in Fig. S3). Parameter estimation on these FRAP curves showed that increasing the number of particles modeled yielded increasingly better recoveries for the key parameters (see Table S1).
Numerical fitting of FRAP data for nonlocalizing molecules yields consistent estimates of diffusion coefficients and fractions
We first apply the parameter fitting procedure to FRAP data for particles that are not actively transported in the cell. The attempts to fit FRAP data for β-globin RNA using the two-state active transport model (model 1) either fail or provide inconsistent results across trials. The parameter sweeps result in initial guesses for the unknown parameters that overestimate velocity c and underestimate diffusion coefficient d, leading to fits with no useful biological conclusions. This suggests that stationary states are essential in the dynamics of β-globin RNA in the cytoplasm, and that active transport is unlikely to occur for this nonlocalizing RNA.
We therefore perform parameter estimation for individual oocyte FRAP data using reaction-diffusion (3a), (3b) and initial conditions (5) corresponding to three bleach spots (see Fig. 4 B). This approach yields consistent results for diffusion coefficient d, which averages 2 μm2/s (with standard deviation 1.3 μm2/s) across nine oocyte trials in an experimental set, and 2.8 μm2/s (with standard deviation 2 μm2/s) for the second set shown in Fig. 6 A. Sample fits of the data are included in Fig. S4. These predictions allow us to analyze the mobility of RNA, because the fractions of particles in the diffusing and stationary states for model 3 are simply given by:
| (7a) |
| (7b) |
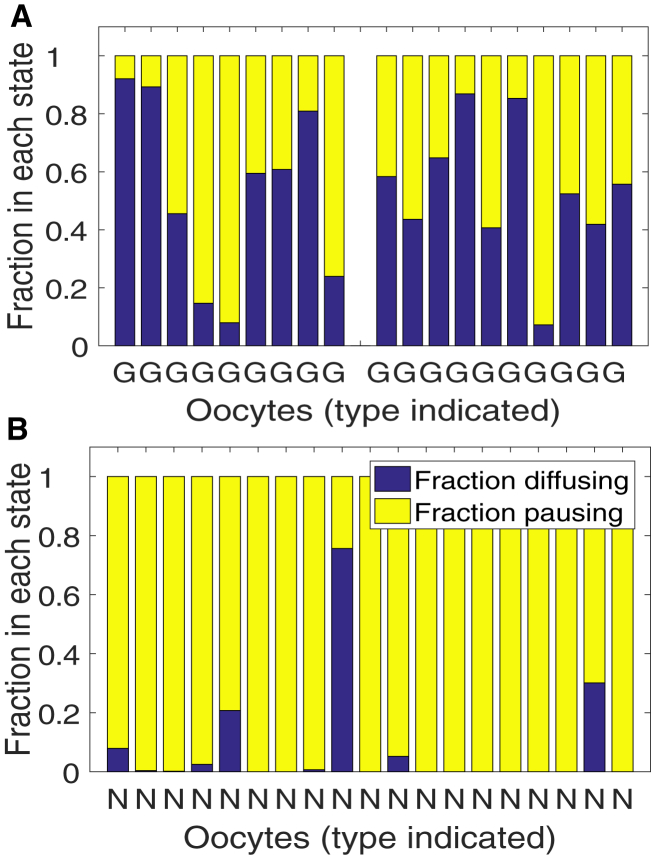
Here we assume that the concentration of RNA particles has reached steady state (see Supporting Materials and Methods) throughout the time course of a FRAP experiment. The estimates for rates β1 and β2, together with (7a), (7b), suggest that nonlocalizing β-globin RNA does not solely diffuse, and may instead spend on average ∼47% of time (with standard deviation 32%) in a paused state for the first set, and 46% of time (with standard deviation 23%) for the second set. The predicted fractions of RNA in each state are displayed in the bar graph in Fig. 6 A, and similar results are provided in Fig. S5 for additional sets of oocytes.
Figure 6.
Predicted fractions of (A) nonlocalizing β-globin RNA (G) in sets of 9 and 10 untreated oocytes and (B) VLE RNA in 19 nocodazole-treated oocytes (N) in diffusing and stationary states for individual oocyte trials. Parameter estimation is performed with a three-bleach spot initial condition for β-globin RNA. To see this figure in color, go online.
The reaction-diffusion model (model 3) is also applied to individual nocodazole-treated oocyte FRAP recoveries. This predicts an average RNA diffusion estimate of 2.3 μm2/s (with standard deviation 1.38 μm2/s), similar to the estimate for nonlocalizing β-globin RNA. At equilibrium, an average of 92.45% of particles (with standard deviation 18.4%) are stationary, compared to ∼46% in the β-globin RNA case (see Fig. 6). We note that the distinct diffusing behavior predicted in a few of the oocytes in Fig. 6 B is a result of the diluted fluorescence signal under nocodazole treatment, where there is a lower effective concentration of mRNA distributed throughout the cytoplasm rather than an accumulation at the cell periphery. These results suggest that, in nocodazole-treated oocytes, active transport of VLE RNA is blocked due to microtubule impairment, and diffusion may be restricted due to the large size of VLE RNA granules. We observe that the reaction dominant simplification of the reaction-diffusion model (model 3) (derived in (6)) is employed for diffusion coefficient estimates for VLE RNA in Gagnon et al. (25). However, mRNAs in healthy Xenopus oocytes are believed to be actively transported by molecular motor proteins (25). As a result, in the next section we consider active transport as a key mechanism in parameter estimation using FRAP experiments for VLE RNA in untreated oocytes.
The application of FRAP parameter estimation to actively transported particles, localizing VLE RNA, using advection-reaction-diffusion models reveals mechanistic differences between different cytoplasm regions
VLE RNA localizes at the vegetal cortex of Xenopus oocytes, and its dynamics are driven by both diffusion and transport by molecular motor proteins. Therefore, we first fit FRAP data from three regions in the vegetal cytoplasm (see Materials and Methods and Fig. 2 A) to the two-state model (model 1). Using averages of FRAP data from five oocytes in each region, we estimate speed c, diffusion coefficient d, unbinding rate β1, and binding rate β2 (see Tables 2 and S2 and fit in Fig. 7 A). We note that estimates of velocity c and diffusion coefficient d are fairly consistent across regions in the cytoplasm. The RNA is predicted to be moving toward the cortex in Region 1 (upper vegetal cytoplasm), while in Regions 2 and 3 (mid- and lower vegetal cytoplasm), a higher proportion of particles are diffusing. This is consistent with the hypothesis in Gagnon et al. (25), which states that transport by motor proteins in the direction of the vegetal cortex is more effective closer to the nucleus (Regions 1 and 2).
Table 2.
Estimated Parameters for FRAP WT Average Data
| Parameter | Region |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1I | 1II | 1III | 2I | 2II | 2III | 3I | 3II | 3III | |
| c (μm/s) | 0.05 | 0.12 | 0.08 | 0.09 | 0.1 | 0.12 | 0.07 | 3e−4 | 0.04 |
| d (μm2 s−1) | 0.26 | 1.63 | 0.37 | 1.42 | 1.02 | 0.99 | 0.83 | 2.64 | 1.85 |
| v (μm/s) | 0.05 | 0.12 | 0.05 | 0.02 | 0.1 | 0.1 | 0.002 | 0.0001 | 4e−6 |
| σ2 (μm2 s−1) | 5e−12 | 1e−7 | 0.36 | 3.03 | 0.005 | 0.37 | 8.53 | 2.62 | 3.71 |
Average data is based on three sets of five oocytes each using model 1 for VLE RNA, for Regions 1–3 in the cytoplasm (see Fig. 2A). The superscripts I, II, and III correspond to the index of the average FRAP data set under consideration.
Figure 7.
(A) Average FRAP data for VLE RNA in Region 2 in five WT oocytes is fit with model 1; estimated parameters are c = 0.09 μm/s, d = 1.42 μm2/s, β1 = 0.003 s−1, and β2 = 8e−4 s−1. (B) Sample FRAP data for VLE RNA in Region 3 in an individual WT oocyte is fit with model 2; estimated parameters are c+ = 0.51 μm/s, c− = 0.91 μm/s, d = 2.29 μm2/s, α+ = 1e−5 s−1, α− = 2e−5 s−1, δ+ = 0.1 s−1, and δ− = 0.02 s−1. To see this figure in color, go online.
As outlined in Materials and Methods, we then use these estimates to inform initial guesses for velocity c+ in the vegetal cortex direction and diffusion d in the four-state model (model 2). We perform ample parameter sweeps for rates α+, α−, δ+, δ−, and velocity c− in the nucleus direction. Parameter estimation for individual FRAP curves yields consistent estimates, and the results for averaged FRAP trial data are summarized in Table 3. We note that the diffusion coefficients are consistent across regions for all sets of oocytes, and that the velocity toward the animal pole is consistently higher in Region 3 compared to Regions 1 and 2. A sample FRAP data fit for an individual oocyte is provided in Fig. 7 B. Mobility of the VLE RNA can be investigated using the predicted fractions of particles in each state derived in Supporting Materials and Methods. Our results confirm the hypothesis that bidirectional transport plays an important role in the dynamics of VLE RNA (25), and further suggest that particles might spend on average ∼72.5% of time in a paused state (with standard deviation 21%; see Fig. S6). The RNA in nocodazole-treated oocytes is predicted to spend most of the time in a paused state, consistent with the results of model 3 in Fig. 6 B.
Table 3.
Estimated Parameters for FRAP WT Average Data
| Parameter | Region |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1I | 1II | 1III | 2I | 2II | 2III | 3I | 3II | 3III | |
| c+ (μm/s) | 0.37 | 1.06 | 0.08 | 1.16 | 0.9 | 0.18 | 2.39 | 0.62 | 0.27 |
| c− (μm/s) | 0.04 | 4e−9 | 4e−6 | 0.15 | 0.43 | 0.009 | 2.93 | 1.96 | 0.89 |
| d (μm2 s−1) | 1.82 | 9.85 | 6.98 | 7.45 | 7.446 | 3.41 | 1.51 | 9.9 | 0.95 |
| v (μm/s) | 0.07 | 0.12 | 0.05 | 0.14 | 0.08 | 0.077 | −0.39 | −0.22 | −0.18 |
| σ2 (μm2 s−1) | 0.39 | 1.22 | 0.38 | 1.36 | 1.68 | 0.67 | 4.18 | 6.5 | 2.42 |
Average data based on three sets of five oocytes each using model 2 for VLE RNA, for Regions 1–3 in the cytoplasm (see Fig. 2A). The superscripts I, II, and III correspond to the index of the average FRAP data set under consideration. The sets considered are the same as used for parameter estimation using model 1 in Table 2.
We note that the ample parameter sweeps and local refinements allow us to determine best choices for initial guesses in parameter estimation. Optimizations carried out in parallel for these guesses yield best parameter fits for velocities and the diffusion coefficient that are consistent across trials. While the estimated kinetic rates have a larger variance across individual oocyte fits, they yield consistent biological predictions when combined in relevant quantities such as fractions of particles in each state and asymptotic velocity and diffusion (next section).
Derivation of effective velocities, expected run lengths and times on microtubules, suggests avenues for transport PDE model selection
Given that particle dynamics can be captured using multiple PDE models of active transport, we investigate the question of model selection through the example of localizing RNA in Xenopus oocytes. The analysis of these PDE systems in Supporting Materials and Methods allows us to compute and compare quantities of interest predicted by the two-state model (model 1) and the four-state model (model 2). These quantities include the effective velocity and diffusion of a particle for large time, the percentage of particles in each state at equilibrium, and the expected run length and time of motor-cargo complexes on microtubules (that is, how far and how long a motor travels on average before dissociating from a microtubule). These asymptotic and dissociation-based quantities are mentioned in the experimental literature (43) and are thus very useful in evaluating models of active transport.
The effective velocity v and effective spread σ2 for the two-state model are the actual long-term speeds and diffusion of particles given the transition rates between particle states. These quantities are given by (see Supporting Materials and Methods for derivation):
| (8) |
| (9) |
Equivalent quantities can be calculated for the four-state model using Mathematica (44) to yield more complex expressions that depend on all the model parameters. These asymptotic quantities are then evaluated using estimated parameters for averaged FRAP data: the results are summarized in Tables 2 and 3. For both the two-state and the four-state models, we note that the effective velocity is either consistently smaller (two-state model) or negative indicating net movement in the animal pole direction (four-state model) for Region 3 in the lower cytoplasm. The effective diffusion also shows a consistent increase in Region 3. Both models therefore support the hypothesis of faster movement in the upper vegetal cytoplasm (Regions 1–2) and higher spread of particles (suggesting bidirectional transport) in the lower vegetal cytoplasm (Region 3). The observations in Tables 2 and 3 show results for average FRAP data from different sets of oocytes, but the differences between regions hold for parameter estimates in individual FRAP data trials as well. Given that the FRAP bleaching experiments are performed at the same time for all three regions in the cytoplasm, we do not expect these differences to be a result of experimental variability.
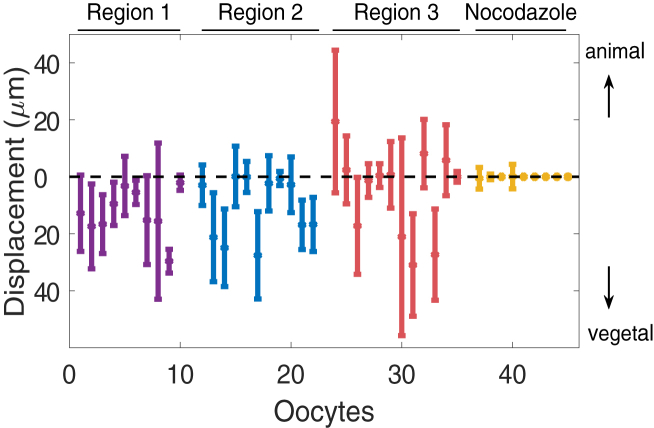
The derivation of the effective velocity and diffusion for large time also provides a tool for comparison of mobility of localizing VLE RNA with mobility of RNA in cells treated with nocodazole. Fig. 8 shows predictions for these particle displacement quantities when fitting both types of data to the four-state model (model 2). We note that the nocodazole-treated trials (Fig. 8, yellow) predict almost no net movement, as is expected when the microtubule structure is disrupted. In untreated oocytes, the transport to the vegetal cortex is more significant close to the nucleus (Region 1, purple) than close to the vegetal cortex (Region 3, red). While we predict that the majority of untreated oocytes spend similar amounts of time in transport in the animal and vegetal directions (see Fig. S6), Fig. 8 also incorporates the velocity predictions to highlight directional bias through effective velocity and diffusion calculations.
Figure 8.
Predicted effective displacement and spread at T = 200 s using the four-state model for individual FRAP data in healthy and nocodazole-treated (N) oocytes. The distance between the dots and the zero axis corresponds to the predicted average displacement of a particle toward the nucleus or the vegetal cortex, and error bars correspond to the predicted spread of displacement due to diffusion for each trial. Purple, blue, and red correspond to Regions 1, 2 and 3, respectively, as in Fig. 2A; yellow corresponds to nocodazole-treated oocytes. To see this figure in color, go online.
The low order-of-magnitude estimates for binding/unbinding rates using the two-state model (see Table S2) would lead to the unlikely suggestion that either all particles are diffusing or they are all being transported at a given location (see (7a), (7b)). By contrast, the four-state model predicts a more uniform distribution of particles in different states (see Fig. S6), with a slight bias to a higher percentage of particles moving in Regions 1 and 2. This suggests that the additional complexity of considering another moving population and a stationary state in the four-state model (model 2) is necessary to model particle mobility in these experiments.
In addition, we compare predictions of the expected run lengths and times of an RNA particle on microtubules to experimental results. The average moving run times and the distances for the two-state model (1/β1, respectively, c/β1) are very large compared to experimental observations of the processivity of molecular motor proteins. Kinesin and dynein motors have been shown to have average run lengths of roughly 1–2 μm (45, 46), and velocities of ∼0.5–1 μm/s (47), so that they are expected to spend a few seconds on an individual microtubule filament. These run lengths may be larger when multiple motors are attached to and transport cargo (41, 42). The time and distance spent by a particle on a microtubule for the four-state model are given by (see Supporting Materials and Methods):
The predictions for these moving states quantities given estimated parameters for experimental FRAP data from individual oocytes are displayed in Fig. 9. We note that run times are on the order of seconds, and run lengths are on the order of micrometers, as expected from previous experimental measurements (42). It is also worth noting that the results for untreated oocytes (Fig. 9) further support the hypothesis of bidirectional transport of RNA in the cytoplasm (25), with a bias to movement in the vegetal cortex direction. In Gagnon et al. (25), this hypothesis was revealed through a more complicated photoactivation experiment, because the standard FRAP data analysis did not account for active transport processes. In the case of nocodazole-treated oocytes (Fig. 9, yellow), both run times and lengths are predicted to be considerably shorter in both transport directions.
Figure 9.
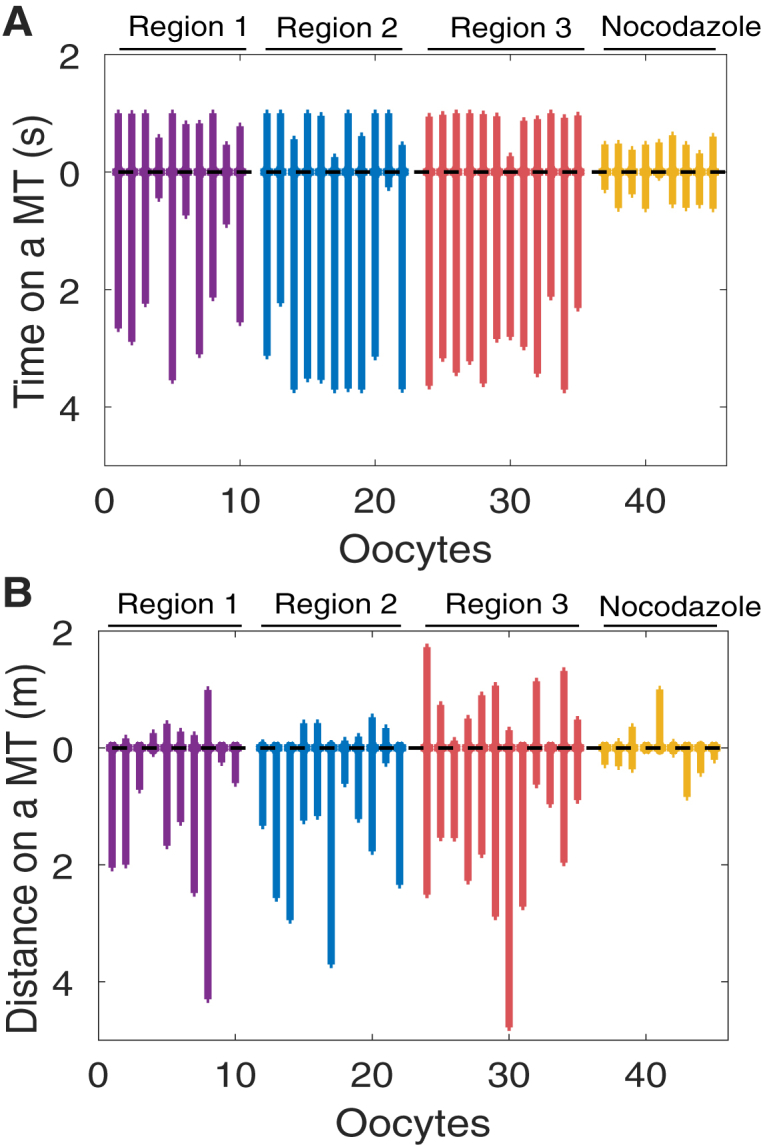
Predicted expected run time (A) and length (B) spent before dissociating from a microtubule for VLE RNA. The length of the segment extending up corresponds to the time or distance for movement up a MT toward the nucleus, and the length of the segment extending down corresponds to the time or distance for movement down a MT toward the vegetal cortex. Purple, blue, and red correspond to Regions 1, 2, and 3, respectively, as in Fig. 2A; yellow corresponds to nocodazole-treated oocytes. To see this figure in color, go online.
Accounting for the dynamics during the photobleach process is needed to estimate the order of magnitude of the diffusion coefficient
In analyzing FRAP recovery curves, the initial condition for (1a), (1b)–(3a), (3b) can play a significant role on parameter estimates. The uniform disk model studied in Axelrod et al. (3) and Braeckmans et al. (5) assumes that the photobleach and dynamics during the photobleach process are instantaneous. The postbleaching intensity is thus assumed to have a flat circular disk profile, which eases the derivation of analytical solutions for FRAP recovery. We compared the results of our parameter estimation methods for β-globin nonlocalizing RNA using the uniform disk model with results obtained using a Gaussian initial condition of the form and with results using the spatial fluorescence distribution after photobleach (fit with a biophysically justified exponential of Gaussian, see Fig. 4).
Fig. S7 shows that the diffusion coefficient estimates for the same set of five oocytes are sensitive to the initial condition. The uniform disk profile assumption yields diffusion coefficients 35 times smaller on average than the ones that use spatial information from postbleach intensity profiles (see additional estimates in Fig. S8, top). Similarly, uniform disk model estimates of the diffusion coefficient in particles engaged in active transport (localizing VLE RNA) were on average 33 times smaller than the postbleach profile ones for individual FRAP data (see Fig. S8, center). These observations indicate that the assumption of instantaneous dynamics during the photobleach process leads to significant underestimation of the diffusion coefficient, as previously noted and explored in multiple studies (7, 9, 10, 11, 13). This suggests that a more practical approach for FRAP data analysis consists of using the spatial distribution of fluorescence from the first postbleach image as the initial condition for the FRAP dynamical equations (1, 8, 9, 11, 14).
Binding rates estimates are also believed to be affected by the assumption of instantaneous diffusion during photobleaching (10). Our tests using advection-reaction-diffusion models such as (1) and (2) reveal similar estimates for velocities toward the vegetal cortex (c and c+) for the two initial conditions. However, estimates of velocities in the animal pole direction, as well as some transport rates, are affected by the uniform disk model assumption. Predictions of the speed of transport c− in the animal pole direction in Region 3 are underestimated when the bleaching dynamics is assumed to be instantaneous (see Fig. S8, bottom). This suggests that the photobleach process should be taken into account to obtain more accurate orders-of-magnitude estimates for model parameters.
Conclusions
We have presented a numerical approach to parameter estimation using FRAP recovery data for models of active transport. These methods apply to intracellular dynamics in any organism where directed movement (e.g., by molecular motor proteins) is believed to play a key role in particle localization (see Fig. 3). The advantage of the proposed method is that it can be applied to any FRAP bleach spot geometry, it does not require normalization of the FRAP data, and it can take into account the postbleach intensity profile distribution. This approach allows us to determine transport parameters for different particle states (active transport, diffusion, etc.) even though FRAP data does not distinguish between these populations. As in Beaudouin et al. (14) and Braga et al. (15), the model equations we consider cannot be solved analytically ((1a), (1b) and (2a), (2b), (2c), (2d)) or have a complex initial condition geometry ((3a), (3b) with initial condition Eq. 5). This motivates the use of efficient numerical integration for systems of advection-reaction-diffusion PDEs (38, 39), and of large parameter sweeps for the model parameters. The computational cost of both these parameter sweeps and optimization with multiple initial conditions is significantly reduced through the use of parallel computation. The method is validated using FRAP recovery curves simulated with PDE models (Figs. 5 and S2) as well as with continuous-time Markov chain models of the dynamical processes (Fig. S3).
Initial conditions for these dynamical systems have been shown to be affected by the temporal limitations of bleaching and scanning in confocal FRAP experiments (13). We used the experimental spatial distribution of fluorescence right after photobleaching to take into account the dynamics that may occur during the bleaching process. In our experimental setup, these initial postbleach profiles were well described by the exponential of a Gaussian (Fig. 4). Our results suggest that failing to account for the postbleach dynamics in our experiments underestimates diffusion coefficients 20- to 30-fold, and can have an impact on the order of magnitude of parameters such as velocities and rate constants. This observation is similar to conclusions in studies of diffusion and binding-diffusion models, where the assumption of negligible diffusion during bleaching leads to significant underestimation of the magnitude of the diffusion coefficient (11, 13).
While analytical solutions for PDE models of active transport are not available, we provide rigorous mathematical derivations for solutions of these systems for large time (Supporting Materials and Methods). This allows us to obtain expressions for the effective velocity and diffusion of a particle for large times, given bidirectional movement, diffusion, and binding dynamics in an arbitrary number of states. These quantities correspond to the bulk movement and diffusion of the particles given their transition rates between states, and provide a useful comparison to observed timescales of intracellular movement. Model selection is facilitated by the derivations of fractions of particles in each state, as well as of expected run times and lengths of cargo on microtubules (Supporting Materials and Methods). Knowledge of biologically relevant timescales and length scales for microtubule travel provides comparison and validation for the models of active transport appropriate in different experimental settings (Fig. 9). This is particularly important in applications where the regime of the parameter space is not known, so that simplifications of the PDE models as considered in Sprague et al. (6) are difficult. For these situations, we propose using general PDE models that build up to the complete range of mechanisms that are believed to influence particle dynamics. These models can then be further validated and compared using derivations of biological quantities of relevance as described above.
We applied the methods described here to study RNA dynamics using FRAP data from Xenopus oocytes. Our results for effective particle speed and diffusion confirm the differences in dynamics between localizing VLE RNA and nonlocalizing RNA (Fig. 8). Moreover, this approach confirms that distinct kinetics and transport directionality can be expected for RNA transport in different cytoplasmic regions of a single cell (25). We provide further evidence that bidirectional transport occurs in all regions of the cytoplasm (Fig. 9), but the different velocities of the molecular motor proteins in different areas of the cell (Fig. 2 A) suggest that vegetal transport has a more clear directional bias in the upper vegetal cytoplasm (Regions 1 and 2) than in the lower vegetal cytoplasm (Region 3). This is consistent with the finding that RNA is transported by kinesin motors on a bidirectional array of microtubules close to the vegetal cortex (26). Parameter estimates for distinct cytoplasm regions will allow for accurate two-dimensional simulations of the transport models similar to Khuc Trong et al. (16), with movement restricted to the microtubule cytoskeleton studied in Messitt et al. (26). This approach would provide a direct comparison with experimentally observed patterns of RNA localization, as well as tools for better understanding the spatial and temporal regulation of different motor proteins in various areas of the cell.
Our methods for extracting velocity, diffusion, and binding rate information from FRAP recovery data are broadly applicable to other systems where active transport is involved in intracellular dynamics, such as mRNA localization in Drosophila oocytes (48) or neurofilament transport along axons in neurons (19). The numerical approach to estimate parameters based on FRAP data can be applied to any biomolecules that are believed to undergo diffusion, active transport, and binding kinetics (see Supporting Material for sample code). In addition, the modeling and parameter estimation of FRAP experiments can also be extended to complementary experiments such as fluorescence correlation spectroscopy and photoactivation, which would provide additional validation of parameters for transport mechanisms.
Author Contributions
M.-V.C. developed the analytical tools, analyzed the data, and wrote the manuscript. B.S. designed the research and contributed to the analytical tools. J.A.K. performed the FRAP imaging and initial analyses to obtain the raw data. J.A.G. performed design of live cell imaging, clone construction, preparation of labeled RNAs, and microinjection. K.L.M. led the design of live cell imaging.
Acknowledgments
Part of this research was conducted using computational resources and services at the Center for Computation and Visualization, Brown University.
M.-V.C. and B.S. were partially supported by NSF grant No. DMS-1408742. This work was supported in part by grant No. GM071049 to K.L.M. from the NIH. J.A.G. was a predoctoral trainee supported in part by grant No. T32-GM07601 from the NIH.
Editor: Anne Kenworthy.
Footnotes
Supporting Materials and Methods, Supporting Data, eight figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30286-2.
Supporting Citations
References (49, 50) appear in the Supporting Material.
Supporting Material
References
- 1.Lorén N., Hagman J., Braeckmans K. Fluorescence recovery after photobleaching in material and life sciences: putting theory into practice. Q. Rev. Biophys. 2015;48:323–387. doi: 10.1017/S0033583515000013. [DOI] [PubMed] [Google Scholar]
- 2.McNally J.G. Quantitative FRAP in analysis of molecular binding dynamics in vivo. Methods Cell Biol. 2008;85:329–351. doi: 10.1016/S0091-679X(08)85014-5. [DOI] [PubMed] [Google Scholar]
- 3.Axelrod D., Koppel D.E., Webb W.W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976;16:1055–1069. doi: 10.1016/S0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blonk J., Don A., Birmingham J. Fluorescence photobleaching recovery in the confocal scanning light microscope. J. Microsc. 1993;169:363–374. [Google Scholar]
- 5.Braeckmans K., Peeters L., Demeester J. Three-dimensional fluorescence recovery after photobleaching with the confocal scanning laser microscope. Biophys. J. 2003;85:2240–2252. doi: 10.1016/s0006-3495(03)74649-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sprague B.L., Pego R.L., McNally J.G. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Braga J., Desterro J.M., Carmo-Fonseca M. Intracellular macromolecular mobility measured by fluorescence recovery after photobleaching with confocal laser scanning microscopes. Mol. Biol. Cell. 2004;15:4749–4760. doi: 10.1091/mbc.E04-06-0496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jonasson J.K., Lorén N., Rudemo M. A pixel-based likelihood framework for analysis of fluorescence recovery after photobleaching data. J. Microsc. 2008;232:260–269. doi: 10.1111/j.1365-2818.2008.02097.x. [DOI] [PubMed] [Google Scholar]
- 9.Mueller F., Wach P., McNally J.G. Evidence for a common mode of transcription factor interaction with chromatin as revealed by improved quantitative fluorescence recovery after photobleaching. Biophys. J. 2008;94:3323–3339. doi: 10.1529/biophysj.107.123182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kang M., Day C.A., DiBenedetto E. A generalization of theory for two-dimensional fluorescence recovery after photobleaching applicable to confocal laser scanning microscopes. Biophys. J. 2009;97:1501–1511. doi: 10.1016/j.bpj.2009.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kang M., Day C.A., Kenworthy A.K. A quantitative approach to analyze binding diffusion kinetics by confocal FRAP. Biophys. J. 2010;99:2737–2747. doi: 10.1016/j.bpj.2010.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sadegh Zadeh K., Montas H.J. A class of exact solutions for biomacromolecule diffusion-reaction in live cells. J. Theor. Biol. 2010;264:914–933. doi: 10.1016/j.jtbi.2010.03.028. [DOI] [PubMed] [Google Scholar]
- 13.Weiss M. Challenges and artifacts in quantitative photobleaching experiments. Traffic. 2004;5:662–671. doi: 10.1111/j.1600-0854.2004.00215.x. [DOI] [PubMed] [Google Scholar]
- 14.Beaudouin J., Mora-Bermúdez F., Ellenberg J. Dissecting the contribution of diffusion and interactions to the mobility of nuclear proteins. Biophys. J. 2006;90:1878–1894. doi: 10.1529/biophysj.105.071241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Braga J., McNally J.G., Carmo-Fonseca M. A reaction-diffusion model to study RNA motion by quantitative fluorescence recovery after photobleaching. Biophys. J. 2007;92:2694–2703. doi: 10.1529/biophysj.106.096693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khuc Trong P., Doerflinger H., Goldstein R.E. Cortical microtubule nucleation can organise the cytoskeleton of Drosophila oocytes to define the anteroposterior axis. eLife. 2015;4:e06088. doi: 10.7554/eLife.06088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen J., Lippincott-Schwartz J., Liu J. Intracellular spatial localization regulated by the microtubule network. PLoS One. 2012;7:e34919. doi: 10.1371/journal.pone.0034919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jung P., Brown A. Modeling the slowing of neurofilament transport along the mouse sciatic nerve. Phys. Biol. 2009;6:046002. doi: 10.1088/1478-3975/6/4/046002. [DOI] [PubMed] [Google Scholar]
- 19.Li Y., Brown A., Jung P. Deciphering the axonal transport kinetics of neurofilaments using the fluorescence photo-activation pulse-escape method. BMC Neurosci. 2014;15(Suppl. 1):132. doi: 10.1088/1478-3975/11/2/026001. [DOI] [PubMed] [Google Scholar]
- 20.Newby J.M., Bressloff P.C. Quasi-steady state reduction of molecular motor-based models of directed intermittent search. Bull. Math. Biol. 2010;72:1840–1866. doi: 10.1007/s11538-010-9513-8. [DOI] [PubMed] [Google Scholar]
- 21.Newby J., Bressloff P.C. Random intermittent search and the tug-of-war model of motor-driven transport. J. Stat. Mech. 2010;2010:P04014. [Google Scholar]
- 22.Reed M.C., Venakides S., Blum J.J. Approximate traveling waves in linear reaction-hyperbolic equations. SIAM J. Appl. Math. 1990;50:167–180. [Google Scholar]
- 23.Friedman A., Craciun G. Approximate traveling waves in linear reaction-hyperbolic equations. SIAM J. Math. Anal. 2006;38:741–758. [Google Scholar]
- 24.Friedman A., Bei H. Uniform convergence for approximate traveling waves in linear reaction-hyperbolic systems. Indiana Univ. Math. J. 2007;56:2133–2158. [Google Scholar]
- 25.Gagnon J.A., Kreiling J.A., Mowry K.L. Directional transport is mediated by a Dynein-dependent step in an RNA localization pathway. PLoS Biol. 2013;11:e1001551. doi: 10.1371/journal.pbio.1001551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Messitt T.J., Gagnon J.A., Mowry K.L. Multiple kinesin motors coordinate cytoplasmic RNA transport on a subpopulation of microtubules in Xenopus oocytes. Dev. Cell. 2008;15:426–436. doi: 10.1016/j.devcel.2008.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Medioni C., Mowry K., Besse F. Principles and roles of mRNA localization in animal development. Development. 2012;139:3263–3276. doi: 10.1242/dev.078626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dale L., Matthews G., Colman A. Secretion and mesoderm-inducing activity of the TGF-β-related domain of Xenopus Vg1. EMBO J. 1993;12:4471–4480. doi: 10.1002/j.1460-2075.1993.tb06136.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thomsen G.H., Melton D.A. Processed Vg1 protein is an axial mesoderm inducer in Xenopus. Cell. 1993;74:433–441. doi: 10.1016/0092-8674(93)80045-g. [DOI] [PubMed] [Google Scholar]
- 30.Birsoy B., Kofron M., Heasman J. Vg1 is an essential signaling molecule in Xenopus development. Development. 2006;133:15–20. doi: 10.1242/dev.02144. [DOI] [PubMed] [Google Scholar]
- 31.Holt C.E., Bullock S.L. Subcellular mRNA localization in animal cells and why it matters. Science. 2009;326:1212–1216. doi: 10.1126/science.1176488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mowry K.L., Melton D.A. Vegetal messenger RNA localization directed by a 340-nt RNA sequence element in Xenopus oocytes. Science. 1992;255:991–994. doi: 10.1126/science.1546297. [DOI] [PubMed] [Google Scholar]
- 33.Hancock W.O. Bidirectional cargo transport: moving beyond tug of war. Nat. Rev. Mol. Cell Biol. 2014;15:615–628. doi: 10.1038/nrm3853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bertrand E., Chartrand P., Long R.M. Localization of ASH1 mRNA particles in living yeast. Mol. Cell. 1998;2:437–445. doi: 10.1016/s1097-2765(00)80143-4. [DOI] [PubMed] [Google Scholar]
- 35.Coller J., Wickens M. Tethered function assays: an adaptable approach to study RNA regulatory proteins. Methods Enzymol. 2007;429:299–321. doi: 10.1016/S0076-6879(07)29014-7. [DOI] [PubMed] [Google Scholar]
- 36.Shaner N.C., Campbell R.E., Tsien R.Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004;22:1567–1572. doi: 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
- 37.Powrie E.A., Ciocanel V., Mowry K.L. Using in vivo imaging to measure RNA mobility in Xenopus laevis oocytes. Methods. 2016;98:60–65. doi: 10.1016/j.ymeth.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cox S., Matthews P. Exponential time differencing for stiff systems. J. Comput. Phys. 2002;176:430–455. [Google Scholar]
- 39.Kassam A.-K., Trefethen L. Fourth-order time-stepping for stiff PDEs. SIAM J. Sci. Comput. 2005;26:1214–1233. [Google Scholar]
- 40.Kang M., Andreani M., Kenworthy A.K. Validation of normalizations, scaling, and photofading corrections for FRAP data analysis. PLoS One. 2015;10:e0127966. doi: 10.1371/journal.pone.0127966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Klumpp S., Lipowsky R. Cooperative cargo transport by several molecular motors. Proc. Natl. Acad. Sci. USA. 2005;102:17284–17289. doi: 10.1073/pnas.0507363102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Müller M.J., Klumpp S., Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc. Natl. Acad. Sci. USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hughes J., Hancock W.O., Fricks J. Kinesins with extended neck linkers: a chemomechanical model for variable-length stepping. Bull. Math. Biol. 2012;74:1066–1097. doi: 10.1007/s11538-011-9697-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wolfram Research. 2014. Mathematica, ver. 10.0. Champaign, IL.
- 45.Sirajuddin M., Rice L.M., Vale R.D. Regulation of microtubule motors by tubulin isotypes and post-translational modifications. Nat. Cell Biol. 2014;16:335–344. doi: 10.1038/ncb2920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Thorn K.S., Ubersax J.A., Vale R.D. Engineering the processive run length of the kinesin motor. J. Cell Biol. 2000;151:1093–1100. doi: 10.1083/jcb.151.5.1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Conway, L., and J. L. Ross. 2014. Kinesin motor transport is altered by macromolecular crowding and transiently associated microtubule-associated proteins. arXiv preprint arXiv:1409.3455.
- 48.Zimyanin V.L., Belaya K., St Johnston D. In vivo imaging of oskar mRNA transport reveals the mechanism of posterior localization. Cell. 2008;134:843–853. doi: 10.1016/j.cell.2008.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Popovic L., McKinley S.A., Reed M.C. A stochastic compartmental model for fast axonal transport. SIAM J. Appl. Math. 2011;71:1531–1556. [Google Scholar]
- 50.Beichelt F. CRC Press; Boca Raton, FL: 2006. Stochastic Processes in Science, Engineering and Finance. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.