Abstract
Background and aim
Estimation of a PET tracer’s non-displaceable distribution volume (VND) is required for quantification of specific binding to its target of interest. VND is generally assumed to be comparable brain-wide and is determined either from a reference region devoid of the target, often not available for many tracers and targets, or by imaging each subject before and after blocking the target with another molecule that has high affinity for the target, which is cumbersome and involves additional radiation exposure. Here we propose, and validate for the tracers [11C]DASB and [11C]CUMI-101, a new data-driven hybrid deconvolution approach (HYDECA) that determines VND at the individual level without requiring either a reference region or a blocking study.
Methods
HYDECA requires the tracer metabolite-corrected concentration curve in blood plasma and uses a singular value decomposition to estimate the impulse response function across several brain regions from measured time activity curves. HYDECA decomposes each region’s impulse response function into the sum of a parametric non-displaceable component, which is a function of VND, assumed common across regions, and a nonparametric specific component. These two components differentially contribute to each impulse response function. Different regions show different contributions of the two components, and HYDECA examines data across regions to find a suitable common VND. HYDECA implementation requires determination of two tuning parameters, and we propose two strategies for objectively selecting these parameters for a given tracer: using data from blocking studies, and realistic simulations of the tracer. Using available test-retest data, we compare HYDECA estimates of VND and binding potentials to those obtained based on VND estimated using a purported reference region.
Results
For [11C]DASB and [11C]CUMI-101, we find that regardless of the strategy used to optimize the tuning parameters, HYDECA provides considerably less biased estimates of VND than those obtained, as is commonly done, using a non-ideal reference region. HYDECA test-retest reproducibility is comparable to that obtained using a VND determined from a non-ideal reference region, when considering the binding potentials BPP and BPND.
Conclusions
HYDECA can provide subject-specific estimates of VND without requiring a blocking study for tracers and targets for which a valid reference region does not exist.
Introduction
Positron Emission Tomography (PET) in the brain involves administration of a tracer dose of a radioactively labeled molecule (i.e., tracer) that binds to a specific target [1]. The tracer signal in the tissue combines signal from tracer “specifically” bound to the target and tracer “non-specifically” bound to other macromolecules or free in tissue water. Estimation of tracer non-displaceable uptake allows quantification of the specific binding potential between tracer and target [2, 3]. The tracer non-displaceable distribution volume (VND), corresponding to “non-specifically” bound and free tracer, is commonly estimated using either the tracer binding level in a reference region that is devoid of the target [2, 3], or a blocking study which involves a baseline PET scan and a second scan with a blocking drug administered just before the tracer [4, 5].
In a valid reference region, the tracer is either free or only “non-specifically” bound, and its volume of distribution (VT) in such a region (VT-RR) is typically assumed to represent the brain-wide VND. For many targets this approach is not appropriate because there is no valid reference region, as the target is present throughout the brain [6–16], and thus the signal in any region includes some specific binding. Using an invalid reference region over-estimates VND, causing underestimation of binding potentials [16], and can confound interpretation of results [17–20]. Automatic extraction of a reference region signal using cluster analysis [7, 10, 12] of the brain PET data is often not successful, or greatly depends on the data used to train the clustering algorithm [21].
Alternatively, a blocking study with tracer injections before and after a saturating dose of an antagonist with high affinity for the same target of interest allows estimation of brain-wide VND using a Lassen plot [4, 5]. However, performing a blocking study in each subject is cumbersome, costly, doubles the radiation exposure, can involve side effects related to the blocking agent, and is therefore generally avoided in clinical research.
A parametric pseudo-reference tissue model was proposed [22] for tracers that have no ideal reference region, which provides estimates only for the binding potential BPND [2] and not for VND and thus not for binding potentials BPP and BPF [2], and assumes that BPND in the pseudo reference region can be estimated from additional competition data. A genomic plot was also recently proposed, which provides VND estimates only at the population level and requires that the brain maps of messenger RNA transcripts of the specific target of interest be available from the Allen Brain Atlas [23].
Based on compartment models (CMs) [24], we proposed to perform at the individual subject level simultaneous estimation of a common VND across regions [25] when no valid reference region is available. However, for some tracers such as [11C]DASB (target: serotonin transporter), the simultaneous estimation of VND across regions often fails to give a unique solution. Separately, we also showed [26] that nonparametric deconvolution is an alternative quantification approach for PET data, which computes binding potentials comparable to estimates by CMs, and for some tracers, shows superior test-retest performance than quantification by CMs [26].
We now propose a new hybrid deconvolution approach (HYDECA) that combines deconvolution and simultaneous search across regions to calculate a brain-wide VND when arterial blood data are available but a valid reference region is not. HYDECA is validated for [11C]DASB and [11C]CUMI-101 (target: serotonin 1A receptor) using simulations and blocking studies [11, 27], and evaluated in test-retest datasets [10, 28].
Materials and methods
Human subjects and animal studies
Data from published blocking studies in baboons [27] and humans [11], and test-retest datasets in humans [10, 28] were used. Human studies were performed in accordance with the 1964 Declaration of Helsinki and its later amendments and approved by The Institutional Review Boards of Columbia University Medical Center (CUMC) and New York State Psychiatric Institute (NYSPI). Animal studies were performed with the approval of the CUMC and NYSPI Institutional Animal Care and Use Committees, according to all applicable regulations governing the use of animals in research.
Nonparametric quantification
According to the extended indicator dilution theory [26, 29], the tracer signal in tissue in a brain region i, CTi(t), after correction for the presence of tracer in vasculature, is a scaled convolution between the metabolite-corrected input function in the arterial plasma, CP(t), and the so-called tissue residue function, Ri(t):
| (1) |
While Ki [mL⋅cm-3⋅min-1] is a proportionality constant, Ri(t) is defined in the theory of the indicator-dilution method as the fraction of indicator that remains in the tissue after an idealized bolus input concentration at time zero. Initially, the residue must be unity (Ri(0) = 1) and from there it decreases (or at least does not increase) with time (refer to [29] for details).
Among many nonparametric approaches that can be used to estimate the impulse response function (IRF) in each region i, IRFi(t) = KiRi(t), from known CP(t) and CTi(t), we proposed using singular value decomposition (SVD) with data-driven selection of the threshold that we described elsewhere [26].
Hybrid deconvolution approach
In the context of PET reversible radiotracers, Ri(t) can be interpreted as the fraction of tracer molecules remaining in the tissue over time, and these molecules can be specifically bound to the target, free in water or bound to other molecules. HYDECA decomposes each region Ri(t) into the sum of a parametric non-displaceable component, which is approximated as a mono-exponential function depending on VND, assumed common across regions (see details below and comments on the validity of this approximation in the Discussion), and a nonparametric specific component. For any choice of VND defining the non-displaceable component, the nonparametric specific component can be estimated by subtraction.
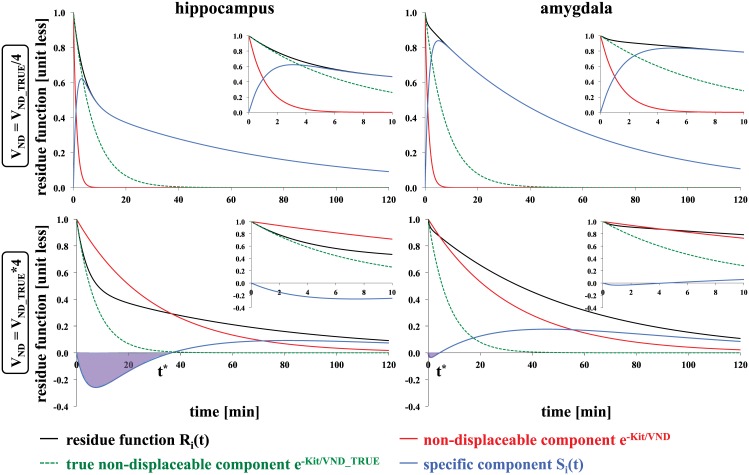
Performing such a decomposition for observed PET data can be challenging, but the goal of HYDECA is to objectively ascertain a “reasonable” VND value by examining data across regions. To illustrate this idea, Fig 1 shows Ri(t) curves in two representative regions, calculated using a two-tissue CM (2TCM) [24] (see Eq 8) and based on kinetic rates derived from data with [11C]DASB [28]. Non-displaceable component curves based on two “unreasonable” choices of VND (a value that is 1/4 and 4 times the magnitude of the true VND, respectively) are compared to the non-displaceable component calculated with the true VND (the “most reasonable” choice). The non-displaceable component and the corresponding specific component differentially contribute to Ri(t) and two effects can be observed. The first effect is that, at time zero, the difference between the slope of Ri(t) and that of the non-displaceable component is small, if the VND value is close to the true VND. The second effect is that, when the VND value used for the non-displaceable component is larger than the true VND, the corresponding specific component results in negative values, violating its positivity constraints. Different regions show different contributions of non-displaceable and specific component to Ri(t). HYDECA is based on finding a VND value that, across regions, provides the best compromise between these two effects.
Fig 1. Illustration of the idea behind the algorithm in the hybrid deconvolution approach.
Ri(t) curves (black lines) calculated using the IRF of the 2TCM and values of the kinetic rates derived from a study with [11C]DASB for 2 representative regions. Red solid lines indicate the non-displaceable component calculated with a VND that is 1/4 the size of (top) and 4 times higher than (bottom) the true underlying VND; green dotted lines indicate the non-displaceable component calculated with the true underlying VND; blue lines indicate the corresponding specific component. Inset plots are added to allow closer inspection of the first 10 minutes after tracer injection. The time t* is derived from the data as the time point after which the specific component has consistently positive values. IRF: impulse response function; 2TCM: two-tissue compartment model; VND: non-displaceable distribution volume.
To do so, HYDECA requires as input CP(t) and CTi(t) curves from a pre-determined set of N brain regions, once corrected for the presence of vasculature. In our implementation we assumed a brain-wide blood volume of 5%. HYDECA estimates VND as follows:
IRFi(t) is estimated in each region i from CTi(t) and CP(t) using SVD as described [26]; Ki is obtained as the value of IRFi(t) at time zero (Ri(0) = 1 by definition for an idealized bolus input; see “Implementation” section below for comments); Ri(t) is then obtained dividing IRFi(t) by the Ki estimate;
Ri(t) is expressed in each region i as the sum of a parametric non-displaceable component (corresponding to an ideal one-tissue CM with distribution volume of VND), RND(t), and a nonparametric specific component, Si(t):
| (2) |
Assuming a mono-exponential for RND(t) represents an approximation (if a 2TCM is needed to describe the data in a given region, RND(t) would be described by two exponentials [24]), whose validity varies across regions (see comments on the validity of this approximation in the Discussion); HYDECA examines data across regions to find a suitable common VND. The property expressed in Eq (2) can be derived from CMs as follows:
| (3) |
| (4) |
| (5) |
with binding potential BPP as in [2]; HYDECA expresses parametrically only RND(t).
For fixed values of the tuning parameters β and γ, the following cost function is minimized over VND using all N regions:
| (6) |
Minimization of the first term in Eq (6), which represents the residual sum of squares between Ri(t) and RND(t), calculated up to time γ after tracer injection, identifies VND values that provide RND(t) curves with a slope close to the slope of Ri(t) at time zero. Given the difficulty in accurately estimating slopes from noisy data, the difference in the slope is approximated as the residual sum of squares between the two curves. The tuning parameter γ controls the number of data points considered for this calculation. Minimization of the second term, which represents the negative area of the curve of the corresponding Si(t), in the case that a portion of Si(t) assumes negative values, penalizes VND values that lead to unphysiological Si(t) values (Fig 1). If Si(t) is everywhere positive then there is no contribution of the second term. If Si(t) has negative values, then the time t* is data-derived as the time point after which Si(t) has consistently positive values. The tuning parameter β weights the contribution of the second term relatively to the first term. We propose and compare two strategies for setting optimal values for the tuning parameters β and γ for a given tracer.
Tuning with simulations
One strategy involves simulating data that imitate characteristics of real data for the tracer at hand, letting β and γ vary over a grid of possible values, and identifying optimal β and γ as those values that allow HYDECA to generate an estimate of VND that, on average across all simulated instances, is closest to the true simulated VND (VND_TRUE).
We considered a metabolite-corrected input function CP(t) and kinetic rate values in the same brain regions we considered in previous publications [25, 26] based on available data [10, 28]: cerebellar gray matter (CGM), temporal lobe (TEM), hippocampus (HIP), dorsal caudate (DCA), amygdala (AMY), and ventral striatum (VST), for [11C]DASB; CGM, HIP, TEM and occipital lobe (OCC), and cingulate (CIN) for [11C]CUMI-101. Noise-free CTi(t) curves were generated for each region using a 2TCM [3, 24]:
| (7) |
| (8) |
| (9) |
where K1i, k2i, k3i, and k4i are the values for the kinetic rate parameters of region i. Table 1 lists the kinetic rate values used in each of two simulated cases per tracer: 1) common VND_TRUE is 3, and 50% of the tracer VT-RR is specific binding (cerebellar grey matter VT ~6); 2) common VND_TRUE is 5, and ~17% of the tracer VT-RR is specific binding (cerebellar grey matter VT ~6).
Table 1. List of kinetic rate values used in the simulations.
| region | K1 [mL·cm-3·min-1] | k2 [min-1] | k3 [min-1] | k4 [min-1] | VT [mL·cm-3] |
|---|---|---|---|---|---|
| [11C]DASB | |||||
| VND = 3 | |||||
| cerebellar grey matter | 0.540 | 0.180 | 0.540 | 0.550 | 5.96 |
| temporal lobe | 0.463 | 0.154 | 0.505 | 0.168 | 12.00 |
| hippocampus | 0.404 | 0.135 | 0.103 | 0.026 | 14.92 |
| dorsal caudate | 0.509 | 0.170 | 2.900 | 0.615 | 17.14 |
| amygdala | 0.380 | 0.127 | 1.510 | 0.270 | 19.78 |
| ventral striatum | 0.476 | 0.159 | 3.452 | 0.357 | 32.02 |
| VND = 5 | |||||
| cerebellar grey matter | 0.542 | 0.108 | 0.542 | 2.816 | 5.96 |
| temporal lobe | 0.463 | 0.093 | 0.505 | 0.361 | 12.00 |
| hippocampus | 0.404 | 0.081 | 0.103 | 0.052 | 14.92 |
| dorsal caudate | 0.509 | 0.102 | 2.900 | 1.194 | 17.14 |
| amygdala | 0.380 | 0.076 | 1.510 | 0.511 | 19.78 |
| ventral striatum | 0.476 | 0.095 | 3.452 | 0.639 | 32.02 |
| [11C]CUMI-101 | |||||
| VND = 3 | |||||
| cerebellar grey matter | 0.450 | 0.150 | 0.050 | 0.050 | 6.00 |
| hippocampus | 0.360 | 0.120 | 0.130 | 0.030 | 16.00 |
| temporal lobe | 0.300 | 0.100 | 0.100 | 0.050 | 9.00 |
| occipital lobe | 0.450 | 0.150 | 0.080 | 0.050 | 7.80 |
| cingulate | 0.330 | 0.110 | 0.090 | 0.050 | 8.40 |
| VND = 5 | |||||
| cerebellar grey matter | 0.450 | 0.090 | 0.050 | 0.250 | 6.00 |
| hippocampus | 0.360 | 0.072 | 0.130 | 0.059 | 16.00 |
| temporal lobe | 0.300 | 0.060 | 0.100 | 0.125 | 9.00 |
| occipital lobe | 0.450 | 0.090 | 0.080 | 0.143 | 7.80 |
| cingulate | 0.330 | 0.066 | 0.090 | 0.132 | 8.40 |
In all cases, we simulated Gaussian noise with zero mean. To ensure realistic noise characteristics, the variance-covariance matrix used to generate simulated noise was estimated from a matrix of residuals, standardized across time points, from the fits for the considered regions using available data [10, 28]. In all cases, we simulated 1000 CTi(t) curves for each region.
For each tracer and VND_TRUE case, we then: 1) considered a grid of β (0.5 to 14; step: 0.5) and γ values (1 to 30 minutes after tracer injection; step: 1); 2) calculated the cost function (Eq 6) corresponding to all combinations of β and γ within the grids, and over a grid of VND values (0.1 to 7; step: 0.1), in each of the simulated instances; 3) considered the average cost function (across instances) corresponding to each of the combinations of β and γ; 4) estimated VND as the value that minimizes each of these average cost functions; and 5) calculated the corresponding absolute estimation error as |VND_TRUE−VND|. After obtaining the association between each combination of β and γ within the grids and the corresponding bias of the VND estimate, we selected as optimal β and γ derived via simulations (βopt-S, γopt-S) the values providing the smallest bias.
Tuning with blocking studies
Another strategy involves using blocking studies, if available, letting β and γ vary over a grid of possible values, and identifying optimal β and γ as those values in correspondence of which HYDECA provides a VND that is, on average across all subjects in the dataset, the closest to the VND estimated using both scans before and after blocking and Lassen plot [5] (VND_LASSEN).
We examined 13 healthy controls imaged with [11C]DASB before and after administration of sertraline [11], and 8 pairs of scans performed on healthy baboons with [11C]CUMI-101 before and after either WAY100635 or 8-OH-DPAT [27].
In each pair, we computed VND_LASSEN using both scans before and after blocking and the same regions considered in simulation. We then: 1) considered the same grids for β and γ as in tuning with simulations; 2) calculated the HYDECA cost function corresponding to all combinations of β and γ within the grids, and over a grid of VND values (0.1 to 30; step: 0.1), using in each pair only the scan before blocking and the same regions considered in simulation; 3) estimated VND as the value that minimizes each of these cost functions; 4) calculated the corresponding absolute estimation error as |VND_LASSEN−VND|; and 5) calculated the average (across all subjects within a tracer) estimation error obtained for each combination of β and γ. After obtaining the association between each combination of β and γ within the grids and the corresponding bias in the VND estimate, we selected as optimal β and γ derived via blocking studies (βopt-B, γopt-B) the values providing the smallest bias.
In each scan before blocking, we calculated the percent difference (PDVND) between VND estimated using HYDECA (with tuning parameters set with either strategy) and the corresponding VND_LASSEN, as PDVND = 100⋅|VND_LASSEN−VND|/ VND_LASSEN.
Implementation
HYDECA, implemented in Matlab R2012b (www.mathworks.com/), is a fast algorithm that runs in ~14 seconds for one subject on an iMac machine, 3.5 GHz Intel Core i7 Processor, once β and γ are determined. The most computationally demanding component is the data-driven selection of SVD threshold [26]. The computational time required to optimize the tuning parameters initially for a given tracer depends on the selected strategy. If this is done using simulations, this can take up to a few hours. Using blocking studies, the computation is complete within a few minutes.
Only with an idealized bolus input does Ri(t) reach its maximum at time zero, and in such a case, Ki could be derived from the value of the reconstructed IRFi(t) = KiRi(t) at time zero. With a realistic bolus infusion of the tracer, Ri(t) reaches its maximum at some time t > 0, and implementation that estimates Ki as the maximum of the reconstructed IRFi(t) is preferable. Furthermore, in our implementation, all deconvolved Ri(t) curves are first shifted to have their maximum value correspond to time zero before calculating the HYDECA cost function in Eq (6). We do not perform any correction for a physiological delay between CTi(t) in the different regions and CP(t).
Estimation using the non-ideal reference region
To investigate the bias of HYDECA VND estimates relative to estimates measured using the Lassen plot, and in comparison to the common practice of setting VND equal to VT-RR even when the reference region is known not to be valid, we utilized only the scans before blocking in the two available datasets to calculate VT in CGM starting from CP(t) and CTi(t), using both a 2TCM [24] and Likelihood Estimation in Graphical Analysis (LEGA) [30]. CGM was chosen as reference region as it has the lowest VT [10, 28] and least displacement of all regions examined in our blocking studies [11, 27]. LEGA provides the best test-retest reproducibility over analysis with CMs and other graphical approaches for estimates with both tracers [10, 28]. PDVND with respect to VND_LASSEN was also calculated for VT-RR obtained with both 2TCM (VT-RR,2TCM) and LEGA (VT-RR,LEGA).
Application to test-retest data
As VND is estimated in order to calculate binding potentials, we considered two available test-retest datasets with [11C]DASB [28] and [11C]CUMI-101 [10] and investigated the reproducibility of binding potentials derived using HYDECA versus using the purported reference region (CGM). Both test-retest datasets included only healthy controls, who were imaged with the radiotracer in question twice in one day (once in the morning, once in the afternoon) in a test-retest study design. In all scans, we calculated VND (using HYDECA with optimal β and γ set with either strategy, and considering the same regions used in simulation), VT-RR,2TCM, and VT-RR,LEGA. For each test-retest pair and region, we calculated the percent difference PDVND-TRT as , where VTEST is the VND or VT-RR estimate in the test scan, and VRETEST the VND or VT-RR estimate in the retest scan. We compared PDVND-TRT values obtained from the different methods using a two-tailed paired t-test, considering all possible pairwise combinations of methods.
In all scans and regions, we then calculated the binding potentials BPP and BPND [2] based on: 1) VND by HYDECA (VND (HYDECA)), as BPP-HYBRID = VT (LEGA)–VND (HYDECA) and BPND-HYBRID = BPP-HYBRID/VND (HYDECA), where VT (LEGA) is the VT obtained in each target region using LEGA; 2) VT-RR,LEGA, as BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA and BPND-RR,LEGA = BPP-RR,LEGA/VT-RR,LEGA; 3) VT-RR,2TCM, as BPP-RR,2TCM = VT (2TCM)–VT-RR,2TCM and BPND-RR,2TCM = BPP-RR,2TCM/VT-RR,2TCM, with VT (2TCM) the VT obtained in each target region using 2TCM; and 4) direct calculation from 2TCM kinetic rates, as BPP-direct,2TCM = K1k3/k2k4 and BPND-direct,2TCM = k3/k4.
For each test-retest pair and region, we calculated the percent difference for the binding potentials (PDBPP and PDBPND) as , (BPT: test estimate; BPRT: re-test estimate), and computed average and standard deviation (SD) (across subjects within a tracer) of PDBPP and PDBPND values in each region. We compared PDBPP and PDBPND values obtained from the different methods using a two-tailed paired t-test, region by region, considering all possible pairwise combinations of methods.
Results
Simulation studies
Tuning parameters optimization
Optimization of β and γ using simulations and effects of β and γ values on VND estimates obtained by HYDECA are shown in Fig 2. As γ (number of points considered for the first term in Eq (6)) increases, β needs to correspondingly increase to weight more the second term in Eq (6)), in order to minimize bias in VND estimation.
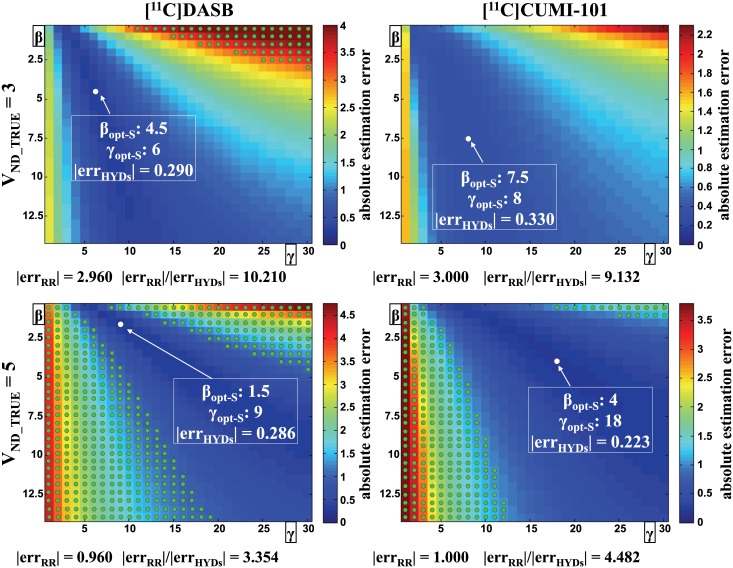
Fig 2. Optimization of tuning parameters β and γ using simulations.
Average absolute error in the estimation of VND as a function of the values for the tuning parameters β and γ, for all simulated cases (VND_TRUE = 3, top; VND_TRUE = 5, bottom) and tracers. Each point in the matrices correspond to a specific combination of β (vertical axis) and γ (horizontal axis) values in the selected grids, and represents the average (across simulated instances) absolute distance between VND estimate obtained by HYDECA, using the corresponding combination of β and γ, and VND_TRUE. The white circle indicates the optimal combination of the tuning parameters (βopt-S, γopt-S) derived using simulations in each case, and the average absolute error in the estimation of VND in correspondence of the optimal tuning parameters is reported (|errHYDs|). Green circles indicate the combinations of β and γ for which HYDECA provides an average absolute error in the estimation of VND that is higher than the absolute error committed by assuming VND equal to the VT in the non-ideal reference region (CGM) (|errRR|), and the ratio between |errRR| and |errHYDs| in correspondence of the optimal β and γ is reported. VND: non-displaceable distribution volume; VND_TRUE: true simulated VND; VT: tracer total volume of distribution; CGM: cerebellum grey matter.
For each tracer and VND_TRUE case, we selected the optimal β and γ values in correspondence of which HYDECA provides the least biased estimation of VND (Fig 2, white circles): for [11C]DASB, βopt-S = 4.5 and γopt-S = 6 (VND_TRUE = 3), βopt-S = 1.5 and γopt-S = 9 (VND_TRUE = 5); for [11C]CUMI-101, βopt-S = 7.5 and γopt-S = 8 (VND_TRUE = 3), βopt-S = 4 and γopt-S = 18 (VND_TRUE = 5).
When 50% of VT-RR is specific binding (VND_TRUE = 3), for [11C]CUMI-101 HYDECA provides an average error in the VND estimation smaller than using VT-RR with any other combination of β and γ. The error committed using a non-ideal reference region (|errRR|) is nine times greater than the error committed using HYDECA (|errHYDs|) (|errRR|/|errHYDs| = 9.132). With [11C]DASB, HYDECA provides an average estimation error smaller than using VT-RR in correspondence of most combinations of β and γ, with exception of a subset of values (green circles in Fig 2) (|errRR|/|errHYDs| = 10.210).
When only 17% of the VT in the non-ideal reference region is specific binding (VND_TRUE = 5), for both tracers the number of combinations of β and γ in correspondence of which HYDECA provides an average estimation error smaller than using VT-RR is reduced. However, HYDECA with optimized β and γ still generated a robustly more accurate estimate of VND than VT-RR ([11C]CUMI-101: |errRR|/|errHYDs| = 4.482; [11C]DASB: |errRR|/|errHYDs| = 3.354).
Cost functions and estimation bias with optimized tuning parameters
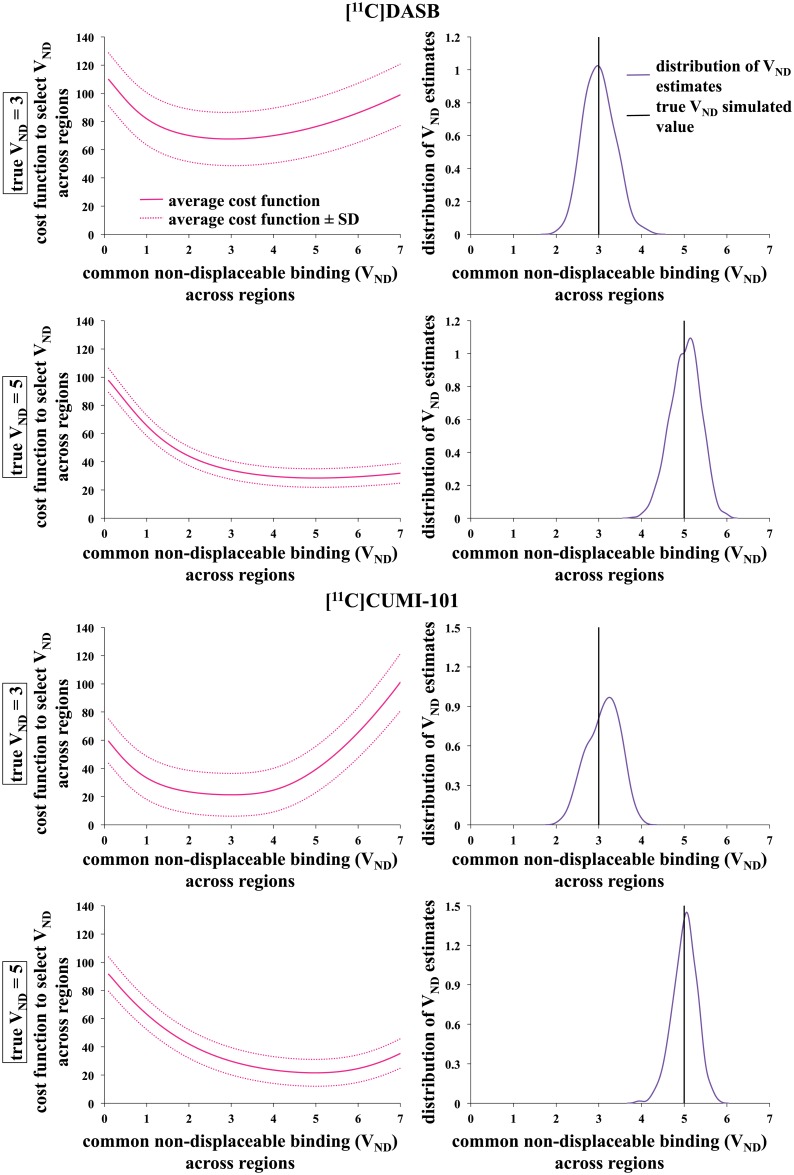
HYDECA cost function curves (Eq 6) using (βopt-S, γopt-S) as determined using simulations are convex and unimodal (Fig 3). The corresponding distributions of VND estimates show a bias, calculated as the average of (VND_TRUE−VND) across instances, of -0.008 (VND_TRUE = 3) and -0.024 (VND_TRUE = 5) ([11C]DASB), and -0.108 (VND_TRUE = 3) and -0.010 (VND_TRUE = 5) ([11C]CUMI-101). The variance of the estimates is 0.133 (VND_TRUE = 3) and 0.126 (VND_TRUE = 5) ([11C]DASB), and 0.144 (VND_TRUE = 3) and 0.082 (VND_TRUE = 5) ([11C]CUMI-101).
Fig 3. Cost functions and estimation bias with tuning parameters β and γ optimized using simulations.
HYDECA cost functions (average across 1000 instances, plus and minus one standard deviation) and corresponding distribution of VND estimates obtained in simulations with VND_TRUE = 3 and VND_TRUE = 5 with [11C]DASB (top) and [11C]CUMI-101 (bottom), using the optimal tuning parameters (βopt-S, γopt-S) derived using simulations in each case. VND: non-displaceable distribution volume; VND_TRUE: true simulated VND.
Blocking studies
Tuning parameters optimization
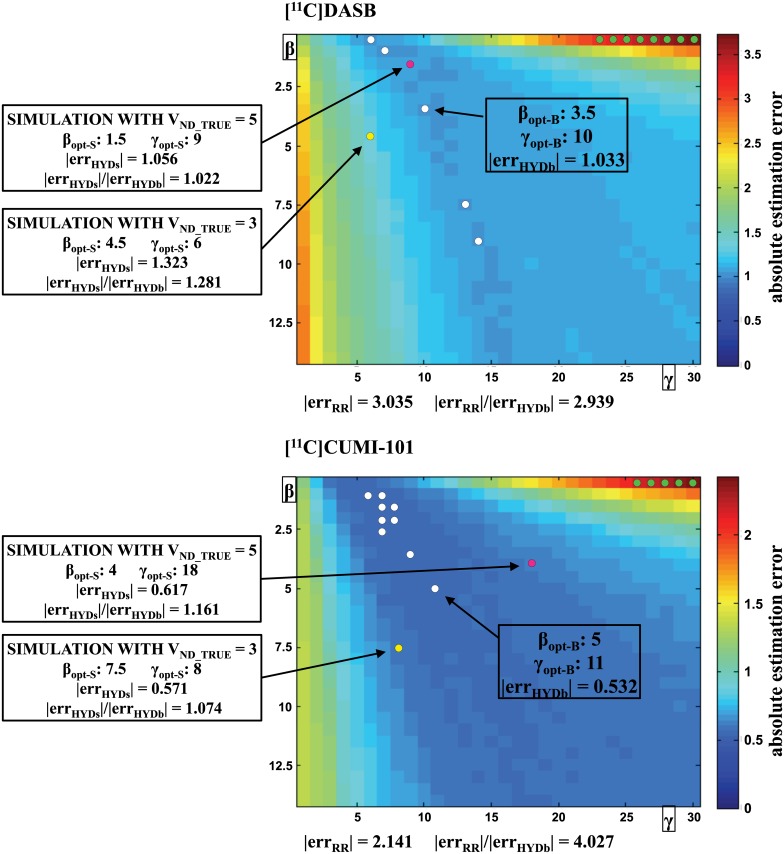
Optimization of β and γ using blocking studies, and effect of β and γ values on HYDECA estimates of VND, are shown in Fig 4. With our data, we found five combinations of β and γ with [11C]DASB and nine with [11C]CUMI-101 that provide the same minimum absolute error in the VND estimation (Fig 4, white circles); any of these combinations could be regarded as the optimal β and γ. We selected: βopt-B = 3.5, γopt-B = 10 for [11C]DASB; βopt-B = 5, γopt-B = 11 for [11C]CUMI-101.
Fig 4. Optimization of tuning parameters β and γ using blocking studies.
Average absolute error in the estimation of VND as a function of the values for the tuning parameters β and γ for both tracers. Each point in the matrices correspond to a combination of β and γ values in the selected grids, and represents the average (across scans within the same tracer) absolute distance between the VND estimated by HYDECA, using the corresponding combination of β and γ, and VND_LASSEN. White circles indicate the optimal combinations of the tuning parameters (βopt-B, γopt-B) derived using the blocking studies, and the average absolute error in the estimation of VND in correspondence of (βopt-B, γopt-B) is reported (|errHYDb|). Green circles indicate the combinations of β and γ for which HYDECA provides an average absolute error in the estimation of VND that is higher than the absolute error committed by using the VT in the CGM as an estimation of VND (|errRR|), and the ratio between |errRR| and |errHYDb| in correspondence of the optimal β and γ is reported. The yellow and pink circle indicates the optimal combination of the tuning parameters (βopt-S, γopt-S) derived using simulation with VND_TRUE = 3 and VND_TRUE = 5, respectively, and the ratio between |errHYDs| (in correspondence of βopt-S and γopt-S) and |errHYDb| (in correspondence of βopt-B and γopt-B) is reported. VND: non-displaceable distribution volume; VND_LASSEN: VND estimated using both scans before and after blocking and Lassen plot; VT: tracer total volume of distribution; CGM: cerebellum grey matter.
With both tracers, only very few combinations of β and γ (Fig 4, green circles) provide an average absolute error in the VND estimation (|errHYDb|) that is larger than the error using VT-RR (|errRR|). The |errRR|/|errHYDb| ratio is 2.939 for [11C]DASB, and 4.027 for [11C]CUMI-101.
For [11C]DASB, HYDECA with (βopt-S, γopt-S) derived using simulation with VND_TRUE = 5 (Fig 4, pink circles) provides the closest results to HYDECA with (βopt-B, γopt-B) derived using blocking studies (|errHYDs|/|errHYDb| = 1.022). A VND_TRUE value of 5 is closer to average VND values obtained using Lassen plot in the available [11C]DASB blocking studies. For [11C]CUMI-101, HYDECA with (βopt-S, γopt-S) derived using simulation with VND_TRUE = 3 (Fig 4, yellow circles) provides the closest results to HYDECA with (βopt-B, γopt-B) derived using blocking studies (|errHYDs|/|errHYDb| = 1.074). A VND_TRUE value of 3 is closer to average VND values obtained using Lassen plot and the available [11C]CUMI-101 blocking studies. In the results that follow, we refer to (βopt-S, γopt-S) for [11C]DASB and [11C]CUMI-101 as those obtained with the simulation studies with VND_TRUE = 5 and VND_TRUE = 3, respectively.
Estimation bias with optimized tuning parameters
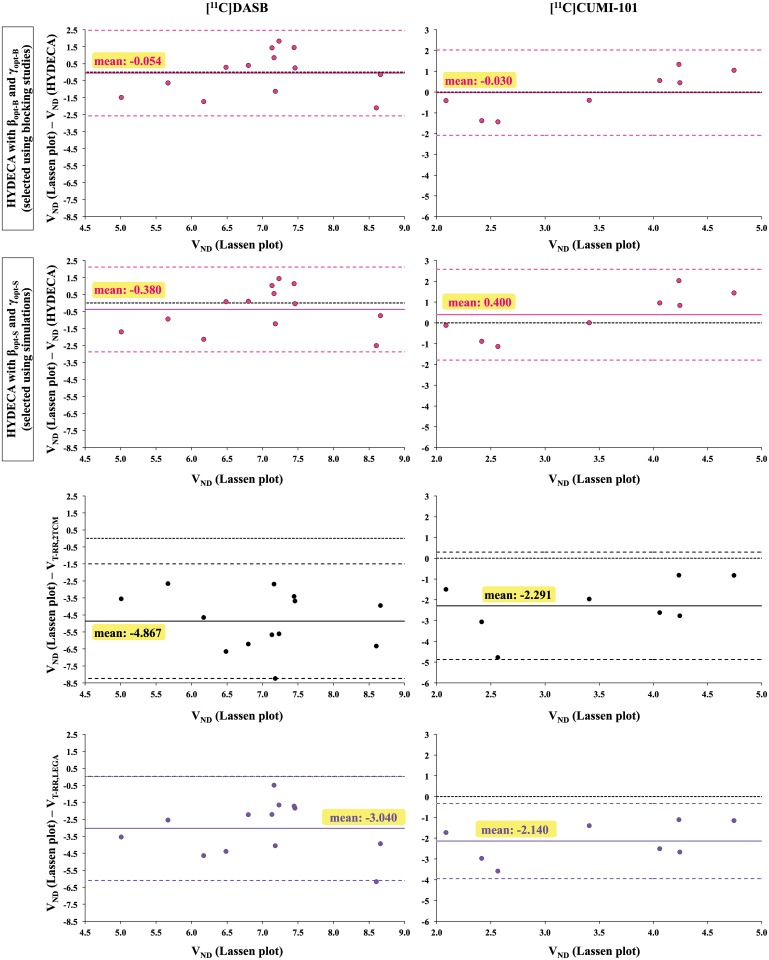
Application of HYDECA to individual scans in the blocking studies, with β and γ optimized using either strategies, in comparison to the use of VT-RR is shown in Fig 5. VND estimates by HYDECA with either sets of tuning parameters are considerably less biased, relative to VND estimates from the Lassen plot, than those using VT-RR. Estimation of VND using 2TCM in the non-ideal reference region is more biased than that obtained by HYDECA and LEGA for both considered tracers. Average (± SD) PDVND values across subjects are: 15.48% (± 9.82) using HYDECA with (βopt-B, γopt-B), 15.40% (± 11.65) using HYDECA with (βopt-S, γopt-S), 44.16% (± 22.52) using VT-RR,LEGA, and 70.04% (± 24.00) using VT-RR,2TCM ([11C]DASB); 27.81% (± 19.03) using HYDECA with (βopt-B, γopt-B), 26.08% (± 17.24) using HYDECA with (βopt-S, γopt-S), 70.26% (± 42.82) using VT-RR,LEGA, and 76.10% (± 56.03) using VT-RR,2TCM ([11C]CUMI-101). All VND and VT-RR estimates for all approaches and both blocking datasets are reported in Table 2. For both tracers, average (across subjects within each tracer) VND estimates by HYDECA, with β and γ optimized using either strategies, are closer than both LEGA and 2TCM to average values calculated using Lassen plot, which is considered standard in the field for in vivo estimation of VND, and SD values are overall lower than those for LEGA and 2TCM.
Fig 5. Estimation bias with tuning parameters β and γ optimized using blocking studies.
Difference between VND_LASSEN and VND estimates obtained by HYDECA with (βopt-B, γopt-B) set using blocking studies (y-axis; first row), between VND_LASSEN and VND estimates obtained by HYDECA with (βopt-S, γopt-S) set using simulations (y-axis; second row), between VND_LASSEN and VND estimated as the VT in the CGM using 2TCM (y-axis; third row), and between VND_LASSEN and VND estimated as the VT in the CGM using LEGA (y-axis; bottom), as a function of VND_LASSEN (x-axis) in individual scans in the blocking study with [11C]DASB (left) and [11C]CUMI-101 (right). Solid lines indicate the average error; dotted lines indicate average error ± 1.96 standard deviation. The zero line is the dotted black line. VND: non-displaceable distribution volume; VND_LASSEN: VND estimated using both scans before and after blocking and Lassen plot; VND (HYDECA): VND estimated using HYDECA; VT-RR,2TCM: distribution volume in the non-ideal reference region calculated using 2TCM; VT-RR,LEGA: distribution volume in the non-ideal reference region calculated using LEGA; VT: tracer total volume of distribution; CGM: cerebellum grey matter; 2TCM: two-tissue compartment model; LEGA: Likelihood Estimation in Graphical Analysis.
Table 2. VND and VT-RR estimates for all approaches in the available blocking datasets and their summary statistics.
| VND ESTIMATES in BLOCKING DATASETS | |||||
|---|---|---|---|---|---|
| HYDECA (βopt-S, γopt-S) (baseline scan) | HYDECA (βopt-B, γopt-B) (baseline scan) | VT-RR,2TCM (baseline scan) | VT-RR,LEGA (baseline scan) | LASSEN (baseline and block scan) | |
| [11C]DASB | |||||
| sub 1 | 6.4 | 6.2 | 13.1 | 10.9 | 6.5 |
| sub 2 | 6.6 | 6.3 | 8.3 | 8.2 | 5.7 |
| sub 3 | 7.5 | 7.2 | 11.1 | 9.3 | 7.5 |
| sub 4 | 6.7 | 6.4 | 13.0 | 9.0 | 6.8 |
| sub 5 | 11.1 | 10.7 | 14.9 | 14.8 | 8.6 |
| sub 6 | 8.4 | 8.3 | 15.4 | 11.2 | 7.2 |
| sub 7 | 6.6 | 6.3 | 9.8 | 7.7 | 7.2 |
| sub 8 | 9.4 | 8.8 | 12.6 | 12.6 | 8.7 |
| sub 9 | 5.8 | 5.4 | 12.8 | 8.9 | 7.2 |
| sub 10 | 6.3 | 6 | 10.9 | 9.2 | 7.4 |
| sub 11 | 6.1 | 5.7 | 12.8 | 9.4 | 7.1 |
| sub 12 | 8.3 | 7.9 | 10.8 | 10.8 | 6.2 |
| sub 13 | 6.7 | 6.5 | 8.6 | 8.6 | 5.0 |
| mean | 7.4 | 7.1 | 11.9 | 10.0 | 7.0 |
| SD | 1.5 | 1.5 | 2.2 | 2.0 | 1.0 |
| [11C]CUMI-101 | |||||
| scan 1 | 3.1 | 3.5 | 6.7 | 6.6 | 4.1 |
| scan 2 | 2.2 | 2.5 | 3.6 | 3.8 | 2.1 |
| scan 3 | 3.4 | 3.8 | 7.0 | 6.9 | 4.2 |
| scan 4 | 2.2 | 2.9 | 5.1 | 5.3 | 4.2 |
| scan 5 | 3.3 | 3.7 | 5.6 | 5.9 | 4.7 |
| scan 6 | 3.4 | 3.8 | 5.4 | 4.8 | 3.4 |
| scan 7 | 3.7 | 4 | 7.3 | 6.1 | 2.6 |
| scan 8 | 3.3 | 3.8 | 5.5 | 5.4 | 2.4 |
| mean | 3.1 | 3.5 | 5.8 | 5.6 | 3.5 |
| SD | 0.6 | 0.5 | 1.2 | 1.0 | 1.0 |
Test-retest studies
Average (across subjects within each tracer) estimates of VND and VT-RR in the test-retest datasets (Table 3) are consistent with corresponding values found in the blocking datasets (Table 2), although in the case of [11C]CUMI-101 the two datasets are in different species. VND values we obtain with HYDECA average 27% of total binding in ventral striatum for [11C]DASB, and 22% of the total binding in hippocampus for [11C]CUMI-101, which is generally in line with reports for other PET tracers [31, 32].
Table 3. VND and VT-RR estimates for all approaches in the available test-retest datasets and their summary statistics.
| VND ESTIMATES in TEST-RETEST DATASETS | ||||||||
|---|---|---|---|---|---|---|---|---|
| HYDECA (βopt-S, γopt-S) | HYDECA (βopt-B, γopt-B) | VT-RR,2TCM | VT-RR,LEGA | |||||
| TEST | RETEST | TEST | RETEST | TEST | RETEST | TEST | RETEST | |
| [11C]DASB | ||||||||
| sub 1 | 10.1 | 10.6 | 9.5 | 10.3 | 14.9 | 15.2 | 14.9 | 15.2 |
| sub 2 | 7.2 | 8.2 | 7 | 7.8 | 10.8 | 10.9 | 10.8 | 10.9 |
| sub 3 | 6.5 | 6.9 | 6.1 | 6.7 | 8.2 | 8.3 | 8.2 | 8.3 |
| sub 4 | 9.8 | 8 | 9.5 | 7.6 | 12.1 | 11.9 | 12.1 | 11.7 |
| sub 5 | 5.6 | 5.1 | 5.2 | 4.7 | 9.0 | 9.1 | 9.0 | 9.1 |
| sub 6 | 7.7 | 8.4 | 7.3 | 8.1 | 11.1 | 9.5 | 9.3 | 9.5 |
| sub 7 | 11.6 | 10.2 | 11.3 | 10 | 14.8 | 14.4 | 14.8 | 13.2 |
| sub 8 | 8.6 | 8.3 | 8.4 | 8 | 15.4 | 11.6 | 11.2 | 11.6 |
| sub 9 | 10.1 | 10.8 | 9.8 | 10.1 | 12.6 | 12.8 | 12.6 | 12.8 |
| sub 10 | 6.9 | 7.8 | 6.8 | 7.4 | 13.6 | 9.7 | 9.2 | 9.7 |
| mean | 8.4 | 8.4 | 8.1 | 8.1 | 12.3 | 11.3 | 11.2 | 11.2 |
| SD | 1.9 | 1.7 | 1.9 | 1.7 | 2.5 | 2.3 | 2.4 | 2.1 |
| [11C]CUMI-101 | ||||||||
| sub 1 | 2.5 | 2.7 | 3.1 | 3.7 | 4.8 | 5.1 | 5.0 | 5.2 |
| sub 2 | 2.6 | 2.3 | 2.9 | 2.7 | 4.8 | 4.8 | 4.9 | 4.8 |
| sub 3 | 2.4 | 2.4 | 3.1 | 2.9 | 4.9 | 4.6 | 5.1 | 4.8 |
| sub 4 | 2.5 | 3.1 | 3.4 | 3.6 | 5.6 | 5.5 | 5.7 | 5.8 |
| sub 5 | 3.1 | 2.6 | 3.6 | 3.7 | 6.1 | 7.2 | 6.1 | 6.7 |
| sub 6 | 1.6 | 2.4 | 2.6 | 3.5 | 5.5 | 5.9 | 5.8 | 6.1 |
| mean | 2.5 | 2.6 | 3.1 | 3.4 | 5.3 | 5.5 | 5.4 | 5.5 |
| SD | 0.5 | 0.3 | 0.4 | 0.4 | 0.5 | 1.0 | 0.5 | 0.8 |
Test-retest PDVND-TRT values for VND (Table 4) from the different methods are not statistically significantly different from each other, with the exception of [11C]DASB, in which case PDVND-TRT values obtained by HYDECA are statistically significantly higher (indicating worse reproducibility) than those derived by LEGA (p-values: 0.003 with β and γ set via simulation; 0.002 with β and γ set via blocking study). See Discussion for factors affecting the reproducibility of VND by HYDECA.
Table 4. Test-retest PDVND percent difference values for HYDECA VND, VT-RR,LEGA and VT-RR,2TCM.
| VND TEST-RETEST PERCENT DIFFERENCE | ||||
|---|---|---|---|---|
| HYDECA (βopt-S, γopt-S) | HYDECA (βopt-B, γopt-B) | 2TCM | LEGA | |
| [11C]DASB | ||||
| pair #1 | 4.83% | 8.08% | 1.65% | 1.68% |
| pair #2 | 12.99% | 10.81% | 0.47% | 0.47% |
| pair #3 | 5.97% | 9.38% | 0.58% | 0.58% |
| pair #4 | 20.22% | 22.22% | 1.30% | 3.01% |
| pair #5 | 9.35% | 10.10% | 1.54% | 1.10% |
| pair #6 | 8.70% | 10.39% | 15.39% | 2.47% |
| pair #7 | 12.84% | 12.21% | 2.82% | 11.49% |
| pair #8 | 3.55% | 4.88% | 28.55% | 2.82% |
| pair #9 | 6.70% | 3.02% | 1.89% | 1.72% |
| pair #10 | 12.24% | 8.45% | 33.27% | 5.78% |
| mean | 9.74% | 9.95% | 8.75% | 3.11% |
| SD | 4.98% | 5.13% | 12.53% | 3.32% |
| [11C]CUMI-101 | ||||
| pair #1 | 7.69% | 17.65% | 5.07% | 3.91% |
| pair #2 | 12.24% | 7.14% | 0.37% | 2.27% |
| pair #3 | 0.00% | 6.67% | 7.05% | 5.99% |
| pair #4 | 21.43% | 5.71% | 2.90% | 1.58% |
| pair #5 | 17.54% | 2.74% | 16.86% | 9.42% |
| pair #6 | 40.00% | 29.51% | 6.79% | 3.62% |
| mean | 16.48% | 11.57% | 6.51% | 4.46% |
| SD | 13.75% | 10.15% | 5.66% | 2.86% |
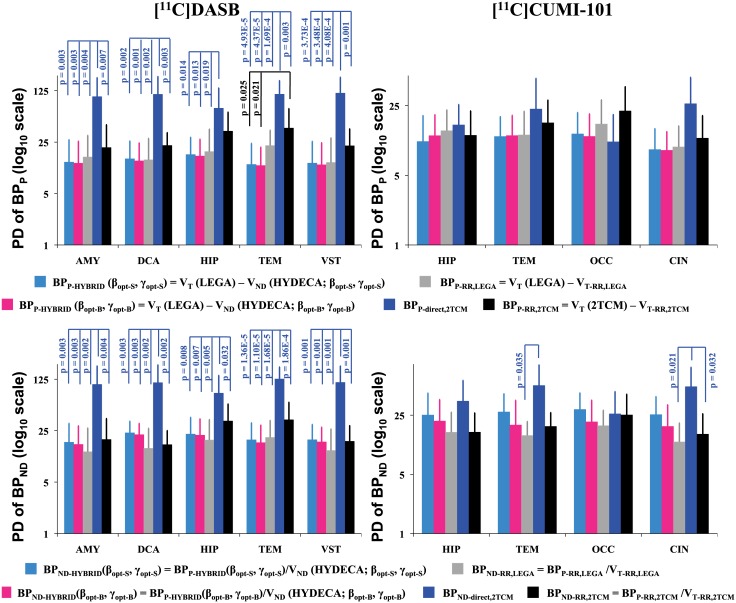
Reproducibility of the binding potentials estimated using HYDECA VND, with β and γ optimized using either strategies, is compared to that of binding potentials based on VT-RR,LEGA, VT-RR,2TCM, or direct estimation by 2TCM in Fig 6. PDBPP values obtained using HYDECA with either sets of optimized tuning parameters are close to each other and comparable to values obtained using VT-RR,LEGA. PDBPP values from the different methods are not statistically significantly different from each other, with the exception of 2TCM direct estimation, where PDBPP values are statistically significantly higher (indicating worse reproducibility) than those of all other methods in the case of [11C]DASB in all brain regions except HIP (range of p-values: 4.37E-5 to 0.019), and of 2TCM indirect estimation in the case of [11C]DASB in TEM, for which PDBPP values are statistically significantly higher than those derived by HYDECA (p-values: 0.025 with β and γ set via simulation; 0.021 with β and γ set via blocking study).
Fig 6. Reproducibility of binding potentials estimated using HYDECA, LEGA, and 2TCM.
Average plus standard deviation (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPP values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using BPP based on VND from HYDECA, BPP based on VT-RR,LEGA, BPP calculated directly from the 2TCM kinetic rates, and BPP based on VT-RR,2TCM (top). Corresponding values for the test-retest percent difference PDBPND (bottom). Vertical axes are reported in logarithmic scale to allow for easier visualization of the direct 2TCM results based on 2TCM kinetic rates. Statistically significant comparisons (p-value ≤ 0.05) are indicated. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP; PDBPND: percent difference for BPND; VND: non-displaceable distribution volume; VT-RR,LEGA: tracer total distribution volume in the non-ideal reference region estimated using LEGA; LEGA: Likelihood Estimation in Graphical Analysis; 2TCM: two-tissue compartment model; VT-RR,2TCM: racer total distribution volume in the non-ideal reference region estimated using 2TCM.
Similarly, PDBPND values from the different methods are not statistically significantly different from each other, with the exception of 2TCM direct estimation in the case of [11C]DASB in all regions (PDBPND values statistically significantly higher than those of all other methods; range of p-values: 1.10E-5 to 0.032), and 2TCM direct estimation in the case of [11C]CUMI-101 in TEM and CIN, for which PDBPND values are statistically significantly higher than those derived by LEGA (p-values: 0.035 in TEM; 0.021 in CIN) and by 2TCM indirect estimation (p-value: 0.032 in CIN).
Overall, the test-retest reproducibility of binding potentials obtained using all methods reported in Fig 6 are comparable, with the exception of 2TCM direct estimation in the case of [11C]DASB.
Discussion
HYDECA is a data-driven approach that estimates VND for each individual based on his/her PET data from multiple brain regions. HYDECA is intended for tracers and targets for which a valid reference region does not exist. If a valid reference region does in fact exist, then binding potentials based on VT-RR or on reference region approaches are likely to be more accurate than those based on HYDECA.
Tuning parameters
HYDECA implementation requires determination of two tuning parameters, herein denoted β and γ, and we propose two possible strategies to make this choice for a given tracer: using data from blocking studies, or realistic simulations of the tracer in question. It should be noted that using the same tuning parameters across subjects imaged with the same tracer does not result in estimating the same VND in each subject.
Of the two strategies, the one using blocking studies involves less subjective judgment. When blocking study data are not available, simulations can be used, but simulated VND values, kinetic rates, and measurement errors should be chosen carefully to obtain realistic representation of the data with the tracer in question. For established tracers, simulations can be set up using kinetic rate values derived from available data or from the literature. For a new tracer, both simulations and validation with blocking studies are recommended.
For [11C]DASB and [11C]CUMI-101, our results suggest that, regardless of the strategy used to optimize the tuning parameters, HYDECA estimates of VND are considerably less biased than those obtained based on VT-RR. Even with a “sub-optimal” choice of the tuning parameters, HYDECA estimates of VND are generally less biased than using a non-ideal reference region (Figs 2 and 4). Although the selection strategies can provide different values for β and γ, the resulting bias in the estimation of VND is similar (|errHYDs|/|errHYDb| ratios in Fig 4).
If we were to optimize β and γ individually for each subject in the blocking datasets, we would observe quite large inter-subject variability in the optimal β and γ: β = 8.85 ± 4.64, γ = 19.77 ± 11.80 ([11C]DASB); β = 9.31 ± 5.04, γ = 18.38 ± 12.37 ([11C]CUMI-101). For subjects in the dataset that is used for tuning parameter selection, using individually optimized β and γ instead of values optimized on average across subjects, as we suggest, would lead to an even less biased VND estimation. However, the question of which β and γ values to use when applying HYDECA to a subject imaged with the same tracer, but for which a blocking scan is not available, would remain. Individually optimized β and γ values are not obtainable in standard practice.
Utility
HYDECA is a workable algorithm that can be applied to estimate individual VND in absence of a reference region or individual blocking data, and could therefore be extremely useful in both clinical and research settings. If the target selected for a given PET application lacks a valid reference region, there is no way to accurately estimate VND (and consequently specific binding to the target), unless one performs a blocking scan for each subject. HYDECA can provide an alternative convenient quantification approach. For tracers for which HYDECA tuning parameters have already been determined, the published optimized tuning parameters can be used. Otherwise, published blocking studies for the tracer in question would constitute the basis to either tune HYDECA directly (if data are accessible) or to set up a simulation.
Reproducibility
HYDECA estimates of VND (with either strategy to set tuning parameters) lead to binding potentials estimates with test-retest reproducibility that are comparable to estimates based on VT-RR. Note that average PDBPP values are overall lower when based on HYDECA compared with values based on VT-RR, and not merely because VND estimates by HYDECA are consistently lower than corresponding VT-RR. Detailed related information is provided in the Supplementary Materials (S3 and S4 Figs, S2 Text). We observe on average worse reproducibility of the estimates based on HYDECA when considering BPND compared to BPP estimates. Because of the nature of the outcome measure and performance metric used here, BPND values and their corresponding test-retest performance are more sensitive than BPP to values and changes (in between test and retest scan) in the VND, which appears at the denominator in the indirect definition of BPND. When using the VT from an invalid reference region to estimate VND, reproducibility of that measure depends on, among other factors, how much the tissue time activity curve from that region changes between the test and the retest scans. HYDECA, instead, uses tissue time activity curves from multiple regions to determine VND, and therefore its test-retest performance is affected, among other factors, by how much the tissue time activity curves from all of these regions change between the test and the retest scans. The test-retest percent difference values for HYDECA VND (Table 4) are on average worse than those for VT-RR calculated using 2TCM and LEGA, especially in the case of [11C]CUMI-101. Reproducibility performance should be considered when deciding which approach to use in longitudinal studies, while the bias of the approach is more important in group comparisons and cross-sectional studies.
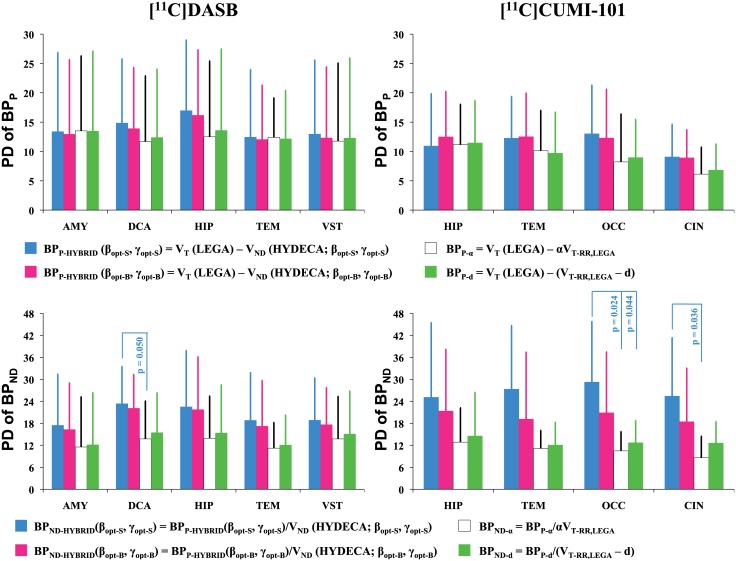
Alternative strategies
If blocking scans are available for a certain tracer, they could be used to estimate a population-based α = VND_LASSEN/VT-RR ratio, which could then be used for studies with the same tracer to scale each subject VT-RR in the non-ideal reference region to estimate VND. We applied such approach to the two available blocking datasets. We found the following VND_LASSEN/VT-RR,LEGA average (± SD) α ratios: 0.710 (± 0.114) for [11C]DASB, and 0.619 (± 0.145) for [11C]CUMI-101. We applied such ratios to the subjects in the available test-retest datasets to calculate a scaled VT-RR,LEGA, and then calculated the corresponding BPP-α = VT(LEGA)—αVT-RR,LEGA and BPND-α = BPP-α/αVT-RR,LEGA values and their test-retest percent difference (Fig 7). Test-retest percent differences values obtained using the different methods reported in Fig 7 are not statistically significantly different from each other in the case of BPP, nor in the case of BPND, with the exception of [11C]DASB BPND in DCA, and [11C]CUMI-101 BPND in OCC and CIN, for which percent differences values obtained using a population-based α ratio are statistically significantly lower (indicating better reproducibility) than those based on HYDECA with β and γ set via simulation (p-value: 0.050, 0.024, and 0.036, respectively). Also see comments on BPND reproducibility in “Reproducibility” section above.
Fig 7. Reproducibility of binding potentials estimated using HYDECA and alternative strategies based on blocking studies.
Average plus standard deviation (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPP values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using BPP based on VND from HYDECA, BPP based on scaled VT-RR,LEGA, and BPP based on average distance d (top). Corresponding values for test-retest percent difference PDBPND (bottom). Statistically significant comparisons (p-value ≤ 0.05) are indicated. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP; PDBPND: percent difference for BPND; VND: non-displaceable distribution volume; VT-RR,LEGA: tracer total distribution volume in the non-ideal reference region estimated using LEGA; LEGA: Likelihood Estimation in Graphical Analysis.
From a compartment modeling point of view, however, if there is specific binding in the non-ideal reference region, this would correspond to an additional compartment, which would require a subtraction (rather than a multiplicative adjustment) from the total VT in the region, in order to be properly accounted for. A population-based distance d = VT-RR−VND_LASSEN can be derived if blocking scans are available for a certain tracer as in the case of the scaled VT-RR. In the two available blocking studies, we found the following average VT-RR,LEGA−VND_LASSEN distance (± SD) d: 3.04 (± 1.56) for [11C]DASB, and 2.14 (± 0.92) for [11C]CUMI-101. We applied such average distance values to the subjects in the available test-retest datasets to calculate BPP-d = VT(LEGA)–(VT-RR,LEGA−d) and BPND-d = BPP-d/(VT-RR,LEGA−d), and their test-retest percent difference (Fig 7). Test-retest percent differences values of binding potentials obtained using a population-based distance d are not statistically significantly different from those of the other methods, with the exception of [11C]CUMI-101 BPND in OCC, where they are statistically significantly lower than those obtained based on HYDECA with β and γ set via simulation (p-value: 0.044). The reproducibility performance of HYDECA with tuning parameters set via blocking study is comparable to that of all the other methods for both binding potentials.
A fixed population-based ratio or distance approach, unlike HYDECA, would not take advantage of the information relative to VND that is implicitly contained in each individual’s PET tissue data across brain regions. Such an approach would rely on blocking studies more heavily than HYDECA, for which tuning parameter selection can alternatively be achieved using simulations.
In the Supplementary Materials (S1 and S2 Figs, S1 Text) we report results obtained on alternative nonparametric binding potentials [26] that can be calculated based on HYDECA, including their test-retest reproducibility and the comparison to 2TCM, LEGA, and alternative strategies.
Choice of regions
Regions that are simultaneously considered should be carefully chosen in all approaches that either take advantage of simultaneous estimation across regions [25, 33–37], or jointly estimate common parameters of interest across regions, like occupancy and VND in the Lassen plot. For simultaneous estimation approaches to perform well, the regions that are considered should in general have kinetic behavior as distinct as possible [36]. Including regions with similar kinetic behavior would serve only to increase the dimensionality of the objective function without adding much useful information [36]. The variety in kinetic behavior depends greatly on the tracer at hand. In our previous experience with simultaneous-type estimation with [11C]DASB [33] and [11C]CUMI-101 [25], we had carefully selected regions to represent a broad range of kinetic behavior, while avoiding regions that tend to be noisy. We had also previously assessed the properties of nonparametric quantification in these regions using both simulated and clinical data [26]. We are therefore using the same regions in this study.
Choice of deconvolution approach
We used here SVD for its speed and ease of implementation, and have characterized its performance in terms of reproducibility and sensitivity to noise in an earlier publication [26]. SVD can however be sensitive to potential delay and dispersion of the injected bolus [38, 39]. More robust approaches to nonparametric deconvolution [39, 40] or functional principal components analysis [41] may further improve HYDECA performance. Here we provide a framework for HYDECA and comparison between different implementations of the algorithm is beyond our scope.
Limitations
Vascular correction
The tracer signal in the brain tissue can be modeled as in Eq (1) only after correction for intravascular activity. Here, following a practice common in the field, we assumed a brain-wide fractional blood volume (VB) of 5%. It is recommended that the VB value be optimized before applying HYDECA (or any other PET quantification approach) if pathological changes in the fractional blood volume are suspected in the population at hand. HYDECA performance, as that of any PET quantification approach, may in fact be affected by an erroneous choice of the VB value used to correct the tissue time activity curves. We ran an additional simulation to investigate the sensitivity of HYDECA estimates of VND to a potentially erroneous vascular correction of the measured time activity curves (details are reported in the Supplementary Materials, S5–S7 Figs, S3 Text). HYDECA estimates of VND appear to be robust to erroneous correction of the time activity curves for errors in VB in the range -4% to +5% for [11C]DASB, and -4% to +7% for [11C]CUMI-101.
As blood volume may vary in the brain, using a brain-wide value may not significantly impact outcome measures such as VT and binding potentials, but may impact the upslope of the tissue signal, and thus the Ri(t) estimated nonparametrically. If VB varies across regions, a case that is not trivial for any of the quantification approaches used in PET, one potential strategy to account for this within HYDECA could be incorporating the vascular correction component into the impulse response function that is nonparametrically deconvolved in each region. The problem may be treatable from a mathematical point of view, but would require careful comparison of more sophisticated approaches to deconvolution than SVD. Another potential strategy could be exploiting the semiparametric nature of HYDECA and adding VB as a free-parameter to be estimated in each of the regions that are simultaneously considered, but this would require a more complex optimization procedure than the simple grid approach that we proposed for VND. Correction for intravascular activity represents just as much of a problem for other approaches proposed as alternatives to compartment models [42, 43].
Assumption of a mono-exponential RND(t) curve
To ensure identifiability of the two components of the residue function curve R(t) (non-displaceable and specific), HYDECA needs to assume a certain shape to describe the non-displaceable component, RND(t). We chose, in part for its simplicity, a mono-exponential function, which would represent the impulse response function in the case of an “ideal” reference region with total distribution volume equal to VND. Assuming a mono-exponential curve for RND(t) represents an approximation: if a 2TCM is needed to describe the data in a given region, the RND(t) curve of the region would be more appropriately described by a two-exponential function (24). We note that a similar assumption is central in the development of the very widely used simplified reference tissue model (SRTM) [44], which assumes that the total (non-displaceable plus specific) impulse response function of the target region (which, as well, would be a two-exponential function) can be reasonably approximated by a mono-exponential curve. The Supplementary Materials (S8 and S9 Figs, S4 Text) report data to evaluate the validity of such approximation for the two tracers considered here. Our evaluation indicates that a mono-exponential approximation for RND(t) would be problematic only in the situation in which k3 >> k4, which means that more tracer molecules transit in a given amount of time from the non-displaceable binding state into the specific binding state than vice versa. We recommend that the simplifying assumption of a mono-exponential RND(t) curve be evaluated for tracers for which it is suspected that k3 >> k4. However, we remind the reader: 1) that HYDECA uses data across many regions, for some of which the mono-exponential assumption may hold better than for others, and provides a brain-wide value of VND that satisfies certain constraints (via the HYDECA cost function) on average across such regions; and 2) that parts of the RND(t) curve that are potentially erroneously determined in a region due to the simplifying mono-exponential assumption are likely to be captured by the corresponding nonparametric RS(t) curve, for which there is no assumption besides being positive and monotonic. We want also to stress that the assumption of a common, brain-wide VND implies that the ratio of the transfer constants (VND = K1/k2) is the same everywhere in the brain for non-specific binding. This same assumption is routinely made when using CMs and/or graphical approaches in a reference region to estimate a brain-wide common VND, when constraining the K1 and k2 parameters in a 2TCM to those of a reference region, or when using SRTM.
Applicability to other populations
The two assumptions required to apply HYDECA are that: a) the non-displaceable distribution volume VND is uniform brain-wide within each subject (which is the same assumption regularly considered in the field when estimating VND from a reference region, or when using SRTM); and b) the non-displaceable component of the residue function, RND(t), is reasonably described by a mono-exponential function (a similar assumption is considered for both reference and target region when using SRTM). So unless there is a population or group of subjects where it is suspected that these two assumptions are seriously violated, HYDECA can be applied. The presence of altered kinetics in the tissue time activity curves of such a population would be problematic for any of the other PET quantification approaches that are based on the assumptions above.
Future investigations
Future investigations include developing a method to provide a measure of precision [45] for HYDECA VND estimates, validating HYDECA across tracers, and assessing whether performing the tuning of β and γ only once for a given tracer will suffice, which should be the case if the noise characteristics and kinetics range of independent data acquired with a tracer for which the HYDECA tuning parameters have been determined will resemble those of the data used in such determination.
Conclusions
We showed, using two PET radiotracers that, in the absence of a valid reference region, HYDECA can provide individual estimates of a brain-wide VND without requiring a blocking study, and these estimates are less biased, with respect to estimation with Lassen plot, which is the method of reference, as it represents a standard in the field for in vivo estimation of VND in humans, than those obtained relying on the VT in a non-ideal reference region.
Supporting information
Average (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPP values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using the two nonparametric definitions of BPP: BPP-END (top), and BPP-NP2 (bottom) (see definitions in S1 Text). In each plot, grey bars refer to BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; black bars refer to BPP-RR,2TCM = VT (2TCM)–VT-RR,2TCM; white bars refer to BPP-α = VT(LEGA)—αVT-RR,LEGA; and green bars refer to BPP-d = VT(LEGA)–(VT-RR,LEGA−d). Error bars indicate standard deviation (across test-retest pairs of scans within each tracer). Vertical axes are reported in logarithmic scale to allow for easier visualization of the 2TCM results. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP. VT (LEGA): tracer total distribution volume (VT) estimated using Likelihood Estimation in Graphical Analysis (LEGA); VT-RR,LEGA: VT in the purported reference region estimated using LEGA; VT (2TCM): VT estimated using a two-tissue compartment model (2TCM); VT-RR,2TCM: VT in the purported reference region estimated using 2TCM; α: population-based ratio of non-displaceable distribution volume (VND) (from available blocking studies) over VT in the purported reference region; d: population-based distance of VT in the purported reference region and corresponding VND (from available blocking studies).
(PDF)
Average (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPND values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using the two nonparametric definitions of BPND: BPND-END (top), and BPND-NP2 (bottom) (see definitions in S1 Text). In each plot, grey bars refer to BPND-RR,LEGA; black bars refer to BPND-RR,2TCM; white bars refer to BPND-α; and green bars refer to BPND-d. Error bars indicate standard deviation (across test-retest pairs of scans within each tracer). Vertical axes are reported in logarithmic scale to allow for easier visualization of the 2TCM results. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP. BPND-RR,LEGA = BPP-RR,LEGA/VT-RR,LEGA = [VT (LEGA)–VT-RR,LEGA]/VT-RR,LEGA; BPND-RR,2TCM = BPP-RR,2TCM/VT-RR,2TCM = [VT (2TCM)–VT-RR,2TCM]/VT-RR,2TCM; BPND-α = BPP-α/αVT-RR,LEGA = [VT(LEGA)—αVT-RR,LEGA]/αVT-RR,LEGA; BPND-d = BPP-d/(VT-RR,LEGA−d) = [VT(LEGA)–(VT-RR,LEGA−d)]/(VT-RR,LEGA−d). VT (LEGA): tracer total distribution volume (VT) estimated using Likelihood Estimation in Graphical Analysis (LEGA); VT-RR,LEGA: VT in the purported reference region estimated using LEGA; VT (2TCM): VT estimated using a two-tissue compartment model (2TCM); VT-RR,2TCM: VT in the purported reference region estimated using 2TCM; α: population-based ratio of non-displaceable distribution volume (VND) (from available blocking studies) over VT in the purported reference region; d: population-based distance of VT in the purported reference region and corresponding VND (from available blocking studies).
(PDF)
Left: Scatter plots of BPP-HYBRID, BPP-END, and BPP-NP2 (see definitions in S1 and S2 Texts) values versus BPP-RR,LEGA values obtained using the non-ideal reference region and Likelihood Estimation in Graphical Analysis (LEGA). The black solid line is the identity line. Right: Distance between test-retest percent difference (PD) values obtained using BPP-HYBRID and PD values obtained using BPP-RR,LEGA (y axis) versus the corresponding distance between BPP-HYBRID (average of test and re-test) and BPP-RR,LEGA (average of test and re-test). Open circles represent values obtained using the non-displaceable distribution volume (VND) from HYDECA with βopt-S and γopt-S; solid circles represent values obtained using the VND from HYDECA with βopt-B and γopt-B. BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; VT (LEGA): tracer total distribution volume (VT) estimated using LEGA; VT-RR,LEGA: VT in the purported reference region estimated using LEGA.
(PDF)
Left: Scatter plots of BPP-HYBRID, BPP-END, and BPP-NP2 (see definitions in S1 and S2 Texts) values versus BPP-RR,LEGA values obtained using the non-ideal reference region and Likelihood Estimation in Graphical Analysis (LEGA). The black solid line is the identity line. Right: Distance between test-retest percent difference (PD) values obtained using BPP-HYBRID and PD values obtained using BPP-RR,LEGA (y axis) versus the corresponding distance between BPP-HYBRID (average of test and re-test) and BPP-RR,LEGA (average of test and re-test). Open circles represent values obtained using the non-displaceable distribution volume (VND) from HYDECA with βopt-S and γopt-S; solid circles represent values obtained using the VND from HYDECA with βopt-B and γopt-B. BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; VT (LEGA): tracer total distribution volume (VT) estimated using LEGA; VT-RR,LEGA: VT in the purported reference region estimated using LEGA.
(PDF)
Percent difference (PDerrVC) between the non-displaceable distribution volume (VND) value estimated at each instance of erroneously corrected time activity curves and the VND value estimated in correspondence of the accurately corrected set of time activity curves (y-axis), as a function of the difference between the true fractional blood volume (VB) value and the value adopted for correction (x-axis); dots and error bars indicate average and standard deviation across subjects, respectively, within each tracer. The dotted horizontal lines indicate the +10%, 0%, and -10% mark, respectively.
(PDF)
Residue function curves R(t) in correspondence of different errors and no error in the fractional blood volume value (VB), and the corresponding HYDECA cost functions, in a representative subject for [11C]CUMI-101. CIN: cingulate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; CGM: cerebellum grey matter.
(PDF)
Residue function curves R(t) in correspondence of different errors and no error in the fractional blood volume value (VB), and the corresponding HYDECA cost functions, in a representative subject for [11C]DASB. AMY: amygdala; DCA: dorsal caudate; HIP: hippocampus; TEM: temporal lobe; VST: ventral striatum; CGM: cerebellum grey matter.
(PDF)
Average (across time points) square distance between the residue function non-displaceable component, RND(t) (see S4 Text), with k3 and k4 >0, and RND(t) with k3 = k4 = 0 as k3 and k4 vary, in 4 cases of (K1, k2) for [11C]DASB. VST: ventral striatum; CGM: cerebellum grey matter. K1, k2 k3 and k4: kinetic rate parameters of a two-tissue compartment model.
(PDF)
Average (across time points) square distance between the residue function non-displaceable component, RND(t) (see S4 Text), with k3 and k4 >0, and RND(t) with k3 = k4 = 0 as k3 and k4 vary, in 4 cases of (K1, k2) for [11C]CUMI-101. HIP: hippocampus; CGM: cerebellum grey matter. K1, k2 k3 and k4: kinetic rate parameters of a two-tissue compartment model.
(PDF)
Supporting information and equations accompanying S1 and S2 Figs.
(PDF)
Supporting information and equations accompanying S3 and S4 Figs.
(PDF)
Supporting information and equations accompanying S5–S7 Figs.
(PDF)
Supporting information and equations accompanying S8 and S9 Figs.
(PDF)
Data Availability
We used data from published blocking studies in baboons (Milak MS, Severance AJ, Ogden RT, Prabhakaran J, Kumar JS, Majo VJ, et al. Modeling considerations for 11C-CUMI-101, an agonist radiotracer for imaging serotonin 1A receptor in vivo with PET. J. Nucl. Med. 2008;49:587-96) and humans (Parsey RV, Kent JM, Oquendo MA, Richards MC, Pratap M, Cooper TB, et al. Acute occupancy of brain serotonin transporter by sertraline as measured by [11C]DASB and positron emission tomography. Biol. Psychiatry. 2006;59:821-8), and test-retest datasets in humans (Milak MS, DeLorenzo C, Zanderigo F, Prabhakaran J, Kumar JS, Majo VJ, et al. In vivo quantification of human serotonin 1A receptor using 11C-CUMI-101, an agonist PET radiotracer. J. Nucl. Med. 2010;51:1892-900; Ogden RT, Ojha A, Erlandsson K, Oquendo MA, Mann JJ, Parsey RV. In vivo quantification of serotonin transporters using [(11)C]DASB and positron emission tomography in humans: modeling considerations. J. Cereb. Blood Flow Metab. 2007;27:205-17). Matlab code that implements HYDECA is freely available through GitHub at the following link https://github.com/FrancescaZanderigo/hybrid-deconvolution-approach.
Funding Statement
The authors received no specific funding for this work.
References
- 1.Laruelle M, Slifstein M, Huang Y. Relationships between radiotracer properties and image quality in molecular imaging of the brain with positron emission tomography. Mol Imaging Biol. 2003;5(6):363–75. Epub 2003/12/12. [DOI] [PubMed] [Google Scholar]
- 2.Innis RB, Cunningham VJ, Delforge J, Fujita M, Gjedde A, Gunn RN, et al. Consensus nomenclature for in vivo imaging of reversibly binding radioligands. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2007;27(9):1533–9. Epub 2007/05/24. [DOI] [PubMed] [Google Scholar]
- 3.Slifstein M, Laruelle M. Models and methods for derivation of in vivo neuroreceptor parameters with PET and SPECT reversible radiotracers. Nuclear medicine and biology. 2001;28(5):595–608. Epub 2001/08/23. [DOI] [PubMed] [Google Scholar]
- 4.Lassen NA, Bartenstein PA, Lammertsma AA, Prevett MC, Turton DR, Luthra SK, et al. Benzodiazepine receptor quantification in vivo in humans using [11C]flumazenil and PET: application of the steady-state principle. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 1995;15(1):152–65. Epub 1995/01/01. [DOI] [PubMed] [Google Scholar]
- 5.Cunningham VJ, Rabiner EA, Slifstein M, Laruelle M, Gunn RN. Measuring drug occupancy in the absence of a reference region: the Lassen plot re-visited. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2010;30(1):46–50. Epub 2009/09/10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ametamey SM, Treyer V, Streffer J, Wyss MT, Schmidt M, Blagoev M, et al. Human PET studies of metabotropic glutamate receptor subtype 5 with 11C-ABP688. Journal of nuclear medicine: official publication, Society of Nuclear Medicine. 2007;48(2):247–52. Epub 2007/02/03. [PubMed] [Google Scholar]
- 7.DeLorenzo C, Kumar JS, Zanderigo F, Mann JJ, Parsey RV. Modeling considerations for in vivo quantification of the dopamine transporter using [(11)C]PE2I and positron emission tomography. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2009;29(7):1332–45. Epub 2009/05/22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ginovart N, Meyer JH, Boovariwala A, Hussey D, Rabiner EA, Houle S, et al. Positron emission tomography quantification of [11C]-harmine binding to monoamine oxidase-A in the human brain. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2006;26(3):330–44. Epub 2005/08/05. [DOI] [PubMed] [Google Scholar]
- 9.Henriksen G, Willoch F. Imaging of opioid receptors in the central nervous system. Brain. 2008;131(5):1171–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Milak MS, DeLorenzo C, Zanderigo F, Prabhakaran J, Kumar JS, Majo VJ, et al. In vivo quantification of human serotonin 1A receptor using 11C-CUMI-101, an agonist PET radiotracer. Journal of nuclear medicine: official publication, Society of Nuclear Medicine. 2010;51(12):1892–900. Epub 2010/11/26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Parsey RV, Kent JM, Oquendo MA, Richards MC, Pratap M, Cooper TB, et al. Acute occupancy of brain serotonin transporter by sertraline as measured by [11C]DASB and positron emission tomography. Biological psychiatry. 2006;59(9):821–8. Epub 2005/10/11. 10.1016/j.biopsych.2005.08.010 [DOI] [PubMed] [Google Scholar]
- 12.Turkheimer FE, Edison P, Pavese N, Roncaroli F, Anderson AN, Hammers A, et al. Reference and target region modeling of [11C]-(R)-PK11195 brain studies. Journal of nuclear medicine: official publication, Society of Nuclear Medicine. 2007;48(1):158–67. Epub 2007/01/06. [PubMed] [Google Scholar]
- 13.Ishibashi K, Robertson C, London E, Mandelkern M. Is the cerebellum the best reference region for a PET study with [F-18]-fallypride? Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2012;32:S178. [Google Scholar]
- 14.Litton JE, Hall H, Pauli S. Saturation analysis in PET—analysis of errors due to imperfect reference regions. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 1994;14(2):358–61. Epub 1994/03/01. [DOI] [PubMed] [Google Scholar]
- 15.Jucaite A, Odano I, Olsson H, Pauli S, Halldin C, Farde L. Quantitative analyses of regional [11C]PE2I binding to the dopamine transporter in the human brain: a PET study. European journal of nuclear medicine and molecular imaging. 2006;33(6):657–68. Epub 2006/03/04. 10.1007/s00259-005-0027-9 [DOI] [PubMed] [Google Scholar]
- 16.Turkheimer FE, Selvaraj S, Hinz R, Murthy V, Bhagwagar Z, Grasby P, et al. Quantification of ligand PET studies using a reference region with a displaceable fraction: application to occupancy studies with [(11)C]-DASB as an example. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2012;32(1):70–80. Epub 2011/08/04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parsey RV, Arango V, Olvet DM, Oquendo MA, Van Heertum RL, John Mann J. Regional heterogeneity of 5-HT1A receptors in human cerebellum as assessed by positron emission tomography. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2005;25(7):785–93. Epub 2005/02/18. [DOI] [PubMed] [Google Scholar]
- 18.Parsey RV, Ogden RT, Miller JM, Tin A, Hesselgrave N, Goldstein E, et al. Higher serotonin 1A binding in a second major depression cohort: modeling and reference region considerations. Biological psychiatry. 2010;68(2):170–8. Epub 2010/05/26. 10.1016/j.biopsych.2010.03.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oquendo MA, Hastings RS, Huang YY, Simpson N, Ogden RT, Hu XZ, et al. Brain serotonin transporter binding in depressed patients with bipolar disorder using positron emission tomography. Archives of general psychiatry. 2007;64(2):201–8. Epub 2007/02/07. 10.1001/archpsyc.64.2.201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ito H, Sudo Y, Suhara T, Okubo Y, Halldin C, Farde L. Error analysis for quantification of [(11)C]FLB 457 binding to extrastriatal D(2) dopamine receptors in the human brain. NeuroImage. 2001;13(3):531–9. Epub 2001/02/15. 10.1006/nimg.2000.0717 [DOI] [PubMed] [Google Scholar]
- 21.Yaqub M, van Berckel BN, Schuitemaker A, Hinz R, Turkheimer FE, Tomasi G, et al. Optimization of supervised cluster analysis for extracting reference tissue input curves in (R)-[(11)C]PK11195 brain PET studies. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2012;32(8):1600–8. Epub 2012/05/17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gunn RN, Murthy V, Catafau AM, Searle G, Bullich S, Slifstein M, et al. Translational characterization of [11C]GSK931145, a PET ligand for the glycine transporter type 1. Synapse. 2011;65(12):1319–32. 10.1002/syn.20966 [DOI] [PubMed] [Google Scholar]
- 23.Veronese M, Zanotti-Fregonara P, Rizzo G, Bertoldo A, Innis RB, Turkheimer FE. Measuring specific receptor binding of a PET radioligand in human brain without pharmacological blockade: The genomic plot. NeuroImage. 2016;130:1–12. 10.1016/j.neuroimage.2016.01.058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gunn RN, Gunn SR, Cunningham VJ. Positron emission tomography compartmental models. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2001;21(6):635–52. [DOI] [PubMed] [Google Scholar]
- 25.Todd Ogden R, Zanderigo F, Parsey RV. Estimation of in vivo nonspecific binding in positron emission tomography studies without requiring a reference region. NeuroImage. 2015;108:234–42. 10.1016/j.neuroimage.2014.12.038 [DOI] [PubMed] [Google Scholar]
- 26.Zanderigo F, Parsey RV, Todd Ogden R. Model-free quantification of dynamic PET data using nonparametric deconvolution. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2015. Epub 2015/04/16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Milak MS, Severance AJ, Ogden RT, Prabhakaran J, Kumar JS, Majo VJ, et al. Modeling considerations for 11C-CUMI-101, an agonist radiotracer for imaging serotonin 1A receptor in vivo with PET. Journal of nuclear medicine: official publication, Society of Nuclear Medicine. 2008;49(4):587–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ogden RT, Ojha A, Erlandsson K, Oquendo MA, Mann JJ, Parsey RV. In vivo quantification of serotonin transporters using [(11)C]DASB and positron emission tomography in humans: modeling considerations. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2007;27(1):205–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.O'Sullivan F, Muzi M, Spence AM, Mankoff DM, O'Sullivan JN, Fitzgerald N, et al. Nonparametric Residue Analysis of Dynamic PET Data With Application to Cerebral FDG Studies in Normals. J Am Stat Assoc. 2009;104(486):556–71. Epub 2009/10/16. 10.1198/jasa.2009.0021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ogden RT. Estimation of kinetic parameters in graphical analysis of PET imaging data. Statistics in medicine. 2003;22(22):3557–68. Epub 2003/11/06. 10.1002/sim.1562 [DOI] [PubMed] [Google Scholar]
- 31.Eberl S, Katsifis A, Peyronneau MA, Wen L, Henderson D, Loc'h C, et al. Preclinical in vivo and in vitro comparison of the translocator protein PET ligands [18F]PBR102 and [18F]PBR111. European journal of nuclear medicine and molecular imaging. 2017;44(2):296–307. 10.1007/s00259-016-3517-z [DOI] [PubMed] [Google Scholar]
- 32.Naganawa M, Jacobsen LK, Zheng MQ, Lin SF, Banerjee A, Byon W, et al. Evaluation of the agonist PET radioligand [(1)(1)C]GR103545 to image kappa opioid receptor in humans: kinetic model selection, test-retest reproducibility and receptor occupancy by the antagonist PF-04455242. NeuroImage. 2014;99:69–79. 10.1016/j.neuroimage.2014.05.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ogden RT, Zanderigo F, Choy S, Mann JJ, Parsey RV. Simultaneous estimation of input functions: an empirical study. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2010;30(4):816–26. Epub 2009/12/10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wong KP, Feng D, Meikle SR, Fulham MJ. Simultaneous estimation of physiological parameters and the input function—in vivo PET data. IEEE Trans Inf Technol Biomed. 2001;5(1):67–76. Epub 2001/04/13. [DOI] [PubMed] [Google Scholar]
- 35.Guo H, Renaut RA, Chen K. An input function estimation method for FDG-PET human brain studies. Nuclear medicine and biology. 2007;34(5):483–92. Epub 2007/06/27. 10.1016/j.nucmedbio.2007.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wong KP, Meikle SR, Dagan F, Fulham MJ. Estimation of input function and kinetic parameters using simulated annealing: application in a flow model. Nuclear Science, IEEE Transactions on. 2002;49(3):707–13. [Google Scholar]
- 37.Riabkov DY, Di Bella EVR. Estimation of kinetic parameters without input functions: analysis of three methods for multichannel blind identification. Biomedical Engineering, IEEE Transactions on. 2002;49(11):1318–27. [DOI] [PubMed] [Google Scholar]
- 38.Knutsson L, Stahlberg F, Wirestam R. Aspects on the accuracy of cerebral perfusion parameters obtained by dynamic susceptibility contrast MRI: a simulation study. Magn Reson Imaging. 2004;22(6):789–98. 10.1016/j.mri.2003.12.002 [DOI] [PubMed] [Google Scholar]
- 39.Zanderigo F, Bertoldo A, Pillonetto G, Cobelli Ast C. Nonlinear stochastic regularization to characterize tissue residue function in bolus-tracking MRI: assessment and comparison with SVD, block-circulant SVD, and Tikhonov. IEEE transactions on bio-medical engineering. 2009;56(5):1287–97. 10.1109/TBME.2009.2013820 [DOI] [PubMed] [Google Scholar]
- 40.Pillonetto G DN G. A new kernel-based approach for linear system identification. Automatica. 2010;46(1):81–93. [Google Scholar]
- 41.Jiang CR, Aston JA, Wang JL. A Functional Approach to Deconvolve Dynamic Neuroimaging Data. J Am Stat Assoc. 2016;111(513):1–13. 10.1080/01621459.2015.1060241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cunningham VJ, Jones T. Spectral analysis of dynamic PET studies. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 1993;13(1):15–23. [DOI] [PubMed] [Google Scholar]
- 43.Gunn RN, Gunn SR, Turkheimer FE, Aston JA, Cunningham VJ. Positron emission tomography compartmental models: a basis pursuit strategy for kinetic modeling. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 2002;22(12):1425–39. [DOI] [PubMed] [Google Scholar]
- 44.Lammertsma AA, Hume SP. Simplified reference tissue model for PET receptor studies. NeuroImage. 1996;4(3 Pt 1):153–8. Epub 1996/12/01. 10.1006/nimg.1996.0066 [DOI] [PubMed] [Google Scholar]
- 45.Ogden RT, Tarpey T. Estimation in regression models with externally estimated parameters. Biostatistics. 2006;7(1):115–29. 10.1093/biostatistics/kxi044 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Average (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPP values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using the two nonparametric definitions of BPP: BPP-END (top), and BPP-NP2 (bottom) (see definitions in S1 Text). In each plot, grey bars refer to BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; black bars refer to BPP-RR,2TCM = VT (2TCM)–VT-RR,2TCM; white bars refer to BPP-α = VT(LEGA)—αVT-RR,LEGA; and green bars refer to BPP-d = VT(LEGA)–(VT-RR,LEGA−d). Error bars indicate standard deviation (across test-retest pairs of scans within each tracer). Vertical axes are reported in logarithmic scale to allow for easier visualization of the 2TCM results. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP. VT (LEGA): tracer total distribution volume (VT) estimated using Likelihood Estimation in Graphical Analysis (LEGA); VT-RR,LEGA: VT in the purported reference region estimated using LEGA; VT (2TCM): VT estimated using a two-tissue compartment model (2TCM); VT-RR,2TCM: VT in the purported reference region estimated using 2TCM; α: population-based ratio of non-displaceable distribution volume (VND) (from available blocking studies) over VT in the purported reference region; d: population-based distance of VT in the purported reference region and corresponding VND (from available blocking studies).
(PDF)
Average (across test-retest pairs of scans within each tracer) test-retest percent difference PDBPND values calculated in each of the considered region for [11C]DASB (left) and [11C]CUMI-101 (right), using the two nonparametric definitions of BPND: BPND-END (top), and BPND-NP2 (bottom) (see definitions in S1 Text). In each plot, grey bars refer to BPND-RR,LEGA; black bars refer to BPND-RR,2TCM; white bars refer to BPND-α; and green bars refer to BPND-d. Error bars indicate standard deviation (across test-retest pairs of scans within each tracer). Vertical axes are reported in logarithmic scale to allow for easier visualization of the 2TCM results. AMY: amygdala; CIN: cingulate; DCA: dorsal caudate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; VST: ventral striatum; PDBPP: percent difference for BPP. BPND-RR,LEGA = BPP-RR,LEGA/VT-RR,LEGA = [VT (LEGA)–VT-RR,LEGA]/VT-RR,LEGA; BPND-RR,2TCM = BPP-RR,2TCM/VT-RR,2TCM = [VT (2TCM)–VT-RR,2TCM]/VT-RR,2TCM; BPND-α = BPP-α/αVT-RR,LEGA = [VT(LEGA)—αVT-RR,LEGA]/αVT-RR,LEGA; BPND-d = BPP-d/(VT-RR,LEGA−d) = [VT(LEGA)–(VT-RR,LEGA−d)]/(VT-RR,LEGA−d). VT (LEGA): tracer total distribution volume (VT) estimated using Likelihood Estimation in Graphical Analysis (LEGA); VT-RR,LEGA: VT in the purported reference region estimated using LEGA; VT (2TCM): VT estimated using a two-tissue compartment model (2TCM); VT-RR,2TCM: VT in the purported reference region estimated using 2TCM; α: population-based ratio of non-displaceable distribution volume (VND) (from available blocking studies) over VT in the purported reference region; d: population-based distance of VT in the purported reference region and corresponding VND (from available blocking studies).
(PDF)
Left: Scatter plots of BPP-HYBRID, BPP-END, and BPP-NP2 (see definitions in S1 and S2 Texts) values versus BPP-RR,LEGA values obtained using the non-ideal reference region and Likelihood Estimation in Graphical Analysis (LEGA). The black solid line is the identity line. Right: Distance between test-retest percent difference (PD) values obtained using BPP-HYBRID and PD values obtained using BPP-RR,LEGA (y axis) versus the corresponding distance between BPP-HYBRID (average of test and re-test) and BPP-RR,LEGA (average of test and re-test). Open circles represent values obtained using the non-displaceable distribution volume (VND) from HYDECA with βopt-S and γopt-S; solid circles represent values obtained using the VND from HYDECA with βopt-B and γopt-B. BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; VT (LEGA): tracer total distribution volume (VT) estimated using LEGA; VT-RR,LEGA: VT in the purported reference region estimated using LEGA.
(PDF)
Left: Scatter plots of BPP-HYBRID, BPP-END, and BPP-NP2 (see definitions in S1 and S2 Texts) values versus BPP-RR,LEGA values obtained using the non-ideal reference region and Likelihood Estimation in Graphical Analysis (LEGA). The black solid line is the identity line. Right: Distance between test-retest percent difference (PD) values obtained using BPP-HYBRID and PD values obtained using BPP-RR,LEGA (y axis) versus the corresponding distance between BPP-HYBRID (average of test and re-test) and BPP-RR,LEGA (average of test and re-test). Open circles represent values obtained using the non-displaceable distribution volume (VND) from HYDECA with βopt-S and γopt-S; solid circles represent values obtained using the VND from HYDECA with βopt-B and γopt-B. BPP-RR,LEGA = VT (LEGA)–VT-RR,LEGA; VT (LEGA): tracer total distribution volume (VT) estimated using LEGA; VT-RR,LEGA: VT in the purported reference region estimated using LEGA.
(PDF)
Percent difference (PDerrVC) between the non-displaceable distribution volume (VND) value estimated at each instance of erroneously corrected time activity curves and the VND value estimated in correspondence of the accurately corrected set of time activity curves (y-axis), as a function of the difference between the true fractional blood volume (VB) value and the value adopted for correction (x-axis); dots and error bars indicate average and standard deviation across subjects, respectively, within each tracer. The dotted horizontal lines indicate the +10%, 0%, and -10% mark, respectively.
(PDF)
Residue function curves R(t) in correspondence of different errors and no error in the fractional blood volume value (VB), and the corresponding HYDECA cost functions, in a representative subject for [11C]CUMI-101. CIN: cingulate; HIP: hippocampus; OCC: occipital lobe; TEM: temporal lobe; CGM: cerebellum grey matter.
(PDF)
Residue function curves R(t) in correspondence of different errors and no error in the fractional blood volume value (VB), and the corresponding HYDECA cost functions, in a representative subject for [11C]DASB. AMY: amygdala; DCA: dorsal caudate; HIP: hippocampus; TEM: temporal lobe; VST: ventral striatum; CGM: cerebellum grey matter.
(PDF)
Average (across time points) square distance between the residue function non-displaceable component, RND(t) (see S4 Text), with k3 and k4 >0, and RND(t) with k3 = k4 = 0 as k3 and k4 vary, in 4 cases of (K1, k2) for [11C]DASB. VST: ventral striatum; CGM: cerebellum grey matter. K1, k2 k3 and k4: kinetic rate parameters of a two-tissue compartment model.
(PDF)
Average (across time points) square distance between the residue function non-displaceable component, RND(t) (see S4 Text), with k3 and k4 >0, and RND(t) with k3 = k4 = 0 as k3 and k4 vary, in 4 cases of (K1, k2) for [11C]CUMI-101. HIP: hippocampus; CGM: cerebellum grey matter. K1, k2 k3 and k4: kinetic rate parameters of a two-tissue compartment model.
(PDF)
Supporting information and equations accompanying S1 and S2 Figs.
(PDF)
Supporting information and equations accompanying S3 and S4 Figs.
(PDF)
Supporting information and equations accompanying S5–S7 Figs.
(PDF)
Supporting information and equations accompanying S8 and S9 Figs.
(PDF)
Data Availability Statement
We used data from published blocking studies in baboons (Milak MS, Severance AJ, Ogden RT, Prabhakaran J, Kumar JS, Majo VJ, et al. Modeling considerations for 11C-CUMI-101, an agonist radiotracer for imaging serotonin 1A receptor in vivo with PET. J. Nucl. Med. 2008;49:587-96) and humans (Parsey RV, Kent JM, Oquendo MA, Richards MC, Pratap M, Cooper TB, et al. Acute occupancy of brain serotonin transporter by sertraline as measured by [11C]DASB and positron emission tomography. Biol. Psychiatry. 2006;59:821-8), and test-retest datasets in humans (Milak MS, DeLorenzo C, Zanderigo F, Prabhakaran J, Kumar JS, Majo VJ, et al. In vivo quantification of human serotonin 1A receptor using 11C-CUMI-101, an agonist PET radiotracer. J. Nucl. Med. 2010;51:1892-900; Ogden RT, Ojha A, Erlandsson K, Oquendo MA, Mann JJ, Parsey RV. In vivo quantification of serotonin transporters using [(11)C]DASB and positron emission tomography in humans: modeling considerations. J. Cereb. Blood Flow Metab. 2007;27:205-17). Matlab code that implements HYDECA is freely available through GitHub at the following link https://github.com/FrancescaZanderigo/hybrid-deconvolution-approach.