Ensemble simulations: folding, unfolding and misfolding of a high-efficiency frameshifting RNA pseudoknot

Abstract

Massive all-atom molecular dynamics simulations were conducted across a distributed computing network to study the folding, unfolding, misfolding and conformational plasticity of the high-efficiency frameshifting double mutant of the 26 nt potato leaf roll virus RNA pseudoknot. Our robust sampling, which included over 40 starting structures spanning the spectrum from the extended unfolded state to the native fold, yielded nearly 120 μs of cumulative sampling time. Conformational microstate transitions on the 1.0 ns to 10.0 μs timescales were observed, with post-equilibration sampling providing detailed representations of the conformational free energy landscape and the complex folding mechanism inherent to the pseudoknot motif. Herein, we identify and characterize two alternative native structures, three intermediate states, and numerous misfolded states, the latter of which have not previously been characterized via atomistic simulation techniques. While in line with previous thermodynamics-based models of a general RNA folding mechanism, our observations indicate that stem-strand-sequence-separation may serve as an alternative predictor of the order of stem formation during pseudoknot folding. Our results contradict a model of frameshifting based on structural rigidity and resistance to mechanical unfolding, and instead strongly support more recent studies in which conformational plasticity is identified as a determining factor in frameshifting efficiency.

INTRODUCTION

The RNA pseudoknot motif is a well-characterized supersecondary structure that contains two (or more) base-paired stem regions in which a strand of one of these stems is intercalated within the two strands of another stem (Figure 1A). Discovery of RNA pseudoknots began in the late 1970s with the observation of tRNA mimicry by the 3΄ terminal pseudoknot of Turnip Yellow Mosaic Virus (TYMV) (1), which shares neither primary nor secondary structure with tRNA^Val, yet achieves recognition by tRNA^Val-specific enzymes (2,3). Mimicry-capable RNAs, such as TYMV, showcase the potential dominance of three-dimensional topology, rather than primary or secondary structure, in determining the biological activity of RNAs (4).

Figure 1.

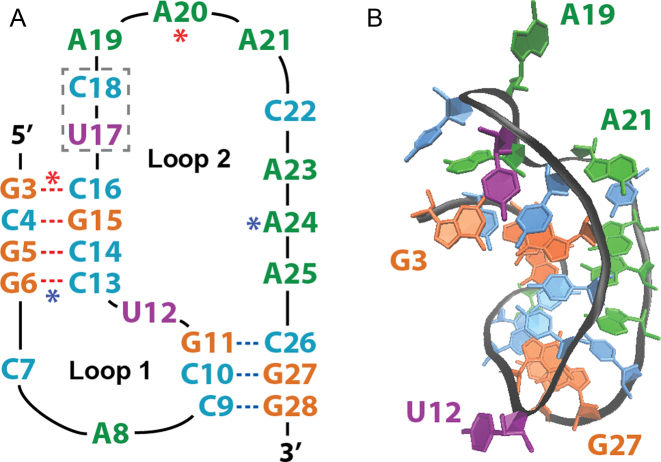
Luteovirus pseudoknot structure. (A) Sequence and secondary structure, with Stem 1 (S1) beginning at the 5΄ terminus, Stem 2 (S2) ending at the 3΄ terminus, and the locations of the C17U/A18C mutations noted by the dashed gray box. Red and blue asterisks denote Loop 2 (L2) residues that form base-triplets with S1 base pairs. (B) Three-dimensional representation of the crystal structure (PDB ID: 2A43) with selected residues labeled to aid in visual orientation.

In recent years, pseudoknots have been observed to play functional roles in structural organization, ribosomal association, and translation via unfolding and refolding (5), and particular attention has been given to the participation of pseudoknots in –1 programmed ribosomal frameshifting (PRF), the register shifting of the mRNA translational reading frame that alters codon recognition, as observed in Luteovirus, HIV-1, and coronaviruses (6,7). Frameshifting, including –1 PRF, is now understood to be enabled through the presence of two fundamental motifs in viral mRNA during translation: an upstream heptanucleotide slippery sequence, where the pausing of the ribosome and displacement of the reading frame occurs, and a downstream stimulatory element (the pseudoknot).

Frameshifting ability thus serves as an important recoding strategy that allows a virus to maximize the number of polypeptides encoded by a relatively small genome (8). While it was previously proposed that rigid, highly stable pseudoknots would resist unfolding and thereby lead to frameshifting (9,10), more recent studies have suggested that frameshifting efficiency instead depends on the overall conformational plasticity of the pseudoknot (11,12), which is defined by the diversity of structural states within the conformational equilibrium in tandem with the tendency to readily transition to these available alternative states (8,13).

The dynamic nature of RNA structure, and the relation of such structural dynamics to function, emphasizes the notion that the lowest energy structure is not always representative of the functional conformation (14), highlighting a key problem with analyses based upon a single energy-minimized structure, and thereby presenting a challenge in better understanding RNA structure-function relationships. Further complicating this matter, the free energy landscape often features an ensemble of partially folded and misfolded states (15,16), some of which may have functional utility enabled through alternative geometries. For example, the tRNA-mimic pseudoknot of TYMV can also modulate ribosome and replicase activity of genomic RNA in TYMV (13).

This study seeks to characterize the free energy surface and conformational dynamics of the potato leaf roll virus (PLRV) RNA pseudoknot via massive all-atom molecular dynamics (MD) simulations, which provide structural information about native, non-native and misfolded states along the folding pathway. PLRV is classified within the Luteoviridae family and shares the Polerovirus genus with beet western yellow virus (BWYV), a widely known and highly studied RNA pseudoknot. The PLRV used herein (PDB 2A43, shown in Figure 1B) is an X-ray crystallographic structure which possesses C17U/A18C mutations that greatly enhance its frameshifting efficiency (9). This PLRV exhibits considerable structural and spatial homology with BWYV (17), making it a strong candidate for studies in RNA folding and dynamics, and pseudoknot structure-activity analysis, such as understanding the role of conformational dynamics in –1 PRF.

MATERIALS AND METHODS

The PLRV pseudoknot was studied via all-atom molecular dynamics simulations using the AMBER potential (18) ported to the GROMACS 3.3 molecular dynamics suite (19). Charge neutrality was obtained through inclusion of 25 Na⁺ ions (20) placed randomly around the solute with a minimum RNA-ion separation of 5.0 Å, resulting in an ionic concentration of ∼100 mM, which is similar in magnitude to most in vitro experimental work of this nature (11). While PLRV has been shown to fold in the absence of divalent ions (21), it is possible that Mg²⁺, a requirement for the folding of many RNAs, would change the folding behavior of PLRV. Although a comparison of the conformational stabilities and dynamics in the presence and absence of Mg²⁺ is beyond the scope of the current study, this comparison is a target for future investigation. Steepest-descent energy minimization was followed by solvation in a periodic 75 Å cubic box with ∼13500 TIP3P water molecules (22) to capture both the bulk and molecular properties of the ionic aqueous solvent, which was then annealed with the RNA held fixed for 1.0 ns prior to the collection of production simulations. All simulations were run in the NPT ensemble (23) at 1 atm and 300 K using a 2.0 fs timestep with bonds constrained using the LINCS algorithm (24) and conformations stored every 100 ps. No artificial or biasing potentials or restraints were employed.

The resulting thermodynamically-stable system served as the starting point for 20 thermal unfolding simulations, which generated thousands of conformations spanning the complete (un)folding pathway. Although high-temperature unfolding simulations are not expected to generate misfolded structures or alternative folds, this method provides the energy necessary to overcome, and thus sample both sides of, large conformational free energy barriers, making it a simple and powerful tool with which to sample conformations along the (un)folding pathway. Our previously reported K-means clustering algorithm (25) was then applied to the structures resulting from these thermal unfolding simulations, each of which was represented by a four dimensional vector defined by the pseudoknot radius of gyration (R_g), the all-atom root-mean-squared deviation (RMSD) from the native starting structure, and the number of native and non-native base-pairing interactions, as determined by the 3DNA analysis tool (26). This clustering resulted in 41 distinct conformational clusters ranging from fully unfolded, with an RMSD of 30.1 Å and a radius of gyration of 31.7 Å, to fully folded (RMSD of 0.0 Å and R_g of 11.9 Å).

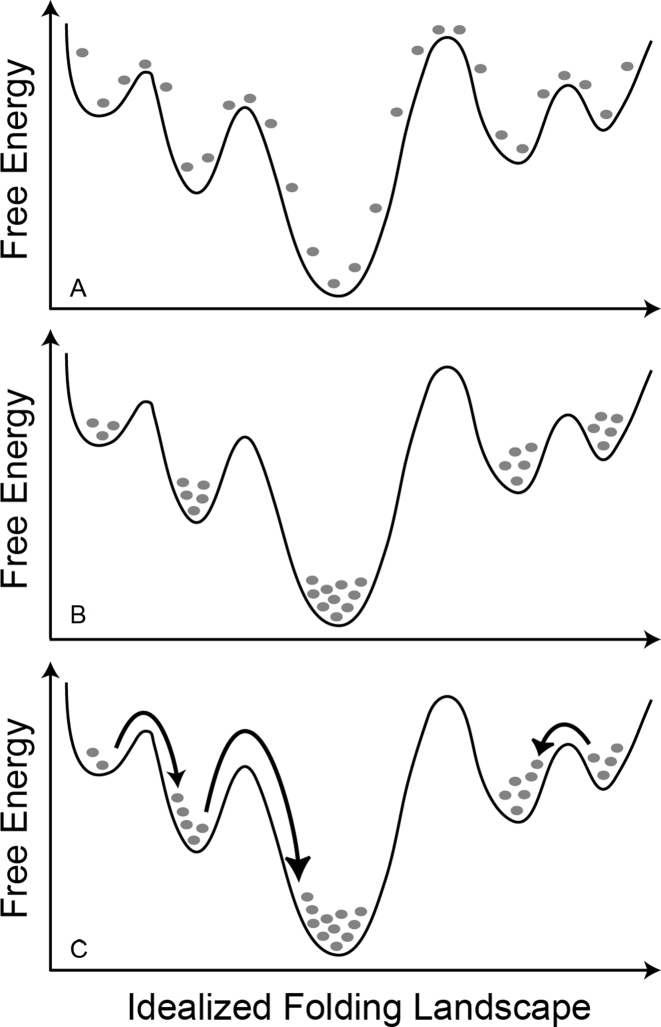
The average structure within each of these 41 clusters was then identified and served as the starting point for 200 all-atom, explicit-solvent MD simulations at 300 K and 1 atm, thereby totaling 8200 independent simulations collected on the Folding@Home distributed computing network (http://folding.stanford.edu) (27). As illustrated in Figure 2, the initial phase of our simulations consisted of ensemble-level annealing of each of the 41 starting structures on the 300 K free energy surface, followed by random transitions between energetic minima. While our use of numerous and conformationally diverse starting structures cannot guarantee that all regions of the conformational space have been sampled, the approach taken herein was designed to optimize the sampling of conformational states, and transitions between these states, and our cumulative sampling time of ∼120 μs represents a significant move forward in making the examination of that space at the all-atom level as thorough as possible, yielding a richly detailed picture of pseudoknot structure and dynamics, as described below.

Figure 2.

Simplified representation of our sampling technique along an idealized folding landscape. Each gray dot represents 200 independent simulations starting in a specific conformation at time t = 0 in (A). After a short annealing period, these simulations rapidly sample from the entire free energy surface (B). At longer times, the ensemble relaxes into conformational equilibrium on this free energy surface and transitions between distinct structural states (examples provided by arrows) are observed (C).

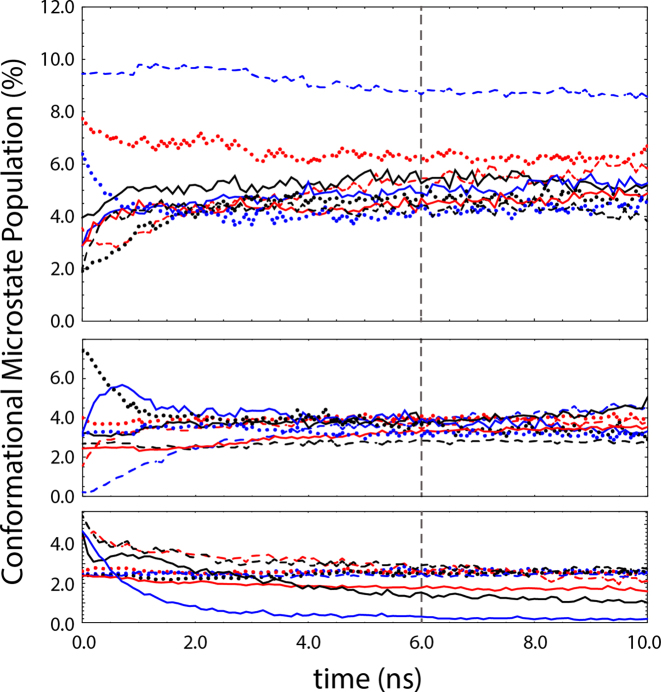
K-means clustering of the resulting data set (∼1.2 million structures) following the protocol described above yielded 27 conformational microstates, with no significant overlap between neighboring clusters, and transitions between neighboring clusters occurring on the 1.0 ns to 10.0 μs timescales. The population of each conformational microstate as a function of time within our simulated ensemble was monitored, with approximate conformational equilibrium reached at 6.0 ns (Figure 3). We emphasize that the approximate equilibrium suggested in Figure 3 represents a steady-state within our simulated ensemble on the 100 μs timescale. Transitions involving larger free energy barriers and longer timescales may, therefore, have gone unobserved within our ensemble simulations. To confirm steady-state behavior, the transition probability and rate matrices, representing the moves from each microstate i to each microstate j after the equilibration period, were evaluated and demonstrated both time-independence and detailed balance. Post-equilibration sampling, which included over 50 μs of simulation time, was therefore used to evaluate the thermodynamics, kinetics, and folding mechanism of the pseudoknot motif.

Figure 3.

Populations of the 27 conformational microstates identified by K-means clustering versus time (split into three panels for visual clarity). Approximate conformational equilibrium is established at 6.0 ns (dashed line).

To quantitatively assess the native structural content of each of our ∼1.2 million simulated conformations, native contacts (NC) were defined as atomic pairs separated by three or more residues that were within 5.0 Å of one another at least 25% of the time in our simulated native state ensemble, thereby accounting for native state structural flexibility (28). Simulations were considered as part of the native state ensemble if they maintained an all-atom RMSD below 5.0 Å, thereby yielding a total native state simulation time of 8.44 μs across 1175 simulations. Native contacts for each conformation were then identified for the full pseudoknot structure and for each substructure within the pseudoknot motif. The resulting native contact counts were then normalized using the mean number of native contacts observed in native state simulations; for tertiary (T) native contacts and those in Loop 2 (L2), both of which displayed multi-modal distributions, normalization was done using the maximum in the highest-valued peak in the NC distribution. Contacts between atomic pairs not observed in the simulated native state ensemble were classified as non-native contacts (NNC), an atomic-level analog of the recently-published NNC definition of Mouro et al. (29), and normalized using the largest quantity of non-native contacts observed. We emphasize that this latter normalization of non-native contacts may understate the overall degree of non-native character, and thus the degree of misfolding, present within a given structure. Further information regarding the approximations made within, and sources of uncertainty inherent to, our simulation methodology and the resulting analysis are provided as Supplement Material.

RESULTS AND DISCUSSION

Pseudoknot structural states

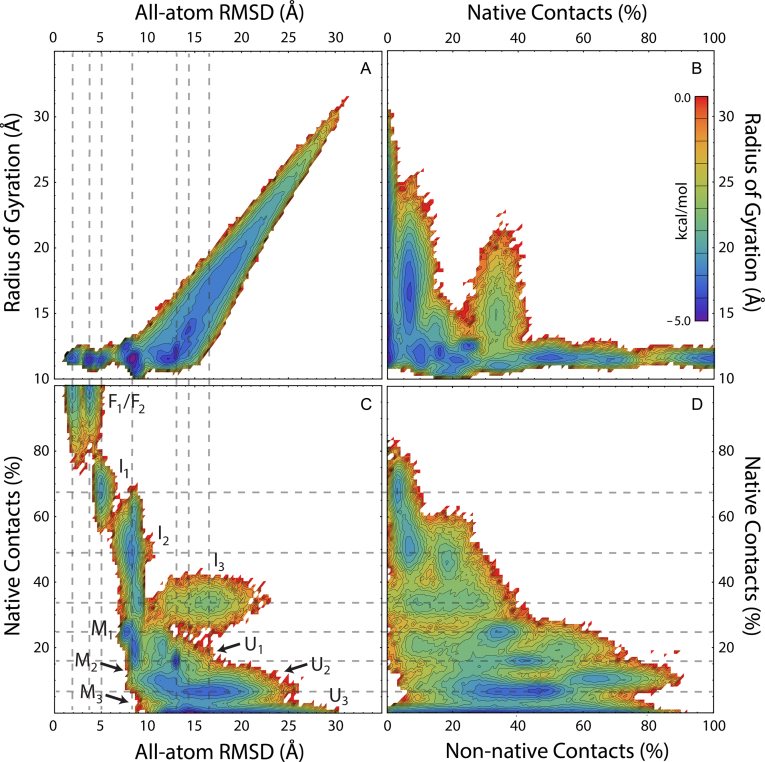
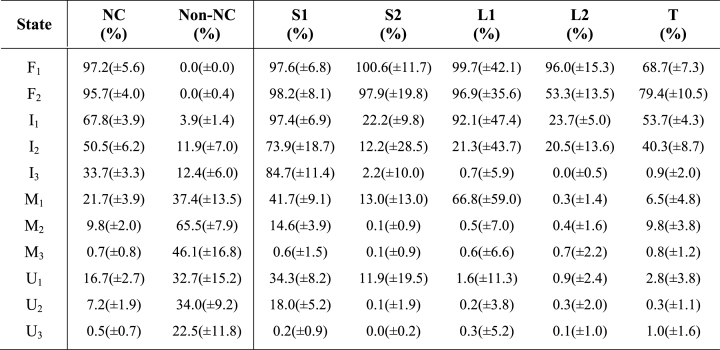
The conformational free energy surfaces shown in Figure 4 are projected onto four metrics: the all-atom RMSD, the radius of gyration, and the normalized quantities of both native and non-native contacts, as defined above. These free energy landscapes were visualized, using only post-equilibration data from our simulated ensemble, by defining the free energy as F = –RT ln Pr at 300 K, where Pr is the normalized probability of finding structures at a given location on the energy landscape. Partitioning of the four-dimensional space depicted in Figure 4 led to the identification of 11 conformational macrostates. In describing these macrostates below, and as labeled in Figure 4C, capital F, I, M and U labels were used to denote folded, intermediate, misfolded and unfolded states, respectively, with numeric subscripts ranging from most native (lower subscript values) to least native (higher subscript values). The overall native and non-native character of these 11 macrostates, alongside the mean native character of substructures within the pseudoknot motif, are provided in Table 1.

Figure 4.

Free energy surface projected onto the RMSD, R_g and percentage of native and non-native contact folding metrics. State labels in (C) indicate observed macrostates participating in the equilibrium folding mechanism. Dashed lines are provided to visually align a given state depicted in neighboring projections. The color-coded energy scale shown in (B) applies to all panels shown.

Table 1. Overall and substructure mean (±SD) native and non-native contacts per macrostate.

Native states

The upper left corners of Figure 4C and D, which represent structures with low RMSD, high NC, and zero NNC, demonstrate the presence of two alternative folded states (NC > 90%, RMSD < 5 Å). The state denoted as F₁ averages only ∼2.0 Å RMSD from the crystal structure and contains a well-structured Loop 2 region. In contrast, the state labeled F₂, with an average RMSD of ∼3.7 Å RMSD from the crystal structure, contains a significantly less-structured Loop 2 region and increased native tertiary contacts (Table 1). As tertiary structure in the PLRV pseudoknot is formed predominantly through interactions of Loop 2 bases with the minor groove of Stem 1 (S1) to form a ‘triple helix’ structure (21), which has been observed in other pseudoknots (30), our observation of alternating Loop 2 and tertiary contacts suggests a twisting mode in which either Loop 2 or tertiary contacts may be optimally sampled to increase the overall stability of the pseudoknot fold.

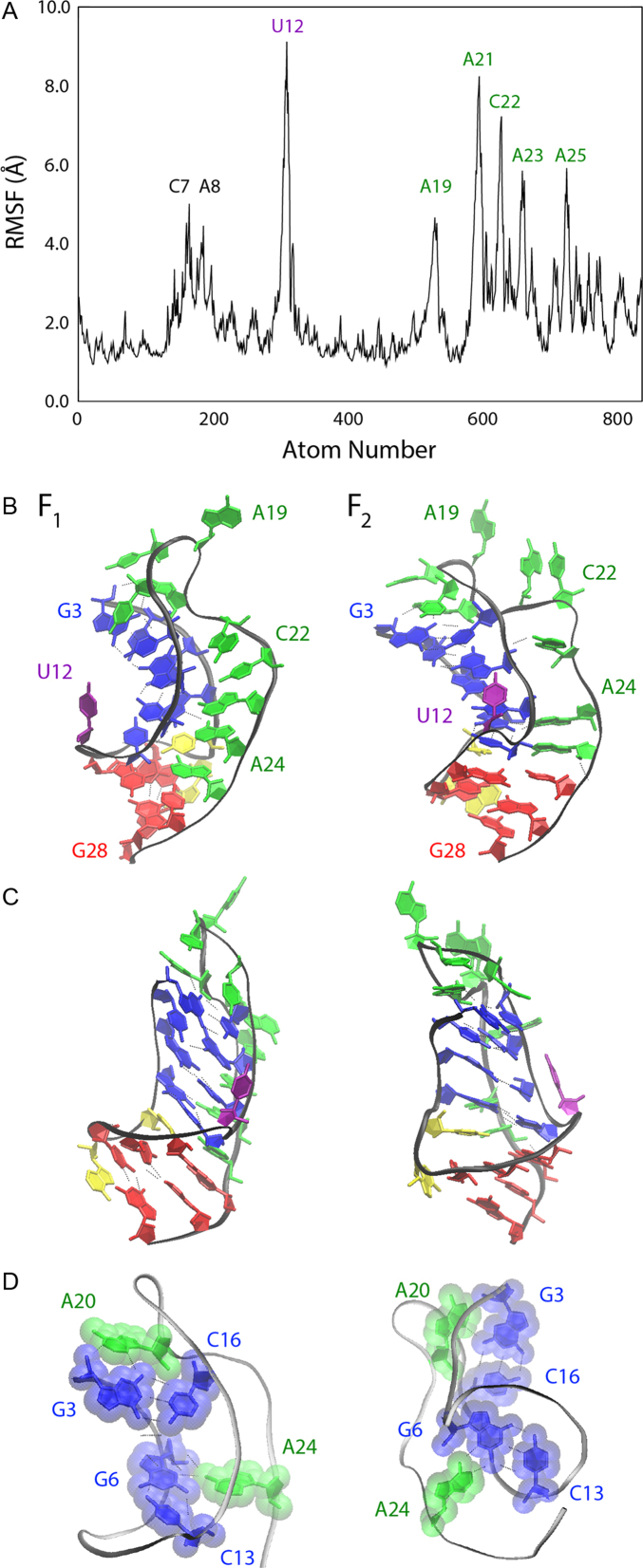
To probe this possibility, and to assess the overall flexibility of each residue in the PLRV pseudoknot, the all-atom root-mean-squared fluctuations (RMSF) were plotted and the mean structures representing these two alternative states were compared. As shown in Figure 5A, which includes only data from our reported 8.44 μs of native state simulations, nearly all Loop 2 residues from A19 to A25 (inclusive) exhibit significant RMSF, with fluctuations of ∼5–8 Å. Only the U12 ‘bridge’ residue between the two stem regions shows more flexibility than Loop 2 residues. In addition, Loop 1 (L1) residues (C7 and A8) show moderate flexibility (RMSF of 4–5 Å), which is clearly limited by the size of the loop and the stability of G·C base-pairs on either side of this loop region.

Figure 5.

(A) The root-mean-squared fluctuation observed in our native state simulated ensemble, with residue labels denoting regions that show larger fluctuations than the baseline of ∼2 Å. (B) Ensemble average structures of the PLRV pseudoknot native states, F₁ (left) and F₂ (right), with specific residues labeled and substructures colored for visual clarity, including Stem 1 (blue), Loop 1 (yellow), Stem 2 (red) and Loop 2 (green). (C) Native structures in (B) rotated 90° about the vertical axis for visual inspection. (D) Native structures shown in (A) and (B) oriented and presented to emphasize interactions of the relatively immobile A20 and A24 residues with Stem 1 base-pairs; hydrogen bonds are represented as dotted lines and transparent molecular surfaces are provided to visualize van der Waals contacts.

The high flexibility of Loop 2 in the PLRV pseudoknot is not surprising given its sequence size of 9 nt: Reiling et al. recently reported a direct correlation between loop size and flexibility, and characterized the optimization of base-pair stacking interactions that can result from such flexibility (31), which contributes to the inherent entropy of Loop 2 while also providing alternative structural interactions within the pseudoknot. A comparison of the mean structures of states F₁ and F₂ is shown in Figure 5B, with Figure 5C showing these same structures rotated 90° about the vertical axis. The primary differences between these two states is the looping out of residues A21 and C22, and a slight unwinding of both helical stem regions to facilitate increased tertiary contacts in state F₂. These include interactions between the Loop 2 backbone and Stem 1, the A23 residue and the Stem 1 backbone, and improved stacking and hydrophobic packing interactions within the two helix stem regions.

Unlike the majority of Loop 2 residues, A20 and A24 show relatively low mobility in Figure 5A, which is due to the participation of these two residues in base-triplets, as shown in Figure 5D. Hydrogen bonding and van der Waals contact between the bases of A20 and A24 with the G3·C16 and G6·C13 base-pairs, respectively, effectively anchor both Stem 1 and these Loop 2 residues in place in both the F₁ and F₂ native states, while leaving U12, Loop 1, and most of Loop 2 flexible enough to allow rapid transitions between F₁ and F₂.

Intermediate states

Below the states labeled F₁ and F₂ in Figure 4C, three intermediate states (labeled I₁ through I₃) were identified by their significant quantities of native structure and low degrees of non-native interactions. Our observation of multiple intermediates in pseudoknot folding agrees with numerous previous observations and predictions including the simple model of Ansari et al. based on laser T-jump experiments (32) and the folding pathways predicted from coarse-grained simulations by Thirumalai et al. (33). While both I₁ and I₂ have undergone collapse to a near-native mean gyration radius of just over 12 Å in our simulated PLRV ensemble, the I₃ state is somewhat less compact with an average gyration radius of 15.5 Å, and significant differences are apparent among these three states.

The least native of these three intermediates, I₃, has a mean RMSD of ∼15 Å and contains limited native structure with 33.7(±3.3)% of native contacts present, which derive solely from the 84.7(±11.4)% of Stem 1 formation, on average, with no other appreciable native structure observed (Table 1). The small degree of non-native interaction observed in I₃, 12.4(±6.0)%, is largely due to interactions between residues 19–23 (Loop 2 residues) that fold back upon Stem 1 to stabilize that stem and to interact with the 5΄ terminus.

In contrast, the I₂ intermediate (mean RMSD of ∼8 Å) contains 50.5(±6.2)% of global native contacts and the more native-like I₁ intermediate (mean RMSD of ∼5 Å) contains an average of 67.8(±3.9)% of global native contacts, demonstrating a significant decrease in RMSD and an increase in native character of nearly 20% as folding progresses from each intermediate to its more native neighboring state. While I₁ contains a fully formed Stem 1 helix and ∼22% of Stem 2 contacts, I₂ has an average Stem 1 native content of only 73.9(±18.7)% (statistically equivalent to Stem 1 content in the I₃ intermediate) and an average Stem 2 native content of 12.2(±28.5)%, indicating that S2 nucleation occurs as intermediate I₂ is reached. Whereas the Loop 2 region shows an average of 20–25% of native structure formed in both the I₁ and I₂ intermediate states, the Loop 1 region, which consists of only two nucleotides and a relatively small number of native contacts, is fully formed in the observed I₁ intermediate but remains unstructured in the less-native I₂ and I₃ states.

As with I₃, the I₂ intermediate is also subject to minor but non-negligible non-native contact formation of 11.9(±7.0)%, while this is minimized in the I₁ state at 3.9(±1.4)%. In addition, the formation of 40.3(±8.7)% of tertiary contacts in I₂ signifies contact of Loop 2 within the minor groove of Stem 1 and initial structuring of this loop, which increases to 53.7(±4.3)% in the I₁ intermediate, thus confirming that additional triple-helix structure is present in the more native I₁ state. Comparing overall size and native character, the I₁ and I₂ intermediates are quite similar, as demonstrated in Figure 4 and Table 1, and we posit that these two intermediates are non-differentiable via many experimental probes. Taken together, I₁ and I₂ are consistent with both the statistical mechanical model of Chen and coworkers that predicted a similar intermediate for BWYV (which shares similar sequence and structure with PLRV) (34) and the simulation-based results of Cho et al. for cases in which one stem is thermodynamically more stable than the other (33).

Unfolded states

Also labeled in Figure 4C are the three unfolded states observed in our simulations, denoted numerically as U₁ through U₃ (from most to least structured), which were identified as having little-to-no native structure and exhibiting a relatively low quantity of non-native structure (less than approximately one third of the maximum observed NNC). While Bian et al., who recently reported 3 μs of bias-exchange metadynamics simulations of a similar H-type pseudoknot, did not report discrete sub-states within their sampling of the unfolded state, our results are in agreement with their observation of multiple clusters of unfolded conformations at various R_g values (35).

The simplest of our observed unfolded states, the relatively extended U₃ state, which has a mean gyration radius of ∼22 Å and a mean RMSD of ∼20 Å, exhibits only 0.05(±0.07)% native character and a mean non-native contact quantity of 22.5(±11.8)%, with these NNC's forming between apparently random segments of the PLRV sequence. The more structured U₁ state represents the collapsed, or globular, portion of the unfolded conformational space, with a near-native mean gyration radius of ∼13 Å and a mean RMSD of ∼12 Å, and exhibits 16.7(±2.7)% of native contacts, including mean Stem 1 and Stem 2 native contact counts of 34.3(±8.2)% and 11.9(±19.5)%, respectively, thereby indicating that stem nucleation may occur within this region of the conformational space, as might the reversing of such nucleation, sans the formation of loop or tertiary contacts. As the mean quantity of non-native contacts for U₁ was 32.7(±15.2)% (Table 1), it could be argued that this is a misfolded rather than unfolded state. Our classification of U₁ as an unfolded state is based primarily upon the presence of this state along the folding pathway, in which it readily transitions to and from the less-native U₂ state and the I₃ intermediate described above, as well as the observation that nearly half of the detected non-native contacts within this state occur between the first three residues (5΄ terminus) and the five residues directly succeeding them, indicating dominance of highly accessible local interactions rather than long-range or large scale structure formation.

Between these extremes, the U₂ state is composed of moderately-collapsed, self-interacting conformations with an average RMSD of ∼16 Å and a mean gyration radius of ∼17 Å. The 7.2(±1.9)% mean native contact percentage accounts for the 18.0(±5.2)% mean Stem 1 native contacts that are observed in this state, again suggesting nucleation of Stem 1 early in the folding process, with no other native structure observed. As with U₁, non-native content is seemingly high for an unfolded state at 34.0(±9.2)%. As with both U₁ and U₃, however, the U₂ state is categorized as unfolded rather than misfolded based on the random occurrence of low-probability non-native contacts across the PLRV sequence and the observation that this state readily transitions to and from both the U₁ and U₃ portions of the configurational space.

Misfolded states

Three misfolded states are observed in Figure 4C, labeled M₁ through M₃, where designation as a misfold was based on high RMSD (>5 Å), low native state structural content (NC), and high degrees of non-native structure (NNC), as is consistent with a recent study of Noe et al. (36). While RNA is known to be easily trapped in metastable misfolded structures (37) and misfolding has been predicted or observed for this and numerous other pseudoknots (38–41), we emphasize that our normalization of the total number of non-native contacts present in a structure (using the largest total quantity of NNC observed) may underscore the overall degree of misfolding present for a given structural state.

The most native-like misfold, M₁, includes a native-like mean gyration radius of 12.3(±0.8) Å, a mean RMSD of only 8.0(±0.7) Å, and 21.7(±3.9)% of native structure formed. This latter value derives predominantly from the partial formation of Loop 1 (∼67%), Stem 1 (∼42%) and Stem 2 (∼13% NC), suggesting that this misfolded state can include nucleation of either, or both, helical stem regions. The M₁ non-native structural content of 37.4(±13.5)% derives from interactions involving Loop 2 residues: in this case, more specifically, residues 21–25 may fold back to interact with either strand within Stem 1 (the 5΄ terminus or residues 15–17).

While the M₂ state also exhibits a native-like gyration radius of 12.3(±0.4) Å, the mean RMSD of ∼11 Å and the limited native structure (∼10%), in tandem with a much higher mean non-native structure, 65.5(±7.9)%, makes it clear that this misfold is only native-like in size. The small quantity of native structure observed in this state includes only the possible nucleation of Stem 1 (∼15% of Stem 1 NC) and minimal, random formation of native tertiary interactions (∼12% of native tertiary NC). The large quantity of non-native structure present in the M₂ state includes mispairing of the 5΄ terminal G3 residue with A8 or C10, or with nucleotides 22–25, as well as possible mid-sequence mispairing of residues 7–14 with residues 11–22, the latter of which would maintain significant entropy in one or more loop regions. In addition, it might be speculated that the M₁ and M₂ misfolds would not be easily differentiable experimentally, given their similar size and lack of native structure.

Unlike the M₁ and M₂ misfolds, the M₃ state exhibits a slightly larger mean gyration radius of 14.5(±1.9) Å and a somewhat higher mean RMSD of 13.8(±1.6) Å. Although collapsed to nearly native-like size, no native structure is observed in this state and the mean quantity of non-native contacts is observed to be 46.1(±16.8)%, which is based largely on interactions between C14/G15/C16 Stem 1 residues with either the 5΄ terminus or with C10/G11 Stem 2 residues. While the M₁ through M₃ misfolds might easily be clustered or classified into a larger number of misfolded states, our analysis has emphasized macroscopically measurable structural characteristics and both M₂ and M₃ represent misfolds predicted by the statistical mechanical model of Ansari et al. (32).

Macrostate folding mechanism

Per the discussion above, Figure 6 presents the conformational dynamics observed within our ensemble simulations, with residues in each structure color coded according to their participation in native state secondary structure following the scheme used in Figure 5. Relative timescales in Figure 6 are indicated by colored arrows representing the nanosecond (green) through microsecond (red) regimes. The observed transition timescales are in agreement with well-characterized timescales reviewed by Isambert (42) and more recently reported by Truex et al. (43), with zipping/unzipping transitions occurring on timescales of 100 ns or less and formation of helix stem regions on longer timescales (44,45), all much more rapid than accepted RNA transcription rates of ∼50 nt/s, which suggests that folding and misfolding can easily occur during this process given the right environmental conditions.

Figure 6.

Pseudoknot macrostate folding mechanism predicted from our ensemble simulations following equilibration. Substructures are colored according to the color scheme used in Figure 5B and arrows are color-coded to represent transition timescales according to the inset key. For each macrostate the average structure is shown alongside the mean RMSD (top) and R_g (bottom).

As depicted in Figure 6, multiple folding pathways may be realized through the multiple intermediate and misfolded states described above. While the observed macrostates are generally distinguishable based on their native and non-native character (Table 1), nearly all exhibit highly-collapsed mean molecular size, with native or near-native gyration radii, thereby emphasizing the prevalence of self-interaction and collapse in initiating non-bonded interactions and folding of the pseudoknot motif, as was reported in the recent computational study of Bian et al. (35). The relative organization of native secondary structural elements and tertiary structure can be inferred from the free energy projections in Figure 7. Specifically, the formation of Stem 1 preceding that of Stem 2 is a prevalent occurrence in our simulations (Figure 7A), as predicted by the statistical mechanical model of Chen et al. (34) and the stability hypothesis put forth by Thirumalai and coworkers (33), the latter of which dictates that base-paired stem regions with higher thermodynamic stability will form before less-stable stem regions.

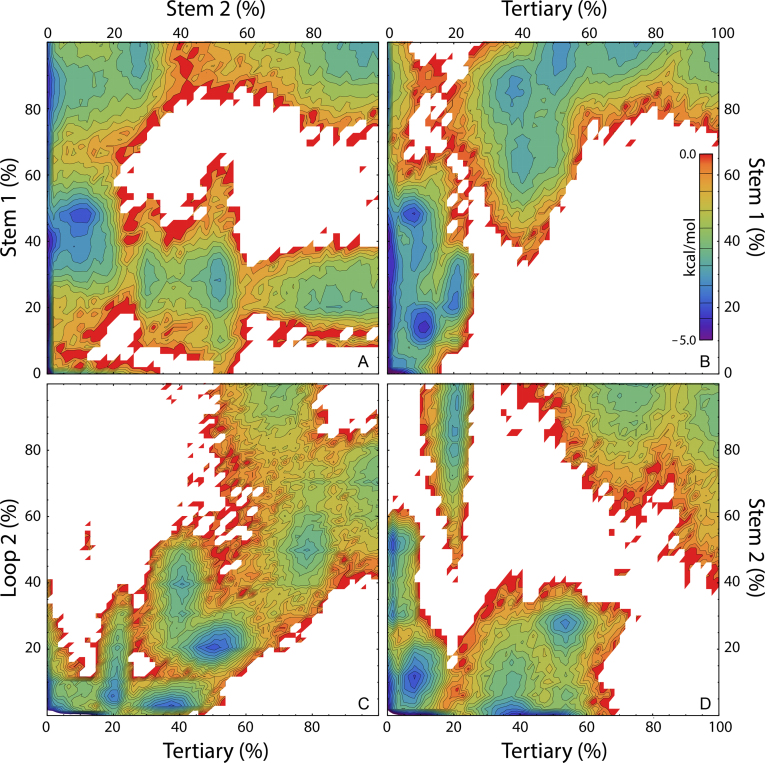
Figure 7.

Sampling of the PLRV pseudoknot conformational free energy landscape projected onto the native content of substructural elements S1, S2, L2 and T. The color-coded energy scale shown in (B) applies to all panels shown.

It is questionable, however, whether our observed prevalence of early Stem 1 formation is kinetically favored based not on relative stem thermodynamic stabilities, but rather on the sequence distance separating the strands within each stem. For example, Figure 1A shows that only 6 nt separate the terminal base-pair residues of Stem 1 in PLRV, whereas 14 nt separate the terminal base-pair of Stem 2, and it is therefore not surprising that a random search of the conformational space would favor Stem 1 nucleation over that of Stem 2. Notably, the use of stem-strand-sequence-separation as a predictor of the order of stem formation accurately accounts for the folding mechanisms of the MMTV, SRV-1 and hTR pseudoknots studied by Thirumalai et al. (33).

As would be expected, given that the formation of native tertiary structure involves interactions of Loop 2 residues with the minor groove of Stem 1, significant tertiary structure is absent until 50% or more of Stem 1, the stem with the much smaller stem-strand-sequence-separation, is formed (Figure 7B). A strong correlation between the formation of Loop 2 and tertiary contacts is evident in Figure 7C at low to moderate native contact values, with somewhat larger quantities of tertiary contacts and somewhat fewer Loop 2 contacts seemingly favored, suggesting that the formation of tertiary structure prompts further formation of Loop 2 structure. In contrast, at high native contact values the existence of alternative states that favor either increased Loop 2 structure or increased tertiary structure, but not both, reinforces our prior description of the transition between the alternative F₁ and F₂ native states. Given the quantitative descriptions of the observed intermediates above, alongside our sampling of the free energy landscape shown in Figure 7D, it can be inferred that Stem 2 largely forms prior to both Loop 2 and tertiary contact formation, but may also form later in the folding process, in tandem with the initiation of Loop 2 and tertiary contacts.

The folding mechanics reported herein are consistent with the unfolding of BWYV described by recent optical tweezer experiments and steered molecular dynamics simulations (46), and add a new level of complexity by accounting for the formation of non-native structure. The presence of multiple misfolded states on the free energy surface is in agreement with the PK5 pseudoknot pathway reported by Cao et al. (47), as well as the broadly applicable Kinetic Partitioning Mechanism (KPM) put forth by Thirumalai et al., in which a population of unfolded molecules is assumed to split into two distinct groups that fold on different time scales defined by the presence of multiple intermediates and misfolds (48–50). From Figure 6, our ensemble simulations predict individual molecular folding events occurring on the hundreds-of-nanoseconds (along the most rapid pathway) to the multiple-microseconds timescales.

Structure-based frameshifting

It was previously speculated that residues A19 and U12 (the latter referred to as the linker, bridge or junction residue), which are looped-out and show both significant flexibility (high RMSF) and a lack of intramolecular interactions in the two native states observed in our simulations (Figures 1, 5A and B), serve as ribosomal recognition sites during translation (9,51). It was also suspected that the U17–C18–A19 linker region plays an important role in initiating ribosomal contact based on proximity to the 5΄ terminus and intermolecular association observed during crystallization (9). As with U12 and A19, the U17 and C18 residues remained virtually unchanged between states F₁ and F₂, and these residues displayed no significant non-native intramolecular associations within our observed macrostate ensembles. Unlike U12 and A19, however, the U17–C18 pair demonstrates high rigidity (low RMSF in Figure 5A), which derives from π-stacking of these bases and the G3·C16–A20 base-triplet at the 5΄ terminus of Stem 1. These observations are consistent with the speculation noted above, with U12 and A19 being most suitable for ribosomal recognition when remaining looped-out and flexible, while the much more rigid U17 and C18 residues serve to anchor the looped-out position of A19 for recognition with the ribosomal machinery.

Though the mechanism of structural recognition has not yet undergone experimental probing at the residue level, direct interactions of these residues with the ribosome during decoding of the viral mRNA would justify a number of observations regarding the dependence of frameshifting efficiency on specific pseudoknot residues. For example, Gao and Simon recently showed that for a structurally similar member of Luteoviridae, pea enation mosaic virus (PEMV), frameshifting efficiency is correlated with Stem 1 stability, but not overall thermodynamic stability (12). This agrees well with our observations of PLRV where Stem 1, which is composed solely of G·C base-pairs, demonstrates high structural rigidity (low RMSF in Figure 5A), and supports a mechanism based on ribosomal recognition via looped-out viral mRNA nucleotides: ample destabilization of Stem 1, and fraying or destruction of 5΄ terminal G3·C16–A20 base-triplet interactions, would disrupt the structure of the U17–C18–A19 linker, leading to potential dislocation of A19 from the looped-out position needed for suitable positioning relative to the ribosome. Analogously, destabilization of the opposite end of Stem 1, the G6·C13–A24 base-triplet, could have a similar impact on the looped-out U12 residue.

Indeed, in both of the observed native states, stable base-triplet interactions between Loop 2 residues and the Stem 1 minor groove are observed (Figures 1A and 5D), which have been shown to be a requirement for high-efficiency –1 PRF (52–54): Olsthoorn et al. reported that the removal of either of these base-triplet interactions, via point mutation of adenine residues in Loop 2 to either pyrimidine (C or U), decreased frameshifting by ∼33% to ∼75% in the simian retrovirus type-1 (SRV-1) pseudoknot, which is similar to PLRV in both structure and efficiency (11). Removal of one or both of these base-triplet interactions, which would weaken the energetic preference to preserve Loop 2 interactions within the minor groove of Stem 1, could lead to a potential preference toward improper alignment of one or both of the looped-out U12 and A19 residues with the ribosome.

Further correlation between these looped-out nucleotides and ribosomal association comes again from SRV-1, where a C24A mutation in Loop 2 of similar size and composition resulted in a frameshifting increase of 24% (11). While the direct result of this mutation would allow for increased preference for contiguous A-stacking within Loop 2, an indirect result of this increased Loop 2 structural stabilization would be an enhanced preference to maintain the looped-out nucleotide atop Loop 2, keeping that residue in place to interact with the ribosome. In addition, SRV-1 displays a third base-triplet between an adenine in Loop 2 and a G·C base pair that acts as the linker between Stems 1 and 2. This linker region in SRV-1 is analogous to the U12 linker in PLRV, the latter of which lacks base pair and triplet interactions altogether. In line with the structural logic presented above, Olsthoorn et al. reported that loss of this third base-triplet interaction in SRV-1 (via mutation to a U·A base pair) decreased PRF by nearly a factor of 4 (11), again supporting Stem 1 stability as a determining factor in PRF efficiency, and suggesting that a lone, looped-out nucleotide linker, such as U12 in PLRV and U13 in BWYV (55), provides some structural advantage which offsets the potential loss from an additional base-triplet and can thereby facilitate more optimal ribosomal recognition.

As a highly efficient PRF-stimulating pseudoknot (9,17), PLRV exhibits structural features in silico that have been correlated with frameshifting efficacy. Previous studies used these structural features as evidence of frameshifting stimulation being favored by high-stability, rigid mRNA pseudoknots that would resist mechanical unfolding at the ribosome (9,10). This supposition was contradicted by the work of Brierley et al., who demonstrated a lack of correlation between –1 PRF and ribosomal pausing (56), and more recently by the work of Woodside et al., which illustrated that –1 PRF is not dependent on resistance to mechanical unfolding (8).

Rather than mechanical blockage of the ribosome, it is now believed that the ribosome itself may act as a helicase, able to disrupt secondary structure during transcription (57,58), and recent work has shown that high –1 PRF efficiency is instead correlated with pseudoknot conformational plasticity (8,11). Our observed conformational dynamics is well in line with this observation: our simulations provide structural evidence for multiple native states, partially-folded intermediates, and misfolded states that would be accessible upon refolding of the pseudoknot motif following mechanical unfolding at the ribosome, with transitions between these states readily occurring on sub-millisecond timescales. In addition, the stability of Stem 1, and of Stem 1–Loop 2 base-triplet interactions, has been shown to enhance PRF efficiency, which our model accounts for in terms of a resulting preference to maintain looped-out residues (U12 and A19) that can participate in ribosomal recognition. Our computational characterization of alternative native states and regions of high flexibility (Loop 1, Loop 2 and the U12 linker), alongside a conformational equilibrium involving numerous available macrostates, thus supports the conformational plasticity-based model of –1 PRF. Indeed, the apparent necessity for regions of high stability and rigidity alongside much more structurally-adaptable regions within the pseudoknot assembly, as a prerequisite for efficient PRF, provides a most intriguing ‘micro-machine’ view of the function of even this relatively miniscule viral RNA sequence.

CONCLUSION

Our rigorous sampling provides a detailed picture of pseudoknot conformational equilibrium and dynamics, and has allowed us to characterize the PLRV pseudoknot motif as incorporating both rigid, highly stable components and highly flexible, mobile regions, with significant fluctuations predicted both within and between numerous macrostates in conformational equilibrium. We report herein the presence of two alternate native state conformations, in which a global topological twisting mode allows for alternation between optimizing Loop 2 contacts and tertiary contacts between that loop and the minor groove of the neighboring base-paired stem region. Three folding intermediates have been identified and characterized, as have multiple misfolded states. While misfolding has been the focus of many protein-oriented studies, less attention has been given to this topic with respect to nucleic acids, and we present here the first all-atom, simulation-based study of this nature to probe RNA misfolding.

Although our results are well-aligned with the stability hypothesis of Thirumalai and coworkers, which emphasizes the importance of helical stem stability in determining the order of stem formation, we offer an alternative quantity upon which stem formation order may be determined, which is consistent with the system studied herein and the systems studied previously by Thirumalai et al. Namely, from geometric and statistical considerations, we propose that stem folding order may be predicted by the relative sequence distances between adjacent strands that must find one another to form properly base-paired native stem regions (i.e. the stem-strand-sequence-separation).

While this effort represents a significant increase in the size of the RNA systems to which we have applied our all-atom computational approach (25,59–61), much is left to be probed with regard to pseudoknot folding and (mal)function, particularly when considering the effects of sequence mutations, deletions, and insertions. We look forward to expanding on these findings: indeed, the diversity of this data set is testament to the level of detail now achievable through MD simulation methods, which we expect will only continue to open new avenues of RNA investigation.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

MARC U*STAR program, funded by NIH/NIGMS [T34GM008074 to A.R.]; CNSM and CSULB (to K.N. and E.S.); Women & Philanthropy for providing undergraduate research scholarships to support their efforts (to Y.G. and D.R.).

Conflict of interest statement. None declared.