Abstract
Population structure can be described by genotypic-correlation coefficients between groups of individuals, the most basic of which are the pairwise relatedness coefficients between any two individuals. There are nine pairwise relatedness coefficients in the most general model, and we show that these can be reduced to seven coefficients for biallelic loci. Although all nine coefficients can be estimated from pedigrees, six coefficients have been beyond empirical reach. We provide a numerical optimization procedure that estimates all seven reduced coefficients from population-genomic data. Simulations show that the procedure is nearly unbiased, even at 3× coverage, and errors in five of the seven coefficients are statistically uncorrelated. The remaining two coefficients have a negative correlation of errors, but their sum provides an unbiased assessment of the overall correlation of heterozygosity between two individuals. Application of these new methods to four populations of the freshwater crustacean Daphnia pulex reveal the occurrence of half siblings in our samples, as well as a number of identical individuals that are likely obligately asexual clone mates. Statistically significant negative estimates of these pairwise relatedness coefficients, including inbreeding coefficients that were typically negative, underscore the difficulties that arise when interpreting genotypic correlations as estimations of the probability that alleles are identical by descent.
Keywords: population structure, population genomics, coancestry, relatedness, identity by descent
MANY phenotypes are influenced by complex interactions between multiple genes and various environmental conditions (Fisher 1918). It may be impossible to isolate all of the genetic factors contributing to a complex phenotype, but the total genetic contribution to phenotypic variation can be estimated using regression coefficients that describe the statistical association between the genotypes of two individuals.
The statistical association of genotypes between individuals, or genotypic correlation, is usually described as those individuals sharing alleles that are descended from the same ancestral allele, in which case the shared alleles are said to be identical by descent (IBD). Two slightly different meanings of IBD are in common use, with IBD sometime being used in the former sense and sometimes more specifically referring to an IBD segment—a pair of haplotypes that have not experienced any recombination during their descent from a single ancestral segment (Cotterman 1940; Malécot 1948; Sved 1971; Powell et al. 2010; Thompson 2013). We use either pedigree IBD or recombinational IBD, respectively, to refer to the more specific meanings when necessary. Recombinational IBD is distinguished from pedigree IBD in that recombinational IBD depends on the locations of recombination events, but pedigree IBD does not. In the absence of recombination, for example over very short mapping distances, recombinational IBD and pedigree IBD are identical (Thompson 2013). Since pedigree IBD is sufficient for estimating the parameters of the quantitative-genetic models used here, pedigree IBD is used throughout the article.
A number of IBD coefficients are necessary to describe the probability that different groups of alleles within diploid individuals are IBD. If the genotype-to-phenotype relationship were very simple, then a single measure of genotypic correlation which described how the number of alleles are correlated between individuals—the coefficient of coancestry (Θ)—would be sufficient to relate genetic covariance to phenotypic covariance. Unfortunately, many genes do not follow a simple additive model of gene action, and as a result, additional genotypic-correlation coefficients are needed.
For example, full siblings tend to have a stronger phenotypic resemblance to each other than either sibling has to their parents. While this may seem surprising, it can be understood as a result of nonadditive gene action. If the parents are unrelated to each other, then at every locus a single parent and offspring share exactly one pair of alleles that are IBD see Supplemental Material, Table S5 in File S1). However, heterozygosity and homozygosity (jointly called zygosity) are defined by the relationship of two haploid genomes to each other. Because each parent gives only one haploid genome to their offspring, the offspring’s zygosity is unassociated with the zygosity of their parent, so the coefficient of fraternity (Δ)—which describes the association of zygosity between individuals—is zero. While siblings share alleles that are IBD with each other with equal probability that offspring share alleles that are IBD with parents, siblings can receive the same alleles from both parents, creating a correlation of zygosity state in addition to the correlation of allele count. Thus, because alleles often exhibit some form of dominance, a pair of siblings generally has greater genetic covariance than a parent-offspring pair, despite having similar coancestry coefficients (Lynch and Walsh 1998).
In a randomly mating, outbred population, knowledge of both and between all individuals is sufficient to relate the genetic covariance of individuals, to the additive and dominance genetic variation in a population (Lynch and Walsh 1998). These terms are used to estimate heritability, and thus IBD coefficients are fundamental to a variety of quantitative-genetic analyses. However, and are only sufficient to estimate genetic variation in panmictic outbred populations. Additional genetic variance terms and IBD coefficients are necessary to describe inbred individuals.
The probability of both pedigree IBD and recombinational IBD can be estimated if the pedigree of the related individuals is known (Wright 1922; Thompson 1988). However, because each round of reproduction involves a limited number of crossover events, typically on the order of one event per chromosome arm; the actual pattern of inheritance can vary substantially from the expectation predicted by path analysis. For instance, a pair of human half siblings have an expected coancestry of but because crossover events separate them, of half siblings will have a coancestry that is <0.092 or >0.158 (Speed and Balding 2015).
Some of the shortcomings of pedigree analysis can be addressed by estimating genotypic-correlation coefficients from molecular markers. The actual pattern of inheritance, rather than the pattern predicted from pedigree analysis, can be estimated from molecular markers. Additionally, defining allele frequencies from the sampled population frees methods using molecular markers from reliance on reference populations (Lynch and Ritland 1999; Wang 2002, 2007, 2011; Fernández and Toro 2006; Kalinowski et al. 2006; Anderson and Weir 2007). However, if a method estimates the probability of IBD, then meaningful estimates are confined to the interval between zero and one. While this property is not undesirable per se, using the probability of IBD within that model as a regression coefficient is undesirable because it creates bias in estimates of heritablity (Lynch and Ritland 1999).
Rather than attempting to estimate the probability of IBD from the statistical association of genotypes, the statistical association between genotypes can be directly described with the goal of describing the statistical association between genotypes at unknown causal loci; an approach which has led to the modern use of genotpyic correlations in genetic relatedness matrices (Lynch and Ritland 1999; Powell et al. 2010). This approach is consistent with the motivations behind the development of IBD (Cotterman 1940; Malécot 1948). We examine how negative correlations arise within genotypic correlations, an aspect of the statistical association of genotypes which is poorly described in both a pedigree- and recombinational-IBD framework.
With these problems in mind, we sought to develop a method for estimating relatedness that makes effective use of the biallelic markers abundantly available in population-genomic data, without making restrictive assumptions about possible values of relatedness coefficients. We show how both genotypic and phenotypic correlation coefficients can be negative, which emphasizes that these coefficients are not probabilities; and also show that seven coefficients, rather than nine, are sufficient to specify the genetic covariance at biallelic loci.
Methods
A statistical view of genealogies
The genotype of one individual often gives us some information about the genotypes of other individuals. We expect the members of a species to be genetically similar, so sequencing a single individual of that species can give us some idea of the genes present in most members of that species. This genetic similarity arises in part from the common ancestry of all members of a species. The metaphor of IBD captures this part of the explanation, but also obscures the influence of mutation and genetic drift on these correlations. This lacuna of understanding is also present in pedigree-based calculations of IBD coefficients, which, despite >100 years of use, can only be calculated from truncated pedigrees. Calculations from exhaustive pedigrees cause pedigree-based calculations of genotypic correlations to approach one (Speed and Balding 2015), differing sharply from the behavior of IBD coefficients calculated using a molecular-marker method. A careful consideration of the statistical processes at work highlights the roles of mutation and drift in generating genotypic correlations, and shows how molecular-marker methods are related to pedigree-based methods.
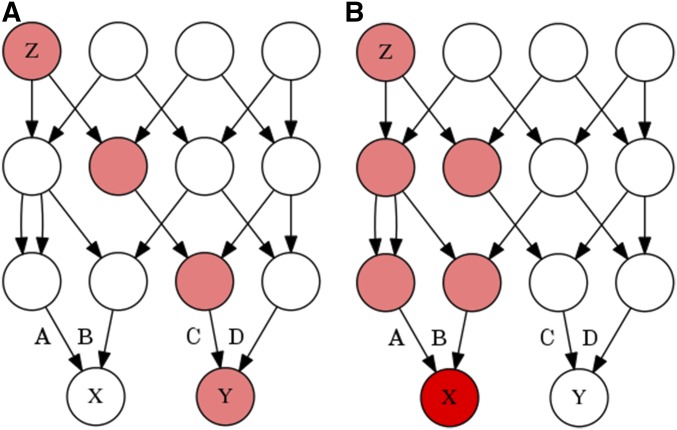
We can imagine that an individual’s genotype is determined by a three step process, in which an allele (SNP) originates in some particular ancestor through mutation (individual Z in Figure 1), and then descends stochastically down a fixed genealogical structure, ultimately coming to rest in the genome of the individual that we have sampled (individual X or Y in Figure 1). The genotypic correlation between two gametes is a measure of the tendency of alleles to cooccur in those gametes, and to calculate this correlation we will need to estimate three probabilities: the probability of sampling a particular allele in some particular gamete A, the probability of sampling that allele in some other gamete B, and the probability of sampling that allele in both gametes simultaneously, (see Table 1 for other symbols and their definitions).
Figure 1.
Two genealogies of identical structure which illustrate the stochastic model of genotypic correlations. In both of these genealogies a mutation is present in ancestor Z, making Z heterozygous for some trait (pink). The allele is then transmitted to Z’s offspring with a probability of 1/2 for each, and thus gamete A has a probability of 1/4, and (A) B and C each have a probability of 1/8 of carrying the mutant allele. If only one individual in the second generation receives the mutant allele, as in (A), then individuals X and Y cannot both receive the mutant allele. However, if in the second generation two individuals possess the mutant allele, as in (B), then A has a probability of 1/2, and B and C each have a probability of 1/4 of carrying the mutant allele. The coefficient of identity between X and Y is calculated depending on whether the probability of the gamete carrying the mutant allele A, B, or C is conditioned merely on Z being heterozygous, or on the genotypes of individuals in generations following Z.
Table 1. Symbols and their meaning.
| Symbol | Meaning |
|---|---|
| The nth of Jacquard’s (1970) nine condensed modes of IBD, described in Table 2 | |
| Without a subscript, is used to symbolize the coefficient of fraternity | |
| A | The event A, typically the event of sampling some particular allele in some particular gamete |
| a | A random variable indicating whether event A occurred, which takes on a value of 1 when event A occurs, and a value of 0 when it does not |
| The probability of event A | |
| The expectation, or mean, of the random variable a. Equivalent to P(A) | |
| An estimate of | |
| The nth central moment of a, defined as | |
| A mixed central moment of a, b, and omitted variables, defined as | |
| The inbred relatedness, which is the probability of sampling a locus where individual X is inbred and also related to individual Y | |
| The coefficient of coancestry, or kinship, between individuals X and Y, which is the probability that an allele in individual X is IBD to an allele in individual Y. Also denoted by θ and in some texts | |
| The second-order zygosity correlation of individuals X and Y, which is the probability that there are two pairs of alleles which are each IBD. Either both individuals are inbred but unrelated, or the individuals are genetically identical but not inbred | |
| The fourth-order zygosity correlation of genotypes between individuals X and Y, which is the probability that all four alleles in the two individuals are IBD | |
| The allele-frequency estimation error, the difference in allele frequencies between individuals X and Y | |
| Quantitative-genetic terms | |
| The additive genetic variation of the population | |
| The dominance genetic variation of the population | |
| The covariance of additive and dominance effects in inbred individuals | |
| The variance of dominance effects in inbred individuals | |
Calculating P(A) and P(B)
Unfortunately, the sampling of a haplotype is a singular event. We cannot directly measure the probability of sampling an allele in a particular haplotype in a particular individual. However, we can use the distribution of genotypes within the population as a whole, in combination with some statistical model, as an estimate of that probability. The simplest statistical model we can use is a uniform distribution, where the presence or absence of an allele is independent and identically distributed among all haplotypes; in this case, our estimate of is simply the frequency of the allele in the population. This is not an unreasonable procedure, but we need to keep in mind that is being calculated on the condition that the frequency of some allele in the population is p, and would be more properly written as and not simply
Conditional independence
By conditioning on the current allele frequency in a panmictic population, p, we can theoretically remove the genotypic correlation created by genetic drift. If an individual X gives no information about the genotype of individual Y, aside from aiding in the estimation of the allele frequency in the population, then the genotypes of X and Y can be made independent by conditioning on that allele frequency. This process implicitly occurs when molecular markers are used to estimate genotypic-correlation coefficients, because allele frequencies must be measured in the current generation. Pedigree-based methods neglect this step by assuming that allele frequencies are known a priori, and as a result, the effects of drift are not removed explicitly or implicitly. As a result, genotypic-correlation coefficients increase monotonically as pedigrees become more extensive (Speed and Balding 2015).
Negative correlations
Conditioning on the allele frequency in the current generation will not, in general, make the genotypes of all distantly related individuals independent. Individuals in a population have varying degrees of relatedness, and different allele frequencies will be necessary to make different pairs of individuals independent. No allele frequency will make all sufficiently distant individuals independent. For instance, in Figure 1, an allele that originates in individual Z has an unconditional probability and of being sampled in individuals X and Y, respectively. The unconditional probabilities of sampling the allele are independent because the allele descends through entirely separate lineages. Because X and Y share no ancestors that possess the mutant allele except for Z, we do not learn anything about the frequency of the mutant allele in Y’s ancestors from X. Yet if we condition on the allele frequency in the parental generation (from which gametes A, B, C, and D were sampled), then individuals X and Y become negatively correlated.
It is easiest to see how this negative correlation arises if we first think of conditioning on the generation containing X and Y. For instance, consider the case where we condition on sampling a single copy of the mutant allele among the four alleles of X and Y. In this case, learning that the allele was sampled in Y tells us with certainty that the allele was not sampled in X, because we already know the allele was sampled only once. A similar, though less severe, process occurs when we condition on the parental generation. Learning that individual Y possesses an allele makes it more likely that copies of that allele were present in Y’s parents, and if the total number of alleles in the parental generation is known, then it becomes less likely that X’s parents had copies of the allele, and vice versa. A negative genotypic correlation indicates that an allele tends to be sampled from either individual X or individual Y, but usually not both.
Negative correlations can occur in large unstructured populations. Stochastic differences in reproductive success occur between families delineated by any level of relatedness (e.g., a family at the level of first cousins, all second cousins, etc.), and just as in the preceding example, larger families will contribute more alleles to estimates of allele frequencies than small families. As a result, conditioning on allele-frequency estimates will create negative correlations between some pairs of individuals. These negative correlations are a fundamental aspect of population structure that describes these differences in reproductive success, and they do not become trivial in large populations. Negative correlations are unfamiliar in the context of population structure because of the tradition of envisioning these correlations as estimates of probabilities, but later we will observe negative genotypic-correlation coefficients among individuals in real populations, so we will need to have some understanding of the mechanisms that create them.
Expression for pairwise genotypic correlation
Two random variables (for example a and b in Figure 1) that can each be in one of two possible states (a = 0 and a = 1) can take on four states jointly (a = 1 and b = 0, b = 1 and a = 0, etc.), each with their own associated probability. These four outcomes have three degrees of freedom (one degree of freedom is lost because the four states sum to one), and thus we need three parameters to describe the overall distribution: the probability that or the probability that or and some parameter that describes the association of a and b. An obvious choice for this association term is the correlation coefficient between a and b, which is a covariance normalized by the geometric mean of the SDs of the univariate distributions, and can be written as:
| (1) |
where and are two different notations for the covariance between a and b, and and are two different notations for the variance of a. In general is the nth central moment of a and is defined as where E denotes the expectation, or raw moment, of a variable.
The covariance is related to the correlation coefficient by so we can write the probability of a and b in terms of the means and and the correlation coefficient as:
| (2) |
By substituting for a, we can write the probabilities that as E[a′b], as E[ab′], and so on, e.g.:
If we ignore the particular genealogy shown in Figure 1, and instead consider the general case: the two gametes composing individual X and the two gametes composing individual Y could have been sampled from different populations, and the frequencies of alleles could differ in these populations, so it may be the case that where and are the allele frequencies in X’s parents and and are the frequencies in Y’s parents. The correlation coefficient can still be used to describe the genotypic correlation between a and b, and the joint probabilities can be written in the form of Equation 2, though determining the allele frequencies may be difficult.
There are six unique ways to choose two items from four items if items can be chosen only once, and the order of choice does not matter (i.e., four choose two is six). As a result there are six “second-moment” correlation coefficients between any four random variables. These are just correlation coefficients in the ordinary sense, but need to be distinguished from the higher moment coefficients describing the statistical association of three or four random variables, which are introduced later. Two of these six “second-moment” coefficients are inbreeding coefficients, which are the correlation coefficients of the gametes that fused to make an individual:
| (3) |
The other four second-moment coefficients are generally not considered separately; instead, their arithmetic average defines the coefficient of coancestry:
| (4) |
The use of the arithmetic average is not an arbitrary choice. If the two diploid individuals X and Y produce two gametes e and f, the gametes will have a second-moment correlation coefficient of
| (5) |
There are 16 possible paired genotypes of two individuals at biallelic loci etc.), and to fully describe the joint probability of these 16 paired genotypes several parameters are needed. Coskewness and cokurtosis coefficients both arise naturally when describing three- and four-variable statistical associations, in the same way that covariance arises when describing two-variable associations. While we will not use the coskewness or cokurtosis themselves, the third- and fourth-moment correlation coefficients are related to coskewness and cokurtosis and share properties with them.
Skewness (rather than coskewness) measures the asymmetry of a probability distribution and is defined as it measures whether observations have a tendency to be either larger (for positive skewness) or smaller (for negative skewness) than the mean. Coskewness is the multivariate analog of skewness that represents the tendency of jointly distributed variables to simultaneously take on values on the same (for positive) or different (for negative) side of the means (i.e., major-allele frequencies) of the distribution, and is defined as While coskewness is a dimensionless parameter—because the numerator and denominator are the of same order—it does not estimate genotypic correlations. The coskewness of a haplotype with itself is simply the skewness, whereas the genotypic correlation of a haplotype with itself is one.
To obtain a statistic that does not vary as a function of allele frequency, and thus estimates genotypic correlations, we normalize the third central mixed moment by the third moments of the univariate distributions, yielding
| (6) |
This notation is adapted to emphasize the similar form and behavior of this parameter to a correlation coefficient, and we will refer to as the third-moment correlation coefficient. (The choice of the geometric mean of central moments is described in more detail in Section SC in File S1.) The third-moment correlation can be used in a fashion similar to the second-moment correlation coefficient to write probabilities of the joint distribution of three variables, e.g.:
A total of four third-moment correlations exist between four haploid genomes, which are grouped into two arithmetic averages:
| (7) |
We call these terms the inbred-relatedness coefficients, because they describe the probability of sampling a site where the first index individual (X for or Y for is inbred and related to the second indexed individual (through either one or both of the alleles in the second indexed individual). The symbols and are adopted from Cockerham (1971). Again, the arithmetic mean is not an arbitrary choice, but instead represents a formulation that allows us to express the third-moment correlation of gametes produced by individuals.
The final term is the fourth-moment correlation coefficient. This coefficient estimates the fraction of sites where zygosity is guaranteed to be identical. There are three modes of IBD (Δ1, Δ2, and Δ7 in Figure 2) where the zygosity of the two individuals is guaranteed to be identical, so the fourth-moment correlation coefficient is defined as
| (8) |
where and are the second central moments, and are the fourth central moments, the dots denote the omission of the moments of c and d, and α is a term that describes the fraction of the fourth-moment correlation coefficient that arises from the fourth-moment component as described below. Unlike the second-moment and third-moment coefficients, where all identity modes contributing to the genotypic correlation describe the same basic kind of relationship (either two alleles that are IBD or three alleles that are IBD), the fourth-moment coefficient is comprised of two different kinds of relationships: a relationship where all four alleles are IBD, and a relationship of two pairs of two alleles, either in the same (Δ2) or different (Δ7) individuals, which are each IBD. These are the second- and fourth-moment components of and and they can be expressed in terms of as:
| (9) |
and
| (10) |
The notation in the subscript specifies which groups of alleles are IBD. This notation becomes necessary when there are several different ways in which the relationship can be partitioned. The coefficient is the sum of the terms and used by Cockerham (Holland et al. 2003) and becomes the coefficient of fraternity, in the absence of inbreeding. The term is Jacquard’s (1970) and is also used by Cockerham (1971). We call the zygosity correlation coefficient because it describes how zygosity (i.e., whether an individual is heterozygous or homozygous) is correlated between individuals, with called the second-moment zygosity correlation component and called the fourth-moment zygosity correlation component because they depend on the second- and fourth-moments of the univariate distributions, respectively.
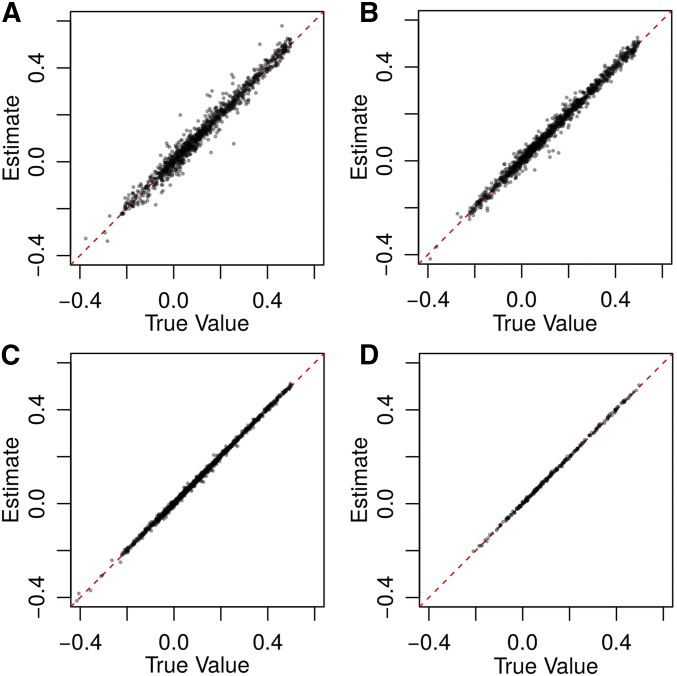
Figure 2.
Results from 10,000 simulations using (A) 3× and (B) 10× coverage at 5000 loci; and (C) 3× and (D) 10× coverage at 100,000 loci. Allele frequencies were drawn from a triangular distribution as described and reported without error. All seven genotypic-correlation coefficients are graphed jointly. A summary of biases and MSEs can be found in Table S3 in File S1.
Every set of nine probabilities for jointly sampling the genotypes of individuals X and Y can be transformed into a unique set of eight parameters. Two of these parameters are the probabilities of sampling the minor allele in individuals X and Y, and the other six are the genotypic-correlation coefficients relating X and Y: and However, the joint genotypic probabilities are only defined for some values of these eight parameters (i.e., the relationship is not a one-to-one correspondence). Strong correlation of the genotypes of the individuals places a constraint on the difference of the probability of sampling the minor allele in both individuals. If correlations are close to +1 then the difference of minor-allele frequencies must be close to 0, but when correlations are close to −1, the difference must be close to 1 − minor allele frequency.
Finally, it is the joint central moment that is specified by a set of nine genotypic probabilities, and not a genotypic-correlation coefficient, either or Finding the values of the coefficients and requires a range of allele frequencies, because and describe how the denominator of Equation 8 changes as a function of allele frequencies. The relationship of these coefficients to the nine condensed modes of IBD is shown in Table 2.
Table 2. Relationship between genotypic-correlation coefficients and modes of IBD.
 |
On the right are the nine identity modes relating two individuals. Alleles a and b belong to individual X, and alleles c and d belong to individual Y. Alleles that are IBD are connected by solid lines. On the left, these nine modes can be used to obtain the coefficients of coancestry (Θ), inbreeding (f), and fraternity (Δ), along with the coefficients that we introduce: the inbred relatedness (γ), identity (δ), and zygosity (ρ).
Three condensed IBD modes can be expressed in terms of these seven coefficients: and Although we do not consider these coefficients for three or more alleles in this article, if more alleles were present could be separated into its components and and the remaining six condensed IBD modes could be estimated from linear combinations of the genotypic-correlation coefficients presented here.
A complete model of genetic covariance in populations
These genotypic-correlation coefficients are important in the analysis of quantitative traits. In the absence of inbreeding and epistasis, the genetic covariance of quantitative traits can be defined as
| (11) |
In the presence of inbreeding, but absence of epistasis, this becomes
| (12) |
where is the covariance of additive and dominance effects in inbred individuals ( in Cockerham 1983), and is the variance of dominance effects in inbred individuals in Cockerham 1983) (see Lynch and Walsh 1998 and Abney et al. 2000). In the absence of inbreeding, the terms and are all 0, and so Equation 12 reduces to Equation 11. However, even in ostensibly outbred populations, particular individuals will have small but statistically significant amounts of inbreeding (or outbreeding) because real populations are not perfectly panmictic (Cockerham and Weir 1983). As a result, estimates of genetic covariance using Equation 12 should be more accurate than estimates that assume a perfectly panmictic population and use Equation 11. As with the additive and dominance genetic variance, care should be taken in the verbal interpretation of the covariance of additive and dominance effects in inbred individuals and the variance of dominance effects in inbred individuals as these parameters describe properties of populations and do not describe modes of gene action.
Estimating IBD coefficients from population-genomic data
There are three steps in computing the coefficients of relatedness using sequence data: (1) an estimate of the allele frequencies in the populations from which the two individuals are sampled must be obtained, (2) the genotypes of the two individuals being compared must be estimated, and (3) a relatedness estimate must be constructed from this information. The first two steps are closely related, because they both involve making inferences about genotypes from sequence data, and we use a framework that jointly estimates sequence error rates and allele frequencies at each site (Maruki and Lynch 2015), implemented in the program mapgd (M. S. Ackerman, T. Maruki, and M. Lynch, unpublished data). A benefit of this approach is that it not only produces unbiased estimates of population parameters when depth of coverage is low, but because we explicitly model sequencing as two discrete events (the random sampling of chromosomes from an individual followed by the random distribution of errors among reads), we can assess whether the observed data are consistent with our statistical model. The likelihood equation used to estimate allele frequencies and genotypic likelihoods, Equation S13 in File S1, can be transformed into a cumulative-distribution function describing the probability of obtaining data of lower likelihood than the observed data, Equation S16 in File S1. By limiting the analysis to genomic sites consistent with the model, we can remove sites that potentially suffer from sequencing or assembly artifacts (Section S6 in File S1).
The third and final step in the process is to estimate the genotypic-correlation coefficients from genotypic probabilities and allele frequencies. We do this by maximizing a likelihood equation that describes the probability of observing the pattern of reads given a set of genotypic-correlation coefficients. For a particular site, the likelihood equation is the product of the three terms: (1) the probability that individual X has genotype given that the “quartet” (i.e., counts of A’s, C’s, G’s, and T’s observed at the site) is observed at site k; (2) the corresponding probability for individual Y; and (3) the probability of observing the pair of genotypes and in the two individuals given a set of genotypic-correlation coefficients When estimating genotypic-correlation coefficients, the terms and are simplified from equation 4b in Lynch (2008), because the error rate and major- and minor-allele identities have been estimated prior to this calculation by mapgd from the population data. The term is taken from the joint genotypic distributions developed in the previous section (defining the coefficients of IBD) with being the vector of the seven genotypic-correlation coefficients. Explicit forms of and in terms of allele frequencies, genotypic-correlation coefficients, error rates, and nucleotide quartets are given in Section S2 in File S1.
Because the genotypes [of which there are three: (1) homozygous for the major-allele, (2) heterozygous, and (3) homozygous for the minor allele] are mutually exclusive events, we sum across them and assume that observations at the n different loci are independent. The product (or the sum of the logs) of the likelihood of the data at each site gives us the likelihood of the data overall:
| (13) |
where and are the quartets of individuals X and Y at site k, respectively.
Equation 13 is maximized to estimate genotypic-correlation coefficients. Because the assumption that observations at different loci are independent is violated, these estimates are quasi-likelihood estimates rather than maximum-likelihood estimates. The maximization is done with the sequential least-squares programming (SLSP) algorithm implemented in the Python module SciPy. Testing of the maximization procedures available in the SciPy module showed that this method offered satisfactory convergence times and stability (Section S4 in File S1). Although the performance of the SLSP algorithm was satisfactory, we have not made a concerted effort to maximize computational efficiency (for instance, use of C++ instead of Python will likely offer computational benefits). Thus future refinements of the numerical estimation procedure may be helpful.
Maximization of the genotypic correlation is unbound, meaning that the maximization procedure examines any real number; however, the quasi-likelihood function is undefined or poorly defined for some parameter values, so in practice all estimates are between −1 and 1. When the quasi-likelihood function is undefined, a value of is returned. More problematic for numerical optimization is that the mutually exclusive probabilities of observing specific genotypes within Equation 13 (written more explicitly in Table S2 in File S1) can become less than zero or greater than one for some parameters and data. While there are a number of potential ways to address this problem, currently we arbitrarily set to 0 when it becomes negative and normalize the remaining probabilities. Because this behavior occurs most frequently when minor-allele frequencies are small, we recommend ignoring sites with minor-allele frequencies <0.05, although this procedure has minimal effect on the bias and mean squared error (MSE) of simulations (Table S7 in File S1).
Simulations
Two kinds of simulations were performed to test our methods. The first simulation was designed to examine the statistical performance of mapgd’s estimation procedure. For these simulations, mapgd was given simulated sequence from two individuals and the allele frequencies in the population from which these individuals were sampled. These allele frequencies could either represent the true population allele frequencies or represent the allele frequencies in a simulated sample. Related individuals were generated by selecting one to seven genotypic-correlation coefficients, which were then assigned a random value between −1 and 1. The remaining coefficients were assigned a value of 0. There are some constraints on what values these coefficients can take (though unlike the condensed IBD modes they do not need to sum to one), so a check was performed to ensure that the joint probability distribution was defined for all minor-allele frequencies between 0.1 and 0.4, and a file was generated with either or SNPs at either or coverage. Allele frequencies were drawn from a triangular distribution with mean 0.1, minimum 0, and maximum 1. Finally, binomially distributed noise representing the sampling error in estimates of allele frequencies was introduced for sampling 10, 100, and 1000 individuals. Simulations that compare the effects of including or excluding alleles from the two individuals being compared are reported in Section S5 in File S1.
We also simulated a genomics study by creating 150-bp reads that were aligned to a simulated reference genome using bwa (Li and Durbin 2010). A total of 98 individuals were simulated: 2 focal individuals with a known relationship and 96 unrelated individuals. Allele frequencies within the population were Pareto-distributed and were estimated from both the 2 focal individuals and the 94 unrelated individuals.
The accuracy of our estimates of relatedness and inbreeding were compared to the programs VCFtools, KING, and PLINK. Unfortunately, no other method currently exists that estimates the coefficients γ or δ; but, several these programs can calculate the coancestry (Θ) and fraternity (Δ) coefficients in the absence of inbreeding, denoting them as either and after Cotterman (1940), or and after Suarez et al. (1978). In the absence of inbreeding these terms are equivalent to and respectively, and are usually verbally described as representing the probability that one (k1 or IBD1) or two (k2 or IBD2) alleles are identical by descent between a pair of individuals. For details on the operation of mapgd, see M. S. Ackerman, T. Maruki, and M. Lynch (unpublished data); for VCFtools, see Yang et al. (2010); for KING, see Manichaikul et al. (2010); and for PLINK, see Purcell et al. (2007).
Data availability
The software used in the simulations and data analysis is freely available from https://github.com/LynchLab/mapgd/. The Daphnia pulex data are available on request.
Results
Simulation results
Our quasi-maximum-likelihood estimation procedure produces accurate and precise estimates of all seven relatedness components, even when depth of coverage is minimal (Figure 2). The bias (the expected error, and the MSE depend on the number of loci sampled, the depth of coverage, and the accuracy of allele-frequency estimates. Individuals in typical metazoan populations may have between and informative SNPs, and even at 3 coverage we can estimate all seven components with MSE When the number of loci used is reduced to 100,000 and 5000, the largest MSE increases to and respectively.
Linkage between loci means that adjacent SNPs are likely to be in similar relatedness modes and do not provide independent estimates of the pedigree relationship between individuals. As a result, the difference between the genotypic correlations observed in a sample and the genotypic correlations expected from the pedigree relationship can be substantial (Table S6 in File S1, left columns). However, loci influencing quantitative traits share the departures from pedigree expectations caused by this nonindependence, so the sample genotypic correlations are better estimates of the state of these causal loci than the expectations based on a known pedigree relationship (Browning and Browning 2013; Speed and Balding 2015). Linkage has no effect on the bias or MSE of these measures when viewed in this way (Table S6 in File S1, right columns).
In these simulations where population allele frequencies are known exactly, the most biased estimators are the inbreeding coefficients and When a very large number of individuals are used, inbreeding is overestimated by 0.003 when coverage is low and only 5000 SNPs are used. This bias arises largely from the small number of SNPs used in the analysis and not from low coverage, with a similar bias occurring at coverage. However, the bias of the method depends on both the number of individuals used to estimate allele frequencies (Table S7 in File S1) and whether focal individuals are included in those estimates (Table S8 in File S1).
Errors in the estimation of allele frequencies upwardly bias estimates of and and downwardly bias This bias is roughly independent of depth of coverage and number of loci used, but does depend on the number of individuals sampled; resulting in an upward bias of 0.01 to and when 48 individuals are used to estimate allele frequencies, and decreasing to 0.005 when 96 individuals are used in the estimates (data not shown). Including the focal individuals being compared in allele-frequency estimates substantially increases the magnitude of the bias and MSE (Table S8 in File S1). Estimates of inbreeding and coancestry from 3× coverage data that excluded the focal individuals from allele-frequency calculations was less biased and more accurate than 20× coverage data that included focal individuals included in allele-frequency calculations.
The errors of estimates of five genotypic-correlation coefficients and are uncorrelated, whereas the errors of the estimates of the two zygosity coefficients and have a strong negative correlation to each other and consequently these two terms also have the largest MSEs. However, when or more loci are used, the MSEs of both and are
We compared the performance of mapgd to VCFtools (Yang et al. 2010), which can estimate (using the –relatedness option) and f (using the –het option); and to KING (Manichaikul et al. 2010) and PLINK (Purcell et al. 2007), which estimates both and on our mock genomics study of 98 individuals. Using the default settings of each program, we find that the quasi-maximum-likelihood method implemented in mapgd substantially reduces the bias and MSE of identity coefficients compared to VCFtools, KING, and PLINK, particularly when genotyping error rates are high. At a coverage of 3×, KING underestimates coancestry by 48%, PLINK by 49%, and VCFtools by 27% for outbred siblings. Increasing the coverage to 10× reduces the bias to 8, 8, and 5%, respectively, and all of the programs are essentially unbiased at 30× coverage (Table 3). However, unlike the method we present here, high coverage does not ensure accurate estimates from VCFtools, PLINK, or KING, because they are all sensitive to assumptions regarding inbreeding to various degrees. The program KING seems to be particularly sensitive to these assumptions, generally estimating that inbred siblings are unrelated (i.e., Θ = 0).
Table 3. Bias and MSE of mapgd, VCFtools, KING, and PLINK in estimating coancestry, fraternity, and inbreeding for outbred and inbred siblings.
| Coancestry (Θ) | Out. | In. | |||
|---|---|---|---|---|---|
| Program | Cov. | Bias (×103) | MSE (×104) | Bias (×103) | MSE (×104) |
| mapgd | 3× | −10 | 2.2 | −11.6 | 2.5 |
| VCFtools | 3× | −68 | 50 | −150 | 230 |
| KING | 3× | −120 | 170 | −450 | 2000 |
| mapgd | 10× | −6.9 | 0.73 | −8.2 | 1.5 |
| VCFtools | 10× | −12.0 | 1.8 | −16 | 3.3 |
| KING | 10× | −21 | 4.7 | −520 | 2700 |
| mapgd | 30× | −6.4 | 0.69 | −7.2 | 1.0 |
| VCFtools | 30× | −5.7 | 0.70 | −4.5 | 1.0 |
| KING | 30× | −3.1 | 0.29 | −500 | 2500 |
| Fraternity | Out. | In. | |||
| Program | Cov. | Bias (×103) | MSE (×104) | Bias (×103) | MSE (×104) |
| mapgd | 3× | −7.2 | 22 | −0.3 | 23 |
| PLINK | 3× | −20 | 7.1 | 72 | 52 |
| KING | 3× | 370 | 1400 | 230 | 520 |
| mapgd | 10× | −1.7 | 4.3 | −1.4 | 5.8 |
| PLINK | 10× | 11 | 2.3 | 110 | 120 |
| KING | 10× | 58 | 36 | 400 | 1700 |
| mapgd | 30× | 1.2 | 4.3 | 8.6 | 6.1 |
| PLINK | 30× | 1.7 | 1.6 | 120 | 150 |
| KING | 30× | −3.5 | 1.7 | 360 | 1300 |
| Inbreeding | Out. | In. | |||
| Program | Cov. | Bias (×103) | MSE (×104) | Bias (×103) | MSE (×104) |
| mapgd | −14 | 7.1 | −33 | 18 | |
| VCFtools | 99 | 100 | −100 | 110 | |
| PLINK | 72 | 54 | −150 | 220 | |
| mapgd | −8.5 | 1.6 | −7.0 | 1.3 | |
| VCFtools | 15 | 3.5 | −11 | 9.5 | |
| PLINK | 12 | 2.4 | −7.4 | 1.2 | |
| mapgd | −9.0 | 1.9 | −7.6 | 1.6 | |
| VCFtools | −0.1 | 1.9 | −3.8 | 1.3 | |
| PLINK | −2.2 | 1.4 | −2.4 | 0.9 | |
The values of all seven IBD coefficients are listed in Table S5 in File S1. Results are from 100 simulations on a 400-kbp, 400-cM genome containing SNPs. See Section S7 in File S1 for SNP filtering parameters. Out., outbred; in., inbred; cov. coverage. See figure S7 for diagram of outbred and inbred siblings.
In contrast to the poor performance of VCFtools, PLINK, and KING on low coverage sequence or with relatives with complex relationships, mapgd gives accurate and unbiased estimates across all simulated coverage and relationships (Table 3). This robust estimation comes with a substantial computational cost, with estimates from mapgd taking longer than the other methods. The major computational hurdle for accurate estimation of relatedness is the accurate calculation of allele frequencies. But, this investment in computational time results in a substantial increase in the accuracy of allele-frequency estimation (Figure 3).
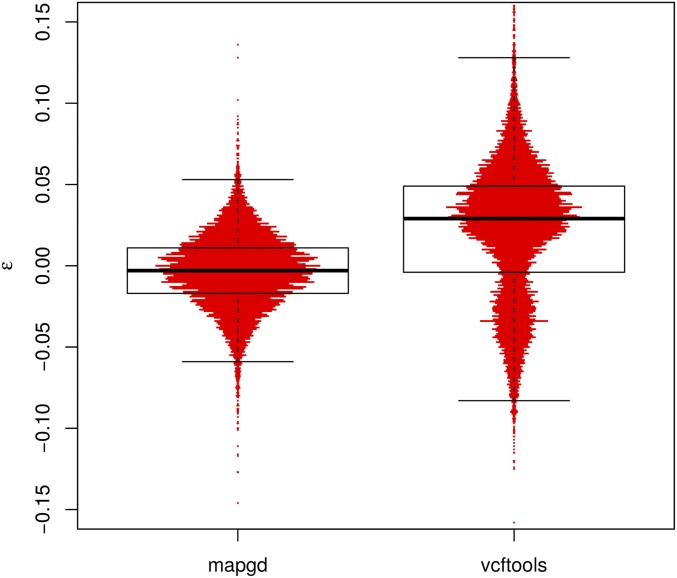
Figure 3.
Violin plots of the errors (ε) of allele-frequency estimates from the programs mapgd and VCFtools. The horizontal width of the red bars represents the frequency of observations with the corresponding values of ε. The black box shows the median (heavy black line), boundaries of the upper and lower quartile (so that 50% of all errors are contained within the box), and the whiskers denote observations within 1.5 interquartile range of the upper and lower quartiles. Results from estimates of a population of 98 individuals with 3× coverage. Alleles are drawn from a neutral spectrum. Allele frequencies in VCFtools are calculated by the VCFtools –freq command.
The surprisingly poor performance of KING in the presence of inbreeding arises from an attempt by the program to compensate for population structure. While this may be successful under other circumstances, here it infers that the single inbred pair of siblings we included in our simulated population are a unique subpopulation. Disabling this option, with the –homo argument, substantially reduces the bias of KING’s coancestry calculations, but it still compares unfavorably with mapgd.
Analysis of Daphnia population-genomic data
D. pulex is a microcrustacean commonly found in ephemeral ponds. During much of the year D. pulex asexually produce offspring that quickly mature within maternal brood chambers, but D. pulex can also produce resting eggs capable of long dormancy, called ephippia, through sexual reproduction (sexuals). Because only resting eggs survive the winter in ephemeral ponds, sexual D. pulex must have sex at least once a year to persist. However, some D. pulex only produce these resting eggs asexually (asexuals), allowing them to persist between years without sex (Hebert and Crease 1980), thought they still produce males capable of reproducing with sexual D pulex.
Samples of 96 Daphnia pulex were collected from four ephemeral ponds: Kickapond (KAP), Portland Arch (PA), Busey (BUS), and Spring Pond South (see Figure S6 for a map of locations). Early season samples were collected to minimize the chance of sampling clone mates (genetically identical individuals), which are produced asexually by all female D. pulex at 1–4 week intervals but cannot survive the winter. Each of these samples was initially evaulated using six allozyme loci to reveal any shared multilocus genotype as a rudimentary screen for asexuals. Because no population appeared to have asexuals in high abundance, all of these populations were sequenced to average coverage on an Illumina MySeq. The reads were aligned to a reference genome (Colbourne et al. 2011) and analyzed with mapgd (Section S8 in File S1).
Three of the four D. pulex populations showed mild but significant outbreeding (Figure 4A), although some of this could result from bias in our methods or artifacts resulting from alignment to the reference genome. The population displaying inbreeding (Spring Pond South) also contained a number of clone mates (12 genetically distinct individuals sampled 74 times). Genetically identical individuals were also isolated from PA (7 genetically distinct individuals sampled 17 times), but not from the two other populations. We analyzed these individuals for asexual markers described in previous studies (Tucker et al. 2013; Xu et al. 2015), and found that 3 of the 12 groups of clone mates in Spring Pond South possessed asexual makers, giving a total of 24 putative asexual individuals. The putative asexuals were outbred compared to the local population vs. Two chromosomes within asexual D. pulex are believed to originate from a hybridization of D. pulex with D. pulicaria and appear to be maintained with little recombination (Tucker et al. 2013; Xu et al. 2013, 2015); individuals should have substantial outbreeding in these hybrid regions. We removed these chromosomes from the analysis (Figure S1A), but individuals with asexual markers still appear outbred compared to the local population.
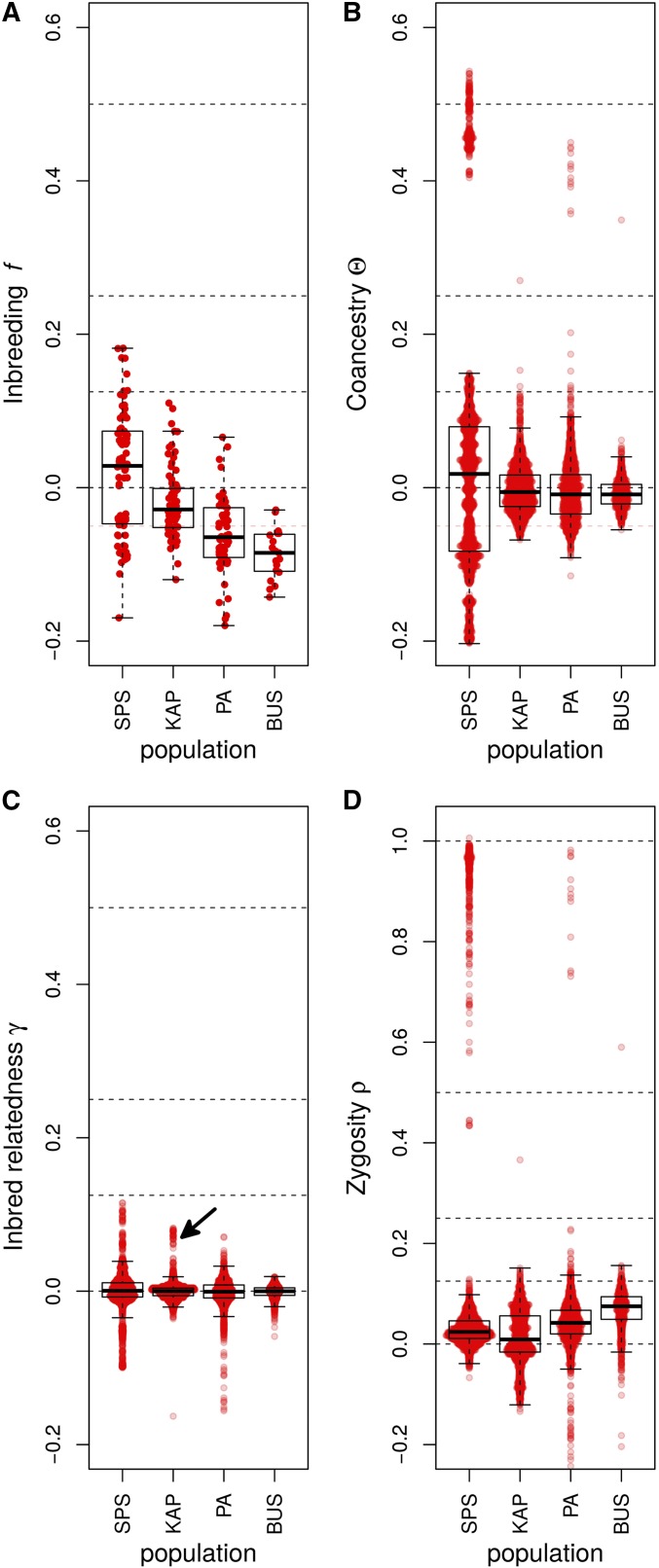
Figure 4.
Box plots of the genotypic-correlation coefficients of (A) inbreeding (f), (B) coancestry (Θ), (C) inbred relatedness (γ), and (D) zygosity estimated in the four Daphnia populations. The arrow in (C) indicates a group of nine individuals analyzed in more detail in Figure S1B. The individual pairwise estimates are shown as red points. Because γ, and ρ are pairwise estimators, comparisons exist in each population for these coefficients, while only estimates exist for f. Dashed lines are placed at 1, 0.5, 0.25, 0.125, and 0 to allow easier assignment of relationship status. SPS, Spring Pond South.
In addition to groups of clone mates displaying and , the expectation for clone mates, (Figure 4, B and D), several other general patterns are apparent. Strongly negative coancestry values separate the individuals with asexual markers from other individuals in Spring Pond South (Figure 4B). These individuals are also separated by negative inbred-relatedness values (Figure 4C).
A group of nine individuals in KAP displayed elevated inbred-relatedness values (Figure 4C, arrow). These individuals had elevated inbreeding, coancestry, and second- and fourth-order zygosity correlations with each other group, and a generally negative coancestry with the rest of the population (Figure S1B).
The second- and fourth-order zygosity correlation components show a strong negative correlation with each other (Figure S2), which is consistent with the behavior of estimation error in our simulations (Figure S3), and is also consistent with the behavior of the estimators when there is population structure (data not shown). Because of these negative correlations, the zygosity correlation coefficient was used in analyses.
KAP and BUS ponds had no clone mates, but PA and BUS both had a pair of first-order relationships Table 4).
Table 4. The values of genotypic-correlation coefficients for the six individuals from KAP, PA, and BUS displaying coancestry of half-sibling relationships or higher (Θ > 1/8), excluding clone mates.
| Clone X | Clone Y | |||||||
|---|---|---|---|---|---|---|---|---|
| BUS-10 | BUS-11 | 0.14a | −0.03a | 0.34a | 0.08a | 0.01a | 0.00 | 0.42a |
| PA-12 | PA-108 | −0.07a | −0.00 | 0.20a | −0.02a | 0.00 | −0.01a | 0.08a |
| PA-024 | PA-051 | −0.06a | −0.08a | 0.13a | 0.00 | −0.00 | 0.01 | 0.05a |
| PA-112 | PA-04 | −0.04a | −0.08a | 0.13a | −0.02a | −0.02a | −0.00 | 0.03 |
| KAP-048 | KAP-099 | −0.00 | 0.03a | 0.15a | −0.01a | 0.01a | −0.00 | 0.01 |
| KAP-113 | KAP-120 | −0.04a | −0.03a | 0.13a | −0.01a | −0.01a | 0.00 | 0.00 |
Spring Pond South is excluded due to small sample size.
Genotypic-correlation coefficients significantly different from zero corrected for the 42 comparisons in the table).
Six pairs of individuals in our samples show coancestry coefficients consistent with half-sibling or sibling relationships (Table 4), and we will briefly discuss each of these relationships. Particular individuals from these populations are referred to by the pond from which they are isolated, and the order in which they were isolated from the initial sample, though this information. The coancestry (Θ) of BUS-10 and BUS-11 is consistent with these two individuals being full siblings, and this is supported by their relatively large fraternity coefficient (Δ), but was somewhat less than expected for full siblings However, BUS-10 has a large inbreeding value and the relationship is inconsistent with some form of inbred half siblings because the inbred-relatedness values are too low. It may be that the low coverage of BUS-10 caused an overestimate of inbreeding and coancestry values, and an underestimate of fraternity, although this error would have to be more severe than errors seen in simulation at coverage. PA-12 and PA-108 also demonstrate a relatively high coancestry, but too low to be full siblings, and they have a low fraternity as well. In this case it may be that PA-12 and PA-108 are half siblings, but that population structure is obscuring their relationship. Two other pairs of individuals in KAP and two pairs in PA are consistent with half siblings with varying degrees of inbreeding (Table 4). The coancestry statistics are all and other genotypic-correlation coefficients are small. However, most of these relationships are still confounded with population structure, as demonstrated by the generally negative inbreeding coefficients. There are also half sibling-like relationships in Spring Pond South; however, the performance of the estimators is very sensitive to estimations of allele frequencies, and the allele-frequency calculations in Spring Pond South are based on the smallest number of individuals due to the large number of clone mates sampled. Because estimation of the genotypic-correlation coefficients depends on accurate allele-frequency estimates, significant bias may exist in these estimates.
Discussion
Here we reemphasize the importance of allowing genotypic-correlation coefficients to take on negative values—not only because doing so decreases the bias of estimates, but also because the expected correlations can indeed be negative. The framework outlined here is the first method to provide accurate estimates of zygosity correlation coefficients in the presence of inbreeding, and also the first method to provide estimates of inbred-relatedness coefficients from population-genomic data. This method provides accurate and nearly unbiased estimates on very low coverage data. The genotypic-correlation coefficients recovered from the four populations of Daphnia provide insight into population structure by recovering close family relationships and separating distinct subpopulations.
Similar results are not obtained in the analysis of the data with the program PLINK, which shows substantial bias in samples with coverage (Figure S4B and Figure S5B). Additionally, PLINK estimates close relatedness between individuals at rates substantially higher than mapgd, which would be consistent with the high MSE of PLINK’s estimates implied by simulations.
Our formulation of the second-order zygosity correlation coefficient, is novel. It differs both from Cockerham’s notation (Cockerham 1971), and from the coefficient of fraternity for inbreed individuals, (Lynch and Walsh 1998). At biallelic loci, the second-order zygosity correlation coefficient estimates dominance genetic variance, unlike the coefficient of fraternity. Caution should be exercised when estimating dominance genetic variance, as the coefficient of fraternity is also sometimes called the coefficient of dominance, and it would be easy to assume that the coefficient of dominance could be relevant to estimating dominance genetic variance. Although it will likely be confusing to use this term in the context of quantitative genetics, because it is already used to refer to the coefficient describing the dominance deviation, if the term is used it would apply more appropriately to the second-order zygosity correlation coefficient.
There is a long history of interpreting IBD coefficients as correlation or regression coefficients, and it has long been recognized that these coefficients can be extended to include coefficients relating an arbitrary number of individuals (Wright 1922; Cockerham 1971). For instance, Wright’s can be thought of as the genotypic correlation of all members of a defined subpopulation to each other. However, it has generally been thought that such extensions would prove impractical to calculate, or that the number of coefficients would increase very quickly. But by grouping partitions of the same order, as we do with the second- and fourth-order zygosity correlation coefficients, the number of coefficients can be substantially reduced. Programs capable of algebraic manipulation may make it possible to extend this method to groups larger than pairs of individuals.
Methods for estimating individual specific allele frequencies have been developed using principal component analysis, and such methods may be necessary to properly remove population stratification when estimating genotypic correlations (Conomos et al. 2016). The phrase individual specific allele frequencies may seem self-contradictory, since an individual does not in an ordinary sense of the word have an allele frequency. But an individual does have a probability of possessing an allele, and, as discussed in the section Calculating P(A) and P(B), this probability is usually taken to be identical with the allele frequency in the population. Because population structure can cause this frequency to differ for different groups of individuals, and these groups do not need to be discrete; every individual can have a unique probability of possessing an allele, and thus, in some sense, can have an individually unique allele frequency. While Equations 3–9 formally allow differences in ancestral allele frequencies between individuals, we have not made an attempt to estimate this parameter. However, even with these limitations, the ability to detect and characterize complex relationships in wild populations, such as that between PA-12 and PA-108, should be a boon to researchers. While many programs can detect some relationships in panmictic populations, mapgd is unique in that its estimates are accurate in the presence of inbreeding, and it provides additional genotypic-correlation coefficients not estimated by other programs.
The draft genome to which reads were aligned in this study is known to suffer from a number of artifacts, particularly “allelic splits,” where the two alleles of a gene assemble as paralogous genes in the reference, and “paralog collapse” where paralogous genes are assembled at a single locus (Denton et al. 2014). While the goodness-of-fit statistic was developed in part to detect and remove these artifacts, its performance has not been carefully analyzed in this article, and it is possible that artifacts undetected by the goodness-of-fit statistic influence our estimates. The inbreeding of an individual is the coancestry of the parents, and while slightly negative coancestry is common in these populations, there are few individuals with but many individuals with (Figure 4, A and B). The difference between average coancestry and average inbreeding suggest that there may be some bias in inbreeding estimation. The inclusion of focal individuals in estimation of allele frequencies may be responsible for some of this bias, since this inclusion biases estimates in simulations by approximately −0.01 (Table S8 in File S1). Currently it is difficult to sequentially exclude the focal individuals from allele-frequency calculations, but methods of removing this bias need to be explored. Additionally, some of the bias may arise from the poor reference. High coverage increases the power of the goodness-of-fit test, and should increase our ability to discern artifacts in the reference. While an elevation of inbreeding is seen in low coverage individuals, inbreeding estimates appear stable once coverage is > implying that mapgd’s estimates are relatively robust once sequencing depth is reasonable. Nevertheless, the robustness of these estimates needs to be reevaluated when a better reference genome becomes available.
In this study, genotypic correlations provided insight into a number of aspects of population structure. The two separate groups of asexuals in Spring Pond South could be distinguished from sexuals by their large negative inbreeding, coancestry, and inbred-relatedness values. This result is consistent with limited or no crossing between the asexuals and the sexuals within the pond. A group of nine individuals in KAP with a coancestry of form a clear subpopulation (Figure 4 and Figure S1), although we have not explored what factors drive this structure.
An average of two close relatives were found in the three Daphnia populations (excluding clone mates), which may seem surprisingly high given that only 96 individuals were sampled. However, 4500 comparisons of relatedness were made between individuals in each population, so the possibility of obtaining related individuals is much greater than naive intuition would suggest. Our ability to find closely related individuals in random samples highlights the potential power of a genomic-based approach in wild populations.
One strength of a maximum-likelihood framework is that it allows the assessment of significance of relationships through a log-likelihood ratio test. A correctly specified likelihood function would account for correlation between loci, rather than assuming that loci are independent, and allow for tests of deviations from pedigree expectations. Because our method is a quasi-maximum-likelihood method, it does not test for these deviations; nevertheless it does correctly test for the significance of sample correlations. In the Daphnia, virtually all pairs of individuals had highly significant departures from an unrelated status (i.e., after multiple correction), in stark contrast to the behavior of our estimators in simulations when the true value of the parameters are known to be zero. Genotypic correlations in these samples may be created by geographic structure of the population and temporal structure created by the dormancy of resting eggs over many seasons. In this case the log-likelihood-ratio test is, at least in a sense, working correctly. Since most populations may have some form of substructure owing to variation in family size, demography, etc., it may be desirable to find a method that considers some aspects of population structure as part of the null model.
While much work remains to be done, our estimators already have excellent performance when coverage is minimal. The ability to use low coverage data for population-genomic studies will greatly reduce the cost of these studies. Even if the additional parameters estimated by methods outlined here are unneeded, the ability to recover accurate and precise estimates of coancestory, inbreeding, and fraternity estimates on low coverage sequence may be of general use. We hope that these properties, and others discussed in the text, will make the general coefficients of genotypic correlation useful to the research community.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.190660/-/DC1.
Acknowledgments
We thank colleagues for their helpful comments on this article, especially Lydia Bright. Thanks to W. Kelley Thomas and the Hubbard Center for Genome Studies for their continued help with the sequencing, the Center for Genomics and Bioinformatics and especially James Ford for the preparation of libraries, Kimberly Young of the Daphnia Growth Facility and her army of undergraduates for their tireless work maintaining lines, and Ben Fulton and others at the Pervasive Technology Institute for their help with mapgd. Finally, M.S.A. would especially like to thank Sadie Carter for her constant encouragement. This research was made possible by a grant from the National Science Foundation to M.L. to support the development of methods for the analysis of population-genomic data (Department of Environmental Biology award 1257806) and a grant from the National Institutes of Health to M.L. to support population genomics research in Daphnia pulex (GM-101672-01A1).
Note added in proof: See Lynch et al. 2017 (pp. 315–332) in this issue and Maruki and Lynch 2017 (pp. 1393–1404) and Ye et al. 2017 (pp. 1405–1416) in the G3 May issue for related work.
Footnotes
Communicating editor: R. Nielsen
Literature Cited
- Abney M., McPeek M. S., Ober C., 2000. Estimation of variance components of quantitative traits in inbred populations. Am. J. Hum. Genet. 66: 629–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson A. D., Weir B. S., 2007. A maximum-likeihood method for the estimation of pairwise relatedness in structured populations. Genetics 176: 421–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning B. L., Browning S. R., 2013. Improving the accuracy and efficiency of identity-by-descent detection in population data. Genetics 194: 459–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockerham C., 1971. Higher order probability functions of identity of alleles by descent. Genetics 69: 235–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockerham C., 1983. Covariances of relatives from self-fertilization. Crop Sci. 23: 1177–1180. [Google Scholar]
- Cockerham C., Weir B. S., 1983. Variance of actual inbreeding. Theor. Popul. Biol. 23: 85–109. [DOI] [PubMed] [Google Scholar]
- Colbourne J. K., Pfrender M. E., Gilbert D., Thomas W. K., Tucker A., et al. , 2011. The ecoresponsive genome of Daphnia pulex. Science 331: 555–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conomos M. P., Reiner A. P., Weir B. S., Thornton T. A., 2016. Model-free estimation of recent genetic relatedness. Am. J. Hum. Genet. 98: 127–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotterman, C., 1940 A calculus for statistico-genetics. Ph.D. Thesis, Ohio State University, Ohio. [Google Scholar]
- Denton J. F., Lugo-Martinez J., Tucker A. E., Schrider D. R., Warren W. C., et al. , 2014. Extensive error in the number of genes inferred from draft genome assemblies. PLoS Comput. Biol. 10: e1003998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández J., Toro M. A., 2006. A new method to estimate relatedness from molecular markers. Mol. Ecol. 15: 1657–1667. [DOI] [PubMed] [Google Scholar]
- Fisher R. A., 1918. The correlation between relatives on the supposition of mendelian inheritance. Trans. R. Soc. Edinb. 52: 399–433. [Google Scholar]
- Fu Y.-X., 1995. Statistical properties of segregating sites. Theor. Popul. Biol. 48: 172–197. [DOI] [PubMed] [Google Scholar]
- Hebert P. D. N., Crease T., 1980. Clonal coexistence in Daphnia pulex leydig: another planktonic paradox. Science 207: 1363–1365. [Google Scholar]
- Holland J. B., Nyquistand W. E., Cervantes-Martinez C. T., 2003. Estimating and interpreting heritability for plant breeding: an update. Plant Breed. Rev. 22: 9–111. [Google Scholar]
- Jacquard S., 1970. The Genetic Structure of Populations. Springer-Verlag, New York. [Google Scholar]
- Kalinowski S. T., Wagner A. P., Taper M. L., 2006. ML-RELATE: a computer program for the maximum likelihood estimation of relatedness and relationship. Mol. Ecol. Notes 6: 576–579. [Google Scholar]
- Li H., Durbin R., 2010. Fast and accurate long-read alignment with burrows-wheeler transform. Bioinformatics 26: 589–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., 2008. Estimation of nucleotide diversity, disequilibrium coefficients, and mutation rates from high-coverage genome-sequencing projects. Mol. Biol. Evol. 25: 2409–2419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Ritland K., 1999. Estimation of pairwise relatedness with molecular markers. Genetics 152: 1753–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Malécot G., 1948. Les Mathématiques de l’hérédité. Barnéoud frères, Paris. [Google Scholar]
- Manichaikul A., Mychaleckyi J. C., Rich S. S., Dal K., Sale M., et al. , 2010. Robust relationship inference in genome-wide association studies. Bioinformatics 26: 2867–2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruki T., Lynch M., 2015. Genotype-frequency estimation from high-throughput sequencing data. Genetics 201: 473–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell J. E., Visscher P. M., Goddard M. E., 2010. Reconciling the analysis of ibd and ibs in complex trait studies. Nat. Rev. Genet. 11: 800–805. [DOI] [PubMed] [Google Scholar]
- Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M., 2007. PLINK: a toolset for whole-genome association and poulation-based linkage analysis. Am. J. Hum. Genet. 81: 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D., Balding D. J., 2015. Relatedness in the post-genomic era: is it still useful? Nat. Rev. Genet. 16: 33–44. [DOI] [PubMed] [Google Scholar]
- Suarez B. K., Rice J., Reich T., 1978. The generalized sib pair IBD distribution: its use in the detection of linkage. Ann. Hum. Genet. 42: 87–94. [DOI] [PubMed] [Google Scholar]
- Sved J., 1971. Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor. Popul. Biol. 2: 125–141. [DOI] [PubMed] [Google Scholar]
- Thompson E. A., 1988. Two-locus and three-locus gene identity by descent in pedigrees. IMA J. Math. Appl. Med. Biol. 5: 261–279. [DOI] [PubMed] [Google Scholar]
- Thompson E. A., 2013. Identity by descent: variation in meiosis, across genomes, and in populations. Genetics 194: 301–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker A. E., Ackerman M. S., Eads B. D., Xu S., Lynch M., 2013. Population-genomic insights into the evolutionary origin and fate of obligately asexual Daphnia pulex. Proc. Natl. Acad. Sci. USA 110: 15740–15745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., 2002. An estimator for pairwise relatedness using molecular markers. Genetics 160: 1203–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., 2007. Triadic IBD coefficients and applications to estimating pairwise relatedness. Genet. Res. 89: 135–153. [DOI] [PubMed] [Google Scholar]
- Wang J., 2011. Coancestry: a program for simulating, estimating and analysing relatedness and inbreeding coefficients. Mol. Ecol. Resour. 11: 141–145. [DOI] [PubMed] [Google Scholar]
- Wright S., 1922. Coefficients of inbreeding and relationship. Am. Nat. 56: 330–338. [Google Scholar]
- Xu S., Innes D. J., Lynch M., Cristescu M. E., 2013. The role of hybridization in the origin and spread of asexuality in Daphnia pulex. Mol. Ecol. 22: 4549–4561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S., Spitze K., Ackerman M. S., Ye Z., Bright L., et al. , 2015. Hybridization and the origin of contagious asexuality in Daphnia pulex. Mol. Biol. Evol. 32: 3215–3225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Benyamin B., McEvoy B. P., Gordon S., Henders A. K., et al. , 2010. Common snps explain a large proportion of heritability for human height. Nat. Genet. 42: 565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The software used in the simulations and data analysis is freely available from https://github.com/LynchLab/mapgd/. The Daphnia pulex data are available on request.