The loop hypothesis: contribution of early formed specific non-local interactions to the determination of protein folding pathways

Abstract

The extremely fast and efficient folding transition (in seconds) of globular proteins led to the search for some unifying principles embedded in the physics of the folding polypeptides. Most of the proposed mechanisms highlight the role of local interactions that stabilize secondary structure elements or a folding nucleus as the starting point of the folding pathways, i.e., a “bottom–up” mechanism. Non-local interactions were assumed either to stabilize the nucleus or lead to the later steps of coalescence of the secondary structure elements. An alternative mechanism was proposed, an “up–down” mechanism in which it was assumed that folding starts with the formation of very few non-local interactions which form closed long loops at the initiation of folding. The possible biological advantage of this mechanism, the “loop hypothesis”, is that the hydrophobic collapse is associated with ordered compactization which reduces the chance for degradation and misfolding. In the present review the experiments, simulations and theoretical consideration that either directly or indirectly support this mechanism are summarized. It is argued that experiments monitoring the time-dependent development of the formation of specifically targeted early-formed sub-domain structural elements, either long loops or secondary structure elements, are necessary. This can be achieved by the time-resolved FRET-based “double kinetics” method in combination with mutational studies. Yet, attempts to improve the time resolution of the folding initiation should be extended down to the sub-microsecond time regime in order to design experiments that would resolve the classes of proteins which first fold by local or non-local interactions.

Electronic supplementary material

The online version of this article (doi:10.1007/s12551-013-0113-3) contains supplementary material, which is available to authorized users.

Introduction

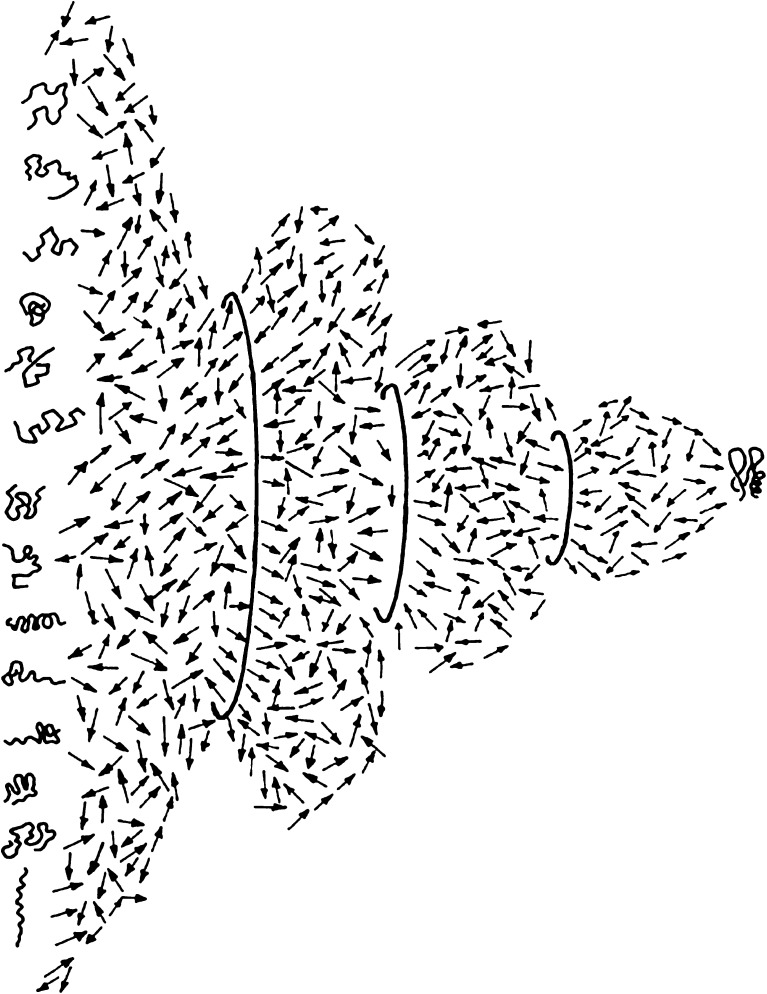
Most globular proteins fold within seconds and even microseconds into a compact structure under physiological conditions. An ensemble of disordered protein molecules, which populates a large conformational space and undergoes fast transition to an ensemble of ordered molecules, must explore a very large number of pathways due to the stochastic nature of the search (Fig. 1). However, the folding transition is fast and efficient, and most of the pathways converge to an ensemble of ordered molecules that occupy only a very small section of the conformational space. This extremely fast and efficient folding transition (in microseconds) of almost all globular proteins led to the hypothesis that the mechanism of the folding transition of globular proteins is not a random search, but rather, an ordered sequence of steps that gradually reduce the conformational space available to the polypeptide chain. The “thermodynamic hypothesis” means that, in principle, one should be able to predict the product of the conformational search (i.e. the folded conformation) by searching for the free energy minimum of the system of protein and solvent (Anfinsen and Scheraga 1975; Goldstein et al. 1992; Shakhnovich and Gutin 1993a, b; Sali et al. 1994; Shakhnovich 1994).

Fig. 1.

Structural view of the folding transition. A two-dimensional slice in the multidimensional conformational hyperspace of a refolding protein molecule. The transition between the large ensemble of disordered chain conformations and the small ensemble of native chain folds is based on purely stochastic thermal motions of all the chain segments driven by the thermal energy of the solvent. The directed folding transition, which is based on these elementary stochastic steps, is achieved by means of the gradual addition of conformational constraints, represented by the circles of smaller and smaller diameters, which represent the reduction of the conformational space. These constraints consist of local and non-local cross links between chain elements that reduce the degrees of freedom of the backbone and the side chains. The search for the interactions that impose these restrictions is a major goal of folding research aimed at deciphering the relationship between the genetic (sequence) information and the formation of the folded state of the protein molecules (reproduced with permission)

This approach does not address the mechanism that determines the rate and efficiency of the folding transition. Thus, efforts were next directed at identifying structural characteristics of the transient ensembles of partially ordered molecules that were assumed to be present along the folding pathway, as indicators of the mechanism underlying the fast transition. The underlying assumption was that the mechanism of folding is hierarchical and that the sequence information encoded in each globular protein includes a set of “instructions” for the construction of the folded states via the gradual formation of sub-domain structures. Thus, the genetic information should be viewed as a “blueprint” for the construction process and, hence, the challenge is to decipher the relationship between the sequence information and specific steps in the transition process.

The challenge inherent in this approach is the need to characterize transient ensembles that include a wide range of conformations, with a large variance of structural characteristics; each of these conformational states is poorly populated and very short lived. The most common methods, which rely on the determination of population averages of structural characteristics, are insufficient, and methods for very fast capture of the mean and the variance of each measured structural characteristic should be developed. Historically, inspired by the chemical concepts of reaction intermediates, it was assumed that the detection of kinetic intermediates along the pathway (Ptitsyn 1973) and residual structures (Shortle and Meeker 1989) should reveal some of the principles of the folding mechanism (Ptitsyn 1973; Karplus and Weaver 1976; Kim and Baldwin 1982). Metastable intermediates, however, may actually slow the transition and might not be the right target for the search (Sosnick et al. 1994; Krantz et al. 2002).

When considering possible mechanisms of stepwise structure formation, the “bottom-up” model would intuitively appear to be the first choice (Kim and Baldwin 1982; Ionescu and Matthews 1999). In this model, local interactions (LI) between near neighbor residues along the chain are assumed to first form and then stabilize short structural elements, such as secondary structures. Those elements then coalesce to form a higher level of contacts. The entropy cost of such a transition is low, and the probability of the formation of pairwise interactions is high. An alternative model is based on the hypothesis that the dominant interactions which are essential for the early determination of the folding pathway, enabling rapid and early elimination of major sections of the conformational space, are non-local interactions (NLI) between monomers separated by ten or more residues along the chain. This model is counter-intuitive since it involves a larger reduction of conformational entropy, and thus these NLIs should be slower to form than LIs. The relative importance of local versus NLIs in determining the rate of folding and for the folded structures has been investigated for many years based on experiments, simulations, and theoretical considerations. The view that non-local contacts can be effective early in the folding transition was first suggested based on simple lattice-based protein folding simulations (Taketomi et al. 1975; Go and Taketomi 1978). Using a cubic lattice simulation, Shakhnovich (Abkevich et al. 1995) found that NLIs contribute to a faster rate of folding. However, the results of many other studies support the counter-hypothesis that the folding mechanism is dominated by LIs, while the non-local ones provide non-specific stabilization of the compact conformers (Anfinsen and Scheraga 1975; Harrison and Durbin 1985; Wright et al. 1988; Rooman et al. 1992; Dill et al. 1993; Weikl and Dill 2003) and nucleation (Wetlaufer 1973; Daggett and Fersht 2003; Kihara 2005) The question of whether the LIs or NLIs are more important or dominant in the initiation of folding, or for determination of the direction and rate of the folding transition remains open, and is the subject of the present review.

Most of the early studies addressing this question were based on analyses of the folded structures or theoretical considerations, as well as simulations. However, to resolve this issue, there is a need for experimental investigation of the role of NLIs versus LIs at the level of the collapsed protein molecules, prior to the formation of the transition state ensemble (TSE). For that purpose, we developed methodologies based on time-resolved fluorescence resonance energy transfer (trFRET) for characterization of the ensembles of unfolded, collapsed, and partially folded globular protein molecules. The method is based on a combination of site-specific labeling of selected pairs of residues by fluorescent probes with donor and acceptor receptors and determination distributions of intramolecular distances in ensembles of the labeled protein molecules by means of trFRET measurements. This method enables monitoring fine changes of the end-to-end distance of preselected chain elements, such as loops or secondary structure elements, one at a time, in situ, in the context of the whole molecule which does not contribute to the signals (Beechem and Haas 1989; Haas 2005). Preparation of series of labeled mutants of one protein enables the monitoring of conformational changes of each sub-domain structure. Very fast data collection enables the determination of series of sequential distance distributions along the folding pathway (Ratner et al. 2000, 2005; Ben Ishay et al. 2012b). Such experiments yield meaningful information on specific conformational changes and the order of their occurrence along the folding pathway. .

Pre-transition state ensemble processes

Under physiological conditions, where the aqueous solution is a poor solvent for globular proteins, these collapse to globules of reduced mean diameter, similar to any other polymer. This is a manifestation of the non-specific reduction of the residue-solvent interactions such as backbone hydrogen bonds (Bolen and Rose 2008; Teufel et al. 2011) or the hydrophobic effect. A common feature of the collapsed state is the burial of hydrophobic chain segments in the interior of the collapsed globule, which amplifies the probability of NLIs, whether specific or non-specific.

Many experiments show that the mean radius of the collapsed globule is about 30 % larger than that of the same molecule in its fully folded state (Finkelstein and Shakhnovich 1989; Bilsel and Matthews 2006). Thus, almost half of its volume is occupied by solvent molecules. This implies that in the collapsed state, few residue–residue interactions are effective, chain dynamics are not inhibited, and the probability of residue–residue encounters is enhanced. Remaining questions regarding this folding stage are the identification of key interactions that appear in the collapsed globule and contribute to the development of the programmed pathway, as well as the residues that supply them.

The loop hypothesis

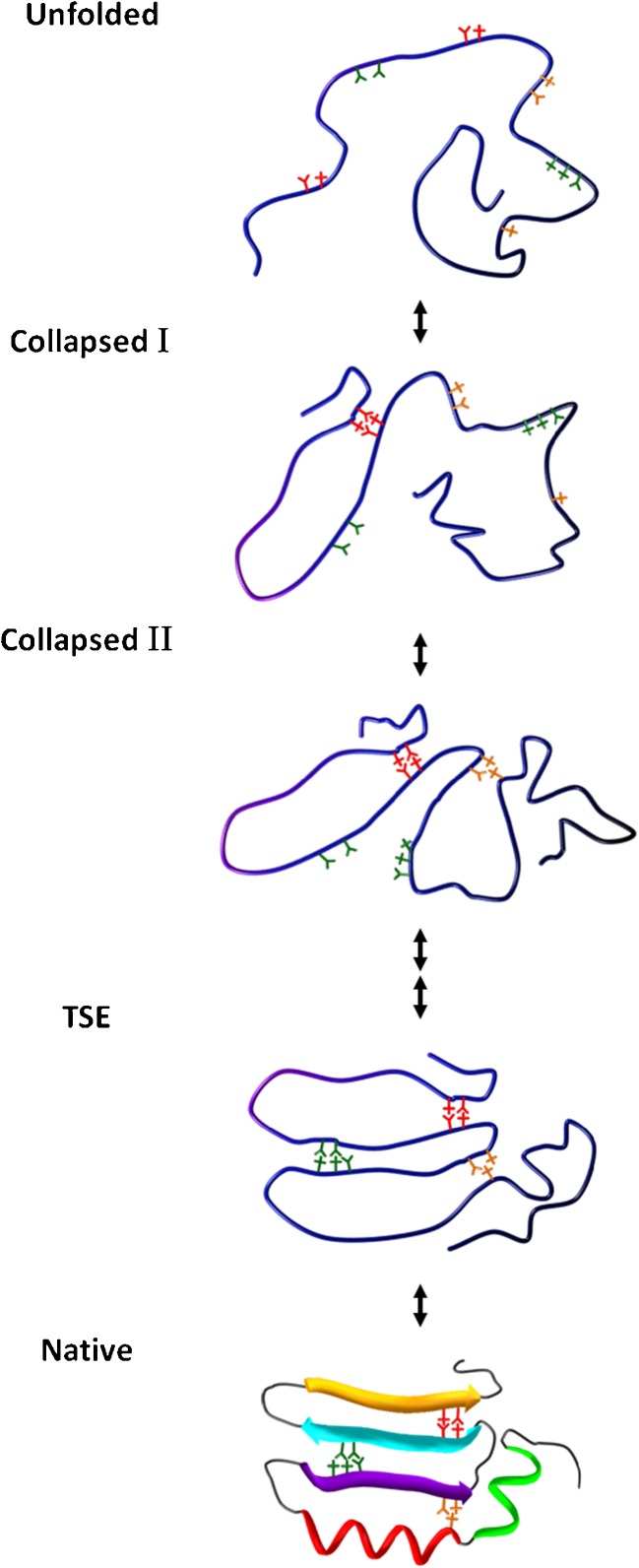
We proposed the “loop hypothesis” in 1995 based on results of trFRET studies on the folding of double-labeled (donor and acceptor) reduced bovine pancreatic trypsin inhibitor (BPTI) (Fig. 2) (Ittah and Haas 1995). We hypothesized that the earliest steps in the folding transition are the closure of few long loop (25–35 residues) segments by NLIs between clusters with mostly non-polar residues at their ends (Ittah and Haas 1995; Haas 2005). In contrast to the “bottom-up” folding mechanism, we assumed a “top–down” pathway, whereby non-local (and less probable)-structure elements are formed at the initiation of folding. Secondary structures can either form at the same time or at a later time along the transition, but the NLIs which close the loops do not depend on secondary structures of interacting clusters. The biological advantages of such a mechanism are (1) maximum backbone entropy reduction per interaction, (2) rapid formation of the overall outline of the native structure and reduced chance for aggregation or misfolding, (3) rapid protection from proteolysis mechanisms in the cell. It was further suggested that very few such closed loops sufficiently restrict the conformational space and force the protein into an ensemble of conformations very close to the TSE and the folded ensembles. Our “closed loop hypothesis” is consistent with the nucleation condensation mechanism (Fersht 1997), but takes it one step further by suggesting that the closed loops, which contribute to the folding nucleus, are formed in a very early step of the folding transition, either during or shortly after the non-specific collapse, well before the formation of the TSE, even in apparent two-state folders. We assumed that the closure of the loops might be of marginal stability and that therefore they could be observed by characterization of the fine changes in the transient distributions of intramolecular distances between the clusters of residues that form the closing interactions. We also assumed that since only very few such interactions are needed and since they are not dependent on the formation of secondary structures, it is possible that these structural elements would not be detected by conventional detection methods used to study the kinetics of protein folding (e.g., tryptophan fluorescence, far UV circular dichroism, etc.). trFRET experiments are ideal for detecting the formation of each closed long loop since it is possible to follow selected distances between two sites that are separated by large number of residues, their distributions, and fast fluctuations (Beechem and Haas 1989; Haas 2005). This led to our efforts towards the development of the trFRET-based “double kinetics” method for the detection of transient intramolecular distance distribution in the rapid collapsed state of globular proteins and during the full folding transition (Ratner et al. 2000; Jacob et al. 2005; Ben Ishay et al. 2012a).

Fig. 2.

Carton description of the “closed loop model”. Five snapshots along the folding trajectory of a model protein. The unfolded state is represented by one of the many possible conformers. The three pairs of clusters of mostly hydrophobic residues that can form the lock of specific loop ends are shown in three colors. Upon change to folding conditions, rapid chain collapse leads to a compact still disordered globule. During or immediately after chain collapse (collapsed I) the loop structure locked by pair of specific hydrophobic clusters is rapidly formed. In the next step (collapsed II, red and orange clusters) the second loop is formed within a very short time. The three closed loops already fix the overall native-like topology of the chain. At this point a diffuse nucleus has been formed and with activation, a limited delay, or right away (in the single domain fast folders) the transition state ensemble (TSE) is formed. Finally, packing and complete desolvation is achieved and the folded state is stabilized (Native)

The NLI-based model for initiation of folding raises several questions that must be addressed. These include: (1) Is it feasible that two distant sites separated by a long chain segment would so rapidly come into contact? (2) How does a single interaction balance the large entropy cost of restricting a large segment of the chain? (3) What are the types of residue clusters that form the loop ends’ NLIs? (4) Do the folding transitions of relatively small single domain proteins that are considered “two-state folders” also have pre-transition state loop closure steps (not detected so far)?

The first question on the speed of contact formation was answered by several studies in which the kinetics of loop closure of long polypeptide segments was measured, mainly in fluorescence quenching experiments. Fast loop closure on the nanosecond time scale has been reported (Lapidus et al. 2000; Buscaglia et al. 2003; Krieger et al. 2003). Concerns about the entropy cost of loop closure can be considered in the context of (1) a study of the probability of loop closure showing less than a one order of magnitude change of the probability between 10 and 40 residue chain segments (Camacho and Thirumalai 1995); (2) several studies showing that the entropy cost is low (Scalley-Kim et al. 2003; Wang et al. 2005). One reason that the entropy change is expected to be balanced by the NLIs is that only the loop ends are constrained, while the rest of the chain between them is free to occupy a large number of conformations under the constraints of the chain collapse. The other questions concerning the nature of the loop end and the pathways taken by two-state folders will be discussed in the following sections where we review two sets of theoretical and experimental results. In these sections, we will first describe experiments, simulations, and theoretical considerations that address the mechanism of folding and its kinetics, and are thus directly relevant to the closed loop hypothesis. We will also describe analyses of the folded structures of proteins that highlight the importance of loop structures in the protein folded state. However, we do not directly address the closed loop hypothesis.

Direct and indirect findings consistent with the closed long loop hypothesis

Set A

Support for the loop hypothesis can be found using several experimental or theoretical and computational approaches. The first approach is the observation of the fast formation of contacts between loop ends at the initiation of refolding transitions using kinetic experiments. This is the most direct test of the hypothesis. An ideal experiment should enable monitoring the time course of changes in the distributions of intramolecular distances between ends of putative loops, as well as changes in secondary structure elements throughout the time course of refolding experiments. Indirect support can also be found in the following experiments and theoretical approaches: (2) observations of any NLI formation at the initiation of folding transitions; (3) detection of characteristics of folding nuclei, which are formed by separate chain sections prior to the formation of the TSE; (4) observation of accelerated folding rate by early formation of NLIs in simulations of the folding transition.

Set B

Analyses of the loop structures in the native (folded) structures of proteins which do not address the mechanism of folding and loop hypothesis but are of interest in light of the loop hypothesis include (1) statistical analysis of the folded structures and folding rates of proteins and (2) bioinformatics analyses.

• A.
  Studies of the mechanism and kinetics of the folding transition.

  1. Experiments that resolve fast and slow loop closure at the initiation of refolding transitions.

     • tr-FRET detection of rapid folding kinetics: the “double kinetics” experiment.
       The “double kinetics” folding/unfolding experiments combine fast initiation of folding/unfolding transitions by rapid change of the solution conditions, synchronized with rapid determination of fluorescence decay curves. This experiment enables a series of time-dependent transient distributions of the distance between pairs of probes attached to the ends of chain segments to be determined during the fast refolding transition. Two time regimes are involved in this experimental approach, namely, the duration of the conformational transition, the ‘chemical time regime’ (t _c) (microseconds to seconds), and the ‘spectroscopic time regime’ (t _s), the nanosecond fluorescence decay of the probes.
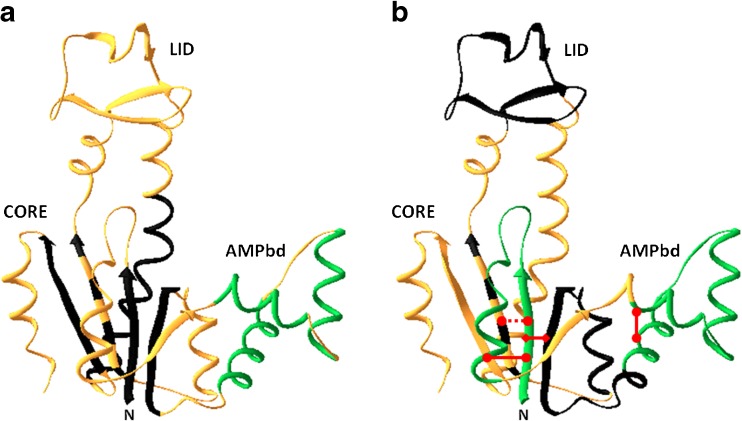
     • This approach was applied in a series of experiments in which Escherichia coli adenylate kinase (AK) was used as the model molecule. AK is a 214-residue, three-domain bacterial protein which catalyzes the transfer of a phosphoryl group between ATP and AMP (Noda et al. 1975; Muller and Schulz 1988, 1992; Schulz et al. 1990). A systematic labeling plan was designed in which pairs of probes were introduced at the ends of long loop structures and at the ends of several known secondary structure elements (Fig. 3) (Orevi et al. 2009). Stopped flow mixing was used for the initiation of refolding (Ben Ishay et al. 2012b). Upon transition to folding conditions, the initial transient collapsed ensemble of AK conformers appeared disordered and refolded to a native structure through an apparent two-state mechanism with a rate constant of 0.3 s⁻¹. At the end of the dead-time of the stopped flow device (5 ms), the distributions of several intramolecular distances were broad, in particular those that are far apart along the primary sequence of the chain, with a mean distance characteristic of the collapsed globule (e.g., the distance between residues 18 and 203, 28 and 203, 58 and 86, and 73 and 203) (Fig 3) (Ben Ishay et al. 2012b). Several secondary structure elements that were monitored showed slow transition to the native mean end-to-end distance at the same rate as the cooperative folding transition (0.3 s⁻¹). These include three β strands (residues 1–8, 79–86, and 188–203) and one α helix (residues 169–188) (Orevi, in preparation). In sharp contrast, the ends of several closed loops associated with the CORE domain already achieved the native-like mean distance at the end of the mixing dead-time (Fig. 4). These include the N-terminal loop (residues 1–26), the AMP_bind loop (residues 28–71) (Fig. 5), and the long loop, which includes the former two loops between residues 1 and 75. Other loops that were tested did not show this very early closure to native distances between their ends. These include the LID domain loop (residues 121–155) and two other sections, residues 58–86 and residues 66–95 (Fig. 4) (Orevi, in preparation). Interestingly, the two helices at the node of the AMP_bind domain long loop and the one in between were also found to have a native-like distribution of their end-to-end distances at the end of the mixing dead-time. This series of experiments show that in the case of AK, selected long loops are closed during or right after the fast collapse, while other sections of the chain fold only at a rate that is three orders of magnitude slower (Fig. 3). The fast closed loops are associated with the N-terminal section of the CORE domain, located within the first third of the chain, and it is reasonable to assume that the folding nucleus is included in that section. These results provide strong evidence in support of the loop hypothesis. However, further tests, must be performed in order to firmly establish the role of the early closed long loop in the initiation and direction of the folding pathway of the AK molecule. One such experiment was already done—the introduction of mutations at the node of the AMP_bind loop. The native structure shows close contact between the clusters of residues 67–68 and 34–35. When both Met34 and Leu67 were replaced by Ala residues, the rate of loop closure was dramatically reduced. When residue Leu35 was replace by Ala, the protein was destabilized and the yield of folding was extremely poor. This clearly shows that the hydrophobic NLIs between these two clusters is crucial for the folding of the AK molecule.
     • In a similar series of FRET measurements, Udgaonkar and coworkers studied the early steps of the folding transition of the protein barstar (89 residues) (Sinha and Udgaonkar 2007) and found fast reduction of the inter-segmental distances in a small number of labeled pairs, while some other pairs showed only slow transition to native intramolecular distances. Such heterogeneity is a hallmark of the formation of specific non-local contacts at some parts of the chain.
     • Winkler used trFRET to determine the distance distributions of two loops/residue pairs in cytochrome c (125 residues), 150 μs after refolding initiation (Kimura et al. 2007). These authors found that one distance distribution (Trp32-heme) was native-like, while the distribution of the second pair (72-heme) was still unfolded. Similar results were obtained by Matthews et al. (Wu et al. 2008) who studied the early steps (30 μs) of the folding transition of the alpha subunit of tryptophan synthase.
       In the context of the loop hypothesis, it is possible that pairs that show native-like distance at an early stage of the transition are located in close proximity to a loop node, or alternatively, are affected by the closure of one or several loops.
  2. Experimental studies that reveal the formation of NLIs at the initial phases of folding transitions.
     Non-local hydrophobic interactions between three helical segments of apomyoglobin at the earliest (microsecond) phases of the refolding transition have been shown by several groups. Dayer and coworkers (Gulotta et al. 2001) reported ultrafast (almost diffusion limited) assembly of a three-helix-terminal (A, G and H) structure by a net of hydrophobic NLIs. These experiments support the conclusion that specific NLIs between hydrophobic residue clusters can develop in a diffusion limited search at the initiation of the refolding transition. The correlation of fast structure formation with the average area buried upon folding that was determined for specific chain segments in the refolding apomyoglobin molecules further demonstrated the role of NLIs in the initiation of the folding transition (Nishimura et al. 2005; Felitsky et al. 2008). Lapidus et al. (2007) used microsecond resolution of a microfluidic device for rapid mixing and resolved the initial phases of refolding of three model proteins. A fast hydrophobic collapse (approx. 20 μs) was followed by the formation of the first native tertiary contacts (approx. 100 and 300 μs). Kato et al. (2010) studied the folding of mutants of S. nuclease, where NLIs were perturbed and concluded that the native NLIs established at the early stage of the folding process facilitate further secondary structure formation. Meisner and Sosnick (2004) studied the kinetics of folding of a two-chain engineered protein in which helicity and collision rate can be varied and concluded that an unstructured encounter complex can successfully initiate rapid folding, with helix formation occurring at a later stage. The collision-first route enables a high basal folding rate of any protein. Mirny and Shakhnovich (2001) reviewed a number of folding kinetics studies and found that in all cases secondary interactions play—at most—a minor role in determining folding kinetics. Instead, strong and specific hydrophobic NLIs seem to be the dominate driving force.

     • Hydrophobicity and the capacity to adopt tight contacts between sidechains contribute to the specificity of early formed NLIs.
       O’Neill et al. (O’Neill and Robert Matthews 2000) reported solid evidence for the role of stereo-specificity in the formation-specific NLIs between non-polar side chains in the fast phases of the folding of the enzyme dihydrofolate reductase. Three hydrophobic residues which are part of the early developed hydrophobic core (I91, I94, and I155) were substituted by similar hydrophobic residues (L or V). These substitutions reduced the extent of the earliest structure formation upon initiation of refolding.
       Similarly, Davidson examined the effect of substitution of nine core residues of the SH3 domain (Northey et al. 2002), and Raleigh substituted six core residues of the NTL9 domain (Anil et al. 2005). In both studies, non-polar (or aromatic) residues were substituted with residues that were designed to change either the local hydrophobicity or the contacting surfaces, and the rate of refolding was measured. Single substitution of non-polar residues resulted in a dramatic change in the folding rate (up to a factor of 55-fold in the experiments reported above and up to 600-fold in those reported by other labs (Munson et al. 1997). Yet the change in the folding rate did not (necessarily) alter the overall thermodynamic stability or structure. In most cases, increased hydrophobicity accelerated folding, while residues involved in the development of the fast core of SH3 (I28, A39, and I50) showed dependence on side-chain structure rather than hydrophobicity. This suggests that tight packing of non-local residue clusters is achieved rapidly and effectively in selected chain segments at the initiation of folding. Steward et al. (2009) studied the folding of a complex all-alpha Greek key domain and concluded that topology is the dominant factor in the folding of this protein.
       To summarize, the data presented above shed light on the mechanism by which specific hydrophobic contacts can rapidly form. The less specific force is the local hydrophobicity that directs parts of the chain to the interior, which in turn increases the probability of forming close contacts with other (non-local) hydrophobic regions. Then, more specific recognition is achieved on the basis of stereo-specific alignment between defined clusters or residues. These features are encoded in the linear sequence of the chain.
  3. The role of NLIs in the early nucleation step of the folding pathway.
     The nucleation step was suggested to be a mechanism ensuring a fast and efficient folding transition (Wetlaufer 1973; Fersht 1995, 1997; Mirny and Shakhnovich 2001). The nucleus is formed by residues from different parts of the chain, and unstructured loops between them. In some proteins, the nucleus does not include secondary structures and some proteins do have secondary structures in their folding nucleus, which depend on stabilization by NLIs (Mirny and Shakhnovich 2001). A very large body of theoretical, simulations and experimental studies further developed the role of nucleation as a step of the folding transition (Daggett and Fersht 2003). The common theme of most of those mechanisms is the presence of a small number NLIs that are formed prior to the main folding transition. In many cases, these contacts form long closed loops.
     Shakhnovich used molecular dynamics (MD) and a Monte Carlo Go model simulation to examine the events that lead to formation of the TSE (Dokholyan et al. 2000; Hubner et al. 2004a, b). A common theme was found for various simulation techniques and/or folding sequences: In all cases, a small number of contacts are formed before the activation barrier is crossed, and all these contacts are necessary for the assembly of the TSE.
     Hubner et al. (2005) concluded that in several SH3-domain variants, essential non local contacts are formed before the appearance of a well defined hydrophobic core or secondary structures. Similarly Dobson (Lindorff-Larsen et al. 2004, 2005) argues that a small network of hydrophobic contacts defines the native topology in the TSE. Further evidence that the requirement for a nucleus, which involves NLIs and directs the formation of the TSE, is a general feature of the folding mechanism was described by many researchers (Fulton et al. 1999; Paci et al. 2003; Geierhaas et al. 2004; Krantz et al. 2004; Sosnick et al. 2004; Lappalainen et al. 2008; Tsong et al. 2008; Samatova et al. 2009).

     • The loop hypothesis and the nucleation-condensation mechanism.
       The loop hypothesis is consistent with the nucleation–condensation mechanism (Daggett and Fersht 2003) with some significant differences. The nucleation condensation mechanism describes the formation of the nucleus, which is the hallmark of the TSE; all conformations belonging to the TSE have an obligate nucleus, which is often a specific well-defined set of contacts, both local and non-local. In the nucleation-condensation mechanism, the nucleation process is coupled to TSE formation, while the “loop hypothesis” describes the formation of the earliest sub-domain structures, which precede the formation of the nucleus and are coupled to the initiation of the folding transition. The loop hypothesis assumes that the first step which follows the transfer of a fully disordered polypeptide to folding conditions is a non-specific adaptation by collapse to an ensemble of disordered molecules whose global dimensions are between those of the unfolded and the folded ensembles. This is followed by the rapid formation of a small set of specific non-local contacts, which are assumed to contribute to the subsequent formation of the folding nucleus. It is assumed that short clusters of (mostly non-polar) residues form the loop ends nodes by specific steric complementarity and that these nodes form marginally stable specific non-local contacts that impose partial order on the overall disordered molecules. In that sense, the experiments that identify the earliest contacts do not demonstrate nucleation, which is a later event coupled to the folding rate-limiting folding step of the formation of the TSE. There is a relationship between the fast formation of first persistent NLIs and nucleation. It is reasonable to assume that the stability of the few earliest native NLIs formed in the disordered collapsed ensemble would facilitate subsequent completion of nucleus formation and determine its overall topology. Thus, the key distinction is that loop formation is a facilitating step for nucleus formation, directing its topology and occurring in the collapsed disordered ensemble, while nucleation is an advanced folding event, indicating the formation of the TSE, which in turn is the rate-limiting step of the global folding transition.
       In addition, the key feature of the nucleation condensation mechanism is the formation “contact-assisted” secondary structure elements that form the folding nucleus in the TSE (Daggett and Fersht 2003); that is, the formation of secondary structures is coupled to formation of “long range contacts” which are stabilized by NLIs. The loop hypothesis assumes an independent role for the formation of non-local contacts stabilized by NLIs which form a diffuse nucleus, followed by stabilization of secondary structures (see Electronic Supplementary Material S1 for details)
  4. Simulations.
     Based on simulations of the folding transition, several research groups have shown the initiation of the pathway by NLIs, although many others assumed secondary structure formation as the first step. Using lattice simulations as mentioned above, Abkevich et al. (1994) observed that a structure with mostly non-local contacts folded two orders of magnitude faster than one with mostly local contacts. Juraszky et al. (Juraszek and Bolhuis 2006) found that in the folding of the small protein, i.e., the WW cage, 80 % of the pathways are initiated by NLI while secondary structures appear later. Zhang and Chan (2013) performed explicit-chain simulations using coarse grained chain models of natural proteins and computed the transient distributions of conformations sampled along the trajectories of many molecules. They found that conformations in the initial phases of the faster pathways were enriched with NLIs. Thus, successful folding is associated with a preference for NLIs at the initiation of the transition.
     Papandreou and Chomilier and coworkers (Lonquety et al. 2009; Papandreou et al. 2004; Prudhomme and Chomilier 2009) used native fold analysis and simulations to further develop the concept of closed loops as early folding structures and to elucidate the mechanism of folding. An algorithm was developed for the recognition of the residues involved in the loop closure interaction, which were named Most Interacting Residues (MIR); this was followed by dynamic simulation of the early folding events. The MIR sequences also correlate with the locations of highly conserved hydrophobic residues (referred to as topohydrophobic), based on structural alignment of the members of a protein topological family. The analysis of MIR positions with respect to the folded chain topology defines elements called Tightened End Residues (TFE)—i.e. segments that close to form loops in the folded state. The correlation of the TFE ends with the MIR sequences and the core of the proteins is very robust. It was suggested that the TFE loops function as autonomous folding units. Dynamic Monte Carlo simulation of the first steps in the folding transition of a 111 representative fold types based on knowledge of their TFEs was performed. The results of the simulation revealed a significant trend of burial of the MIR elements at the initiation of the folding process. The importance of the MIR elements was further validated by the simulation of mutations in these sequences and correlation with the known stabilities of 385 proteins with published stability data (Lonquety et al. 2009). These studies of the MIR elements, which are located are at the ends of long loops, strongly support the loop hypothesis.
• B.
  Evidence for the importance of loop structures in the folded states of proteins.

  1. The loop as a basic folding unit based on analysis of folded structures.
     Berezovsky and Trifonov (Berezovsky and Trifonov 2001, 2002; Berezovsky et al. 2002) analyzed the outline of the chain fold of the crystal structures of 302 proteins and proposed that protein structures can be viewed as compact linear arrays of closed loops. They proposed that protein folding progresses through the consecutive looping of the chain, with the loops ending primarily at hydrophobic nuclei termed “locks.” No relationship was found between secondary structure and the loop ends, but rather only 25 % of closed loop end residues reside in the middle of α-helix or β-sheet sections, in agreement with the closed loop hypothesis.
     An alternative approach to identify closed loop folding units was developed by Reynolds’ group (Chintapalli et al. 2010). Their strategy is based on the presence of insertions and deletions in structurally aligned pairs of proteins that share essentially the same fold but not necessarily high sequence similarity. The algorithm was able to capture loop units that correspond to the closed loops found by Berezovsky and colleagues in the above studies. Reynolds and coworkers showed that (1) the folding rate correlates extremely closely with total contact distance evaluated only over the lock residues, and (2) the lock residues tend to have high ϕ-values, “as would be expected for residues that play an important role in the transition structure for folding” (Chintapalli et al. 2010). Reynolds further suggests that the closed loop hypothesis is able to give an alternative description of the data obtained by Englander’s group (Bai et al. 1995; Hoang et al. 2003; Englander et al. 2007) for cytochromes c and b562 (as well as for triosephosphate-isomerase) initially interpreted in terms of independent folding units (foldons). The closed loop hypothesis-based mechanism was said to be “as elegant as the published explanations as it does not invoke discontinuous foldons.”
  2. Bioinformatics.
     The growth of protein structure databases and advances in bioinformatics methods have enabled large-scale analysis within structural types and homologs addressing the question of the role of local versus non-local interactions in protein folding. The work of Govindarajan and Goldstein was mentioned in the Introduction. A very different result was obtained by Unger and Moult (Moult and Unger 1991; Unger and Moult 1996) who concluded that foldability of a sequence is determined primarily by LIs.
     In a recent bioinformatics study using the contemporary database, Ofran and Unger (Noivirt-Brik et al. 2013) assessed the importance of the two types of interactions through their evolutionary and structural conservation. The underlying assumption was that positions which form more critical contacts for the folding, stability and function are likely to be more conserved. These researchers found that for the majority of proteins found in the current database, non-local contacts are structurally and evolutionary more conserved than the local ones.

     • Support for the “bottom-up” mechanisms of folding.
       The up–down mechanism of folding reviewed in the sections above is not supported by a large number of researchers who have provided evidence for dominant role of LIs in the initiation of the folding transition and the stabilization of the final folded structures of globular proteins. Most of these studies are based on computational structure prediction methods. Here, we mention some examples of proposed mechanisms. On the basis of entropic considerations, Rose et al. suggest that helix and strand formation will be guiding events in protein folding (Aurora et al. 1997; Baldwin and Rose 1999a, b; Dadlez 1999). Folding prediction by the fragment assembly mechanism, which is based mainly on early formed LIs, was successfully used by many groups (Levitt 1992; Bowie and Eisenberg 1994; Simons et al. 1997; Lee et al. 1999; Chikenji et al. 2006; Haspel et al. 2003a, b). The success of this method in different versions (e.g. successful prediction of native folds in chimera proteins (Chikenji et al. 2006) strongly support the importance of early formed LIs in stabilizing the final fold of small proteins. In these models, the NLIs are assumed to have smaller role and can be non-specific. In the zipping and assembly (ZA) mechanism suggested by Dill’s group (Dill et al. 1993), local structuring happens first at independent sites along the chain, then those structures either grow (zip) or coalescence (assemble) with other structures (Ozkan et al. 2007; Dill et al. 2008; Shell et al. 2009). Dill argues that the ZA mechanism is a model for the physical pathways of protein folding. The fragment assembly (FA) (or ZA) procedures for protein folding predictions show impressive success when applied to small proteins. Does the success of the FA methods mean that it predicts the folding routes? This should be tested by experiments. Fersht (Fersht and Daggett 2002; Daggett and Fersht 2003) concludes that only when the propensity of stable secondary structures is high can such structures form first and then assembly. However, in the majority of proteins, the unstable secondary structures are stabilized by NLIs.
     • The contact order folding rate correlation and the loop hypothesis.
       The observation that low “contact order”, which implies a high ratio of LIs to NLIs in the folded structures of proteins, is correlated with high rate of folding seems to give strong support to the role of LIs in determining the folding rate (Plaxco et al. 1998; Ivankov et al. 2003). Weikl (Weikl and Dill 2003; Weikl 2008) introduced the concept of effective contact order and showed that closure of small loops shows improved correlation with the global folding rate. Gromiha (Gromiha and Selvaraj 2001) introduced the measure of longer range order and found that proteins with more local structures (e.g., alpha-helix proteins) fold faster than proteins with more non-local structures (e.g., beta-sheet proteins). However, the fact that a higher content of local native folded structures correlates with fast folding does not contradict the loop hypothesis. The various contact order correlations are impressive, but it should be kept in mind that the correlation is global, i.e., summed over many proteins, and between native structures and the rate-limiting step of the folding transitions. Such correlations mainly reflect the contribution of LIs in the TSE and the rate of the main folding transition, where the effect of the earlier formation of only few key specific NLIs has very small weight. Moreover, the folded conformation of every protein includes a large number of LIs and NLIs. The loop hypothesis assumes that of all the native state NLIs, only a few specific interactions are effective at the initiation of folding, while the contact order computation, which sums all of the native interactions, cannot single out the contribution of these few initial interactions. Furthermore, Chan et al. (Chan et al. 2011) presented a set of coarse-grained models for real proteins that can successfully capture the experimental contact order-related folding rates. However, in the recent detailed simulation of the folding transition paths of a similar set of model proteins (mentioned above in section A-d), Zhang and Chan (2013) found that the transition paths of folding have more non-local contact than typical conformations in the folding quasi-preequilibrium with the same number of native contacts. Fersht (Fersht 2000) also asserts that the correlation cannot exclude the role of some tertiary interactions in formation of the extended nucleus. Taken together, these considerations and simulation results show that the Plaxco–Simmons–Baker (Plaxco et al. 1998) folding rate correlation does not necessarily preclude early formation of a relatively higher number of non-local contacts along folding transition paths.

Fig. 3.

Ribbon diagram representing the fast and slow folding sub-domain loop and secondary structure elements marked on the native state chain fold of the backbone of the Escherichia coli AK molecule (PDB ID code: 4AKE). a Fast and slow folding secondary structure elements that were studied so far are color coded. Those that remain disordered at 5 ms after initiation of mixing into folding buffer (the dead-time) are colored in black. Those that gain native-like mean end-to-end distance at the 5 ms detection time are colored green. The three short helices in the AMP_bind loop gain native-like end-to-end distance within the mixing dead-time (green). Parts of the chain that were not tested are colored in gold. Most of the segments which form secondary structures that constitute the core domain of AK are still disordered in the initial phase of the folding transition. b The non-local interactions between chain segments that are effective at the 5 ms collapsed ensemble are marked by a red line. At least three long loops are closed within the mixing time, i.e., at least within the initial 5 ms of refolding: the N terminal loop and the AMP_bind loop (green), as well as a long loop between residues 1–75 (red diamond) that includes the two elementary loops. Chain segments that form a loop structure in the folded state but not in the intermediate state are colored in black

Fig. 4.

Intra-molecular distance distribution between residue 203 and residue 18. The distance distribution at the 5 ms time point and at equilibrium starts as a single population with a mean distance of the compact collapsed globule. As time proceeds slowly (seconds) a second population characterized by native mean distance between the labeled sites grows and the collapsed subpopulation is decreasing (reproduced with permission)

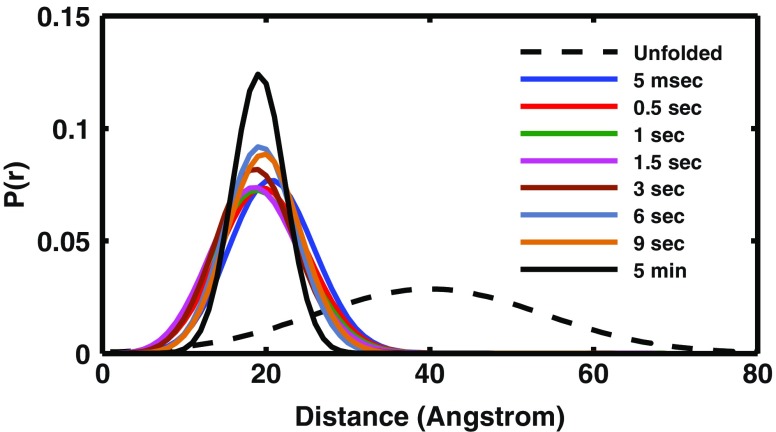
Fig. 5.

Fast closure of the AMP_bind loop in AK refolding ensemble. Intra-molecular distance distribution between residues 71 and 28 during refolding and at equilibrium. The broken black line indicates the distance distribution under denaturing conditions (2M Guanidinium-HCl) measured by the double kinetics method. The mean and full width at half maximum FWHM in the denatured state are 38 Ǻ and 34 Ǻ, respectively. The blue and black solid lines mark the 5 ms transient distribution, and the distribution at 5 min after mixing, respectively. The overlap of all the distributions obtained during the refolding transition from 5 ms to 5 min provides solid evidence for very fast closure of the loop structure (reproduced with permission)

Concluding remarks

The structure of both globular proteins and intrinsically disordered proteins is dominated by weak interactions, and hence, depends on cooperativity and is in most cases metastable. The role of the LIs versus NLIs involves two related questions: (1) the contribution of each type of interaction to the rate and efficiency of the folding transition which is, in the current context, the earliest specific interactions, and (2) the importance of the two types of interactions to the folded structures, their stability, functionality, and variance. The NLIs that essentially crosslink the structure of globular proteins might enhance their stability, similar to the function of disulfide crosslinks. Early stabilization of compact conformations at the initiation of folding is also important for favoring the folding transition relative to the competing intracellular processes of alternative folding (misfolding) and degradation.

Due to the large number of weak interactions and the stochastic nature of the elementary steps of the transitions, it is difficult to answer the question discussed in the present review by analyses of the final products of the folding transition. The search for the very few native NLIs or LIs that are formed first after transfer to folding conditions and which are just a small fraction of many such interactions that are formed during the transition should be done by targeting them specifically. The kinetics of the formation of specific key sub-domain structures should be probed directly, in situ, in the background of the rest of the chain. Even then, studying the rate of folding by simply monitoring only changes of a probe located at one site, or studying just a single global parameter such as the radius of gyration, yields limited information.

The ideal experiment should be able to monitor key intramolecular distances in all parts of the molecule, in situ, with a submicrosecond time resolution and spatial resolution of single Å. Moreover, since the folding transition starts from an ensemble of a very large number of conformations (Fig. 1), the early folding transitions should be studied by methods that can yield the distributions of selected intramolecular distances that report the folding status of key segment structures and their development from the moment of transition to folding conditions. For these reasons, we chose to develop the trFRET-based methods and, in particular, the double kinetics method. Similarly, FRET-based single molecule experiments can be developed for that goal. Yet the currently available probes needed for detection of acceptable photon flux at the high resolution of the chemical time base might cause significant structural biases in the ensemble of disordered collapsed molecules at the initiation of the folding transition.

Most of the experiments and computations that were reviewed here either support or do not contradict the closed loop hypothesis, but these provide indirect evidence. Statistical analysis of structures and folding rates and the determination of correlations between them are important guides for research, but the answer to the questions discussed here can come only from a combination of kinetic and mutational studies of selected structural elements. The ϕ-value experiments, which are very powerful, are also indirect and contain information regarding the main kinetic barrier, rather than the earliest events of the pathway. The question of the order of formation of LIs and NLIs in the nucleation events should also be investigated by the high time resolution of kinetic experiments monitoring the time-dependent status of secondary and tertiary structure elements. It is clear that both LIs and NLIs contribute to the folding transition; nevertheless, the results reviewed here give strong support to the counter-intuitive mechanism whereby the NLIs play a dominant role in the initiation and determination of the folding pathways. It is possible that there are two types of folding mechanism, one in which NLIs are dominant, and the other in which the LIs predominate. This possibility was suggested by Fersht (Daggett and Fersht 2003) and is supported by several of the results reviewed here. It should be of interest to test this possibility. Yet a major task for the near future is enhancement of the resolution of the “chemical time base” of the double kinetics experiments. We hope that improvement of the double kinetics methods with fast resolution and specific labeling will allow us to resolve this question.