Human Q fever incidence is associated to spatiotemporal environmental conditions

Abstract

Airborne pathogenic transmission from sources to humans is characterised by atmospheric dispersion and influence of environmental conditions on deposition and reaerosolisation. We applied a One Health approach using human, veterinary and environmental data regarding the 2009 epidemic in The Netherlands, and investigated whether observed human Q fever incidence rates were correlated to environmental risk factors.

We identified 158 putative sources (dairy goat and sheep farms) and included 2339 human cases. We performed a high-resolution (1 × 1 km) zero-inflated regression analysis to predict incidence rates by Coxiella burnetii concentration (using an atmospheric dispersion model and meteorological data), and environmental factors – including vegetation density, soil moisture, soil erosion sensitivity, and land use data – at a yearly and monthly time-resolution.

With respect to the annual data, airborne concentration was the most important predictor variable (positively correlated to incidence rate), followed by vegetation density (negatively). The other variables were also important, but to a less extent. High erosion sensitive soils and the land-use fractions “city” and “forest” were positively correlated. Soil moisture and land-use “open nature” were negatively associated. The geographical prediction map identified the largest Q fever outbreak areas. The hazard map identified highest hazards in a livestock dense area.

We conclude that environmental conditions are correlated to human Q fever incidence rate. Similar research with data from other outbreaks would be needed to more firmly establish our findings. This could lead to better estimations of the public health risk of a C. burnetii outbreak, and to more detailed and accurate hazard maps that could be used for spatial planning of livestock operations.

1. Introduction

1.1. Background

Q fever is a worldwide livestock-associated disease caused by the gram-negative bacterium Coxiella burnetii. The largest Q fever outbreak ever described occurred in The Netherlands from 2007 to 2010 with over 4,000 notified human cases [1]. In this epidemic, human Q fever was mainly associated with dairy goats, and to a lesser degree with dairy sheep [2]. The main reservoirs of C. burnetii are the goats' and sheep's placentas and birth products; the main clinical symptom is late abortion of lambs [3], [4], [5]. The birth products may contain up to about one billion C. burnetii bacteria per gram [4], [5], [6]. Other, but less important, excretion routes are milk [7], [8], [9] and feces and urine [9]. Excretion of the bacterium can last up to months after infection by C. burnetii [6].

Since goat stables are only partially enclosed, excreted bacteria can be transmitted from the indoor to the outdoor environment. C. burnetii has been detected in outdoor air samples in several particle size fractions in the surroundings of positive farms [10], [11]. The bacterium and its spore-like forms may survive for weeks to months in the outdoor environment [12], [13], [14].

1.2. Human infection

Human infection generally occurs by inhaling the C. burnetii bacterium. The dose for 50% human illness (ID50) is about 1.18 bacteria [15]. There is no evidence for human illness being transmitted by the foodborne pathway [14].

Human Q fever is a notifiable disease in The Netherlands since 1978. Prior to the large epidemic in 2007–2010, the number of notified cases varied between 5 and 20 per year, with a maximum estimated seroprevalence of antibodies against C. burnetii in the general population of 2.3% in 2006 [16]. The total number of (a)symptomatic human infections during the epidemic was estimated to be about 12.6 times larger than the total number of notified cases [17]. The seroprevalence in the centre of the epidemic was estimated at 12.2% in 2009 [18] and 10.7% in 2010–2011 [19]. The Q fever prevalence on large dairy goat farms (> 50 animals) was estimated to be 43.1% in 2009 [20].

1.3. Problem description

The number of humans infected by an airborne pathogen depends on:

• (1)emission strength;
• (2)airborne transmission from source to receptor as a function of meteorological and environmental conditions [21], [22], [23], [24], [25], [26], [27], [28]; and
• (3)human exposure: the exposure level is dependent on, among others, duration [29], location [30] and physical activity [31].

In the current study we mainly focused on the second point to investigate the possible effects of the transmission pathway (outdoor environment) between source (farms) and receptors (humans). The outdoor environment could play a threefold role: first, meteorological conditions (including wind speed/direction, precipitation and vertical motions in the atmosphere) influence the degree and pre-dominant direction of the airborne transmission of C. burnetii bacteria that were released from a farm's stable into the air [22], [32]; secondly, landscape elements (including vegetation) are able to remove particles from the atmosphere by deposition (e.g., [33], [34]). Thirdly, these landscape elements and specific environmental conditions possibly affect the reaerosolisation of bacteria [35], [36].

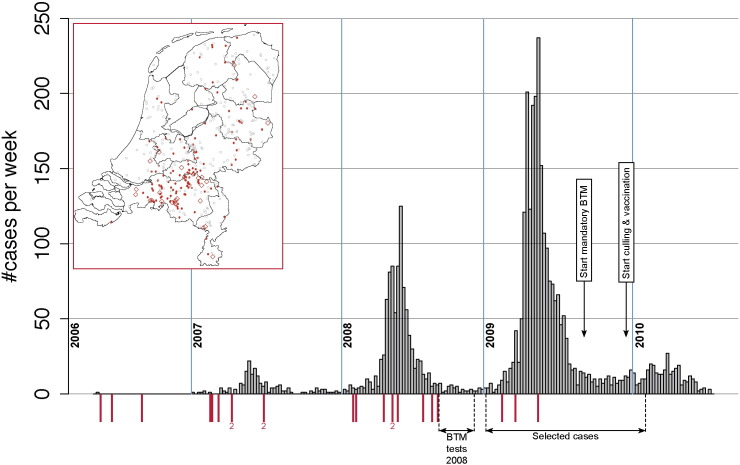
The Dutch Q fever cases were spatially clustered with large regional differences in incidence rates. Highest rates were reported in the southeast of The Netherlands [1]; in several other regions positive farms were identified without hardly any reported human cases nearby (Fig. 1). Therefore, an explorative statistical analysis was performed in 2011 to investigate the correlation between Q fever incidence rate and specific environmental conditions (vegetation greenness, land use, soil texture, soil moisture content, wind velocity, temperature, and global radiation) [27]. The authors concluded that relatively low vegetation greenness and low soil moisture content levels were correlated to higher transmission levels of C. burnetii.

Fig. 1.

Time course of the Q fever epidemics in The Netherlands with the number of notified cases per week (gray bars). Red bars indicate the week in which an abortion wave was registered at one (or two: ‘2’) farms. The non-systematic bulk tank milk (BTM) tests were performed in the autumn of 2008; the mandatory and systematic BTM tests were performed from September 2009. Mandatory and systematic vaccination and culling started at the end of December 2009. The geographic map of The Netherlands shows the location of all large dairy goat farms with abortion waves (♢), all other positive (•) and negative (○) farms.

Since that study was explorative, several important assumptions were made:

• -Cases were assumed to have been infected only by the nearest positive farm.
• -Only farms with reported abortion waves (i.e. > 5% of the parturitions [37]) (n = 27) were assumed to have emitted bacteria, while in practice many more had tested positive in one or multiple tests (see Methods section).
• -Soil moisture content was based on static ground water level data with no temporal component.
• -“Farm status” was dichotomised to months with “no transmission” (if the incidence rate was ≤ 1/10,000 within 5 km) or “transmission”.

1.4. Aim

The aim of this research was to refine the study of [27] to test the hypothesis that transmission of C. burnetii from farms to humans was associated to environmental conditions and their spatial and temporal heterogeneity using a zero inflated regression analysis. In addition, we included additional variables: concentration and deposition of C. burnetii modeled by means of an hourly-based atmospheric dispersion model (which includes among others precipitation amount/duration, atmospheric stability, and wind speed/direction, and the relative geographical position of cases with respect to the position of putative sources), leaf area index, soil wind erosion sensitivity, and time-dependent soil moisture levels at a high spatial and temporal resolution. Results of this study might lead to environmental transmission risk mapping.

2. Method

2.1. Data description

2.1.1. Research period

The Q fever epidemic lasted four years (2007–2010) [1] (Fig. 1), but in the current study we focused primarily on the epidemic in 2009, since:

• 1)A systematic farm monitoring program was not organised until September 2009, hence the infection status was not known for all goat farms during the previous years;
• 2)Dairy goats and dairy sheep were systematically and mandatory vaccinated or culled from the beginning of 2010 onward, resulting in sharply decreasing numbers of human cases in that year; and
• 3)The number of human notifications was largest in 2009, both due to the larger number of positive farms (hence a larger infection pressure) and a possibly increased awareness.

We performed our analyses at a monthly resolution and for the full research year (1 January 2009–31 December 2009).

2.1.2. Human data

The regional Municipal Health Services made the dates of disease onset of notified human Q fever cases available, including their six-figure zip codes (referred to as PC6, i.e. at street-level resolution). Combining these dates of disease onset with the Q fever incubation period of 8–33 days (95% CI, μ = 20.7 days) [38], we selected all notified human Q fever cases with a date of onset of disease between 9-Jan.-2009 and 2-Feb.-2010 (n = 2339). Monthly incidence rate were based on all cases that could have been infected symptomatically during that particular month (Fig. 2), and we assumed that notified cases were infected within their street of residence [30].

Fig. 2.

Timeline of the number of attributed human Q fever cases per month based on a case's day of onset of disease and the Q fever incubation period of 8–33 days (95% CI) [38].

In addition, we used population density data at the PC6-level (reference date 1 January 2010), made available by Statistics Netherlands (CBS). We aggregated the population density data and case data to a 1-km² grid and selected all cells with one or more inhabitants (“inhabited grid cells”) (n = 25,339).

2.1.3. Veterinary data

The Ministry of Economic Affairs made the coordinates available of all goat and sheep farms in The Netherlands (n = 42,509) and the number of goats and sheep per farm in November 2008 and November 2009. The majority of these farms were small hobby farms. We selected all large dairy goat farms (i.e. > 50 animals; n = 373 in 2008 and n = 405 in 2009), since those were associated to the Q fever outbreaks [37].

We assumed a farm was positive for C. burnetii in 2009 if at least one of the following conditions was met (most farms met multiple conditions):

• -The farm's tank milk tested positive in the non-systematic and non-mandatory Bulk Tank Milk (BTM) sampling program implemented by the Animal Health Service (GD) in the autumn of 2008. This program included approximately 66% of the large dairy goat farms [8].
• -The farm's tank milk tested positive in the mandatory BTM sampling program, systematically conducted at all large dairy goat and sheep farms by the Animal Health Service on authority of The Netherlands Food and Consumer Product Safety Authority (nVWA) from September 2009 [2].
• -An abortion rate of > 5% was reported by the Animal Health Service either in the years 2007, 2008 or 2009 [37].
• -At least one vaginal or environmental swab was confirmed positive in a non-systematic sampling investigation [39], [40] in 2008 and 2009.

This resulted in a list of 158 positive dairy goat farms (Fig. 1), of which most kept > 50 goats in both 2008 and 2009 (Supplementary Table A1). Some also kept sheep; thirteen farms started after November 2008; two farms terminated their activities after November 2008.

2.1.4. Concentration data (airborne transmission)

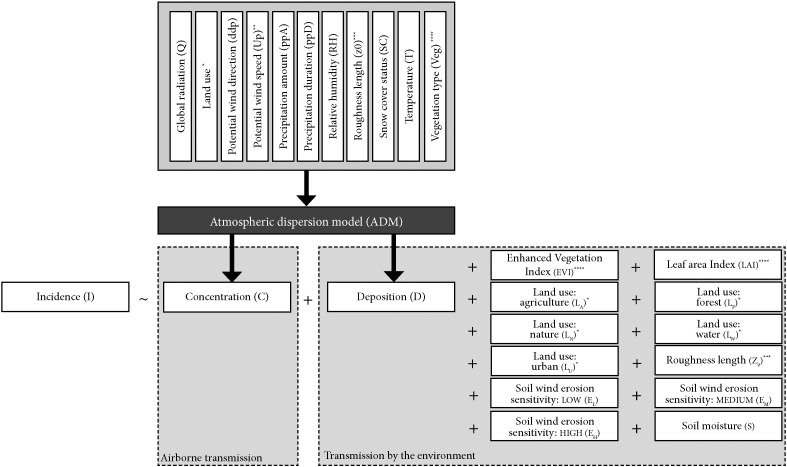
We correlated observed Q fever incidence rate to the concentration modeled by an atmospheric dispersion model (airborne transmission), modeled deposition levels, and other environmental conditions (related to deposition and reaerosolisation) (Fig. 3).

Fig. 3.

Overview of all variables. Incidence rate is explained by concentration (airborne transmission) and variables related to deposition and reaerosolisation. Concentration and deposition were calculated by the OPS-ST model using meteorological data and data of land use, roughness length, and vegetation type. Variables indicated by one or more asterisks (*) are related to each other, but are not necessarily equal.

We calculated airborne concentration levels of C. burnetii by means of the OPS-ST model (Operational Priority Substances – Short Term, version 10.3.2), which is an atmospheric dispersion model (ADM) developed by The Netherlands National Institute for Public Health and the Environment (e.g., [41], [42], [43], [44]).

In a previous study it was concluded that modeled log-transformed ADM-concentrations correlated better to observed Q fever incidence rate than either a distance-based model or a model with no predictors [21]. That is, meteorological conditions (including wind and precipitation) are correlated with observed Q fever incidence rates.

We applied their ADM-configurations and considered each positively classified farm as a putative source of C. burnetii. Although the bulk tank milk status of the majority of the farms was known, it was unclear how to convert these values to emission strengths [45]. Therefore, we used each farm's herd size as a proxy for the steady-state emission strength:

$$E_j=max\left(A_{j,2008},A_{j,2009}\right).$$ (1)

With A_j,2008 as the number of animals at farm j in November 2008, and A_j,2009 in November 2009.

Required meteorological data as input data for the ADM included hourly averaged global radiation, precipitation amount and duration, relative humidity, snow cover status, temperature, and wind speed and direction (Fig. 3), retrieved from the Royal Netherlands Meteorological Institute (KNMI) and interpolated to farm levels [21]. Precipitation data were available at a 1 km² resolution; we spatially interpolated the other hourly data to get values at farm levels. We aggregated the hourly output concentration and deposition maps to monthly and yearly averaged values at a 1 km² resolution.

2.1.5. Environmental data related to deposition and reaerosolisation

Important environmental variables potentially influencing the reaerosolisation and deposition of particles/bacteria/spores are: soil texture, roughness elements, soil moisture content, and wind speed [35]. Therefore, we added soil moisture content [%] [46], vegetation greenness (Enhanced Vegetation Index) [−] [47], vegetation density (Leaf Area Index) [m² leaf per m² ground surface] [48], soil erosion sensitivity [categorical: low/moderate/high] [49], land use (categorical: agriculture/forest/open nature/water/urban) [50], and roughness length [41] to the model (Fig. 3). Data were averaged to yearly and monthly values (Supplementary Text A). Note that vegetation, land use and roughness length are related to both deposition and reaerosolisation.

Assuming that the notified cases were infected at their residential addresses [30], not only the environmental conditions within an inhabited grid cell of 1 km², but also the conditions in the surrounding of a grid cell will have positive or negative effects on deposition and reaerosolisation. Since the risk of a Q fever infection has been estimated to be largest within 5 km of a positive farm [51], we spatially averaged the monthly and yearly averaged numerical environmental parameters within 5 km to a single numerical value per inhabited grid cell per month and per year (Supplementary Text A). In addition, we calculated fractions of the categorical parameters (land use and soil erosion sensitivity classes) within the 5 km radius (Supplementary Text A).

2.2. Statistical analyses

2.2.1. Preparation

In order to prevent too high skewness of the predictor variables, we transformed the concentration and environmental data to normal distributions (e.g., log-transformation or (square) root) by visual inspection and by application of a Kolmogorov–Smirnov test on normality (p < 0.05).

In addition, we determined the correlation coefficients of all combinations of (transformed) predictor variables. If two variables highly correlated (r ≥ 0.7) and if there was a plausible physical explanation for their high correlation, we excluded one of them from the analysis to prevent collinearity.

2.2.2. Zero inflated regression

We correlated the number of observed cases, corrected for population density, to all remaining environmental variables. To deal with the large number of zero incidence rates in the inhabited grid cells, we used a zero inflated regression model (using R version 3.0.3 and package ‘pscl’) [52], [53], which accounts for large amounts of true zeros (not exposed, so not infected) and accidental zeros (exposed but not infected).

The model consists of a mixture of two components: firstly, a ‘zero’ (binomial) model to distinguish between exposure and no exposure, i.e. the probability of observing ≥ 1 cases:

$$Y=\left\{Z>0\right\}~\mathit{Bin}\left(1,p\right)$$ (2)

$$\text{logit}\left(p\right)={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_n{X}_n$$ (3)

where Z is the number of cases, Y is the binomial event that > 0 cases were notified (or the event that ‘exposure’ occurs), and X_i is the value of predictor variable i; p is the binomial probability;

Secondly, a ‘count’ model is included to determine the correlation of predictors to the actual number of observed cases, given exposure. For the count model we applied a negative binomial model to allow for over-dispersion (extreme incidence rates):

$$Z|Y~\mathit{NegBin}\left(\lambda ,\theta \right)$$ (4)

$$\lambda =n\bullet \mathit{exp}\left({\beta }_0+{\beta }_1{X}_{1,}+\dots +{\beta }_n{X}_n\right).$$ (5)

With λ being the expected number of cases, n being the number of inhabitants per inhabited grid cell, and θ being the dispersion parameter. If no fit could be found, a Poisson model was applied, which is basically a negative binomial distribution with θ = 0:

$$Z|Y~\mathit{Pois}\left(\lambda \right)$$ (6)

We first performed univariate analyses at the month and year level to detect all correlating variables at the 80% confidence level (p < 0.20). Secondly, we performed a multivariate analysis at the 95% confidence level (p < 0.05) using the step function in R (package ‘stats’) for forward and backward model selection.

Subsequently, we retrieved the fitted values of the coefficients to create a geographical prediction map per month and for the full research period using the predict.zeroinfl() function in R. We extracted the model's Akaike's Information Criterion (AIC) that is a measure for the model's goodness of fit. We also extracted the differences in AIC (ΔAIC) of the model with respect to the same model in case each of the variables would be removed. The AIC-differences are a measure for the contribution of a variable to the prediction of Q fever incidence rate.

2.2.3. Validation

We applied validation of the results by

(1) visual inspection of the geographical observed, predicted, and residual incidence rate maps;

(2) performing a linear regression analysis of the log-transformed predicted and observed incidence rates for all grid cells with > 0 observed cases. We applied orthogonal linear regression and assumed 0.3 < | r | < 0.6 (Pearson's correlation coefficient) to correspond to a moderate, and | r | ≥ 0.6 to correspond to a strong linear relationship. In addition, we determined the 95% confidence intervals of the slope and intercept of the regression line by bootstrapping 10,000 times; and

(3) applying spatial cross-validation to the yearly averaged data. That is, we trained the model based on the annually averaged data with all variables that were significant (p < 0.05) in the negative binomial model by randomly selecting 2/3 of the inhabited grid cells and applied that model to the remaining 1/3 of the inhabited grid cells. We repeated this process 1,000 times and calculated the mean predicted number of cases in each inhabited grid cell, both for the binomial and the negative binomial model. By applying cut off values (from 0.001 through 1.00 with steps of 0.001) to the binomial probability p, we created a plot of the sensitivity versus the specificity and extracted the area under the curve (AUC). We then retrieved the ‘optimal cut-off’ (i.e. the value corresponding to the maximum sum of the sensitivity and specificity). We then calculated the mean squared error (MSE) as a measure for the difference between the observed and predicted number of cases of these true positive grid cells.

2.2.4. Environmental hazard maps

Finally, we calculated an environmental hazard map using the fitted multivariate model, under absence of positive (C. burnetii emitting) farms and human cases. These hazard maps reflect the potential risk for an infection if C. burnetii would be emitted. They could give insight in the spatial variation in potential relative risks for transmission.

3. Results

3.1. Data preparation

3.1.1. Transformation of variables

Supplementary Table 2 shows the transformation functions that we applied to the environmental data.

Supplementary Fig. 1, Supplementary Fig. 2, Supplementary Fig. 3, Supplementary Fig. 4, Supplementary Fig. 5, Supplementary Fig. 6, Supplementary Fig. 7, Supplementary Fig. 8 show geographical plots of the yearly and monthly averaged concentration, LAI, and soil moisture, and the aggregated land use and soil wind erosion sensitivity map.

3.1.2. One to one regression analysis

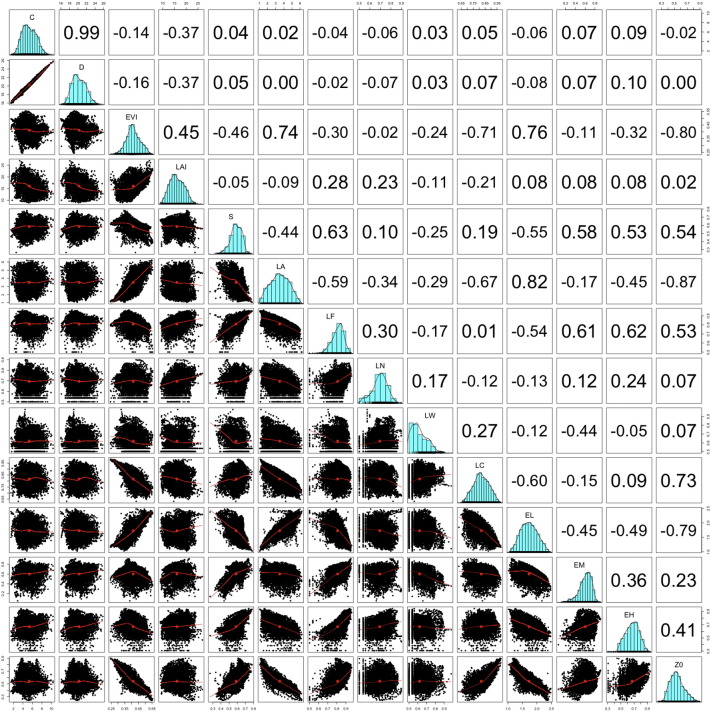
From the one to one regression analysis we excluded the variables deposition, Enhanced Vegetation Index, and roughness length from any further analysis due to collinearity. The land-use fraction “agriculture” and the soil erosion sensitivity fraction “moderate” were considered as reference variables (in the intercept). See Supplementary Fig. 9 for the Pearson's regression coefficients (r) of all combinations of predictor variables (yearly averaged).

Supplementary Fig. 9.

Linear regression coefficients (Pearson's r) of the one-to-one analysis. Zero-data were excluded from the datasets of concentration, deposition, the land use fractions, and the soil erosion sensitivity fractions to optimise the linear regression analysis. Abbreviations: C = concentration, D = deposition, EVI = enhanced vegetation density, LAI = leaf area index, S = soil moisture, LA = land use ‘agriculture’, LF = land use ‘forest’, land use ‘open nature’, LW = land use ‘water’, LC = land use ‘city’, EL = low soil erosion sensitivity, EM = moderate soil erosion sensitivity, EH = high soil erosion sensitivity, Z0 = roughness length.

3.1.3. Univariate analyses

Supplementary Fig. 10, Supplementary Fig. 11 show the effects of the variables on the incidence rates in case of a one-unit increase of the (transformed) variable. Values larger respectively smaller than 1 correspond to positive respectively negative effects on the incidence rate.

• (1)Model part 1: zero (binomial) model (Supplementary Fig. 10): no clear, consistent correlations at the 80% confidence level are found. Concentration is never correlated to incidence rate. In general, values are very high or very low, indicating high uncertainties.
• (2)Model part 2: count (negative binomial/Poisson) model (Supplementary Fig. 11): concentration is positively correlated to incidence rate (mean effect of ± 2.0). The leaf area index is negatively correlated to incidence rate. (± 0.75.) Soil moisture shows inconsistent results with mostly very negative effects. High soil erosion sensitivity is positively correlated (± 1.9). The land use fractions are alternately correlated, with ‘water’ and ‘city’ generally consistent.

Supplementary Figs. 10 and 11 show the effects of the variables on the incidence rates in case of a one-unit increase of the (transformed) variable. Values larger respectively smaller than 1 correspond to positive respectively negative effects on the incidence rate.

• (1)Model part 1: zero (binomial) model (Supplementary Fig. 10): no clear, consistent correlations at the 80% confidence level are found. Concentration is never correlated to incidence rate. In general, values are very high or very low, indicating high uncertainties.
• (2)Model part 2: count (negative binomial/Poisson) model (Supplementary Fig. 11): concentration is positively correlated to incidence rate (mean effect of ± 2.0). The leaf area index is negatively correlated to incidence rate. (± 0.75.) Soil moisture shows inconsistent results with mostly very negative effects. High soil erosion sensitivity is positively correlated (± 1.9). The land use fractions are alternately correlated, with ‘water’ and ‘city’ generally consistent.

We excluded variables not significant at the 80% confidence level (in case of white cells in both Supplementary Fig. 10, Supplementary Fig. 11) for the multivariate analysis.

3.2. Multivariate analysis

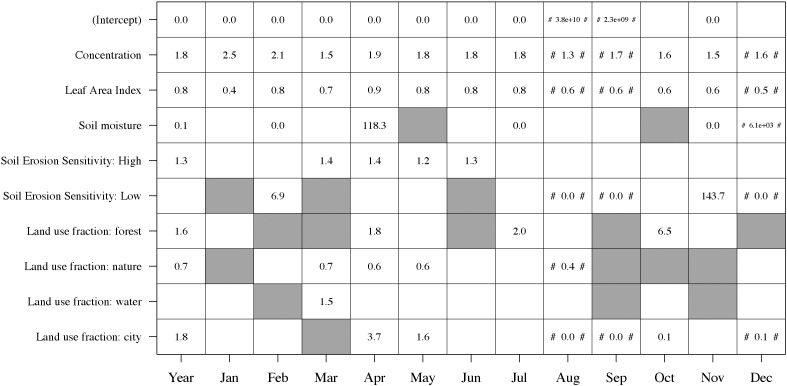
Table 1 shows the AIC-differences (ΔAIC) if each of the individual variables would be removed from the final multivariate model. These results show that concentration is by far the most important predictor for Q fever incidence rate. The second most important predictor is the leaf area index (both yearly and monthly data). For the yearly averaged data all variables had p < 0.05. For the monthly averaged data most correlations with p < 0.05 are found during the months April and May (reflected by the highest number of human cases (Fig. 2)).

Table 1.

Difference in Akaike's Information Criterion (ΔAIC) if each of the individual variables would be removed from the multivariate model per month. A difference of approximately 3 points in AIC is considered to be significant. White cells correspond to non-significance in the zero-inflated model.

	YEAR	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
Concentration	947	190	235	384	657	552	530	188	145	100	63	64	58
Leaf area index	186	61	49	135	60	81	118	98	78	66	69	28	66
Land use: open nature	57				65	26		7.2	5.2
Soil moisture	49		19	3.1	55			16		23		6.0	21
Land use: forest	45	9.1			61	14		12	3.4		14
Erosion sensitivity: low	40		22		22	12			6.1	6.7	3.0	27	19
Land use: city	36		27		46	7.4			22	28	5.5		15
Land use: water	36	5.2		38		9.2	19	24
Erosion Sensitivity: high	34			13	49	12	14	6.8			18	3.9

Fig. 4 shows the effects of the predictor variables on the incidence rate in case of a one-unit increase of the back-transformed predictor variables (count model, i.e. negative binomial/Poisson). It shows that concentration is positively correlated to observed incidence rate (mean effect of ± 1.8), and that leaf area index is negatively correlated (± 0.7). The other variables did not always have p < 0.05: soil moisture, and the fraction land use ‘open nature’ are generally negatively correlated; high soil erosion sensitivity and the fraction land use ‘forest’ are positively correlated. High numbers refer to large standard errors. Supplementary Fig. 12 shows the effects of the predictor variables for the binomial model. Similar to the univariate analyses, these results are inconsistent and the standard errors are large.

Fig. 4.

Mean effects of the back-transformed predictor variables in the multivariate zero-inflated negative binomial or Poisson regression analysis. All values were the result of a negative binomial regression analysis, except for those indicated by hash tags (#) (Poisson). White cells refer to variables with p ≥ 0.05; gray cells refer to variables excluded from the analysis (since p ≥ 0.20 in the univariate analysis). Values represent the effect of the predictor variable in case of a one-unit increase. The results of the binomial part of the regression analysis are shown in Supplementary Fig. 12.

Mean effects of the back-transformed predictor variables in the multivariate zero-inflated negative binomial or Poisson regression analysis. All values were the result of a negative binomial regression analysis, except for those indicated by hash tags (#) (Poisson). White cells refer to variables with p ≥ 0.05; gray cells refer to variables excluded from the analysis (since p ≥ 0.20 in the univariate analysis). Values represent the effect of the predictor variable in case of a one-unit increase. The results of the binomial part of the regression analysis are shown in Supplementary Fig. 12.

3.3. Validation

At the 1 km² level, the observed incidence rates are highly heterogeneous, whereas the predicted incidence rates are much more smoothed (Supplementary Fig. 13). To reduce the occurrence of random spatial attribution, we aggregated the observed and predicted incidence rates to different geographical levels: 5 km² (Supplementary Fig. 14), 10 km² (Supplementary Fig. 15), and to the municipality level (Fig. 5). These figures are based on yearly averaged environmental data.

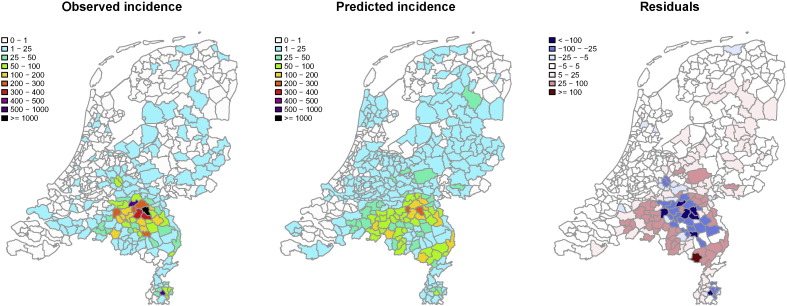
Fig. 5.

(Left, Middle) Observed and predicted incidence rate per 100,000 inhabitants, aggregated to the municipality level; (Right) Predicted incidence rate minus the observed incidence rate per 100,000 inhabitants per municipality.

By visual inspection of Fig. 5, regions with the highest observed incidence rate (in the southeast of The Netherlands) are identified by the multivariate model, although the observed incidence rate numbers are smaller (negative residuals). Overestimation of the incidence rate is found around this high incidence rate area.

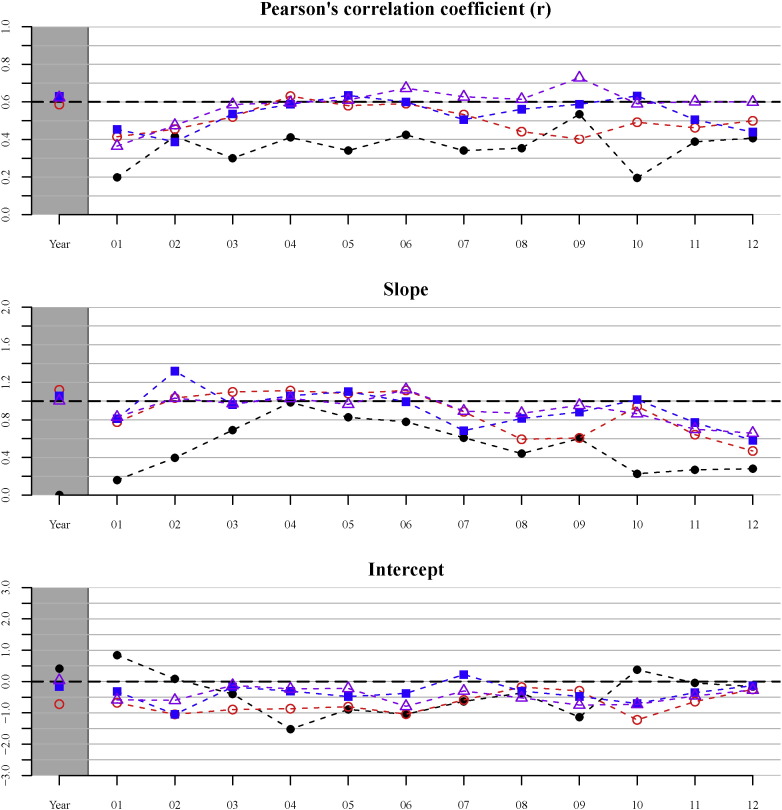
Fig. 6 shows Pearson's correlation coefficient (r) and the slopes and intercepts of the orthogonal regression curves as function of time at four geographical aggregation levels. The correlation coefficient is highly influenced by the geographical aggregation level. Lowest values are found at the 1 km² level (0.3–0.4); at the other geo-aggregation levels the differences are smaller with values around r = 0.6. Supplementary Table 3 shows the values of Fig. 6 in a table, including the 95% confidence intervals of the slopes and intercepts.

Fig. 6.

Statistics for four geo-aggregation levels (1 km², 5 km², 10 km², and municipality level) for yearly and monthly averaged data: Pearson's correlation coefficient (r), and slopes and intercepts of the linear regression line. Most ideal values for slope and intercept, and the minimum level for a ‘strong’ correlation (r = 0.60) are indicated by a dashed horizontal line. Symbols: (•) 1 km² level, (○) 5 km² level, (■) 10 km² level, and (△) municipality level.

The slopes of the regression curves are close to 1 in the yearly analysis and during the months with the highest number of cases (March – June), indicating that there is a positive, one-to-one, correlation between predicted and observed incidence rates. During the rest of the year and at the 1 km² aggregation level the values are generally much smaller. The intercepts are generally negative, but best values (i.e. close to zero) are found at the 10 km² and municipality level.

Finally, Supplementary Fig. 17 shows the curves of the sensitivity versus the specificity, resulting from the spatial cross-validation analysis (as a function of a cut-off value of 0.001…1.00 with steps of 0.001). The resulting area under the curve is equal to 0.453 (1 km resolution), 0.60 (5 km), 0.63 (10 km), and 0.73 (municipality level). The mean squared error (MSE) is equal to 18.9, 320.1, 1295, and 1227 respectively.

3.4. Environmental hazard maps

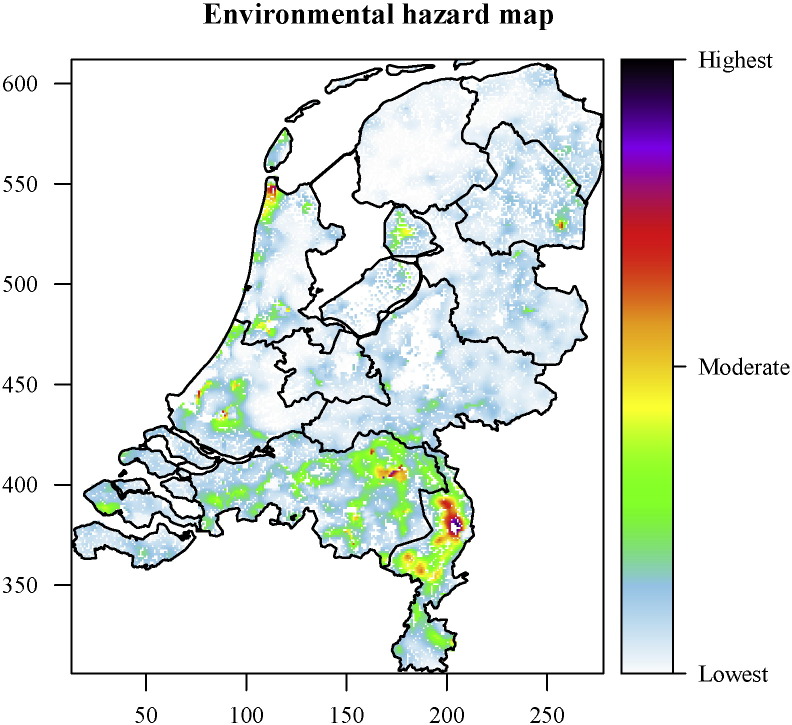
Fig. 7 shows a dimensionless environmental hazard map based on yearly averaged data. These hazards are related to the effect of the environment (deposition and reaerosolisation), under absence of any emissions. Regions with the highest hazards are located in the southeast, and are related to low vegetation density (Supplementary Fig. 3), low soil moisture levels (Supplementary Fig. 5), and high soil erosion sensitivity (Supplementary Fig. 8).

Fig. 7.

Environmental hazard map for yearly averaged data at the 1 km² level.

4. Discussion

4.1. Conclusions

We performed a spatiotemporal regression analysis to investigate the correlation between observed human incidence rates and observed and modeled environmental risk factors during the large Q fever epidemic in The Netherlands in 2009. We conclude that C. burnetii concentration is positively correlated to incidence and that it is the best predictor variable for human Q fever, followed by the mean spatial vegetation density (Leaf Area Index) (negative). High soil erosion sensitivity fractions (positive), soil moisture (generally negative), and the land use classes ‘forest’ (positive) and open nature (negative) had p < 0.05 as well, but less frequent in time. Low soil erosion sensitivity and the land use fractions ‘water’ and ‘city’ did generally not have p < 0.05 or at least not consistently. The effects of the land use classes ‘forest’ and ‘open nature’ on incidence are counter-intuitive, which is caused by the coincidental presence of large forest areas and absence of large open nature areas in the major Q fever outbreak area. Best results are found for the 2009-averaged data and the monthly averaged data of March, April and May – which corresponds to the large number of notified human cases.

In other words, airborne transmission is the most powerful predictor for observed human Q fever incidence rates. The effect of the environment on the transmission (deposition and reaerosolisation, mainly covered by LAI, but also by soil moisture, soil erosion sensitivity and the land use class fractions) is also of importance, but to a lesser degree. In general, our results are in line with those of the previous pilot study [27], where it was concluded that vegetation, soil moisture and arable land were risk factors for C. burnetii exposure.

4.2. Research context

Our results are consistent with previously published literature on the physical effects of meteorological conditions (e.g., atmospheric stability, wind speed/direction, temperature, and precipitation) on survival and transmission of airborne pathogens [22], [44], [54], [55], [56], and the effects of vegetation, objects, and surface roughness on deposition and reaerosolisation [35]. For instance, precipitation increases the amount of wet deposition, while a smoother surface results in further spread. For the Dutch situation, this means that most exposure could be expected in regions with little vegetation, dry conditions, and arable land. Despite the fact that presence of C. burnetii in outdoor environments has been demonstrated [10], [11], [57], [58], studies concerning the possible effects of vegetation and soil conditions on airborne pathogens do exist [59], [60], [61], [62], but are scarce. The study of [63] is comparable to our study, although it does not include an atmospheric dispersion model.

4.3. Uncertainties

Uncertainties in the predictor data will be relatively small, for they are environmental data that are systematically measured at high spatial and temporal resolutions by official institutes (e.g., Royal Netherlands Meteorological Institute, NASA, Wageningen University & Research Centre). Uncertainties in the human and farm data, however, will be much larger: human Q fever data do not include non-notified infected persons. With respect to the farm data, a systematic and mandatory test was not implemented before September 2009.

Fig. 5 showed that the residual incidence rates (predicted minus observed) were spatially clustered. In the area with the highest Q fever incidence rates the observations are underestimated; in other areas overestimations occurred. The total number of predicted cases is however almost identical to the total number of observed cases (data not shown). However, the curves of the sensitivity versus the specificity (based on the binomial model) might be further improved (Suppl. Fig. 17). Possible explanations might be that:

• 1)The incidence rates are extremely peaked: for the yearly averaged data and during springtime the variance was much larger than the mean indicating that a zero inflated Poisson model was not applicable. Instead, we applied a zero inflated negative binomial model to account for extreme values. Nevertheless, this could not prevent underestimations still to occur.
• 2)Large differences in emissions between farms might have occurred (as also suggested by [64] in the 2006-Bluetongue outbreak in northwest Europe). This includes that large shedding animals might have been present at the positive farms, possibly represented by ‘abortion farms’: the 27 farms at which abortion waves have occurred during the years 2007–2009 [37] (Fig. 1). Since, abortion waves are a symptomatic indication for the presence of C. burnetii [3], [4], [5], ‘abortion farms’ were associated to high emission strengths of C. burnetii [2]. However, their geographical location does not always coincide to high-observed incidence rates (Fig. 4A).
• 3)An over-simplified emission profile: judging from the epidemic curve in Fig. 1, a steady-state emission profile is hard to defend. Although it was previously shown that such a steady-state profile fitted better to the human data than a lognormal temporal emission profile [21], the current study included multiple sources. That is, several lognormal emission profiles form multiple sources could have led to a more temporarily smoothed exposure curve.

Although environmental conditions could either have a positive or negative effect on the transmission of C. burnetii, the source term remains a very important variable. Thus, further investigations on the source strength and its temporal behavior is recommended.

Also, this study does not necessarily reflect direct causal relationship between the outcome (incidence rates) and its predictors. However, detected relationships are supported by literature [35], augmenting the probability of a true, direct, physical correlation as well as the confidence in the hazard maps.

4.4. Binomial and count model

Strictly speaking, the population is divided into two groups in case of a large-scale outbreak: those who were exposed and those who were not. Non-exposed humans cannot have been infected. Those exposed could either be infected or not be infected; those infected could either developed clinical symptoms or not. Since the majority of the people were not infected [18], [19] and a large amount of them were not exposed as well (Supplementary Fig. 2), we applied a zero inflated regression analysis. After all, zeros could either be explained by the absence of exposure, or by the probability of non-infection or asymptomatic infection despite exposure [53].

This might be an explanation for the variable ‘concentration’ to have p ≥ 0.05 in the binomial (zero) part of the univariate and multivariate analysis (Supplementary Fig. 10, Supplementary Fig. 12), whereas it had p ≪ 0.05 in the negative binomial/Poisson (count) part (Supplementary Fig. 11, Supplementary Fig. 4). After all, non-zero concentrations were modeled in many inhabited grid cells (Supplementary Fig. 1, Supplementary Fig. 2), whereas in many of these grid cells the observed incidence rates were equal to zero: that is, the specificity in a dichotomous situation is relatively low. There is, however, a clear relationship between the modeled concentration and the number of observed cases (count model). Note that the effects of each variable represent mean effects, as the values were back-transformed to original values that were not normally distributed.

4.5. Time-dependency

The correlation analysis in the current study was performed quasi-temporally. That means that we performed a regression analysis for each month separately and for the year 2009. The reason for that is that it is complicated to include the variable ‘time’. For example, ‘temperature’ is a variable that is highest values during the summer; if now the emission strengths were also highest in summer, there still would not be a causal relationship yet. High temperatures and high emission strengths happen to occur at the same time; nevertheless, conditions could be different compared to climatological averages, resulting in a possible positive or negative effect.

‘Soil moisture’ is a typical variable for which its effect should be tested in a time-dependent analysis. In the current study design, only its spatial differences are included. That is, we included the spatial heterogeneity of the variable into the model, but not the difference with respect to other months or other years, thereby excluding the effect of a dry season. In a multivariate statistical model the absolute values of a variable are not as important as the deviation of individual values with respect to their common mean.

If a time-dependent analysis would be performed (comparable to [55]), it would be advisable to focus on specific outbreak areas (e.g., those of [30]) to exclude spatial variations and to be able to compare the effects in different areas. A Fourier-transformation applied to the temporal variables would be one of the possibilities [65].

4.6. Hazard map

The hazard map should be interpreted prudently. It shows the spatial potential risk for a C. burnetii infection modulated by environmental factors. That is, neither meteorological conditions nor emission strengths were included, but the possible effects of spatial variations in vegetation density, land use, soil moisture and soil erosion sensitivity were.

Based on this study, the highest hazards were found in the south-eastern Netherlands, with additional hotspots in the northeast and the coastal areas. These maxima were in general correlated to relatively low vegetation densities, dry soil conditions and high soil erosion sensitivities.

The Dutch livestock industry is, however, highly concentrated in the southeast of The Netherlands, partly due to the relatively poor arable farming conditions there (oligotrophic soils and dry soil conditions). The combination of high livestock densities and ‘high’ hazards for spatial spread of airborne pathogens as a function of environmental conditions could result in enhanced human incidence rates in case of an outbreak among animals.

4.7. Recommendations

In particular, we would recommend focusing on the uncertainties in the human and farm data for future research. As noticed, the human data set included only those who passed through four stages: (1) symptomatic infection; (2) occurrence of disease; (3) seeking medical care; and (4) being diagnosed as Q fever case. All other infected persons were not included in the data set (this group is estimated to be 92% of all infected humans [17]). Serological data could be used as well, but only if they cover a large geographical area.

Next to the human data, the source data is neither complete, despite all efforts. We would recommend formulating a protocol in case of a future veterinarian outbreak concerning zoonotic pathogens with an airborne transmission route. Such a protocol could include criteria on (intensive) air sampling within and outside infected stables. In case of Coxiella burnetii, it could include criteria on vaginal sampling and tank milk monitoring and their temporal dynamics as well. That way, more effort could be invested in determining time-dependent emission rates for C. burnetii. Such, more detailed modeled concentrations could be calculated (with more realistic between-farm variations) and a subsequent exposure assessment could be elaborated.

In addition, similar research with data from other outbreaks would be needed to more firmly establish our findings. This could lead to better estimations of the public health risk of a C. burnetii outbreak, and to more detailed and accurate hazard maps that could be used for spatial planning of livestock operations.

The following are the supplementary data related to this article.

Supplementary Fig. 1

Mean modeled log-transformed concentration per km² (yearly averaged). White colors correspond to zero log-transformed concentrations.

Supplementary Fig. 2

Mean modeled log-transformed concentration per km² (monthly averaged).

Supplementary Fig. 3

Mean leaf area index [m²/m²] per km² (yearly averaged), spatially averaged within 5 km of each inhabited grid cell.

Supplementary Fig. 4

Mean leaf area index [m²/m²] per km² (monthly averaged), spatially averaged within 5 km of each inhabited grid cell.

Supplementary Fig. 5

Mean soil moisture content [%] per km² (yearly averaged), spatially averaged within 5 km of each inhabited grid cell.

Supplementary Fig. 6

Mean soil moisture content [m²/m²] per km² (monthly averaged), spatially averaged within 5 km of each inhabited grid cell.

Supplementary Fig. 7

Land use map of The Netherlands (LGN6) aggregated to five main classes: (1) agriculture, (2) forest, (3) open nature, (4) water, and (5) city.

Supplementary Fig. 8

Soil wind erosion sensitivity map of The Netherlands (Hack-ten Broeke et al., 2009).

Supplementary Fig. 10

Mean effects of the back-transformed predictor variables in the univariate binomial regression analysis. White cells refer to variables with p ≥ 0.20; gray cells refer to variables with 0.05 ≤ p < 0.20. Values represent the effect of the predictor variable in case of a one-unit increase.

Supplementary Fig. 11

Same as S11, but from the univariate negative binomial or Poisson regression analysis. All values were the result of a negative binomial regression analysis, except for those indicated by hash tags (#) (Poisson).

Supplementary Fig. 12

Mean effects of the back-transformed predictor variables in the multivariate zero-inflated binomial regression analysis. White cells refer to variables with p ≥ 0.05; gray cells refer to variables excluded from the analysis (since p ≥ 0.20 in the univariate analysis). Values represent the effect of the predictor variable in case of a one-unit increase.

Supplementary Fig. 13

(Left, Middle) Observed and predicted incidence per 100,000 inhabitants at the 1 km² level; (Right) Predicted incidence minus the observed incidence per 100,000 inhabitants.

Supplementary Fig. 14

(Left, Middle) Observed and predicted incidence per 100,000 inhabitants at the 5 km² level; (Right) Predicted incidence minus the observed incidence per 100,000 inhabitants.

Supplementary Fig. 15

(Left, Middle) Observed and predicted incidence per 100,000 inhabitants at the 10 km² level; (Right) Predicted incidence minus the observed incidence per 100,000 inhabitants.

Supplementary Fig. 16.

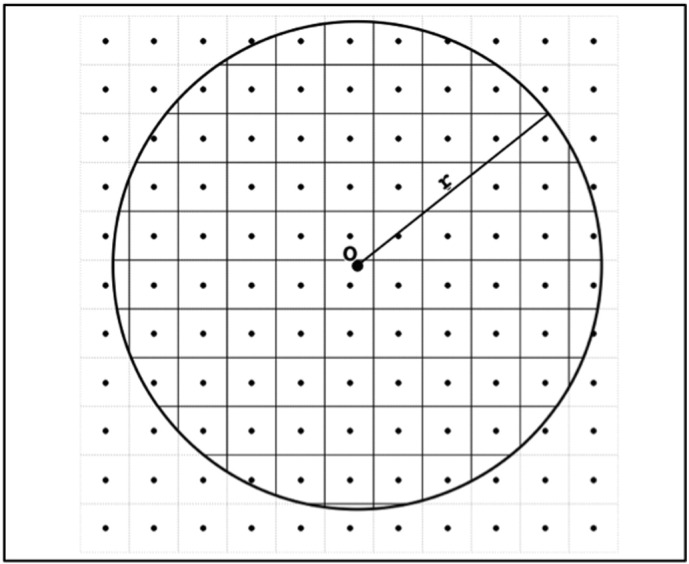
Spatial averaging of all (parts of) grid cells within a distance of five kilometer (r) of a source farm (O).

Supplementary Fig. 17

Sensitivity versus the specificity resulting from the spatial cross-validation analysis. A cut-off value of 0.01 to 1.00 with steps of 0.01 was applied to the predicted number of cases. Line colors refer to the spatial aggregation level: 1 km² (black), 5 km² (red), 10 km² (blue), and municipality level (purple).

Supplementary Tables.

Supplementary Text 1

“Data preparation”.