Structure and Intermolecular Interactions between L-Type Straight Flagellar Filaments

Abstract

Bacterial mobility is powered by rotation of helical flagellar filaments driven by rotary motors. Flagellin isolated from the Salmonella Typhimurium SJW1660 strain, which differs by a point mutation from the wild-type strain, assembles into straight filaments in which flagellin monomers are arranged in a left-handed helix. Using small-angle x-ray scattering and osmotic stress methods, we investigated the structure of SJW1660 flagellar filaments as well as the intermolecular forces that govern their assembly into dense hexagonal bundles. The scattering data were fitted to models, which took into account the atomic structure of the flagellin subunits. The analysis revealed the exact helical arrangement and the super-helical twist of the flagellin subunits within the filaments. Under osmotic stress, the filaments formed two-dimensional hexagonal bundles. Monte Carlo simulations and continuum theories were used to analyze the scattering data from hexagonal arrays, revealing how the bundle bulk modulus and the deflection length of filaments in the bundles depend on the applied osmotic stress. Scattering data from aligned flagellar bundles confirmed the theoretically predicated structure-factor scattering peak line shape. Quantitative analysis of the measured equation of state of the bundles revealed the contributions of electrostatic, hydration, and elastic interactions to the intermolecular forces associated with bundling of straight semi-flexible flagellar filaments.

Introduction

Bacterial locomotion is powered by rotating long (∼$10-15\mathit{\mu }\text{m}$), helical flagellar filaments, which are attached to the bacterial surface through a molecular motor embedded in the bacterial membrane. The complete flagellum-motor complex contains ∼25 proteins. The flagellin homopolymer, however, comprises >$99\text{\%}$ of the flagellum length, providing the structural stiffness necessary to generate the thrust that powers bacterial motility (1, 2). Each flagellar filament can be described as a helical assembly of flagellin protein monomers, with nearly 11 subunits per two turns of a one-start helix, or as a hollow cylinder comprising 11 protofilaments staggered in a nearly longitudinal helical arrangement (2, 3). Each protofilament is a linear structure consisting of flagellin monomers stacked onto each other.

The flagellin monomers can exist in two distinct conformational states denoted as left-handed (L) or right-handed (R). Within each protofilament, all the monomers switch in a highly cooperative fashion, and thus, each protofilament also has either an L or an R configuration. If all the protofilaments within a single flagellum have the same conformational state, the entire assemblage assumes the shape of a straight hollow cylinder made of an L or R helical arrangement of the flagellin monomers (4). In many cases, however, a flagellum contains a mixture of L and R protofilaments, leading to a packing frustration that is resolved by the formation of a helical super-structure along the entire flagellum length, a unique feature that is essential for bacterial motility. Depending on the ratio of R to L filaments, there are a number of distinct structures of varying pitch and radius. In addition, point mutations in the flagellin amino acid sequence affect the helical structure (5). Flagellin mutants, in which all the protofilaments assume an L or an R conformational state, have been isolated and were shown to assemble into straight flagellar filaments (6, 7). Another unique feature of flagella is that they can switch between different helical states in response to external stimuli, including ionic strength, pH, external forces, or temperature (3, 8, 9). Besides their obvious biological importance, their unique helical structure and intriguing stimuli-induced polymorphic transitions make flagella a highly promising, yet poorly explored, building block for assembly of soft materials and biologically inspired nano/micro machines (10).

To better understand bacterial taxis, which is driven by hydrodynamically bundled flagellar filaments, as well as to assemble flagellum-based soft materials, it is essential to elucidate the structure, as well as the intermolecular forces between flagellar filaments (11, 12). Using small-angle x-ray scattering (SAXS), we investigated the behavior of L-type straight flagellar filaments isolated from the SJW1660 strain, which differs from the wild-type SJW1103 flagellin strain by the point mutation G426A. The structure of the flagellar filament was determined in solution. Under osmotic stress, the filaments formed bundles. To quantitatively model scattering patterns from flagellar bundles, we performed Monte Carlo simulations that accounted for the effect of thermal fluctuations on the arrangement of the filaments within the bundles. The line shape of the structure-factor correlation peak and the measured osmotic pressure-distance curves were consistent with theoretical predications (13, 14). These experiments and models allowed us to determine the contributions of hydration, electrostatic, and elastic interactions to the equation of state describing the lateral forces acting between the flagellar filaments within the bundles and the bending stiffness of the filaments.

Materials and Methods

Experimental

The L-type straight filament SJW1660, with flagellin point mutation G426A, was isolated from a mutant strain of the wild-type SJW1103 purified from Salmonella enterica serovar Typhimurium (15) according to a previously published protocol (10). Briefly, bacteria were grown to a log phase, sedimented at 8000 × g, and redispersed in a minimal volume by repeated pipetting with a 1 mL pipette. A very dense foamy bacterial solution was vortex mixed at the highest power setting for 5 min to separate flagella from the bacterial bodies (Genie 2 Vortex, Scientific Industries, Bohemia, NY). Subsequently, this suspension was diluted with a buffer and centrifuged at 8000 × g for 20 min to sediment bacterial bodies. The supernatant contained flagellar filaments, which were then concentrated by two centrifugation/resuspension steps at 100,000 × g for 1 h. For all experiments the flagella were resuspended in 100 mM NaCl and 10 mM K₂HPO₄ at pH 7, adjusted with a few mM of NaOH. To apply osmotic stress to the flagellar filaments and induce bundle formation, we used polyethylene glycol (PEG) of molecular mass 20 kDa (purchased from Sigma-Aldrich (St. Louis, MO) and used as received). Osmotic stress samples were prepared by mixing PEG and flagellar filament solutions, as described elsewhere (16, 17, 18, 19). The osmotic pressure, $\text{Π}$, of each polymer solution was measured using a vapor pressure osmometer (Vapro 5520, Wescor, Pittsburgh, PA) and verified against the well-established (20) expression $\text{log}\pi =a+b\times {\left(wt\text{\%}\right)}^c$, where $a=1.57$, $b=2.75$, and $c=0.21$. Samples were first prepared in Eppendorf tubes, in which they were vortex mixed. Before SAXS measurements, each sample was transferred to a quartz capillary that was flame sealed and centrifuged at 6000 × g, using a Sigma 1-15PK centrifuge and rotor no. 11024, suitable for capillaries. The structural changes at each osmotic pressure were measured by SAXS.

Solution x-ray scattering data analysis

Most of the solution SAXS measurements were performed using our in-house setup. The x-ray source was a rotating anode MicroMax-007 HF (Rigaku, Tokyo, Japan) with a copper target, whose wavelength is 1.54 Å. The optics was a Confocal Max-Flux, CMF-12-100Cu8 focusing unit (Osmic, Rigaku). The detector was a MAR345 image plate (MarXperts, Norderstedt, Germany), the sample-to-detector distance was 1.8 m, and the exposure time was 2 h. The setup also includes scatterless slits (Forvis Technologies, Santa Barbara, CA) (21). More details about the setup are described in our earlier publication (22). Some of the data were measured at ID02 beamline at the European Synchrotron Radiation Facility. ID02 beamline optics consist of a cryogenic cooled Si-111 channel-cut monochromator and a focusing toroidal mirror. The beam size was 200 × 400 μm² (vertical and horizontal, respectively), with divergence of 20 × 40 μrad. The photon energy was 12.4 keV. The detector was a FReLoN 16M Kodak CCD, the sample-to-detector distance was 2 m, and the exposure time was 0.1 s. A more detailed description of the beamline characteristics is provided elsewhere (23).

To analyze the data, we simulated the real-space structure of the flagellar bundle and the interactions between neighboring filaments, and calculated the bundle’s scattering intensity, I, as a function of q, which is the magnitude of the momentum transfer vector (or scattering vector), $\overrightarrow{q}$ (24, 25, 26, 27, 28). By comparing the simulation results with the data, we determined the structural parameters and physical properties of the bundles.

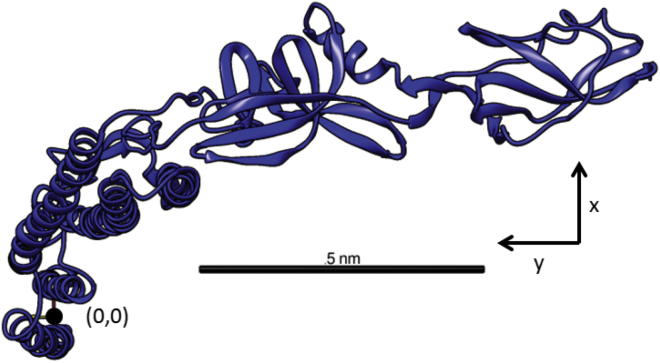
The initial estimate of structural parameters by the model was taken from electron cryo-microscopy data (29). The atomic structure (at 4 Å resolution) of an L-type flagellin monomer was taken from the Protein Data Bank (PDB: 3A5X) (15, 30) and placed in a Cartesian coordinate system (Fig. 1). The origin was not placed at the subunit center of mass, but rather between the two α-helices at the z axis which points along the filament’s long axis. This choice allowed a simpler relation between translations and rotations of the monomer with the filament axes. In particular, the scattering amplitude of atom i was calculated using the International Union of Crystallography (IUCR) atomic form factor:

$$f_i^0\left(q\right)=\sum _{j=1}^4{a}_j\text{exp}\left(-b_j{\left(\frac{\left|\overrightarrow{q}\right|}{4\pi }\right)}^2\right)+c,$$ (1)

where $a_j,b_j$, and c are the Cromer-Mann coefficients, given in Table 2.2B of the International Tables for X-ray Crystallography (31) and its subsequent corrections (32).

Figure 1.

A 3D representation of the flagellin monomer, based on PDB: 3A5X (15). The coordinate system used in our computation model is indicated by the origin and the x and y axes, and the scale bar represents 5 nm. To see this figure in color, go online.

The scattering amplitude of the entire flagellin monomer is given by

$$F_{\text{Monomer}}\left(\overrightarrow{q}\right)=\sum _j{f}_j^0\left(q\right)\cdot \text{exp}\left(i\overrightarrow{q}\cdot {\overrightarrow{r}}_j\right),$$ (2)

where ${\overrightarrow{r}}_j$ is the location of the jth atom in the monomer with respect to the origin, and $\overrightarrow{q}$ is the momentum transfer vector in reciprocal space. To account for the contribution of the solvent, its displaced volume should be estimated (33, 34, 35). A uniform sphere (dummy atom) with a mean solvent electron density, ${\rho }_0$, and atomic radius, $r_j^{\text{s}}$, could have been placed at the center of each atom j in the PDB file. This approach, however, may generate errors at low q (36). Therefore, the uniform spheres were replaced by spheres with Gaussian electron density profiles (36),

$${\rho }_j\left(\overrightarrow{r}\right)={\rho }_0\text{exp}\left[-{\left(\frac{\overrightarrow{r}}{r_j^{\text{s}}}\right)}^2\right],$$

where ${\rho }_0$ is the mean electron density of the solvent $\left({\rho }_0^{\text{water}}=333\left(e/{\text{nm}}^3\right)\right)$, and the $r_j^{\text{s}}$ radii were published previously (33). When absent, empirical radii (37) were used. The scattering amplitude contribution of the Gaussian dummy atom is

$$F_j\left(\overrightarrow{q}\right)=$$

$${\int }_0^{2\pi }d{\varphi }_r{\int }_0^{\pi }d{\theta }_r{\int }_0^{\infty }{\rho }_0\text{exp}\left[-{\left(\frac{r}{r_j^s}\right)}^2\right]\text{exp}\left[i\overrightarrow{q}\cdot \overrightarrow{r}\right]r^2\text{sin}{\theta }_{r}dr.$$

The result depends on the radius and q, owing to the spherical symmetry, and is given by

$$F_j\left(q\right)={\rho }_0{\pi }^{\frac{3}{2}}{\left(r_j^{\text{s}}\right)}^3\text{exp}\left[-{\left(\frac{r_j^{\text{s}}q}{2}\right)}^2\right].$$ (3)

In this approach, the overall excluded volume, $V_{\text{ex}}^{\text{Gaussian}}$ is ${\pi }^{\left(3/2\right)}{\left(r_j^{\text{s}}\right)}^3$, and it is larger by a factor of $\left(3\sqrt{\pi }/4\right)\approx 1.33$ than the volume of the uniform sphere, $V_{\text{ex}}^{\text{Uniform}}=\left(4\pi /3\right){\left(r_j^{\text{s}}\right)}^3$, in agreement with previous work (36). To better fit the data, the value of the mean electron density, ${\rho }_0$, was adjusted to some extent (Fig. S1). When the solvent contribution was taken into account, the scattering amplitude from a monomer became:

$$F_{\text{Monomer}}\left(\overrightarrow{q}\right)=\sum _j\left[f_j^0\left(q\right)-F_j\left(q\right)\right]\cdot \text{exp}\left(i\overrightarrow{q}\cdot {\overrightarrow{r}}_j\right).$$ (4)

To describe the entire filament, we first translated the ith monomer, with respect to its origin reference point (Fig. 1), by the translation vector $\overrightarrow{R_i}\left(x_i,y_i,z_i\right)$. The monomer was then rotated by its Tait-Bryan (38) rotation angles, ${\alpha }_i,{\beta }_i,\mathrm{and}{\gamma }_i$, around the x, y, and z axes, respectively, using the rotation matrix

$$\mathbf{A}\left(\alpha \mathrm{,}\beta \mathrm{,}\gamma \right)=\left[\begin{array}{ccc}\text{cos}\beta \text{cos}\gamma & -\text{cos}\beta \text{sin}\gamma & \text{sin}\beta \\ \text{cos}\alpha \text{sin}\gamma +\text{cos}\gamma \text{sin}\alpha \text{sin}\beta & \text{cos}\alpha \text{cos}\gamma -\text{sin}\alpha \text{sin}\beta \text{sin}\gamma & -\text{cos}\beta \text{sin}\alpha \\ \text{sin}\alpha \text{sin}\gamma -\text{cos}\alpha \text{cos}\gamma \text{sin}\beta & \text{cos}\gamma \text{sin}\alpha +\text{cos}\alpha \text{sin}\beta \text{sin}\gamma & \text{cos}\alpha \text{cos}\beta \end{array}\right].$$

The location and orientation of the ith subunit were described as

$$\begin{array}{c}{\alpha }_i={\beta }_i=0,{\gamma }_i=i\times \frac{4\pi }{NU}\\ x_i=R\cos \left({\gamma }_i\right),y_i=R\sin \left({\gamma }_i\right),z_i=i\times \frac{P}{NU}\end{array},$$ (5)

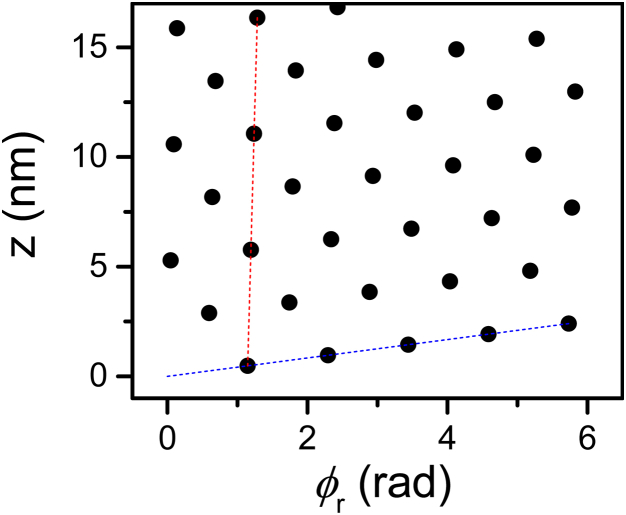
where R is the radius of the reference point, P is the two-pitch distance, and $NU$ is the number of subunits in a two-pitch turn. Our model assumes that thermal fluctuations within each flagellum are negligible. Fig. 2 shows a two-dimensional (2D) projection of the helical lattice of the filament.

Figure 2.

A projection of the helical lattice showing the monomer axial rise, z ($0.48\pm 0.01\text{nm}$ per monomer), and the packing arrangement at the radius of the reference point ($R=2.42\pm 0.02\text{nm}$). The dotted red line shows the shift between monomers that are on top of one another. The dotted blue line shows the axial rise between adjacent monomers. ${\varphi }_r={\gamma }_i\text{mod}2\pi$, where ${\gamma }_i$ is defined in Eq. 5. To see this figure in color, go online.

Using the reciprocal-grid (RG) algorithm (28), the flagella scattering form factor, $FF$, was numerically calculated,

$$FF\left(\overrightarrow{q}\right)=\sum _{i=1}^n{F}_{\text{Monomer}}\left({\mathbf{A}}_i^{-1}\left({\alpha }_i,{\beta }_i,{\gamma }_i\right)\cdot \overrightarrow{q}\right)\cdot \text{exp}\left(i\overrightarrow{q}\cdot \overrightarrow{R_i}\right),$$ (6)

and orientationally averaged to give the solution scattering intensity,

$$I\left(q\right)=\frac{{\int }_0^{2\pi }d{\varphi }_q{\int }_0^{\pi }{\left|FF\left(q,{\theta }_q,{\varphi }_q\right)\right|}^2\text{sin}{\theta }_{q}d{\theta }_q}{{\int }_0^{2\pi }d{\varphi }_q{\int }_0^{\pi }\text{sin}{\theta }_{q}d{\theta }_q},$$ (7)

where ${\mathbf{A}}_i$ and ${\overrightarrow{R}}_i$ are the rotation matrix and the translation vector, respectively, of the ith monomer.

Osmotic stress exerted by non-adsorbing polymers induced bundling of straight flagellar filaments. The scattering intensity owing to the packing of the flagellar filaments was computed using the form factor of a single filament, $FF$, as a unit cell. The form factor was multiplied by a structure factor (lattice sum), $SF\left(\overrightarrow{q}\right)$, of a 2D lattice and orientationally averaged, $\left(FF\left(\overrightarrow{q}\right)\cdot SF\left(\overrightarrow{q}\right)\right)$, in $\overrightarrow{q}$-space. We assumed a perfect hexagonal 2D lattice as our starting point (Fig. S5). This assumption is equivalent to assuming that the chains are very stiff. The fitting parameters of a hexagonal lattice were the spacing between the centers of neighboring filaments, a, and the domain size (the distance over which two lattice points maintain positional correlation). These parameters determined the position and width of the correlation peaks in the scattering intensity. Since samples were in solution at room temperature, the lattice exhibited significant thermal fluctuations, which washed away the sharp peaks of the structure factor (Fig. S5).

In real space, a finite 2D lattice, at zero temperature, is described by

$$S{F}_r\left(\overrightarrow{r}\right)=\delta \left(z\right)\sum _i^M\delta \left(x-x_i\right)\delta \left(y-y_i\right),$$ (8)

where ${\overrightarrow{r}}_i=\left(x_i,y_i,z_i\right)$ is the location of the ith point in a lattice with M unit cells. At a finite temperature, thermal fluctuations work against the intermolecular forces, affecting the lattice structure. Assuming a harmonic potential between nearest neighbors, we calculated the pairwise energetic cost, $\text{Δ}{E}_i$, for a small displacement, $\text{Δ}\overrightarrow{r}$, of the ith lattice point from its mean location, ${\overrightarrow{r}}_i$, at a given temperature:

$$3\text{Δ}{E}_i=\frac{1}{2}\kappa \sum _{j\in nn}\left[{\left({\overrightarrow{r}}_{\perp i}+\text{Δ}{\overrightarrow{r}}_{\perp }-{\overrightarrow{r}}_{\perp j}\right)}^2-{\left({\overrightarrow{r}}_{\perp i}-{\overrightarrow{r}}_{\perp j}\right)}^2\right].$$ (9)

Here, ${\overrightarrow{r}}_{\perp i}=\left(x_i,y_i,0\right)$ and $nn$ denote nearest neighbors and κ is the lattice elastic constant between neighbors. The factor of 3 accounts for the fact that on average, each chain has six neighbors and the interaction is shared between the interacting pairs (39). The probability of a deviation, $\text{Δ}{E}_i$, in the energy is

$$P_i\left(\text{Δ}{E}_i\right)\sim \text{exp}\left(-\frac{\text{Δ}{E}_i}{k_{\text{B}}T}\right),$$ (10)

where $k_{\text{B}}$ is the Boltzmann constant and T is the absolute temperature. To estimate the effect of thermal fluctuations, we performed Monte Carlo simulations. In each iteration, we tested the probability of a random displacement at a random lattice point against a random number between 0 and 1. If the random number was smaller than the calculated probability, $P_i\left(\text{Δ}{E}_i\right)$, the displacement was accepted. Repeating this process for ∼${10}^9$ iterations, using periodic boundary conditions, converged into a stable, slightly (depending on the value of κ) disordered 2D hexagonal lattice. Fig. S6 shows how the value of κ affected the calculated intensity in this model.

In real space, the total electron density is a convolution of the electron density of a filament, ${\rho }_{\text{filament}}\left(\overrightarrow{r}\right)$, and the 2D bundle lattice, $S{F}_r\left(\overrightarrow{r}\right)$. In reciprocal space, the convolution becomes a multiplication; hence, the total scattering amplitude is

$$F\left(\overrightarrow{q}\right)=FF\left(\overrightarrow{q}\right)\cdot SF\left(\overrightarrow{q}\right),$$ (11)

where

$$SF\left(\overrightarrow{q}\right)=\sum _{i=1}^M\text{exp}\left(i\overrightarrow{q}\cdot {\overrightarrow{r}}_i\right).$$ (12)

To obtain the scattering intensity, $I_{\text{bundle}}\left(q\right)$, we calculated the square of the scattering amplitude, ${\left|F\left(q,{\theta }_q,{\varphi }_q\right)\right|}^2$, and averaged over all the orientations in reciprocal space (${\theta }_q$ and ${\varphi }_q$), as in Eq. 7 (28). $I_{\text{bundle}}\left(q\right)$ was then compared with the experimental SAXS data.

Results and Discussion

Scattering from flagellar suspensions

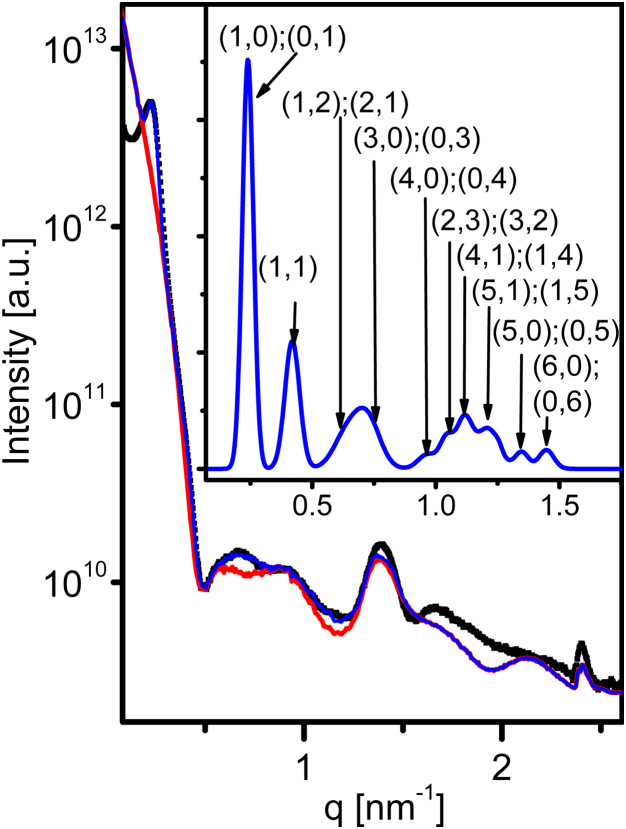
The x-ray scattering 2D pattern from a dense solution of straight flagella, isolated from strain SJW 1660, was azimuthally averaged, yielding an experimental scattering intensity curve (Fig. 3). The experimental data were compared with the scattering curve computed from a flagellar model in which the atomic structure of flagellin monomers (Fig. 1) was arranged on a flagellar one-start left-handed helical lattice. The relevant microscopic parameters in Eq. 5 (R, P, and $NU$) were varied to obtain the best fit of our theoretical computed curve to the experimental scattering data and to estimate the error in the form-factor fitting parameters (Figs. S2–S4). During this procedure, the atomic structure of the flagellin subunit, obtained from PDB: $3A5X$ (15), was preserved and the subunits were not allowed to overlap.

Figure 3.

Azimuthally integrated scattering intensity as a function of q (the magnitude of the momentum transfer vector, $\overrightarrow{q}$), from isotropic solution of the SJW1660 strain in 100 mM NaCl (black solid squares). The form factor (red curve) of a flagellar filament was computed using Eqs. 2 and 7 and fitted to experimental data yielding the following essential flagellar structural parameters: filament diameter, $D=23.1\text{nm}$; two-turn pitch, $p=5.2\text{nm}$; 10.96 flagellin subunits per two-turn pitch; and the radius of the reference point, $R=2.42\text{nm}$. The blue curve corresponds to the same form factor when multiplied by the structure factor of a 2D hexagonal phase with a lattice constant, a, of 30.0 nm. The structure factor and its peak indexes are shown in the inset. To see this figure in color, go online.

In our experiments, the average length of flagellar filaments was 4 ± 2 μm (10). The SAXS measurements, however, were insensitive to objects longer than a few hundred nanometers; hence, in our theoretical computations, the filament length, L, was fixed at 300 nm (in other words, the filament contained $n=660$ monomers). Models with longer filaments required more computational resources and did not change the scattering intensity profile, or better fit the data, in the q-range of our data. A quantitative comparison of experimental measurements to the theoretical model revealed a filament diameter, D, of 23.1 $\pm$ 0.1 nm, a two-turn pitch, P, of 5.2 ± 0.1 nm, $NU=10.96\pm 0.01$ flagellin subunits/two-turn pitch, and a radius of the reference point, R, of 2.42 ± 0.02 nm (Fig. 4). These values are consistent with electron cryo-microscopy and x-ray fiber diffraction data ($D=23-24\text{nm}$ (30, 40), $P=5.27\text{nm}$, $NU=11.26$ (15, 40), and $R=2.5\text{nm}$ (15)).

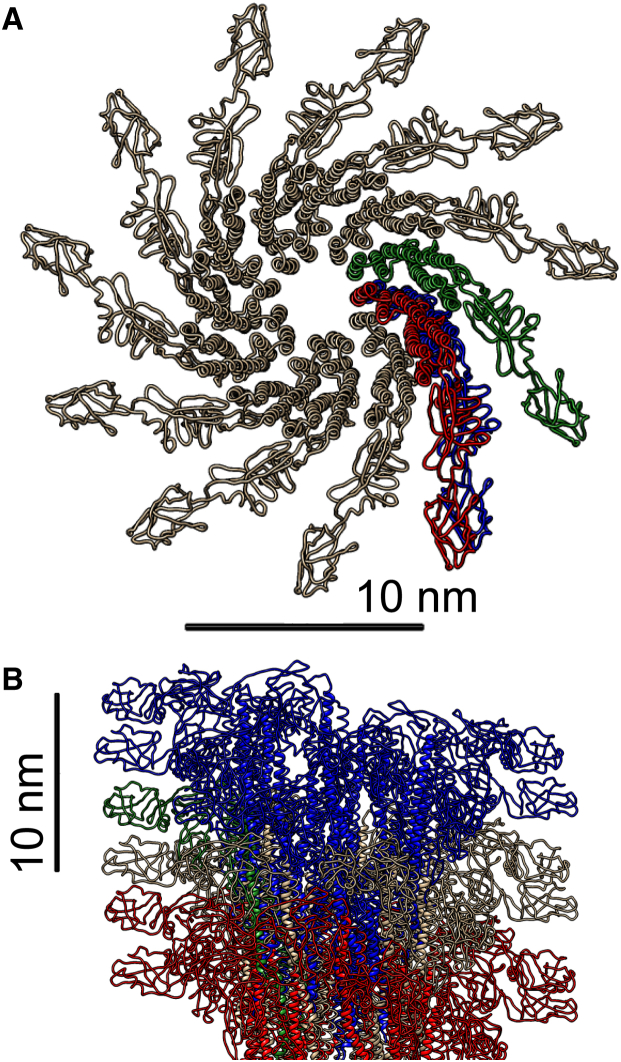
Figure 4.

3D atomic model of a two-turn pitch (11 flagellin subunits). (A) Top view. (B) Side view of a three-pitch filament along the filament long axis. The blue subunit is the first monomer (at $z=0$), and the red subunit is the monomer unit of the second two-turn pitch, which is slightly shifted (see Fig. 2). To see this figure in color, go online.

Using Gaussian dummy atoms (Eqs. 4 and 7) to account for the contribution of the solvent with reasonable values for the solvent electron density, ${\rho }_0$ (in Eq. 3), did not significantly improve the fit of our form-factor model to the experimental data (Fig. S1). The contribution of the solvent was therefore not computed in subsequent models (in other words, Eqs. 2 and 7 were used). By varying the model parameters, we determined the effect of each parameter on the locations and magnitudes of various features in the calculated intensity. The first minimum was mainly controlled by the flagellar filament diameter (see Fig. S2), the peak at $q=1.4{\text{nm}}^{-1}$ was closely associated with the helical pitch (see Fig. S3), and the peak at $q=2.4{\text{nm}}^{-1}$ was attributed to the axial rise (Fig. S4). The high sensitivity of our model to these structural parameters and their weak interdependency is demonstrated in Figs. S2–S4.

To obtain high signal/noise scattering patterns, we used a 27 ± 0.1 mg/mL (or 0.524 ± 0.002 mM) flagellar suspension. Based on the structure of the flagellar filaments, the mean filament volume fraction, $\varphi$, in this sample was $\simeq 0.062$. Previous work has demonstrated that rigid rods form a nematic phase when $\left(\varphi L/D\right)>4$. This relationship becomes quantitatively valid in the Onsager limit in which $L\text{/}D>100$ (41, 42). Consequently, because our flagellar filaments were >2 μm, and thus satisfied the Onsager criterion, the filament suspension formed nematic liquid crystals. We note that inherently, polydispersity of flagellar filaments significantly widens isotropic-nematic co-existence. This makes it possible that shorter filaments partitioned into an isotropic phase (43). Furthermore, rigorous analysis would have to account for the contribution of electrostatic repulsion, which leads to an effective diameter that can be significantly larger than the bare one. The high ionic strength of our suspension, however, significantly reduced this contribution (44).

Although the majority of the measured scattering pattern from flagellar filaments is owing to the form factor, the signal also contained weak structure-factor correlation peaks, at $q_{\left(\mathrm{1,0}\right)}=0.24{\text{nm}}^{-1}$ and its higher harmonics (Fig. 3). The presence of these peaks suggests that a fraction of the filaments within our sample formed hexagonal bundles with a lattice constant, a, of $30.0\pm 0.1\text{nm}$ (Fig. 3, inset). Within such bundles, the volume per chain is $\left(\sqrt{3}L{a}^2/2\right)$, where L is the mean filament length. The volume of a chain is $\left(L\pi D^2/4\right)$; hence, the volume fraction of the filaments in our lattice, given by the ratio of the two, $\varphi =\left(\pi D^2/2\sqrt{3}{a}^2\right)$, was $\simeq 0.54$. The average volume fraction of the filaments, however, was $\simeq 0.062$, suggesting that a low-density nematic liquid crystal coexisted with a low fraction of filaments that formed high-density hexagonal bundles.

Lindemann stability criterion asserts that the root mean-square displacement (RMSD), ${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\left(1/2\right)}$, in a lattice should be small compared with the lattice constant $\left(<0.1a\right)$. In a lattice with purely steric interactions (13),

$${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\frac{1}{2}}=3^{\frac{1}{2}}\left(a-D\right).$$ (13)

The lattice is expected to melt when $a_{\text{max}}\approx 1.2D$, which in the case of our flagellar filaments corresponds to $a\approx 28\text{nm}$ (13). For the filaments in the hexagonal phase, a was $\approx 1.3D$, suggesting that the van der Waals attractive interactions between the filaments were not negligible and stabilized the bundle structure. The structure-factor peaks were relatively wide (with a full width at half-maximum of $\approx 0.06{\text{nm}}^{-1}$), suggesting that the hexagonal bundles had small lateral dimensions. Applying Warren’s approximation revealed that, on average, there were only $\sim 3$ filaments that maintained positional correlation in the lattice (45).

Measuring the equation of state for flagellar solutions using the osmotic stress technique

To induce large-bundle formation, we applied osmotic stress to the flagellar filaments by adding increasing concentrations of an inert polymer (PEG: molecular mass, 20 kDa) to our SJW 1660 flagellar filament solution (Fig. 5). We then determined the structure of the forming flagellar filament bundles and the interactions between filaments in the bundles. To obtain the mean interfilament lateral separation, a, and the average coherence length, along which the positional order of filaments within the bundle is maintained, we modeled the scattering from a filamentous bundle and compared it with experimental measurements (Fig. 5 B). We multiplied the single-filament form factor (Eq. 6) by a hexagonal lattice sum (Eqs. 11 and 12) and orientation averaged the product in $\overrightarrow{q}$-space (Eq. 7). To take into account the effect of thermal fluctuations, we assumed a harmonic potential between nearest-filament neighbors and calculated the energetic cost of random small displacements in the hexagonal lattice (Eq. 9). We performed Monte Carlo simulation (using Eq. 10) that equilibrated the lattice structure. A lattice of $40\times 40$ with $\kappa =1.2\pm 0.1\text{mN}\cdot {\text{m}}^{-1}=0.29\pm 0.02{\text{k}}_{\text{B}}\text{T}\cdot {\text{nm}}^{-2}$ (κ is defined in Eq. 9) was kept constant. Based on the locations of the filament centers that were obtained from the simulations, we calculated the structure factor (Eq. 12) and $I_{\text{bundle}}\left(q\right)$ (Eq. 7), and compared these predictions with the experimental SAXS data.

Figure 5.

Scattering from an isotropic suspension containing bundles of SJW1660 straight flagellar filaments in 100 mM NaCl. The bundles were assembled using a 5 wt % PEG (molecular mass, 20 kDa) concentration, corresponding to an osmotic pressure of 47 kPa (20). (A) Two-dimensional x-ray scattering image. (B) Azimuthally integrated scattering intensity as a function of q. The experimental measurements (black squares) were fitted to our computational hexagonal lattice model (red curve) with a lattice constant of $a=23.5\text{nm}$. Good agreement can be seen over a wide q-range in both the location and magnitude of the peaks, whose indexes are indicated in brackets. To see this figure in color, go online.

Three lattice parameters affected the scattering intensity, $I_{\text{bundle}}\left(q\right)$: 1) the 2D hexagonal lattice size, a, which determined the locations of the structure-factor correlation-peak centers (Fig. S7); 2) the lattice coherence length (i.e., the positional correlation length of the lattice), which mainly influenced the width of the structure-factor correlation-peaks (Fig. S8); and 3) the elastic constant, κ, which affected the intensity and number of structure-factor peaks (Fig. S6). High κ values correspond to weaker thermal fluctuations and, hence, sharper correlation peaks. Our computational model quantitatively fitted the experimental scattering curve over a wide range of q values (Fig. 5 B). Results for other osmotic pressures, which show comparable agreement with the computational model, are shown in Fig. S9. From the equipartition theorem and the value of κ, we can estimate the RMSD of a single flagellar chain confined in the hexagonal lattice to be (39) ${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\left(1/2\right)}=\sqrt{\left(k_{\text{B}}T/\kappa \right)}=1.85\pm 0.08\text{nm}\text{.}$

Taking into account hydration repulsion, the bending stiffness, ${\kappa }_{\text{s}}$, of the flagellar filaments, and the electrostatic interactions between them, the equation of state for a bundle of long semi-flexible chains like DNA in solution is (14)

$$\frac{\partial G}{\partial d}\left(d\right)=\frac{\partial H_0}{\partial d}\left(d\right)+c{k}_{\text{B}}T{\kappa }_{\text{s}}^{-\frac{1}{4}}\frac{\partial }{\partial d}\sqrt[4]{\frac{{\partial }^2{H}_0}{\partial d^2}},$$ (14)

where G is the free energy, $d=a-D$ is the spacing between filaments, ${\kappa }_{\text{s}}$ is the bending stiffness, $H_0$ is

$$H_0\left(d\right)=a_{\text{h}}\frac{e^{-d/{\lambda }_{\text{H}}}}{\sqrt{d/{\lambda }_{\text{H}}}}+b\frac{e^{-d/{\lambda }_{\text{D}}}}{\sqrt{d/{\lambda }_{\text{D}}}},$$ (15)

where ${\lambda }_{\text{H}}$ and ${\lambda }_{\text{D}}$ are the hydration and electrostatic screening lengths, respectively. The explicit expression of $\left(\partial G/\partial d\right)\left(d\right)$ is given in Section S6 in the Supporting Material.

In a hexagonal lattice, the relation between the free energy and the osmotic pressure is (14)

$$\text{Π}\left(d\right)=-\frac{1}{\sqrt{3}d}\frac{\partial G}{\partial d}\left(d\right).$$ (16)

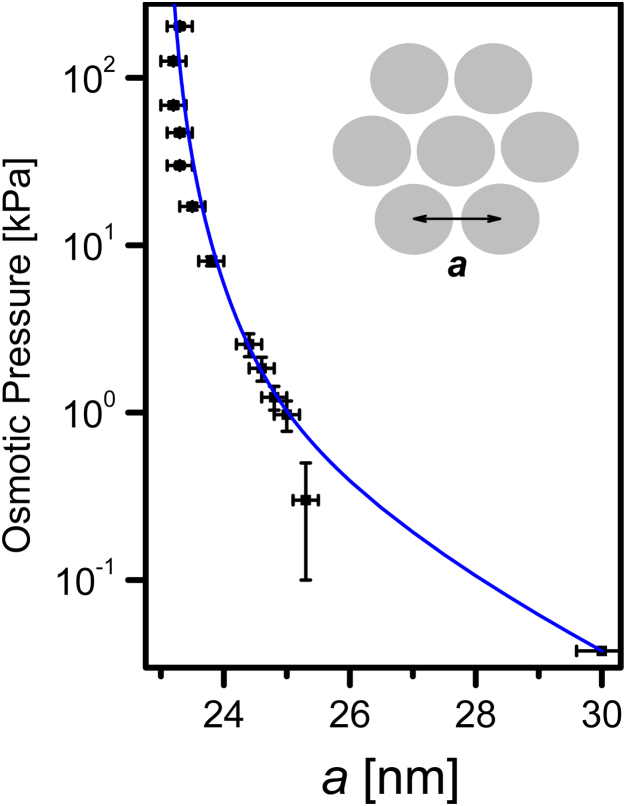
As expected, the lateral filament spacing, a, obtained from fitting the scattering data to our model (as demonstrated in Fig. 5) decreased with increasing osmotic pressure (Fig. 6). The experimental pressure-distance curve could be quantitatively fitted to the theoretical equation of state (Eqs. 14–16). We fixed the filament hard-core diameter, D, to the value obtained from the form-factor analysis (23 nm) when performing the fit. The fit yielded the parameters $a_{\text{h}}=40\pm 5\text{Pa}\cdot {\text{nm}}^2$, $b=40\pm 5\text{Pa}\cdot {\text{nm}}^2$, $c=1.7\pm 0.1$, ${\kappa }_{\text{s}}=2.9\pm 0.4\cdot {10}^{-15}\text{J}\cdot \text{nm}$, ${\lambda }_{\text{H}}=0.26\pm 0.03\text{nm}$, and ${\lambda }_{\text{D}}=0.82\pm 0.03\text{nm}$. ${\lambda }_{\text{H}}$ is close to the expected value of ∼3 Å (46). ${\lambda }_{\text{D}}$ can be calculated from the calculated ionic strength of the sample, 0.84 nm (47). The small difference between the calculated and the measured ${\lambda }_{\text{D}}$ could be explained by the small amount of NaOH that was added to the solution to maintain natural pH. We kept the value of the prefactor c close to unity, as obtained in an earlier study (14). $a_{\text{h}}$ and b were first fitted to the high-pressure data, where the contribution of the hydration and electrostatic forces should dominate.

Figure 6.

The equation of state of bundled straight filaments shows how the lattice constant, a, of a hexagonal bundle (see inset for a schematic top view) of straight filaments depends on the applied osmotic pressure. The blue curve indicates the fit of the theoretical model (Eq. 14) to the data. To see this figure in color, go online.

The bending stiffness, ${\kappa }_{\text{s}}$, terms dominated the lower pressure data and are associated with the persistence length of the filaments (13): $P=\left(k_{\text{s}}/k_{\text{B}}T\right)=700\pm 100$ μm. This value is significantly higher than the persistence length of actin (18 μm), which has a smaller cross section, and comparable to the persistence length of a taxol-free microtubule (700–1500 μm), which has a slightly larger cross section (48). A taxol-stabilized microtubule has, as expected, a longer persistence length (5200 μm) (48). The latter values were measured from thermal fluctuations in the shape of the filaments. Note that the persistence length that we found is higher than the value determined from electron micrographs of isolated, negatively stained filaments (41 μm) (11). Finally, a constant weak negative effective pressure of 37 Pa was added to account for the contribution of the van der Waals interaction, which led to the hexagonal phase when no osmotic stress was applied (Fig. 3).

Whereas the theoretical model quantitatively fits the data over a wide range of applied osmotic pressures, when the filaments were far apart, the model (Eq. 14) predicted a slightly more repulsive interaction than measured. At very high pressures (490 kPa or higher), the filaments assumed lattice-spacing values, a, that were smaller than the unstressed filament diameter. Our data, however, show that at these high pressures, the first minimum of the azimuthally integrated scattering curve moves toward higher q values, suggesting that the form factor has changed owing to deformation of the filaments (Fig. 7). This change is consistent with a tighter monomer packing resulting in a smaller filament diameter, D. From the structure of the flagellar filaments we can calculate the cross-section geometrical moment of inertia, $I\approx \left(\pi /4\right)\left[{\left(D/2\right)}^4-R^4\right]=1.4\times {10}^4{\text{nm}}^4$. The filament Young’s modulus, E, is then given by (48)

$$E=\frac{P}{I}\approx 0.20\pm 0.03\text{GPa},$$

where we have assumed that $P=700\pm 100\mathit{\mu }\text{m}$. Table 1 summarizes the parameters determined in this study.

Figure 7.

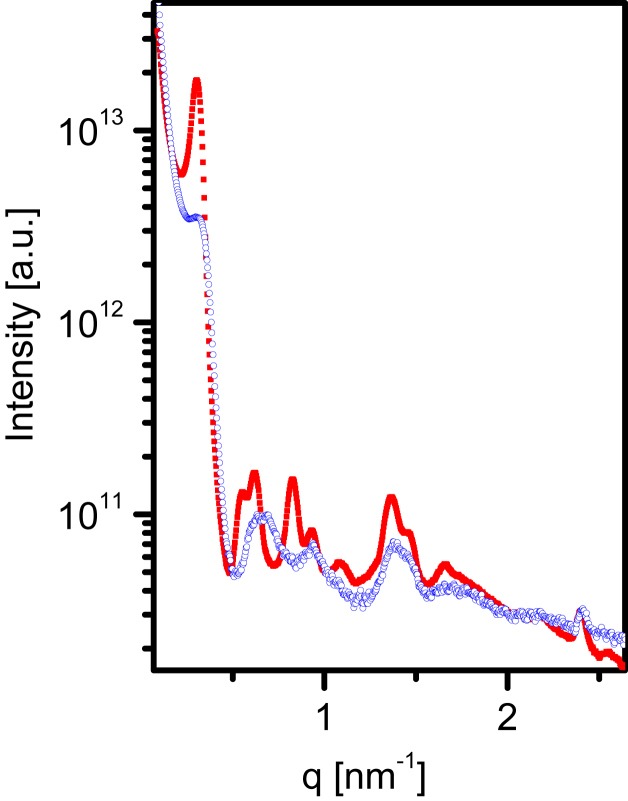
At high osmotic pressures, the scattering profiles exhibited a discontinuous change indicating a structural change of the constituent flagella. A comparison between SAXS patterns measured for moderate (30 kPa; red solid symbols; hexagonal lattice spacing, 23.3 nm) and high (490 kPa; blue open symbols; hexagonal lattice spacing, 21 nm) osmotic pressures. To see this figure in color, go online.

Table 1.

Summary of the Parameters Determined In This Study

Parameter Name, Symbol	Value	Error	Units
Filament diameter, D	23.1	0.1	nm
Two-turn pitch, P	5.2	0.1	nm
Radius of the reference point, R	2.42	0.01	nm
Number of flagellin subunits per two-turn pitch, $NU$	10.96	0.01
Hexagonal lattice elastic constant between neighbors, κ	1.2	0.1	mN $\cdot$ m−1
RMSD of a flagellar chain in the hexagonal lattice, ${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\left(1/2\right)}$	1.85	0.08	nm
Flagellar bending stiffness, ${\kappa }_{\text{s}}$	2.9	0.4	${10}^{-15}$ J $\cdot$ nm
Flagellar Young’s modulus, E	0.20	0.03	GPa

Within the hexagonal lattice, semi-flexible flagellar filament chains are confined to an effective “tube” within the hexagonal lattice. It has been argued that fluctuations of this type of confined filaments can be described by a single characteristic length scale, which points along the long axis, $\hat{z}$, direction of the filaments. This length scale is the Odijk deflection length, ${\lambda }_{\text{def}}$, which is the average displacement between successive collisions along the chain within the confined lattice and is given by (49, 50)

$${\lambda }_{\text{def}}\approx P^{\frac{1}{3}}{d}^{\frac{2}{3}}.$$ (17)

Equation 17 is based on scaling theory and agrees well with Monte Carlo simulations up to a prefactor of order 2 (51). The mean fluctuations in the nematic director can then be estimated from the deflection length (13):

$$\langle {\left|n_{\perp }\right|}^2\rangle \approx {\left[\frac{d}{{\lambda }_{\text{def}}}\right]}^2.$$ (18)

Therefore, it follows that the measurement of d directly yields the Odijk deflection length.

The bulk modulus,

$$B\equiv -V\frac{d\text{Π}}{dV},$$ (19)

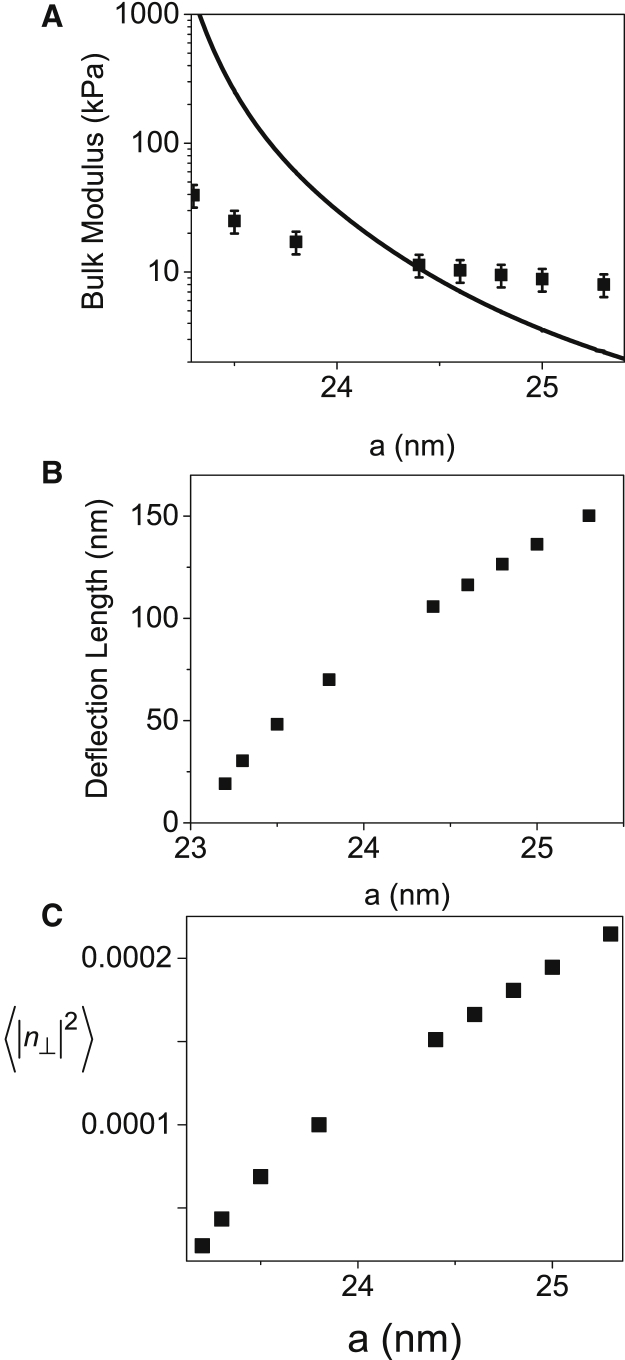
can be computed from the theoretical $\text{Π}\left(d\right)$ (Eq. 16). The compressed volume, V, is taken to be the volume of solution per chain inside the hexagonal lattice (52) and is given by $V\text{/}L=\left(\sqrt{3}{a}^2/2\right)-\pi \left(D^2/4\right)\equiv A_{\text{c}}$, where L is the chain length and $A_{\text{c}}$ is the compressed area per chain. Assuming that L remained unchanged under the osmotic pressures applied in our experiment, $dV=L\cdot d{A}_{\text{c}}$, $B=-A_{\text{c}}\left(d\text{Π}/d{A}_{\text{c}}\right)$ and is independent of L. Using the above formula we can determine how the calculated bulk modulus, deflection length, and mean fluctuations in the nematic director vary with the lattice spacing, a (Fig. 8). The bulk modulus decreased with a, whereas the deflection length and the mean fluctuations in the nematic director increased with a.

Figure 8.

Elastic constants of the hexagonal phase as a function of the lattice spacing, a. (A) The bulk modulus, calculated based on the osmotic stress data (solid curve) or on the Monte Carlo simulation results (solid symbols). (B) The deflection length (the average displacement between successive collisions along the chain within the confined lattice). (C) The fluctuations in the nematic director. To see this figure in color, go online.

The bulk modulus can also be estimated from κ by scaling analysis. To obtain units of pressure, κ should be divided by a length scale. The relevant length scale in this case is the deflection length, ${\lambda }_{\text{def}}$, which is the length scale over which the displacement of the filament is kept within the tube around the filaments, which is in the original lattice site. Hence, we obtain

$$B\approx \frac{\kappa }{{\lambda }_{\text{def}}}.$$ (20)

Fig. 8 confirms that the bulk modulus, which was estimated from the Monte Carlo simulations by scaling analysis (Eq. 20), yields bulk moduli that are of the same order of magnitude as those obtained from the osmotic stress data (Eq. 19). When a was smaller than ∼23.5 nm, the scaling analysis deviated from the bulk modulus, which was computed from the osmotic stress data. The deviation might be attributed to the fact that as a gets shorter, κ might change (13); hence, Eq. 20 does not provide a good estimate of B at low a values.

Twist of the flagellar bundle could have contributed to disorder in the bundles (53). Twist distortions, however, are expected to occur on length scales of the filament curvature, which in our case was much longer than the accessible length scale in our SAXS experiments.

Scattering from aligned flagella samples

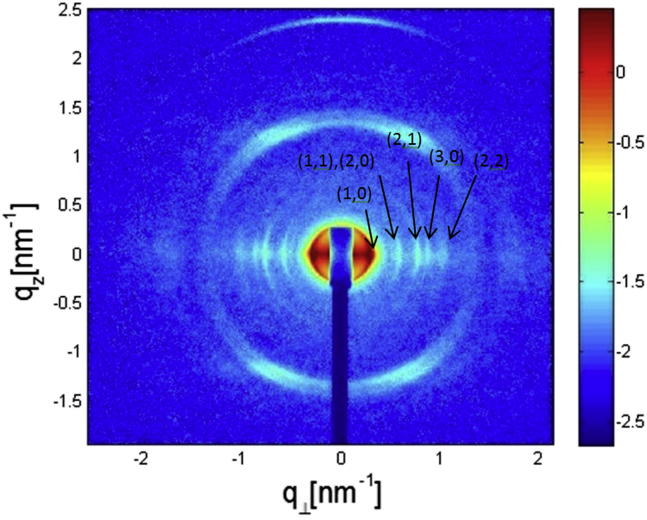
In most of our samples, the solutions were isotropic, as demonstrated in the 2D scattering pattern shown in Fig. 5 A. In a few samples, however, without any special treatment (54, 55, 56), we accidentally obtained 2D scattering images from partially aligned bundles of SJW1660 filaments. These data were taken at the ID02 beamline, European Synchcrotron Radiation Facility (Grenoble, France). The 2D scattering data showed local bundle alignment, owing to the flow of the high bundle concentration in the narrow (∼2 mm) quartz flow-cell capillary (Fig. 9). The 2D structure-factor peaks, associated with lateral packing, were located along the perpendicular axis, $q_{\perp }$. The peak at $1.4{\text{nm}}^{-1}$, attributed to the two-turn helical pitch, was along a diagonal line situated between the vertical $\left(q_z\right)$ and horizontal $\left(q_{\perp }\right)$ axes, and the peak at $2.4{\text{nm}}^{-1}$, which shows the helical axial rise, was along the vertical, $q_z$, axis, as expected.

Figure 9.

2D x-ray scattering image from a partially aligned bundle of straight filaments. The filaments were aligned along their long, z, axis. Using Cartesian coordinates in reciprocal space, the scattering vector, $\overrightarrow{q}$, has three components, $q_x,q_y$, and $q_z$. On a 2D detector, we can observe the $q_z$ component and the $q_{\perp }$ component, which is the projection of the scattering vector on the $\left(q_x,q_y\right)$ plan and is given by $q_{\perp }=\sqrt{q_x^2+q_y^2}$. To see this figure in color, go online.

To calculate the structure factor, $S\left(q_{\perp },q_z\right)$, both the density, $\rho \left(\overrightarrow{r}\right)$, and the local displacement field, $u\left(\overrightarrow{r}\right)$, should be evaluated. $u\left(\overrightarrow{r}\right)$ was calculated from the elastic free energy for fluctuations in the hexagonal phase (13). ${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\left(1/2\right)}$ is directly related to the stability of the hexagonal bundle (in other words, the lattice is unstable when ${\langle {\left|\overrightarrow{u}\right|}^2\rangle }^{\left(1/2\right)}$ diverges).

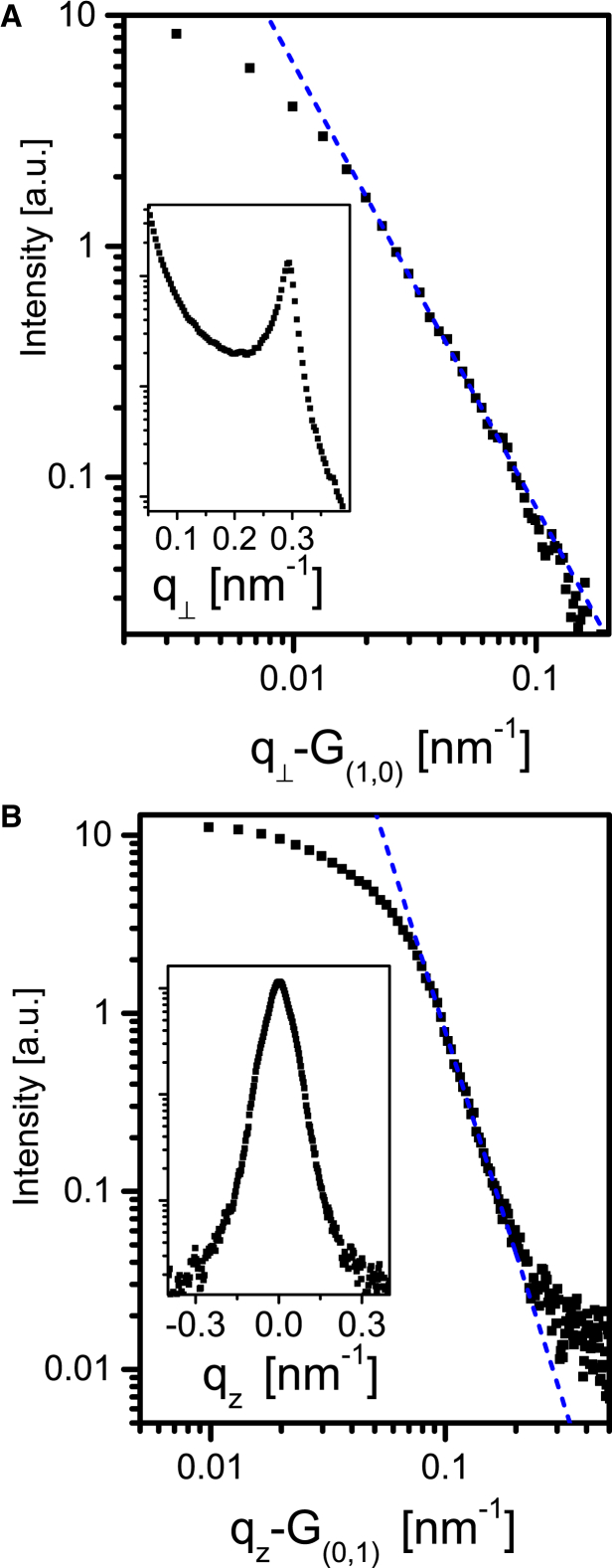
By alignment of the filaments in the flow-cell capillary we obtained 2D scattering data from the hexagonal flagellar bundles that we could compare with the theoretical structure factor calculated for semi-flexible long chains (13). The model, which takes into account the elastic free energy of undulations in a hexagonal phase of chains, predicts that the line shape of the hexagonal structure-factor peaks should decay as power laws in the tails of the peaks. In particular, for the $\left(\mathrm{1,0}\right)$ and $\left(\mathrm{0,1}\right)$ peaks, the data contained enough points to confirm the predicted power lows. Fig. 10 A presents a log-log plot of the $\left(\mathrm{1,0}\right)$ peak along the perpendicular direction, $q_{\perp }$, with a linear fit, using a slope of $-2.0\pm 0.1$, confirming the predicated (13) structure-factor line shape of: $SF\left(q_{\perp }-G_{\left(\mathrm{1,0}\right)},q_z=0\right)\propto q_{\perp }^{-2}$, where $G_{\left(\mathrm{1,0}\right)}$ is the $\left(\mathrm{1,0}\right)$ peak center. Fig. 10 B presents a log-log plot of the $\left(\mathrm{0,1}\right)$ peak along the vertical, $q_z$, axis using a linear fit with a slope of $-4.0\pm 0.1$, confirming the predicted structure-factor line shape of $SF\left(q_{\perp }=0,q_z-G_{\left(\mathrm{0,1}\right)}\right)\propto q_z^{-4}$, where $G_{\left(\mathrm{0,1}\right)}$ is the center of the $\left(\mathrm{0,1}\right)$ peak. Similar structure-factor line shapes can be expected for other semi-flexible filament bundles, including microtubule or neurofilament bundles (57).

Figure 10.

(A) A log-log plot of the (1,0) peak tail (solid symbols) along $q_{\perp }$, showing a linear tail. $G_{\mathrm{1,0}}$ is the peak center. The broken line is a linear fit with a slope of $-2.0\pm 0.1$, as theoretically predicted (13). The inset shows the shape of the peak on a log-linear scale. (B) A log-log plot of the (0,1) peak tail (solid symbols) along $q_z$, averaged over 5 pixels in $q_{\perp }$, showing a linear tail. The center of the peak is at $G_{\mathrm{0,1}}$. The broken line is a linear fit with a slope of $-4.0\pm 0.1$, as theoretically predicted (13). The inset shows the shape of the peak on a log-linear scale. To see this figure in color, go online.

Conclusions

We have used solution SAXS to determine the structure of the L-type straight flagellar filament strain SJW 1660. Using the atomic model of the flagellin subunit, we calculated the scattering curve from the helical lattice of the entire filament and compared with our scattering data. We found that the helix had a diameter of $23.1\pm 0.1\text{nm}$, a two-turn pitch of $5.2\pm 0.1\text{nm}$, and $10.96\pm 0.01$ flagellin subunits/two-turn pitch. Under osmotic stress, the filaments formed 2D hexagonal bundles. To fit the solution x-ray scattering curves of 2D hexagonal bundles, Monte Carlo simulations were used to account for thermal fluctuation effects and the interactions between filaments in the bundles, assuming harmonic pairwise potentials between neighboring filaments with an elastic constant, κ, of $1.2\pm 0.1\text{mN}\cdot {\text{m}}^{-1}$. We determined the distance between the semiflexible flagellar filaments in the bundles as a function of osmotic stress. We could fit the resulting pressure-distance curve to the equation of state of hexagonal bundles of semi-flexible chains like DNA (14), from which the parameters associated with the electrostatic, hydration, and undulation interactions were determined. The undulation energy was associated with a bending stiffness, which corresponds to a chain persistence length of $\approx 700\pm 100\mathit{\mu }\text{m}$. Table 1 summarizes the parameters determined in this study.

We then computed the bundle bulk modulus, the deflection length of the filaments within the bundle, and the mean fluctuations in the nematic director, as well as the variation of these parameters with the hexagonal lattice spacing. Using scaling arguments, we confirmed that the bundle bulk modulus obtained from the Monte Carlo simulations is in agreement with the bulk modulus obtained from the osmotic stress data. Furthermore, the tails of the bundle structure-factor peak line shapes followed the theoretically predicted (13) power-law behavior (for semi-flexible chains) with exponents of $-2$ and $-4$ in the perpendicular and axial directions, respectively. The persistence length of flagellar filaments is similar to that of a microtubule. However, owing to the larger microtubule lumen, osmotic stress deforms the microtubule at low pressures. Higher pressures lead to 2D hexagonal bundles like those of DNA and flagella (14, 17, 18). The stiffness of the flagellar filaments is important for bacteria to swim efficiently using propeller-like beating motions of these filaments.

Author Contributions

D.L., W.S., Z.D., and U.R. designed research; D.L., A.G., T.D., W.S., Z.D., and U.R. performed research; D.L., A.G., T.D., and U.R. contributed analytic tools; D.L., Z.D., and U.R. analyzed data; D.L., Z.D., and U.R. wrote the manuscript.

Editor: Kazuhiro Oiwa.