Abstract
The influence of the membrane on transmembrane proteins is central to a number of biological phenomena, notably the gating of stretch activated ion channels. Conversely, membrane proteins can influence the bilayer, leading to the stabilization of particular membrane shapes, topological changes that occur during vesicle fission and fusion, and shape-dependent protein aggregation. Continuum elastic models of the membrane have been widely used to study protein-membrane interactions. These mathematical approaches produce physically interpretable membrane shapes, energy estimates for the cost of deformation, and a snapshot of the equilibrium configuration. Moreover, elastic models are much less computationally demanding than fully atomistic and coarse-grained simulation methodologies; however, it has been argued that continuum models cannot reproduce the distortions observed in fully atomistic molecular dynamics simulations. We suggest that this failure can be overcome by using chemically and geometrically accurate representations of the protein. Here, we present a fast and reliable hybrid continuum-atomistic model that couples the protein to the membrane. We show that the model is in excellent agreement with fully atomistic simulations of the ion channel gramicidin embedded in a POPC membrane. Our continuum calculations not only reproduce the membrane distortions produced by the channel but also accurately determine the channel’s orientation. Finally, we use our method to investigate the role of membrane bending around the charged voltage sensors of the transient receptor potential cation channel TRPV1. We find that membrane deformation significantly stabilizes the energy of insertion of TRPV1 by exposing charged residues on the S4 segment to solution.
Introduction
During the past decade there have been great advancements in the understanding and modeling of proteins embedded in the membrane (1, 2, 3). One of the first lessons from experiment was that membrane structural and mechanical properties can induce proteins to undergo conformational changes to carry out their function. Early experiments on the antibiotic ion channel forming peptide gramicidin A showed that the thickness of the membrane drives dimerization of the channels (4), whereas later experiments on the mechanosensitive channel MscL (5) showed that in-plane tension and the hydrophobic thickness of the membrane bias the opening and closing of MscL. In addition to the influences of membrane rigidity and thickness, further advancements in experimental techniques have shed light on how membrane shape is coupled to protein function, localization, diffusional properties, and protein-protein interactions (3). For instance, membrane curvature plays a crucial role in the mobility of proteins in the membrane (6). Curvature is thought to affect the probability of alamethicin conductance states (7) and to play an allosteric regulatory role for ion channel function of α-hemolysin (8). Moreover, proteins are not static. Proteins push back on the bilayer, potentially acting as shape remodeling elements that may even influence how cells carry out their biological function (9, 10) For example, protein coats composed of COPI or COPII complexes have been associated with the distinct shapes of spherical vesicles that shuttle between the endoplasmic reticulum and Golgi (11), whereas the homotypic fusion of embedded proteins on opposing membranes is believed to induce endoplasmic reticulum tubular networks (12). Also, there is growing evidence that rows of transmembrane F-ATPase dimers are partially responsible for the complex folds of the cristae (inner mitochondrial membrane) (13, 14), and recent experiments using electron microscopy and electron paramagnetic resonance of endophilin A1 show that vesiculation and tubulation are likely a function of the depth of protein insertion (15).
Parallel to this experimental evidence, several theoretical efforts to study the interaction between transmembrane proteins and their host membranes have also emerged. Fully atomistic simulation (16), coarse-grained models (17), purely analytic continuum approaches (18), and hybrid models (19, 20) have been developed to explain what is observed in experiment and to further explore these interactions beyond the spatial and temporal resolutions of current experimental techniques. A key characteristic of molecular dynamic simulations is the possibility of extracting a lateral pressure profile that describes the nonhomogeneous membrane stress inside a bilayer arising from hydrophobic, electrostatic, and steric interactions (21). The membrane stress profile can then be used to study the mechanical coupling between the protein and the bilayer but results are affected by the level of coarsening in the simulation (22). Protein-driven membrane deformations require system sizes and timescales that are challenging for fully atomistic simulation. Continuum approaches, however, are less computationally demanding and have proven to be an effective tool to study these systems (3). Numerous continuum models for the membrane exist, most of which predict the deformation of the membrane that minimizes the mismatch between the hydrophobic core of the membrane with the hydrophobic belt of amino acids around the protein (2, 23, 24, 25, 26, 27). The models calculate the shape of membrane surfaces and also provide the resulting membrane compression and curvature energies.
Gramicidin-A function in the membrane has been well characterized using experimental techniques (4, 28), and for this reason it serves as a model system for the validation of continuum and computational approaches. This antimicrobial, short peptide forms anchors in either upper and lower monolayers, and individual peptides come together to create a homodimer that spans the membrane. The ion channel is only functional as a dimer, and in thicker membranes, gramicidin must pinch the upper and lower leaflets to dimerize. For this reason, dimer formation is a function of the hydrophobic mismatch between the dimer hydrophobic region and the membrane hydrophobic thickness. Membrane bilayer energetics are related to the changes of the average gramicidin channel lifetimes (26, 29), and this phenomenon provides experimentally measurable evidence of the underlying physical interactions between the membrane and the protein. Many groups have successfully studied these lifetimes using continuum membrane models (23, 24, 25, 27, 30, 31). These theoretical approaches have provided deep insight into the effects of membrane elastic properties and protein boundary conditions on the energetics of the system and the equilibrium shapes of the membrane near the protein. Nevertheless, the majority of these continuum-based studies have represented the protein as an idealized cylinder lacking chemical detail. Consequently these continuum models have failed to reproduce outcomes of detailed atomistic studies (16, 18, 22). This observation has prompted the field to refine the continuum approaches and include atomistic detail (19, 32, 33), geometric effects (34, 35), or both (20, 36). For example, the Weinstein group (20, 36) developed a novel method to account for deformations of the bilayer by noncylindrical shape inclusions. Their model represents the membrane as two uncoupled single sheets. They used a finite difference solver on a Cartesian grid where the membrane is represented by a continuum elastic model but the boundary conditions for the model are directly extracted from the membrane heights at the protein-membrane interface from molecular dynamics (MD) simulations. This coupling to observations from MD proved useful in quantifying the hydrophobic mismatch-driven remodeling of membranes by G protein-coupled receptors (20) and studying the coupling between membrane shape and conformational states of the bacterial leucine transporter (36). Similarly, Haselwandter and co-workers developed sophisticated analytic and numerical treatments of the membrane-protein contact boundary to explore the influence of protein shape on the membrane deformation energies of MscL (34, 35, 37). Those authors used a continuum elastic representation of the membrane together with mixed finite element formulation to solve for the membrane energies. Although currently their methods do not include atomistic detail, their approach yields rapid numerical convergence for complex domains and have successfully been applied to study the relations between the shape of MscL and the supramolecular architecture of MscL lattices and clusters (35).
Here, we present a hybrid continuum-atomistic model that can describe membrane deformations induced by membrane proteins of arbitrary shape. The model uses the structural information from the protein inclusion (19, 32, 38) together with a finite volume, continuum representation of the membrane (39). In contrast to previous models (19, 20, 35), we include protein chemistry and geometrical effects, but our methods are self-consistent and do not require any input from molecular dynamics. The finite volume numeric scheme for describing the membrane shape allows us to distort the grid near the protein interface, resulting in smooth membrane-protein boundaries and a distorted grid that increases the accuracy of our solver with fewer discrete elements than a Cartesian grid. The membrane is allowed to undergo asymmetric bilayer deformations, where the effects of possible redistribution of the membrane lipids near the inclusion are captured by the space-dependent behavior of the elastic moduli (27). The deformation profile is calculated by minimizing the sum of the elastic, electrostatic, and nonpolar energies. Incorporating all three energies provides a more sophisticated and realistic view of global membrane-protein energetics than provided by membrane-only models. In the next section, we derive our continuum model for bilayer deformations in response to the insertion of an integral protein. Then we validate our method by comparing membrane shapes produced by fully atomistic simulations of gramicidin with membrane shapes produced from our continuum calculations. Our model is able to accurately reproduce the membrane height profiles, boundary conditions, and protein orientation seen in our simulations. We discuss how care must be taken when producing average membrane surfaces from MD trajectories with a particular emphasis on periodic boundary effects and fluctuations in protein position. Finally, to illustrate the capability of our model to handle complex protein shapes, we study the membrane-induced deformations by the thermosensitive ion channel, TRPV1. These deformations significantly reduce the electrostatic penalties caused by exposing charged and polar residues to the membrane core.
Materials and Methods
Model description
As in our previous works (19, 32, 38), the total energetic stability of the membrane-protein system is approximated as the following:
| (1) |
where G(me) is the membrane elastic energy due to the shape distortions in the membrane, G(e) is the electrostatic penalty caused by inserting a charged protein into the low-dielectric environment of the membrane, G(np) is the nonpolar energy associated with burying protein surface area in the membrane (hydrophobic effect), and G(o) represents the orientational entropy cost of a protein constrained to only explore a subset of tilted configurations. We calculate the change in free energy of the protein-membrane system with respect to a reference state where the protein is completely in solution, far away from the undistorted (flat) membrane. For transmembrane proteins, the hydrophobic effect tends to be the largest component, and it stabilizes the protein in the membrane through the nonpolar energy G(np). Typically, G(np) is approximately three times larger than the electrostatic interactions G(e), which in turn tend to destabilize the protein; however, these two components can vary significantly depending on the size and charge makeup of the protein in question. Whereas G(np) and G(e) play the major role in determining the insertion energy, the membrane can still deform to accommodate a charged protein leading to an unfavorable elastic penalty G(me) that is approximately an order-of-magnitude smaller than G(np), in many cases. Finally, the orientational entropy G(o) has a very modest effect in stabilizing the protein. In this section, we outline the elements of our theory that allow us to account for arbitrary shape protein inclusions. First, we describe the general geometry of the protein-membrane system, and then we present the theory behind the membrane elasticity G(me) term in Eq. 1. For details on the energetic description on the nonelastic energetic terms (G(e) + G(np) + G(o)), we refer the reader to our previous publications (3, 19, 32, 38, 40) and the Supporting Material.
Geometry: matched and unmatched regions
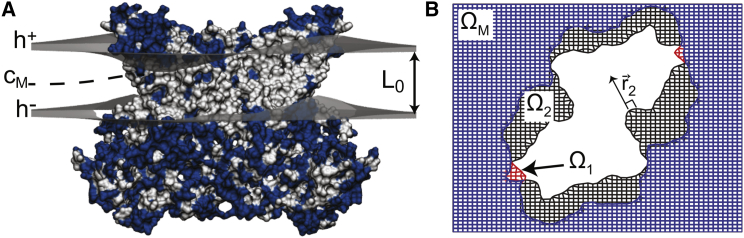
We consider a bilayer membrane made up of two monolayers (leaflets) of identical lipid composition with an embedded protein of arbitrary shape (a graphical representation is given in Fig. 1). Due to the nonuniform cross-sectional area of the protein, the area projections in the x-y plane of the upper and lower leaflets do not coincide (see Fig. 1 B). The projected area in the x-y plane covered by the upper leaflet is denoted Ω+, and it is described by the field variable h+(x,y). Similarly, Ω− is the projected area of the lower leaflet, where the leaflet’s height is given by h−(x,y). Because the leaflets do not coincide at all x-y values, it is useful to characterize the matched and unmatched regions between the projected areas. The region ΩM = Ω+ ∪ Ω− is defined as the matched x-y region, where h+ and h− are well defined. On the other hand, Ω1 = Ω− − ΩM represents the unmatched region in the x-y plane where only the lower leaflet variable h− is well defined, while Ω2 = Ω+ − ΩM represents the unmatched area where only the upper leaflet variable h+ is well defined. Finally, we define the shape variables u± as the difference between the height h± of the upper and lower leaflets with respect to the flat equilibrium height of the membrane h0 = L0/2 as follows:
| (2) |
Figure 1.
Continuum membrane model for proteins of arbitrary shape. (A) Shown here is a wide view of membrane deformation around an embedded membrane protein from the continuum model. The membrane headgroup-tail interfaces are shown as gray surfaces, where h+(x,y) describes the upper leaflet shape and h−(x,y) describes the lower leaflet shape. The membrane dividing (compression) surface CM is shown by the dashed line and the unperturbed membrane thickness is labeled L0. The protein is shown in molecular surface representation. Residues are blue and white for hydrophilic and hydrophobic residues, respectively. (B) Given here is the top-down view of grid used in membrane solver. The blue area denotes the region where the upper and lower leaflets are matched ΩM, meaning u+ = h+ − L0/2 and u− = h− + L0/2 are defined. The red areas near the boundary correspond to the unmatched Ω1 region where only the lower leaflet variable u− is defined. The black areas near the boundary represent the unmatched region Ω2 where only the upper leaflet variable u+ is defined and is the normal vector to the curve describing the protein/upper-monolayer interface. For illustrative purposes, the grid spacing has been enlarged and truncated around the protein. To see this figure in color, go online.
Membrane deformation energy G(me)
As mentioned earlier, G(me) represents the elastic energetic penalty due to membrane deformation in the presence of an inserted protein. We chose to use a continuum theory to describe the shape deformations of the bilayer by considering independent variables for each monolayer (23, 38). For a general configuration (e.g., Fig. 1) where there are two unmatched regions Ω1 and Ω2, we define the total membrane free energy as the sum of the independent contributions of each monolayer, as follows:
| (3) |
where GM(me) is the elastic energy contribution of the two monolayers over the region ΩM where both u+(x,y) and u−(x,y) are defined, G1(me) is the contribution over the unmatched region Ω1 where only u− is defined, and G2(me) is the contribution over unmatched Ω2 where only u+ is defined. The energy GM(me) over the matched region ΩM is given by the following (23):
| (4) |
where we have used the u± definitions in Eq. 2, the “+” refers to the upper monolayer and “−” the lower one, and factors of two are present due to a monolayer versus bilayer description. Kc is the bilayer bending modulus, α is the surface tension parameter, Ka is the bilayer area compression modulus, and KG is the bilayer Gaussian modulus. The variables J0+ and J0− are the spontaneous curvatures of the upper and lower leaflets, respectively. We have defined J0± using the standard sign convention, such that a lipid at equilibrium with a positive spontaneous curvature is one with a large headgroup with a preference for a micelle geometry (41). Above, we have written the compression term as a function of the surface cM(x,y) separating the two leaflets (Fig. 1 A). For more details, we refer the reader to the literature (42, 43, 44, 45) and the Supporting Material accompanying this article.
Minimizing the free energy in Eq. 4 with respect to cM(x,y) yields: cM = (u+ + u−)/2, which corresponds to the midplane of the bilayer (42). Using this last result for cM in the compression term of Eq. 4 recovers the liquid crystal-based energy expression proposed by Huang (23) and used in our previous works (19, 32, 38).
The functional forms of G1(me) and G2(me) over the unmatched regions are analogous to the expression Eq. 4, but each term only has contributions from a single leaflet. Where the in-plane areas of the inserted protein do not match in the upper and lower leaflets there are projected regions where the bilayer midplane does not exist. For such scenarios, the lipids in opposing monolayers will still be compressed against a dividing surface c(x,y), which is constrained by the protein’s geometry. We define the field variables c1(x,y) and c2(x,y) as the dividing (compression) surface over regions Ω1 (upper monolayer) and Ω2 (lower monolayer), respectively. The functions c1(x,y) and c2(x,y) are protein specific, but for transmembrane proteins spanning both leaflets, where the mismatched region is small compared to the total protein surface area projection (i.e., gramicidin, TRPV1), we propose an approximation, as follows:
| (5) |
where is the boundary condition of the field variable u+ enforced at the contact curve between the upper leaflet and the protein. Similarly is the boundary condition of u− at the contact curve between the lower leaflet and protein. Equation 5 assumes that the monolayer dividing surfaces c1 and c2 are not heavily distorted with respect to cM and can be approximated by extending the bilayer midplane cM = (u+ + u−)/2 by using the boundary values in regions where either the upper or lower leaflets are not defined. Equation 5 ensures that the resulting surface dividing the two monolayers is continuous in space. For more detail, please refer to the Supporting Material.
We can write the free energy contribution G1(me) over region Ω1, as follows:
| (6) |
and the contribution G2(me) over region Ω2, as follows:
| (7) |
As before, we have assumed that both monolayers have equal elastic moduli, and we have expressed the energy contributions in terms of bilayer moduli to be consistent with Eq. 4.
Membrane equilibrium configurations
The membrane equilibrium shape equations associated with the elastic energy G(me) are determined by minimization of (4), (5), (6), (7) resulting in the following Euler-Lagrange equations:
| (8) |
| (9) |
| (10) |
| (11) |
where we have made use of Eq. 5 and defined the following:
| (12) |
Under the assumption of constant or vanishing spontaneous curvatures J0±, we recover the equations of our earlier work (19, 32, 38). Note that Gaussian terms do not appear in the Euler-Lagrange equations (8), (9), (10), (11). The Gaussian curvature terms can be transformed into boundary integrals by means of the divergence theorem (46, 47) and consequently do not contribute to the shape equations of the system.
The equilibrium equations (8), (9), (10), (11) can be readily solved for u+ and u− given a suitable set of boundary conditions. First, it is physically reasonable to assume that far away from the protein the perturbation effects on the membrane deformations vanish. As the perturbations vanish, the membrane asymptotically approaches its unstressed equilibrium configuration, as follows:
| (13) |
Meanwhile, at the protein-membrane boundary, we impose the following fixed set of boundary conditions:
| (14) |
where is the normal vector to the curve describing the protein/lower-monolayer interface and is the corresponding vector at the protein/upper-monolayer interface (see Fig. 2). This last set of conditions in Eq. 14 depends on the geometry and atomic structure of the protein, and for this reason is optimized by an iterative procedure that attempts to minimum the total energy of the system, GT (32, 38). Details on the minimization procedure are in the next section.
Figure 2.
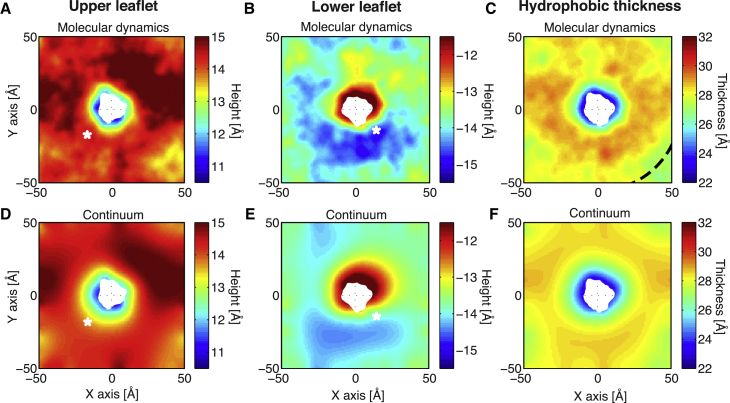
Comparison of protein-induced membrane deformations from molecular dynamics and continuum elasticity. (A–C) Shown here are the average membrane height profiles for the upper leaflet (A), lower leaflet (B), and hydrophobic thickness (C) from one 250-ns MD simulation of gramicidin in a POPC bilayer. (D)–(F) show the corresponding continuum membrane surfaces. For the continuum calculations (D)–(F), we used boundary conditions at the protein-membrane boundary and at the edges of the box that were extracted from the MD data in (A)–(C). The region where the membrane is compressed near the protein (compression ring) can be clearly seen in the hydrophobic mismatch panels of both the MD (C) and continuum calculations (F). Dashed arc line in (C) shows a 55 Å radial distance measured from the center of the protein. White asterisks show the location of maximum difference between leaflet heights calculated using simulation (A) and (B) when compared to continuum (D) and (E). For reference, in Fig. S8 we show the gramicidin-induced membrane deformations calculated using our hybrid-atomistic model without any input from MD. To see this figure in color, go online.
Although we have chosen to use the fixed boundary conditions given in Eq. 14, there are other alternative conditions that still satisfy (8), (9), (10), (11). In the Supporting Material, we address in detail the treatment of boundary conditions for elastic continuum models and the proposed version of a hybrid continuum-atomistic model.
Minimization of the total energy GT
In 2013, Lee et al. (18) suggested that elastic continuum descriptions fail to reproduce the membrane deformations near the protein boundary observed in MD simulations. The disparity between MD and continuum methods has been argued to result from the lack of explicit chemical and geometrical effects of the inserted protein (3, 18, 20). The contact conditions between membrane and protein will have a large effect not only on the membrane deformation energy but also on nonpolar and electrostatic penalties. Therefore, determining the minimum energy of the system GT (Eq. 1) requires a thoughtful choice of the prescribed boundary conditions at the protein-membrane interface. Our hybrid-continuum approach is equipped to determine the correct boundary conditions. We search for the optimal set of fixed boundary conditions Eq. 14 that minimize the total energy GT and consequently play the key role in coupling the elastic and nonelastic effects (see Eq. 1). To find the optimal value of the displacement boundary conditions and , we use a simulated annealing algorithm (48), where an iterative search is performed over all displacement parameters to obtain the membrane shape that minimizes GT. The displacement boundary conditions are further optimized using Powell’s method (49), then the slope boundary conditions are optimized using a Nelder-Mead simplex method (50). The Powell and Nelder-Mead optimizations are performed one more time to ensure convergence. We express the variables and in Fourier series representation of order n (three or higher) where the search is over the (2n + 1) amplitude coefficients. The upper and lower slope variables, S+ and S−, are set as proportional to the upper and lower displacement boundary conditions, as follows:
| (15) |
where α+ and α− are the scalar parameters that are optimized. This simplification reduces the parameter space and the search time. More information can be found in Callenberg (48).
Identifying the membrane-protein contact curve
Within the dual monolayer framework, there are two contact curves—one for the upper leaflet and one for the lower leaflet. These curves represent the lipid excluded surface, which is the surface of closest contact between a spherical lipid probe and the protein atoms (51). To identify these curves, we first erect a flat Cartesian grid for the upper and lower leaflets, and then use level set theory to move grid points near the membrane-protein surface onto the boundary curve representing the lipid excluded surface (39). The mathematical details on how to obtain the distorted grid representing the monolayer surfaces with geometrically accurate boundary curves can be found in Wolgemuth and Zajac (39).
For both upper and lower leaflets, we define the smooth curve C(x,y) that represents the lipid-excluded surface. Next, we find the level set function L(x,y) (isocontour) rendering the signed minimum distance from every coordinate point (i,j) in the Cartesian grid to the curve C(x,y). Therefore, the interface C(x,y) is represented implicitly by the zero of the level set function L(x,y) = 0 and the unit normal to the curve C(x,y) is given by the following:
| (16) |
Fig. 1 shows the unit vector corresponding to the upper leaflet. Next, from the distance map L(x,y) we identify the set B of all Cartesian grid points (iB, jB) within one Cartesian grid-edge length gl of the curve C as follows:
| (17) |
The collection of points in set B define the curve that most closely describes each leaflet boundary curve in a Cartesian grid. Finally, we distort the Cartesian grid points at the boundary by spatially moving all points in set B from their initial position onto the curve C(x,y) using the following transformation:
| (18) |
where the new position vector describes the location of the distorted grid points representing the protein-membrane interface. In Eq. 18 the function L(iB, jB) tells how far the points (iB, jB) in the regular Cartesian grid are from the curve C, while tells the direction in which the position vector needs to be displaced. One of the convenient features of this procedure is that the distorted grid (see Fig. 1) retains four-point connectivity and results in smooth boundaries (39). As with all numeric solutions of PDEs, an accurate description of the boundary is important for faithfully representing the shape of the system and properly applying boundary conditions. Once the boundaries are established, we solve the shape equations ((8), (9), (10), (11)) using a finite volume method. Details of the numerical procedure can be found in Wolgemuth and Zajac (39).
Continuum model parameters
Here, we only consider homogeneous POPC membrane systems, and we have summarized the elastic and continuum parameters used throughout our calculations in Table 1. We assume the area compression modulus in the bulk for the upper and lower monolayers is half of the reported area compression modulus of the bilayer (Ka,B). This condition is justified over the bulk region ΩM if we assume a constant and equal density of lipids per leaflet (see Supporting Material). We point out that although constant elastic rigidity is commonly used in continuum elastic models of the membrane (3), this assumption likely breaks down near the protein interface (18, 27). From a physical point of view, one can expect spatial changes of the elastic constants due to limitation on the mobility and packing of the lipid molecules near the inclusion (shell hardening) (17, 22, 25, 26, 27). For this reason, it has been previously suggested that the common assumption of constant elastic parameters might be an oversimplification at the shorter length scales of a protein-membrane system (25). Partenskii and Jordan (27) implemented a model where values of the elastic constants near the inclusion are larger than the values in the bulk. In their work, this shell hardening effect has a decay length (∼15 Å) comparable to the width of lipid molecules. In their work the bending and compression moduli are both increased near the protein, but the authors found that only the perturbation of the compression bilayer constant Ka has a significant effect on the membrane energy. Comparison to gramicidin experiments showed that the compression modulus is ∼5 times larger at the protein-membrane boundary than in the bulk (Ka,B) (27). In this model, we have incorporated shell hardening through a spatially dependent compression modulus that is greatest at the protein-membrane boundary, and exponentially decays to the bulk monolayer value as distance increases. Hardening primarily affects the first and second lipid shells surrounding the protein (for detail, see Supporting Material). We point out that in this model the function can be arbitrary, and this does not change the governing Euler-Lagrange equations (8), (9), (10), (11). As in our previous work (32), we found that the surface tension (α) does not contribute significantly to the energy and for this reason we assume it to be a constant over all space. Finally, the last integral term in Eq. 4 is the Gaussian curvature energy contribution. In our problem, the membrane does not change topology between the initially flat surface and final distorted surface because both states include the protein hole. In addition to topological changes, the Gaussian term can be formally shown to contribute only through the boundary effects (24, 47, 52, 53). When using fixed boundary conditions, as we do here, the equilibrium shape is independent of the Gaussian term, but the total energy GT of any given configuration still depends on the Gaussian curvature. Consequently, this term will affect the search for the optimal equilibrium shape as described in Minimization of the Total Energy GT. We have chosen to use Gaussian modulus KG values from simulation (54, 55), which are in reasonable agreement with reported experimental values. Also, in writing our energies we have assumed the Gaussian monolayer modulus to be half of the measured bilayer modulus KG. This assumption is justified in our calculation, given that we use zero spontaneous curvature for each monolayer. In general, the relation between the monolayer and bilayer Gaussian curvature moduli has a correction term involving the monolayer spontaneous curvature and the position of the monolayer pivotal plane (41, 56).
Table 1.
Elastic Membrane Material Properties Specific to POPC and Prescribed Parameters for All Continuum Calculations
| Parameters | Values | Reference |
|---|---|---|
| Membrane thickness (L0) | 28.5 Å | Kim et al. (16) |
| Surface tension (α) | 3.00 × 10−13 N/Å | Latorraca et al. (32) |
| Bending modulus (KC) | 8.5 × 10−10 NÅ | Kim et al. (16) |
| Gaussian modulus (KG) | ∼−0.9 × Kc | Hu et al. (54) |
| Shell hardening factora (Θ) | ∼4.27 | Partenskii and Jordan (27) |
| Area compression modulus (bulk)a (Ka,B) | 2.13 × 10−11 N/Å | Latorraca et al. (32) |
| Protein dielectric (εp) | 2.0 | Latorraca et al. (32) |
| Membrane dielectric (εhc) | 2.0 | Latorraca et al. (32) |
| Headgroup dielectric (εhg) | 80.0 | Latorraca et al. (32) |
| SASA prefactor for nonpolar energy (a) | 0.028 kcal/(molÅ2) | Sitkoff et al. (91) |
We have used nonuniform values of the compression modulus Ka (see Supporting Material). For the remaining parameters necessary for the electrostatic calculations (i.e., electrostatic grid dimensions), we use the same values presented in our previous publication (32).
We point out that our model, like any continuum membrane representation, is limited by the phenomenological nature of the parameters describing the membrane mechanical properties (41). Experiments have shown that there are still uncertainties regarding the specific values of mechanical parameters (57, 58), and the MD reported values do not always agree with experiment (59, 60). In this work, we constrain ourselves to a smectic liquid-crystal model (23) where the mechanical parameters (Table 1) have been picked from the gramicidin-POPC literature (16, 18), keeping in mind that our goal is a comparison between our hybrid continuum model and MD simulations.
Simulation methods
Simulations were prepared using the NMR gramicidin structure (PDB: 1JNO) (61). With CHARMM-GUI (62), the structure was inserted into a 97 × 97 Å2 POPC membrane, and solvated with TIP3P water molecules (63), and 150 mM KCl. The total system size was 38,876 atoms. The system was run in the software NAMD (http://www.ks.uiuc.edu/Research/namd/) (64) using the CHARMM36 lipid force field (http://mackerell.umaryland.edu/charmm_ff.shtml) (65) with an anisotropic Nosé-Hoover-Langevin barostat and Langevin thermostat. Equilibration and production simulations were carried out using the default parameters provided by CHARMM-GUI (http://www.charmm-gui.org/). Two independent gramicidin simulations were separately prepared and run for 250 ns each, and another membrane-only simulation was prepared and run for 100 ns.
The hydrophobic interfaces of the upper and lower leaflets were averaged over time to obtain a single MD-generated membrane surface to compare with the continuum predictions. The goal of such averaging is to provide a physically accurate representation of the equilibrium shape of the membrane, but we note that the average of a solution set is not necessarily a solution itself. That is, averaging the membrane surface may produce physically unrealistic shapes. To reduce possible artifacts from averaging, we used an interpolation method. When comparing membrane surfaces between MD and our continuum model, each frame from MD was aligned to the initial snapshot by centering the protein. Then the upper and lower surfaces were interpolated from the C2 carbon atoms of the POPC acyl chains (66) using a cubic spline method. After the alignment, the upper and lower surfaces were averaged over all frames. When comparing the predicted boundary conditions of our continuum model to MD, the protein was further aligned by rotating in the x-y plane to minimize the root mean square deviation of the protein backbone. Because the continuum model assumes the membrane lies in the x-y plane, the simulations were only allowed to rotate about the z axis during the alignment. Other rotations were not allowed because this would rotate the membrane out of the x-y plane. Additional details are provided in the Supporting Material.
Results and Discussion
Gramicidin induces asymmetric deformations
We first applied our model to study the membrane deformations created around the antibacterial ion channel gramicidin. This protein is often used to explore protein-membrane interactions, because its ability to conduct ions is intimately connected to the properties of the membrane (4), and experimental studies have demonstrated membrane thinning/thickening at the protein interface (28). Continuum elastic models have proven useful in predicting the energetics of gramicidin induced deformations and using these energies to accurately estimate open channel lifetimes (18, 26, 67). All of these models use a simplified cylindrical description of gramicidin leading to radially symmetric membrane distortions. In 2012, Kim et al. (16) rigorously compared the continuum distortions to those observed from all-atom molecular dynamics simulations. Interestingly, despite their reliability in determining channel function, the authors noted that simplified continuum elastic models fail to reproduce the deformations observed in simulation (16).
We chose to revisit this analysis using a more accurate treatment of the channel chemistry and geometry to determine if these features could overcome the deficiencies inherent in simpler continuum models. We started by running two independent simulations of gramicidin in a 100 × 100 Å2 membrane patch of POPC membrane for 250 ns each (500 ns total). The average membrane deformation profiles from the two MD simulations are shown in Fig. 2, A–C. Similar to previous studies (16, 22), we observe highly nonsymmetric deflections in the upper and lower leaflets with respect to the bilayer midplane (Fig. 2, A and B). The greatest distortion in the upper leaflet is the blue region adjacent to the protein (Fig. 2 A), whereas the greatest distortion in the lower leaflet is the red region adjacent to the protein but on the opposite side (Fig. 2 B). Both distortions result in membrane compression as summarized in the plot of the membrane hydrophobic thickness (Fig. 2 C). The bulk, equilibrium POPC thickness is 28.5 Å, and at the protein the membrane is 22 Å whereas along the outer edge (∼50 Å away) the membrane thickness is between 27 and 30 Å. The thickness at the middle of the simulation box edges is ∼1 Å thicker than the equilibrium value indicating that it has not returned to equilibrium. However, in the corners the membrane is quite close to the bulk value. This observation indicates that care must be taken when interpreting protein-membrane coupling on small patches of membrane where the boundary conditions of the box enter, as has been highlighted previously (32, 68).
As a first test of our continuum model, we asked whether it could reproduce the membrane surfaces observed in fully atomistic simulation if we extracted the boundary conditions at the membrane-protein interface and the outer boundary directly from the simulation. Thus, we focused only on the elastic component of our model (G(me)), ignoring for now the electrostatic (G(e)) and nonpolar (G(np)) contributions. For consistency between the MD calculations and our continuum approach, we calculated the most probable protein orientation from MD, and then used the same orientation in our continuum calculations. To obtain the boundary conditions, we first identified the boundary curve of a single snapshot from the MD simulations using the level set method described earlier. The displacements at the boundaries were found by interpolation from the MD membrane surfaces, and the slope boundary conditions were calculated by taking the dot product of the surface gradient and the normal of the boundary. The corresponding continuum surfaces are plotted in Fig. 2, D, E, and F, under their respective averaged surfaces from MD (Fig. 2). In the solution domain, the continuum membrane surfaces match remarkably well with the surfaces seen in MD, indicating that continuum elastic models can accurately describe membrane distortions on protein-sized length scales. Both methods predict very similar damped oscillating profiles where the membrane first pinches down by ∼4 Å near the protein forming a ring where the membrane is compressed (compression ring), then the membrane expands to overshoot the bulk value before finally returning to equilibrium values at the corners of the simulation box (Fig. 2). The upper leaflet height in Fig. 2 D differs by <1.0 Å with the MD results (Fig. 2 A) over the entire surface, and the mean absolute deviation between both surfaces is only 0.2 Å. Similarly, the continuum and MD surfaces for the lower leaflet are at most 1.5 Å different from each other with a mean absolute deviation of 0.3 Å. The most notable difference between the continuum calculations and the MD simulations is the size of the compression ring around the protein (Fig. 2, C and F). The ring extends radial from the center of the protein for 25–30 Å in the continuum calculations, but only 20–25 Å in the MD simulations.
It has been suggested that the bilayer becomes harder near embedded proteins (27), and in Fig. 2, we used a variable compression modulus with a hardening factor Θ = 4.27 (taken from Partenskii and Jordan (27)) to capture this effect. We found that this hardening factor is essential for modulating the radial extent of the membrane compression ring. In the absence of hardening (Θ = 1), gramicidin-induced distortions extend over a larger ring (30–35 Å) (data not shown), which results in a poorer match with what is observed in MD. Increasing the hardening factor beyond 4.27 produces an even better match to MD, but the deformation energy increases significantly and there is no experimental estimate of Θ for the gramicidin-POPC system.
Continuum elastic models readily provide estimates of the membrane distortion energy, whereas MD simulations do not, and extracting boundary conditions from MD to solve continuum elasticity equations to determine deformation energies has been used previously (13, 20). The gramicidin membrane configuration in Fig. 2 produces a POPC membrane distortion energy of 10.4 kcal/mol. The energy is equally shared by the upper and lower leaflets, with the compression mode accounting for most of the energetic penalty (49%), followed by the mean curvature effects (33%) and Gaussian curvature effects (17%). As in previous studies, we find that the surface tension has a negligible contribution (<1%) (18, 19, 23, 25, 27). Returning to the full energetic calculation of our implicit membrane model, the elastic deformation (∼10 kcal/mol) and electrostatic component (∼25 kcal/mol) are unfavorable, but overall gramicidin is stabilized in the membrane by the nonpolar energy (∼−83 kcal/mol), which arises from the significant fraction of buried protein surface area.
Predicting protein orientation in the membrane
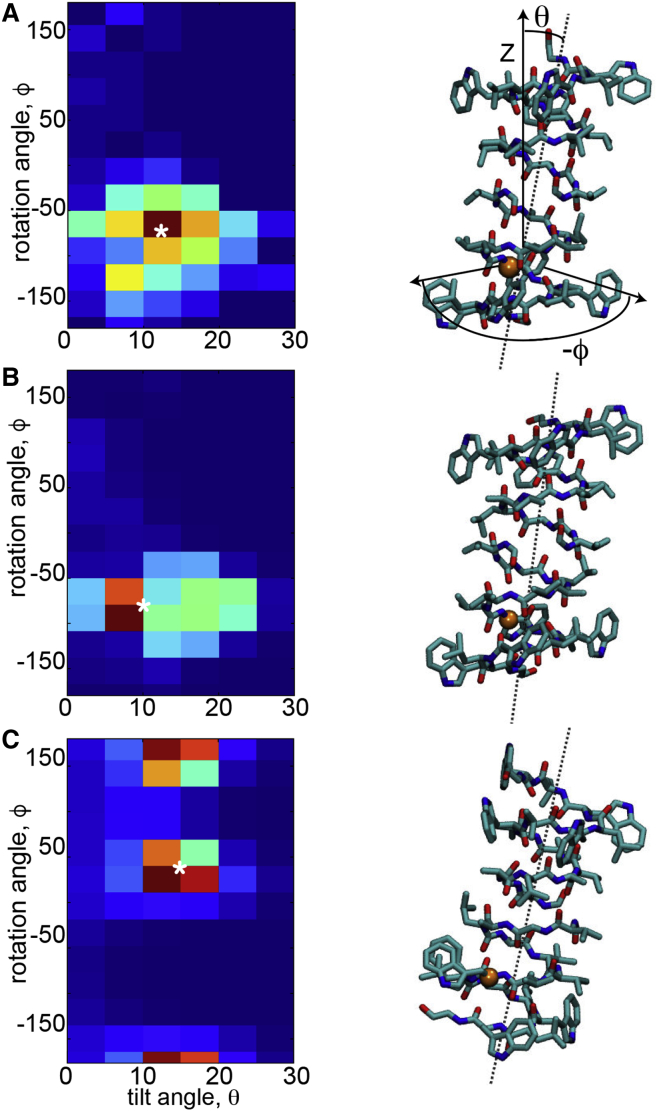
Next, we wanted to determine if we could use our full continuum energy model to predict the orientation of gramicidin in the membrane. The full model (Eq. 1) includes electrostatic and nonpolar contributions in addition to the membrane deformation energy. The boundary conditions at the membrane-protein interface are extracted from the protein structure using our proposed methodology in Minimization of the Total Energy GT. Starting with the long axis of the protein aligned with the z axis and the protein center of mass in the middle of the membrane, we carried out a search over the upper and lower membrane-protein contact curves to determine the optimal membrane deformation profile that minimizes the total energy. We applied flat outer boundary conditions on a 150 × 150 Å2 outer boundary, far enough from the protein that our MD simulations predicted that the membrane should return to its equilibrium value. Once the optimal membrane contact curve and energy were determined for this one orientation, we scanned through a series of tilt and rotation angles and identified the minimum energy membrane configuration for each orientation, E(θ, ρ). Tilting of gramicidin breaks the bilayer symmetry about the midplane, leading to different membrane-protein interfaces in the upper and lower leaflets. Our model and numeric scheme is equipped to handle symmetry breaking that arises from complex protein shape as well as protein orientation in the membrane caused by tilt. With these energies, we created a two-dimensional pseudo-histogram of gramicidin orientation, H(θ, ρ), using the relation: H(θ, ρ) = exp(−E(θ, ρ)/kBT). The map generated by our continuum model provides good agreement with the histogram obtained from simulation (Fig. 3, A and B). Additionally, the minimum energy orientation matches remarkably well with the average orientation seen in simulation (Fig. 3, A and B). The model predicts an optimal orientation of 10° tilt and 77° rotation, while the MD predicts 12.5° tilt and 62° rotation. The orientational entropy term G(o) slightly stabilizes the predicted tilted configuration by ∼1 kcal/mol with respect to the vertical configuration, which is expected given the increase in accessible states for moving off axis. For both the MD and the hybrid continuum-atomistic model, the protein orients to maximally expose the hydrophilic indole nitrogens on the tryptophan residues. Because the POPC bilayer is thicker than gramicidin, the membrane must also pinch to expose these hydrophilic groups. We hypothesized, therefore, that this orientation would no longer be the most energetically favorable if the membrane was very stiff. To test this idea, we carried out the same search with a nondeformable membrane. The predicted orientation no longer matches MD or our deformable membrane model (Fig. 3, C), demonstrating that membrane deformation is necessary to predict protein orientation in the membrane in this instance.
Figure 3.
The continuum model predicts the correct protein orientation in the membrane. Given here is the orientation of gramicidin in the membrane predicted from MD simulations (A), our hybrid continuum-atomistic model (Eq. 1) (B), and the continuum model without membrane bending (C). In all panels, the heat map on the left shows the probability of finding gramicidin at specific tilt θ and rotation ρ-angles, where θ is the angle between the z axis and the long axis of the helix, and ρ corresponds to rotation about the long axis of the channel. To define the rotation ρ, we use as reference points the projection of the z axis together with the vector formed by the helical principal axis and the Cα position in residue W9 (16). The most probable configuration has been marked with a white asterisk (∗). The right panel shows the protein configuration corresponding to the most probable configuration, as well as the pictorial description of θ and ρ. Probabilities were obtained by calculating the energy at each orientation, then using Boltzmann weighting to convert the energies to probabilities. To see this figure in color, go online.
Predicting the membrane-protein contact curve
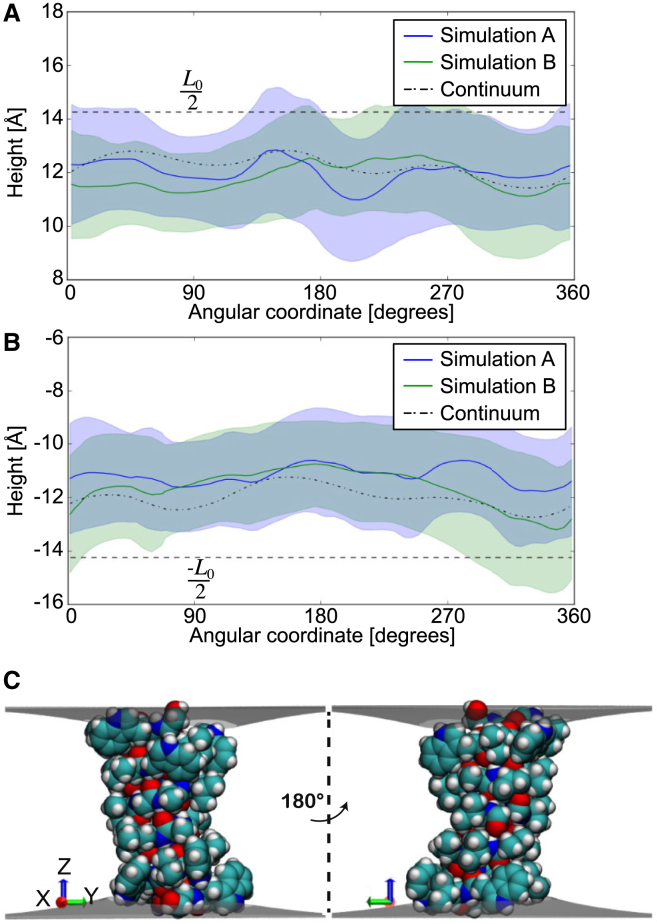
Next, we wanted to determine if our hybrid continuum-atomistic model (Eq. 1) could actually predict the shape of the membrane-protein contact curve observed in the MD simulations. First, we investigated our two independent MD simulations to determine if the contact curve is characterized by a single contour with very little variation, or if it fluctuates wildly, which would be impossible for our deterministic model to reproduce. Individually averaging the results from both simulations showed pronounced membrane pinching at the contact interface by as much as 2 Å at the upper leaflet and 2 Å at the lower leaflet (solid green and blue curves compared to the constant dashed line; Fig. 4), but there are subtle differences between the simulations because the membrane thickness varied in the azimuthal direction and it showed fluctuations over time. Calculating the SD of the contact curve in time revealed that it fluctuates up to 4 Å in both leaflets (blue and green shaded intervals in Fig. 4). The variance in the height arises from changes in side-chain rotamer conformation, changes in protein tilt and rotation angle, and thermal motion of the membrane-protein system. Thus, the average membrane surfaces and contact curves result from a superposition of many different protein configurations. With this in mind, we identified 32 snapshots from our MD simulations that populated the most probable bin in Fig. 3 A, and we used our continuum model (Eq. 1) together with the protein structure to calculate the optimal membrane boundary for each snapshot configuration. The average membrane-protein contact curves for the upper and lower boundary from these continuum calculations are shown in Fig. 4 where we see good agreement with both MD simulations (dash/dotted line). Moreover, Fig. 4 C shows one of the continuum solutions revealing that membrane-anchoring tryptophans are the primary determinants of the membrane height around the protein. The membrane thins to expose these nitrogens to the high dielectric environment of the headgroup region, in agreement with our simulations and previous work (16). We observe the indole nitrogen creating transient hydrogen bonds with the headgroup phosphate or backbone carbonyls of the adjacent lipids, whereas the tryptophan ring interacts with the positively charged choline through cation-π interactions.
Figure 4.
Comparison of protein-membrane boundary distortions from the continuum model and MD simulation. Given here are the membrane height values at the protein-membrane boundary for the upper leaflet (A) and lower leaflet (B). The dotted line corresponds to the average solution calculated from 32 protein snapshots by our continuum model. The blue and green solid lines are the average membrane height values from the two independent 250 ns MD simulations. The blue- and green-shaded regions correspond to MD solutions within 1 SD and the overlap between the blue- and green-shaded region has been highlighted in a darker color. The equilibrium height of the undeformed monolayer L0/2 is shown by dashed lines. (C) Shown here are the membrane surface profiles calculated from the model. The angular coordinate in (A) and (B) are with respect to the x axis shown here. The protein-membrane boundaries align with the indole nitrogens of the tryptophans and the hydroxyl of the terminal ethanolamine. The right view corresponds to a 180° rotation about the z axis. To see this figure in color, go online.
Elasticity equations require two boundary conditions, and here we impose membrane height and membrane slope conditions. Earlier gramicidin studies that used similar boundary conditions found that it was necessary to impose a zero slope on the surface to match experimental results (18, 25, 31), and later studies with shell hardening revealed that a zero slope condition was no longer needed to match experiment (27). Here, we optimized for the slope that minimizes the total energy, and we found that the most favorable contact slope is moderately positive (but not equal to zero) with a slight variability along the boundary (see Fig. S6).
TRPV1 residues bend the membrane
The numeric advances described here let us explore membrane distortions around embedded proteins with complex shapes, and the continuum nature of our model scales well to large systems. Thus, we used our approach to predict the membrane deformations around TRPV1, a large nonselective cation channel with four voltage-sensor-like domains that harbor basic residues buried in the membrane interface. Previously, we used our software APBSmem (https://apbsmem.sourceforge.io/) to scan through all multipass membrane proteins of known structure and calculate the electrostatic energy (Ge) associated with embedding the protein in a flat, low-dielectric lipidlike environment (40). We found that the closed, capsaicin-bound (partially open), and RTX-bound (fully open) structures returned >10 residues that incurred large electrostatic penalties for being in or near the membrane (Fig. 5 A). Examination of the structures revealed that many of these residues were near the hydrophobic interface, but buried in the membrane according to the hydrophobic thickness estimated by the Orientations of Proteins in the Membrane database (69). We reasoned that minor distortions in the membrane may expose these charged and polar residues to water relieving the electrostatic penalty, and we also hypothesized that these membrane deformations may be coupled to the function of the channel. We used our continuum model (Eq. 1) and searched for the membrane configuration that minimized the total energy of the system. As reasoned, the optimal solution exhibits large deformations around the protein, and these deformations significantly reduce the electrostatic insertion penalty of the high energy residues (Fig. 5, B and C). The membrane deformation energies induced by the closed, partially open, and fully open structures are 38, 52, and 64 kcal/mol, respectively. These energies indicate that as the TRPV1 channel opens, it generates larger membrane deformations. K464 and R491 are two membrane-anchoring residues that are partially responsible for these deformations. In an undeformed membrane, K464 and R491 cause very large 12.8 and 19.9 kcal/mol electrostatic penalties in the open structure, respectively, but these penalties are almost completely relieved when the membrane is allowed to bend. It is tempting to speculate that these residues are involved in thermosensitivity or voltage sensing, and their displacement may bias the opening of the channel. However, more detailed experimental analysis on the mechanistic role of K464 and R591 is required.
Figure 5.
The hybrid continuum-atomistic model predicts that TRPV1 deforms the membrane. (A) Shown here are the electrostatic membrane insertion penalties for membrane-exposed residues when the membrane is represented as a rigid slab. Hydrophobic interfaces are shown as transparent surfaces. Residues are colored by electrostatic insertion penalty. We calculate this penalty as the electrostatic energy of the protein in membrane minus the electrostatic energy of the protein in solution. (B) Electrostatic insertion penalty after the membrane is allowed to deform. In (A) and (B), only residues with a penalty >1 kcal/mol are shown. (C) Given here is the reduction in electrostatic penalty after the membrane is allowed to deform. This is the penalty of (A) subtracted from the penalty in (B). For clarity, only residues with reductions >1 kcal/mol are shown. Tyr-511 and TM helices are labeled. To see this figure in color, go online.
Conclusions
Although continuum elasticity theory has been successful at reproducing the long-wavelength equilibrium shapes of membrane structures (41), whether such models can accurately describe membrane deformations at the Ångström length scale has been debated. A 2013 comparison to fully atomistic MD simulations suggests that continuum models fail to reproduce key features observed in the simulations (18). Here, we presented a self-consistent continuum approach to model protein-mediated distortions in the bilayer, which overcomes much of the shortcomings of simpler continuum treatments. Our model builds off of our earlier work in which we accurately represent the protein at the atomic level and incorporates a biophysically meaningful energy model of the system that includes electrostatic, nonpolar, and membrane elastic energies (19, 32, 38). Here, we have significantly advanced our geometric handling of the protein shape and elasticity calculations by employing a finite volume solver (39) to address insertions of arbitrary shape. The membrane calculations are performed in a distorted grid that is mapped to the membrane-protein boundary, which increases the fidelity of our solver with lower grid densities than a strictly Cartesian grid. We show that the method matches results from MD simulations with high accuracy, and our approach highlights how the boundary conditions of the elastic solver preserve the chemical information of the protein. Nonetheless, the method is computationally fast because it relies on implicit energy models at all stages. Thus, we assert that continuum membrane models have the potential to provide deep insight into membrane-protein interactions involved in a wide range of biological phenomena with high spatial resolution, but with minimal computational overhead.
We validate our continuum model by comparing to MD simulations of gramicidin in a POPC membrane. First, we test our continuum membrane description by only using our elastic solver and boundary conditions extracted from MD. As seen in Fig. 2, the continuum predictions nicely match MD membrane deformation profiles and the extent of the membrane compression ring around gramicidin. We then move on to make predictions for gramicidin orientation and depth of penetration using the full energy model given by Eq. 1 without any input from MD. Our continuum model agrees with the atomistic predictions for membrane contact heights and tilt as shown in Figs. 3 and 4. We show that a flat-slab representation of the membrane fails to determine the preferred protein orientation, indicating that membrane deformation plays a crucial role in determining the final equilibrium configuration. Finally, as an application of our self-consistent continuum model, we study POPC membrane deformations induced by the transient receptor potential cation channel TRPV1. We found that allowing the membrane to deform greatly reduces the electrostatic penalty of charged residues near the headgroup-tail interfaces of the membrane. Our calculations further showed that TRPV1-charged residues generate much larger deformations in the open and partially open structures than the closed structure. Based on this observation, we speculate that the same residues involved in the membrane distortions could be involved in thermosensitivity or voltage sensing. More detailed experimental analysis is required to uncover the mechanistic role of these residues.
When comparing to continuum descriptions of the membrane, the MD surface profiles require careful analysis of periodic boundary effects (32, 68) and spatial fluctuations of the protein orientation and side-chain movements. Our MD simulations of the gramicidin channel in a 100 × 100 Å2 patch reveal that the membrane is not fully relaxed at the edges (Fig. 2). If one desires to match MD simulation results, continuum elastic membrane models should explicitly impose similar far-field conditions. Although gramicidin has been a test case for exploring continuum models of the membrane and comparing these solutions to MD, we believe that it is likely one of the harder systems to match due to the small size of the protein, which allows it to change its orientation in the membrane on a fast timescale resulting in sizable fluctuations in the protein-membrane contours (Fig. 4). Care must be taken when averaging the membrane surfaces from the MD simulations to avoid unphysical artifacts (see Supporting Material), and our experience suggests that comparison between MD and our continuum model is much easier for larger proteins that are better anchored in the membrane (3). Additionally, the computational demand is significantly lower for continuum calculations as opposed to MD. For gramicidin, the boundary conditions and energies can be calculated within 3 h on a desktop CPU, whereas the converged MD surfaces required 54 days of computation time using GPU-accelerated NAMD with 1 GPU and 32 CPUs.
Elastic moduli are key elements of the model that directly impact the membrane deformation energy and surface profiles. Previous work has suggested that these moduli vary spatially due to protein effects (18, 27), and we found that including a lipid hardening factor as suggested in Partenskii and Jordan (27) significantly improves the quantitative match between continuum results and atomistic MD. As membrane elastic models become increasingly more sophisticated through the inclusion of spatially dependent elastic moduli that vary with membrane composition (60), we believe that our solver can serve as an efficient tool to test models and elastic constants by quickly calculating energetics and membrane shapes to compare with experiments (23, 25, 70) and atomistic simulations. Additional experimental estimates of the energetics of the gramicidin-POPC system would be needed to further parameterize continuum models. Lastly, we point out that whereas hardening is a compelling candidate to explain differences between continuum predictions and MD, certainly there are other factors that are known to affect membrane energetics such as lipid tilt (71), entropic cost of lipid confinement (72, 73), line tension effects on lipid ordering (74, 75, 76), and additional terms penalizing the changes in area per lipid molecule (77). In future work, we plan to refine our elastic model by adding these elements.
Our hybrid continuum-atomistic model offers a distinct advantage over fully atomistic simulations for studying protein-membrane interactions due to its speed and accuracy, and this advantage grows with the size of the system. Because the model accurately reproduces results from MD simulations, we now plan to use it to probe larger, more complex biological situations such as multiprotein problems like the F-ATPase complexes that form rows of proteins along the inner membrane of the mitochondrial cristae (13), M2 channel-mediated fission (78), and SNARE-mediated fusion (79). Because continuum calculations are inexpensive and fast, our model provides a promising framework for exploring these multiprotein phenomena, where we can not only address geometrical effects in the membrane and the protein shape (34, 35, 37), but also extract membrane deformation energy values and reveal how specific protein structure and chemistry drives the processes.
Author Contributions
D.A. designed research, performed research, analyzed data, and wrote the paper. N.P.B. designed research, performed research, analyzed data, and wrote the paper. F.V.M. performed research and analyzed data. C.W.W. contributed numerical tools. M.G. designed research, analyzed data, and wrote the paper.
Acknowledgments
This work was supported by National Institutes of Health (NIH) grant No. R01-GM117593 and National Science Foundation (NSF) CAREER Award No. MCB-0845286. Computations were performed, in part, at the Texas Advanced Computing Center through the support of grant No. MCB-80011 and the Extreme Science and Engineering Discovery Environment (XSEDE) and the University of California San Francisco.
Editor: Markus Deserno.
Footnotes
David Argudo, Neville P. Bethel, and Frank V. Marcoline all contributed equally to this work.
Supporting Materials and Methods and eight figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30394-6.
Supporting Citations
References (80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90) appear in the Supporting Material.
Supporting Material
References
- 1.Zimmerberg J., Kozlov M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 2.Andersen O.S., Koeppe R.E., 2nd, Koeppe E. Bilayer thickness and membrane protein function: an energetic perspective. Annu. Rev. Biophys. Biomol. Struct. 2007;36:107–130. doi: 10.1146/annurev.biophys.36.040306.132643. [DOI] [PubMed] [Google Scholar]
- 3.Argudo D., Bethel N.P., Grabe M. Continuum descriptions of membranes and their interaction with proteins: towards chemically accurate models. Biochim. Biophys. Acta. 2016;1858:1619–1634. doi: 10.1016/j.bbamem.2016.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Urry D.W. The gramicidin A transmembrane channel: a proposed pi(L,D) helix. Proc. Natl. Acad. Sci. USA. 1971;68:672–676. doi: 10.1073/pnas.68.3.672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Perozo E., Cortes D.M., Martinac B. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 2002;418:942–948. doi: 10.1038/nature00992. [DOI] [PubMed] [Google Scholar]
- 6.Quemeneur F., Sigurdsson J.K., Lacoste D. Shape matters in protein mobility within membranes. Proc. Natl. Acad. Sci. USA. 2014;111:5083–5087. doi: 10.1073/pnas.1321054111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Keller S.L., Bezrukov S.M., Parsegian V.A. Probability of alamethicin conductance states varies with nonlamellar tendency of bilayer phospholipids. Biophys. J. 1993;65:23–27. doi: 10.1016/S0006-3495(93)81040-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tonnesen A., Christensen S.M., Stamou D. Geometrical membrane curvature as an allosteric regulator of membrane protein structure and function. Biophys. J. 2014;106:201–209. doi: 10.1016/j.bpj.2013.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shibata Y., Hu J., Rapoport T.A. Mechanisms shaping the membranes of cellular organelles. Annu. Rev. Cell Dev. Biol. 2009;25:329–354. doi: 10.1146/annurev.cellbio.042308.113324. [DOI] [PubMed] [Google Scholar]
- 10.Cogliati S., Enriquez J.A., Scorrano L. Architecture and function of mechanosensitive membrane protein lattices. Trends in Biomedical Sciences. 2015;41:261–273. [Google Scholar]
- 11.Aridor M., Bannykh S.I., Balch W.E. Sequential coupling between COPII and COPI vesicle coats in endoplasmic reticulum to Golgi transport. J. Cell Biol. 1995;131:875–893. doi: 10.1083/jcb.131.4.875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Orso G., Pendin D., Daga A. Homotypic fusion of ER membranes requires the dynamin-like GTPase atlastin. Nature. 2009;460:978–983. doi: 10.1038/nature08280. [DOI] [PubMed] [Google Scholar]
- 13.Davies K.M., Anselmi C., Kühlbrandt W. Structure of the yeast F1Fo-ATP synthase dimer and its role in shaping the mitochondrial cristae. Proc. Natl. Acad. Sci. USA. 2012;109:13602–13607. doi: 10.1073/pnas.1204593109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jiko C., Davies K.M., Gerle C. Bovine F1Fo ATP synthase monomers bend the lipid bilayer in 2D membrane crystals. eLife. 2015;4:e06119. doi: 10.7554/eLife.06119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ambroso M.R., Hegde B.G., Langen R. Endophilin A1 induces different membrane shapes using a conformational switch that is regulated by phosphorylation. Proc. Natl. Acad. Sci. USA. 2014;111:6982–6987. doi: 10.1073/pnas.1402233111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kim T., Lee K.I., Im W. Influence of hydrophobic mismatch on structures and dynamics of gramicidin a and lipid bilayers. Biophys. J. 2012;102:1551–1560. doi: 10.1016/j.bpj.2012.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yoo J., Cui Q. Membrane-mediated protein-protein interactions and connection to elastic models: a coarse-grained simulation analysis of gramicidin A association. Biophys. J. 2013;104:128–138. doi: 10.1016/j.bpj.2012.11.3813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee K.I., Pastor R.W., Im W. Assessing smectic liquid-crystal continuum models for elastic bilayer deformations. Chem. Phys. Lipids. 2013;169:19–26. doi: 10.1016/j.chemphyslip.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Choe S., Hecht K.A., Grabe M. A continuum method for determining membrane protein insertion energies and the problem of charged residues. J. Gen. Physiol. 2008;131:563–573. doi: 10.1085/jgp.200809959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mondal S., Khelashvili G., Weinstein H. Quantitative modeling of membrane deformations by multihelical membrane proteins: application to G-protein coupled receptors. Biophys. J. 2011;101:2092–2101. doi: 10.1016/j.bpj.2011.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ollila O.H.S., Risselada H.J., Marrink S.J. 3D pressure field in lipid membranes and membrane-protein complexes. Phys. Rev. Lett. 2009;102:078101. doi: 10.1103/PhysRevLett.102.078101. [DOI] [PubMed] [Google Scholar]
- 22.Yoo J., Cui Q. Three-dimensional stress field around a membrane protein: atomistic and coarse-grained simulation analysis of gramicidin A. Biophys. J. 2013;104:117–127. doi: 10.1016/j.bpj.2012.11.3812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang H.W. Deformation free energy of bilayer membrane and its effect on gramicidin channel lifetime. Biophys. J. 1986;50:1061–1070. doi: 10.1016/S0006-3495(86)83550-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ring A. Gramicidin channel-induced lipid membrane deformation energy: influence of chain length and boundary conditions. Biochim. Biophys. Acta. 1996;1278:147–159. doi: 10.1016/0005-2736(95)00220-0. [DOI] [PubMed] [Google Scholar]
- 25.Nielsen C., Goulian M., Andersen O.S. Energetics of inclusion-induced bilayer deformations. Biophys. J. 1998;74:1966–1983. doi: 10.1016/S0006-3495(98)77904-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Harroun T.A., Heller W.T., Huang H.W. Theoretical analysis of hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 1999;76:3176–3185. doi: 10.1016/S0006-3495(99)77469-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Partenskii M.B., Jordan P.C. Membrane deformation and the elastic energy of insertion: perturbation of membrane elastic constants due to peptide insertion. J. Chem. Phys. 2002;117:10768–10776. [Google Scholar]
- 28.Harroun T.A., Heller W.T., Huang H.W. Experimental evidence for hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 1999;76:937–945. doi: 10.1016/S0006-3495(99)77257-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.May S. Theories on structural perturbations of lipid bilayers. Curr. Opin. Colloid Interface Sci. 2000;5:244–249. [Google Scholar]
- 30.Helfrich P., Jakobsson E. Calculation of deformation energies and conformations in lipid membranes containing gramicidin channels. Biophys. J. 1990;57:1075–1084. doi: 10.1016/S0006-3495(90)82625-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nielsen C., Andersen O.S. Inclusion-induced bilayer deformations: effects of monolayer equilibrium curvature. Biophys. J. 2000;79:2583–2604. doi: 10.1016/S0006-3495(00)76498-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Latorraca N.R., Callenberg K.M., Grabe M. Continuum approaches to understanding ion and peptide interactions with the membrane. J. Membr. Biol. 2014;247:395–408. doi: 10.1007/s00232-014-9646-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Panahi A., Feig M. Dynamic heterogeneous dielectric generalized born (DHDGB): an implicit membrane model with a dynamically varying bilayer thickness. J. Chem. Theory Comput. 2013;9:1709–1719. doi: 10.1021/ct300975k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Haselwandter C.A., Phillips R. Connection between oligomeric state and gating characteristics of mechanosensitive ion channels. PLOS Comput. Biol. 2013;9:e1003055. doi: 10.1371/journal.pcbi.1003055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kahraman O., Koch P.D., Haselwandter C.A. Architecture and function of mechanosensitive membrane protein lattices. Sci. Rep. 2016;6:19214. doi: 10.1038/srep19214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mondal S., Khelashvili G., Weinstein H. The cost of living in the membrane: a case study of hydrophobic mismatch for the multi-segment protein LeuT. Chem. Phys. Lipids. 2013;169:27–38. doi: 10.1016/j.chemphyslip.2013.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haselwandter C.A., Phillips R. Directional interactions and cooperativity between mechanosensitive membrane proteins. Europhys. Lett. 2013;101:1–6. doi: 10.1209/0295-5075/101/68002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Callenberg K.M., Latorraca N.R., Grabe M. Membrane bending is critical for the stability of voltage sensor segments in the membrane. J. Gen. Physiol. 2012;140:55–68. doi: 10.1085/jgp.201110766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wolgemuth C.W., Zajac M. The moving boundary node method: a level set-based, finite volume algorithm with applications to cell motility. J. Comput. Phys. 2010;229:7287–7308. doi: 10.1016/j.jcp.2010.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Marcoline F.V., Bethel N., Grabe M. Membrane protein properties revealed through data-rich electrostatics calculations. Structure. 2015;23:1526–1537. doi: 10.1016/j.str.2015.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Deserno M. Fluid lipid membranes: from differential geometry to curvature stresses. Chem. Phys. Lipids. 2015;185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001. [DOI] [PubMed] [Google Scholar]
- 42.Fošnarič M., Iglič A., May S. Influence of rigid inclusions on the bending elasticity of a lipid membrane. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:051503. doi: 10.1103/PhysRevE.74.051503. [DOI] [PubMed] [Google Scholar]
- 43.Bingham R.J., Olmsted P.D., Smye S.W. Undulation instability in a bilayer lipid membrane due to electric field interaction with lipid dipoles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:051909. doi: 10.1103/PhysRevE.81.051909. [DOI] [PubMed] [Google Scholar]
- 44.Watson M.C., Penev E.S., Brown F.L.H. Thermal fluctuations in shape, thickness, and molecular orientation in lipid bilayers. J. Chem. Phys. 2011;135:244701. doi: 10.1063/1.3660673. [DOI] [PubMed] [Google Scholar]
- 45.Watson M.C., Morriss-Andrews A., Brown F.L.H. Thermal fluctuations in shape, thickness, and molecular orientation in lipid bilayers. II. Finite surface tensions. J. Chem. Phys. 2013;139:084706. doi: 10.1063/1.4818530. [DOI] [PubMed] [Google Scholar]
- 46.Kamien R.D. The geometry of soft materials: a primer. Rev. Mod. Phys. 2002;74:953–971. [Google Scholar]
- 47.Brannigan G., Brown F.L.H. Contributions of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys. J. 2007;92:864–876. doi: 10.1529/biophysj.106.094953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Callenberg, K. M. 2013. Membrane bending is critical for assessing the thermodynamic stability of proteins in the membrane. Ph.D. thesis, University of Pittsburgh, Pittsburgh, PA.
- 49.Powell M. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964;7:155–162. [Google Scholar]
- 50.Nelder J., Mead R. A simplex method for function minimization. Comput. J. 1965;7:308–313. [Google Scholar]
- 51.Richards F.M. Areas, volumes, packing and protein structure. Annu. Rev. Biophys. Bioeng. 1977;6:151–176. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 52.Hardt R., Kinderlehrer D., Lin F.-H. Existence and partial regularity of static liquid crystal configurations. Commun. Math. Phys. 1986;105:547–570. [Google Scholar]
- 53.Stewart I.W. Taylor and Francis; London, UK: 2004. The Static and Dynamic Continuum Theory of Liquid Crystals. [Google Scholar]
- 54.Hu M., Briguglio J.J., Deserno M. Determining the Gaussian curvature modulus of lipid membranes in simulations. Biophys. J. 2012;102:1403–1410. doi: 10.1016/j.bpj.2012.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hu M., de Jong D.H., Deserno M. Gaussian curvature elasticity determined from global shape transformations and local stress distributions: a comparative study using the MARTINI model. Faraday Discuss. 2013;161:365–382. doi: 10.1039/c2fd20087b. [DOI] [PubMed] [Google Scholar]
- 56.Helfrich W. Lyotropic lamellar phases. J. Phys. Condens. Matter. 1994;6:A79–A92. [Google Scholar]
- 57.Dimova R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014;208:225–234. doi: 10.1016/j.cis.2014.03.003. [DOI] [PubMed] [Google Scholar]
- 58.Nagle J.F., Jablin M.S., Akabori K. What are the true values of the bending modulus of simple lipid bilayers? Chem. Phys. Lipids. 2015;185:3–10. doi: 10.1016/j.chemphyslip.2014.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Levine Z.A., Venable R.M., Brown F.L.H. Determination of biomembrane bending moduli in fully atomistic simulations. J. Am. Chem. Soc. 2014;136:13582–13585. doi: 10.1021/ja507910r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Venable R.M., Brown F.L.H., Pastor R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Townsley L.E., Tucker W.A., Sham S., Hinton J.F. Structures of gramicidins A, B, and C incorporated into sodium dodecyl sulfate micelles. Biochemistry. 2001;40:11676–11686. doi: 10.1021/bi010942w. [DOI] [PubMed] [Google Scholar]
- 62.Lee J., Cheng X., Im W. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016;12:405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 64.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Klauda J.B., Venable R.M., Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.de Planque M.R.R., Killian J.A. Protein-lipid interactions studied with designed transmembrane peptides: role of hydrophobic matching and interfacial anchoring. Mol. Membr. Biol. 2003;20:271–284. doi: 10.1080/09687680310001605352. [DOI] [PubMed] [Google Scholar]
- 67.Goulian M., Mesquita O.N., Libchaber A. Gramicidin channel kinetics under tension. Biophys. J. 1998;74:328–337. doi: 10.1016/S0006-3495(98)77790-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hu Y., Ou S., Patel S. Free energetics of arginine permeation into model DMPC lipid bilayers: coupling of effective counterion concentration and lateral bilayer dimensions. J. Phys. Chem. B. 2013;117:11641–11653. doi: 10.1021/jp404829y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lomize M.A., Lomize A.L., Mosberg H.I. OPM: orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 70.Elliott J., Needham D., Haydon D. The effects of bilayer thickness and tension on gramicidin single-channel lifetime. Biochim. Biophys. Acta. 1983;735:95–103. doi: 10.1016/0005-2736(83)90264-x. [DOI] [PubMed] [Google Scholar]
- 71.Hamm M., Kozlov M.M. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E. 2000;3:323–335. [Google Scholar]
- 72.May S. Membrane perturbations induced by integral proteins: the role of conformational restrictions of the lipid chains. Langmuir. 2002;18:6356–6364. [Google Scholar]
- 73.Bohinc K., Kralj-Iglič V., May S. Interaction between two cylindrical inclusions in a symmetric lipid bilayer. J. Chem. Phys. 2003;119:7435–7444. [Google Scholar]
- 74.Kuzmin P.I., Akimov S.A., Cohen F.S. Line tension and interaction energies of membrane rafts calculated from lipid splay and tilt. Biophys. J. 2005;88:1120–1133. doi: 10.1529/biophysj.104.048223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.García-Sáez A.J., Chiantia S., Schwille P. Effect of line tension on the lateral organization of lipid membranes. J. Biol. Chem. 2007;282:33537–33544. doi: 10.1074/jbc.M706162200. [DOI] [PubMed] [Google Scholar]
- 76.Katira S., Mandadapu K.K., Chandler D. Pre-transition effects mediate forces of assembly between transmembrane proteins. eLife. 2016;5:e13150. doi: 10.7554/eLife.13150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bitbol A.F., Constantin D., Fournier J.-B. Bilayer elasticity at the nanoscale: the need for new terms. PLoS One. 2012;7:e48306. doi: 10.1371/journal.pone.0048306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Rossman J.S., Jing X., Lamb R.A. Influenza virus M2 protein mediates ESCRT-independent membrane scission. Cell. 2010;142:902–913. doi: 10.1016/j.cell.2010.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Weber T., Zemelman B.V., Rothman J.E. SNAREpins: minimal machinery for membrane fusion. Cell. 1998;92:759–772. doi: 10.1016/s0092-8674(00)81404-x. [DOI] [PubMed] [Google Scholar]
- 80.Sharp K.A., Honig B. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 81.Baker N.A., Sept D., McCammon J.A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Sanner M.F., Olson A.J., Spehner J.-C. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 1996;38:305–320. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 83.Sitkoff D., Ben-Tal N., Honig B. Calculation of alkane to water solvation free energies using continuum solvent models. J. Phys. Chem. 1996;100:2744–2752. [Google Scholar]
- 84.Fournier J.-B. Microscopic membrane elasticity and interactions among membrane inclusions: interplay between the shape, dilation, tilt and tilt-difference modes. Eur. Phys. J. B Cond. Matter Complex Syst. 1999;11:261–272. [Google Scholar]
- 85.Schmid F. Are stress-free membranes really “tensionless”? EPL. 2011;95:28008. [Google Scholar]
- 86.Diamant H. Model-free thermodynamics of fluid vesicles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:061123. doi: 10.1103/PhysRevE.84.061123. [DOI] [PubMed] [Google Scholar]
- 87.Safran A.S. Westview Press; Boulder, CO: 2003. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. Frontiers in Physics. [Google Scholar]
- 88.Boal D. 2nd. Cambridge University Press; Cambridge, UK: 2012. Mechanics of the Cell, [Google Scholar]
- 89.Aranda-Espinoza H., Berman A., Safran S. Interaction between inclusions embedded in membranes. Biophys. J. 1996;71:648–656. doi: 10.1016/S0006-3495(96)79265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Bolza O. Dover Publications; Mineola, NY: 1961. Lectures on the Calculus of Variations. [Google Scholar]
- 91.Sitkoff D., Sharp K.A., Honig B. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 1994;98:1978–1988. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.