Statistical Mechanics of Allosteric Enzymes

Abstract

The concept of allostery in which macromolecules switch between two different conformations is a central theme in biological processes ranging from gene regulation to cell signaling to enzymology. Allosteric enzymes pervade metabolic processes, yet a simple and unified treatment of the effects of allostery in enzymes has been lacking. In this work, we take a step toward this goal by modeling allosteric enzymes and their interaction with two key molecular players—allosteric regulators and competitive inhibitors. We then apply this model to characterize existing data on enzyme activity, comment on how enzyme parameters (such as substrate binding affinity) can be experimentally tuned, and make novel predictions on how to control phenomena such as substrate inhibition.

Graphical abstract

1. INTRODUCTION

All but the simplest of cellular reactions are catalyzed by enzymes, macromolecules that can increase the rates of reactions by many orders of magnitude. In some cases, such as phosphoryl transfer reactions, rate enhancements can be as large as 10²⁰-fold or more.¹ A deeper understanding of how enzymes work can provide insights into biological phenomena as diverse as metabolic regulation or the treatment of disease.^2–4 The basic principles of enzyme mechanics were first proposed by Michaelis and Menten⁵ and later extended by others.^6–8 While the earliest models considered enzymes as single-state catalysts, experiments soon revealed that some enzymes exhibit richer dynamics.^9,10 The concept of allosteric enzymes was introduced by Monod–Wyman–Changeux (MWC) and independently by Pardee and Gerhart,^7,11–13 providing a much broader framework for explaining the full diversity of enzyme behavior. Since then, the MWC concept in which macromolecules are thought of as having both an inactive and active state has spread into many fields, proving to be a powerful conceptual tool capable of explaining many biological phenomena.^14–16

Enzymology is a well studied field, and much has been learned both theoretically and experimentally about how enzymes operate.^17–20 With the vast number of distinct molecular players involved in enzymatic reactions (for example, mixed, competitive, uncompetitive, and noncompetitive inhibitors as well as cofactors, allosteric effectors, and substrate molecules), it is not surprising that new discoveries continue to emerge about the subtleties of enzyme action.^9,21,22 In this paper, we use the MWC model to form a unifying framework capable of describing the broad array of behaviors available to allosteric enzymes.

Statistical mechanics is a field of physics that describes the collective behavior of large numbers of molecules. Historically developed to understand the motion of gases, statistical physics has now seen applications in many areas of biology and has provided unexpected connections between distinct problems such as how transcription factors are induced by signals from the environment, the function of the molecular machinery responsible for detecting small gradients in chemoattractants, the gating properties of ligand-gated ion channels, and even the accessibility of genomic DNA in eukaryotes which is packed into nucleosomes.^23–29

The remainder of the paper is organized as follows. In section 2.1, we show how the theoretical treatment of the traditional Michaelis–Menten enzyme, an inherently non-equilibrium system, can be stated in a language remarkably similar to equilibrium statistical mechanics. This sets the stage for the remainder of the paper by introducing key notation and the states and weights formalism that serves as the basis for analyzing more sophisticated molecular scenarios. In section 2.2, we discuss how the states and weights formalism can be used to work out the rates for the simplest MWC enzyme, an allosteric enzyme with a single substrate binding site. This is followed by a discussion of how allosteric enzymes are modified by the binding of ligands, first an allosteric regulator in section 2.3 and then a competitive inhibitor in section 2.4. We next generalize to the much richer case of enzymes with multiple substrate binding sites in section 2.5. Lastly, we discuss how to combine the individual building blocks of allostery, allosteric effectors, competitive inhibitors, and multiple binding sites to analyze general enzymes in section 2.6. Having built up this framework, we then apply our model to understand observed enzyme behavior. In section 3.1, we show how disparate enzyme activity curves can be unified within our model and collapsed onto a single curve. We close by examining the exotic phenomenon of substrate inhibition in section 3.2 and show how the allosteric nature of some enzymes may be the key to understanding and controlling this phenomenon.

2. MODELS

2.1. Michaelis–Menten Enzyme

We begin by briefly introducing the textbook Michaelis–Menten treatment of enzymes.¹⁸ This will serve both to introduce basic notation and to explain the states and weights methodology which we will use throughout the paper.

Many enzyme-catalyzed biochemical reactions are characterized by Michaelis–Menten kinetics. Such enzymes comprise a simple but important class where we can study the relationship between the traditional chemical kinetics based on reaction rates with a physical view dictated by statistical mechanics. According to the Michaelis–Menten model, enzymes are single-state catalysts that bind a substrate and promote its conversion into a product. Although this scheme precludes allosteric interactions, a significant fraction of nonregulatory enzymes (e.g., triosephosphate isomerase, bisphosphoglycerate mutase, adenylate cyclase) are well described by Michaelis–Menten kinetics.¹⁸

The key player in this reaction framework is a monomeric enzyme E which binds a substrate S at the substrate binding site (also called the active site or catalytic site), forming an enzyme–substrate complex ES. The enzyme then converts the substrate into product P which is subsequently removed from the system and cannot return to its original state as substrate. In terms of concentrations, this reaction can be written as

$$[\mathrm{E}]+[\mathrm{S}]\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftarrows }}[\text{ES}]\stackrel{k_{\text{cat}}}{\to }[\mathrm{E}]+[\mathrm{P}]$$ (1)

where the rate of product formation equals

$$\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[\text{ES}]k_{\text{cat}}$$ (2)

Briggs and Haldane assumed a time scale separation where the substrate and product concentrations ([S] and [P]) slowly change over time while the free and bound enzyme states ([E] and [ES]) changed much more rapidly.⁶ This allows us to approximate this system over short time scales by assuming that the slow components (in this case [S]) remain constant and can therefore be absorbed into the k_on rate³⁰

$$[\mathrm{E}]\underset{k_{\text{off}}+k_{\text{cat}}}{\overset{k_{\text{on}}[\mathrm{S}]}{\rightleftarrows }}[\text{ES}]$$ (3)

Assuming that the system (3) reaches steady state (over the short time scale of this approximation) quickly enough that the substrate concentration does not appreciably diminish, this implies

$$[\mathrm{E}][\mathrm{S}]k_{\text{on}}=[\text{ES}](k_{\text{off}}+k_{\text{cat}})$$ (4)

which we can rewrite as

$$\frac{[\text{ES}]}{[\mathrm{E}]}=\frac{[\mathrm{S}]k_{\text{on}}}{k_{\text{off}}+k_{\text{cat}}}\equiv \frac{[\mathrm{S}]}{K_{\mathrm{M}}}$$ (5)

where $K_{\mathrm{M}}=\frac{k_{\text{off}}+k_{\text{cat}}}{k_{\text{on}}}$ is called the Michaelis constant. K_M incorporates the binding and unbinding of ligand as well as the conversion of substrate into product; in the limit k_cat = 0, K_M reduces to the familiar dissociation constant $K_{\mathrm{D}}=\frac{k_{\text{off}}}{k_{\text{on}}}$. Using eq 5 and the fact that the total enzyme concentration is conserved, [E] + [ES] = [E_tot], we can solve for [E] and [ES] separately as

$$[\mathrm{E}]=[{\mathrm{E}}_{\text{tot}}]\frac{1}{1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}\equiv [{\mathrm{E}}_{\text{tot}}]p_{\mathrm{E}}$$ (6)

$$[\text{ES}]=[{\mathrm{E}}_{\text{tot}}]\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}{1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}\equiv [{\mathrm{E}}_{\text{tot}}]p_{\text{ES}}$$ (7)

where $p_{\mathrm{E}}=\frac{[\mathrm{E}]}{[{\mathrm{E}}_{\text{tot}}]}$ and $p_{\text{ES}}=\frac{[\text{ES}]}{[{\mathrm{E}}_{\text{tot}}]}$ are the probabilities of finding an enzyme in the unbound and bound forms, respectively. Substituting the concentration of bound enzymes [ES] from eq 7 into the rate of product formation eq 2,

$$\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=k_{\text{cat}}[{\mathrm{E}}_{\text{tot}}]\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}{1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}$$ (8)

Figure 1 shows the probability of free and bound enzyme as well as the rate of product formation. The two parameters k_cat and [E_tot] scale $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ vertically (if k_cat is increased by a factor of 10, the y-axis values in Figure 1B will be multiplied by that same factor of 10), while K_M effectively rescales the substrate concentration [S]. Increasing K_M by a factor of 10 implies that 10 times as much substrate is needed to obtain the same rate of product formation; on the semilog plots in Figure 1, this corresponds to shifting all curves to the right by one power of 10.

Figure 1.

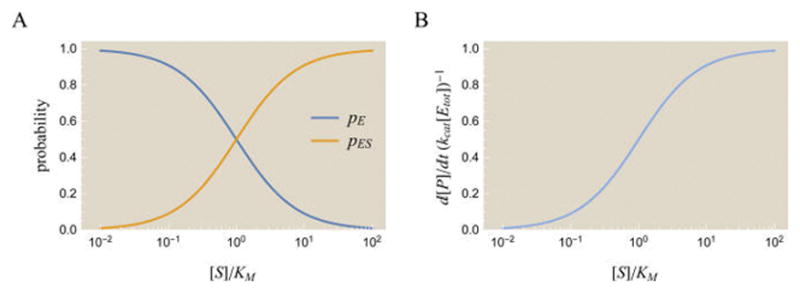
Dynamics of the Michaelis–Menten enzyme. (A) Probabilities of the free enzyme p_E and bound enzyme p_ES states as a function of substrate concentration. As the amount of substrate [S] increases, more enzyme is found in the bound state rather than the free state. (B) The rate of product formation for a nonallosteric enzyme. The rate of product formation has the same functional form as the probability p_ES of the enzyme– substrate complex, as illustrated by eqs 2 and 7.

We can visualize the microscopic states of the enzyme using a modified states and weights diagram shown in Figure 2.³¹ The weight of each enzyme state is proportional to the probability of its corresponding state (w_E ∝ p_E, w_ES ∝ p_ES)—the constant of proportionality is arbitrary but must be the same for all weights. For example, from eqs 6 and 7, we can multiply the probability that the enzyme will be unbound (p_E) or bound to substrate (p_ES) by $1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}$ which yields the weights

Figure 2.

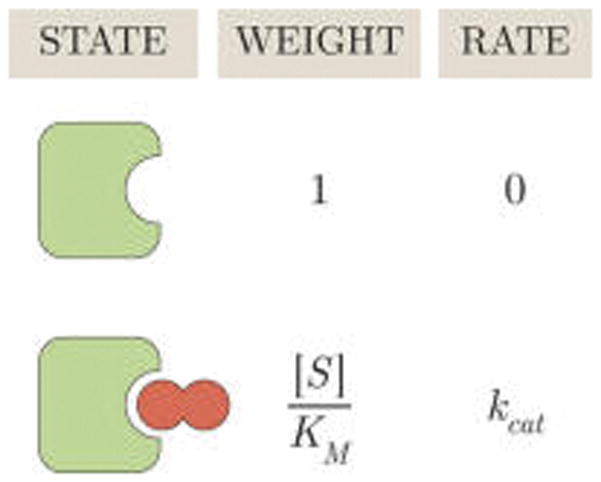
States and weights for the Michaelis–Menten enzyme. Each enzyme conformation is shown together with its weight and its catalytic rate. The probability of finding an enzyme (green) in either the free or bound state equals the weight of that state divided by the sum of all weights ( $1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}$) where [S] is the concentration of substrate (dark red) and $K_{\mathrm{M}}=\frac{k_{\text{off}}+k_{\text{cat}}}{k_{\text{on}}}$ is the Michaelis constant. At [S] = K_M, half of the enzyme population exists in the free form and half exists in the bound form. For [S] > K_M, more than half of all enzymes will be bound to substrate.

$$w_{\mathrm{E}}=1$$ (9)

$$w_{\text{ES}}=\frac{[\mathrm{S}]}{K_{\mathrm{M}}}$$ (10)

Given the weights of an enzyme state, we can proceed in the reverse direction and obtain the probability for each enzyme state using

$$p_{\mathrm{E}}=\frac{w_{\mathrm{E}}}{Z_{\text{tot}}}=\frac{1}{1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}$$ (11)

$$p_{\text{ES}}=\frac{w_{\text{ES}}}{Z_{\text{tot}}}=\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}{1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}}}$$ (12)

where

$$Z_{\text{tot}}=w_{\mathrm{E}}+w_{\text{ES}}$$ (13)

is the sum of all weights. Dividing by Z_tot ensures the total probability of all enzyme states equals unity, p_E + p_ES = 1. The rate of product formation eq 8 is given by the product of the enzyme concentration [E_tot] times the average catalytic rate over all states, weighed by each state’s (normalized) weights. In the following sections, we will find this trick of writing states and weights very useful for modeling other molecular players.

The weights in Figure 2 allow us to easily understand Figure 1A: when [S] < K_M, w_E > w_ES so that an enzyme is more likely to be in the substrate-free state; when [S] > K_M, w_E < w_ES and an enzyme is more likely to be found as an enzyme–substrate complex. Increasing K_M shifts the tipping point of how much substrate is needed before the bound ES enzyme state begins to dominate over the free E state.

It should be noted that the formal notion of states and weights employed in physics applies only to equilibrium systems. For example, a ligand binding to a receptor in equilibrium will yield states and weights similar to Figure 2 but with the Michaelis constant K_M replaced by the dissociation constant K_D.³² However, the ligand–receptor states and weights can also be derived from the Boltzmann distribution (where the weight of any state j with energy E_j is proportional to e^−βE_j) while the enzyme states and weights cannot be derived from the Boltzmann distribution (because the enzyme system is not in equilibrium). Instead, the nonequilibrium kinetics of the system are described by the modified states and weights in Figure 2, where K_D for substrate must be replaced with K_M. These modified states and weights serve as a mathematical trick that compactly and correctly represents the behavior of the enzyme, enabling us to apply the well established tools and intuition of equilibrium statistical mechanics when analyzing the inherently nonequilibrium problem of enzyme kinetics. In the next several sections, we will show how to generalize this method of states and weights to MWC enzymes with competitive inhibitors, allosteric regulators, and multiple substrate binding sites.

2.2. MWC Enzyme

Many enzymes are not static entities but dynamic macromolecules that constantly fluctuate between different conformational states. This notion was initially conceived by Monod–Wyman–Changeux (MWC) to characterize complex multisubunit proteins such as hemoglobin and aspartate transcarbamoylase (ATCase).^7,11,12 The authors suggested that the ATC enzyme exists in two supramolecular states: a relaxed “R” state, which has high affinity for substrate, and a tight “T” state, which has low affinity for substrate. Although in the case of ATCase the transition between the T and R states is induced by an external ligand, recent experimental advances have shown that many proteins intrinsically fluctuate between these different states even in the absence of ligand.^33–35 These observations imply that the MWC model can be applied to a wide range of enzymes beyond those with multisubunit complexes.

We will designate an enzyme with two possible states (an Active state E_A and an Inactive state E_I) as a MWC enzyme. The kinetics of a general MWC enzyme are given by

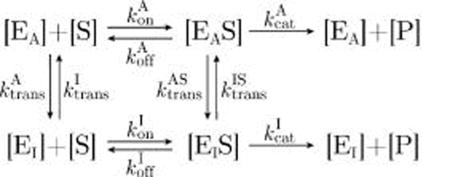(14)

which relates the active and inactive enzyme concentrations ([E_A], [E_I]) to the active and inactive enzyme–substrate complexes ([E_AS], [E_IS]). In this two-state MWC model, similar to that explored by Howlett et al.,³⁶ the rate of product formation is given by

$$\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=k_{\text{cat}}^{\mathrm{A}}[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]+k_{\text{cat}}^{\mathrm{I}}[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]$$ (15)

The active state will have a faster catalytic rate (often much faster) than the inactive state, $k_{\text{cat}}^{\mathrm{A}}>k_{\text{cat}}^{\mathrm{I}}$.

As in the case of a Michaelis–Menten enzyme, we will assume that all four forms of the enzyme (E_A, E_I, E_AS, and E_IS) quickly reach steady state on time scales so short that the substrate concentration [S] remains nearly constant. Therefore, we can incorporate the slowly changing quantities [S] and [P] into the rates, a step dubbed the quasi-steady-state approximation.³⁰ This allows us to rewrite eq 14 in the following form

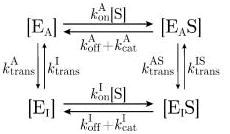(16)

Assuming the quasi-steady-state approximation holds, the four enzyme states will rapidly attain steady-state values

$$\frac{\mathrm{d}[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]}{\mathrm{d}t}=\frac{\mathrm{d}[{\mathrm{E}}_{\mathrm{A}}]}{\mathrm{d}t}=\frac{\mathrm{d}[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]}{\mathrm{d}t}=\frac{\mathrm{d}[{\mathrm{E}}_{\mathrm{I}}]}{\mathrm{d}t}=0$$ (17)

In addition, a separate constraint on the system that is necessary and sufficient to apply the method of states and weights is given by the cycle condition: the product of rates going clockwise around any cycle must equal the product of rates going counterclockwise.³⁰ It should be noted that, to violate the cycle condition, a system must continuously pay energy, since at least one step in any cycle must be energetically unfavorable. We shall proceed with the assumption that there are no such cycles in our system. For the MWC enzyme (eq 16), this implies

$$(k_{\text{on}}^{\mathrm{A}}[\mathrm{S}])k_{\text{trans}}^{\text{AS}}(k_{\text{off}}^{\mathrm{I}}+k_{\text{cat}}^{\mathrm{I}})k_{\text{trans}}^{\mathrm{I}}=(k_{\text{off}}^{\mathrm{A}}+k_{\text{cat}}^{\mathrm{A}})k_{\text{trans}}^{\mathrm{A}}(k_{\text{on}}^{\mathrm{I}}[\mathrm{S}])k_{\text{trans}}^{\text{IS}}$$ (18)

or equivalently

$$\underset{\frac{[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]}{[{\mathrm{E}}_{\mathrm{A}}]}}{\underbrace{\frac{k_{\text{on}}^{\mathrm{A}}[\mathrm{S}]}{k_{\text{off}}^{\mathrm{A}}+k_{\text{cat}}^{\mathrm{A}}}}}\underset{\frac{[{\mathrm{E}}_{\mathrm{A}}]}{[{\mathrm{E}}_{\mathrm{I}}]}}{\underbrace{\frac{k_{\text{trans}}^{\mathrm{I}}}{k_{\text{trans}}^{\mathrm{A}}}}}=\underset{\frac{[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]}{[{\mathrm{E}}_{\mathrm{I}}]}}{\underbrace{\frac{k_{\text{on}}^{\mathrm{I}}[\mathrm{S}]}{k_{\text{off}}^{\mathrm{I}}+k_{\text{cat}}^{\mathrm{I}}}}}\underset{\frac{[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]}{[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]}}{\underbrace{\frac{k_{\text{trans}}^{\text{IS}}}{k_{\text{trans}}^{\text{AS}}}}}$$ (19)

The validity of both the quasi-steady-state approximation (17) and the cycle condition (19) will be analyzed in section A of the Supporting Information. Assuming both statements hold, we can invoke detailed balance—the ratio of concentrations between two enzyme states equals the inverse of the ratio of rates connecting these two states. For example, between the active states [E_AS] and [E_A] in eq 16

$$\frac{[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]}{[{\mathrm{E}}_{\mathrm{A}}]}=\frac{k_{\text{on}}^{\mathrm{A}}[\mathrm{S}]}{k_{\text{off}}^{\mathrm{A}}+k_{\text{cat}}^{\mathrm{A}}}\equiv \frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}$$ (20)

where we have defined the Michaelis constant for the active state, $K_{\mathrm{M}}^{\mathrm{A}}$. Similarly, we can write the equation for detailed balance between the inactive states [E_IS] and [E_I] as

$$\frac{[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]}{[{\mathrm{E}}_{\mathrm{I}}]}=\frac{k_{\text{on}}^{\mathrm{I}}[\mathrm{S}]}{k_{\text{off}}^{\mathrm{I}}+k_{\text{cat}}^{\mathrm{I}}}\equiv \frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}$$ (21)

An enzyme may have a different affinity for substrate or a different catalytic rate in the active and inactive forms. Typical measured values of K_M fall into the range 10⁻⁷–10⁻¹ M.³⁷ Whether $K_{\mathrm{M}}^{\mathrm{A}}$ or $K_{\mathrm{M}}^{\mathrm{I}}$ is larger depends on the specific enzyme.

As a final link between the language of chemical rates and physical energies, we can recast detailed balance between [E_A] and [E_I] as

$$\frac{[{\mathrm{E}}_{\mathrm{A}}]}{[{\mathrm{E}}_{\mathrm{I}}]}=\frac{k_{\text{trans}}^{\mathrm{I}}}{k_{\text{trans}}^{\mathrm{A}}}\equiv {\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}$$ (22)

where ε_A and ε_I are the free energies of the enzyme in the active and inactive states, respectively, and $\beta =\frac{1}{k_{\mathrm{B}}T}$, where k_B is Boltzmann’s constant and T is the temperature of the system. Whether the active state energy is greater than or less than the inactive state energy depends on the enzyme. For example, ε_I < ε_A in ATCase, whereas the opposite holds true, ε_A < ε_I, in chemoreceptors.^9,32

Using eqs 20–22, we can recast the cycle condition (19) (as shown in the underbraces) into a simple relationship between the steady-state enzyme concentrations. Additionally, we can use these equations to define the weights of each enzyme state in Figure 3. Following section 2.1, the probability of each state equals its weight divided by the sum of all weights

Figure 3.

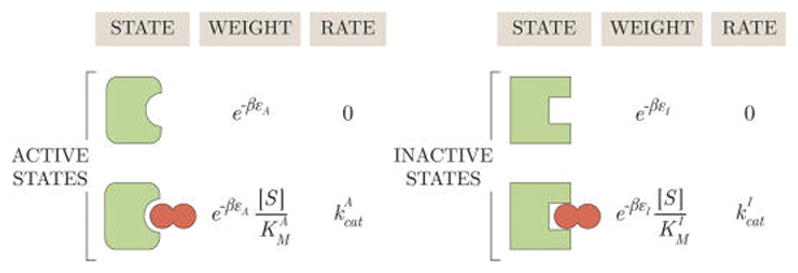
States and weights for a MWC enzyme. The energies ε_A and ε_I provide the free energy scale for the substrate-free conformations, dictating their relative probabilities. Decreasing the energy ε_A of the active state would increase the probability of all the active enzyme conformations relative to the inactive conformations. $K_{\mathrm{M}}^{\mathrm{A}}$ denotes the substrate concentration at which half of the active enzymes are bound and half of the active enzymes are unbound, as indicated by the crossing of the (p_EA, blue) and (p_EAS, gold) curves at $[\mathrm{S}]=K_{\mathrm{M}}^{\mathrm{A}}$ in Figure 4. $K_{\mathrm{M}}^{\mathrm{I}}$ serves an analogous role for the inactive states.

$$p_{{\mathrm{E}}_{\mathrm{A}}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{1}{Z_{\text{tot}}}$$ (23)

$$p_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}}{Z_{\text{tot}}}$$ (24)

$$p_{{\mathrm{E}}_{\mathrm{I}}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{1}{Z_{\text{tot}}}$$ (25)

$$p_{{\mathrm{E}}_{\mathrm{I}}\mathrm{S}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{Z_{\text{tot}}}$$ (26)

where

$$Z_{\text{tot}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)$$ (27)

Note that multiplying all of the weights by a constant c will also multiply Z_tot by c, so that the probability of any state will remain unchanged. That is why in Figure 2 we could neglect the e^−βε factor that was implicitly present in each weight.

The total amount of enzyme is conserved among the four enzyme states, [E_tot] = [E_A] + [E_AS] + [E_I] + [E_IS]. Using this fact together with eqs 20–22 enables us to solve for the concentrations of both types of bound enzymes, namely,

$$[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]=[{\mathrm{E}}_{\text{tot}}]\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}=[{\mathrm{E}}_{\text{tot}}]p_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}}$$ (28)

$$[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]=[{\mathrm{E}}_{\text{tot}}]\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}=[{\mathrm{E}}_{\text{tot}}]p_{{\mathrm{E}}_{\mathrm{I}}\mathrm{S}}$$ (29)

Substituting these relations into eq 15 yields the rate of product formation

$$\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}$$ (30)

The probabilities (23) – (26) of the different states and the rate of product formation (30) are shown in Figure 4. Although we use the same parameters from Figure 1 for the active state, the p_EA and p_EAS curves in Figure 4A look markedly different from the p_E and p_ES Michaelis–Menten curves in Figure 1A. This indicates that the activity of a MWC enzyme does not equal the activity of two independent Michaelis–Menten enzymes, one with the MWC enzyme’s active state parameters and the other with the MWC enzyme’s inactive state parameters. The interplay of the active and inactive states makes a MWC enzyme inherently more complex than a Michaelis–Menten enzyme.

Figure 4.

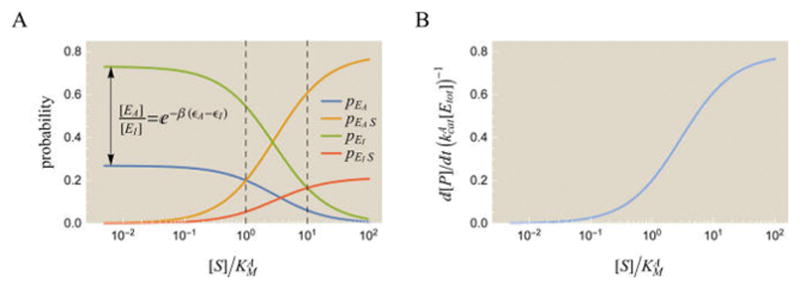
Quantitative description of a MWC enzyme. (A) Probabilities of each enzyme state. While the active state has the same catalytic rate $k_{\text{cat}}^{\mathrm{A}}$ and Michaelis constant $K_{\mathrm{M}}^{\mathrm{A}}$ as the Michaelis–Menten enzyme in Figure 1A, the inactive state significantly alters the forms of p_EA and p_EAS. The dashed vertical lines indicate where the substrate concentration equals $K_{\mathrm{M}}^{\mathrm{A}}$ and $K_{\mathrm{M}}^{\mathrm{I}}$, respectively. (B) The rate of product formation, $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. Assuming $\frac{k_{\text{cat}}^{\mathrm{A}}}{k_{\text{cat}}^{\mathrm{I}}}\gg 1,\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ (blue curve in part B) is dominated by the active enzyme–substrate complex, p_EAS (gold curve in part A). Parameters were chosen to reflect “typical” enzyme kinetics values: $\frac{k_{\text{cat}}^{\mathrm{A}}}{k_{\text{cat}}^{\mathrm{I}}}={10}^2,\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}={10}^{-1}$, and e^{−β(ε_A−ε_I)} = e^−1.38 Substrate concentrations are shown normalized relative to the active state parameter $\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}$, although the inactive state parameter $\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}$ could also have been used.

When [S] = 0, the enzyme only exists in the unbound states E_A and E_I whose relative probabilities are given by $\frac{p_{{\mathrm{E}}_{\mathrm{A}}}}{p_{{\mathrm{E}}_{\mathrm{I}}}}={\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}$. When [S] → ∞, the enzyme spends all of its time in the bound states E_AS and E_IS which have relative probabilities $\frac{p_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}}}{p_{{\mathrm{E}}_{\mathrm{I}}\mathrm{S}}}={\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}$. The curves for the active states (for free enzyme p_EA and bound enzyme p_EAS) intersect at $[\mathrm{S}]=K_{\mathrm{M}}^{\mathrm{A}}$, while the curves of the two inactive states intersect at $[\mathrm{S}]=K_{\mathrm{M}}^{\mathrm{I}}$. For the particular parameters shown, even though the unbound inactive state (green) dominates at low substrate concentrations, the active state (gold) has the largest statistical weights as the concentration of substrate increases. Thus, adding substrate causes the enzyme to increasingly favor the active state.

Using this framework, we can compute properties of the enzyme kinetics curve shown in Figure 4B. One important property is the dynamic range of an enzyme, the difference between the maximum and minimum rate of product formation. In the absence of substrate ([S] → 0) and a saturating concentration of substrate ([S] → ∞), the rate of product formation (eq 30) becomes

$$\underset{[\mathrm{S}]\to 0}{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=0$$ (31)

$$\underset{[\mathrm{S}]\to \infty }{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}}{K_{\mathrm{M}}^{\mathrm{I}}}}{\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}}{K_{\mathrm{M}}^{\mathrm{A}}}+\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}}{K_{\mathrm{M}}^{\mathrm{I}}}}$$ (32)

From these two expressions, we can write the dynamic range as

$$\begin{array}{c}\text{dynamic}\text{range}=\left(\underset{[\mathrm{S}]\to \infty }{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)-\left(\underset{[\mathrm{S}]\to 0}{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)\\ =[{\mathrm{E}}_{\text{tot}}]k_{\text{cat}}^{\mathrm{A}}\left(1-\frac{1-\frac{k_{\text{cat}}^{\mathrm{I}}}{k_{\text{cat}}^{\mathrm{A}}}}{1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}}\right)\end{array}$$ (33)

where every term in the fraction has been written as a ratio of the active and inactive state parameters. We find that the dynamic range increases as $\frac{k_{\text{cat}}^{\mathrm{I}}}{k_{\text{cat}}^{\mathrm{A}}}$, e^{−β(ε_A−ε_I)}, and $\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}$ increase (assuming $k_{\text{cat}}^{\mathrm{A}}>k_{\text{cat}}^{\mathrm{I}}$).

Another important property is the concentration of substrate at which the rate of product formation lies halfway between its minimum and maximum value, which we will denote as [S₅₀]. It is straightforward to show that the definition

$$\underset{[\mathrm{S}]\to [{\mathrm{S}}_{50}]}{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=\frac{1}{2}\left(\underset{[\mathrm{S}]\to \infty }{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}+\underset{[\mathrm{S}]\to 0}{lim}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)$$ (34)

is satisfied when

$$[{\mathrm{S}}_{50}]=K_{\mathrm{M}}^{\mathrm{A}}\frac{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}+1}{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}+\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}}$$ (35)

With increasing e^{−β(ε_A−ε_I)}, the value of [S₅₀] increases if $K_{\mathrm{M}}^{\mathrm{A}}>K_{\mathrm{M}}^{\mathrm{I}}$ and decreases otherwise. [S₅₀] always decreases as $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}$ increases. Lastly, we note that, in the limit of a Michaelis–Menten enzyme, ε_I → ∞, we recoup the familiar results

$$\text{dynamic}\text{range}=[{\mathrm{E}}_{\text{tot}}]k_{\text{cat}}^{\mathrm{A}}({\epsilon }_{\mathrm{I}}\to \infty )$$ (36)

$$[{\mathrm{S}}_{50}]=K_{\mathrm{M}}^{\mathrm{A}}({\epsilon }_{\mathrm{I}}\to \infty )$$ (37)

2.3. Allosteric Regulator

The catalytic activity of many enzymes is controlled by molecules that bind to regulatory sites which are often different from the active sites themselves. As a result of ligand-induced conformational changes, these molecules alter the substrate binding site which modifies the rate of product formation, $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. Allosterically controlled enzymes represent important regulatory nodes in metabolic pathways and are often responsible for keeping cells in homeostasis. Some well-studied examples of allosteric control include glycogen phosphorylase, phosphofructokinase, glutamine synthetase, and aspartate transcarbamoylase (ATCase). In many cases the data from these systems are characterized phenomenologically using Hill functions, but the Hill coefficients thus obtained can be difficult to interpret.³⁹ In addition, Hill coefficients do not provide much information about the organization or regulation of an enzyme, nor do they reflect the relative probabilities of the possible enzyme conformations, although recent results have begun to address these issues.⁴⁰ In this section, we add one more layer of complexity to our statistical mechanics framework by introducing an allosteric regulator.

Consider a MWC enzyme with one site for an allosteric regulator R and a different site for a substrate molecule S that will be converted into product. We can define the effects of the allosteric regulator directly through the states and weights. As shown in Figure 5, the regulator R contributes a factor $\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}$ when it binds to an active state and a factor $\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}$ when it binds to an inactive state where $R_{\mathrm{D}}^{\mathrm{A}}$ and $R_{\mathrm{D}}^{\mathrm{I}}$ are the dissociation constants between the regulator and the active and inactive states of the enzyme, respectively. Unlike the Michaelis constants $K_{\mathrm{M}}^{\mathrm{A}}$ and $K_{\mathrm{M}}^{\mathrm{I}}$ for the substrate, the dissociation constants $R_{\mathrm{D}}^{\mathrm{A}}$ and $R_{\mathrm{D}}^{\mathrm{I}}$ enter the states and weights because the regulator can only bind and unbind to the enzyme (and cannot be transformed into product). In other words, if we were to draw a rates diagram for this enzyme system, detailed balance between the two states where the regulator is bound and unbound would yield a dissociation constant ( $\frac{k_{\text{off}}}{k_{\text{on}}}$) rather than a Michaelis constant ( $\frac{k_{\text{off}}+k_{\text{cat}}}{k_{\text{on}}}$).

Figure 5.

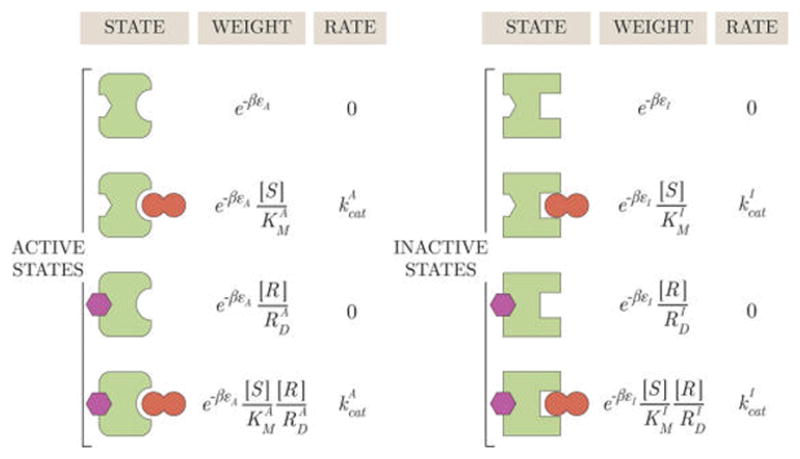
States and weights for a MWC enzyme with an allosteric regulator. The allosteric regulator (purple) does not directly interact with the substrate (dark red) but instead introduces a factor $\frac{[\mathrm{R}]}{R_{\mathrm{D}}}$ into the weights where R_D is a dissociation constant. Note that the regulator can only associate to and dissociate from the enzyme, whereas substrate can be turned into product as shown by the Michaelis constant K_M. An allosteric activator binds more tightly to the active state enzyme, $R_{\mathrm{D}}^{\mathrm{A}}<R_{\mathrm{D}}^{\mathrm{I}}$, which leads to an increased rate of product formation because the active state catalyzes substrate at a faster rate than the inactive state, $k_{\text{cat}}^{\mathrm{A}}>k_{\text{cat}}^{\mathrm{I}}$. An allosteric inhibitor would satisfy $R_{\mathrm{D}}^{\mathrm{A}}>R_{\mathrm{D}}^{\mathrm{I}}$.

Using the states and weights in Figure 5, we can compute the probability of each enzyme state. For example, the probabilities of the four states that form product are given by

$$p_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}}{Z_{\text{tot}}}$$ (38)

$$p_{{\mathrm{E}}_{\mathrm{A}}\text{SR}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}}{Z_{\text{tot}}}$$ (39)

$$p_{{\mathrm{E}}_{\mathrm{I}}\mathrm{S}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{Z_{\text{tot}}}$$ (40)

$$p_{{\mathrm{E}}_{\mathrm{I}}\text{SR}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}}{Z_{\text{tot}}}$$ (41)

where

$$Z_{\text{tot}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)$$ (42)

is the sum of all weights in Figure 5. An allosteric activator has a smaller dissociation constant $R_{\mathrm{D}}^{\mathrm{A}}<R_{\mathrm{D}}^{\mathrm{I}}$ for binding to the active state enzyme, so that for larger [R] the probability that the enzyme will be in the active state increases. Because the active state catalyzes substrate at a faster rate than the inactive state, $k_{\text{cat}}^{\mathrm{A}}>k_{\text{cat}}^{\mathrm{I}}$, adding an activator increases the rate of product formation $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. An allosteric inhibitor has the flipped relation $R_{\mathrm{D}}^{\mathrm{A}}>R_{\mathrm{D}}^{\mathrm{I}}$ and hence causes the opposite effects.

Proceeding analogously to section 2.2, the total enzyme concentration [E_tot] is a conserved quantity which equals the sum of all enzyme states ([E_A], [E_AS], [E_AR], [E_ASR], and their inactive state counterparts). Using the probabilities in eqs 38–41, we can write these concentrations as [E_AS] = [E_tot]p_EAS, [E_ASR] = [E_tot]p_EASR, …, so that the rate of product formation is given by

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=k_{\text{cat}}^{\mathrm{A}}([{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]+[{\mathrm{E}}_{\mathrm{A}}\text{SR}])+k_{\text{cat}}^{\mathrm{I}}([{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]+[{\mathrm{E}}_{\mathrm{I}}\text{SR}])\\ =[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}\end{array}$$ (43)

The rate of product formation (43) for different [R] values is shown in Figure 6. It is important to realize that, by choosing the weights in Figure 5, we have selected a particular model for the allosteric regulator, namely, one in which the regulator binds equally well to an enzyme with or without substrate. There are many other possible models. For example, we could add an interaction energy between an allosteric regulator and a bound substrate. However, the simple model in Figure 5 already possesses the important feature that adding more allosteric activator yields a larger rate of product formation $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$, as shown in Figure 6.

Figure 6.

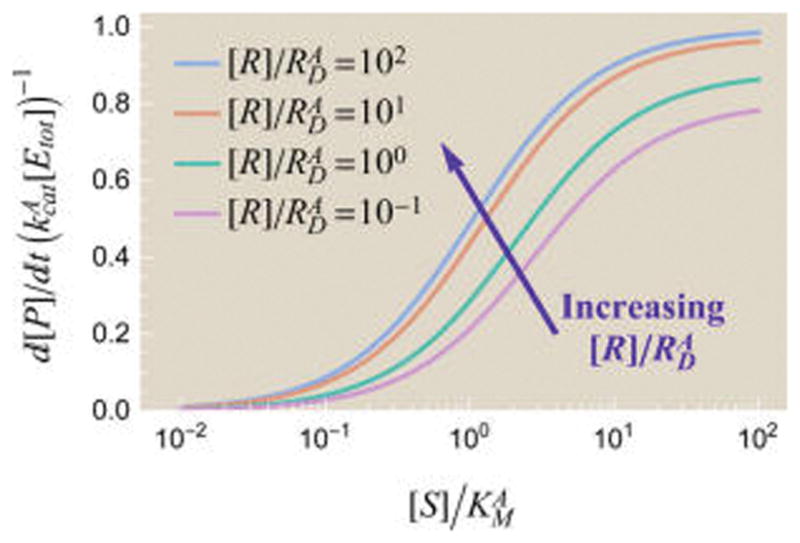
Effects of an allosteric regulator R on the rate of product formation $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. The regulator’s greater affinity for the active enzyme state increases the fraction of the active conformations and hence $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. Parameters used were $\frac{R_{\mathrm{D}}^{\mathrm{A}}}{R_{\mathrm{D}}^{\mathrm{I}}}={10}^{-2}$ and the parameters from Figure 4.

An allosteric regulator effectively tunes the energies of the active and inactive states. To better understand this, consider the probability of an active state enzyme–substrate complex (with or without a bound regulator). Adding eqs 38 and 39,

$$\begin{array}{l}{p}_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}}+p_{{\mathrm{E}}_{\mathrm{A}}\text{SR}}=\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}\\ \equiv \frac{{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}}{{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}\end{array}$$ (44)

where

$${\stackrel{\sim }{\epsilon }}_{\mathrm{A}}={\epsilon }_{\mathrm{A}}-\frac{1}{\beta }log\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)$$ (45)

$${\stackrel{\sim }{\epsilon }}_{\mathrm{I}}={\epsilon }_{\mathrm{I}}-\frac{1}{\beta }log\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)$$ (46)

We now compare the total probability that an active state enzyme will be bound to substrate in the presence of an allosteric regulator (eq 44) to this probability in the absence of an allosteric regulator (eq 24). These two equations show that a MWC enzyme in the presence of regulator concentration [R] is equivalent to a MWC enzyme with no regulator provided that we use the new energies ε̃_A and ε̃_I for the active and inactive states. An analogous statement holds for all of the conformations of the enzyme, so that the effects of a regulator can be completely absorbed into the energies of the active and inactive states! In other words, adding an allosteric regulator allows us to tune the parameters ε_A and ε_I of an allosteric enzyme, and thus change its rate of product formation, in a quantifiable manner. This simple result emerges from our assumptions that the allosteric regulator and substrate bind independently to the enzyme and that the allosteric regulator does not affect the rate of product formation.

One application of this result is that we can easily compute the dynamic range of an enzyme as well as the concentration of substrate for half-maximal rate of product formation discussed in section 2.2. Both of these quantities follow from the analogous expressions for a MWC enzyme (eqs 33 and 35) using the effective energies ε̃_A and ε̃_I, resulting in a dynamic range of the form

$$\text{dynamic}\text{range}=[{\mathrm{E}}_{\text{tot}}]k_{\text{cat}}^{\mathrm{A}}\left(1-\frac{1-\frac{k_{\text{cat}}^{\mathrm{I}}}{k_{\text{cat}}^{\mathrm{A}}}}{1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{A}}}{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{I}}}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}}\right)$$ (47)

and an [S₅₀] value of

$$[{\mathrm{S}}_{50}]=K_{\mathrm{M}}^{\mathrm{A}}\frac{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{A}}}{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{I}}}+1}{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{A}}}{1+[\mathrm{R}]/R_{\mathrm{D}}^{\mathrm{I}}}+\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}}$$ (48)

As expected, the dynamic range of an enzyme increases with regulator concentration [R] for an allosteric activator ( $R_{\mathrm{D}}^{\mathrm{A}}<R_{\mathrm{D}}^{\mathrm{I}}$). Adding more activator will shift [S₅₀] to the left if $K_{\mathrm{M}}^{\mathrm{A}}<K_{\mathrm{M}}^{\mathrm{I}}$ (as shown in Figure 6) or to the right if $K_{\mathrm{M}}^{\mathrm{A}}>K_{\mathrm{M}}^{\mathrm{I}}$. The opposite effects hold for an allosteric inhibitor ( $R_{\mathrm{D}}^{\mathrm{I}}<R_{\mathrm{D}}^{\mathrm{A}}$).

2.4. Competitive Inhibitor

Another level of control found in many enzymes is inhibition. A competitive inhibitor C binds to the same active site as substrate S, yet unlike the substrate, the competitive inhibitor cannot be turned into product by the enzyme. An enzyme with a single active site can either exist in the unbound state E, as an enzyme–substrate complex ES, or as an enzyme–competitor complex EC. As more inhibitor is added to the system, it crowds out the substrate from the enzyme’s active site which decreases product formation. Many cancer drugs (e.g., lapatinib, sorafenib, erlotinib) are competitive inhibitors for kinases involved in signaling pathways.⁴¹

Starting from our model of a MWC enzyme in Figure 3, we can introduce a competitive inhibitor by drawing two new states (an enzyme–competitor complex in the active and inactive forms), as shown in Figure 7. Only the enzyme–substrate complexes in the active (E_AS) and inactive (E_IS) states form product. The probabilities of each of these states is given by eqs 24 and 26 but using the new partition function (which includes the competitive inhibitor states)

Figure 7.

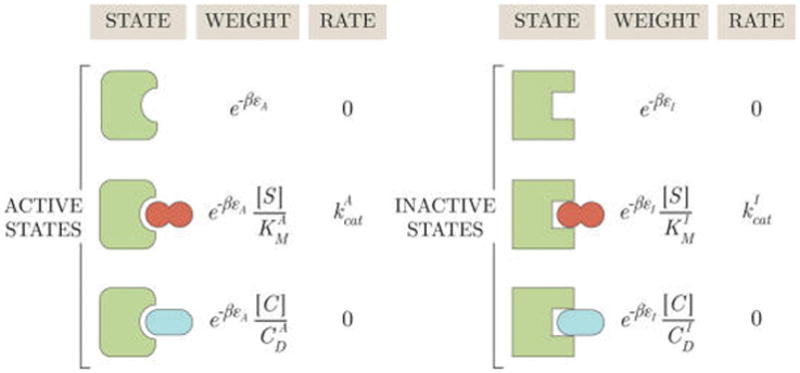
States and weights for a MWC enzyme with a competitive inhibitor. While the substrate S (dark red) can be transformed into product, the inhibitor C (light blue) can occupy the substrate binding site but cannot be catalyzed. As seen with the allosteric regulator in section 2.3, the competitive inhibitor contributes a factor $\frac{[\mathrm{C}]}{C_{\mathrm{D}}}$ to the statistical weight of a state where C_D is the inhibitor’s dissociation constant.

$$Z_{\text{tot}}={\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)$$ (49)

Repeating the same analysis from section 2.2, we write the concentrations of bound enzymes as [E_AS] = [E_tot]p_EAS and [E_IS] = [E_tot]p_EIS, where [E_tot] is the total concentration of enzymes in the system and p_EA,IS is the weight of the bound (in)active state enzyme divided by the partition function, eq 49. Thus, the rate of product formation equals

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=k_{\text{cat}}^{\mathrm{A}}[{\mathrm{E}}_{\mathrm{A}}\mathrm{S}]+k_{\text{cat}}^{\mathrm{I}}[{\mathrm{E}}_{\mathrm{I}}\mathrm{S}]\\ =[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}\end{array}$$ (50)

Figure 8 shows the rate of product formation for various inhibitor concentrations [C]. Adding more competitive inhibitor increases the probability of the inhibitor-bound states and thereby drains probability out of those states competent to form product, as expected. Similarly to our analysis of allosteric regulators, we can absorb the effects of the competitive inhibitor ( $C_{\mathrm{D}}^{\mathrm{A},\mathrm{I}}$) in eq 50 into the enzyme parameters (ε_A,I, $K_{\mathrm{M}}^{\mathrm{A},\mathrm{I}}$)

Figure 8.

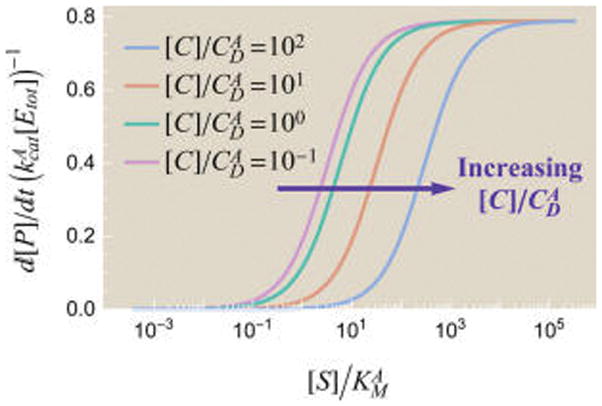
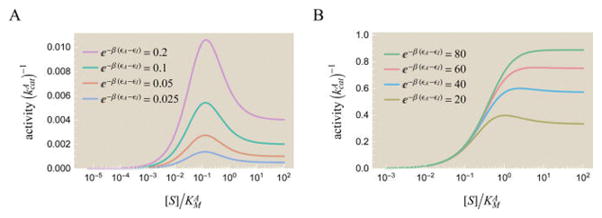
Effects of a competitive inhibitor C on the rate of product formation $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. When $[\mathrm{C}]\lesssim C_{\mathrm{D}}^{\mathrm{A}},C_{\mathrm{D}}^{\mathrm{I}}$, the inhibitor cannot out-compete the substrate at high substrate concentrations, while the free form of enzyme dominates at low substrate concentrations. Therefore, increasing [C] up to values of $~C_{\mathrm{D}}^{\mathrm{A}}$ or $C_{\mathrm{D}}^{\mathrm{I}}$ has little effect on $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$. Once $[\mathrm{C}]\gtrsim C_{\mathrm{D}}^{\mathrm{A}},C_{\mathrm{D}}^{\mathrm{I}}$, the inhibitor can out-compete substrate at large concentrations, pushing the region where the enzyme–substrate complex dominates further to the right. Parameters used were $\frac{C_{\mathrm{D}}^{\mathrm{A}}}{C_{\mathrm{D}}^{\mathrm{I}}}=1$ and the parameters from Figure 4.

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}\right)}\\ \equiv [{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{A}}}\frac{[\mathrm{S}]}{{\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{I}}}\frac{[\mathrm{S}]}{{\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{{\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\stackrel{\sim }{\epsilon }}_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{{\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{I}}}\right)}\end{array}$$ (51)

where we have defined the new energies and Michaelis constants

$${\stackrel{\sim }{\epsilon }}_{\mathrm{A}}={\epsilon }_{\mathrm{A}}-\frac{1}{\beta }log\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)$$ (52)

$${\stackrel{\sim }{\epsilon }}_{\mathrm{I}}={\epsilon }_{\mathrm{I}}-\frac{1}{\beta }log\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)$$ (53)

$${\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{A}}=K_{\mathrm{M}}^{\mathrm{A}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)$$ (54)

$${\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{I}}=K_{\mathrm{M}}^{\mathrm{I}}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)$$ (55)

Note that eq 51 has exactly the same form as the rate of product formation of a MWC enzyme without a competitive inhibitor, eq 30. In other words, a competitive inhibitor modulates both the effective energies and the Michaelis constants of the active and inactive states. Thus, an observed value of K_M may not represent a true Michaelis constant if an inhibitor is present. In the special case of a Michaelis–Menten enzyme (e^−βε_I → 0), we recover the known result that a competitive inhibitor only changes the apparent Michaelis constant.¹⁷

As shown for the allosteric regulator, the dynamic range and the concentration of substrate for half-maximal rate of product formation [S₅₀] follow from the analogous expressions for a MWC enzyme (section 2.2, eqs 33 and 35) using the parameters ε̃_A,I and ${\stackrel{\sim }{K}}_{\mathrm{M}}^{\mathrm{A},\mathrm{I}}$. Hence, an allosteric enzyme with one active site in the presence of a competitive inhibitor has a dynamic range given by

$$\text{dynamic}\text{range}=[{\mathrm{E}}_{\text{tot}}]k_{\text{cat}}^{\mathrm{A}}\left(1-\frac{1-\frac{k_{\text{cat}}^{\mathrm{I}}}{k_{\text{cat}}^{\mathrm{A}}}}{1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}}\right)$$ (56)

and an [S₅₀] value of

$$[{\mathrm{S}}_{50}]=K_{\mathrm{M}}^{\mathrm{A}}\frac{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}+\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}}$$ (57)

Notice that eq 56, the dynamic range of a MWC enzyme in the presence of a competitive inhibitor, is exactly the same as eq 33, the dynamic range in the absence of an inhibitor. This makes sense because in the absence of substrate ([S] → 0) the rate of product formation must be zero and at saturating substrate concentrations ([S] → ∞) the substrate completely crowds out any inhibitor concentration. Instead of altering the rate of product formation at these two limits, the competitive inhibitor shifts the $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ curve, and therefore [S₅₀], to the right as more inhibitor is added.

Said another way, adding a competitive inhibitor effectively rescales the concentration of substrate in a system. Consider a MWC enzyme in the absence of a competitive inhibitor at a measured substrate concentration [S_no[C]]. Now consider a separate system where an enzyme is in the presence of a competitive inhibitor at a concentration [C] and at a measured substrate concentration [S_with[C]]. It is straightforward to show that the rate of product formation $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ is the same for both enzymes

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[{\mathrm{S}}_{\text{no}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[{\mathrm{S}}_{\text{no}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[{\mathrm{S}}_{\text{no}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[{\mathrm{S}}_{\text{no}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}\\ =[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[{\mathrm{S}}_{\text{with}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[{\mathrm{S}}_{\text{with}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[{\mathrm{S}}_{\text{with}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{A}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[{\mathrm{S}}_{\text{with}[\mathrm{C}]}]}{K_{\mathrm{M}}^{\mathrm{I}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}\end{array}$$ (58)

provided that

$$[{\mathrm{S}}_{\text{with}[\mathrm{C}]}]=\frac{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}+1}[{\mathrm{S}}_{\text{no}[\mathrm{C}]}]$$ (59)

For any fixed competitive inhibitor concentration [C], this rescaling amounts to a constant multiplicative factor which results in a horizontal shift on a log scale of substrate concentration [S], as is indeed shown in Figure 8.

As we have seen, the effects of both an allosteric regulator and a competitive inhibitor can be absorbed into the parameters of a MWC enzyme. This suggests that experimental data from enzymes that titrate these ligands can be collapsed into a one-parameter family of curves where the single parameter is either the concentration of an allosteric effector or a competitive inhibitor. Indeed, in section 3.1, we shall find that this theory matches well with experimentally measured activity curves.

2.5. Multiple Substrate Binding Sites

In 1965, Gerhart and Schachman used ultracentrifugation to determine that ATCase can be separated into a large (100 kDa) catalytic subunit where substrate binds and a smaller (30 kDa) regulatory subunit which has binding sites for the allosteric regulators ATP and CTP.⁴² Their measurements correctly predicted that ATCase had multiple active sites and multiple regulatory sites, although their actual numbers were off (they predicted two active sites and four regulatory sites, whereas ATCase has six active sites and six regulatory sites).¹³ Three years later, more refined sequencing by Weber and crystallographic measurements by Wiley and Lipscomb revealed the correct quaternary structure of ATCase.^43–45

Many enzymes are composed of multiple subunits that contain substrate binding sites (also called active sites or catalytic sites). Having multiple binding sites grants the substrate more locations to bind to an enzyme which increases the effective affinity between both molecules. A typical enzyme will have between one and six substrate binding sites, and binding sites for allosteric regulators can appear with similar multiplicity. However, extreme cases exist such as hemocyanin which can have as many as 48 active sites.⁴⁶ Interestingly, across different species, the same enzyme may possess different numbers of active or regulatory sites, as well as be affected by other allosteric regulators and competitive inhibitors.^10,47 Furthermore, multiple binding sites may interact with each other in a complex and often uncharacterized manner.⁴⁸

We now extend the single-site model of a MWC enzyme introduced in Figure 3 to a MWC enzyme with two substrate binding sites. Assuming that both binding sites are identical and independent, the states and weights of the system are shown in Figure 9. When the enzyme is doubly occupied E_AS², we assume that it forms product twice as fast as a singly occupied enzyme E_AS.

Figure 9.

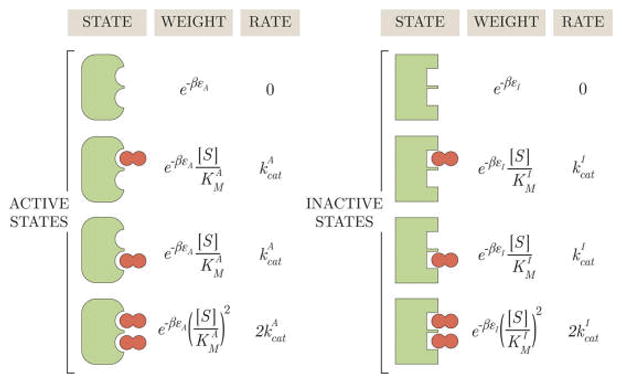
States and weights for a MWC enzyme with two substrate binding sites. Each binding site acts independently, and the rate of product formation of a doubly bound state is twice the rate of the corresponding singly bound state.

It has been shown that, in MWC models, explicit cooperative interaction energies are not required to accurately model biological systems; cooperativity is inherently built into the fact that all binding sites switch concurrently from an active state to an inactive state.¹⁶ For example, suppose an inactive state enzyme with two empty catalytic sites binds with its inactive state affinity $K_{\mathrm{M}}^{\mathrm{I}}$ to a single substrate, and that this binding switches the enzyme from the inactive to the active state. Then, the second, still empty, catalytic site now has the active state affinity $K_{\mathrm{M}}^{\mathrm{A}}$, an effect which can be translated into cooperativity. Note that an explicit interaction energy, if desired, can be added to the model very simply.

As in the proceeding sections, we compute the probability and concentration of each enzyme conformation from the states and weights (see eqs 23–29). Because the active and inactive conformations each have two singly bound states and one doubly bound state with twice the rate, the enzyme’s rate of product formation is given by

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=k_{\text{cat}}^{\mathrm{A}}(2p_{{\mathrm{E}}_{\mathrm{A}}\mathrm{S}})+2k_{\text{cat}}^{\mathrm{A}}(p_{{\mathrm{E}}_{\mathrm{A}}{\mathrm{S}}^2})+k_{\text{cat}}^{\mathrm{I}}(2p_{{\mathrm{E}}_{\mathrm{I}}\mathrm{S}})+2k_{\text{cat}}^{\mathrm{I}}(p_{{\mathrm{E}}_{\mathrm{I}}{\mathrm{S}}^2})\\ =2[{\mathrm{E}}_{\text{tot}}]\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}{\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)}^2+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}{\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}^2}\end{array}$$ (60)

We will have much more to say about this model in section 3.2.2, where we will show that $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ as a function of substrate concentration [S] may form a peak. For now, we mention the well-known result that a Michaelis–Menten enzyme with two independent active sites will act identically to two Michaelis–Menten enzymes each with a single active site (as can be seen in the ε_I → ∞ limit of eq 60).¹⁷ It is intuitively clear that this result does not extend to MWC enzymes: $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ for a two-site MWC enzyme, eq 60, does not equal twice the value of $\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ for a one-site MWC enzyme, eq 30.

2.6. Modeling Overview

The above sections allow us to model a complex enzyme with any number of substrate binding sites, competitive inhibitors, and allosteric regulators. Assuming that the enzyme is in steady state and that the cycle condition holds, we first enumerate its states and weights and then use those weights to calculate the rate of product formation. Our essential conclusions about the roles of the various participants in these reactions can be summarized as follows:

1. The (in)active state enzyme contributes a factor (e^−βε_I) e^−βε_A to the weight. The mathematical simplicity of this model belies the complex interplay between the active and inactive states. Indeed, a MWC enzyme cannot be decoupled into two Michaelis–Menten enzymes (one for the active and the other for the inactive states).

2. Each bound substrate contributes a factor $(\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}})\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}$ in the (in)active state where $K_{\mathrm{M}}=\frac{k_{\text{off}}+k_{\text{cat}}}{k_{\text{on}}}$ is a Michaelis constant between the substrate and enzyme. It is this Michaelis constant, and not the dissociation constant, which enters the states and weights diagram.

3. Each bound allosteric regulator or competitive inhibitor X contributes a factor $(\frac{[\mathrm{X}]}{X_{\mathrm{d}}^{\mathrm{I}}})\frac{[\mathrm{X}]}{X_{\mathrm{d}}^{\mathrm{A}}}$ in the (in)active state where $X_{\mathrm{D}}=\frac{k_{\text{off}}^{\mathrm{X}}}{k_{\text{on}}^{\mathrm{X}}}$ is the dissociation constant between X and the enzyme. An allosteric regulator R effectively tunes the energies of the active and inactive states, as shown in eqs 45 and 46. A competitive inhibitor C effectively changes both the energies and Michaelis constants of the active and inactive states, as described by eqs 52–55.

4. The simplest model for multiple binding sites assumes that each site is independent of the others. The MWC model inherently accounts for the cooperativity between these sites, resulting in sigmoidal activity curves despite no direct interaction terms.

In section B of the Supporting Information, we simultaneously combine all of these mechanisms by analyzing the rate of product formation of ATCase (which has multiple binding sites) in the presence of substrate, a competitive inhibitor, and allosteric regulators. In addition, the supplementary Mathematica notebook lets the reader specify their own enzyme and see its corresponding properties.

Note that while introducing new components (such as a competitive inhibitor or an allosteric regulator) introduces new parameters into the system, increasing the number of sites does not. For example, a MWC enzyme with one (Figure 3), two (Figure 9), or more active sites would require the same five parameters: e^{−β(ε_A−ε_I)}, $K_{\mathrm{M}}^{\mathrm{A}},K_{\mathrm{M}}^{\mathrm{I}},k_{\text{cat}}^{\mathrm{A}}$, and $k_{\text{cat}}^{\mathrm{I}}$.

3. APPLICATIONS

Having built a framework to model allosteric enzymes, we now turn to some applications of how this model can grant insights into observed enzyme behavior. Experimentally, the rate of product formation of an enzyme is often measured relative to the enzyme concentration, a quantity called activity

$$A\equiv \frac{1}{[{\mathrm{E}}_{\text{tot}}]}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$$ (61)

Enzymes are often characterized by their activity curves as substrate, inhibitor, and regulator concentrations are titrated. Such data not only determines important kinetic constants but can also characterize the nature of molecular players such as whether an inhibitor is competitive, uncompetitive, mixed, or noncompetitive.^49–51 After investigating several activity curves, we turn to a case study of the curious phenomenon of substrate inhibition, where saturating concentrations of substrate inhibit enzyme activity, and propose a new minimal mechanism for substrate inhibition caused solely by allostery.

3.1. Regulator and Inhibitor Activity Curves

We begin with an analysis of α-amylase, one of the simplest allosteric enzymes, which only has a single catalytic site. α-Amylase catalyzes the hydrolysis of large polysaccharides (e.g., starch and glycogen) into smaller carbohydrates in human metabolism. It is competitively inhibited by isoacarbose⁵¹ at the active site and is allosterically activated by Cl⁻ ions at a distinct allosteric site.⁵²

Figure 10 plots substrate concentration divided by activity, [S]/A, as a function of substrate [S]. Recall from section 2.3 that an enzyme with one active site and one allosteric site has activity given by eq 43

Figure 10.

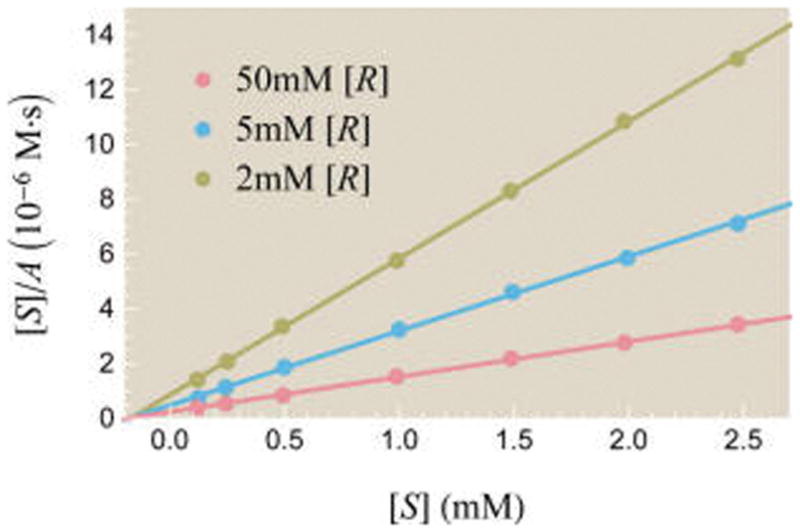
Theoretically and experimentally probing the effects of an allosteric regulator on activity. Data points show experimentally measured activity from Feller et al. for the enzyme α-amylase using substrate analogue [S] (EPS) and allosteric activator [R] (NaCl).⁵² Best fit theoretical curves described by eq 63 are overlaid on the data. The best fit parameters are e^{−β(ε_A−ε_I)} = 7.8 × 10⁻⁴, $K_{\mathrm{M}}^{\mathrm{A}}=0.6\text{mM},K_{\mathrm{M}}^{\mathrm{I}}=0.2\text{mM},R_{\mathrm{D}}^{\mathrm{A}}=0.03\text{mM},R_{\mathrm{D}}^{\mathrm{I}}=7.9\text{mM},k_{\text{cat}}^{\mathrm{A}}=14{\mathrm{s}}^{-1}$, and $k_{\text{cat}}^{\mathrm{I}}=0.01{\mathrm{s}}^{-1}$.

$$A=\frac{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}$$ (62)

Thus, we expect the [S]/A curves in Figure 10 to be linear in [S]

$$\frac{[\mathrm{S}]}{A}=\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{1}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{A}}}\right)+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{1}{K_{\mathrm{M}}^{\mathrm{I}}}\left(1+\frac{[\mathrm{R}]}{R_{\mathrm{D}}^{\mathrm{I}}}\right)}$$ (63)

Figure 10 shows that the experimental data is well characterized by the theory so that the rate of product formation at any other substrate and allosteric activator concentration can be predicted by this model. The fitting procedure is discussed in detail in section B of the Supporting Information.

In the special case of a Michaelis–Menten enzyme (ε_I → ∞), the above equation becomes

$$\frac{[\mathrm{S}]}{A}=\frac{K_{\mathrm{M}}^{\mathrm{A}}+[\mathrm{S}]}{k_{\text{cat}}^{\mathrm{A}}}({\epsilon }_{\mathrm{I}}\to \infty )$$ (64)

The x-intercept of all lines in such a plot would intersect at the point ( $-K_{\mathrm{M}}^{\mathrm{A}}$, 0) which allows an easy determination of $K_{\mathrm{M}}^{\mathrm{A}}$. This is why plots of [S] vs [S]/A, called Hanes plots, are often seen in enzyme kinetics data. Care must be taken, however, when extending this analysis to allosteric enzymes where the form of the x-intercept is more complicated.

We now turn to competitive inhibition. Figure 11A plots the inverse rate of product formation ${\left(\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)}^{-1}$ of α-amylase as a function of the competitive inhibitor concentration [C]. The competitive inhibitor isoacarbose is titrated for three different concentrations of the substrate α-maltotriosyl fluoride (αG3F).

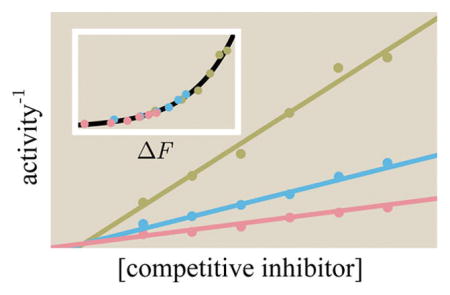
Figure 11.

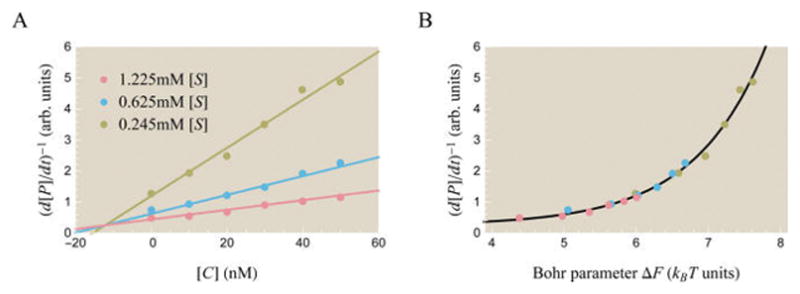
Theoretically and experimentally probing the effects of a competitive inhibitor on activity. (A) Data points show experimentally measured activity in arbitrary units from Li et al. for the enzyme α-amylase using substrate analogue [S] (α-maltotriosyl fluoride) and competitive inhibitor [C] (isoacarbose).⁵¹ Best fit theoretical curves described by the inverse of eq 65 are overlaid on the data. The best fit parameters are e^{−β(ε_A−ε_I)} = 36, $K_{\mathrm{M}}^{\mathrm{A}}=0.9\text{mM},K_{\mathrm{M}}^{\mathrm{I}}=2.6\text{mM},C_{\mathrm{D}}^{\mathrm{A}}=12\text{nM},C_{\mathrm{D}}^{\mathrm{I}}=260\text{nM}$, and $\frac{k_{\text{cat}}^{\mathrm{A}}}{k_{\text{cat}}^{\mathrm{I}}}=1.4$. Note that the x-axis varies [C] rather than [S] as in most other plots. (B) A data collapse of the three curves using the Bohr parameter ΔF from eq 68 which encompasses the effects of both the substrate and inhibitor upon the system.

Recall from section 2.4, eq 50 that the rate of product formation for an allosteric enzyme with one active site in the presence of a competitive inhibitor is given by

$${\left(\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)}^{-1}=\frac{1}{[{\mathrm{E}}_{\text{tot}}]}\frac{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}{k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}$$ (65)

so that the best fit ${\left(\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)}^{-1}$ curves in Figure 11A are linear functions of [C]. Rather than thinking of eq 65 as a function of the competitive inhibitor concentration [C] and the substrate concentration [S] separately, we can combine these two quantities into a single natural parameter for the system. This will enable us to collapse the different activity curves in Figure 11A onto a single master curve, as shown in Figure 11B. Algebraically manipulating eq 65,

$$\begin{array}{l}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=[{\mathrm{E}}_{\text{tot}}]\frac{\left(k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}+k_{\text{cat}}^{\mathrm{I}}\right)\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{\left({\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}+1\right)\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}\\ \equiv [{\mathrm{E}}_{\text{tot}}]\frac{(k_{\text{cat}}^{\mathrm{A}}K+k_{\text{cat}}^{\mathrm{I}}){\mathrm{e}}^{-\beta \mathrm{\Delta }F}}{(K+1){\mathrm{e}}^{-\beta \mathrm{\Delta }F}+1}\end{array}$$ (66)

where

$$K={\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}}$$ (67)

$$\mathrm{\Delta }F=-\frac{1}{\beta }log\left[\frac{\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}}{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{A}}}\right)+\left(1+\frac{[\mathrm{C}]}{C_{\mathrm{D}}^{\mathrm{I}}}\right)}\right]$$ (68)

Therefore, ${\left(\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}\right)}^{-1}$ curves at any substrate and inhibitor concentrations can be compactly shown as data points lying on a single curve in terms of ΔF, which is called the Bohr parameter. Such a data collapse is also possible in the case of allosteric regulators or enzymes with multiple binding sites, although those data collapses may require more than one variable ΔF. In section C of the Supporting Information, we show that the Bohr parameter corresponds to a free energy difference between enzyme states and examine other cases of data collapse.

3.2. Substrate Inhibition

We now turn to a striking phenomenon observed in the enzyme literature: not all enzymes have a monotonically increasing rate of product formation. Instead, peaks such as those shown schematically in Figure 12 can arise in various enzymes, displaying behavior that is impossible within Michaelis–Menten kinetics. By exploring these two phenomena with the MWC model, we gain insight into their underlying mechanisms and can make quantifiable predictions as to how to create, amplify, or prevent such peaks.

Figure 12.

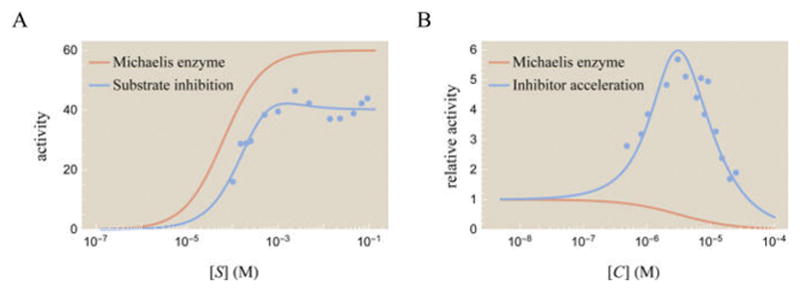
Enzyme activity curves do not need to be monotonic as predicted by Michaelis–Menten enzyme kinetics. (A) As many as 20% of enzymes exhibit substrate inhibition, where at high substrate concentrations activity decreases, in contrast to a Michaelis–Menten enzyme shown for reference.^53,54 Activity for acetylcholinesterase is shown in units of (nanomol of product)·min⁻¹·(mL of enzyme)^−1.55 (B) Some enzymes exhibit inhibitor acceleration, where adding a small amount of a competitive inhibitor increases the rate of product formation. This generates a peak in activity, in stark contrast to a Michaelis–Menten enzyme which only decreases its activity as more competitive inhibitor is added. Relative activity is shown for ATCase, where relative activity equals activity at [C] divided by the activity with no competitive inhibitor.¹⁰ The data and best fit parameters for the substrate inhibition and inhibitor acceleration curves are discussed in section C of the Supporting Information.

In Figure 12A, the monotonically increasing Michaelis– Menten curve makes intuitive sense—a larger substrate concentration implies that at any moment the enzyme’s active site is more likely to be occupied by substrate. Therefore, we expect that the activity, $A=\frac{1}{[{\mathrm{E}}_{\text{tot}}]}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$, should increase with the substrate concentration [S]. However, many enzymes exhibit a peak activity, a behavior called substrate inhibition.⁵³

Even more surprisingly, when a small amount of competitive inhibitor—a molecule whose very name implies that it competes with substrate and decreases activity—is mixed together with enzyme, it can increase the rate of product formation. This latter case, called inhibitor acceleration, is shown in Figure 12B.^10,56 In contrast, a Michaelis–Menten enzyme shows the expected behavior that adding more competitive inhibitor decreases activity. We will restrict our attention to the phenomenon of substrate inhibition and relegate a discussion of inhibitor acceleration to section D of the Supporting Information.

Using the MWC enzyme model, we can make predictions about which enzymes can exhibit substrate inhibition. We first formulate a relationship between the fundamental physical parameters of an enzyme that are required to generate such a peak and then consider what information about these underlying parameters can be gained by analyzing experimental data.

3.2.1. Single-Site Enzyme

As a preliminary exercise, we begin by showing that an enzyme with a single active site cannot exhibit substrate inhibition. Said another way, the activity, eq 61, of such an enzyme cannot have a peak as a function of substrate concentration [S]. For the remainder of this paper, we will use the fact that all Michaelis and dissociation constants (K_M’s, C_D’s, and R_D’s) are positive and assume that both catalytic constants ( $k_{\text{cat}}^{\mathrm{A}}$ and $k_{\text{cat}}^{\mathrm{I}}$) are strictly positive unless otherwise stated.

Consider the MWC enzyme with a single substrate binding site shown in Figure 3. Using eq 30, it is straightforward to compute the derivative of activity with respect to substrate concentration [S], namely,

$$\frac{\mathrm{d}A}{\mathrm{d}[\mathrm{S}]}=\frac{({\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}})\left({\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{k_{\text{cat}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{A}}}+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\frac{k_{\text{cat}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}{{\left({\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)\right)}^2}$$ (69)

Since the numerator cannot equal zero, this enzyme cannot have a peak in its activity when [S] is varied. Note that the numerator is positive, indicating that enzyme activity will always increase with substrate concentration.

The above results are valid for an arbitrary MWC enzyme with a single site. In particular, in the limit ε_I → ∞, a MWC enzyme becomes a Michaelis–Menten enzyme. Therefore, a Michaelis–Menten enzyme with a single active site cannot exhibit a peak in activity. In section E of the Supporting Information, we discuss the generalization of this result: a Michaelis–Menten enzyme with an arbitrary number of catalytic sites cannot have a peak in activity. However, as we shall now see, this generalization cannot be made for a MWC enzyme, which can indeed exhibit a peak in its activity when it has multiple binding sites.

3.2.2. Substrate Inhibition

As many as 20% of enzymes are believed to exhibit substrate inhibition, which can offer unique advantages to enzymes such as stabilizing their activity amid fluctuations, enhancing signal transduction, and increasing cellular efficiency.⁵⁴ This prevalent phenomenon has elicited various explanations, many of which rely on nonequilibrium enzyme dynamics, although some equilibrium mechanisms are known.⁵³ An example of this latter case is seen in the enzyme aspartate transcarbamoylase (ATCase) which catalyzes one of the first steps in the pyrimidine biosynthetic pathway. Before ATCase can bind to its substrate asparatate (Asp), an intermediate molecule carbamoyl phosphate (CP) must first bind to ATCase, inducing a change in the enzyme’s shape and electrostatics which opens up the Asp binding slot.^57,58 Because Asp can weakly bind to the CP binding pocket, at high concentrations Asp will outcompete CP and prevent the enzyme from working as efficiently, thereby causing substrate inhibition.⁵⁹

To the list of such mechanisms, we add the possibility that an enzyme may exhibit substrate inhibition without any additional effector molecules. In particular, an allosteric enzyme with two identical catalytic sites can exhibit a peak in activity when the substrate concentration [S] is varied. We will first analyze the properties of this peak and then examine why it can occur. For simplicity, we will assume $k_{\text{cat}}^{\mathrm{I}}=0$ throughout this section and leave the general case for section E of the Supporting Information.

Using eqs 60 and 61, the activity of a MWC enzyme with two active sites is given by

$$A=\frac{1}{[{\mathrm{E}}_{\text{tot}}]}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}=\frac{2k_{\text{cat}}^{\mathrm{A}}{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)}{{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{A}}}{\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{A}}}\right)}^2+{\mathrm{e}}^{-\beta {\epsilon }_{\mathrm{I}}}{\left(1+\frac{[\mathrm{S}]}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}^2}$$ (70)

A peak will exist provided that $\frac{\text{dA}}{\mathrm{d}[\mathrm{S}]}=0$ has a positive [S] root. The details of differentiating and solving this equation are given in section E of the Supporting Information, the result of which is that a peak in activity A occurs as a function of [S] provided that

$$1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}<{\left(\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}-1\right)}^2(k_{\text{cat}}^{\mathrm{I}}=0)$$ (71)

The height of such a peak is given by

$$A_{\text{peak}}=k_{\text{cat}}^{\mathrm{A}}\frac{K_{\mathrm{M}}^{\mathrm{I}}}{K_{\mathrm{M}}^{\mathrm{A}}-K_{\mathrm{M}}^{\mathrm{I}}}(\sqrt{1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}}-1)$$ (72)

Examples of peaks in activity are shown in Figure 13 for various values of e^{−β(ε_A−ε_I)}. Substituting in the peak condition eq 71, the maximum peak height is at most

Figure 13.

Peaks in enzyme activity $A=\frac{1}{E_{\text{tot}}}\frac{\mathrm{d}[\mathrm{P}]}{\mathrm{d}t}$ as a function of substrate concentration [S]. Activity is shown in units of $k_{\text{cat}}^{\mathrm{A}}$, which rescales the activity curves vertically. The peak for (A) small and (B) large ratios of the enzyme’s energy in the active versus inactive state, e^{−β(ε_A−ε_I)}. The height of the peak increases with e^{−β(ε_A−ε_I)}. The activity is computed from eq 70 using the parameters $k_{\text{cat}}^{\mathrm{I}}=0,\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}=10$, and the different values of e^{−β(ε_A−ε_I)} shown. As predicted by eq 71, every value in the range ${\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}<{\left(\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}-1\right)}^2$ will yield a peak in activity. While the peak is more pronounced when the active state is energetically favorable (e^{−β(ε_A−ε_I)} < 1) in part A, the maximum peak height is much larger in part B, as seen by the different scale of the y-axis.

$$A_{\text{peak}}<k_{\text{cat}}^{\mathrm{A}}\frac{\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}-2}{\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}-1}$$ (73)

If we consider the maximum value of e^{−β(ε_A−ε_I)} allowed by the peak condition eq 71, the peak height approaches $k_{\text{cat}}^{\mathrm{A}}$ for large $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}$ (as seen by the green curve e^{−β(ε_A−ε_I)} = 80 in Figure 13B). In this limit, the active bound state dominates over all the other enzyme states so that the activity reaches its largest possible value, $k_{\text{cat}}^{\mathrm{A}}$. Although the “peak height” is maximum in this case, the activity curve is nearly sigmoidal, making the peak hard to distinguish. To that end, it is reasonable to compare the peak height to the activity at large substrate concentrations

$$A_{[\mathrm{S}]\to \infty }=2k_{\text{cat}}^{\mathrm{A}}\frac{{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}}{{\left(\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}\right)}^2+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}}$$ (74)

As the energy difference between the active and inactive states e^{−β(ε_A−ε_I)} increases, the peak height A_peak monotonically increases but the relative peak height $\frac{A_{\text{peak}}}{A_{[\mathrm{S}]\to \infty }}$ monotonically decreases. These relations might be used to design enzymes with particular activity curves; conversely, experimental data of substrate inhibition can be used to fix a relation between the parameters e^{−β(ε_A−ε_I)} and $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}$ of an enzyme.

We now turn to the explanation of how such a peak can occur. One remarkable fact is that a peak cannot happen without allostery. If we consider a Michaelis–Menten enzyme (by taking the limit $k_{\text{cat}}^{\mathrm{I}}\to 0$ and ε_I → ∞), then the peak condition eq 71 cannot be satisfied.

To gain a qualitative understanding of how a peak can occur, consider an enzyme that inherently prefers the active state (e^{−β(ε_A−ε_I)} > 1) but with substrate that preferentially binds to the inactive state ( $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}>1$). Such a system is realized in bacterial chemotaxis, where the chemotaxis receptors are active when unbound but inactive when bound to substrate.³² This setup is shown schematically in Figure 14. At low substrate concentrations, $[\mathrm{S}]\ll K_{\mathrm{M}}^{\mathrm{A}}$, most enzymes will be unbound and therefore in the active state. At intermediate substrate concentrations, $[\mathrm{S}]\approx K_{\mathrm{M}}^{\mathrm{A}}$, many enzymes will be singly bound. Because $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}>1$, the substrate will pull these bound enzymes toward the inactive state. For large substrate concentrations, $[\mathrm{S}]\gg K_{\mathrm{M}}^{\mathrm{A}}$, most of the enzymes will be doubly bound and hence will be predominantly in the inactive form. Because the inactive state does not catalyze substrate ( $k_{\text{cat}}^{\mathrm{I}}=0$), only the number of substrates bound to active state enzymes increases the rate of product formation, and because more of these exist in the intermediate regime, a peak forms. To be more quantitative, the activity eq 70 at the medium substrate concentration ( $[\mathrm{S}]=K_{\mathrm{M}}^{\mathrm{A}}$) is given by

Figure 14.

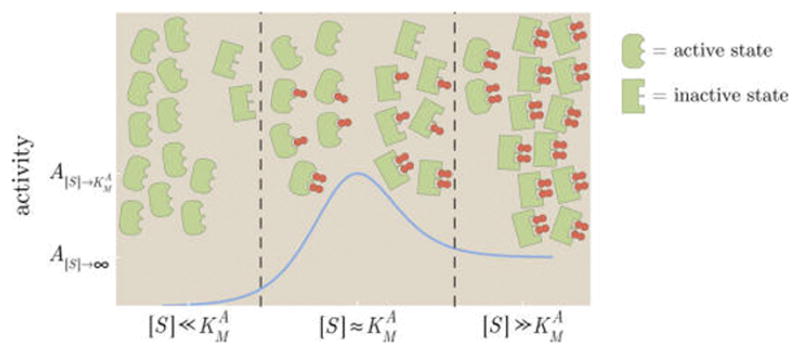
Mechanism underlying the peak in activation by substrate S. At low substrate concentrations (left region), all enzymes are unbound and are mostly in the active form (rounded, green). As the amount of substrate is increased (middle region), the probability that an enzyme is singly bound and then doubly bound increases. Because the substrate prefers to bind to an inactive state (sharp, green) enzyme–substrate complex, binding more substrate pushes the enzymes into the inactive state. At medium substrate concentrations, more active state enzyme–substrate complexes exist than at high substrate concentrations (right region) which yields a peak. Each enzyme fluctuates between its different configurations, and the cartoons show the distributions of the most prevalent states.

$$A_{[\mathrm{S}]\to K_{\mathrm{M}}^{\mathrm{A}}}=k_{\text{cat}}^{\mathrm{A}}\frac{4{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}}{{\left(\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}+1\right)}^2+4{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}}$$ (75)

Comparing this to A_[S]→∞ in eq 74, we find that $A_{[\mathrm{S}]\to K_{\mathrm{M}}^{\mathrm{A}}}>A_{[\mathrm{S}]\to \infty }$ provided that

$$1+{\mathrm{e}}^{-\beta ({\epsilon }_{\mathrm{A}}-{\epsilon }_{\mathrm{I}})}<\frac{1}{4}{\left(\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}-1\right)}^2$$ (76)

This is in close agreement with the peak condition eq 71, and the factor of $\frac{1}{4}$ is due to the fact that the peak need not occur precisely at $[\mathrm{S}]=K_{\mathrm{M}}^{\mathrm{A}}$.

Note that the peak condition eq 71 does not necessarily force the unbound enzyme to favor the active state (e^{−β(ε_A−ε_I)} > 1), since this condition can still be satisfied if e^{−β(ε_A−ε_I)} < 1. However, the peak condition does require that substrate preferentially binds to the inactive state enzyme (in fact, we must have $\frac{K_{\mathrm{M}}^{\mathrm{A}}}{K_{\mathrm{M}}^{\mathrm{I}}}>2$ to satisfy the peak condition).

Recall that as many as 20% of enzymes exhibit substrate inhibition, and this particular mechanism will not apply in every instance. To be concrete, an allosteric enzyme that obeys the mode of substrate inhibition proposed above (1) must have at least two catalytic sites and (2) must be driven toward the inactive state upon substrate binding. Therefore, an enzyme such as ATCase which exhibits substrate inhibition but where the substrate preferentially binds to the active state enzyme must have a different underlying mechanism.⁶⁰ Various alternative causes including the effects of pH due to substrate or product buildup^17,61 or the sequestering effects of ions^62,63 may also be responsible for substrate inhibition. However, the mechanism of substrate inhibition described above exactly matches the conditions of acetylcholinesterase whose activity, shown in Figure 12A, is well categorized by the MWC model.⁵⁵ It would be interesting to test this theory by taking a well characterized enzyme, tuning the MWC parameters so as to satisfy the peak condition eq 71 (or an analogous relationship for an enzyme with more than two catalytic sites), and checking whether the system then exhibits substrate inhibition. Experimentally, tuning the parameters can be undertaken by introducing allosteric regulators or competitive inhibitors as described by eqs 45 and 46 and eqs 52–55, respectively. For example, in section E of the Supporting Information, we describe an enzyme system where introducing a competitive inhibitor induces a peak in activity.

4. DISCUSSION

Allosteric molecules pervade all realms of biology from chemotaxis receptors to chromatin to enzymes.^15,64–66 There are various ways to capture the allosteric nature of macromolecules, with the MWC model representing one among many.^8,67,68 In any such model, the simple insight that molecules exist in an active and inactive state opens a rich new realm of dynamics.

The plethora of molecular players that interact with enzymes serve as the building blocks to generate complex behavior. In this paper, we showed the effects of competitive inhibitors, allosteric regulators, and multiple binding sites, looking at each of these factors first individually and then combining separate aspects. This framework matched well with experimental data and enabled us to make quantifiable predictions on how the MWC enzyme parameters may be tuned upon the introduction of an allosteric regulator (eqs 45 and 46) or a competitive inhibitor (eqs 52–55).

As an interesting application, we used the MWC model to explore the unusual behavior of substrate inhibition, where past a certain point adding more substrate to a system decreases its rate of product formation. This mechanism implies that an enzyme activity curve may have a peak (see Figure 12), a feat that is impossible for a Michaelis–Menten enzyme. We explored a novel minimal mechanism for substrate inhibition which rested upon the allosteric interactions of the active and inactive enzyme states, with suggestive evidence for such a mechanism in acetylecholinesterase.

The power of the MWC model stems from its simple description, far-reaching applicability, and its ability to unify the proliferation of data gained over the past 50 years of enzymology research. A series of activity curves at different concentrations of a competitive inhibitor all fall into a one-parameter family of curves, allowing us to predict the activity at any other inhibitor concentration. Such insights not only shed light on the startling beauty of biological systems but may also be harnessed to build synthetic circuits and design new drugs.