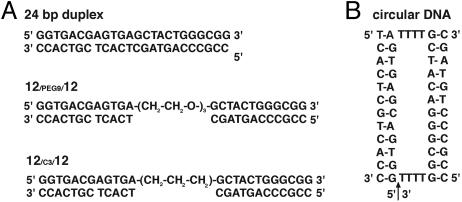Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution

Abstract

Understanding biological and physical processes involving nucleic acids, such as the binding of proteins to DNA and RNA, DNA condensation, and RNA folding, requires an understanding of the ion atmosphere that surrounds nucleic acids. We have used a simple model DNA system to determine how the ion atmosphere modulates interactions between duplexes in the absence of specific metal ion-binding sites and other complicated interactions. In particular, we have tested whether the Coulomb repulsion between nucleic acids can be reversed by counterions to give a net attraction, as has been proposed recently for the rapid collapse observed early in RNA folding. The conformation of two DNA duplexes tethered by a flexible neutral linker was determined in the presence of a series of cations by small angle x-ray scattering. The small angle x-ray scattering profiles of two control molecules with distinct shapes (a continuous duplex and a mimic of the compact DNA) were in good agreement with predictions, establishing the applicability of this approach. Under low-salt conditions (20 mM Na⁺), the tethered duplexes are extended because of a Coulombic repulsion estimated to be 2–5 kT/bp. Addition of high concentrations of Na⁺ (1.2 M), Mg²⁺ (0.6 M), and spermidine³⁺ (75 mM) resulted in electrostatic relaxation to a random state. These results indicate that a counterion-induced attractive force between nucleic acid duplexes is not significant under physiological conditions. An upper limit on the magnitude of the attractive potential under all tested ionic conditions is estimated.

Nucleic acids play a central role in the storage, transmission, and control of genetic information. DNA and RNA associate with numerous protein and nucleic acid partners to form the complexes that participate in and regulate cellular metabolism and form catalytic components of biological machines such as the ribosome. A comprehensive understanding of these biological processes requires understanding the fundamental physical and chemical principles underlying the behaviors of the participating molecules.

Nucleic acids are highly charged biopolymers, with one formal negative charge per monomeric unit. There are many examples of specific interactions of nucleic acids with ions in nucleic acid–protein complexes and in folded RNAs (1, 2). Nevertheless, the vast majority of cations associated with a nucleic acid are nonspecifically bound. These counterions condense onto DNA or RNA and form a thermally fluctuating sheath commonly referred to as the ion atmosphere (3, 4). Indeed, order-of-magnitude calculations estimate enormous repulsive energies for RNA in the absence of counterions (e.g., ≈10³ kT for a folded RNA with ≈400 nucleotides, the size of the Tetrahymena group I intron).∥ This repulsive energy is predominantly overcome by electrostatic interactions with the ion atmosphere (3–5).

Despite the clear importance of the ion atmosphere, experimental investigation has been difficult. The dynamic nature of the ion atmosphere renders it invisible in crystallographic structures. Progress has been made in the direct “visualization” of ion distributions around DNA duplexes in recent neutron scattering (6) and anomalous small angle x-ray scattering (SAXS) experiments that provide constraints on the shape of the ion atmosphere (7). Nevertheless, the energetic effects of this atmosphere still remain unclear.

The widely used nonlinear Poisson Boltzmann (NLPB) model can estimate the electrostatic energies for nucleic acid conformations in different ionic condition (8–12). However, this model is incomplete. It does not account for the finite sizes of ions and, of particular importance to this work, positional correlations between discrete ions beyond a mean-field approximation (13). Recent theoretical work indicates that such ion–ion correlation effects can lead to a net attraction for strongly charged polyelectrolytes in the presence of multivalent cations (13–16). This effect can be thought of as analogous to attractive London dispersion forces caused by correlations of electron clouds between two nearby molecules, with the counterions arranged to minimize repulsion between one another and to maximize attractive interactions with both polyelectrolytes. Indeed, DNA condensation has been observed in numerous studies (refs. 17 and 18 and references therein), and a counterion-correlation-attractive force is a leading candidate for explaining this phenomenon (18). More recently, Murthy and Rose (15) have proposed that a counterion-induced attractive force is responsible for parallel helical arrangements common in nucleic acid crystal structures. Furthermore, a rapid “collapse” early in Mg²⁺-promoted RNA folding has been suggested to arise from analogous attractive forces induced by Mg²⁺ ions (5, 19, 20).

Precise and extensive osmotic stress measurements by Parsegian and colleagues (21–26) have yielded quantitative descriptions of screened electrostatic repulsion, hydration forces, and long-range attractive forces in dense, parallel arrays of DNA double helices with several types of counterions. However, many-body effects (24) and disrupted water structure in these highly dehydrated arrays hinder the direct application of these stress measurements to isolated nucleic acids in solution. Here, we have used a simple tethered DNA in which two DNA duplexes of defined length are connected by a neutral flexible linker (Figs. 1A and 2) to isolate the counterion-modulated interactions between two helices. The results provide estimates for repulsive forces in the presence of low concentrations of monovalent cations and an upper limit for any attractive force in the presence of multivalent cations.

Fig. 1.

The schemes of the model DNA constructs applied herein. (A) The 24-bp duplex, 12_/PEG9/12 and 12_/C3/12.(B) The circular DNA.

Fig. 2.

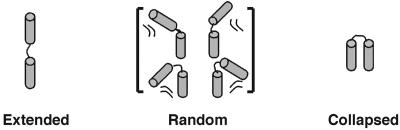
The three conformational states of the tethered DNA (12_/PEG9/12, Fig. 1 A) distinguished herein.

Materials and Methods

Construction of 12-bp Tethered DNAs and 24-bp Duplex DNA. The 12-bp tethered DNAs (12_/PEG9/12 and12_/C3/12) and 24-bp duplex were assembled from chemically synthesized oligonucleotides (Qiagen, Valencia, CA, and Integrated DNA Technologies, Coralville, IA) as shown in Fig. 1A. Oligonucleotides were purified by ion-exchange HPLC chromatography, dried to solid pellets, and resuspended in doubly distilled water. Equimolar complementary oligonucleotides were annealed in 5, 25, or 100 mM sodium 3-(N-morpholino)propanesulfonic acid (Mops), (2, 10, or 40 mM Na⁺, respectively), pH 7.0, with strand concentrations determined by absorbance at 260 nm. The concentrated DNA stocks were then diluted into different salt solutions, with final DNA concentrations of 0.1–0.4 mM. Nondenaturing PAGE with DNA staining by StainsAll (Sigma) indicated that the samples were annealed properly and contained negligible amounts of free single strands.

Construction of 80-bp Tethered DNA and 160-bp Duplex DNA. Long tethered DNA 80_/PEG9/80 was constructed by ligating seven chemically synthesized oligonucleotides using T4 DNA ligase (Fig. 7, which is published as supporting information on the PNAS web site). The 160-bp duplex DNA was assembled by primerless PCR using seven oligonucleotides and then amplified by standard PCR. The 80-bp tethered DNA and the 160-bp duplex DNA were purified by nondenaturing PAGE (6% polyacrylamide/50 mM Tris·borate, pH 8.0/2 mM MgCl₂, 10°C), eluted in 100 mM sodium-acetate (pH 7) overnight, and desalted by using Sep-Pak cartridges (Waters). Dried pellets were resuspended in 100 mM sodium-Mops, pH 7.0, before adding salts.

Construction of Model for the Compact State Using a Circular DNA. A linear 32-nt DNA oligonucleotide (Fig. 1B, with the initial 5′ end indicated by the arrow) was circularized by annealing the ends to a DNA splint and ligating with T4 DNA ligase (27); the product was purified by denaturing PAGE (10% polyacrylamide/7 M urea/10 mM Tris-borate). The circularized single-stranded DNA was then hybridized to two 12-nt complementary oligonucleotides to form the circular DNA as a mimic of the collapsed state (Figs. 1B and 2).

Data Acquisition by SAXS. SAXS data were acquired at 25°C at beamline 4–2 of the Stanford Synchrotron Radiation Laboratory and the BESSRC-CAT beamline 12-ID of the Advanced Photon Source. Scattering was independent of DNA concentration (0.1–0.4 mM), indicating that interparticle ordering, aggregation, and duplex disassociation are negligible. Data shown were obtained with 0.2 mM DNA.

Correction of the Scattering Data for Ion Atmosphere Effects. The total scattering profile I(s) [s = 2 sin(θ/2)/λ; θ is the scattering angle, λ is the x-ray wavelength] is dominated by the contributions from the DNA itself but also includes a smaller contribution (≈20%) from the correlations between DNA and its surrounding ion atmosphere (28). The observed scattering profile can be divided by an s-dependent correction factor to yield the profile from the DNA scattering alone. We have theoretically estimated this correction factor for different DNA conformations in the presence of monovalent (1.2 M Na⁺) or divalent (0.6 M Mg²⁺) cations by using procedures described in ref. 7. The difference in correction factors obtained for tethered DNAs in a fully extended conformation and a collapsed conformation is less than ≈2%; the standard deviation among all conformations is ≈1%, considerably smaller than the statistical error of the data at all scattering angles (Fig. 8, which is published as supporting information on the PNAS web site). Thus, this correction factor is nearly independent of DNA configuration. The factor appropriate to each solution condition was therefore determined as the ratio of the observed scattering profile of a control DNA duplex (in a single conformation) to the predicted scattering profile from the DNA duplex alone (29); 24- and 160-bp duplexes were used as controls for 12- and 80-bp tethered duplexes, respectively.

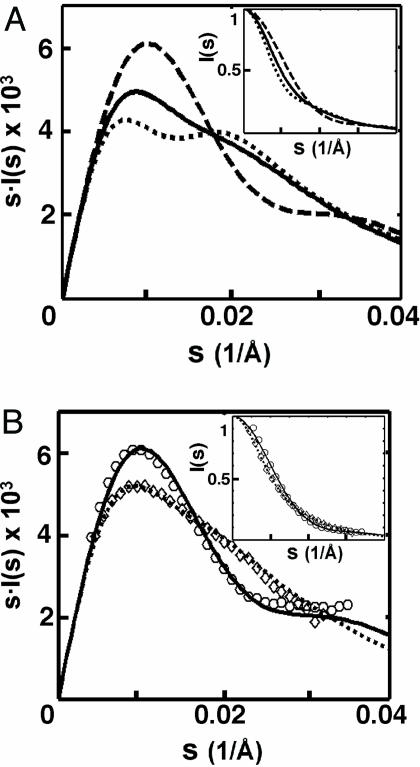
Prediction of SAXS Profiles for Random, Collapsed, and Extended States of the Tethered DNAs. SAXS profiles of individual tethered DNA conformations were calculated as described from atomic models of the DNA (7), including a prediction for a 24-bp duplex (Fig. 3B) as a mimic of the extended state of the tethered 12-bp duplex. To obtain predictions for random, collapsed, and low-salt extended states of the tethered duplex (Fig. 3A), SAXS profiles were averaged for the ensembles of conformations, as described below.

Fig. 3.

Monitoring conformational states of the tethered DNA duplexes by SAXS. (A) Predicted SAXS profiles of the extended (dotted line), random (solid line), and collapsed (dashed line) states of 12-bp tethered DNA (12_/PEG9/12, Fig. 1A). Scattering intensity I(s) has been multiplied by the scattering angle s to help illustrate SAXS profile differences; Inset shows the unweighted profile with intensity normalized to unity at s = 0. (B) Experimental SAXS profiles of 24-bp duplex DNA (diamonds) and circular DNA (circles) compared to the predicted SAXS profiles of the duplex (dotted line) and circular (solid line) DNA. (Inset) Plots of I(s), normalized as in A. SAXS data were obtained with 0.2 mM DNA in 1.2 M NaCl/100 mM Na-Mops, pH 7.0.

For the random state, the two duplexes were allowed to take random orientations and positions, with the tether attachment points constrained to be no further than the maximum tether length. Conformations with any pair of duplex atoms closer than the sum of their van der Waals radii were eliminated. The tether elasticity was taken into account by weighting the contributions of each conformation to the SAXS profile by the end-to-end distance distribution predicted for a freely jointed polymer chain with bond lengths appropriate to the tether and with free rotations around each joint; the distribution matched that expected for a polymer with persistence length of 3.1 Å, consistent with the experimentally measured value of ≈3.5 Å (30). Varying the C—C and C—O bond length (from 1 to 2 Å) and C—C—C and C—C—O bond angles (from 90° to 180°) resulted in negligible changes in the predicted SAXS profiles below (data not shown). Varying the sampling size (from 1,000 to 10,000 molecules) did not affect the predicted SAXS profile significantly (data not shown).

The collapsed state ensemble was generated by the same procedure as the random ensemble, except that only conformations with both distances between tether attachment points of the two duplexes within 22 Å (the average length of four T's, ref. 31; Fig. 1B), were retained. Variation of this distance cutoff (18–26 Å) had negligible effects on the resulting profile.

For the low-salt extended ensemble, the contributions of each conformation in the random ensemble were weighted by a Boltzmann distribution determined by the electrostatic energy at each conformation. The energy was calculated by the numerical integration of the nonlinear Poisson–Boltzmann model at 20 mM monovalent salt in Delphi (49).

Estimation of Allowed Potentials Between Two Duplexes. SAXS profiles for tethered DNAs can be readily calculated for different assumed interhelical potentials by applying Boltzmann weighting to the random ensemble described above. We used two models to describe the interhelical potentials, as described below.

Pairwise Yukawa Potential Model. A Yukawa potential (32, 33) was used as a general functional form for describing the repulsion, or the effective attraction meditated by ions, between two phosphates, as a function of their separation r:

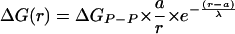[1]

where a is the minimal distance between two phosphates (4 Å). The interhelical potential energy for a given tethered DNA conformation is then the sum of potential energies associated with all pairs of phosphates (Eq. 2; see also Fig. 9 and Supporting Text, which are published as supporting information on the PNAS web site).

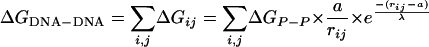[2]

Orientation-Constrained Model. Ion-induced attractive forces have been suggested to be highly orientation-dependent (21, 25, 26, 34). An “orientation-constrained model” was therefore also used to model geometrical constraints of hypothetical attractive forces and to obtain estimates of the upper limit of attraction in high salt.

We first made a binary classification of all conformations in the random ensemble (10,000 molecules, Materials and Methods). Molecules that have the dihedral angle (θ) and centermass distance (R_cm) between the two helices smaller than defined cutoffs for θ and R_cm are defined as “collapsed”; the remainder are “noncollapsed.” We then assumed a constant attractive potential existing between the helices, ΔG_attr, for the collapsed molecules.

Estimating Allowed Potentials by SAXS Comparison. The interhelical potentials of all molecules can be defined by using either the “pairwise Yukawa potential” or “orientation-constrained” model. We can then readily predict a SAXS profile for the tethered DNA by applying Boltzmann weighting to the these molecules (7) (Eq. 3).

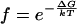[3]

where f is the Boltzmann weight for each molecule given its interhelical potential, ΔG (i.e., ΔG_DNA-DNA in the pairwise Yukawa potential or ΔG_attr in the orientation-constrained model). The allowed parameters in the pairwise Yukawa potential model (ΔG_DNA-DNA and λ) or in the orientation-constrained model (ΔG_attr) that are consistent with the data were determined by the goodness-of-fit of the predicted scattering profiles to the observed profile, quantitated as a χ² statistic (35), with errors estimated from photon counting statistics. Systematic errors due to uncertainty in the ion atmosphere correction (≤1%; see Supporting Text) and sample preparation (<1% difference in independently prepared samples at different beamlines, data not shown) were smaller than the statistical error (1–6%) at all scattering angles and were therefore neglected.

Results and Discussion

Collapse of nucleic acids in high valence ions has been observed in several large DNA and RNA systems (17, 18, 26, 36) and is predicted from theory (13, 37, 38). Nevertheless, the experimental systems used to date are complex or form ill-defined states upon compaction. Therefore, we designed a simple system that allows straightforward modeling and experimental detection, the tethered DNA duplex (Figs. 1A and 2). Here, we first demonstrated that SAXS can distinguish between different conformational states of the tethered duplex (Fig. 2). We then determined the system's state in the presence of different cations. Finally, we used these results to provide quantitative estimates and limits for repulsive and attractive electrostatic forces.

Use of SAXS to Monitor Tethered DNA Conformational States. SAXS provides information about the global shape of molecules in solution (28). The profile represents the instantaneous average of the scattering by all conformational states, weighted solely by the number of molecules in each of those states. Other techniques that are more commonly used to assay conformational states often have unequal weighting. For example, the nanosecond time scale of fluorescence and the 1/R⁶ dependence of FRET can obscure the average or “typical” behavior of molecules within the population.

We explored whether SAXS would be sensitive to the different conformational states of the tethered DNA (Fig. 2) by using calculational and experimental controls. SAXS profiles can be readily calculated for a molecule with known atomic coordinates (29). The calculated SAXS profiles for the tethered duplexes in three conformational states, extended, random, and collapsed, are shown in Fig. 3A; these states should be readily distinguishable by SAXS. As an experimental calibration, we then predict the SAXS profiles for two control molecules with distinct shapes (Fig. 3B), a 24-bp continuous duplex (Fig. 1A) and a circular DNA that is a mimic of the collapsed state (Fig. 1B). These molecules give clearly distinguishable SAXS profiles that agree well with their experimental profiles.

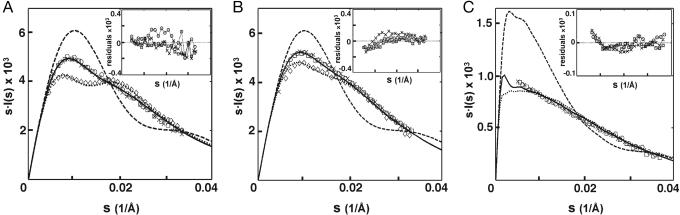
Tethered DNA Conformation in Low Salt. At very low concentration of monovalent salt (20 mM Na⁺), the 12-bp tethered DNA, 12_/PEG9/12 (Fig. 1A), gives a SAXS profile expected for the “extended state” (Fig. 4A, diamonds and dotted line). The extended configuration suggests a repulsive force between the tethered duplexes. The possibility that the duplexes stack on one another to give this extended state is inconsistent with the two maxima that are present in the scattering-angle-weighted SAXS profile calculated for the extended tethered duplex but not calculated or observed for the continuous duplex (Fig. 3, dotted lines). Thus, the results suggest that Coulomb repulsion between the duplexes dominates under these conditions. This force must overcome an entropic bias favoring the random conformations. A quantitative estimate of this repulsive force is given below.

Fig. 4.

Experimental SAXS profiles of the tethered DNA constructs: 12_/PEG9/12 (A); 12_/C3/12 (B); and 80_/PEG9/80 (C) (see Figs. 1 A and 7) in different salt conditions: 20 mM Na⁺ (diamonds), 1.2 M Na⁺ (squares), 0.6 M Mg²⁺ (circles), and 75 mM spermidine³⁺ (×), compared to the predicted SAXS profiles for the extended (dotted line), random (solid line), and collapsed (dashed line) states for each of the tethered duplexes. SAXS profiles were obtained with DNA concentrations of 0.2 mM (12_/PEG9/12), 0.2 mM (12_/C3/12), and 0.015 mM (80_/PEG9/80), in 100 mM Na-Mops, pH 7.0. (Insets) Residuals of experimental SAXS profiles of tethered DNA compared to their corresponding random state predictions, plotted against s from 0 to 0.04 (1/Å).

High Concentration of Monovalent Cation Relaxes the Tethered DNA. We next determined the effect of a high concentration of monovalent cations, 1.2 M Na⁺, on this tethered DNA. Under these conditions, the SAXS profile is consistent with a family of relaxed, entropically disordered conformations, i.e., the random state (Fig. 4A, squares and solid line). This result is consistent with the screening effects predicted by mean-field treatment of the ion atmosphere (8).

Testing Collapse with Multivalent Cations. The divalent cation Mg²⁺ is especially important for the structure and function of nucleic acids (1, 2, 5, 9–12). It has been suggested that divalent cations (e.g., Mg²⁺) may induce an attractive potential that mediates nucleic acid collapse through counterion-correlation effects (15, 36, 39, 40). Other theoretical approaches have suggested that significant attraction in water occurs only for cations of higher charge (≥3+) (13).

Here, we tested Mg²⁺ and ions with higher valence (spermidine³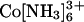⁺, and spermine⁴⁺). In the presence of high concentration of Mg²⁺ (0.6 M), the tethered duplex gives the SAXS profile predicted for the random state rather than the collapsed state (Fig. 4A, circles). The same results were observed with the divalent polyamine putrescine²⁺ (0.6 M, circles in Fig. 10, which is published as supporting information on the PNAS web site) and the trivalent polyamine spermidine³⁺ (75 mM, Fig. 4A).

Although not common in experiments on RNA folding and catalysis, the multivalent ions 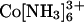and spermine⁴⁺ are widely used as condensing agents that precipitate DNA out of solution at moderate total ion concentrations (e.g., 6.5 and 3.2 mM, respectively, with 40 mM Na⁺ and 0.2 mM 24-bp DNA duplex) (refs. 17 and 18 and references therein). Because we are interested in probing the properties of isolated nucleic acids and not the condensed DNA phase (17, 41), we placed the tethered DNA construct at concentrations of these ions just below (5–8%) their precipitation thresholds with different background concentrations of Na⁺ (2, 10, and 40 mM). In each case, the SAXS profile obtained was identical to that expected for the relaxed molecule ensemble, as in high Na⁺ and Mg²⁺ (Fig. 10).

The absence of significant compaction implies that the proposed counterion correlation-induced attraction is not strong enough to drive collapse with monovalent or multivalent cation concentrations well above typical physiological concentrations [≈200 mM monovalents, ≈5 mM divalents, and ≈100 μM polyamines, the estimated total concentrations (42, 43) and above the concentrations typically used in in vitro folding and catalysis experiments with nucleic acids in solution (36, 44)]. Thus, an attractive electrostatic force, if present, is insufficient to compete with the “repulsive” force from conformational entropy to achieve a net attraction. Therefore, we attempted to alter this balance of forces. We diminished the entropic barrier by ≈1 kT by shortening the linker to favor the collapse (using the 12_/C3/12 tethered duplex instead of the 12_/PEG9/12 tethered duplex, Fig. 1A). Fig. 4B shows that, as with the 12_/PEG9/12 tethered duplex, this molecule is in an extended state at low Na⁺. High concentrations of Na⁺, Mg²⁺, and spermidine³⁺ (as well as concentrations of 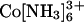and spermidine⁴⁺ below their aggregation thresholds; Fig. 10B) all give profiles expected for the random state, with no evidence of collapse. Next, we extended the duplex length to 80 bp to increase the potential attractive force. Again, no indication of collapse was obtained (Figs. 4C and 10C). Therefore, we conclude that the attractive force is weak or absent under the conditions tested. We then obtained a quantitative limit for the magnitude of this force as described below.

Quantitative Estimation of the Forces in Nucleic Acid Relaxation and Compaction. We first quantified the repulsive force between the tethered duplexes in low salt and an upper limit of the repulsion in high salt by using a general form of the electrostatic forces, a Yukawa potential (Eqs. 1 and 2), as described in Materials and Methods. Control calculations demonstrated that this procedure reasonably describes the repulsive forces calculated by numerical NLPB treatments of electrostatics for this tethered duplex system (Fig. 9).

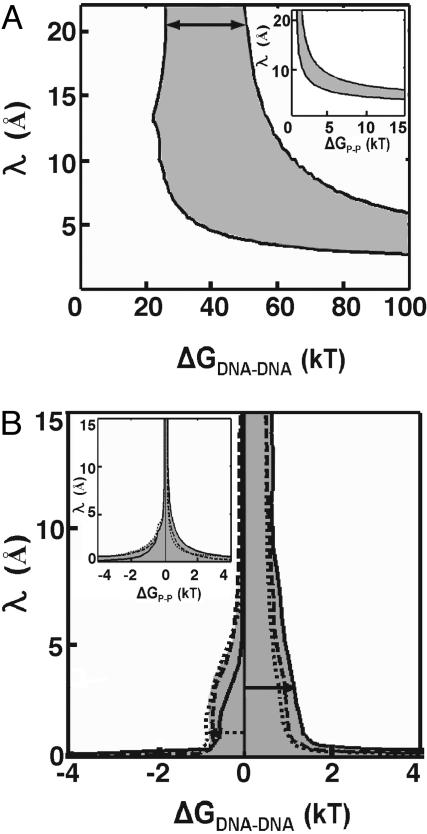
The quantitative results for data in low (20 mM Na⁺) and high (1.2 M Na⁺, 0.6 M Mg²⁺, 75 mM spermidine³⁺) concentrations of counterions are plotted in Fig. 5 A and B, respectively. The shaded areas in the insets represent the 95% confidence region of the pairwise phosphate potential ΔG_P-P and the decay length λ (Eq. 1), i.e., the set of ΔG_P-P and λ values consistent with the data. We then expressed these values in terms of the interhelical potential, ΔG_DNA-DNA (Fig. 5 and Eq. 2), to easily convert the energetic values into a “per base pair” scale. We defined ΔG_DNA-DNA as the potential for the DNA conformation with the two DNA duplexes side-by-side at their distance of closest approach (25 Å, representing twice the helix radius plus the excluded volume for approach of two phosphoryl oxygen atoms and the diameter of an ion: 20 + 4 +1 Å) as a reference scale from a particular conformation is required for plotting the allowed values of the decay length λ in Fig. 5. Thus, the reported per base pair repulsive energies and limits represent the values for this closely packed state.

Fig. 5.

Estimate of repulsive potential between the tethered DNA duplexes in low salt (A) and the maximal repulsion and attraction in high salt (B). Eqs. 1 and 2 were used to determined the values of λ and ΔG_P-P (Insets) or ΔG_DNA-DNA that are consistent with the observed SAXS profiles for the 12_/PEG9/12 in 20 mM Na⁺ (A) or 1.2 M Na⁺ (solid line), 0.6 M Mg²⁺ (dashed line), and 75 mM spermidine³⁺ (dotted line) (B). The shaded areas represent 95% confidence regions for parameters that are consistent with the observed SAXS profiles. The solid arrows indicate the range (25–55 kT) of interhelical repulsion at low salt (A) and the upper limit (≈1.4 kT) in high salt (B), at decay length of 20 Å and 3 Å, respectively, the Debye screening lengths under the low and high salt conditions, respectively (see Supporting Text). The dotted arrow indicates the strongest attractive potential (–1 kT) in multivalent ions for which the decay length is not less than the smallest diameter of one cation (1.3 Å).

Fig. 5A indicates that the repulsive potential consistent with the data in low salt ranges from 25 to 55 kT (or 2.1–4.6 kT per bp) (Fig. 5A, solid arrow), assuming a decay length of 20 Å, the Debye–Hückel electrostatic screening length at 20 mM Na⁺ obtained from NLPB treatment (Supporting Text). In high salt (1.2 M Na⁺), the repulsion is reduced to ≤1.4 kT (or ≤0.12 kT per bp) (Fig. 5B, solid arrow), at the Debye–Hückel screening length of 3 Å obtained from an NLPB treatment (Supporting Text).

The Yukawa potential (Eqs. 1 and 2) also provides a simple means to describe attractive interactions between two charged particles (32, 33). A negative sign for ΔG_P-P in Eq. 1 and 2 could represent the effective attraction between two phosphates through interactions with ions. Assuming that the phosphate–phosphate interactions are “pairwise” additive, the upper limit for the attractive potential in high concentrations of multivalent salt can be calculated. This approach yields an upper limit of –0.1 kT per bp in high-salt conditions (1.2 M Na⁺, 0.6 M Mg²⁺, 75 mM spermidine³⁺) (Fig. 5B, dotted arrow), using a minimum decay length λ of 1.3 Å, the smallest diameter possible of a counterion (e.g., a bare Mg²⁺) that would be needed to participate in the electrostatic attraction.

Ion correlation-induced attraction has been suggested to be highly orientation dependent (34). Such an attraction could also be cooperative, i.e., the interactions between regions of the DNA are larger than the sum of the interactions of the regions in isolation; for example, cooperativity might be a feature of the observed attractive force from the rearrangement of structured hydration layers between closely spaced parallel double helices (24). Forces that are cooperative or exhibit a high orientation dependence will not be well described by the “pairwise Yukawa potential” used above. Therefore, we used a simple “orientation-constrained model” to account for the geometry demands of such attractive forces. In this model, a constant attractive potential, ΔG_attr, is assumed for all molecules with a conformation within a defined interhelical distance and angle (R_cm and θ, respectively), as described in Materials and Methods.

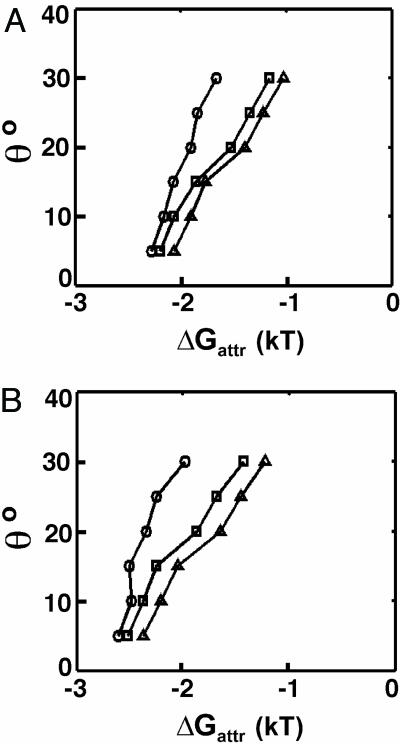
Fig. 6 shows the attractive potentials, ΔG_attr, that are consistent with SAXS data (i.e., the values give 95% confidence in χ² test) in 0.6 M Mg²⁺and 75 mM spermidine³⁺. The cutoffs of the dihedral angle (θ) and the center-mass distance (R_cm) between two helices were systematically varied. Smaller cutoffs of θ and R_cm leave a smaller group of molecules in the defined collapsed state. The smaller this population, the larger the force (ΔG_attr) consistent with the data, because fewer conformers can each be weighted more heavily. To estimate the upper limit of attraction, we used a minimum R_cm value of 25 Å (twice the DNA radius plus the excluded volume of the phosphoryl oxygen atoms and the diameter of an ion) and a threshold of θ = 15° below which attraction is observed in simulations (34). The resulting upper limit of attraction is ≈–2.5 kT, or, –0.21 kT/bp, similar to the estimate obtained from the Yukawa potential model.

Fig. 6.

Estimate of maximal attractive potential between the tethered DNA 12_/PEG9/12 in high salt by the orientation constrained model. The values of ΔG_attr are consistent with data (values give 95% confidence in χ² test) in 0.6 M Mg²⁺ (A) and 75 mM spermidine³⁺ (B), given different cutoffs for dihedral angle θ, and the center-mass distance R_cm [25 Å (circles), 30 Å (squares), and 35 Å (triangles)] between the two DNA helices.

Above, we have shown no evidence of significant attraction between two helices. Nevertheless, there is the possibility that more than two neighboring helices are required to generate a pronounced attraction; for example, attractive forces were observed in an array of multiple aligned helices (26). Such many-body effects cannot be probed in the system studied herein.

Conclusions and Implications

Attractive forces between helices have been proposed to drive collapse of RNA early in folding and to stabilize the compact folds of structured RNAs (5, 19, 20). There is extensive experimental evidence for such attractive forces between long helices in the presence of multivalent cations or alcohols (refs. 17 and 18 and references therein), and counterion correlations and surface hydration effects have been suggested to explain this phenomenon (ref. 18 and references therein, and ref. 26). However, these studies have used long genomic DNAs (typically ≥10⁴ bp) and typically several DNA molecules are incorporated into the condensed structure (ref. 18 and references therein), in contrast to the situation typical for folding of an isolated RNA molecule.

In this work, a simple and defined model system was chosen to systematically and quantitatively evaluate effects of the ion atmosphere on nucleic acid folding. We chose a 12-bp tethered DNA duplex because the duplexes in RNA structures are typically no longer than this length; the results were extended to 80-bp tethered DNA to provide a more sensitive probe for attractive forces. The DNA helices were linked by a neutral polyethylene glycol tether to minimize conformational and electrostatic constraints present with nucleic acid tethers; analogous results were obtained with a tether of five T residues (data not shown). Probing the conformational ensemble by SAXS allowed quantitative evaluation of pairwise intramolecular forces over a wide range of solution conditions that do not lead to intermolecular aggregation. These conditions span those used in RNA folding studies of isolated molecules.

We first probed the low-salt conditions that have commonly been used for the initial unfolded state in thermodynamic and kinetic studies of RNA folding (5, 19, 39, 45, 46). The results provide strong evidence for a dominant repulsive force, consistent with the extended states of complex RNAs under analogous conditions (36, 44, 46). In high concentrations of monovalent and other salts, a “random” conformation of the tethered duplexes is observed. The difference between the extended low-salt state and the random high-salt state of the tethered duplex model parallels the electrostatic relaxation process recently proposed for more complex RNAs early in their folding pathways (ref. 46; see also refs. 5, 8, and 47). The inability of high concentrations of Mg²⁺ or other cations of higher valence to compact the tethered duplexes provides no indication of significant attractive force induced by the ion atmosphere. Upper limits for an attractive force of 0.1–0.2 kT/bp have been calculated by using two general energetic models with simplifying assumptions.

Because typical physiological and in vitro folding conditions contain lower concentrations of cations than used herein, we do not expect a significant role of counterion-modulated attractive forces in RNA folding. Thus, the energetic consequences of ion atmospheres may be accounted for by simple electrostatic theories (8–12), a viewpoint that can continue to be tested and refined by using well defined model systems such as the tethered duplexes studied herein.