Abstract
Researchers estimating causal effects are increasingly challenged with decisions on how to best control for a potentially high-dimensional set of confounders. Typically, a single propensity score model is chosen and used to adjust for confounding, while the uncertainty surrounding which covariates to include into the propensity score model is often ignored, and failure to include even one important confounder will results in bias. We propose a practical and generalizable approach that overcomes the limitations described above through the use of model averaging. We develop and evaluate this approach in the context of double robust estimation. More specifically, we introduce the model averaged double robust (MA-DR) estimators, which account for model uncertainty in both the propensity score and outcome model through the use of model averaging. The MA-DR estimators are defined as weighted averages of double robust estimators, where each double robust estimator corresponds to a specific choice of the outcome model and the propensity score model. The MA-DR estimators extend the desirable double robustness property by achieving consistency under the much weaker assumption that either the true propensity score model or the true outcome model be within a specified, possibly large, class of models. Using simulation studies, we also assessed small sample properties, and found that MA-DR estimators can reduce mean squared error substantially, particularly when the set of potential confounders is large relative to the sample size. We apply the methodology to estimate the average causal effect of temozolomide plus radiotherapy versus radiotherapy alone on one-year survival in a cohort of 1887 Medicare enrollees who were diagnosed with glioblastoma between June 2005 and December 2009.
1 Introduction
Methods for causal inference are predicated on knowledge of the covariates necessary to satisfy the no unmeasured confounding assumption, but the exact set of covariates needed to control confounding is rarely known. With the growing use of causal inference methods in large observational studies, such as administrative databases used in comparative effectiveness research, the set of potential confounders can be quite large. Practical tools that acknowledge uncertainty in confounder selection and are robust to model misspecification are imperative for correct estimation of the average causal effect (Vansteelandt et al., 2012; Wang et al., 2012; Zigler and Dominici, 2014; Wang et al., 2015). Extracting the minimal and necessary set of covariates for confounding adjustment in the final data analysis becomes more difficult as the set of potential confounders grows. Failure to adjust for even one important confounder may lead to a biased estimate of the causal effect of interest.
Several attempts have been made to develop methods for confounder selection in causal inference (Joffe et al., 2004; Brookhart et al., 2006; Schneeweiss et al., 2009; Wang et al., 2012; De Luna et al., 2011; Gruber and van der Laan, 2012; Shahar, 2013; Vansteelandt et al., 2012; VanderWeele and Shpitser, 2011; Wilson and Reich, 2014; Zigler and Dominici, 2014; Wang et al., 2015). Most of these authors note that statistical methods to select confounders pose unique challenges, and methods designed for prediction may not be directly applicable. Statistical methods to select potential confounders based on the outcome model prioritize covariates strongly associated with the outcome, while variable selection based on a treatment model prioritize covariates that are strongly associated with the treatment. Both these approaches can result in inefficient and biased inferences because they can fail to identify the full set of necessary confounders.
One set of methods for confounder selection builds on Bayesian model averaging (Wang et al., 2012, 2015). These authors propose an approach, called Bayesian adjustment for confounding (BAC), to estimate the effect of a continuous exposure (or treatment) on an outcome, while accounting for the uncertainty in the choice of confounders. Their approach is based on specifying two models: (1) the outcome as a function of the exposure and the potential confounders; and (2) the exposure as a function of the potential confounders. They assume a priori that if a covariate is highly predictive of the exposure then the same covariate will have a large prior probability of being included into the outcome model.
Zigler and Dominici (2014) use similar ideas in the context of a propensity score analysis for binary treatment (Rosenbaum and Rubin, 1983). They propose a Bayesian model averaging approach that adjusts for confounding by using the propensity score as a linear predictor in an outcome model. To handle the so-called “feedback” issue (McCandless et al., 2010; Zigler et al., 2013), the proposed method forces variables that are included in the propensity score model to also be included as linear predictors in the outcome model.
Although these methods have, in our view, formulated the problem of confounder selection soundly and proposed workable solutions, they rely on parametric assumptions to estimate causal effects. For example, the methods of Wang et al. (2012), Zigler and Dominici (2014), and Wang et al. (2015) specify a sampling distribution for the outcome model and rely on covariate adjustment through a linear predictor in an outcome model. Also, these methods do not provide an easily generalizable procedure for extending widely used non-Bayesian causal inference methodologies, including useful nonparametric and semi-parametric methodologies that rely on on selection of confounders. The goal of this paper is to provide a practical and generalizable strategy for robustifying a broad range of causal inference methodologies with regard to model choice. Our approach borrows and simplifies Bayesian ideas, but strays from a fully coherent Bayesian specification.
We wish to leverage existing non-Bayesian tools to mitigate the negative effects of overlooking the uncertainity due to model selection. We are particularly interested in applications presenting a large number of potential confounders relative to the sample size. In this setting, uncertainty on confounder selection is especially important. In a setting where we estimate a regression coefficient, we often make several assumptions regarding the sampling distribution of the outcome, the functional form relating the covariates to the outcome, and which covariates we include into the the regression model. In causal inference, it is common to assume a model for the propensity score, thus leading to uncertainty regarding which covariates the analyst decides to include into the propensity score model, including the functional form.
We develop and evaluate our model averaging approach focusing on the double robust estimator. The result is a newly proposed family of estimators, the model averaged double robust estimators, formally accounting for model uncertainty through the use of model averaging while extending the desirable double robustness property. We consider a model space including a large collection of combinations of the outcome model and propensity score model, where each of these models can include a different subset of all the potential confounders. We compute model-specific double robust estimators as a function of the outcome model and a propensity score model, and then average over these using weights that are motivated by posterior model probabilities, though not always interpretable as such. We introduce a prior distribution on the model space that (1) a priori links the outcome and the propensity score model, (2) assigns higher prior probabilities to propensity score models that include necessary confounders (i.e. covariates that are associated with both the treatment and the outcome), and (3) assigns low prior probability to propensity score models that include covariates that are only associated with the treatment. By conducting several simulation studies with varying sample sizes, number of potential confounders, and strength of confounding bias, we show that by specifying this prior distribution, and using the resulting posterior model probabilities as weights in a model averaged double robust estimate, we substantially increase efficiency.
In Section 2, we introduce a general framework for model averaging in causal inference and model averaged double robust estimation. In Section 3, we provide asymptotic results about our proposed estimators. In Section 4, we provide a simulation study that illustrates the finite sample performance of model averaged double robust estimators. In Section 5, we apply the model averaged double robust estimator to estimate the comparative effectiveness of temazolomide on 1-year survival after diagnosis with glioblastoma.
2 Methods
2.1 Notation and General Approach
To facilitate the presentation of our framework for model averaging in causal inference, consider first the estimation of the causal effect Δ of a binary treatment using an inverse probability of treatment weighted estimator (IPW). Instead of selecting a single propensity score model, let’s consider the class of propensity score models ℳ that includes logistic and probit regression models with all possible subsets of the potential confounders as linear predictors. If, within class ℳ, we choose the ith model ℳi ∈ ℳ for analysis, then the resulting estimator of the causal effect will inherit properties that depend on that choice, a fact we record via the notation Δ̂(ℳi). To robustify the estimation process with respect to choice of model, a generic approach is to compute a weighted average of model specific estimates Δ̂(ℳi):
| (1) |
where wi ∈ [0, 1] is the weight assigned to model ℳi and ∑i wi = 1.
Beyond the IPW example, this defines a general class of model averaged estimators built using any desired combination of estimated weights and estimated model-specific causal effects. In Section 3, we will show that, under standard regularity conditions, if the underlying causal estimate is consistent under the true model ℳtrue, then the weighted version will also be consistent, as long as the true model belongs to the model class ℳ and the weights converge to a degenearte distribution on the true model. This provides the general motivation for the approach. In this paper, we investigate it specifically for double robust estimation.
Looking ahead, the implementation of a model averaged estimate requires a strategy for assigning weights wi to models. The focus of this paper will be on the case where the weights wi corresponds to the posterior model probabilities, but one could consider model weights derived from other criteria such as minimizing mean squared error (Longford, 2006).
2.2 Double robust estimator
Let Y (x) be the potential outcome that would have been observed under treatment X = x, x ∈ {0, 1}. The observed outcome Y is related to the potential outcomes Y (x) by Y = I(X = x)Y (x), where I(X = x) is the indicator that X = x. Consider a p-dimensional set of potential confounders C, and assume strong ignorable treatment assignment (Rosenbaum and Rubin, 1983), so that (Y (0), Y (1)) ╨ X|C. Let (Yh, Xh, Ch) be independent observations for h = 1, …, n. We are interested in estimating the average causal effect:
| (2) |
Given a model for the propensity score, P(X = 1|C) = e(C), and models for the outcome under each treatment, E(Y|X = 1, C) = m1(C) and E(Y|X = 0, C) = m0(C), we define the well known double robust (Δ̂DR) estimator as:
| (3) |
where m̂1h, m̂0h, and êh are the estimates of m1(C), m0(C), and e(C) for individual h (Bang and Robins, 2005). The double robust estimator is regarded as semi-parametric because the estimation procedure only depends on the specification of the conditional means P(X = 1|C), E(Y|X = 1, C), and E(Y|X = 0, C) and does not rely on a fully parametric specification of the models.
The propensity score model and the outcome models can be selected in any number of ways. A researcher may rely on expert knowledge to decide both the functional form and the confounders to include in each model, or may rely on a model selection procedure that chooses the best model from a set of candidate models. For the remainder of this paper, we will refer to as the “model selected double robust estimate” in which both the propensity score and the outcome models have been selected independently using BIC.
2.3 A model averaged double robust estimator
Next we apply the model averaging outlined in Section 2.1 to the double robust estimator. We chose to consider the double robust estimator because of its wide use and strong asymptotic properties. Also, it will highlight the flexibility of our approach because it relies on the specification of multiple models.
Let and be finite collections of models for the observed data likelihoods p(X = 1|C), p(Y|X = 0, C), and p(Y|X = 1, C), respectively. In this paper, the models can vary depending on inclusion of potential confounders in linear predictors. Similar approaches could consider distributional assumptions, link functions, specification of the functional form of the predictors (e.g. inclusion of interactions) and more. Let ℳom = ℳ1 × ℳ0 denote all combinations of models in ℳ1 and ℳ0. Further, define as the double robust estimate corresponding to the models and . Similarly to (1), we define the model average double robust estimate as a weighted average of model specific double robust estimates , that is:
| (4) |
Here is the joint (approximate) posterior probability of models and and is the double robust estimate that uses the plug in estimates of m̂1h, m̂0h, and êh corresponding to and . The estimation of the weights wij is performed independently of the estimation of .
Posterior model probabilities depend on the likelihoods of the models in the model space, along with the prior distribution on the model space. The specification of the likelihood used in deriving the weights plays no role (except through the conditional means) in the estimation of the model specific effects , which remains semiparametric and robust to higher order moments of the true data generating mechanism.
2.4 Priors on the model space
2.4.1 Uniform prior on the model space
To derive weights, we specify a prior distribution on the model class, and compute approximate posterior probabilities. The simplest choice is to assume that all models are independent and equally likely a priori, which we will refer to as a uniform prior on the model space. This implies that the prior odds of each model is 1, and that the prior distribution on the propensity score model class is independent of the prior distribution on the outcome model class. Because of the independence assumption, the posterior model probabilities factor as . Therefore, and can be computed separately, which substantially simplifies the computation.
The resulting posterior distribution assigns high weights to propensity score models that include Cs strongly associated with X and does not consider relationships with Y. The current literature in causal inference suggests that inclusion of covariates that are only related to the treatment into a propensity score model adds to the variance of the resulting estimator (Rubin et al., 1997; Hahn, 2004; Brookhart et al., 2006; Wooldridge, 2009; Pearl, 2009; Vansteelandt et al., 2012).
2.4.2 Dependent prior on the model space
In view of this consideration, efficiency can be gained through the use of a prior distribution on the propensity score model space that favors inclusion of potential confounders that are associated with both treatment and outcome, instead of predictors associated only with treatment (Rubin et al., 1997; Hahn, 2004; Brookhart et al., 2006; Wooldridge, 2009; Pearl, 2009; Groenwold et al., 2011; Vansteelandt et al., 2012). With this goal in mind, we propose an alternative prior distribution on the model space that links the propensity score model to the outcome model through prior model dependence. We assume that the prior odds of including a potential confounder in the propensity score model given that it is included in the outcome model is 1, and that the prior odds of including a potential confounder in the propensity score model given that it is excluded from the outcome model is small. This dependence also implies that the prior odds of including a potential confounder in the outcome model given that it is included in the propensity score model is high.
Specifically, we assume that both ℳps and ℳom contain models with linear preditors comprising potential confounders. We let indicate that the terms in the linear predictor of are a subset of those of . Since ℳom is the product space of ℳ0 and ℳ1, we evaluate the inclusion relation above using the union of terms in the linear predictors from the corresponding models in ℳ0 and ℳ1. To specify the prior, we choose a reference propensity score model such that for all j. Thus, is either a null model or a model that includes the potential confounders that will be included in all models. We set the prior odds of propensity score model to model conditional on the outcome model to be:
| (5) |
for τ ∈ [0, 1]. Lastly, we assume that the prior distribution on the outcome model space is uniform.
The choice of τ is important. First, τ = 1 corresponds to the uniform prior on the model space of the previous section. Second, when τ = 0, the prior model dependency given by (5) restricts the set of potential confounders included in the propensity score model to be a subset of those included in the outcome model.
Third, when τ is nonzero but smaller than 1, the prior dependency of (5) gives small weight a priori to propensity score models including terms that are not included in the outcome model. Finally, when τ > 1, the prior assigns small weights to outcome models including a larger set of covariates than that included into the propensity score model. We generally avoid this choice, as terms that are predictive of the outcome but not the treatment can still contribute to more efficient estimation of the causel effect.
2.5 Estimation of model weights
2.5.1 BIC approximation of posterior model probabilities
The posterior model probabilities, which are used as model weights in (4), are a function of the Bayes factors and the choice of prior distribution on the model space. In general, the Bayes factor for comparing model ℳi to model ℳj is defined as Bij = p(𝒟|ℳi)/p(𝒟|ℳj), where 𝒟 denotes the data and p(𝒟|ℳi) = ∫ p(𝒟|ℳi, ηi)p(ηi|ℳi)∂ηi is the integrated likelihood over all model-specific parameters ηi within ℳi. A simple transformation of the Bayes factors gives the posterior model probabilities, P(ℳi|𝒟) = AiBi1/∑j:ℳj∈ℳ AjBj1, where Ai is the prior odds of ℳi versus a reference model ℳ1. Outside of a few special cases, the Bayes factor Bij will not have a closed form, and an approximation will be necessary. A widely used approximation of Bayes factors is based on the Bayesian Information Criterion (BIC) (Schwarz, 1978), which we adopt in this paper. Other information criteria can be used to derive model weights, such as the Akaike Information Criteria (AIC) (Akaike, 1998). See Yang (2003, 2005) for a discussion of the relative merits of using AIC versus BIC in model averaging. As the number of models in ℳ increases, evaluating the Bayes’ factor for every model becomes computationally infeasible. Instead, we can use a Markov chain Monte Carlo algorithm such as MC3 (Madigan et al., 1995) to search the model space.
2.5.2 Two-stage posterior weights
Model weights based on the prior given in (5) still have the potential limitation that the resulting posterior model probabilities will favor outcome models that include potential confounders that are only associated with the treatment. This can result in a loss of efficiency. Specifically, the prior was described with the goal of limiting the inclusion of potential confounders in the propensity score model to covariates associated to both the treatment and the outcome. However, the prior can have a different effect: potential confounders strongly associated with only treatment are included in both the propensity score and outcome models. As previously discussed, inclusion of such covariates reduces efficiency.
As an alternative, we propose a two-stage approach for calculating the model weights motivated by De Luna et al. (2011), who suggested to first identify the covariates associated with the outcome, and then identify the covariates associated with the treatment among those associated with the outcome. First, they suggest to find a reduced covariate vector, CY, such that p(Y0, Y1|C) = p(Y0, Y1|CY) holds. Second, CY is further reduced into Z such that p(X = 1|CY) = p(X = 1|Z) holds. They show that the covariate sets CY and Z are sufficient for the identification of the average causal effect, and that using Z in nonparametric estimation improves efficiency.
With this in mind, we propose the following two-stage approach for calculating model weights:
Compute the marginal posterior probability qj of the jth outcome model, assuming a uniform prior and without considering the propensity score model;
Compute the conditional posterior probability of the ith propensity score model, conditional on knowing the terms included in the linear predictor of the outcome model, using prior model dependence given by (5);
Multiply the estimates from Stage 1 and 2 to calculate model weight .
The model weights under this two-stage approach can be calculated easily because they are a transformation of the model probabilities assuming a uniform prior on the model space. The difference between the two-stage model weights and the proper posterior model probabilities under the same prior is that the two-stage approach restricts the marginal outcome model weights to be equal to the marginal posterior outcome model probabilities under a uniform prior on the model space. Thus the qj in Stage 1 of the two-stage method does not correspond to the marginal posterior under the dependent prior, while the estimation of in Stage 2 does correspond to the conditional posterior under this prior. A further discussion of this two-stage procedure can be found in Web Appendix A.
3 Asymptotic properties
For a general Δ̂MA defined in (1), we show that, if the underlying causal estimate is consistent under the true model ℳtrue, and the true model belongs to the model class ℳ, then the model averaged estimator will also be consistent:
Theorem 1
Let ℳ be a finite collection of models. Assume: (1) ℳ contains the true model, ℳtrue, (2) the regularity conditions necessary for , are met and (3) Δ̂(ℳi) is bounded in probability for all i. Then .
For the model averaged double robust estimator, we show that if the posterior model probabilities are converging to the true models and if the true propensity score model OR the true outcome model is contained in the corresponding model space, then is consistent for the average causal effect (2). We regard this as an important relaxation of the robustness properties of the double robust estimator, as we only need the true models to be included in a potentially large collection of models.
Theorem 2
Assume conditions (2) and (3) of Theorem 1. Let ℳom, ℳps be collections of models. If
(1) ℳom contains the true models, , for both E(Y|X = 1, C) and E(Y|X = 0, C), and ,
or (2) ℳps contains the true model, , for P(X = 1|C), and , then, .
For proofs, see Web Appendix B.
We chose to specify conditions of Theorem 2 in relation to the true data generating models to be consistent with the literature on double robustness. However, the same conclusion could be reached using weaker conditions, as long as the model space includes a model pair that produces a consistent effect estimate. One such example may be a model that is sufficient for controlling confounding (Greenland et al., 1999; De Luna et al., 2011; Vansteelandt et al., 2012). To see this, consider Lemma 2. First, we note that the true propensity model is not necessary to maintain the consistency of the doubly robust estimator. Instead, we only require a propensity score model, , such that . Assume that the model class ℳps contains this consistent model, . If , then . A similar argument can be made with regard to the outcome model, to relax Theorem 2.
4 Simulation study
4.1 Setup
In this section, we illustrate the finite sample behavior of relative to alternatives. We consider: (1) the double robust estimate using model selection separately for the propensity score and the outcome model (); (2) the model averaged double robust estimate that assumes the prior model dependence of (5) with τ ∈ {1, 0.1, 0.01, 0} (); (3) the model averaged double robust estimate that uses the two-stage approach for calculating model weights with τ ∈ {1, 0.1, 0.01, 0} (); and (4) the collaborative double robust targeted maximum likelihood estimator (van der Laan and Gruber, 2010; Gruber and van der Laan, 2010) (Δ̂C−TMLE). See Table 1 for a description of the estimators considered in these simulations. A description of the C-TMLE algorithm can be found in Web Appendix C.
Table 1.
Description of all estimators used in the simulations. Included is (1) the type of estimator; and (2) the choice of prior distribution for the model space. All Bayes factors are estimated using the BIC approximation.
| Estimator | Description | |
|---|---|---|
| model selected double robust estimator that chooses the propensity score model and the outcome model separately based on the BIC |
||
| MA-DR estimator assuming prior model dependence defined by (5) | ||
| MA-DR estimator assuming prior model dependence defined by (5) and using the two-stage approach for calculating model weights |
||
| Δ̂C−TMLE | Collaborative double robust targeted maximum likelihood estimator using the super learner to select the outcome regression with prediction algorithms including the full model, stepwise selection, and ridge regression |
We generate the data as follows: (1) ; (2) X ~ Bernoulli(p = expit(Cαps)); and (3) Y ~ N(βX + Cαom, σ2). We consider different values of the unknown parameters αps and αom to capture different levels of confounding, and vary both the sample size n and the number of potential confounders p. In all simulations, β = 1, implying that Δ = 1. The simulation scenarios are defined in Table 2. We restrict ℳps and ℳom to only include linear combinations of the p potential confounders so that there are 2p models for both the propensity score and the outcome. The number of models in each class may be large depending on the number of potential confounders.
Table 2.
Summary of Parameters for Simulation Group 1. In each of the 4 scenarios considered, we generate data as follows: (1) ; (2) X ~ Bernoulli(p = expit(Cαps)); and (3) Y ~ N(βX + Cαom, σ2) with β = 1 and σ2 = 4. All effects of confounders are linear on both the treatment and outcome.
| Scenario | Description | αps (PS model) | αom (Outcome model) |
|---|---|---|---|
| 1 | No confounding | (0.4,0.3,0.2,0.1,0) | (0,0,0,0,0) |
| 2 | Moderate confounding | (0.5,0.5,0.1,0,0) | (0.5,0,1,0.5,0) |
| 3 | Strong predictors of outcome, weak predictors of treatment |
(0.1,0.1,1,1,1) | (2,2,0,0,0) |
| 4 | Strong confounding | (0.5,0.4,0.3,0.2,0.1) | (0.5,1,1.5,2,2.5) |
4.2 Results for n = 200, p = 5, and σ2 = 4
The simulations of this section are intended to explore whether, even in simple scenarios with only 5 covariates and strong signals (i.e. αom and αps), model averaging has benefits over model selection. We consider as gold standard the results obtained using the true outcome model. For each of the simulation scenarios defined in Table 2, Table 3 provides the mean, standard error, bootstrapped 95% confidence interval coverage, and relative efficiency compared to the gold standard. All estimators show very small bias compared to the true Δ = 1. The proposed model averaged estimators tend to have smaller standard errors than their model selected counterparts.
Table 3.
The mean, standard error, relative efficiency (variance of the gold standard divided by the variance of the estimator), and 95% confidence interval coverage probability of various estimators when n = 200 and p = 5 for 1000 replications of the data.
| Scenario 1 | Scenario 2 | |||||||||
| τ | Mean | Std. Error | Rel. Eff. | Coverage | Mean | Std. Error | Rel. Eff. | Coverage | ||
| Gold standard | - | 1.00 | 0.27 | 1.00 | 0.95 | 1.00 | 0.30 | 1.00 | 0.94 | |
| - | 1.00 | 0.29 | 0.89 | 0.95 | 1.00 | 0.32 | 0.95 | 0.94 | ||
| Δ̂C−TMLE | - | 1.00 | 0.29 | 0.89 | 0.95 | 1.00 | 0.31 | 0.97 | 0.94 | |
|
|
1 | 1.00 | 0.29 | 0.90 | 0.95 | 1.00 | 0.32 | 0.95 | 0.93 | |
| 0.1 | 1.00 | 0.29 | 0.91 | 0.95 | 1.00 | 0.31 | 0.96 | 0.94 | ||
| 0.01 | 1.00 | 0.29 | 0.92 | 0.95 | 1.00 | 0.31 | 0.96 | 0.94 | ||
| 0 | 1.00 | 0.28 | 0.93 | 0.95 | 1.00 | 0.31 | 0.96 | 0.94 | ||
| 0.1 | 1.00 | 0.29 | 0.91 | 0.95 | 1.00 | 0.31 | 0.96 | 0.93 | ||
| 0.01 | 1.00 | 0.28 | 0.93 | 0.95 | 1.00 | 0.31 | 0.97 | 0.93 | ||
| 0 | 1.00 | 0.28 | 0.98 | 0.95 | 1.02 | 0.31 | 0.97 | 0.93 | ||
| Scenario 3 | Scenario 4 | |||||||||
| τ | Mean | Std. Error | Rel. Eff. | Coverage | Mean | Std. Error | Rel. Eff. | Coverage | ||
| Gold standard | - | 0.99 | 0.29 | 1.00 | 0.95 | 0.99 | 0.30 | 1.00 | 0.95 | |
|
|
- | 1.00 | 0.53 | 0.55 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | |
| Δ̂C−TMLE | - | 0.98 | 0.39 | 0.74 | 0.94 | 1.00 | 0.30 | 1.00 | 0.95 | |
|
|
1 | 1.00 | 0.52 | 0.55 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | |
| 0.1 | 1.00 | 0.52 | 0.55 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | ||
| 0.01 | 0.99 | 0.52 | 0.56 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | ||
| 0 | 0.99 | 0.50 | 0.57 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | ||
|
|
0.1 | 1.00 | 0.52 | 0.55 | 0.93 | 1.00 | 0.31 | 0.97 | 0.95 | |
| 0.01 | 1.00 | 0.52 | 0.55 | 0.93 | 1.01 | 0.31 | 0.96 | 0.94 | ||
| 0 | 0.99 | 0.30 | 0.98 | 0.95 | 1.02 | 0.32 | 0.95 | 0.92 | ||
Model averaging assuming prior model independence, with τ = 1, is comparable to model selection across all four simulation scenarios, with only negligible gains in efficiency. This suggests that even a relatively unsophisticated implementation of model averaging to account for model uncertainty may do no worse than model selection. The estimators assuming prior model dependence have standard errors that are generally smaller than that of .
Scenario 3 is worth further discussion as it illustrates a substantial difference in the relative performance of the model averaged estimators. Here only C1 and C2 are confounders, while C3, C4, and C5 are strongly associated with the exposure only (i.e. they are instruments). The model averaged estimators (except with τ = 0) have relative efficiencies less than 0:6, Δ̂C−TMLE has relative efficiency of 0.74, and with τ = 0 has relative efficiency of 0:98. Here, all potential confounders are linear in both the propensity score and the outcome model, yet model averaging can reduce the variance of the double robust estimator dramatically if we assume prior model dependence and use the two-stage approach for estimating the model weights with τ = 0. Also, note that using model selection on the propensity score model independently of the outcome model will tend to choose propensity score models that include C3, C4, and C5. As these three potential confounders are unrelated to the outcome, their inclusion in the propensity score model only adds to the variance of the model selected estimator.
To better characterize the relative performance of the model averaged estimates, Table 5 provides the mean posterior inclusion probability of the covariates in the outcome model and in the propensity score model. First, considering , we observe that as τ goes to zero, the posterior concentrates on outcome models that include C3, C4, and C5. This is an unintended consequence of the prior model dependence, which was designed in the hope that it would exclude these instruments from the propensity score model instead of including them in the outcome model. Inclusion of instruments in the outcome model can inflate the variance of the estimated causal effect. Next observe that, for where we use the two-stage procedure for calculating the model weights, the inclusion probabilities for the instruments are 0.12 when τ = 0. For other choices of τ, there is no change in the inclusion probabilities. This occurs because these three covariates are strong predictors of treatment and the signal overwhelms the prior. Only very small choices of τ will influence the posterior inclusion probabilities in this scenario. The estimator with τ = 0 has smaller variance than the other estimators because it effectively down weights propensity score models that include C3, C4, and C5.
Table 5.
Scenario 3: the mean posterior inclusion probabilities when n = 200 and p = 5 for 1000 replications of the data.
| Outcome | Propensity score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ | C1 | C2 | C3 | C4 | C5 | C1 | C2 | C3 | C4 | C5 | ||
| 1 | 1 | 1 | 0.12 | 0.12 | 0.12 | 0.15 | 0.15 | 1 | 1 | 1 | ||
| 0.1 | 1 | 1 | 0.13 | 0.14 | 0.13 | 0.15 | 0.15 | 1 | 1 | 1 | ||
| 0.01 | 1 | 1 | 0.22 | 0.23 | 0.23 | 0.15 | 0.15 | 1 | 1 | 0.99 | ||
| 0 | 1 | 1 | 0.99 | 0.99 | 0.98 | 0.15 | 0.15 | 0.99 | 0.99 | 0.98 | ||
| 1 | 1 | 1 | 0.12 | 0.12 | 0.12 | 0.15 | 0.15 | 1 | 1 | 1 | ||
| 0.1 | 1 | 1 | 0.12 | 0.12 | 0.12 | 0.15 | 0.15 | 1 | 1 | 1 | ||
| 0.01 | 1 | 1 | 0.12 | 0.12 | 0.12 | 0.15 | 0.15 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 0.12 | 0.12 | 0.12 | 0.14 | 0.14 | 0.12 | 0.12 | 0.12 | ||
These simulations demonstrate that the model averaged double robust estimator with a two-stage dependent prior with τ = 0 performs nearly as well as the gold standard in many of the scenarios considered and performs substantially better than all of the competitors in Scenario 3.
4.3 Results for n = 200, p = 100, and σ2 = 1
An important motivation for model averaging approaches is their applicability to analyses with a large sets of potential confounders, where substantive knowledge can be of limited help in specifying models, and where several models receive support from the data. Rather than ignoring model uncertainty, we can leverage information from the data to reduce the set of potential confounders to a manageable size through the use of model averaging and a carefully chosen prior distribution on the model space.
To illustrate, we now consider a set of potential confounders that is half the size of the number of observations (p = 100 and n = 200). The model space of the propensity score alone has 2100 = 1.27 * 1030 potential models while the joint model space has 2200 models. It is impossible to enumerate a set of models this large, and evaluating balance within even a small set of these models can be challenging. Instead, our prior distribution on the model space prioritizes propensity score and outcome models that share potential confounders. We then search for these models stochastically using a Markov chain Monte Carlo model composition (MC3) (Madigan et al., 1995). For computational efficiency, we focus on with τ = 0 and do not consider any of the other model averaged estimators with the dependent prior.
Overall, the prior model dependence given by (5) with τ = 0 in the two-stage approach appears to be very effective at reducing the propensity score model space. This reduction increases both statistical and computational efficiency, while promoting inclusion of the correct confounders. By searching a smaller space of models, we may also be more likely to find regions of the model space with higher posterior probabilities. The resulting estimator dramatically improves efficiency when compared with model selection.
Specifically, we repeated the simulations from Section 4.2, but generate a total of p = 100 potential confounders and reduced σ2 to be 1. We consider the same four scenarios given in Table 2, but include an additional 95 covariates that are unrelated to both the treatment and outcome. In addition to these simulations, we consider one additional scenario (Scenario 5) to mimic a situation where the sets of covariates associated with only the outcome or only the exposure are large, but the overlap between these two sets is small. Specifically, we generate 20 covariates only related to the outcome, 10 related to both the outcome and the exposure (and hence confounders), 20 covariates related only to the exposure, and 50 additional noise covariates. This adds to a total of p = 100 potential confounders, while the sample size remains n = 200. The strength of the relationships between the potential confounders, the outcome, and the exposure were randomly generated. Details can be found in Web Appendix D.
Table 4 provides the mean, standard error, bootstrapped 95% confidence interval coverage, and relative efficiency compared to the gold standard for each simulation scenario defined in Table 2 but with p = 100. The superiority of compared to alternatives is even more striking when p = 100. Relative efficiencie is above 0.80 for all five scenarios, while the other estimators suffer from a severe loss of efficiency. The model averaged double robust estimator assuming prior model independence continues to have smaller standard error when compared with model selection. However, the differences in efficiency between the two are no longer negligible, with with τ = 1 having less variance.
Table 4.
The mean, standard error, relative efficiency (variance of the gold standard divided by the variance of the estimator), and 95% confidence interval coverage probability of various estimators when n = 200 and p = 100 for 500 replications of the data.
| Scenario 1 | Scenario 2 | |||||||||
| τ | Mean | Std. Error | Rel. Eff. | Coverage | Mean | Std. Error | Rel. Eff. | Coverage | ||
| Gold standard | - | 1.00 | 0.14 | 1.00 | 0.95 | 1.00 | 0.15 | 1.00 | 0.94 | |
| - | 1.00 | 0.17 | 0.66 | 0.93 | 1.00 | 0.19 | 0.62 | 0.95 | ||
| Δ̂C−TMLE | - | 1.01 | 0.20 | 0.45 | 0.93 | 0.99 | 0.26 | 0.34 | 0.98 | |
| 1 | 1.00 | 0.16 | 0.72 | 0.95 | 1.00 | 0.18 | 0.71 | 0.94 | ||
| 0 | 1.00 | 0.14 | 0.91 | 0.94 | 1.00 | 0.16 | 0.94 | 0.93 | ||
| Scenario 3 | Scenario 4 | |||||||||
| τ | Mean | Std. Error | Rel. Eff. | Coverage | Mean | Std. Error | Rel. Eff. | Coverage | ||
| Gold standard | - | 1.00 | 0.14 | 1.00 | 0.95 | 1.00 | 0.16 | 1.00 | 0.95 | |
| - | 1.00 | 0.33 | 0.19 | 0.95 | 1.00 | 0.19 | 0.70 | 0.96 | ||
| Δ̂C−TMLE | - | 0.97 | 0.36 | 0.16 | 1.00 | 1.01 | 0.30 | 0.27 | 0.97 | |
| 1 | 1.00 | 0.35 | 0.17 | 0.96 | 1.00 | 0.17 | 0.80 | 0.96 | ||
| 0 | 1.00 | 0.15 | 0.87 | 0.97 | 1.01 | 0.16 | 0.95 | 0.95 | ||
| Scenario 5 | ||||||||||
| τ | Mean | Std. Error | Rel. Eff. | Coverage | ||||||
| Gold standard | - | 0.998 | 0.162 | 1.000 | 0.94 | |||||
| - | 1.006 | 0.189 | 0.735 | 0.93 | ||||||
| Δ̂C−TMLE | - | 1.005 | 0.217 | 0.555 | 0.96 | |||||
| 1 | 1.004 | 0.183 | 0.787 | 0.93 | ||||||
| 0 | 0.999 | 0.176 | 0.851 | 0.96 | ||||||
The gains in efficiency of the model averaged double robust estimator over the model selected estimator illustrates that with n = 200 observations, the sample size is not large enough to reflect the fact that model selection and model averaging are asymptotically equivalent. With and τ = 0 specifically, the use of the two-stage approach for calculating model weights is effective at identifying the models that include potential confounders that are associated with both the treatment and the outcome. This feature becomes increasingly important as the set of potential confounders increases. In Scenario 5, there are p = 100 potential confounders but only 10 are actual confounders, while 30 are related to only the exposure. Therefore, the gains in efficiency observed in Scenario 5 are likely due to placing higher weights on the propensity score models that include the 10 confounders, as opposed to selecting a propensity score model that includes all 30 potential confounders only associated with the exposure.
We have focused our simulations on situations where the model classes include models that vary only by the confounders that are selected, and the data generating model is included in the class. More work is needed to determine the relative merits of the model averaged double robust estimators when these assumptions are relaxed. With regard to the first, suppose that the set of confounders was known, but the exact functional forms relating the confounders to the outcome and treatment are unknown. The model averaged double robust estimator can be used in this setting as well; the model classes would contain various specifications of how the confounders appear in the models (e.g. interactions, polynomials, splines, etc.). In this setting, we expect the model averaged double robust estimator to perform well provided that the model classes are flexible enough to capture important features of the data.
5 Comparative effectiveness of temozolomide for treating glioblastoma
The SEER linked Medicare database was used to construct a cohort of 1887 Medicare beneficiaries who were diagnosed with glioblastoma from June 2005 to December 2009 to compare the effectiveness of temozolomide plus radiotherapy (X = 1) vs. radiotherapy alone (X = 0) for lowering the probability of death within 1 year of diagnosis. For more background on glioblastoma and temozolomide see Arvold and Reardon (2014) and Arvold et al. (2014).
Table 6 summarizes 33 baseline characteristics of patients who were treated with temozolomide plus radiotherapy (n = 776) and those who were treated with radiotherapy alone (n = 1111). Younger patients were more likely and older patients were less likely to received temozolomide. Other differences in baseline characteristics between the treatment groups include the use of diagnostic tests (MRI and CT scan), the extent of resection, income, race, and the patient comorbidities atherosclerosis and COPD as measured by the Hierarchical Condition Categories (Pope et al., 2004). The unadjusted rate of death within 1 year of diagnosis is 11.7% (7.6–16.0%) lower in the patients receiving temozolomide plus radiotherapy compared to radiotherapy alone (63.7% versus 75.4%).
Table 6.
Baseline characteristics (% experiencing) and 1-year mortality rate for patients treated with temozolomideplus radiotherapy and radiotherapy alone, along with estimated inclusion probabilities (assuming prior model dependence defined by (5) and using the two-stage approach with τ = 0) for the analyses of the Medicare data.
| Radiotherapy only (n = 1111) |
Temozolomide (n = 776) |
Pr (Inclusion in outcome model) |
Pr (Inclusion in propensity score) |
|
|---|---|---|---|---|
| Age group: | ||||
| 65–69 | 25.6 | 30.7 | Reference | Reference |
| 70–74 | 28.1 | 32.1 | 1.00 | 0.07 |
| 75–79 | 23.8 | 23.3 | 1.00 | 0.09 |
| ≥80 | 22.5 | 13.9 | 1.00 | 0.95 |
| Gender (female/male) | 47.1 | 48.5 | 0.09 | 0.08 |
| Married (yes/no) | 64.9 | 71.0 | 0.03 | 0.03 |
| Race (white/other) | 85.4 | 89.9 | 0.10 | 0.10 |
| Income (high/low) | 63.0 | 67.8 | 1.00 | 0.23 |
| Region: | ||||
| Northeast | 21.7 | 20.3 | Reference | Reference |
| Midwest | 14.5 | 13.1 | 0.06 | 0.06 |
| South | 17.6 | 21.5 | 0.01 | 0.01 |
| West | 46.2 | 45.1 | 0.03 | 0.03 |
| Dual eligible (yes/no) | 14.3 | 11.6 | 0.02 | 0.02 |
| Biopsy (yes/no) | 31.1 | 28.9 | 0.02 | 0.02 |
| Resection (yes/no) | 73.2 | 79.1 | 1.00 | 0.48 |
| CT scan(yes/no) | 79.6 | 76.8 | 1.00 | 0.08 |
| MRI (yes/no) | 76.5 | 83.4 | 0.13 | 0.13 |
| Initial discharge (home/other) | 45.4 | 55.3 | 1.00 | 0.94 |
| Number of tumors (1 tumor/>1 tumor) | 97.5 | 98.2 | 0.02 | 0.02 |
| Location of tumors (supratentorial/other) | 77.6 | 78.5 | 0.04 | 0.04 |
| Tumor size (≥ 3cm) | 70.3 | 70.4 | 0.03 | 0.03 |
| Palliative care (yes/no) | 10.6 | 10.4 | 0.02 | 0.02 |
| Extent of resection (major/minimal) | 28.5 | 29.9 | 1.00 | 0.14 |
| Atherosclerosis (yes/no) | 17.8 | 14.4 | 0.72 | 0.05 |
| Hypertension (yes/no) | 61.5 | 61.5 | 0.02 | 0.02 |
| Cerebrovascular disease (yes/no) | 1.40 | 0.8 | 0.04 | 0.04 |
| COPD (yes/no) | 10.3 | 7.7 | 0.03 | 0.03 |
| Pneumonia (yes/no) | 1.0 | 1.3 | 0.01 | 0.01 |
| Malnutrition (yes/no) | 1.7 | 1.3 | 0.01 | 0.01 |
| Dementia (yes/no) | 7.6 | 5.9 | 0.02 | 0.02 |
| Functional disability (yes/no) | 0.3 | 0.0 | 0.02 | 0.02 |
| Prior trauma (yes/no) | 2.8 | 2.6 | 0.03 | 0.03 |
| Psychological disease (yes/no) | 2.3 | 2.1 | 0.01 | 0.01 |
| Parkinson or Huntington (yes/no) | 0.9 | 0.6 | 0.01 | 0.01 |
| Anemia (yes/no) | 8.2 | 9.1 | 0.02 | 0.01 |
| Depression (yes/no) | 5.0 | 5.2 | 0.06 | 0.05 |
| Asthma (yes/no) | 3.0 | 1.7 | 0.01 | 0.01 |
| Diabetes (yes/no) | 21.0 | 20.4 | 0.99 | 0.06 |
| Deyo score: | ||||
| 0 | 57.9 | 61.1 | Reference | Reference |
| 1 | 27.6 | 27.8 | 0.04 | 0.04 |
| 2+ | 14.5 | 11.1 | 0.01 | 0.01 |
| Death within 1-year | 75.4 | 63.7 | ||
We estimate the average causal effect of temozolomide plus radiotherapy (vs. radiotherapy alone) on the probability of death within 1 year of diagnosis using the model averaged double robust estimator assuming prior model dependence defined by (5) with τ = 0 and using the two stage approach for calculating model weights. We specify logistic regression models for both the propensity score model and outcome model. The propensity score model class contains logistic regressions with all possible subsets of the covariates as main effects. The outcome model class contains logistic regressions that include the treatment and all possible subsets of the covariates as main effects. With 33 covariates, the joint model space has 22*33 = 7.4 * 1014 possible models. MCMC chains were run for 10,000 iterations. We estimate the rate of death within 1 year of diagnosis is 6.7% (2.4–10.7%) lower in the patients receiving temozolomide using the model averaged double robust estimator. This compares with the double robust estimator that includes all covariates in both the outcome and propensity score models that estimates a 6.4% (2.5–10.4%) lower mortality rate within 1 year of diagnosis for the patients receiving temozolomide. We also performed model selection, where we selected the propensity score and outcome model independently using BIC, and estimated the effect of temozolomide at 7.3% (3.5–11.1%). Notice that the 95% confidence intervals are slightly wider for the model averaged double robust estimator. This is expected, as the model averaged double robust estimator accounts for model uncertainty. As we will now discuss, the confidence intervals for the model averaged double robust estimator are only slightly wider because there is very little uncertainty in the selection of confounders in this example.
One benefit of utilizing model averaging is that the posterior probability of inclusion can be calculated for each potential confounder. Included in Table 6 are posterior inclusion probabilities in both the propensity score and outcome models. One can loosely interpret the probability of inclusion in the propensity score model as the probability of being a confounder because of the prior distribution and the two stage method used for calculating the model weights. Note that the age category 80+ years has a posterior inclusion probability in the propensity score model of 0.95, and the indicator of a home discharge after diagnosis has a posterior inclusion probability of 0.94. These large inclusion probabilities suggest that the data indicates that age and initial discharge location are related to both 1-year survival and receipt of temozolomide; therefore, age and discharge type are important confounders. The only other patient characteristic to have considerable posterior probability in the propensity score model is an indicator of resection, with a probability of 0.48.
These results suggest that there are only a few important confounders of the relationship between 1-year survival and receipt of temozolomide. This is not completely unexpected, as glioblastoma patients have poor prognosis and complications tend to arise from disease progression. This is reflected in the decision to treat with temozolomide, where the youngest and the healthiest patients are more likely to receive treatment.
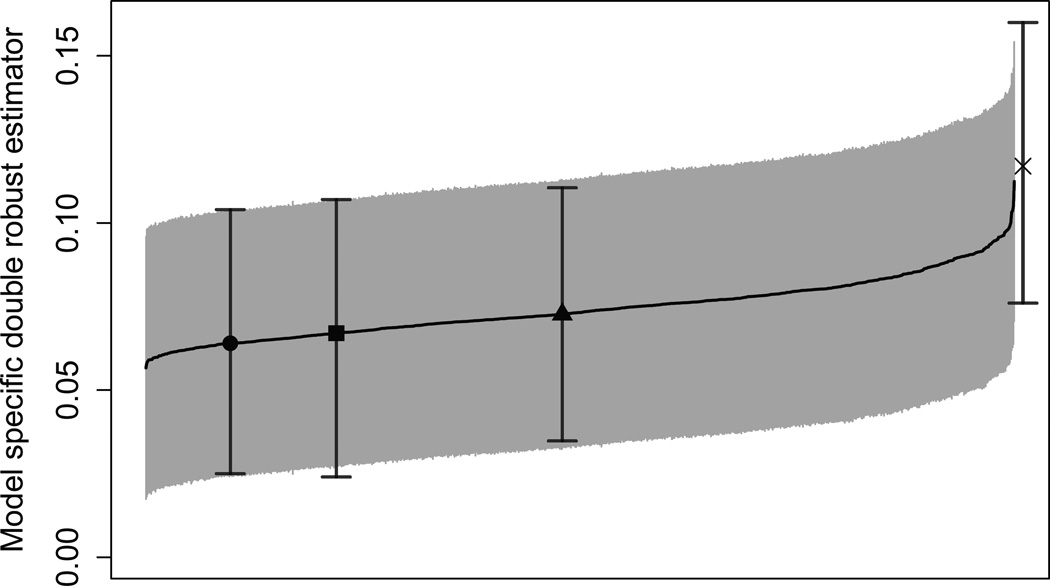
Figure 1 provides the model specific double robust estimators and corresponding 95% confidence intervals for 1000 randomly chosen outcome models and 1000 randomly chosen propensity score models. The unadjusted estimator of 11.7% (7.6–16.0%) is beyond the upper end of the distribution of the model specific estimates, while the model averaged double robust estimator of 6.7% (2.4–10.7%) is near the lower end of distribution. All of the model specific estimates are lower in magnitude than the unadjusted estimator, suggesting that any choice of models leads to a more conservative estimate of the difference in 1-year mortality when compared to the unadjusted estimator. The model averaged double robust estimator allows us to incorporate this model uncertainty into our final estimator by taking a weighted average of these model specific estimates. Figure 1 nicely provides a fully transparent illustration of the sensitivity of Δ̂DR to the choice of potential confounders in the outcome and propensity score models. We also see that the model selected estimate is anti-conservative when compared to the model averaged estimate or the double robust estimate that includes all of the covariates.
Figure 1.
Model specific double robust estimator for the glioblastoma example and corresponding 95% confidence intervals for 1000 randomly chosen outcome models and 1000 randomly chosen propensity score models, sorted by point estimates. The unadjusted estimator (X), the model averaged double robust estimator (square), the double robust estimator that includes all covariates into both models (circle), and the model selected double robust estimator (triangle) are included. Model selection is performed using BIC.
These results highlight the usefulness of the estimator at providing researchers with data-driven indications of the uncertainty surrounding the choice of confounders while returning consistent estimation of the causal effect of interest.
6 Discussion
In this paper we present a model averaging framework that can be used to robustify any causal estimator that depends on the specification of a model. We focused on the double robust estimator to highlight that model averaging is possible in contexts not yet explored in causal inference. The model weights used in this paper were derived from approximate posterior model probabilities, but one could consider weights derived from other criteria (e.g. model weights based on the balance of covariates between treatment groups). Studying the properties of alternate weights and the use of model averaging on other estimators in causal inference is an exciting line of research.
Our results build on the most basic double robust estimator for the average causal effect. It has been demonstrated elsewhere that this double robust estimator can be biased especially when some of the estimated propensity scores are close to zero or are highly variable, and several adjustments to the estimator have been proposed (Robins et al., 2007; Cao et al., 2009; Tan, 2010). We expect that results similar to those presented here may hold for these other estimators. Additionally, the model averaged double robust estimator does not assume that the confounders’ effect on the potential outcomes is the same between treatment groups, as a model for the outcome under each treatment can be specified.
Our model averaged double robust estimator shares some similarities with the work of Han and Wang (2013) who propose a method that allows the specification of multiple models for both the propensity score and the outcome regression. One difference in the methods lies in how the models are combined to produce the final estimator. We propose to take a weighted average of the model specific estimates, whereas Han and Wang (2013) combine the models to produce a subject specific weight, ŵi and define their estimator as μ̂ = ∑ŵiYi. While we propose a general procedure for model averaging in causal inference, it is not immediately clear to us whether the method of Han and Wang (2013) extends to other estimators.
A central piece in the construction of a model averaged estimator is the prior placed on the space of possible models. In this area there are opportunities to expand our work and potentially improve it substantially. For example, while our prior guarantees consistency in asymptotics with fixed p and increasing n, it would be interesting to investigate consistency when both p and n grow; in this setting a uniform prior on the model space can lead to inconsistency and priors that penalize model complexity may have better properties. The prior of (5) controls the prior probability of model combinations that do not meet the restriction ℳps ⊂ ℳom through τ. However, model combinations that do not meet this restriction have the same prior probability. This implies that, given an outcome model, the prior probability of a propensity score model that includes all the potential confounders included in the outcome model plus one additional potential confounder is the same as that of a propensity score model that includes all of the potential confounders that were excluded from the outcome model. In other words there is no prior penalization for complexity within these subspaces. In related work we have explored selecting priors that achieve a good balance between confounding adjustment and model parsimony. See Wang et al. (2012, 2015).
Scott et al. (2010) investigate priors that control for multiplicities in Bayesian variable selection. They stress that multiplicities are essential when one uses variable selection methods as exploratory tools whose resulting list of predictor is more important than the final model itself. This differ from what we do in two important ways: first, in our case, the final model and associated causal effect estimate are the main focus; secondly we do not select, we average. Nonetheless multiplicity properties may be a desirable property for a prior, achievable by allowing prior model probabilities to depend upon the data in an appropriate way. Our prior does not automatically adjust for multiplicities in this sense.
Causal inference approaches are increasingly used to analyze large observational studies, such as administrative databases in comparative effectiveness research. In these applications, there seldom is a clear-cut way of determining a priori the precise set of confounders of scientific relevance. At the same time, improvements in computing speed and parallelization are creating the opportunity for a more systematic investigation of alternative specifications for confounding adjustment. In these settings, the proposed model averaging strategy shows great promise as a data analysis tool to perform robust and consistent inferences with good small sample properties.
Supplementary Material
Acknowledgments
Support for this research was provided by National Institute of Environmental Health Sciences grants T32 ES007142, R01 ES012054, R01 ES024332, and R01 ES026217, National Institute of Health grant R01 GM111339, National Cancer Institute grant P01 CA134294, Environmental Protection Agency grants RD-83479801 and RD-83587201, Health Effects Institute grant (Dominici), and National Cancer Institute grants 5P30 CA006516-50 and R35 CA197449. This project was supported by grant number K18 HS021991 from the Agency for Healthcare Research and Quality. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Agency for Healthcare Research and Quality. We would like to thank Eric Tchetgen Tchetgen and Mireille Schnitzer for their useful discussions, and we would like to acknowledge the anonymous reviewers for their role in substantially improving this work. We are genuinely grateful for their thoughtful and creative suggestions.
Footnotes
Supplementary Materials
Web Appendices and Tables referenced in Sections 2, 3, and 4 are available with this paper at the Biometrics website on Wiley Online Library. A freely available R package (madr) can be downloaded from the CRAN package repository (R Core Team, 2016; Cefalu, 2016).
References
- Akaike H. Selected Papers of Hirotugu Akaike. Springer; 1998. Information theory and an extension of the maximum likelihood principle; pp. 199–213. [Google Scholar]
- Arvold N, Wang Y, Zigler C, Schrag D, Dominici F. Hospitalization burden and survival among older glioblastoma patients? Neuro-oncology. 2014;16(11):1530. doi: 10.1093/neuonc/nou060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arvold ND, Reardon DA. Treatment options and outcomes for glioblastoma in the elderly patient. Clinical interventions in aging. 2014;9:357. doi: 10.2147/CIA.S44259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61(4):962–973. doi: 10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- Brookhart MA, Schneeweiss S, Rothman KJ, Glynn RJ, Avorn J, Stürmer T. Variable selection for propensity score models. American journal of epidemiology. 2006;163(12):1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao W, Tsiatis AA, Davidian M. Improving efficiency and robustness of the doubly robust estimator for a population mean with incomplete data. Biometrika. 2009;96(3):723–734. doi: 10.1093/biomet/asp033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cefalu M. madr: Model Averaged Double Robust Estimation. R package version 1.0.0. 2016 doi: 10.1111/biom.12622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luna X, Waernbaum I, Richardson TS. Covariate selection for the nonparametric estimation of an average treatment effect. Biometrika. 2011;98(4) [Google Scholar]
- Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Statistical Science. 1999:29–46. [Google Scholar]
- Groenwold RH, Klungel OH, Grobbee DE, Hoes AW. Selection of confounding variables should not be based on observed associations with exposure. European journal of epidemiology. 2011;26(8):589–593. doi: 10.1007/s10654-011-9606-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber S, van der Laan MJ. An application of collaborative targeted maximum likelihood estimation in causal inference and genomics. The International Journal of Biostatistics. 2010;6(1) doi: 10.2202/1557-4679.1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber S, van der Laan MJ. Consistent causal effect estimation under dual misspecification and implications for confounder selection procedures. Statistical methods in medical research. 2012 doi: 10.1177/0962280212437451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn J. Functional restriction and efficiency in causal inference. Review of Economics and Statistics. 2004;86(1):73–76. [Google Scholar]
- Han P, Wang L. Estimation with missing data: beyond double robustness. Biometrika. 2013;100(2):417–430. [Google Scholar]
- Joffe MM, Ten Have TR, Feldman HI, Kimmel SE. Model selection, confounder control, and marginal structural models. The American Statistician. 2004;58(4) [Google Scholar]
- Longford NT. Missing data and small-area estimation: Modern analytical equipment for the survey statistician. Springer Science & Business Media; 2006. [Google Scholar]
- Madigan D, York J, Allard D. Bayesian graphical models for discrete data. International Statistical Review/Revue Internationale de Statistique. 1995:215–232. [Google Scholar]
- McCandless LC, Douglas IJ, Evans SJ, Smeeth L. Cutting feedback in bayesian regression adjustment for the propensity score. The international journal of biostatistics. 2010;6(2) doi: 10.2202/1557-4679.1205. [DOI] [PubMed] [Google Scholar]
- Pearl J. On a class of bias-amplifying covariates that endanger effect estimates. Technical report, Citeseer. 2009 [Google Scholar]
- Pope GC, Kautter J, Ellis RP, Ash AS, et al. Risk adjustment of medicare capitation payments using the cms-hcc model. Health Care Financing Review. 2004;25(4):119. [PMC free article] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2016. [Google Scholar]
- Robins J, Sued M, Lei-Gomez Q, Rotnitzky A. Comment: Performance of double-robust estimators when “inverse probability” weights are highly variable. Statistical Science. 2007;22(4):544–559. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Rubin D, et al. Estimating causal effects from large data sets using propensity scores. Annals of internal medicine. 1997;127:757–763. doi: 10.7326/0003-4819-127-8_part_2-199710151-00064. [DOI] [PubMed] [Google Scholar]
- Schneeweiss S, Rassen JA, Glynn RJ, Avorn J, Mogun H, Brookhart MA. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology. 2009 Jul;20(4):512–522. doi: 10.1097/EDE.0b013e3181a663cc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the Dimension of a Model. The Annals of Statistics. 1978;6(2):461–464. [Google Scholar]
- Scott JG, Berger JO, et al. Bayes and empirical-bayes multiplicity adjustment in the variable-selection problem. The Annals of Statistics. 2010;38(5):2587–2619. [Google Scholar]
- Shahar E. A new criterion for confounder selection? neither a confounder nor science. Journal of evaluation in clinical practice. 2013;19(5):984–986. doi: 10.1111/jep.12010. [DOI] [PubMed] [Google Scholar]
- Tan Z. Bounded, efficient and doubly robust estimation with inverse weighting. Biometrika. 2010;97(3):661–682. [Google Scholar]
- van der Laan MJ, Gruber S. Collaborative double robust targeted maximum likelihood estimation. The international journal of biostatistics. 2010;6(1) doi: 10.2202/1557-4679.1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Shpitser I. A new criterion for confounder selection. Biometrics. 2011;67(4):1406–1413. doi: 10.1111/j.1541-0420.2011.01619.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Bekaert M, Claeskens G. On model selection and model misspecification in causal inference. Statistical methods in medical research. 2012;21(1):7–30. doi: 10.1177/0962280210387717. [DOI] [PubMed] [Google Scholar]
- Wang C, Dominici F, Parmigiani G, Zigler CM. Accounting for uncertainty in confounder and effect modifier selection when estimating average causal effects in generalized linear models. Bio-metrics. 2015 doi: 10.1111/biom.12315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Parmigiani G, Dominici F. Bayesian effect estimation accounting for adjustment uncertainty. Biometrics. 2012;68(3):661–671. doi: 10.1111/j.1541-0420.2011.01731.x. [DOI] [PubMed] [Google Scholar]
- Wilson A, Reich BJ. Confounder selection via penalized credible regions. Biometrics. 2014;70(4):852–861. doi: 10.1111/biom.12203. [DOI] [PubMed] [Google Scholar]
- Wooldridge J. Technical report, Tech. Rep.¡. MI: Michigan State University; 2009. Should instrumental variables be used as matching variables. https://www.msu.edu/ec/faculty/wooldridge/current%20research/treat1r6.pdf¿. [Google Scholar]
- Yang Y. Regression with multiple candidate models: selecting or mixing? Statistica Sinica. 2003:783–809. [Google Scholar]
- Yang Y. Can the strengths of aic and bic be shared? a conflict between model indentification and regression estimation. Biometrika. 2005;92(4):937–950. [Google Scholar]
- Zigler CM, Dominici F. Uncertainty in propensity score estimation: Bayesian methods for variable selection and model-averaged causal effects. Journal of the American Statistical Association. 2014;109(505):95–107. doi: 10.1080/01621459.2013.869498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigler CM, Watts K, Yeh RW, Wang Y, Coull BA, Dominici F. Model feedback in bayesian propensity score estimation. Biometrics. 2013;69(1):263–273. doi: 10.1111/j.1541-0420.2012.01830.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.