Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1990 Sep;87(18):7110–7114. doi: 10.1073/pnas.87.18.7110

Interactions of neural networks: models for distraction and concentration.

L P Wang 1, J Ross 1
PMCID: PMC54693  PMID: 2402493

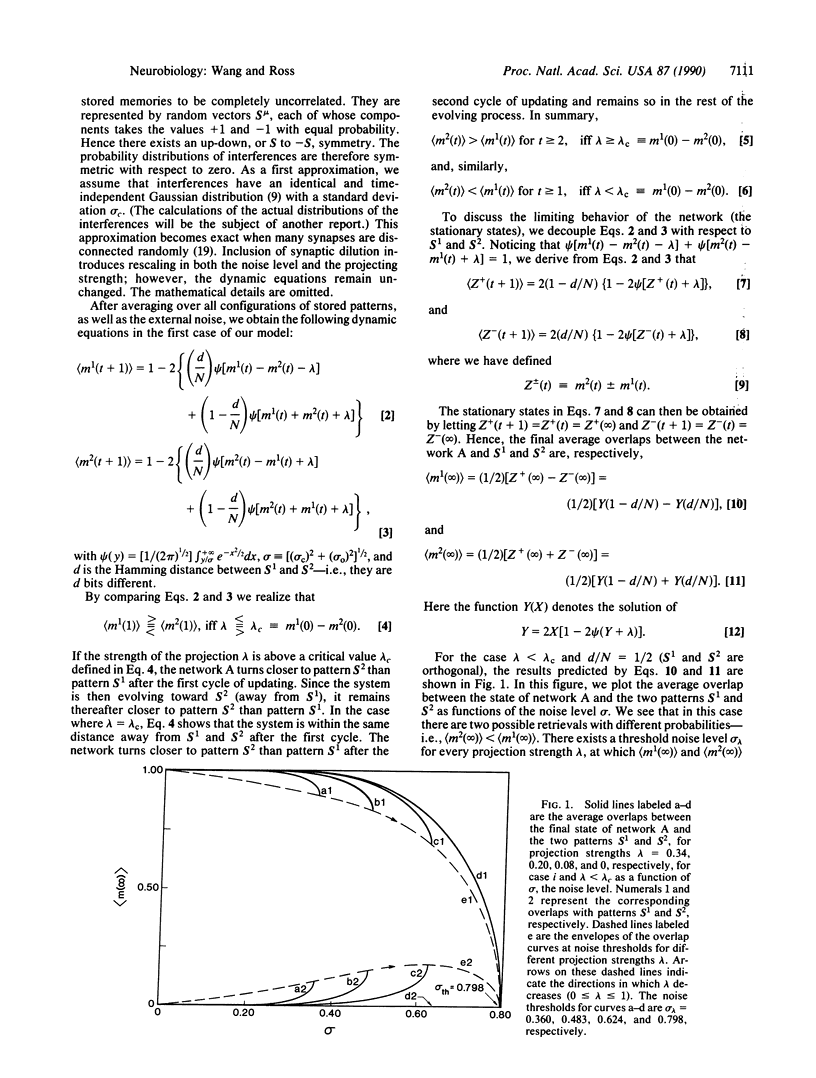
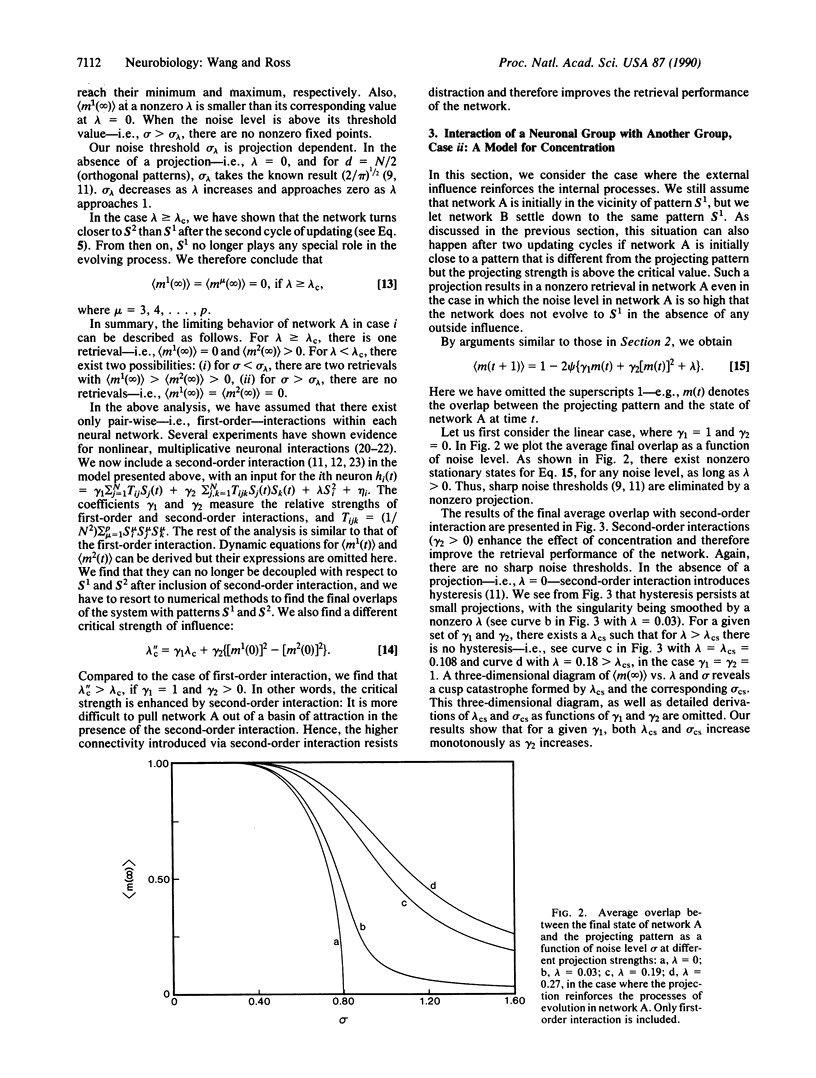
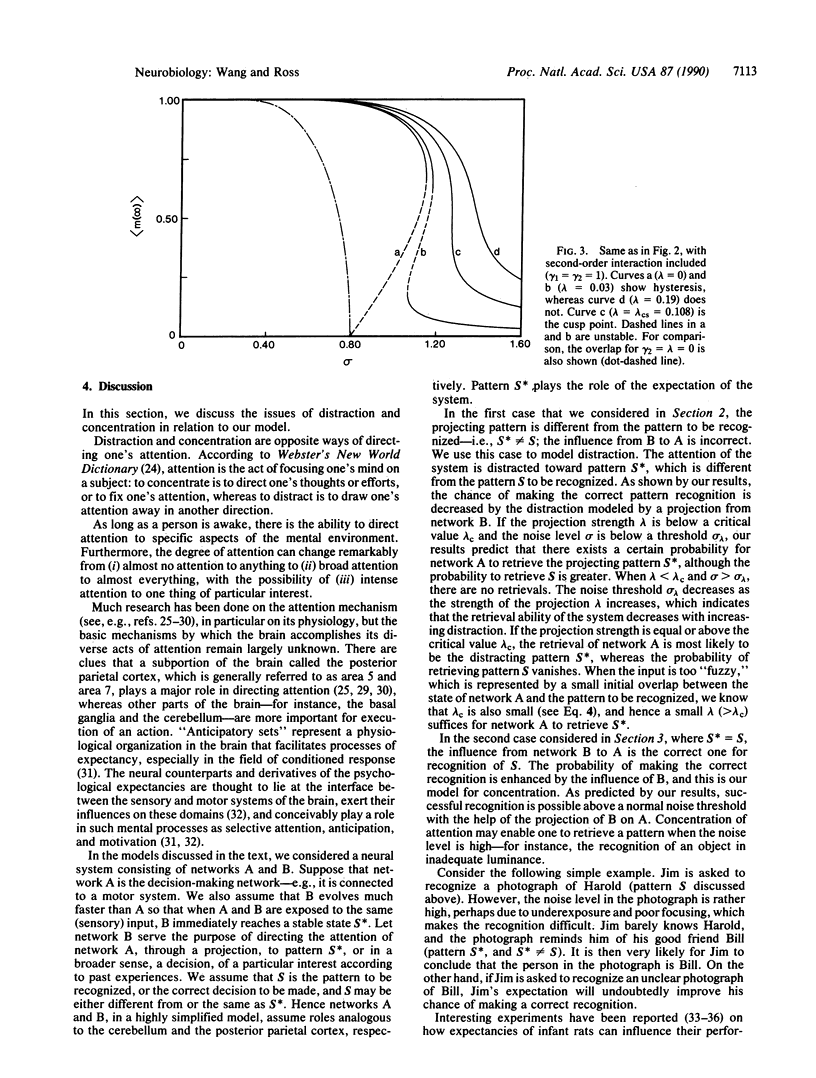
Abstract

We present a model of neural group interactions, which are projections from one neural network (network B) of McCulloch-Pitts neurons connected via a Hebbian rule, to another network (network A) of the same structure. We first consider the case in which the projecting network B is in a pattern different from the initial attracting state of network A. A critical projecting strength lambda c is found such that for lambda below this value there exists a noise threshold sigma lambda corresponding to each lambda. For the case where lambda less than lambda c and the noise level sigma less than sigma lambda, there are two possible retrievals, with different probabilities: the initial attracting state of network A and the projecting pattern. If lambda less than lambda c and sigma greater than sigma lambda, stable states of network A disappear. In the case lambda greater than lambda c, network A is pulled out of its initial basin of attraction and into that of the projecting pattern. This analysis provides a model for distraction. Second-order interactions reduce the distraction. When the projecting network B is in the same pattern as the initial attracting state of network A, the projection acts as an external reinforcement, which enables network A to retrieve in highly noisy conditions. Sharp noise thresholds for nonzero retrievals are shown to be eliminated by the projection. Higher-order connectivity improves the retrieval ability of the network. The second case serves as a model of concentration. We discuss the model of distraction and concentration (i) in connection with common experience of expectation of recognition and (ii) in connection with recent T-maze experiments on infant rats; finally, we suggest a refined version of the Bruner-Potter experiment to test our prediction of the disappearance of hysteresis.

Full text

PDF

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Amit DJ, Gutfreund H, Sompolinsky H. Spin-glass models of neural networks. Phys Rev A Gen Phys. 1985 Aug;32(2):1007–1018. doi: 10.1103/physreva.32.1007. [DOI] [PubMed] [Google Scholar]
  2. BRUNER J. S., POTTER M. C. INTERFERENCE IN VISUAL RECOGNITION. Science. 1964 Apr 24;144(3617):424–425. doi: 10.1126/science.144.3617.424. [DOI] [PubMed] [Google Scholar]
  3. Crick F. The recent excitement about neural networks. Nature. 1989 Jan 12;337(6203):129–132. doi: 10.1038/337129a0. [DOI] [PubMed] [Google Scholar]
  4. Hopfield J. J. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A. 1982 Apr;79(8):2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Kandel E. R., Tauc L. Heterosynaptic facilitation in neurones of the abdominal ganglion of Aplysia depilans. J Physiol. 1965 Nov;181(1):1–27. doi: 10.1113/jphysiol.1965.sp007742. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Keeler J. D., Pichler E. E., Ross J. Noise in neural networks: thresholds, hysteresis, and neuromodulation of signal-to-noise. Proc Natl Acad Sci U S A. 1989 Mar;86(5):1712–1716. doi: 10.1073/pnas.86.5.1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Peretto P., Niez J. J. Long term memory storage capacity of multiconnected neural networks. Biol Cybern. 1986;54(1):53–63. doi: 10.1007/BF00337115. [DOI] [PubMed] [Google Scholar]
  8. Roney K. J., Scheibel A. B., Shaw G. L. Dendritic bundles: survey of anatomical experiments and physiological theories. Brain Res. 1979;180(2):225–271. doi: 10.1016/0165-0173(79)90006-7. [DOI] [PubMed] [Google Scholar]
  9. Shaw G. L., Harth E., Scheibel A. B. Cooperativity in brain function: assemblies of approximately 30 neurons. Exp Neurol. 1982 Aug;77(2):324–358. doi: 10.1016/0014-4886(82)90249-7. [DOI] [PubMed] [Google Scholar]
  10. Smith G. J., Bogomolny A. Appetitive instrumental training in preweanling rats: I. Motivational determinants. Dev Psychobiol. 1983 Mar;16(2):119–128. doi: 10.1002/dev.420160205. [DOI] [PubMed] [Google Scholar]
  11. Smith G. J., Croft E. R. Analysis of appetitive motivation in preweanling rats: application of bromocryptine mesylate. Behav Neural Biol. 1985 May;43(3):250–259. doi: 10.1016/s0163-1047(85)91593-6. [DOI] [PubMed] [Google Scholar]
  12. Smith G. J., Spear N. E. Effects of the home environment on withholding behaviors and conditioning in infant and neonatal rats. Science. 1978 Oct 20;202(4365):327–329. doi: 10.1126/science.694538. [DOI] [PubMed] [Google Scholar]
  13. Wang L., Ross J. Synchronous neural networks of nonlinear threshold elements with hysteresis. Proc Natl Acad Sci U S A. 1990 Feb;87(3):988–992. doi: 10.1073/pnas.87.3.988. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES