Abstract
An extension of Generalized Structured Component Analysis (GSCA), called Functional GSCA, is proposed to analyze functional data that are considered to arise from an underlying smooth curve varying over time or other continua. GSCA has been geared for the analysis of multivariate data. Accordingly, it cannot deal with functional data that often involve different measurement occasions across participants and a large number of measurement occasions that exceeds the number of participants. Functional GSCA address these issues by integrating GSCA with spline basis function expansions that represent infinite-dimensional curves onto a finite-dimensional space. For parameter estimation, functional GSCA minimizes a penalized least squares criterion by using an alternating penalized least squares estimation algorithm. The usefulness of functional GSCA is illustrated with gait data.
Keywords: Generalized structured component analysis, Functional data analysis, Basis function expansion, Splines, Penalized least squares, Alternating least squares
1. Introduction
Generalized Structured Component Analysis (GSCA; Hwang & Takane, 2004) represents component-based structural equation modeling, which enables to examine directional relationships among multiple sets of responses by combining data reduction with path modeling. In GSCA, a component or a weighted composite is obtained from each set of responses, considering hypothesized relationships among observed responses and components simultaneously.
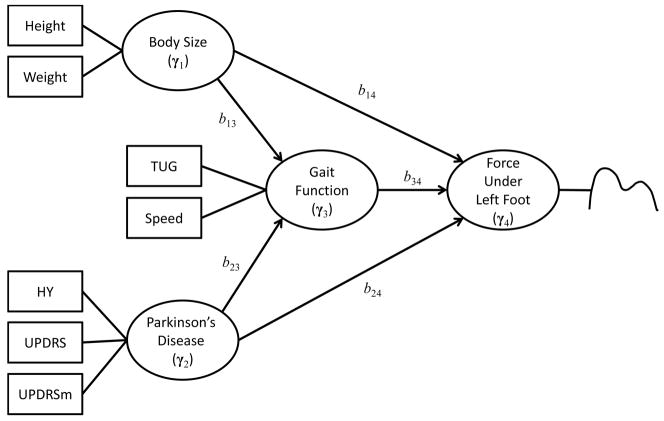
Figure 1 shows an example of the hypothesized relationships among multiple sets of responses that will be further discussed in Section 5. In this example, there are four sets of responses: body size, severity of Parkinson’s disease, gait function, and force under left foot. It is hypothesized that the body size and severity of Parkinson’s disease affect the force under left foot and these effects are mediated by the gait function. If all of these four sets of responses consisted of multivariate data, the original GSCA can be used to fit this model to the data. However, the force under left foot involves so-called functional data, which have distinct characteristics and cannot be easily handled by the original GSCA.
Figure 1.
The hypothesized directional relationships among the four sets of responses. In the path diagram, a circle represents a set; a square indicates an observed variable in the set; a curve right next to the set, force under left foot, indicates that this set consists of functional data. A more detailed description of the observed variables is given in Section 5.
In this paper, we propose an extension of GSCA, called functional GSCA, to deal with functional data. The emergence of sophisticated measurement tools, such as motion capture devices, handheld computers, Bluetooth devices, eye-trackers, and brain scanners, has facilitated the collection of functional data, which refer to the data that are considered to arise from an underlying smooth function varying over a continuum (Ferraty & Vieu, 2006, Chapter 1; Ramsay & Silverman, 2005, Chapter 3). The continuum is often time, but it can be any dimension such as spatial location, wavelength, probability, etc. Researchers in many disciplines have collected a variety of functional data, including motion capture data (e.g., Ormoneit, Black, Hastie, & Kjellström, 2005), motor control data (e.g., Mattar & Ostry, 2010), music perception data (e.g., Vines, Krumhansl, Wanderley, & Levitin, 2006), neuroimaging data (e.g., Tian, 2010), pupil dilation data (e.g., Jackson & Sirois, 2009), and face temperature data (e.g., Park, Suk, Hwang, & Lee, 2013).
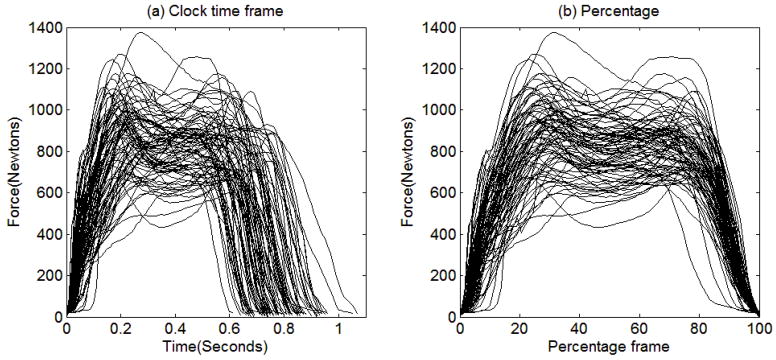
Figure 2(a) displays the functional data that will be analyzed in Section 5. In this example, we have a total of 83 Parkinson’s disease patients who were instructed to walk at their normal pace for two minutes. The force under left foot was measured at a rate of 100 Hz while they were walking. Each trajectory presented in Figure 2(a) is the force under left foot for the first gait cycle completed by each patient. We defined a gait cycle to begin when the force under left foot reaches up to 20 Newtons and to end when it returns back to 20 Newtons.
Figure 2.
The force under left foot for the first gait cycle completed by each patient plotted against (a) clock time (in seconds) and (b) percentage completed (%).
Figures 2(a) and 2(b) illustrate the unique characteristics of functional data. First, as shown in Figure 2(a), each patient has a different walking speed and thus the time to complete a gait cycle varies from patient to patient. The shortest gait cycle took 0.61 second and thus it was measured over 62 time points (from second 0 to second 0.61 by 0.01 second). The longest one took 1.07 seconds and thus it was measured over 108 time points. The original GSCA assumes that each participant is measured on the same number of variables (i.e., time points) and each variable has the same meaning across all participants. However, in functional data, each participant can be measured at different numbers of time points and each time point might have a different meaning for different participants. For example, if a patient walks at a period of 0.7 second/cycle, the second 0.7 indicates the time when the cycle is completed for this patient. However, if a patient walks at a period of 1 second/cycle, the second 0.7 indicates the time when the 70% of the cycle is completed for this patient.
If we transform the original clock time into how much percentage of the gait cycle is completed, we can line up the data according to the percentage frame of reference as shown in Figure 2(b). In this case, each value on the percentage frame has the same meaning across all participants. For example, the value 70% indicates the time when the 70% of the gait cycle is completed for all participants. However, even if we align the data according to the percentage frame of reference, the original GSCA still cannot analyze such aligned data because each trajectory has a different number of measurement occasions.
Second, in functional data, the number of time points often exceeds the number of participants. For the gait data shown in Figures 2(a) and 2(b), the longest gait cycle was measured over 108 time points, which is greater than the number of patients, 83. The original GSCA breaks down when the number of participants is smaller than the number of variables. Even when the number of time points does not exceed the number of participants, the responses measured at adjacent time points tend to be highly correlated, which can lead to a singularity problem when estimating parameters in the original GSCA.
To address these issues, one might be tempted to summarize functional data using summary measures such as component scores obtained by functional principal components analysis (functional PCA; Ramsay & Dalzell, 1991; Ramsay & Silverman, 2005, Chapter 8), and to use the component scores for further analyses. Even though the component scores can be used in the original GSCA framework as indicator variables, this way of analysis might not be desirable. As Abdi (2003) pointed out, the principal components are extracted to maximally explain the variation in the functional data without considering the hypothesized relationships with other sets of variables. There is no guarantee that the extracted components are relevant to other sets of variables. We will discuss this point further in Section 5.3.
The proposed method aims to extend GSCA so that we can analyze functional data properly in the framework of GSCA. Technically, the proposed method integrates GSCA with basis function expansions in order to represent functional data as smooth curves as well as to estimate parameter functions. The idea of basis function expansions is that any smooth curve can be approximated arbitrarily well by taking a weighted sum of a sufficiently large number of basis functions such as spline basis functions and Fourier basis functions (Ramsay & Silverman, 2005, Chapter 3.3). Basis function expansions enable to deal with variation in measurement occasions across participants; the smoothed curves expressed by basis function expansions are defined over the entire range of time or argument and can be evaluated at any value of time within the range. Basis function expansions also enable to deal with the issue of high dimensionality of functional data due to a large number of measurement occasions; we can represent smooth curves on a relatively low-dimensional space spanned by the basis functions.
The proposed method is distinguished from other statistical methodologies that can handle multiple sets of functional data. Functional multiple-set canonical correlation analysis (Hwang, Jung, Takane, & Woodward, 2012) can examine non-directional associations among multiple sets of functional data whereas the proposed method can examine directional relationships. Functional extended redundancy analysis (Hwang, Suk, Lee, Moskowitz, & Lim, 2012) and generalized functional extended redundancy analysis (Hwang, Suk, Takane, Lee, 2015) assume a model that can be represented by a single equation in which a scalar response variable is predicted from multiple sets of functional data. Contrarily the proposed method can examine more complicated directional relationships among multiple sets of functional and/or multivariate data as illustrated in Figure 1 that can be represented by a set of simultaneous equations. Functional linear models including functional ANOVA (Ramsay & Silverman, 2005, Chapter 13; Zhang, J.-T., 2013), varying-coefficient model (Hastie & Tibshirani, 1993; Ramsay & Silverman, 2005, Chapter 15), and time-varying effect model (Tan, Shiyko, Li, Li, & Dierker; Ramsay & Silverman, 2005, Chapter 14) can examine directional relationships among multiple sets of functional data but they also assume a model that can be represented by a single equation only. The linear functional structural equation modeling (lfSEM; Lindquist, 2012) can examine a mediation model that involves a set of simultaneous equations. However, the lfSEM can only handle a model in which the relationship between a scalar input variable and a scalar output variable is mediated by a functional mediator variable. The proposed method can deal with more complicated models in which any of the input, output, and mediation variables can be functional.
This paper is organized as follows. Section 2 provides a brief description of the original GSCA. Section 3 discusses the technical details of functional GSCA. It provides the functional GSCA model and a penalized least squares criterion for parameter estimation, which is minimized by an alternating penalized least squares algorithm. It also expounds the relationship between functional GSCA and the original GSCA, and discusses additional computational issues. Section 4 presents the results of simulation studies which focus on the accuracy of parameter recovery of functional GSCA and stability of the algorithm. Section 5 illustrates the applicability and usefulness of functional GSCA by analyzing the gait data and comparing the results with those obtained from existing methods. The final section summarizes the previous sections and discusses limitations and possible extensions of functional GSCA.
2. Generalized Structured Component Analysis
For model specification, GSCA involves three sub-models: measurement, structural, and weighted relation models. The measurement model specifies relationships between components and observed variables. Assume that N participants are measured on K sets of variables, each of which consists of Pk variables (k = 1, …, K). The measurement model can be generally expressed as:
| (1) |
where zijk indicates a response of participant i (i = 1, …, N) on variable j (j = 1, …, Pk) in the kth set (k = 1, …, K), γik is the kth component score of participant i, cjk is a component loading relating the kth component score to the jth observed variable in the kth set, and εijk is the residual or measurement error. The measurement models for all N participants on all Pk variables in the kth set can be combined into a single equation as follows:
| (2) |
where Zk is an N by Pk matrix of observed responses on the Pk variables in the kth set whose (i, j)th element is zijk, γk = [γ1k, …, γNk]′ is an N by 1 vector of the kth component scores, ck = [c1k, …, cPkk]′ is a Pk by 1 vector of loadings relating the kth component score to the corresponding set of observed response variables, and εk is an N by 1 vector of residuals for the kth set of responses.
The structural model specifies hypothesized directional relationships among the component scores. It can be expressed in matrix notation, as follows:
| (3) |
where Γ is an N by K matrix of component scores, i.e., Γ = [γ1, …, γK], B is a K by K matrix of path coefficients reflecting directional relationships among the component scores, and E is an N by K matrix of residuals. For example, the structural model given in Figure 1 specifies the hypothesized directional relationships among the four component scores: body size (γ1), severity of Parkinson’s disease (γ2), gait function (γ3), and force under left foot (γ4). The matrix of the path coefficients (B) is given by:
| (4) |
where bkl is a parameter to be estimated that indicates the effect of the kth component score on the lth component score and 0’s and 1’s are fixed values. The structural model in Figure 1 can be written as follows:
| (5) |
which contains the following four simultaneous equations:
| (6) |
where ek indicates a vector of residuals for the kth component scores. The first two equations in (6) show that body size (γ1) and severity of Parkinson’s disease (γ2) are exogenous component scores that involve no residuals, gait function (γ3) is predicted from body size (γ1) and severity of Parkinson’s disease (γ2), and force under left foot (γ4) is predicted from body size (γ1), severity of Parkinson’s disease (γ2), and gait function (γ3).
The weighted relation model is used to explicitly define each component score as a weighted composite of observed variables as follows:
| (7) |
where wk is a Pk by 1 vector of weights to define the kth component score.
From (2), (3), and (7), we can see that there are three sets of parameters to estimate: component scores (γk), loadings (ck), and path coefficients (B). In particular, estimating the kth component scores reduces to estimating the corresponding weight vector wk.
In GSCA, the data matrices Zk are typically columnwise standardized to have zero mean and unit variance for each variable. The parameters, {wk}, {ck}, and B are estimated by minimizing the following objective function, subject to the constraint that the variance of each component score equals to unity:
| (8) |
where SS(E) = tr(E′E) indicates the sum of squares of all elements in E. The first term of the objective function represents the sum of squared residuals in the measurement model and the second term is the sum of squared residuals in the structural model. An alternating least squares algorithm (de Leeuw, Young, & Takane, 1976; Hwang, Desarbo, & Takane, 2007; Hwang & Takane, 2004) was developed to minimize this objective function.
An overall fit of a hypothesized model can be measured by FIT (Hwang & Takane, 2004), which is given by:
| (9) |
where ϕ is the objective function value as given in (8) and SS(Z) + SS(Γ) is the total variation in observed variables and component scores. The FIT indicates the proportion of variation in observed variables and component scores that is accounted for by the hypothesized GSCA model. The FIT ranges from 0 to 1; a larger FIT value indicates a better fit.
3. Functional Generalized Structured Component Analysis
In this section, the functional GSCA model is developed to deal with directional relationships among multiple sets of functional responses by combining the original GSCA with basis function expansions and penalized least squares smoothing.
3.1 Data Structure
Assume that N participants are measured on K variables over multiple measurement occasions, thus yielding K sets of functional responses. Let Jik denotes the number of measurement occasions over which the kth variable (k = 1, …, K) was repeatedly measured for the ith participant. Note that the number of measurement occasions might vary across individuals. However, we will assume that the range Tk, over which the measurements are obtained, does not vary across individuals. In the gait data presented in Figure 2(b), for example, each patient’s total force under left foot was measured at different numbers of measurement occasions. However, the range over which the responses were obtained is common to all the patients, i.e., Tk = [0%, 100%].
The response of participant i (i = 1, …, N) at measurement occasion j (j = 1, …, Jik) for variable k (k = 1, …, K) is denoted by zijk, which can be modeled as:
| (10) |
where tijk ∈ Tk is an argument value corresponding to the jth measurement occasion of the ith participant for variable k, vik(tijk) is a smooth curve underlying zijk evaluated at tijk, and εijk is the residual or measurement error. We will call vik(t) data function hereafter (t ∈ Tk). Functional GSCA uses data functions vik(t) as an input instead of raw functional data zijk.
Considering that data functions tend to be (often complex) nonlinear functions of t as illustrated in Figure 2, it is not satisfactory to use simple linear models of t to represent data functions. A popular method for going beyond linearity but still exploiting the simplicity of linear models is to replace t with its transformations and use a linear combination of these transformed values. That is, the data function vik(t) can be represented by:
| (11) |
where Lk is the number of transformations of t used to represent the kth set of functional responses, θkl(t) indicates the lth transformation of t, xikl is the coefficient of θkl(t) for participant i, xik = [xik1, …, xikLk]′ and θk(t) = [θk1(t), …, θkLk(t)]′.
This representation is referred to as a linear basis function expansion in t, and θkl(t) is called the lth basis function for the kth set of functional responses (for more comprehensive discussion on basis function expansions, see Hastie, Tibshirani, and Friedman, 2009, Chapter 5). By using a linear basis function expansion, a function is approximated as a linear combination of a certain number of basis functions that span a function space. This is just as a vector is represented as a linear combination of a certain number of basis vectors that span a vector space. In this way, an infinite-dimensional curve can be represented as a finite-dimensional vector of the coefficients of basis functions.
There are various types of basis functions, θk(t), that can be used. Most functional data analyses involve either Fourier basis functions for periodic data or spline basis functions for non-periodic data (Ramsay & Silverman, 2005, p.45). The proposed method will be developed and illustrated with using spline basis functions, more specifically, B-spline basis functions. However, it will work with any other types of basis functions.
The basis function coefficients, xik, can be estimated by minimizing a penalized least squares criterion (Ramsay & Silverman, 2005, Chapter 5) with generalized cross-validation (Craven & Wahba, 1979). Refer to Ramsay and Silverman (2005; Chapters 3, 4, and 5) for more detailed discussions on how to estimate basis function coefficients and to Ramsay, Hooker, and Graves (2009; Chapters 3, 4, and 5) for MATLAB and R codes for smoothing.
3.2 The functional GCSA model
Like the original GSCA, functional GSCA involves the same three sub-models for model specification. The measurement model specifies the relationships between data functions and component scores as follows:
| (12) |
where γik is the kth component score of participant i, ck(t) is a loading function evaluated at time t, and εik(t) is a residual function. As will be discussed in Section 3.5, the data function will be mean-centered. That is, the data function represents the deviation from the mean curve. Note that ck(t) does not have subscript i, which indicates that the loading function is assumed to be common to all individuals. In other words, functional GSCA assumes that there is a mode of temporal variation, which can be characterized by ck(t), and individuals vary in terms of how much their trajectories reflect this mode of variation, or the amplitude of this variation, represented by the component score, γik. Therefore, the kth loading function captures the representative shape of temporal variation from the mean curve on the kth variable and the corresponding component scores reflect the between-subjects variability in terms of amplitude.
The structural model specifies hypothesized directional relationships among the components, or amplitudes of response trajectories, which is identical to that of the original GSCA:
| (13) |
The weighted relation model defines a component score as a weighted integration of a data function as follows:
| (14) |
where wk(t) indicates a weight function to define the kth component score. The value of a weight function at time t indicates the amount of contribution of the data function at time t to forming the component score. That is, a weight function represents which time interval is crucial for capturing the variability in data functions as well as component scores.
In functional GSCA, there are three sets of parameters to estimate: component scores (γik), loading functions (ck(t), and path coefficients (B). In particular, estimating the component scores reduces to estimating the corresponding weight functions wk(t). To estimate loading and weight functions, we need to represent them by using basis function expansions:
| (15) |
| (16) |
where yk is an Lk by 1 vector of the coefficients for the kth weight functions and ak is an Lk by 1 vector of the coefficients for the kth loading function.
Based on (11) and (15), we can rewrite (14) as:
| (17) |
where Qk = ∫Tk θk(t)θk(t)′dt. By stacking the kth component scores of N participants into one vector, we obtain
| (18) |
where γk = [γ1k, …, γNk]′ and Xk = [x1k, …, xNk]′. Likewise, by using (11), (16), and (18), the measurement model (12) for all N participants can be compactly expressed as:
| (19) |
where εk(t)= [ε1k(t), …, εNk(t)]′.
Consequently, estimating the three sets of parameters, i.e., the weight functions {wk(t)}, loading functions {ck(t)}, and path coefficients B, reduces to estimating the following three sets of parameters: {yk}, {ak}, and B.
3.3 Parameter estimation
Functional GSCA estimates the three sets of parameters, {yk}, {ak}, and B, by minimizing the following objective function:
| (20) |
subject to the constraint that the norm of each component score should equal to the number of participants N. The first term of the objective function indicates the integrated squared residuals in the measurement model (19) summed over all N participants and all K sets of responses. The second term of the objective function indicates the sum of squared residuals in the structural model (13).
The third and the last terms are penalty terms that control the degree of roughness of weight and loading functions, respectively. When estimating parameter functions such as weight and loading functions, it is important to select an optimal number of basis functions. In general, using too many basis functions leads to a highly fluctuating function, often associated with the risk of overfitting, whereas using too few leads to failure to capture important temporal variations. One way to address the issue of selecting the optimal number of basis functions is to use rather a large number of basis functions while preventing the estimated curve from being highly fluctuated by using a penalty term (Eilers & Marx, 1996). For example, the following penalty term can be used for the weight function wk(t):
| (21) |
where D2 is the second derivative operator. The penalty term (21) indicates the squared second derivative of wk(t) integrated over the range Tk. A straight line, which has no curvature or roughness, will have a zero second derivative. As a function becomes more fluctuating at time t, the second derivative of the function at time t will deviate farther away from zero. Therefore, the squared second derivative of a function at time t indicates its curvature or roughness at time t and the squared second derivative of a function integrated over the whole range of t indicates its overall curvature or roughness over the entire range. The penalty term (21) can be rewritten based on (15):
| (22) |
where Rk = ∫Tk D2θk(t)D2θk(t)′dt. Similarly, based on (16), the overall curvature of the kth loading function ck(t) can be written as:
| (23) |
The nonnegative smoothing parameters, λk and ρk, in (20) control the importance of the corresponding penalty terms in yielding final solutions. When λk = ρk = 0 for all k, minimizing the objective function is equivalent to minimizing the sum of squared residuals in the measurement and structural models. Minimizing these residuals, i.e., maximizing the fit to a given data set, takes the risk of overfitting, which may yield highly fluctuating weight and loading functions. By using greater values of the smoothing parameters, the risk of overfitting can be reduced and thus smoother weight and loading functions can be obtained. The optimal values of the smoothing parameters can be determined by a cross-validation method, which will be further discussed in Section 3.5.
An alternating penalized least squares algorithm is developed to minimize (20). This algorithm starts with assigning random initial values to {yk}, {ak}, and B and iterates the following three steps until convergence.
STEP 1
Update {yk} for fixed {ak} and B to minimize the objective function f subject to the constraint that the squared norm of the component score is equal to the number of participants, i.e.,
| (24) |
for all k. This step requires solving a constrained nonlinear optimization problem; the objective function f is a nonlinear function of the parameters {yk} and the objective function should be minimized with respect to the parameters {yk} subject to the K constraints given in (24). The interior-point algorithm (Byrd, Gilbert, & Nocedal, 2000; Byrd, Hribar, & Nocedal, 1999) is used to solve this constrained nonlinear optimization problem by using the fmincon function implemented in MATLAB and to obtain the updated {yk}.
STEP 2
Update {ak} for fixed {yk} and B. Each ak can be updated separately since the objective function f can be written as the sum of K terms, kth term of which contains ak only. To update ak, we solve ∂f/∂ak = 0. The first term of the objective function can be written as:
| (25) |
and ∂f/∂ak = 0 can be rewritten as:
| (26) |
Solving (26) yields the updated ak :
| (27) |
STEP 3
Update B for fixed {yk} and {ak}. Note that B contains parameters to estimate as well as fixed values as illustrated in (4). The second term of the objective function can be written as:
| (28) |
where vec(B) is a super-vector obtained by stacking the columns of B in order, ⊗ indicates the Kronecker product, b is a vector containing only free parameters in vec(B), and Φ is a matrix containing the columns of Ik ⊗ Γ corresponding to the free parameters in vec(B). We can update b by solving ∂f/∂b = 0, which is equivalent to solving ∂f2/∂b = 0. The updated b is given by:
| (29) |
and the updated B can be obtained by putting the elements of b̂ in the appropriate locations in B.
The goodness-of-fit of a hypothesized model can be measured by the FIT index as in the original GSCA, which is given by:
| (30) |
The FIT represents the amount of variation in data functions and component scores that can be explained by the specified model. The first term in the denominator in (30) indicates the total variation in data functions, which can be shown by:
| (31) |
The second term in the denominator represents the total variation of component scores; there are K component scores and each component score has the norm of N. In the numerator, f1 and f2 indicate the amount of squared residuals in the measurement and structural models, respectively. Therefore, the FIT ranges from 0 to 1 and a larger value indicates a better fit. One can use the FIT to compare different models and choose one associated with the highest FIT value as the best model.
3.4 Constrained models
In practice, we may encounter situations in which some observed variables are functional whereas others are multivariate, as illustrated in Figure 1. Functional GSCA can easily accommodate this situation. We can see that the components (18) in functional GSCA reduces to the components (7) in GSCA by constraining Xk = Zk, and Qk = IPk. Note that the corresponding penalty parameters, λk and ρk, should be set to zero. The updated âk and the updated ŷk reduce to the updated loading and weight vectors in the original GSCA (see Hwang et al., 2007; Hwang & Takane, 2004). The matrix of path coefficients B will be updated in the same way in both the original and functional GSCA.
In sum, functional GSCA can deal with both functional and multivariate data by constraining Xk = Zk, Qk = IPk, and λk = ρk = 0 for the kth set of observed variables when it is multivariate. Thus, the original GSCA can be viewed as a special case of functional GSCA, where Xk = Zk, Qk = IPk, and λk = ρk = 0 for all k.
3.5 Other computational considerations
In functional GSCA, B-spline basis functions (de Boor, 2001) are used for basis function expansions because they are appropriate to capture local fluctuations, well-conditioned, numerically stable, and computationally efficient (Dierckx, 1993, Chapter 1). For mathematical definitions and more comprehensive discussions on B-spline basis functions, see de Boor (2001, Chapters 9, 10, and 11), Dierckx (1993, Chapter 1), Hastie et al. (2009, Chapter 5), and Ramsay and Silverman (2005, Chapter 3).
The optimal values of smoothing parameters λk and ρk in (20) are determined by using G-fold cross-validation (Hastie et al., 2009, Chapter 7.10) with assuming λ1 = ··· = λK = λ and ρ1 = ··· = ρK = ρ to reduce computational burden. To perform a G-fold cross-validation, a grid of values for λ and that for ρ are set to test. And the data set is divided into G subsets of similar sizes. Under each pair of values for λ and ρ, one subset of data, called test data, is set aside and the other G−1 subsets of data, called training data, are used to estimate parameters. By using the estimated weight functions, we can obtain the component scores for the test data based on (14). By using the estimated loading functions and obtained component scores, we can obtain the measurement error functions for the test data based on (12). By using the estimated path coefficients and obtained component scores, we can obtain the structural errors for the test data based on (13). The prediction error is defined as the sum of the two errors obtained for the test data: integrated squared measurement error functions and the squared structural errors. We repeat this process G times by using each subset of data as test data each time and obtain G prediction errors. The mean prediction error under each pair of values for λ and ρ is obtained by averaging these G prediction errors. Finally we choose the pair of λ and ρ values that are associates with the smallest mean prediction error as the optimal one.
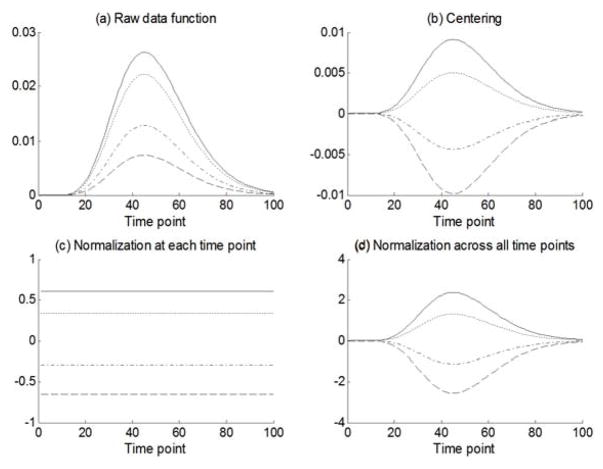
Like GSCA, the estimated parameters in functional GSCA are unique up to scale only because the scale of components is necessarily arbitrary. In order to address this indeterminacy, the original GSCA preprocesses observed data and component scores as follows. First, the data matrix is columnwise centered. That is, each variable is centered to have a mean of zero, which leads the mean of each component to be zero as well. In addition, both observed variables and component scores are standardized to have unit variances so that they become comparable in size. In functional GSCA, data functions are centered to have zero mean over the entire range of t, which leads the mean of each component to be zero just as in the original GSCA. However, standardizing data functions to have the same variance at each value of t as in the original GSCA will yield an undesirable result. Figure 3(a) shows a set of four synthetic data functions. Figure 3(b) shows the four data functions centered to have zero mean over the entire range of t. Centering changes the raw data functions to deviation functions. The shapes and amplitudes of the data functions are affected by centering. However, the information about how much each data function deviates from the mean trajectory is entirely preserved. Figure 3(c) shows that the data functions are centered to have zero mean plus standardized to have the same variance at each measurement occasion. We can see that this type of standardization leads to a total loss of the information about how much each data function deviates from the mean trajectory. In order to address this issue, functional GSCA standardizes data functions to satisfy the following constraint:
| (32) |
where vik(t) is a mean-centered data function. As we can see in Figure 3(d), this type of standardization preserves the deviation information of each trajectory. In addition, functional GSCA standardizes each component score to have its squared norm equal to N, which makes observed data and component scores comparable in size.
Figure 3.
The results of different scaling methods on four synthetic data functions, each of which is represented by a line with different style: (a) raw data functions, (b) centering only, (c) centering plus columnwise normalization, and (d) centering plus matrixwise normalization.
In addition to the estimates, functional GSCA also provides the confidence interval of each estimate based on the bootstrap method (Efron, 1982; Hastie et al., 2009, Chapter 7.11) as the original GSCA.
4. Simulation Studies
4.1 Simulation 1: Accuracy in parameter recovery
A Monte Carlo simulation study was conducted to investigate the accuracy in parameter recovery of functional GSCA under a variety of conditions. Three factors were manipulated for generating data: the number of participants (N) varied at three levels (25, 50, 100), the number of time points (J) varied at three levels (10, 25, 50), and the amount of errors in the measurement model (σ2) varied at three levels (0.5, 1, 2). A total of 3×3×3 = 27 conditions were used and under each condition 100 replications were generated.
4.1.1 Data generation process
To generate each data set under each condition, the structural model depicted in Figure 4 was used, in which two component scores, γi1 and γi2, for the ith individual (i = 1,…, N), were assumed to predict another component score, γi3, as described by the following structural model:
| (33) |
Figure 4.
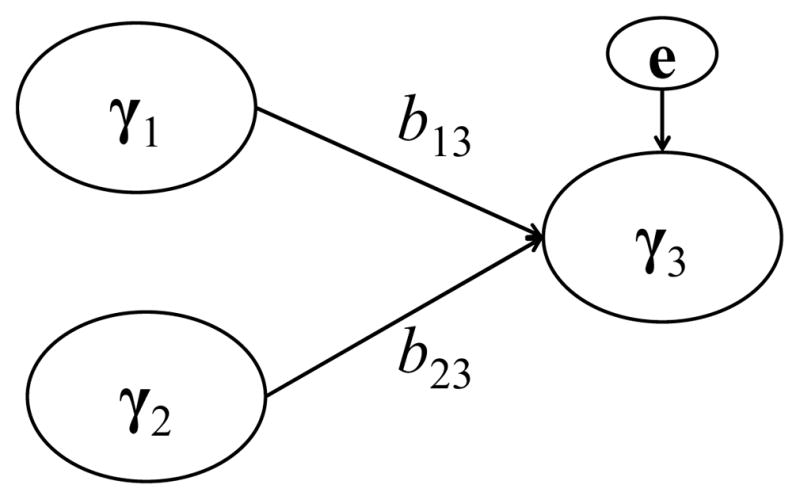
The structural model used for generating data in the simulation study.
The structural models for all N individuals can be combined into a single equation by using the matrix notation as follows:
| (34) |
where γk = [γ1k,…, γNk]′ and e= [e1,…, eN]′.
The two exogenous component scores, γi1 and γi2, and the error term in the structural model, ei, were generated from the following multivariate normal distribution:
| (35) |
which indicates that γi1, γi2, and ei are assumed to be uncorrelated with each other; the variances of the two exogenous component scores are unity; the variance of the structural error is 0.6, which was arbitrarily chosen. After the two exogenous component scores and the error were generated by (4), the endogenous component score, γi3, was generated by the following structural model:
| (36) |
in which b13 = 0.6 and b23 = 0.2 were chosen so as to make the variance of γ3 unity as follows:
| (37) |
Once the three component scores were generated for each of the N individuals, the corresponding functional data were generated as follows. For simplicity, it was assumed that the responses of all individuals on all variables were measured at the equally spaced time points, tj (j = 1,…, J), in which t1 = 0 and tJ = 1. The functional data were generated from the following measurement model:
| (38) |
where zjk is an N by 1 vector of measured responses of N individuals on the kth variable at time tj, γk is an N by 1 vector of the kth component score of N individuals generated as described above, and the loading functions ck(t) were defined as:
| (39) |
| (40) |
| (41) |
over t ∈ [0,1]. The three loading functions were manipulated to have three different degrees of roughness, i.e., the frequency of 1, ½, and ¼, for c1(t), c2(t), and c3(t), respectively. The higher the frequency of a function is the rougher it is. Finally, an N by 1 vector of measurement errors or residuals, εk, was generated from a normal distribution with mean 0 and variance σ2. The error variance σ2 in the measurement model was assumed to be equal across all variables and all measurement occasions.
Before functional GSCA was applied, each set of functional responses was smoothed by the penalized least squares cubic spline smoothing with using 23 B-spline basis functions (Ramsay & Silverman, 2005, Chapter 5). For smoothing the raw data for each set, the smoothing parameter was varied at 11 levels, [10−5, 10−4, 10−3, 10−2, 10−1, 100, 101, 102,103, 104, 105], and the optimal smoothing parameter was chosen among them based on the generalized cross-validation procedure (Craven & Wahba, 1979; Ramsay & Silverman, 2005, Chapter 5). Under the optimal smoothing parameter value, we smoothed raw functional data for each set to obtain data functions.
After obtaining data functions, we analyzed them using functional GSCA. The optimal values of the smoothing parameters, λ and ρ, for functional GSCA were determined by five-fold cross-validation. Each smoothing parameter was varied at 9 levels, [10−4, 10−3, 10−2, 10−1, 100, 101, 102,103, 104], which yielded 9×9 = 81 pairs of smoothing parameter values to test. The optimal pair of smoothing parameter values was chosen based on the first data set under each condition and then used for all 100 data sets belonging to the same condition1. Based on the simulation study presented in Section 4.2, which showed that the functional GSCA algorithm is very stable and highly unlikely to converge to different solutions with different initial values, we used a single random starting value for estimation to reduce computation time.
4.1.2 Results
To evaluate the accuracy of parameter recovery of the loading functions and component scores, the congruence coefficients (Tucker, 1951) between true parameters and their estimates were examined. The congruence coefficient of a vector of true parameters, η, and a vector of their estimates, η̂, is calculated by:
| (42) |
which ranges between −1 and 1 and measures the agreement or similarity in terms of the direction of two vectors regardless of their size. A larger value of the congruence coefficient indicates a better agreement of the two vectors. Conventionally a value greater than 0.9 of the congruence coefficient is regarded as an acceptable degree of similarity or agreement (Mulaik, 1971). In order to calculate the congruence coefficient between two functions, i.e., a true loading function and its estimated loading function, each function is evaluated at 100 equally spaced time points and the vector of 100 evaluated values was used instead.
To examine the accuracy of parameter recovery of the path coefficients, the mean squared errors of the estimates were calculated as given by:
| (43) |
where β is a true path coefficient and β̂ is an estimate of the true path coefficient and the expectation E[·] is taken over 100 replications. The mean squared error of an estimate indicates the average squared distance between the estimate and its true value. A smaller value of the mean squared error indicates a better estimate.
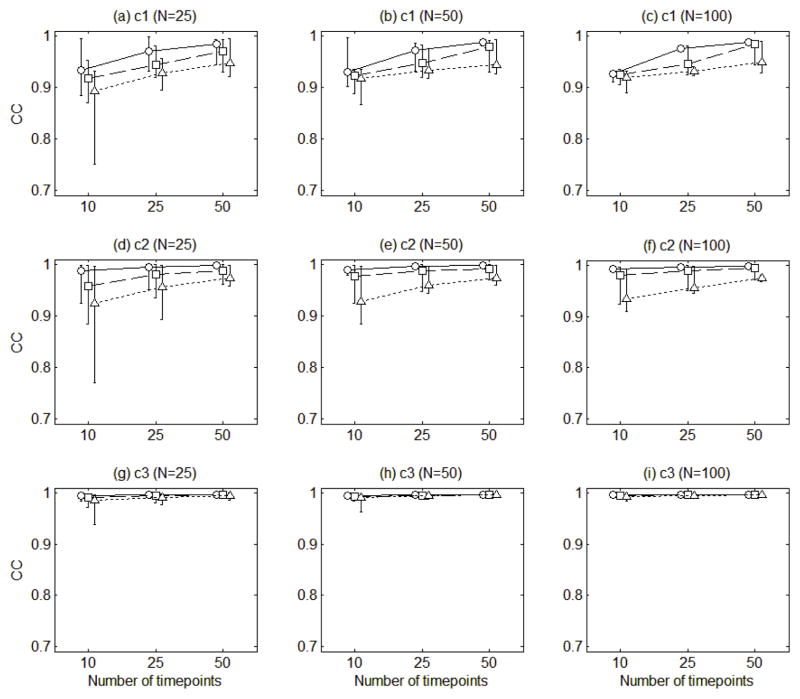
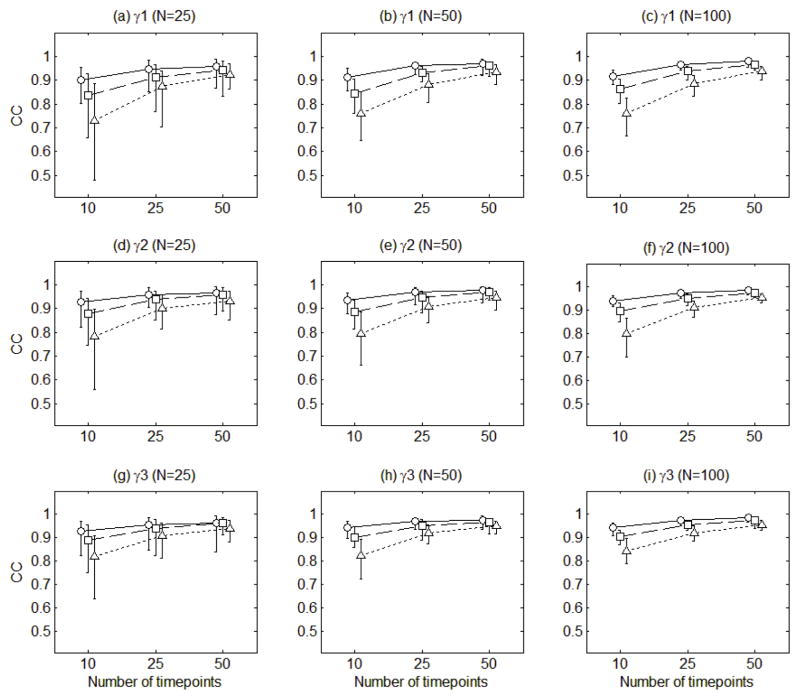
Figure 5 presents the means of the congruence coefficients for the estimates of the three loading functions averaged across 100 replications. The mean congruence coefficients were ranging from 0.89 to 1.00. Figure 5 shows that the loading functions tended to be more accurately estimated as the amount of errors in the measurement model decreased, the number of time points increased, and the roughness of loading functions decreased (the loading function 1 is rougher than the loading function 2, which in turn is rougher than the loading function 3). However, the estimation accuracy was not noticeably affected by the number of individuals (N).
Figure 5.
The mean congruence coefficients of the estimates of the three loading functions (c1, c2, c3) averaged across 100 replications. The circles connected with solid lines are for the error variance of 0.5, the squares connected with dashed lines for error variance of 1, and the triangles connected with dotted lines for error variance of 2. The error bars indicate the ranges of the congruence coefficients.
Figure 5 also displays the ranges of the congruence coefficients for the loading functions. The congruence coefficients tended to widely vary across 100 replications when responses were collected at a smaller number of time points from a smaller number of individuals with a larger amount of error. This indicates that the estimation accuracy of the loading functions can deteriorate when data are noisy and sparsely collected at a small number of time points for a small number of individuals.
Figure 6 presents the mean congruence coefficients of the estimates of the three component score vectors averaged across 100 replications. The mean congruence coefficients were ranging from 0.73 to 0.99. On average, the component scores tended to be more accurately estimated as the amount of errors in the measurement model decreased, the number of time points increased, and the roughness of loading functions decreased. However, the mean congruence coefficients did not noticeably vary depending on the number of individuals.
Figure 6.
The mean congruence coefficients of the estimates of the three component scores (γ1, γ2, γ3) averaged across 100 replications. The circles connected with solid lines are for the error variance of 0.5, the squares connected with dashed lines for error variance of 1, and the triangles connected with dotted lines for error variance of 2. The error bars indicate the ranges of the congruence coefficients.
Figure 6 also displays the ranges of the congruence coefficients for the component score vectors. The congruence coefficients tended to widely vary across 100 replications when responses were collected at a smaller number of time points from a smaller number of participants with a larger amount of error. The congruence coefficients went even below 0.5 when the number of time points was 10, the number of individuals was 25, and the error variance was 2. This indicates that the estimation accuracy of the component scores can substantially deteriorate when data are noisy and sparsely collected at a small number of time points for a small number of individuals.
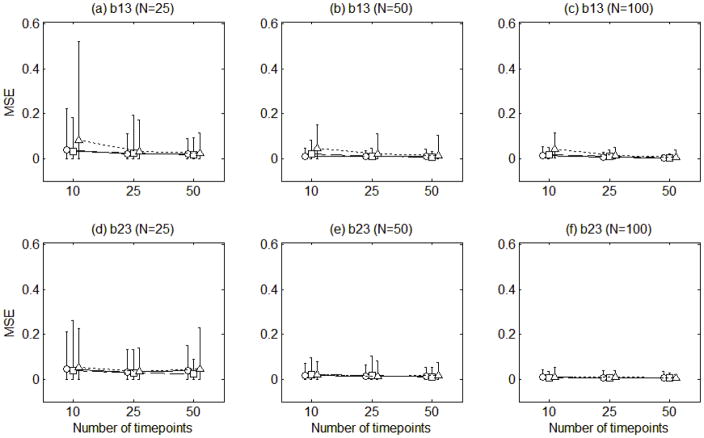
Figure 7 displays the mean squared errors of the path coefficient estimates under each condition. The mean squared errors were ranging from 0.00 to 0.08. Although there is no clear-cut standard for an acceptable level of mean squared errors, the mean squared errors of the estimated path coefficients seemed relatively small compared to the true parameter values. Overall, the mean squared errors tended to decrease when the number of individuals increased, the number of time points increased, and the amount of measurement error decreased.
Figure 7.
The mean squared errors of the estimates of the two path coefficients (b13, b23). The circles connected with solid lines are for the error variance of 0.5, the squares connected with dashed lines for error variance of 1, and the triangles connected with dotted lines for error variance of 2. The error bars indicate the ranges of the mean squared errors.
Figure 7 also displays the ranges of the mean squared errors. Similar to the loading functions and component scores, the ranges of the mean squared errors tended to be wider as the number of time points was smaller, the number of individuals was smaller, and the error variance was larger.
In sum, the simulation study revealed that functional GSCA works as it is supposed to. On average, the estimation became more accurate as the responses were measured at more time points with lower errors. The estimation became more stable as the responses were measured at more time points from more individuals with lower errors. When the responses were measured at a large number of time points with a small amount of measurement error from a large number of individuals, functional GSCA performed reasonably well. The results of the simulation study also suggest that it is beneficial to increase the number of time points and the number of individuals to obtain more accurate and stable estimates of loading functions, component scores, and path coefficients especially when loading functions are expected to be rough and measurements are noisy.
4.2 Simulation 2: Stability of the algorithm
The objective function is bounded above zero and each step of the algorithm decreases the value of the objective function. Therefore, this algorithm will converge to a solution. However, this does not guarantee that the solution is the global minimum. In order to increase the probability of convergence to the global minimum, the algorithm can be repeated a number of times with different initial values each time and the solution associated with the smallest objective function value is chosen as the final one.
In this simulation study, we examined how the solutions may vary with different initial values. We analyzed one data set for each of the 27 conditions examined in Section 4.1 using 100 different initial values. Each initial value was randomly generated from a standard normal distribution.
In each condition, we examined how the objective function value obtained at convergence changed with different initial values. For all 27 conditions, the highest objective function value reached at convergence out of the 100 analyses with different starting values and the lowest one were different only in their 6th or lower decimal place. The reason that the objective function values differ in their 6th or lower decimal place is because the functional GSCA algorithm stops when the change in the objective function value at adjacent iterations is smaller than the stopping criterion, 10−6.
This result shows that the functional GSCA algorithm is highly stable and very unlikely to converge to different solutions with different initial values. Therefore, we used a single starting value when analyzing the example data set in Section 5 to reduce computation time.
5. An Empirical Example: Gait Data
5.1 Functional GSCA
The example data set comes from the three studies of gait behavior of Parkinson’s disease patients including Yoget et al. (2005), Hausdorff et al. (2007), and Frenkel-Toledo et al. (2005). The data are publicly available on the PhysioNet website (Goldberger et al., 2000; http://physionet.org/physiobank/database/gaitpdb/). The MATLAB codes for downloading and preprocessing the data as well as for analyzing the preprocessed data are provided as online supplemental materials.
A total of 93 patients diagnosed as having idiopathic Parkinson’s disease participated in one of the three studies. Out of the 93 patients, 10 patients had missing values in at least one of the observed variables. Therefore, we ended up with 83 patients excluding these 10 patients from the analyses.
In all three studies, patients were measured on the following four sets of responses. First, the body size was measured by two observed variables, height (in centimeters) and weight (in kilograms). Second, the severity of Parkinson’s disease was measured by the three scales – the Hoehn and Yahr staging scale (HY; Hoehn & Yahr, 1967), unified Parkinson’s disease rating scale (UPDRS; Fahn, Elton, & members of the UPDRS Development Committee, 1987), and the motor section score of the UPDRS (UPDRSm). Higher values of these scales indicate more severe cognitive impairment. Third, the gait function was measured by two variables, the Timed Up and Go (TUG; Podsiadlo & Richardson, 1991) score and walking speed. The TUG measures the time that a patient takes to complete a series of movement including rising from a chair, walking a short distance, turning around, returning back to the chair, and sitting down. A higher score of TUG indicates a longer time to complete the task, in other words, a lower gait function. The walking speed indicates the average distance walked per second measured in meter/second with a higher score indicating a better gait function.
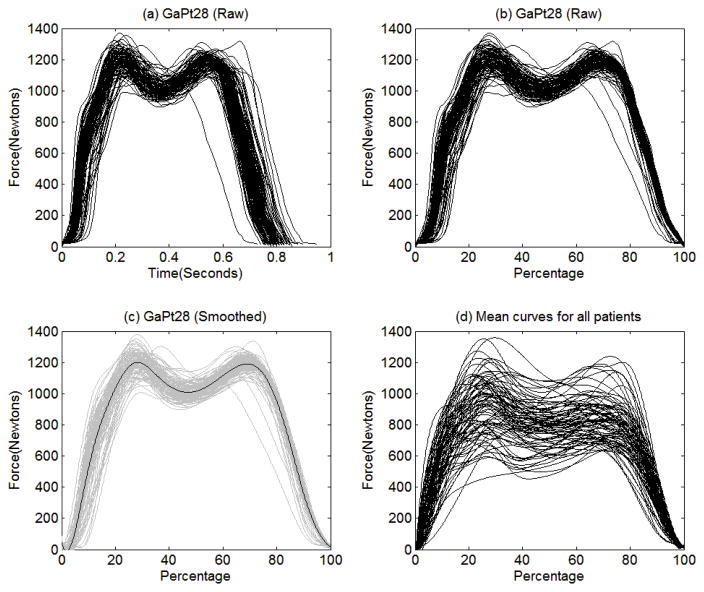
Besides the three sets of responses, patients were also measured on the force under left foot (in Newtons) at 100 Hz for two minutes while they walked at their usual pace, which yielded functional data as shown in Figure 2. As we discussed in the Introduction, each patient had a different walking speed and completed different numbers of gait cycles in two minutes. Therefore, we needed to preprocess the functional data as follows. First, we obtained the trajectories of the force under left foot for all cycles completed by each patient. For example, a patient (GaPt282) completed 104 cycles in two minutes and these 104 trajectories are shown in Figure 8(a). Then we aligned the trajectories obtained from each patient according to the percentage frame of reference as shown in Figure 8(b). And we smoothed each trajectory for each patient by using the penalized least squares cubic spline smoothing with 13 B-spline basis functions (Ramsay & Silverman, 2005, Chapter 5). For smoothing the trajectories for each patient, the smoothing parameter was varied at 11 levels, [10−5, 10−4, 10−3, 10−2, 10−1, 100, 101, 102,103, 104, 105], and the optimal smoothing parameter was chosen based on the generalized cross-validation procedure (Craven & Wahba, 1979; Ramsay & Silverman, 2005, Chapter 5). Under the optimal smoothing parameter value, we smoothed all the trajectories for each patient. The smoothed curves for the patient are presented in Figure 8(c) in gray. Then we obtained the mean curve for each patient by averaging all the curves (or cycles) completed by the patient, which is the black solid curve in Figure 8(c). Each curve presented in Figure 8(d) is the mean curve for each of the 83 patients, which is used for the subsequent analyses.
Figure 8.
The raw data of the 104 gait cycles completed by the patient (GaPt28) are plotted against (a) clock time (in seconds) and (b) percentage completed. The gray curves in (c) are the smoothed curves for the 104 gait cycles and the black line indicates the mean curve of the 104 smoothed curves. The mean curve obtained from each of the 83 patients is plotted in (d).
The structural model used for analyzing this data set is given in Figure 1. The body size and severity of Parkinson’s disease are hypothesized to have effects on the force under the left foot and these effects are mediated by the gait function. The optimal values of the smoothing parameters λ and ρ were determined by five-fold cross-validation, in which each of the smoothing parameters was varied at 5 different values, [101, 102, 103, 104, 105]. The resultant optimal smoothing parameter values were λ = 103 and ρ = 103, which were used in estimating the parameters.
The FIT value was 0.5911, which indicates that 59.11% of the total variation in data functions and component scores can be captured by the functional GSCA model. Table 1 presents the estimated loadings and weights for the body size, severity of Parkinson’s disease, and gait function with 95% bootstrap confidence intervals based on 500 bootstrap samples. In the set of body size, the weight for height has a wide confidence interval, [−.62, .28], whereas the weight for weight has a much narrower confidence interval, [.70, .99], around a high weight value. This indicates that weight is more crucial than height in predicting gait function and force under left foot. In the set of severity of Parkinson’s disease, the weight for HY has a wide confidence interval around zero, [−.07, .33], whereas the confidence intervals of the weights for UPDRS and UPDRSm are much narrower and around higher values, [.40, .58] and [.37, .59], respectively. This indicates that UPDRS and UPDRSm are more important than HY in predicting gait function and force under left foot. In our data, all the patients have HY scores of 2, 2.5, or 3 and there is not much variation in HY. This explains why HY is not so much important as UPDRS and UPDRSm in predicting gait function and force under left foot. In the set of gait function, the weights for TUG and walking speed have relatively narrow confidence intervals around higher values (in absolute values), [−.60, −.39] and [.50, .67], respectively. This indicates that both variables contribute to predicting force under left foot.
TABLE 1.
The estimated weights and loadings of the body size, severity of Parkinson’s disease, and gait function on their indicator variables obtained from functional GSCA
| Component | Indicator Variable | Weight | 95% Confidence Interval
|
Loading | 95% Confidence Interval
|
||
|---|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | Lower Limit | Upper Limit | ||||
| Body Size | Height | −.40 | −.62 | .28 | −.52 | −.74 | .33 |
|
|
|
|
|||||
| Weight | .86 | .70 | .99 | .92 | .78 | 1.00 | |
|
|
|
|
|||||
| Severity of Parkinson’s Disease | HY | .16 | −.07 | .33 | .26 | −.15 | .54 |
|
|
|
|
|||||
| UPDRS | .49 | .40 | .58 | .97 | .94 | .98 | |
|
|
|
|
|||||
| UPDRSm | .51 | .37 | .59 | .95 | .89 | .98 | |
|
|
|
|
|||||
| Gait Function | TUG | −.51 | −.60 | −.39 | −.91 | −.94 | −.87 |
|
|
|
|
|||||
| Walking Speed | .57 | .50 | .67 | .93 | .88 | .97 | |
By examining the loadings, we can see that the component score on body size is highly and positively correlated with weight. The component score on severity of Parkinson’s disease is highly and positively correlated with UPDRS and UPDRSm. The component score on gait function is highly and negatively correlated with TUG, and highly and positively correlated with walking speed. Considering that a higher score on TUG indicates a lower gait function and a higher walking speed indicates a better gait function, a higher component score on gait function indicates that the patient manifests a better gait function.
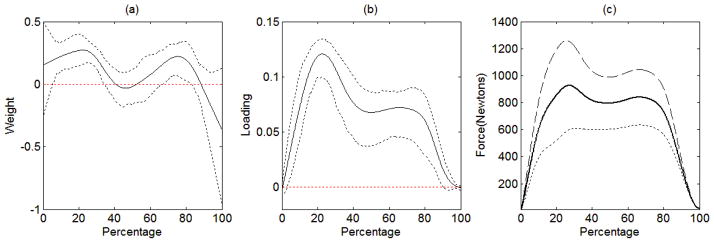
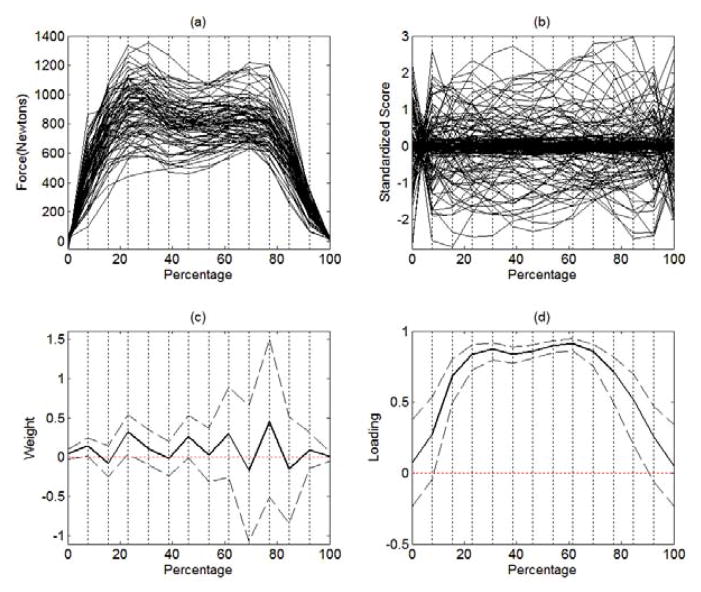
The estimated weight function of force under left foot with 95% pointwise bootstrap confidence interval based on 500 bootstrap samples is given in Figure 9(a). The estimated weight function has higher weight values with relatively narrower confidence intervals over 10% to 30% completion of the gait cycle. This indicates that the force under left foot exerted over 10% to 30% completion of the gait cycle and that over 70% to 85% completion of the gait cycle are crucial in examining the relationship of force under left foot with body size, severity of Parkinson’s disease, and gait function.
Figure 9.
The estimated weight function (solid line) with the pointwise 95% bootstrap confidence interval (dashed lines) is displayed in (a). The estimated loading function (solid line) with 95% pointwise bootstrap confidence interval (dashed lines) is displayed in (b). The predicted data functions associated with different values of component scores are displayed in (c). The thick line is the mean curve of the 83 patients, the thin dashed line indicates the predicted data function when the component score is 2 standard deviations above the mean, and the thin dotted line indicates the predicted data function when the component score is 2 standard deviations below the mean.
The estimated loading function of force under left foot is depicted in Figure 9(b) with the pointwise 95% bootstrap confidence interval based on 500 bootstrap samples. To facilitate the interpretation of the estimated loading function, we plotted the loading function with the mean curve of force under left foot. Considering that the data functions are mean-centered, the data functions indicate the deviations from the mean function. Considering that the component scores are also mean-centered, the measurement model (12) implies that we expect to obtain the mean function when the component score γik is zero, i.e., the mean component score. For a patient whose kth component score is 2 standard deviations above the mean, his data function can be predicted from the measurement model (12) as given by:
| (44) |
where v̄k(t) indicates the mean function, , sk is the standard deviation of the kth component score, and ĉk(t) is the estimated loading function. Similarly, for a patient whose kth component score is 2 standard deviations below the mean, his data function can be predicted by:
| (45) |
Figure 9(c) shows the predicted data functions (44) and (45) on top of the mean function. We can see that a patient whose component score is above the mean tends to manifest stronger force under left foot with having a peak at around 20% and 70%. Contrarily, a patient whose component score is below the mean tends to manifest a relatively flat pattern of change in force under left foot over 30% to 70%.
The estimated path coefficients and their 95% bootstrap confidence intervals based on 500 bootstrap samples are given in Table 2. As expected, if a patient has a higher component score on body size, his component score on force under left foot tends to be larger (b14 = .59 ). In other words, a heavier patient tends to have a higher component score on force under left foot, which in turn is related with elevated amplitude at around 20% and 70%. As a patient has a higher component score on severity of Parkinson’s disease, his component score on gait function tends to be lower (b23 = −.28 ) while controlling for the effect of body size. However, the strength of this relationship is rather uncertain as indicated by a relatively wide confidence interval, [−.49, −.02]. A lower component score on gait function, in turn, is associated with a lower component score on force under left foot (b34 = 0.35 ) while controlling for the effect of body size and that of severity of Parkinson’s disease. However, this relationship is rather uncertain as indicated by its wide confidence interval, [.08, .60]. The effect of body size on gait function (b13 = .22 ) does not seem to exist as indicated by its confidence interval close to zero, [−.08, .43]. A higher component score on severity of Parkinson’s Disease tends to be associated with a lower component score on force under left foot (b24 = −.21 ). However, this relationship might again be rather uncertain as indicated by its wide confidence interval, [−.41, −.01].
TABLE 2.
The estimated path coefficients and their 95% bootstrap confidence intervals of the gait data obtained from functional GSCA
| Path
|
Estimate | 95% Confidence Interval
|
|||
|---|---|---|---|---|---|
| From | To | Lower Limit | Upper Limit | ||
| Body Size | Gait Function | b13 | .22 | −.08 | .43 |
|
|
|||||
| Severity of Parkinson’s Disease | Gait Function | b23 | −.28 | −.49 | −.02 |
|
|
|||||
| Body Size | Force Under Left Foot | b14 | .59 | .39 | .77 |
|
|
|||||
| Severity of Parkinson’s Disease | Force Under Left Foot | b24 | −.21 | −.41 | −.01 |
|
|
|||||
| Gait Function | Force Under Left Foot | b34 | .35 | .08 | .60 |
5.2 The original GSCA with discretizing data functions
We analyzed the gait example data again using the original GSCA in order to illustrate the usefulness of the proposed method over the original GSCA. To deal with functional data in the framework of the original GSCA, we evaluated the data functions (force under left foot) shown in Figure 8(d) at 14 equally spaced percentage occasions3. The evaluated curves are presented in Figure 10(a). We used these 14 responses evaluated at the 14 percentage occasions as indicator variables for force under left foot.
Figure 10.
(a) The evaluated mean curves: the dotted vertical lines indicate the locations of the 14 equally spaced percentage occasions at which the mean curves are evaluated. (b) The standardized data: the mean of each percentage occasion is zero and the standard deviation of each percentage occasion is unity. (c) The estimated weights for the 14 percentage occasions (in solid line) with 95% pointwise bootstrap confidence interval (in dashed line). (d) The estimate loadings for the 14 percentage occasions (in solid line) with 95% pointwise bootstrap confidence interval (in dashed line).
The same structural model was used as in Section 5.1. The estimated weights and loadings for the body size, severity of Parkinson’s disease, and gait function are given in Table 3, which are quite similar to those in Table 1. This indicates the component scores on the body size, severity of Parkinson’s disease, and gait function obtained by the original GSCA with discretizing the data functions are comparable to those obtained by functional GSCA.
TABLE 3.
The estimated weights and loadings of the body size, severity of Parkinson’s disease, and gait function on their indicator variables obtained from the original GSCA
| Component | Indicator Variable | Weight | 95% Confidence Interval
|
Loading | 95% Confidence Interval
|
||
|---|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | Lower Limit | Upper Limit | ||||
| Body Size | Height | −.44 | −.66 | .06 | −.56 | −.77 | .05 |
|
|
|
|
|||||
| Weight | .84 | .66 | .99 | .90 | .76 | 1.00 | |
|
|
|
|
|||||
| Severity of Parkinson’s Disease | HY | .16 | −.10 | .32 | .26 | −.18 | .55 |
|
|
|
|
|||||
| UPDRS | .48 | .37 | .57 | .97 | .94 | .99 | |
|
|
|
|
|||||
| UPDRSm | .51 | .41 | .62 | .95 | .89 | .98 | |
|
|
|
|
|||||
| Gait Function | TUG | −.53 | −.64 | −.45 | −.92 | −.95 | −.88 |
|
|
|
|
|||||
| Walking Speed | .55 | .45 | .62 | .93 | .86 | .96 | |
The estimate path coefficients are presented in Table 4. All the estimated path coefficients in Table 4 are quite similar to those given in Table 2 except for the path from gait function to force under left foot (b34). When the original GSCA was used, the estimated path coefficient was .12 with the confidence interval close to zero, [−.07, .33]. When the functional GSCA was used, the estimated path coefficient was .35 with the confidence interval of [.08, .60]. This difference implies that the original GSCA and functional GSCA might extract different components on force under left foot. Comparing the loadings on force under left foot given in Figure 10(d) and the loading function given in Figure 9(b) also reveals that the original GSCA and functional GSCA extracted different components on force under left foot.
TABLE 4.
The estimated path coefficients and their 95% bootstrap confidence intervals of the gait data obtained from the original GSCA
| Path
|
Estimate | 95% Confidence Interval
|
|||
|---|---|---|---|---|---|
| From | To | Lower Limit | Upper Limit | ||
| Body Size | Gait Function | b13 | .23 | −.05 | .43 |
|
|
|||||
| Severity of Parkinson’s Disease | Gait Function | b23 | −.28 | −.49 | −.01 |
|
|
|||||
| Body Size | Force Under Left Foot | b14 | .62 | .44 | .79 |
|
|
|||||
| Severity of Parkinson’s Disease | Force Under Left Foot | b24 | −.21 | −.38 | .01 |
|
|
|||||
| Gait Function | Force Under Left Foot | b34 | .12 | −.07 | .33 |
Figure 10(c) displays the estimated weights for the responses evaluated at the 14 percentage occasions, which are noticeably different from the weight function given in Figure 9(a). The estimated weights in Figure 10(c) are highly zigzagged and very difficult to interpret. It seems that none of the 14 percentage occasions are crucial in examining the relationships with the body size, severity of Parkinson’s disease, and gait function. The reason that the original GSCA yielded a zigzagged pattern of the weights can be explained by the way data are preprocessed. As already discussed in Section 3.5, in the original GSCA each indicator variable is standardized to have a mean of zero and a standard deviation of unity as shown in Figure 10(b). In other words, the responses at the 14 percentage occasions are standardized without taking it into account that the responses at adjacent percentage occasions are more highly correlated. Therefore, this way of standardization destroys the smooth nature of the trajectories, which in turn can lead to zigzagged weights as shown in Figure 10(c).
5.3 The original GSCA combined with functional PCA
In this section, we analyzed the gait example data using the original GSCA combined with functional PCA (Ramsay & Silverman, 2005, Chapter 8). To summarize functional data, we performed a functional PCA on the data functions of force under left foot and obtained component scores, which were used as indicator variables for force under left foot. A total of four components were extracted so as to retain at least 95% of the total variation in the data function. Figure 11 displays the four obtained eigenfunctions associated with the largest four eigenvalues.
Figure 11.
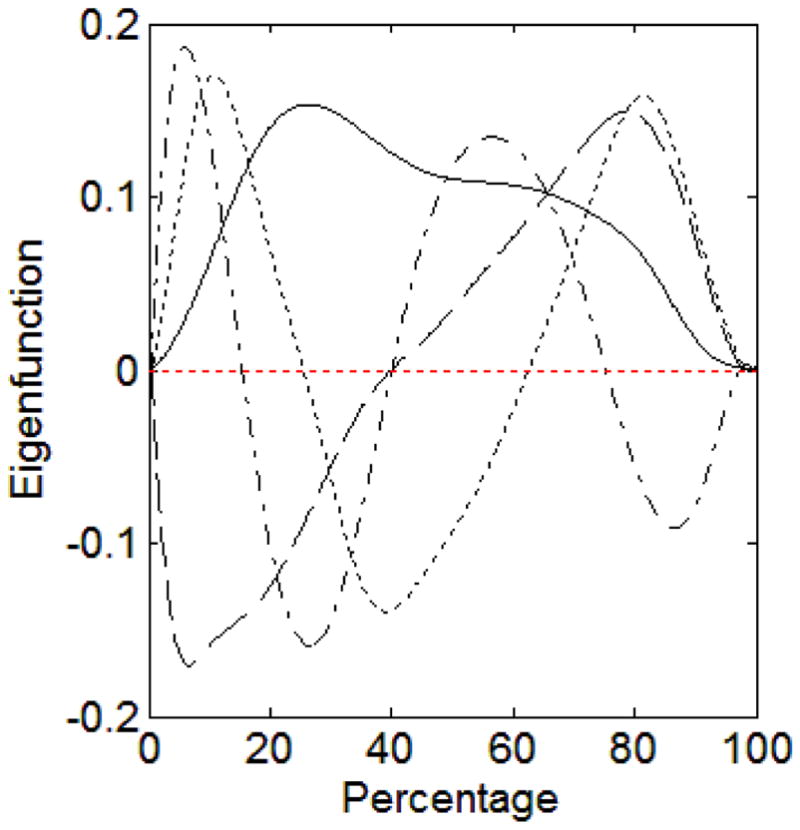
The solid curve is the eigenfunction associated with the largest eigenvalue. The dashed curve is the eigenfunction associated with the second largest eigenvalue. The dotted curve is the eigenfunction associated with the third largest eigenvalue. The dash-dotted curve is the eigenfunction associated with the fourth largest eigenvalue.
The same structural model was used as in Sections 5.1 and 5.2. The estimated weights and loadings are given in Table 5 where Component 1 indicates the component scores that capture the maximal variance; Component 2 indicates the component scores that capture the second maximal variance; and so on. All the estimated weights in Table 5 are quite similar to those given in Table 1 except for the weights for height and weight. When using functional GSCA, weight turned out to be more crucial than height for examining the relationship with body size and other sets of responses including force under left foot. This result makes sense; the force under left foot will be stronger for a heavier person with the same height, but it doesn’t have to be the case for a taller person with the same weight. However, when using the original GSCA combined with functional PCA, it turned out that height has a higher weight with a narrower confidence interval compared to weight. This means that height is more important than weight for examining the relationship with body size and other sets of responses including force under left foot, which is somewhat counter intuitive.
TABLE 5.
The estimated weights and loadings of the body size, severity of Parkinson’s disease, gait function, and force under left foot on their indicator variables obtained from the original GSCA combined with functional PCA
| Component | Indicator Variable | Weight | 95% Confidence Interval
|
Loading | 95% Confidence Interval
|
||
|---|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | Lower Limit | Upper Limit | ||||
| Body Size | Height | .59 | .10 | .93 | .69 | .13 | .95 |
|
|
|
|
|||||
| Weight | −.72 | −.98 | .82 | −.81 | −.99 | .86 | |
|
|
|
|
|||||
| Severity of Parkinson’s Disease | HY | .17 | −.07 | .33 | .27 | −.15 | .55 |
|
|
|
|
|||||
| UPDRS | .51 | .39 | .61 | .97 | .95 | .99 | |
|
|
|
|
|||||
| UPDRSm | .48 | .36 | .58 | .94 | .89 | .98 | |
|
|
|
|
|||||
| Gait Function | TUG | −.38 | −.59 | −.31 | −.87 | −.93 | −.81 |
|
|
|
|
|||||
| Walking Speed | .69 | .51 | .76 | .96 | .88 | .98 | |
|
|
|
|
|||||
| Force Under Left Foot | Component 1 | .51 | −.40 | .89 | .51 | −.60 | .91 |
|
|
|
|
|||||
| Component 2 | −.33 | −.56 | .31 | −.33 | −.69 | .53 | |
|
|
|
|
|||||
| Component 3 | .77 | .02 | .89 | .77 | −.08 | .90 | |
|
|
|
|
|||||
| Component 4 | −.19 | −.46 | .29 | −.19 | −.61 | .49 | |
Considering the wide confidence intervals of the weights of force under left foot on the four component scores, none of the four component scores seem to be substantially contributing to examining the relationship of force under left foot with body size, severity of Parkinson’s disease, and gait function. In addition, all the components extracted by functional PCA shown in Figure 11 are quite different from the component extracted by functional GSCA as shown in Figure 9(a). This example illustrates that functional GSCA and functional PCA can extract different components from the same functional data; functional GSCA extracts components considering the hypothesized relationships with other variables whereas functional PCA extracts components only considering the variation in the functional data.
The estimated path coefficients are presented in Table 6. Compared to the estimated path coefficients in Table 2, we can see that the component score on body size is no longer strongly associated with the component score on force under left foot. This difference comes from the fact that functional GSCA and the original GSCA combined with functional PCA extract different components. In functional GSCA, the component score on body size is more highly related with weight whereas in the original GSCA combined with functional PCA the component score on body size seems to reflect height rather than weight. Moreover, in functional GSCA, the component score on force under left foot reflects the variation in trajectory as depicted by the loading function in Figure 9(b). On the contrary, in the original GSCA combined with functional PCA, the component score on force under left foot may not be strongly related with any of the four component scores extracted by the functional PCA as indicated by the loadings in Table 5 with wide confidence intervals around zero.
TABLE 6.
The estimated path coefficients and their 95% bootstrap confidence intervals of the gait data obtained from the original GSCA combined with functional PCA
| Path
|
Estimate | 95% Confidence Interval
|
|||
|---|---|---|---|---|---|
| From | To | Lower Limit | Upper Limit | ||
| Body Size | Gait Function | b13 | −.27 | −.47 | .07 |
|
|
|||||
| Severity of Parkinson’s Disease | Gait Function | b23 | −.29 | −.53 | −.04 |
|
|
|||||
| Body Size | Force Under Left Foot | b14 | −.23 | −.68 | .48 |
|
|
|||||
| Severity of Parkinson’s Disease | Force Under Left Foot | b24 | −.12 | −.31 | .16 |
|
|
|||||
| Gait Function | Force Under Left Foot | b34 | .69 | .09 | .83 |
6. Summary and Discussion
In this paper, functional GSCA was proposed for the analysis of functional data by integrating the original GSCA with basis function expansions and penalized least squares smoothing into a unified framework. Functional GSCA enables to analyze path-analytic relationships among multiple sets of functional responses without losing information on temporal variations in the data. The usefulness of functional GSCA was investigated by using both synthetic and real data sets. The Monte Carlo study demonstrated that functional GSCA recovered parameters reasonably well and the estimation algorithm was stable. The gait data example illustrated that functional GSCA could examine directional relationships among multiple sets of functional or multivariate responses, while identifying the variation in functional responses relevant to other sets of responses as well as the range of time that is crucial for examining the relationships. We also compared functional GSCA with two other possible ways of analyzing the data in the framework of the original GSCA. The results illustrated that functional GSCA is more useful over the original GSCA with discretizing data functions since functional GSCA can take into account the fact that responses at adjacent measurement occasions are connected. The results also showed that functional GSCA is more useful over the original GSCA combined with functional PCA since functional GSCA extracts components that are more relevant to other responses of main interest.
Despite its usefulness, functional GSCA has limitations. It is not applicable when data functions exhibit not only a certain kind of amplitude variation but also other variations such as a phase variation. For example, Wiesner and Windle (2004) studied adolescent delinquency trajectories and revealed six different trajectory groups: rare offenders, moderate late peakers, high late peakers, decreasers, moderate-level chronics, and high-level chronics. These six trajectory groups differ in terms of two different types of variation. First, these groups have different delinquency levels, i.e., amplitude variation: rare, moderate, and high. Second, these groups also differ in terms of the location of the peak: no peak (rare or chronics), late peak, and early peak (decreases). If these two different types of variation are related with other responses in a different way, functional GSCA might not handle it because the loading function can capture one specific kind of variation. For example, the loading function in Figure 9(b) captures the amplitude variation mainly around earlier occasion. One might think that registering data could resolve this problem to some extent. However, in some cases, researchers are reluctant to register data because the phase variation in data reflects an important characteristic of data that should not be ignored.
A promising way of extending functional GSCA to uncover such cluster-level heterogeneity is to combine functional GSCA with a clustering method. Hwang et al. (2007) already showed that the original GSCA can be nicely combined with fuzzy clustering to deal with heterogeneous groups of subjects. Functional GSCA can be readily extended to fuzzy clusterwise functional GSCA in a similar way. Another promising approach is a multilevel extension of functional GSCA, which can be used when one is interested in examining differences in trajectories as well as in path coefficients across already existing groups, such as gender, geographical regions, treatment conditions, etc. The original GSCA has been extended to multilevel GSCA (Hwang, Takane, & Malhotra, 2007), in which loadings and path coefficients are allowed to vary across different groups. Similarly, functional GSCA can be generalized to incorporate such multilevel structures.
In addition, functional GSCA is not suitable for investigating how the relationships among variables evolve over time. For example, Li, Root, and Shiffman (2006) revealed that the effect of negative mood on urge to smoke changed over various stages of the smoking-cessation process. Functional GSCA is currently based on the assumption that the relationships among components, or path coefficients, remain invariant over time. Thus, it may be useful to extend functional GSCA to deal with time-varying path coefficients (e.g., Hastie & Tibshirani, 1993; Ramsay & Silverman, 2005; Tan, Shiyko, Li, Li, & Dierker, 2012).
Technically, functional GSCA can be regarded as a two-step approach in which functional data are smoothed and then the smoothed curves are used for further analyses. In other words, functional data should be pre-processed for functional GSCA analysis. It would be desirable to incorporate the pre-processing step into the estimation process in functional GSCA so that the functional data are smoothed in an optimal way for examining the hypothesized relationships among the sets of responses in the model.
Supplementary Material
Acknowledgments
The authors are very grateful for the insightful and constructive comments made by the associate editor and three anonymous reviewers that have greatly improved the paper. The work of the first author was supported by the National Institute On Drug Abuse of the National Institutes of Health under Award Number R01DA009757. The final publication is available at link.springer.com.
Footnotes
This means that the chosen smoothing parameter values might have been suboptimal for the other 99 data sets. Therefore, the simulation results may be a bit conservative in the sense that the results would be better if the smoothing parameters have been chosen for every data set optimally.
This is the ID of the patient used in the PhysioNet website.
The original GSCA broke down when we used more than 15 equally spaced percentage occasions due to the high correlations between the responses evaluated at adjacent percentage occasions. Therefore, we ended up evaluating the mean curves at 14 percentage occasions.
References
- Abdi H. Partial least squares (PLS) regression. In: Lewis-Beck M, Bryman A, Futing T, editors. Encyclopedia for research methods for the social sciences. Thousand Oaks: Sage; 2003. pp. 792–795. [Google Scholar]
- Byrd R, Bilbert JC, Nocedal J. A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming. Mathematical Programming A. 2000;89:149–185. [Google Scholar]
- Byrd RH, Hribar ME, Nocedal J. An Interior Point Algorithm for Large Scale Nonlinear Programming. SIAM Journal of Optimization. 1999;9:877–900. [Google Scholar]
- De Boor C. A practical guide to splines. New York, NY: Springer; 2001. [Google Scholar]
- de De Leeuw J, Young FW, Takane Y. Additive structure in qualitative data: An alternating least squares method with optimal scaling features. Psychometrika. 1976;41(4):471–503. [Google Scholar]
- Dierckx P. Curve and surface fitting with splines. Oxford: Clarendon; 1993. [Google Scholar]
- Efron B. The jackknife, the bootstrap, and other resampling plans. Philadelphia: Society for Industrial and Applied Mathematics; 1982. [Google Scholar]
- Eilers PHC, Marx BD. Flexible Smoothing with B-splines and Penalties. Statistical Science. 1996;11(2):89–102. [Google Scholar]
- Fahn S, Elton RL . members of the UPDRS Development Committee. Unified Parkinson’s disease rating scale. In: Fahn S, Marsden D, Calne D, Goldstein M, editors. Recent development in Parkinson’s disease. Florham Park, NJ: MacMillan Healthcare Information; 1987. [Google Scholar]
- Ferraty F, Vieu P. Nonparametric functional data analysis theory and practice. New York: Springer; 2006. [Google Scholar]
- Frenkel-Toledo S, Giladi N, Peretz C, Herman T, Gruendlinger L, Hausdorff JM. Treadmill Walking as an External Pacemaker to Improve Gait Rhythm and Stability in Parkinson’s Disease. Movement Disorder. 2005;20(9):1109–1114. doi: 10.1002/mds.20507. [DOI] [PubMed] [Google Scholar]
- Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov P Ch, Mark RG, Mietus JE, Moody GB, Peng CK, Stanley HE. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation. 2000;101:e215–e220. doi: 10.1161/01.cir.101.23.e215. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R. Varying-Coefficient Models. Journal of the Royal Statistical Society. Series B (Methodological) 1993;55(4):757–796. [Google Scholar]
- Hastie T, Tibshirani R, Friedman JH. The elements of statistical learning data mining, inference, and prediction. New York: Springer; 2009. [Google Scholar]
- Hausdorff JM, Lowenthal J, Herman T, Gruendlinger L, Peretz C, Giladi N. Rhythmic auditory stimulation modulates gait variability in Parkinson’s disease. European Journal of Neuroscience. 2005;26:2369–2375. doi: 10.1111/j.1460-9568.2007.05810.x. [DOI] [PubMed] [Google Scholar]
- Hoehn MM, Yahr MD. Parkinsonism: onset, progression and mortality. Neurology. 1967;17(5):427–442. doi: 10.1212/wnl.17.5.427. [DOI] [PubMed] [Google Scholar]
- Hwang H, DeSarbo WS, Takane Y. Fuzzy Clusterwise Generalized Structured Component Analysis. Psychometrika. 2007;72(2):181–198. [Google Scholar]
- Hwang H, Jung K, Takane Y, Woodward T. Functional multiple-set canonical correlation analysis. Psychometrika. 2012;77:48–64. doi: 10.1007/s11336-015-9478-5. [DOI] [PubMed] [Google Scholar]
- Hwang H, Suk HW, Lee JH, Moskowitz DS, Lim J. Functional extended redundancy analysis. Psychometrika. 2012;77:524–542. doi: 10.1007/s11336-012-9268-2. [DOI] [PubMed] [Google Scholar]
- Hwang H, Suk HW, Takane Y, Lee JH, Lim J. Generalized functional extended redundancy analysis. Psychometrika. 2015;80:101–125. doi: 10.1007/s11336-013-9373-x. [DOI] [PubMed] [Google Scholar]
- Hwang H, Takane Y. Generalized structured component analysis. Psychometrika. 2004;69(1):81–99. doi: 10.1007/s11336-015-9440-6. [DOI] [PubMed] [Google Scholar]
- Hwang H, Takane Y, Malhotra N. Multilevel Generalized Structured Component Analysis. Behaviormetrika. 2007;34(2):95–109. [Google Scholar]
- Jackson I, Sirois S. Infant cognition: going full factorial with pupil dilation. Developmental science. 2009;12(4):670–679. doi: 10.1111/j.1467-7687.2008.00805.x. [DOI] [PubMed] [Google Scholar]
- Li R, Root TL, Shiffman S. A Local Linear Estimation Procedure for Functional Multilevel Modeling. In: Walls TA, Schafer JL, editors. Models for Intensive Longitudinal Data. New York: Oxford University Press; 2006. pp. 63–83. [Google Scholar]
- Lindquist MA. Functional Causal Mediation Analysis With an Application to Brain Connectivity. Journal of the American Statistical Association. 2012;107(500):1297–1309. doi: 10.1080/01621459.2012.695640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar AAG, Ostry DJ. Generalization of dynamics learning across changes in movement amplitude. Journal of neurophysiology. 2010;104(1):426–438. doi: 10.1152/jn.00886.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulaik SA. The foundations of factor analysis. New York: McGraw-Hill; 1971. [Google Scholar]
- Ormoneit D, Black MJ, Hastie T, Kjellström H. Representing cyclic human motion using functional analysis. Image and Vision Computing. 2005;23(14):1264–1276. [Google Scholar]
- Park KK, Suk HW, Hwang H, Lee JH. A functional analysis of deception detection of a mock crime using infrared thermal imaging and the Concealed Information Test. Frontiers in human neuroscience. 2013;7:70. doi: 10.3389/fnhum.2013.00070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podsiadlo D, Richardson S. The Timed “Up & Go”: A Test of Basic Functional Mobility for Frail Elderly Persons. Journal of the American Geriatrics Society. 1991;39(2):142–148. doi: 10.1111/j.1532-5415.1991.tb01616.x. [DOI] [PubMed] [Google Scholar]
- Ramsay JO, Dalzell CJ. Some Tools for Functional Data Analysis. Journal of the Royal Statistical Society: Series B (Methodological) 1991;53(3):539–572. [Google Scholar]
- Ramsay JO, Hooker G, Graves S. Functional data analysis with R and MATLAB. New York: Springer; 2009. [Google Scholar]
- Ramsay JO, Silverman BW. Functional data analysis. New York: Springer; 2005. [Google Scholar]
- Reinsch CH. Smoothing by spline functions. Numerische Mathematik. 1967;10(3):177–183. [Google Scholar]
- Tan X, Shiyko MP, Li R, Li Y, Dierker L. A time-varying effect model for intensive longitudinal data. Psychological Methods. 2012;17(1):61–77. doi: 10.1037/a0025814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian TS. Functional Data Analysis in Brain Imaging Studies. Frontiers in Psychology. 2010;1:35. doi: 10.3389/fpsyg.2010.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker LR. A method for synthesis of factor analysis studies. Washington: Department of the Army; 1951. (Personnel Research Section Report No. 984) [Google Scholar]
- Vines BW, Krumhansl CL, Wanderley MM, Levitin DJ. Cross-modal interactions in the perception of musical performance. Cognition. 2006;101(1):80–113. doi: 10.1016/j.cognition.2005.09.003. [DOI] [PubMed] [Google Scholar]
- Yogev G, Giladi N, Peretz C, Springer S, Simon ES, Hausdorff JM. Dual tasking, gait rhythmicity, and Parkinson’s disease: which aspects of gait are attention demanding? The European journal of neuroscience. 2005;22(5):1248–1256. doi: 10.1111/j.1460-9568.2005.04298.x. [DOI] [PubMed] [Google Scholar]
- Zhang J-T. Analysis of Variance for Functional Data. Boca Raton: CRC Press; 2013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.