Cation effects on haemoglobin aggregation: balance of chemisorption against physisorption of ions

Abstract

A theoretical model of haemoglobin is presented to explain an anomalous cationic Hofmeister effect observed in protein aggregation. The model quantifies competing proposed mechanisms of non-electrostatic physisorption and chemisorption. Non-electrostatic physisorption is stronger for larger, more polarizable ions with a Hofmeister series Li⁺< K⁺< Cs⁺. Chemisorption at carboxylate groups is stronger for smaller kosmotropic ions, with the reverse series Li⁺ > K⁺ > Cs⁺. We assess aggregation using second virial coefficients calculated from theoretical protein–protein interaction energies. Taking Cs⁺ to not chemisorb, comparison with experiment yields mildly repulsive cation–carboxylate binding energies of 0.48 k_BT for Li⁺ and 3.0 k_BT for K⁺. Aggregation behaviour is predominantly controlled by short-range protein interactions. Overall, adsorption of the K⁺ ion in the middle of the Hofmeister series is stronger than ions at either extreme since it includes contributions from both physisorption and chemisorption. This results in stronger attractive forces and greater aggregation with K⁺, leading to the non-conventional Hofmeister series K⁺ > Cs⁺ ≈ Li⁺.

1. Introduction

Hofmeister effects refer to differences in the behaviour of a solution arising from the specific identity of the electrolyte. Hofmeister originally observed the effect of salts on protein solubility [1]. He reported a series in the ability of cations (in sulphate and other salts) to precipitate egg-white protein in the order Li⁺< Na⁺< K⁺< NH₄⁺, alongside a similar series in anions for which the effect was stronger. Specific ion effects have subsequently been observed in a wide range of systems, animal [2–5], mineral [6–9] and otherwise [10–13] in nature. Hofmeister's series was found widely across these systems, even in ionic liquids [14]. An observation could be made that smaller, strongly hydrated ions ‘kosmotropes’ such as Li⁺, Na⁺ are found at one end of the series, while larger, weakly hydrated ions like K⁺, NH₄⁺ are found at the other. So the Hofmeister effect could be understood to be controlled by a single property of the ions, whether size, polarizability or ion–water interaction [15].

Depending on the specific conditions (pH, surface hydrophobicity), the Hofmeister series can be found in both the forward and reverse series [3,16,17]. Unsurprisingly, minor permutations between ions frequently appear. But a more intriguing ‘violation’ of the conventional Hofmeister series was observed by Medda et al. [18] in the aggregation of haemoglobin molecules. Turbidity measurements showed a cation series in aggregation of Li⁺< Cs⁺< Na⁺< K⁺ ≈ Rb⁺. The lighter cations appeared in the conventional order, Li⁺< Na⁺< K⁺. The anomaly here was Cs⁺. As a large chaotropic ion, we would conventionally expect Cs⁺ to appear to the right of K⁺. Instead, it had an effect similar to that of Li⁺. The same anomalous cation sequence was found in an independent experiment devoted to measuring the Brownian motion of BSA protein [19].

Medda et al. [18] interpreted the Cs⁺ anomaly to be a consequence of the highly heterogeneous nature of protein surfaces. Proteins have both charged and uncharged surface residues, thus ions specifically compete for these sites through two different types of ion–surface interaction. The process is illustrated in figure 1. On the one hand, ions adsorb to the protein surface or backbone through physisorption (interaction at a distance from the surface). Electrostatic physisorption is not ion-specific, but non-electrostatic physisorption is ion-specific. Depending on the nature of the surface, whether hydrophobic or hydrophilic, non-electrostatic physisorption alone may lead to a standard or reversed Hofmeister series [17,20]. In this work, we quantify non-electrostatic physisorption through ionic dispersion forces [21,22] using a standard dielectric model of the protein surface [23]. This model gives the surface (the protein backbone) a somewhat hydrophobic character with non-electrostatic physisorption following the series Cs⁺> K⁺> Li⁺.

Figure 1.

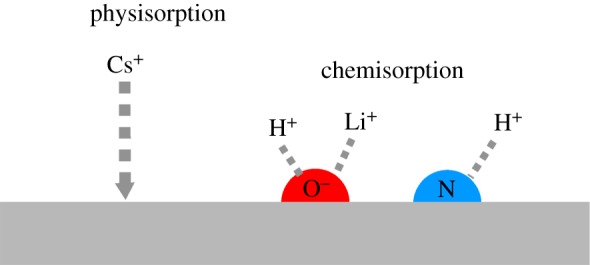
Illustration of physisorption and chemisorption processes.

Alongside non-electrostatic physisorption, however, ions may also interact directly with the surface through chemisorption, binding to specific sites scattered across the protein surface; see figure 2. Non-electrostatic physisorption is expected to be greater for the more polarizable Cs⁺ ion, with an effect on aggregation in the series Li⁺< K⁺< Cs⁺. But we would expect the kosmotropic Li⁺ to bind more strongly to kosmotropic carboxylate sites, leading to a chemisorption series in the reverse order, Cs⁺< K⁺< Li⁺. The observed behaviour is a combination of the two effects of physisorption and chemisorption. Chemisorption of Li⁺ and physisorption of Cs⁺ are both relatively (and equally) strong compared with K⁺. It is the ion giving a higher effective surface charge that inhibits aggregation [18,19].

Figure 2.

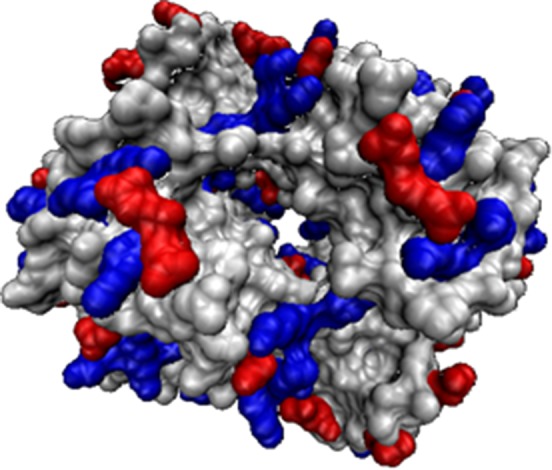
Structural image of the haemoglobin tetramer indicating surface heterogeneity. Negatively charged residues (carboxylates) are red and positively charged residues (amines) are blue; grey regions are uncharged.

Understanding specific cation interactions with proteins is of fundamental importance in life sciences. It is indeed well established that most cells have developed an energy-consuming mechanism to keep low concentrations of sodium and high concentrations of potassium in the cytosol. This is done against concentration gradients by means of ATP energy and an enzyme machine. In this paper, we show how the notions of competing physisorption and chemisorption may be quantified in a theoretical model that provides an estimate of the chemisorption binding energy of kosmotropic cations.

2. Physisorption model

The physisorption profile of ions between two protein surfaces separated by distance L may be estimated using a Poisson–Boltzmann description of the electrolyte. The concentration profile of ion i at a distance z from the surface is given by the Boltzmann relation

2.1

where c_i0 is the bulk concentration of the ion and μ_i(z) is its interaction energy with the surface (i.e. excess chemical potential) which contains two parts, μ_i(z) = q_iψ(z) + μ^NES_i(z). The first is an electrostatic component q_iψ(z) determined by the charge q_i of the ion and the electrostatic potential ψ(z) at that point. The second is a non-electrostatic interaction μ^NES_i(z). For this component, we apply Ninham's ion dispersion interaction [25] with each protein surface, μ^NES_i(z) = μ^disp_i(z) + μ^disp_i(L − z), where

2.2

with 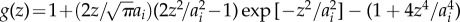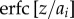. Here, ion specificity is determined by two parameters, the ion radius [24] a_i and the dispersion parameter B_i. B_i is predominantly determined by ion polarizability [25], although also modulated by ion size. Calculation of the B_i coefficient uses the dielectric function of water [26] and a model dielectric function for the protein molecules [23]. Dispersion coefficients and ion radii are given in table 1. The dispersion coefficient of Cs⁺ is augmented by a factor of 1.5 to enable non-electrostatic physisorption of Cs⁺ stronger than that of K⁺ (see μ^disp_i(0) in the table). Ion–protein dispersion interactions of this kind have proved useful in anticipating reversal in the anionic Hofmeister series at pH above and below the isoelectric point of lysozyme [16,27], attributed to charge reversal due to non-electrostatic physisorption [28].

Table 1.

Gaussian radii a_i of ions, static polarizability α₀ (in vacuum), dispersion coefficients B_i and non-electrostatic physisorption energy (ion dispersion energy at contact) for ions in water interacting with a model protein surface.

ion	ai (Å)	α0 (Å3)	Bi (10−50 J m3)	μdispi(0) (kBT)
Li+·5H2O	2.56	6.648	−0.700	−20.754
K+	0.96	0.814	−0.322	−26.591
Cs+	0.96	2.402	−1.371	−27.805
Cl−	1.86	4.861	−1.258	−23.538
H3O+	0.97	0.963	−0.382	−27.496
OH−·3H2O	2.39	7.305	−1.498	−21.983

The non-electrostatic interaction energy μ^NES_i(z) (or μ^disp_i(z)) falls with distance from the surface. But the non-electrostatic physisorption energy is its value when the ion is located at the surface, μ^ps_i = μ^disp_i(z = 0), and is a balance between polarizability (through B_i) and ion size, μ^ps_i = 16B_i/[3(π)^1/2a³].

The electrostatic potential ψ(z) is determined by solving Poisson's equation for the given charge distributions q_ic_i(z) with surface charge determined by chemisorption.

3. Chemisorption model

We apply a competitive site-binding model of chemisorption [29], involving ion binding to surface sites with a finite surface density. This model quantifies the notion of ion site binding which has been proposed as a mechanism that disrupts standard Hofmeister series [18,30]. We take haemoglobin in the form of a tetramer, spherical with diameter 5.5 nm. The surface charge of the haemoglobin tetramer is pH-dependent through charge regulation [31]. We consider H⁺ binding to both carboxylate and amine sites,

3.1

and

3.2

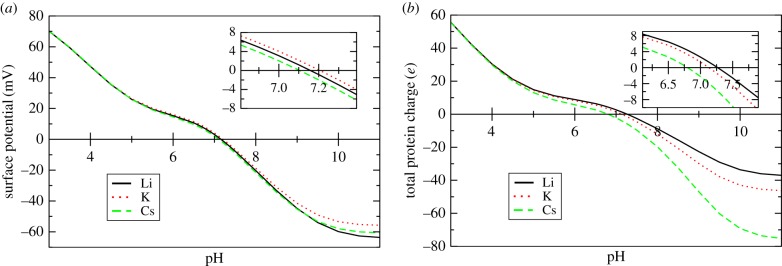
The pK binding constants here are intrinsic equilibrium constants, meaning they are evaluated using ion concentrations c_i(z = 0) at the site rather than bulk concentrations c_i0. We adapt acid constants and site densities for haemoglobin from Matthew et al. [32], averaging over values measured for individual amino acids. Their acid constants are pK^MHG_c = 5.46 averaged over acidic (carboxylate) residues and pK^MHG_a = 8.97 for basic (amine) residues. Matthew, Hanania and Gurd presented ‘intrinsic’ acid constants, already adjusted for the electrostatic physisorption energy of H⁺ (adjusting acid constants is discussed further in [33]). We adjust the acid constants further in order to match the IEP. We take pK_c = pK^MHG_c + ΔG_K/(kT ln 10), where the adjustment ΔG_K =−5.32 k_BT, is fitted to ensure that the surface potential in 100 mM CsCl (including ion dispersion interactions) is zero at the IEP, pH 7.1. We interpret this fitted adjustment as a correction for non-electrostatic physisorption, and as compensation for averaging the various pK values of the different amino acid residues. The final acid constants used are pK_c = 3.15 and pK_a = 6.66. Site densities are N_c = 0.800 nm⁻² and N_a = 0.863 nm⁻² for carboxylate and amine sites, respectively. Site densities are determined from the total number of unmasked (titratable) residues (76 carboxylate sites and 82 amine sites in a haemoglobin tetramer), smeared over the surface of the spherical tetramer. Surface potentials and total protein charge are shown below as a function of pH in figure 4.

Figure 4.

(a) Surface potential and (b) total haemoglobin tetramer charge as a function of pH in 100 mM solutions of LiCl, KCl or CsCl.

Ion-specific chemisorption is modelled through competitive cation binding [29,34] at carboxylate sites,

3.3

We assume here that ion binding (apart from H⁺) at amine sites is weak [35]. Likewise, we assume that anion binding at carboxylate sites is negligible. Cations compete with hydrogen ions to bind to the carboxylate sites. In this work, we treat pK_M as a fitting parameter to align theory with experiment.

The total surface charge is the sum of charges at carboxylate and amine sites:

3.4

The charge at each site is determined by the amount Γ of ion (H⁺ and M⁺) chemisorbed [29]

3.5

and

3.6

Here, q_e refers to the elementary charge, q_e = 1.6022 × 10⁻¹⁹ C. Chemisorption quantities Γ are determined from physisorbed concentrations c^ps_i = c_i(z = 0) and binding constants,

3.7

3.8

3.9

The A parameters here are a measure of the total degree of binding at each site,

3.10

and

3.11

4. Protein interaction free energy

Protein aggregation is determined by the interaction free energy G(L) between two protein tetramers. We estimate the interaction free energy of the spherical haemoglobin tetramers from the interaction free energy G_flat (taken as a surface energy, the free energy per unit area) of an idealized flat haemoglobin surface. That is, the Poisson–Boltzman model-determining ion concentration profiles and electrostatic potential is solved for the flat surface. The relationship between the spherical and flat interaction energies is given by the proximity force approximation of Derjaguin [36], 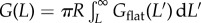, where R is the radius of a tetramer.

The free energy G_flat(L) is composed of various contributions [33,37],

4.1

Here, G_vdW refers to the protein–water–protein van der Waals interaction G_vdW =−A/12πL². We use a Hamaker constant A = 3.522 kT (1.450 × 10⁻²⁰ J). G_en accounts for the configuration entropy of the ion concentration profiles [38]. G_el describes the electrostatic energy of the electric field generated by surface and ion charges [37,38]. For brevity, we omit details of these terms.

G_NES accounts for non-electrostatic physisorption, through the non-electrostatic interaction energy μ^NES_i(z),

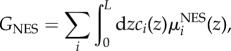4.2

G_chem accounts for chemisorption, the charge transfer energy required to form the surface site charges σ_c and σ_a. Using the framework for describing competitive site binding [29], the chemisorption energy is G_chem = G^c_chem + G^a_chem, with

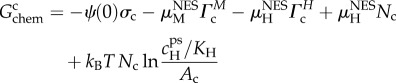4.3

and

4.4

Three qualitatively distinct parts of the chemisorption free energy can be noted. The first is an electrostatic energy, −ψ(0)σ, which partially cancels [39] against G_el. The middle term involves ‘μ^NESΓ’. This is significant since it means that the magnitude of the chemisorption energy is determined in part by the non-electrostatic physisorption energy μ^NES of potential-determining ions. The third part involves ‘k_BT N lnA’ which describes the entropy of surface sites.

5. Matching theory to experiment

The experiment we are modelling in this paper is based on turbidimetric pH titrations of haemoglobin [18]. This technique provided us information on the effect of pH on the aggregation/disaggregation of haemoglobin molecules in the presence of different chloride salts. In figure 3, the extent of aggregation is estimated by the ratio of transmittance at different pH values (T₀ is the transmittance of the optically clear haemoglobin solution). The protein suspension is optically clear below pH 5 (T/T₀ = 1); then the transmittance falls as aggregation of haemoglobin proceeds as a consequence of the increase in pH. T/T₀ reaches a minimum at about pH 7.4 (IEP); then it increases due to the re-dissolution of protein aggregates, reaching a T/T₀ of about 1 at pH > 9. Optically clear protein solutions are obtained at pH values far from the IEP due to repulsive forces as a consequence of ion adsorption due to the electric charges carried by the protein surface at a pH far from the IEP. Figure 3 shows how haemoglobin solubility is modulated by the presence of different 50 mM chloride salts in a cation-specific way. At the starting pH 4.5 haemoglobin carries a positive net charge, so that cations behave as coions. In figure 3, if we consider the trends at , cations promote haemoglobin aggregation in the order Rb⁺ > K⁺ ≈ Na⁺ > Cs⁺ > Li⁺ (50 mM salts) or K⁺ ≈ Rb⁺ > Na⁺ > Cs⁺ > Li⁺ (100 mM).

Figure 3.

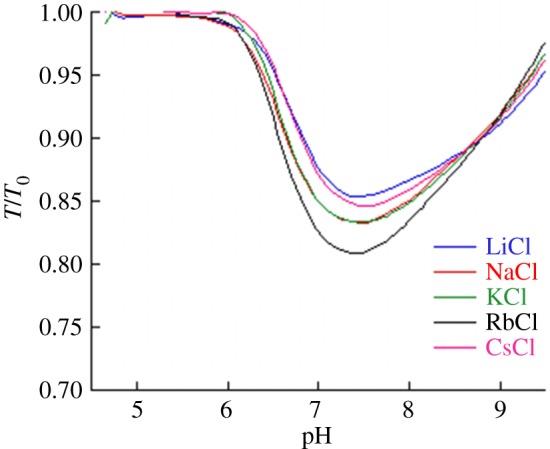
Experimental turbidity measurements of haemoglobin in 50 mM alkali chloride salts. Adapted from [18].

The transmittance measured in turbidity experiments falls as aggregation of haemoglobin tetramers proceeds. That is, the turbidance (absorbance) 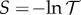rises, proportional to the concentration c_agg of aggregates. If aggregation is dominated by association of two tetramers, then c_agg is proportional [40,41] to the second virial coefficient [42–44]

5.1

b is evaluated here with respect to the separation distance L between protein surfaces, rather than the distance between protein centres r = L + 2R, assuming hard sphere contact between tetramers. Hence, the concentration of aggregates c_agg is determined by the protein–protein interaction G(L). Experimental second virial coefficients have often been used to characterize protein aggregation [45–48]. If particles are non-interacting (G = 0), then b = 0, corresponding to an ideal transmittance of 100%. If particles aggregate (G < 0), then b becomes negative and transmittance is reduced. We use the absorbance relationship 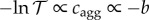to deduce plausible estimates for cation binding constants pK_M. Algebraic details are given in the electronic supplementary material.

The chaotropic ion Cs⁺ is likely to bind weakly to the kosmotropic-like carboxylate site. We remove ambiguity by assuming it does not bind at all, with pK_Cs =−∞.

The experimental transmittance 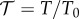of 1 mg ml⁻¹ haemoglobin in 50 mM chloride solution is shown [18] in figure 3. We focus on Li⁺, K⁺ and Cs⁺ representatives of the opposing ends and the middle of the cation Hofmeister series. Transmittances at pH 7 are 0.8541, 0.8324 and 0.8465 for Li⁺, K⁺ and Cs⁺, respectively. With the second virial coefficient b proportional to 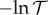, we adjust cation binding constants to achieve the least error in

5.2

(see the electronic supplementary material for the derivation).

The resulting binding constants are pK_Li =−0.21 and pK_K =−1.31, equivalent to a binding energy of 0.484 k_BT for Li⁺ and 3.02 k_BT for K⁺, positive values indicating that binding is relatively unfavourable. Curiously, even for Li⁺ the binding energy is positive (unfavourable), indicating that cation binding to carboxylate sites is relatively weak. By comparison, the carboxylate binding energy of H⁺ (with pK_c = 3.15) is −7.25 k_BT. Chemisorption of Li⁺ is 12.6 times stronger than K⁺, which, combined with different non-electrostatic physisorption, is sufficient to drive the difference in transmittance observed experimentally.

The 2.5 k_BT difference in Li⁺ and K⁺ binding energies found here is in reasonable agreement with the difference of 0.9 kcal mol⁻¹ (1.5 k_BT) found by molecular dynamics simulations [49], although the absolute binding energies from MD are more attractive. The discrepancy may be tentatively attributed to the mean-field smeared surface charge applied here, neglecting the discrete nature of binding sites as well as the specific amino acid residues hosting the carboxylate and amine sites, which is included in molecular dynamics simulations. Discrete surface charges tend to increase counterion physisorption, increasing repulsion (or diminishing attraction) between surfaces [50]. Anions are counterions for the mildly positive haemoglobin surface charge found in our model. To balance against this effect in order to maintain the same interaction under conditions of discrete surface charge, we would expect the slightly stronger cation binding which was found in MD simulation.

The calculated surface potential and total protein (haemoglobin) charge are shown in figure 4 as a function of pH in 100 mM salt solution. The anomalous Hofmeister series K⁺>Li⁺ > Cs⁺ is found in the surface potential. Cs⁺ and Li⁺ swap above pH 9 but remain anomalous with respect to K⁺. Interestingly, the Hofmeister effect is much stronger in the total protein charge, and follows the conventional series Li⁺ > K⁺ > Cs⁺. This observation in the total charge supports our interpretation that the overall Hofmeister effect is a competition between the two mechanisms of chemisorption and non-electrostatic physisorption, each with opposing Hofmeister series.

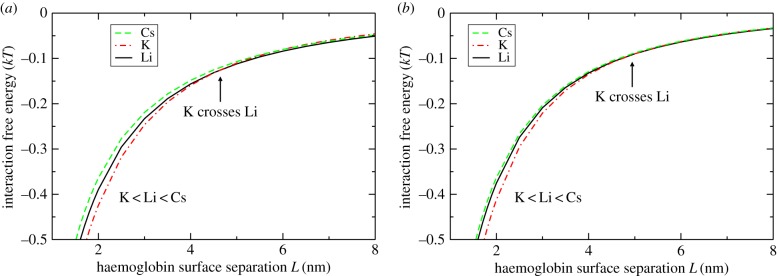
Calculated short-range interaction free energies G(L) for haemoglobin in 50 mM and 100 mM LiCl, KCl, CsCl at pH 7 are shown in figure 5. We find that at small separations the interactions follow the anomalous Hofmeister series, K⁺<Cs⁺≤Li⁺. At 50 mM salt concentrations we can additionally observe that, above a separation of 4.5 nm, the interaction for K⁺ crosses that of Li⁺, with the interaction for Li⁺ becoming the more attractive. A crossover point (not significant on the scale shown in figure 5) also occurs in 100 mM salts at 5 nm. It is apparent that the experimentally observed anomaly in the Hofmeister series for aggregation behaviour is controlled by short-range protein interactions.

Figure 5.

Theoretical short-range interaction energies between two haemoglobin tetramers (diameter 5.5 nm) at pH 7 in (a) 50 mM and (b) 100 mM LiCl, KCl and CsCl.

The reason why K⁺ induces stronger attraction at short separations can be attributed in part to the hydration model used for the ions. Li⁺ is taken as strongly hydrated, hence carrying a larger hydrated ion radius. Although lithium's dispersion B coefficient is larger, its dispersion interaction is weakened over the larger radius and so the short-range non-electrostatic physisorption of K⁺ is stronger. Consequently, the amount of K⁺ at the protein surface is greater than Li⁺, leading to a larger positive electrostatic potential (stronger attractive electrostatic energy G_el) and a stronger attractive chemisorption energy G_chem, due to the component −μ^NES_KΓ^K_c in equation (4.3).

In the case of Cs⁺, the attractive non-electrostatic chemisorption term −μ^NES_CsΓ^Cs_c is not present, so the overall interaction in Cs⁺ is relatively less attractive than K⁺, leading to less aggregation. In the case of Li⁺, as discussed above, non-electrostatic physisorption is weaker, leading to less aggregation. K⁺ has a sufficient amount of both mechanisms, physisorption and chemisorption, that leads to a more attractive short-range interaction and therefore stronger aggregation.

6. Conclusion

Physisorption at the protein backbone and chemisorption at protein charge sites present as two competing mechanisms, each with a cationic Hofmeister series reverse to the other. The K⁺ ion, lying in the middle of a standard Hofmeister sequence between Li⁺ and Cs⁺, experiences a sufficient amount of both mechanisms that results in greater K⁺ adsorption than the other cations. The consequence is a more attractive short-range interaction leading to higher protein aggregation. Overall, the specific ion effect in any given salt is governed by the relative weights of the two mechanisms.

The model was tested against haemoglobin turbidity measurements, fitting chemisorption binding energies to carboxylate sites (assuming no chemisorption of Cs⁺) with the help of calculated second virial coefficients. Fitted binding energies are realistic with weakly unfavourable (positive) binding energies of 0.484 k_BT for Li⁺ and 3.02 k_BT for K⁺. This indicates that Li⁺ binds 12.6 times more strongly than K⁺, consistent with the notion that the kosmotropic Li⁺ should have greater affinity with the kosmotropic carboxylate site [49,51].

Chemisorption binding energies were fitted in this study. Improvements can be made by evaluating binding energies from first principles rather than fitting. A model of ion–ion interactions, already found to be useful in bulk solutions [44,52], may help achieve this.

In the model applied here, accessible chemisorption sites (carboxylates, amines) were located only at the surface of a protein, taken to be impenetrable to ions. In some situations, particularly for denatured proteins, it may be worthwhile exploring a model which allows ions to penetrate into the volume of the protein molecule, with chemisorption taking place at sites throughout the protein volume [53]. Anisotropy in the distribution of ions bound at charge sites is also an important factor in protein aggregation, requiring a more sophisticated three-dimensional modelling [54]. The methodology presented here can be extended to these kinds of three-dimensional models.

Competing interests

We declare we have no competing interests.

Funding

We acknowledge the grant of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. A.S. thanks FIR 2016 and Fondazione di Sardegna (L.R. 7/2007 year 2016—DGR 28/21 17.05.2015) for support.