Identifying tissue-selective transcription factor binding sites in vertebrate promoters

Abstract

We present a computational method aimed at systematically identifying tissue-selective transcription factor binding sites. Our method focuses on the differences between sets of promoters that are associated with differentially expressed genes, and it is effective at identifying the highly degenerate motifs that characterize vertebrate transcription factor binding sites. Results on simulated data indicate that our method detects motifs with greater accuracy than the leading methods, and its detection of strongly overrepresented motifs is nearly perfect. We present motifs identified by our method as the most overrepresented in promoters of liver- and muscle-selective genes, demonstrating that our method accurately identifies known transcription factor binding sites and previously uncharacterized motifs.

Dissecting the transcription-regulation networks in higher eukaryotes is an immediate challenge for systems biology. Techniques like microarray analysis and chromatin immunoprecipitation have produced a significant volume of expression and localization data that can be used to investigate this machinery. Transcription factors play a prominent role in transcription regulation; identifying and characterizing their binding sites is central to annotating genomic regulatory regions and understanding gene-regulatory networks.

Computational methods that use both sequence and expression data to identify transcription factor binding sites (TFBS) are becoming increasingly accurate (1), but binding-site identification in vertebrates remains a difficult problem. Tissue-selective transcription regulation requires more complex regulatory machinery, contributing to less predictable binding-site location (2) and a greater role for combinatorial control (3). Fortunately, knowledge of gene expression in different tissues can facilitate the detection of tissue-selective regulatory elements through comparative analysis of regulatory sequences.

Tools for discovering binding sites associated with specific tissues need to be able to identify highly degenerate motifs that are overrepresented in one set of promoters relative to another. Motif-discovery algorithms, such as consensus (4), meme (5), and gibbs motif sampler (6) represent motifs as position-weight matrices and can express sufficient degeneracy, but none of these algorithms focus on relative overrepresentation between two sets of sequences. dmotifs (7) identifies the motifs that best discriminate between two sets of sequences, but an initial, and often prohibitively large, set of candidate motifs must be provided. Other methods that allow the user to give a background set (1, 8) use the background to fit a statistical model, which is then used to determine overrepresentation.

We describe a general method for discovering TFBSs by identifying motifs based on a relative overrepresentation between two sets of promoters. Our method, dme (discriminating matrix enumerator), uses an enumerative algorithm to exhaustively and efficiently search a discrete space of matrices, scoring each matrix according to its relative overrepresentation. The highest-scoring matrices are refined by using a local search procedure that optimizes the relative overrepresentation score. As soon as a motif is discovered, its occurrences are erased from the data and the procedure is repeated to discover additional motifs. In describing our method, we focus on the objective function that measures relative overrepresentation and on the strategy of exhaustively searching discrete spaces of matrices. We do not discuss issues of how to perform such exhaustive searches, because our focus is accuracy rather than efficiency, within practical time constraints.

We tested the ability of dme to recover planted motifs from simulated data and to identify known binding-site motifs in regulatory regions associated with muscle and liver. Results on simulated data suggest that dme accurately identifies highly degenerate and sparse motifs. Results on promoters of liver- and muscle-selective genes demonstrate that dme accurately identifies overrepresented motifs in regulatory regions of higher eukaryotes. dme identified motifs highly similar to HNF-1, HNF-3, C/EBP, and POU2F1 as the most overrepresented in promoters associated with liver, and motifs highly similar to binding sites of serum-response factor (SRF), myocyte-specific enhancer factor 2 (MEF-2), and myogenic determination factor (MyoD) as the most overrepresented in promoters associated with muscle. We present these, along with other overrepresented motifs that may be binding sites of additional factors or different characterizations for binding sites of factors already associated with these tissues.

dme is the appropriate tool for discovering overrepresented binding-site motifs by using expression or chromatin-immunoprecipitation data. Both experimental protocols present natural foreground and background sets; dme can identify motifs overrepresented in promoters of genes showing strong expression relative to those of weakly expressed genes or in promoters with strong binding affinity relative to those with weak binding affinity. The enumerative strategy used by dme provides the exact computational technology necessary in these applications, in which the strongest motifs may be highly degenerate and have sparse occurrences that are difficult to detect by using sampling-based strategies. dme is freely available for the academic community upon request.

Methods

To measure motif quality, we use a likelihood model (6) for motif overrepresentation in a set of foreground sequences relative to a set of background sequences, or a base composition. We work with the multisets F and B of length w substrings from the foreground and background, respectively. Considering only these multisets, we ignore dependence between consecutive length w substrings, but for large data sets, the error introduced by this approximation is negligible.

First, we describe the model for motif overrepresentation in the foreground relative to the base composition (6). Let F = {s_i|1 ≤ i ≤ n} be a multiset of length w strings; the subset F₁ F consists of observations from a product-multinomial model M = (M₁,..., M_w), called the motif. Members of F₁ are called occurrences of the motif, and they correspond to binding sites. Component M_i,1 ≤ i ≤ w, of M describes the distribution of bases at position i in the set of occurrences; M_i = (M_iA, M_iC, M_iG, M_iT) is a vector of probabilities with unit sum. For any string s of width w, the probability that s is generated by the motif is

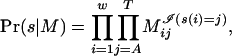where 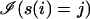indicates that base j appears at position i in s. If F₁ is a set of independent observations, the likelihood of M given F₁ is L_F1(M) = Π_s∈F1 Pr(s|M).

The set F₀ = F\F₁ consists of nonoccurrences. We assume that positions within nonoccurrence sites are generated from a multinomial distribution with parameter f = (f_A, f_C, f_G, f_T), representing the base composition of strings in F₀. For each string s with length w,

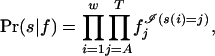and the corresponding likelihood for f, having observed F₀, is L_F0(f) = Π_s∈F0 Pr(s|f).

We use maximum likelihood to measure motif quality and search for the maximum-likelihood partition F₀, F₁ for a given motif model M and base-composition model f. Define the indicator variables Z = {z_i|1 ≤ i ≤ n}, where z_i = 1 exactly when s_i ∈ F₁ and 0 otherwise. The likelihood of M and f given F and values for the missing data Z is

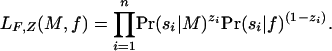[1]

Under this formulation, the quality of M and f depends on the maximum-likelihood values for Z. For a fixed base composition f, our goal is to identify the highest-quality motif, which reduces to finding the maximum-likelihood estimates for variables of Z. This formulation is similar to the formulation by Lawrence and Reilly (9), except that our f is fixed and we make no assumptions about the distribution of motif occurrences across the sequence set. When a set of background sequences is used, the motifs that are the most overrepresented in the foreground relative to the background are those for which the ratio of likelihood in the foreground to likelihood in the background is maximized:

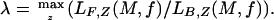[2]

Note that when the motif M and the base composition f are fixed, maximum-likelihood value z_i = 1 exactly when the corresponding substring is more likely to be an observation from M than f.

Objective Function. Taking f as the base composition of 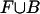, we aim to find a value for M with the highest quality (as defined by Eq. 3). Computationally, finding such a value is simplified by taking the logarithm of the likelihood ratio, resulting in the formula

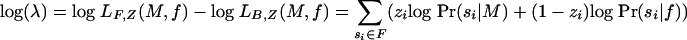[3]

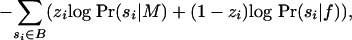where, as in the previous section, z_i indicates that s_i was generated from M. If |F₀| >> |F₁| and |B₀| >> |B₁| (i.e., motif occurrences are not too dense), the base composition of 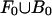should be approximately equal to that of . Under this assumption, the terms in Eq. 3 containing a factor of (1 - z_i) have little influence, and the above formula is maximized with respect to M at approximately the same location as

[4]

Eq. 4 is our objective function, and it is calculated more easily than Eq. 3 because the sums involve only terms corresponding to occurrences, rather than all substrings. We remark that when base compositions of F and B differ greatly, terms multiplied by (1 - z_i) can have a large influence, and differences between F and B may reflect more than just motif content.

The dme Algorithm. dme iterates the following steps, with each iteration producing a motif: (i) initial search to discover the motif with the highest relative overrepresentation (from a restricted class, see below), (ii) local search procedure to optimize the motif based on relative overrepresentation, and (iii) erase the motif from the data set so that motifs discovered in subsequent iterations will not be variants of motifs discovered in earlier iterations.

Initial Search. dme enumerates motifs by constructing all possible matrices built from a specific finite set of “column types.” In theory, the only restriction on the set of permissible column types is that it must be of finite size. Larger sets of column types give a greater number of matrices in the space dme searches, potentially leading to greater accuracy. The quality of each matrix enumerated by dme is calculated by using Eq. 4, and the matrix with the highest quality is maintained. As in a grid search, we assume the set of tested points represents the entire space of solutions. Analogous to using uniformly positioned points in a grid search, it is desirable to select column types so that the matrices enumerated will cover the space of matrices uniformly.

Information content has been used to measure the quality of a motif (10), and it is defined as

Previous methods for matrix-based motif discovery have optimized the information content of the matrix for a fixed number of occurrences (9, 11). In contrast to previous methods, we assume a matrix and maximize a likelihood function that increases with the number of occurrences and occurrence quality. We have observed that the number of occurrences generally has a greater influence on our objective function than the strength of those occurrences, resulting in a tendency for the highest-scoring motifs to be extremely degenerate. To solve this problem, dme enumerates only motifs with information content above a preset threshold, allowing control over the specificity of discovered motifs. The threshold is given in bits per column, and all enumerated motifs have at least the threshold bits per column on average across positions.

Local Search Procedure. Given a matrix, our local search procedure attempts to identify similar matrices with greater values for the objective function. Other studies (12, 13) have used expectation maximization (EM) to improve motifs, but EM does not optimize “relative” overrepresentation. Given a matrix M, and value g ∈ (0, 1), the g-neighborhood of column M_i is the set

where d₁ is the rectilinear metric. The g-neighborhood of M consists of all matrices M′, such that M_i′ ∈ N_g(M_i). We begin with a matrix (called the “original” matrix), and we must determine whether a matrix in the neighborhood of the original has a higher score (as defined by Eq. 4). The refinement procedure consists of enumerating and scoring all motifs in the g-neighborhood of the original motif, for a particular value of g. The optimal motif in the g-neighborhood replaces the original, and the process is repeated with the value g/2 replacing g until the optimal motif is equal to the original motif or until g has reached some specified minimum (e.g., 0.01).

Results

We tested dme on recovering planted motifs from simulated data sets and identifying binding-site motifs in promoters of genes expressed in liver and muscle. dme out-performs other motif-discovery methods on recovering realistic planted motifs, and dme can identify degenerate binding-site motifs in real data. We present and discuss some of the motifs discovered by dme in these promoter sets.

Motif Discovery in Simulated Data Sets. We compared dme, projection (12), gibbs motif sampler (6), and mdscan (1) on the task of recovering planted motifs from simulated foreground sequences without a background set. We also compared dme and mdscan on recovering planted motifs in a foreground set when provided with a background set with motif occurrences probabilistically removed. Sequence sets were constructed by generating 100 DNA sequences of length 1,000 bp from a random multinomial distribution around the uniform. When motifs were planted, occurrences were inserted at positions selected uniformly at random from among all sites in all sequences. Each occurrence was generated by considering the motif as the set of parameters to a product multinomial distribution and by sampling sequences from that distribution. Motif models were generated by randomly sampling sets of columns from a Dirichlet distribution, with motif-information content (a measure of binding specificity) restricted to a particular range.

Data sets were constructed for one to four motif models with widths of 8, 10, or 12, and information content of 1.15 and 1.35 (±0.025) bits per column (see Methods for the definition of information content). For trials without a background set, 100 occurrences from each motif model were planted, and for trials with a background set, 40 occurrences were planted. Background sets were constructed from the same multinomial distribution as their corresponding foreground sets. For each motif model planted in a foreground set, occurrences were probabilistically replaced in the corresponding background set with bases generated at random from the base composition. The probability of an occurrence being replaced was 0.9 times the score for the occurrence divided by the maximum possible score, with scores obtained by using the log-likelihood ratio scoring matrix (14) corresponding to the motif model. Data sets without a background sequence set were generated for widths of 8 and 10, with 1.15 and 1.35 bits per column. Data sets with background sets were generated for width 8, with both 1.15 and 1.35 bits per column, and widths of 10-12 with 1.35 bits per column.

To measure detection quality, we compared produced motifs with those that were planted. Programs could output three candidate motifs for each planted motif in the data set. Motifs were compared by using an information-theoretic distance measure, in which matrix columns are viewed as a multinomial distribution (6) and the distance between two motifs is the average “divergence” (15) between corresponding columns (see Supporting Methods, which is published as supporting information on the PNAS web site, for definition of divergence). For each combination of parameters, the score received by a program is the average over the 100 data sets for that combination, of the average divergence between each planted motif and the recovered motif that most resembles it. Results presented in Tables 1 and 2 indicate that dme recovers planted motifs with greater accuracy than the other methods. We emphasize that dme outperforms those methods on both problem types, and the detection-quality gap between dme and the other methods increases with planted motif-information content.

Table 1. Performance on recovering planted motifs given only a foreground.

Motif	dme	projection	gibbs	mdscan
	Width 8, 1.15 bits per column (±0.025)
1	0.49	0.96	2.46	2.11
2	0.35	0.72	2.06	1.68
3	0.36	0.80	1.86	1.66
4	0.34	0.75	1.77	1.46
	Width 8, 1.35 bits per column (±0.025)
1	0.12	0.32	2.74	1.10
2	0.21	0.28	2.36	1.31
3	0.19	0.28	2.21	1.20
4	0.12	0.28	2.04	1.22
	Width 10, 1.15 bits per column (±0.025)
1	0.04	0.44	2.48	1.12
2	0.05	0.39	2.28	1.37
3	0.06	0.48	2.09	1.35
4	0.06	0.49	1.97	1.60
	Width 10, 1.35 bits per column (±0.025)
1	0.02	0.12	2.81	0.36
2	0.02	0.13	2.52	1.63
3	0.02	0.15	2.41	1.84
4	0.02	0.14	2.29	1.84

Values are mean divergence scores over 100 trials.

Table 2. Performance on recovering planted motifs given both a foreground and a background.

	Motif width 8, 1.15 bits per column		Motif width 8, 1.35 bits per column		Motif width 10, 1.35 bits per column		Motif width 12, 1.35 bits per column
Motifs	dme	mdscan	dme	mdscan	dme	mdscan	dme	mdscan
1	0.27	1.89	0.17	2.38	0.05	2.16	0.02	1.78
2	0.24	1.80	0.16	2.10	0.05	1.93	0.02	1.64
3	0.29	1.60	0.20	1.98	0.06	1.84	0.02	1.61
4	0.27	1.57	0.16	1.91	0.05	1.78	0.02	1.66

Values are mean divergence scores over 100 trials.

Motif Discovery in Tissue-Selective Promoter Sets. We used dme to search for overrepresented motifs in promoters of liver- and muscle-selective genes. For liver, we used a set of nonhomologous promoters, called the liver-selective promoter set (LSPS). For muscle, we used a set of promoters and enhancers curated by Wasserman and Fickett (16), which we refer to as the Wasserman-Fickett set. We also used subsets of promoters from the Eukaryotic Promoter Database (EPD, release no. 78; ref. 17), based on EPD annotations, EPD liver consists of promoters of genes expressed in liver, and EPD muscle consists of promoters of genes expressed in muscle (all types of muscle). Promoters with high sequence similarity were removed from both of these sets. As background, we used the vertebrate subset of EPD, with promoters associated with liver and muscle removed for analysis of liver and muscle, respectively. The base composition of sets associated with liver and muscle differ consistently. Both LSPS and EPD liver have a CG content of 0.48. The Wasserman-Fickett and EPD muscle sets have a high CG content of 0.56 and 0.58, respectively, similar to the base composition of the vertebrate subset of EPD (0.58 CG) (see Data Sets 1-10, which are published as supporting information on the PNAS web site).

We ran dme on each foreground-background set combination. We searched for motifs of width 8, 10, and 12 while varying initial bits per column between 1.45 and 1.8 (see Methods for an explanation of this parameter). dme produces motifs sequentially, with stronger motif produced earlier; hereafter, the rank of a motif refers to this order. We compare discovered motifs to previously characterized motifs from transfac (release no. 8.2; ref. 18) and jaspar (ref. 19; search date, July 2004). Full results are given as Data Sets 11-30, which are published as supporting information on the PNAS web site. Although the curated sets were known to contain functional sites, no evidence suggested that those binding sites were associated with the most overrepresented motifs.

Motif Discovery in Liver-Selective Promotor Sets. Liver-associated factors with well characterized binding-site motifs include the hepatocyte nuclear factors HNF-1, -3, -4, and -6 (20) and the CCAAT/enhancer-binding proteins C/EBP and C/EBPβ (21).

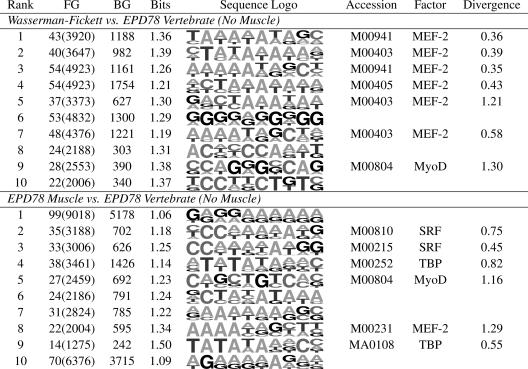
Table 3 shows examples of motifs that were identified as overrepresented in liver-selective promoters and match well with previously characterized motifs. The first and second motifs were found to be overrepresented in LSPS, and they are both similar to binding sites of POU-domain factors (22). The first motif contains both halves of the palindromic TTAATNATTAA pattern characteristic of HNF-1-binding sites. This motif ranked sixth, and on the same run, 7 of the top 10 motifs strongly resembled the entire length of the known HNF-1 motif. The second motif includes the TTAAT pattern. Although it is similar to known HNF-1 and HNF-3 motifs, this motif most closely matches the motif for POU2F1 (23), which is a ubiquitous factor with a critical role in liver (24). The third through fifth motifs are overrepresented in EPD liver, and they include motifs that are similar to those for C/EBP, HNF-1, and POU2F1.

Table 3. Selected results from liver.

Each record corresponds to a motif produced by DMEonruns using various parameter combinations. The rank assigned by DME, thenumberof occurrences in the foreground (FG) and background (BG), and the average bits per column (Bits) of the motif are given. Values given in parentheses with the foreground occurrences is the number of foreground occurrences multiplied by the ratio of the size of the background to the size of the foreground. The sequence logo (28) is given for the motif, along with the sequence logo of a similar previously characterized motif (from transfac or jaspar), the accession no. of the motif (jaspar accession nos. begin with "MA"), the name of the associated factor, and the divergence (Div.) between the two motifs.

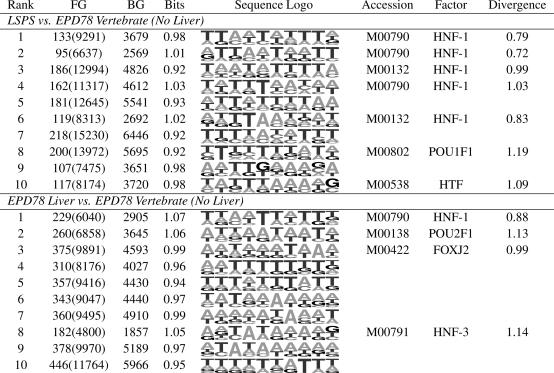
Table 4 shows, for both liver foreground sets, the top 10 motifs of length 10 found by using a minimum information content of 1.6 bits per column. For LSPS, dme found the HNF-1 motif to be the strongest signal, with the known HNF-1 motif closely matching most of the top motifs (although dme erases occurrences of motifs discovered, if the true motif width is greater than the specified width, dme might find multiple “pieces” of the same motif). The motif ranked eighth resembles the binding motif for POU1F1. The motif ranked 10th most resembles the motif for HTF, a known liver factor (25). dme also found the HNF-1 motif to be the most overrepresented in the EPD liver set relative to other vertebrate promoters from EPD, with the top-ranking motif resembling the HNF-1 motif. The motif ranked second resembles the POU2F1-binding motif, and the motif ranked third resembles the binding motif for FOXJ2, which is an expression regulator in liver (26).

Table 4. Top results from liver.

The top-10-ranked motifs produced by dme for both sets of promoters associated with liver. dme was set to identify motifs of width 10, with the minimum bits per column set at 1.6. For each motif, the number of occurrences in the foreground (FG) (with the size-corrected value) and background (BG) are given, along with the average bits per column (Bits) of the produced motif and the sequence logo for the motif. If the motif is a strong match to a previously characterized transfac or jaspar motif associated with liver, the GenBank accession no. (jaspar accession nos. begin with "MA") and corresponding factor name are given, along with the divergence between the two motifs.

Motif Discovery in Muscle-Selective Promoter Sets. Transcription factors with well characterized binding sites have also been identified as essential to regulating gene expression in muscle. These factors include the SRF (16), the MyoD from the myogenin family of basic helix-loop-helix factors (27), MEF-2, the HeLa transcription enhancer factor (TEF), and the ubiquitous zinc-finger transcription factor Sp1 (16).

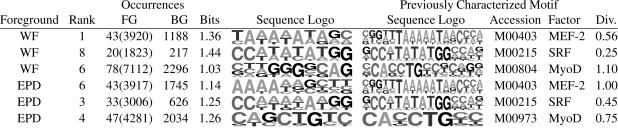
Table 5 shows examples of motifs that were identified as overrepresented in muscle promoters and match well with previously characterized motifs. The first three were identified in the Wasserman-Fickett set, and the first resembles a known binding site for MEF-2, which is strongly expressed in muscle (skeletal and cardiac). The second strongly resembles the CArG-box motif for SRF(human homolog of yeast MCM1), with consensus CC(A/T)₆GG. Motifs resembling the CArG-box appear frequently among the top-ranked motifs identified by dme in the EPD muscle set, consistent with the important role of SRF in muscle cells. The third motif resembles (the reverse complement of) a known binding site for MyoD, which is essential to muscle cell regulation. The remaining three motifs were found in the EPD muscle promoters. The fourth and fifth motifs resemble previously characterized motifs for MEF-2 and SRF. The sixth motif contains the palindrome CAGCTG and is similar to the E-box (i.e., CANNTG) associated with MyoD-binding sites. Table 6 shows, for each muscle foreground set, the top 10 motifs of length 10 found by using at least 1.6 bits per column. dme identified motifs that mostly resemble previously characterized motifs for MEF-2 and SRF. In the Wasserman-Fickett set, each of the top five motifs bears a strong resemblance to known MEF-2-binding sites, indicating extreme overrepresentation for this pattern. The existence of MEF-2-binding sites in the Wasserman-Fickett set was already known, and dme has confirmed that MEF-2 sites are the most overrepresented in the set relative to other vertebrate promoters in EPD. The motifs with ranks 8 and 10 do not match well with any previously characterized motifs associated with muscle, and they may represent important, but yet unknown, binding sites. For motifs of width 10 discovered by using 1.6 bits per column, the MEF-2 motif is sufficiently strong to obscure other motifs. By using other combinations of width and bits per column, motifs identified in the Wasserman-Fickett set usually resemble MEF-2- or SRF-binding sites. dme produces a more diverse set of motifs when EPD muscle promoters are examined. The first motif in Table 6 is purine-rich and does not resemble any previously characterized binding-site motif. The second and third motifs closely match the CArG-box bound by SRF, the fourth matches the TATA-box motif, the fifth motif matches the E-box motif bound by myogenin family members, and the eighth motif matches the MEF-2 motif.

Table 5. Selected results from muscle.

Details are as described for Table 1.

Table 6. Top results from muscle.

Details are as described for Table 2.

Supporting Information. See Tables 7-10, which are published as supporting information on the PNAS web site, for results of mdscan and gibbs motif sampler. mdscan performed well on the liver sets but not as well on the muscle sets. gibbs motif sampler did not perform well on either set.

Discussion

dme identifies motifs that are overrepresented in one set of sequences relative to another set. dme departs significantly from the current paradigm by searching for the best motifs with a specified lower bound on information content, instead of maximizing information content for motifs with a specified lower bound on the number of occurrences. dme uses an enumerative strategy; until recently (13), every matrix-based motif-discovery method used iterative sampling of occurrences (5, 6, 9, 11).

dme correctly identifies highly degenerate and sparse motifs. On recovering planted motifs from a synthetic data set, dme consistently outperformed projection, mdscan, and gibbs motif sampler. dme consistently outperformed mdscan on the task of recovering planted motifs when provided with a background set deficient in motif occurrences. We note that the programs were allowed to run with parameter values promoting correctness rather than efficiency. The performance of dme improves with signal strength, with nearly perfect detection for motifs of width 12 and 1.35 bits per column. The performance of DME on such data is encouraging, because the average width and bits per column of mouse, rat, and human motifs in transfac is 13 and 1.35, respectively.

When applied to liver- and muscle-selective promoters, dme identified motifs that are similar to previously characterized binding motifs of factors known to be active in these tissues. These results validate the effectiveness of dme in discovering binding sites in real data.

Selecting appropriate background sets is critical in comparative analysis. Background sets can control the influence of specific sequence properties. We examined promoters of liver-selective genes, which are AT-rich, relative to other vertebrate promoters, which are CG-rich. An AT-rich background would have controlled the influence of base composition, eliminating the expectation of AT-rich motifs. Using backgrounds to control specific properties of sequence sets also ignores two issues. First, motifs overrepresented in liver promoters relative to a nonvertebrate background might be common to vertebrate promoters in general, and not specific to promoters of liver selective genes. The vertebrate promoters better “mirror” the liver promoters; their use as a background likely controls some other, unknown variables. Second, particular features, such as base composition, may be important for binding behavior. Although motifs that are overrepresented in liver promoters relative to other vertebrate promoters are AT-rich in general, the important HNF-1-binding motif was still ranked highest among them (see Table 4). Base composition in liver promoters may be constrained by binding-site requirements or other functional constraints. Our model assumes that foreground and background have a similar base composition outside of motif occurrences (see Eq. 3 in Methods); in the ideal situation, the two sets differ only in their motif content. In general, background set selection should be guided by the hypothesis being tested, and it is as important as choosing the right priors in Bayesian analysis.

The fact that similar motifs were identified in the curated data sets (LSPS and Wasserman-Fickett set) and the corresponding subsets of EPD suggests that classifications used by EPD are accurate enough for motif identification. We believe that sufficient sequence and expression data exist to warrant large-scale computational studies of tissue-selective TFBSs in multiple tissues and that dme is sufficiently accurate to be used in such a large scale effort.