Stretched exponential decay and correlations in the catalytic activity of fluctuating single lipase molecules

Abstract

Single-molecule techniques offer a unique tool for studying the dynamical behavior of individual molecules and provide the possibility to construct distributions from individual events rather than from a signal stemming from an ensemble of molecules. In biological systems, known for their complexity, these techniques make it possible to gain insights into the detailed spectrum of molecular conformational changes and activities. Here, we report on the direct observation of a single lipase-catalyzed reaction for extended periods of time (hours), by using confocal fluorescence microscopy. When adding a profluorescent substrate, the monitored enzymatic activity appears as a trajectory of “on-state” and “off-state” events. The waiting time probability density function of the off state and the state-correlation function fit stretched exponentials, independent of the substrate concentration in a certain range. The data analysis unravels oscillations in the logarithmic derivative of the off-state waiting time probability density function and correlations between off-state events. These findings imply that the fluctuating enzyme model, which involves a spectrum of enzymatic conformations that interconvert on the time scale of the catalytic activity, best describes the observed enzymatic activity. Based on this model, values for the coupling and reaction rates are extracted.

Dynamics of chemical reactions are conventionally investigated by ensemble measurements. Recent advances in single-molecule spectroscopy have enabled the real-time study of biophysical processes (1–10) and conformational changes (11, 12) of single biomolecules. These studies have demonstrated that new information about such processes can be extracted from single-molecule measurements. In particular, deviations from the standard Michaelis–Menten behavior (13, 14), which is expected for bulk enzymatic activity, have been observed (6–8, 12).

Motivated by these findings, we examined the enzymatic activity of individual molecules of the 33-kDa lipase B from Candida antarctica molecules (15, 16) by using confocal fluorescence microscopy. This lipase catalyzes the hydrolysis of esters in aqueous solution following the same reaction mechanism as that of a serine protease (17). To study the catalysis by single lipase, we used a fluorogenic substrate, namely the non fluorescent ester 2′,7′-bis-(2-carboxyethyl)-5-(and-6)-carboxy fluorescein acetoxymethyl ester, which upon hydrolysis forms a highly fluorescent carboxylic acid product (18, 19). This method enabled us to probe the enzymatic activity by monitoring the fluorescence emission from single enzymes. The fluorescence emission displayed blinking of “on” and “off” events depending on the presence (or absence) of the fluorescent product in the confocal focus (20). By using this approach, we have been able to obtain long trajectories (for time periods of hours) suitable for reliable statistical analysis while varying the concentration of the substrate, thus allowing the study of the effect of changing the substrate concentration on the observed trajectories.

Our analysis demonstrates that the waiting time probability density function (PDF) of the nonfluorescent (off) state follows a stretched exponential with the same fitting parameters for a certain range of substrate concentrations. The highly nonexponential stretched behavior that is also evident in the state-correlation function is interpreted as a manifestation of a spectrum of active enzymatic conformations, which is supported by the oscillations in the logarithmic derivative of the off waiting time PDF. By performing previously undescribed methods of analyses on the data, we obtained information that is used to build a microscopic kinetic model most suitable to account for the experimental findings, namely the fluctuating enzyme model. Within the model, which involves both conformational changes and enzymatic activity, we were able to extract average values for the fast conformational fluctuations and reaction rates.

Single Enzyme Measurements

We start with a brief overview of the experimental setup. A full description is given in ref. 20. Individual lipase B molecules from Candida antarctica were nonspecifically labeled with Alexa Fluor 488 dye molecules (21, 22) and immobilized onto a surface derivatized with dichloro-dimethyl silane by using a hydrophobic glass. A laser-scanning stage confocal microscope was used to detect the lipase molecules. Focusing the laser on a single molecule, we used the attached dye fluorophores to zoom in on an enzyme molecule. The dye was then photobleached before the addition of the substrate. The recorded fluorescence emission showed a blinking (on/off) behavior, which was attributed to the enzymatic turnover cycle (ETOC). Several control measurements were performed to verify this conclusion (e.g., a signal was recorded from a system that contains enzyme in the absence of substrate and vice versa; see also ref. 20).

To analyze the recorded trajectories of the photon counts (Figs. 1 A–C), the ETOC was viewed as a two-state process. The two distinct states are naturally defined by the absence (off state) and the presence (on state) of fluorescence emission. Note that the two-state picture is not an assumption but a consequence of the way the experiments were designed (20). The two-state ETOC dynamics is basically described by the waiting time PDFs of the off state, ϕ_off(t), and of the on state, ϕ_on(t). Namely, ϕ_off(t)dt[ϕ_on(t)dt] is the probability that a given off (on) event along the trajectory lasts between t and t + dt. In principle, these functions do not fully describe the process (O.F., J.K., and A. Szabo, unpublished data). However, they do give its basic characteristics, primarily the number of substates in each of the states of the kinetic scheme. Based on our findings, we suggest below a kinetic scheme for the enzymatic activity.

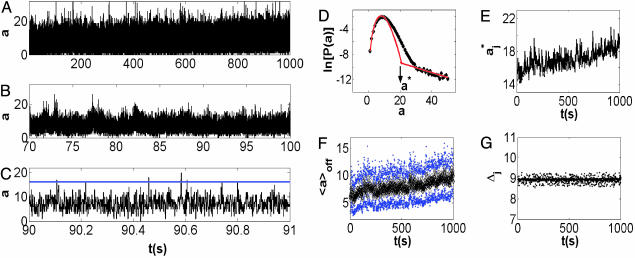
Fig. 1.

The photon count trajectory and its analysis. (A) A photon count trajectory as a function of time (Δt = 1 ms) of a single lipase B from Candida antarctica during catalysis. (B and C) Zooming into segments of the trajectory in A. A local threshold value is shown in C. (D) A ln-linear histogram of P(a) (black curve). The arrow indicates the threshold value, a^*. Also shown are the fitting functions for the two parts of P(a) (red curves). (E) The floating threshold 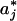as a function of time measured in bins of 1s (J = 1s). (F and G) 〈a_j〉_off ± σ_j, the black sign corresponds to 〈a_j〉_off, and the blue sign corresponds to ±σ_j, as a function of t with J = 1 s (F), and the corresponding Δ_j (G). In all figures, [S] = 1.4 μM.

To get ϕ_off(t) and ϕ_on(t), the photon count trajectory 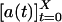(Fig. 1 A–C), where a(t) is a random photon count value at time t ≡ iΔt (Δt = 1 ms) and X is the measurement time (length of the trajectory), is transformed into a two-state (digital) trajectory. This transformation should be performed by applying on the trajectory a threshold photon count value a^*. Namely, by using a^*, the two states composing the trajectory were separated, so that each a(t) was attributed either to an off state, a_off(t) for a(t) < a^*, or an on state, a_on(t) for a(t) ≥ a^*. To estimate a^*, we constructed the stationary histogram of the recorded photon counts P(a) (Fig. 1D). P(a) was composed of two contributions, a peaked off-state noise part and a monotonically decaying on-state part. The noise off-state part of P(a) was fitted with a Poisson PDF (although a Gaussian PDF fits equally well this part). The noise off-state part did not provide any information about the enzymatic process because it originates from background processes. The on-state part of P(a) was fitted by an exponential decay. This part did supply information about the enzymatic activity because it reflected the escape of the “newly formed” fluorescent product molecule from the enzyme and its vicinity. For example, the combination of an exponential on-state waiting time PDF and a Poissonian photon statistics leads to an exponential decay photon counts per bin for a wide range of parameters (O.F. and J.K., unpublished data). In this sense, P(a) shape supports the two-state picture. Now, the intersection between the two fitting functions of the two parts of P(a) can provide estimation for a^* (Fig. 1D). However, another complication prevents such a straightforward use of a^*. This complication is the increase in the noise level as the reaction progresses, which is attributed to the accumulation of the product molecules. To handle this issue, we performed a separate local treatment on the photon count trajectory to transform it into a digital trajectory. The photon count trajectory was divided into L intervals of duration J = X/L = 1 s. In each 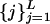interval, the average 〈a_j〉_off and standard deviation 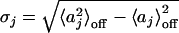of the off-state photon counts were calculated by using first 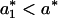. Defining 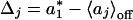and δ_j = σ_j/Δ_j, iterations were performed in each j interval until the local threshold 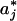was such that the inequality Δ₁ - δ_j ≤ Δ_j ≤ Δ₁ + δ_j was fulfilled. Δ₁ was chosen as a reference value because it defines a zero product trajectory accumulation. We note that 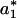was chosen to be smaller than the intersection value because P(a) already contains contribution from the product accumulation. For example, to transform the trajectory shown in Fig. 1 A–C into a digital trajectory, we used several values for 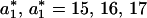= 15,16,17, in the algorithm presented above. All three values for 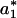led to digital trajectories with the same statistical properties.

By using the above algorithm, we fixed the difference between the average of the off photon counts and the threshold value along the trajectory within some small fluctuations window, whose width was set by the local features of the j interval. This algorithm resulted in a shift (on average) of the threshold to higher values as the reaction progressed (Fig. 1E) (j increased) while taking into account the basic characteristics of the noise part of P(a). Shown in Fig. 1 F and G are 〈a_j〉_off ± σ_j and Δ_j, respectively.

When applying this method, the photon count trajectory is translated into a digital trajectory whose statistical properties can be analyzed. We stress that the threshold value method used here provides reliable results for ϕ_off(t) and ϕ_on(t) for a fairly wide range of photon count parameters (O.F. and J.K., unpublished data).

Statistical Analysis of the Digital Trajectory

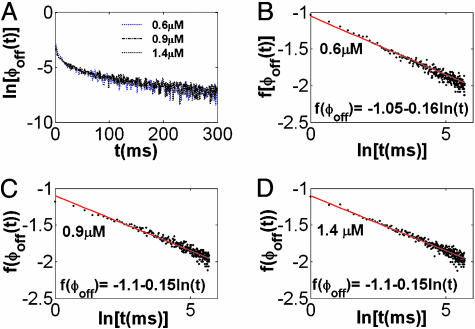
The digital trajectory is characterized by the random process 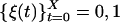, made of on, ξ = 1, and off, ξ = 0, values. ϕ_off(t) and ϕ_on(t) can be constructed by building a histogram from the time durations of the corresponding events along the trajectory. Fig. 2A shows ϕ_off(t) on a ln-linear scale for a set of three different substrate concentrations, [S] = 0.6, 0.9, and 1.4 μM, demonstrating that the relaxation patterns are nonexponential. All of the three curves correspond to the kinetic behavior of the same lipase molecule, obtained by the sequential addition of substrate while monitoring the enzymatic activity for ≈30 min for each [S]. The best fit for these curves is found to be a normalized stretched exponential function (23),

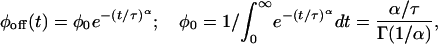[1]

where Γ(·) is the gamma function (24), and the value of the normalization factor, ϕ₀, is valid when assuming that the stretched behavior characterizes the process for all times (namely, for t → ∞). The stretching exponent α and the parameter τ are independent of [S] within the investigated range, α = 0.15 and τ = 1.15 μs (see Fig. 2 B–D). Note that the pair α and τ, rather than each of these parameters alone, is the relevant quantity, which can be seen when calculating, for example, the average off-state duration time: .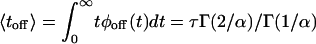

Fig. 2.

The off-state waiting time PDFs. (A) A ln-linear scale plot of the off-state waiting time PDF emphasizes its nonexponential relaxation pattern. (B–D) ϕ_off(t) for a set of three different substrate concentrations [S] = 0.6, 0.9, and 1.4 μM, shown in B, C, and D, respectively. Also shown are the corresponding fitting functions. Here f[ϕ_off(t)] =-ln{-ln[ϕ_off(t)]} is plotted vs. ln(t), where the slope corresponds to the exponent -α, the stretching exponent. For all curves the normalization used was such that ϕ_off(t = 0) = 1, chosen for a convenient parameters extraction.

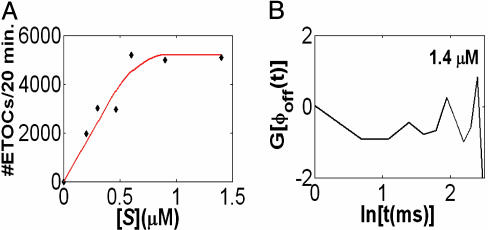
To check the insensitivity of the ϕ_off(t) shape to the substrate concentration for values >0.6 μM, we plotted the number of ETOCs per 20 min as a function of [S]. As shown in Fig. 3A, we observed a saturation profile for this quantity, which reaches its plateau at [S] = 0.6 μM. This observation supports the argument that the stretched exponential decay pattern does not originate, for these concentrations, from anomalous diffusion of the substrate to the enzyme vicinity but reflects an intrinsic feature of the enzymatic activity.

Fig. 3.

The stretched behavior from many subprocesses, which are [S]-independent. (A) A plot of the number of ETOCs during a period of 20 min, as a function of the substrate concentration [S]. The plot reveals a saturation profile similar to that observed for enzymes in solution. Saturation is reached at ≈0.6 μM. The red curve is drawn to guide the eye. (B) The logarithmic derivative (natural log) of ϕ_off(t), G[ϕ_off(t)], for [S] = 1.4 μM displays oscillations, which implies a multiexponential off-state process.

Information about the ETOC mechanism can be obtained by a closer examination of the behavior of ϕ_off(t). We gained insight into the origin of the stretched exponential off-state behavior by plotting the logarithmic derivative of ϕ_off(t), G[ϕ_off(t)] ≡ ∂ ln[ϕ_off(t)]/∂ln(t). Fig. 3B shows that G[ϕ_off(t)] displays oscillations when plotted against ln(t). In principle, such behavior implies that the observed process consists of a spectrum of simple events, each contributing an exponential factor to the overall decay process, where the time scales of these exponentials exhibit some scaling (25). Here, we cautiously interpret the oscillations in G[ϕ_off(t)] as an indication that the off state consists of a sum of exponential terms (parameter extraction would be too speculative in our case).

The waiting-time PDF of the on state, ϕ_on(t), displays a fast decay spanning only a few milliseconds, independent of [S] (data not shown). Being [S]-independent is the expected behavior, as each on event is terminated when the product diffuses away from the enzyme vicinity, a process that should indeed be [S]-independent. We approximate ϕ_on(t) by ϕ_on(t) ≈ κe^-κt with κ^-1 = 1 ms. Deviations from exponential decay are possible, but the fast decay (κ^-1 = Δt) prevents a more accurate fitting.

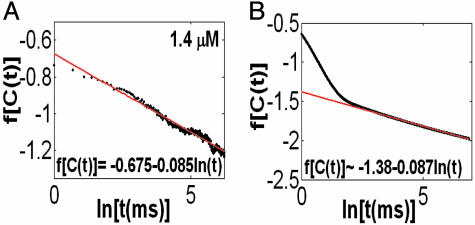
In addition to the calculations of the waiting-time PDFs of the two states, one can compute directly from the experimental trajectory the state-correlation function, C(t) = 〈Δξ(t)Δξ(0)〉/〈Δξ²〉, where Δξ(t) = ξ(t) - 〈ξ〉. This function is the bulk relaxation function (O.F., J.K., and A. Szabo, unpublished data). The decay pattern of C(t) is also a stretched exponential over three time decades, 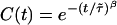, with β = 0.085 and 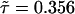μs (Fig. 4A). Now, the state-correlation function obtained directly from the experimental trajectory can be confronted with a theoretical state-correlation function for a two-state semi-Markov (TSSM) process. The Laplace transform 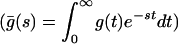of C(t) for a TSSM process with arbitrary waiting time PDFs is known (26–28),

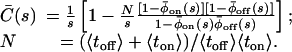[2]

The theoretical TSSM C(t) can be calculated by inverting Eq. 2 with the Laplace transform of the experimental ϕ_off(t) and ϕ_on(t). This function is shown in Fig. 4B by numerically inverting Eq. 2 (using the algorithm by K. J. Hollenbeck called INVLAP.M, 1998). The theoretical TSSM C(t) displays a stretched exponential decay pattern with an exponent β = 0.0876 and 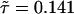ns. The discrepancy at the short time regime of the two state-correlation functions might be related to the estimation of ϕ_on(t). The different 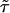values, however, indicate that the system is not fully described as a TSSM process, which means that there are correlations between successive events (O.F., J.K., and A. Szabo, unpublished data). Indeed, we show below that such correlations exist, by considering a different trajectory that displays the chronologically ordered time duration of the off-state events (Fig. 5A). On this trajectory, the height of the i^th line corresponds to the time duration of the i^th off event, where the events appear in the same order of their occurrence in the original time-series. A nontrivial correlation function calculated from this trajectory, which was used in ref. 6, and treated theoretically in O.F., J.K., and A. Szabo (unpublished data) and in refs. 29–31, serves, in principle, as an indication for conformational changes. In our case, the second point of such correlation function, which measures the correlation between successive events, 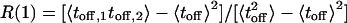, has a value of R(1) = 0.35. However, it is difficult to relate this quantity to the details of a kinetic scheme (see below). Nevertheless, by using an alternative analysis method of the ordered off waiting times trajectory, we extract more precise information about the ETOC mechanism.

Fig. 4.

The state–correlation functions. (A and B) Both the experimental (A) and theoretical (B) autocorrelation function C(t) display a stretched exponential decay pattern [f(·) is defined in Fig. 2], with similar stretching exponent values but different 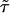values. See text for discussion.

Fig. 5.

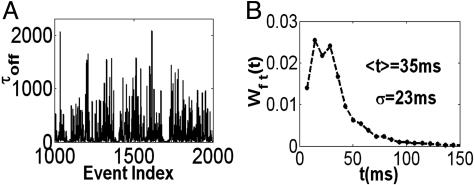
The ordered off waiting times trajectory. (A) The trajectory of the time durations of the off-state events as a function of chronological event index for [S] = 1.4 μM. Noticeable along this trajectory are groups of successive fast events (each event in the group has a τ_off value of <35 ms). (B) The histogram of the time durations of the groups of successive fast events, W_ft(t). W_ft(t) estimates the PDF to occupy a fast conformation (or conformations) for a time duration t before conformational changes occur.

Observing the ordered off waiting times trajectory, we noticed local trends (for all three concentrations) where events of similar short durations followed each other. Namely, along this trajectory fast events (each event is faster than 35 ms) were clustered together, with an average of 3.5 (±1.1) events per group and an average duration time of 10 (±2) ms per event in the group. Binning the times of the fast successive events in each group, we obtained a set of random variables from which we constructed a histogram denoted by W_ft(t) (Fig. 5B). This histogram should be interpreted in view of a kinetic model. When considering our findings, the most natural choice for a kinetic model is the fluctuating enzyme model (Fig. 6A). With this model in mind, W_ft(t) estimates the PDF to occupy a fast conformation (or conformations) for an overall duration t, in which several on/off cycles can occur, before conformational changes to a slow conformation is taking place.

Fig. 6.

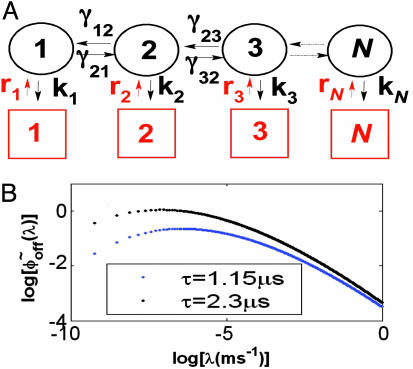
The fluctuating enzyme model and the generalized density of rates. (A) A schematic model of the enzymatic process. The off state consists of a spectrum of N-coupled substates. Also indicated are the coupling rates between the conformations and the enzymatic reaction rates. (B) 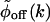for a stretched exponential ϕ_off(t) with α = 0.15 and τ = 1.15 μs, blue curve, and with α = 0.15 and τ = 2.3 μs, black curve.

Modeling

Consider a Michaelis–Menten type of model of a three-stage reaction mechanism (13),

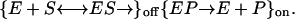The symbols E, S, and P stand for the enzyme, substrate, and product molecules, respectively, and the symbols ES and EP stand for the enzyme–substrate and enzyme–product complexes, respectively. In this model, the first two stages, which are the formation of the complex ES and the transformation of the substrate into product, constitute the off state. The third stage, which is the escape of the product away from the enzyme and its vicinity, constitutes the on state. The off waiting time PDF for this model does not lead to a stretched exponential waiting time PDF. In particular, given a high enough substrate concentration, the expression for ϕ_off(t) is simply a biexponential [the expression for ϕ_on(t) is a single exponential]. Thus, the observed trajectory requires going beyond the Michaelis–Menten type of description. As known from other systems (23, 25, 32, 33), a stretched exponential decaying pattern can arise from contributions of a large number of weighted exponentials. In the present case, the stretched exponential decay pattern of ϕ_off(t) serves as an indication that the system exhibits dynamic disorder. In other words, the ϕ_off(t) form, which is [S]-independent over some concentration range, indicates that a spectrum of enzymatic conformations is involved in the catalytic activity. Any suggested model should incorporate this feature.

We therefore consider a model that involves simultaneously enzymatic activity and conformational changes. The model describes an off state that consists of a broad spectrum of conformational substates, with nearest neighbors connectivity (Fig. 6A). The dynamics of the conformational changes are governed by the coupling rates γ_m±1m, where γ_m±1m is the coupling rate from conformation m to m ± 1. Each of these conformations is active and can react with a reaction rate k_m for substate m. This picture is consistent with experiments that probe conformational changes in proteins and report on fingerprints of a large number of conformations (11). While conformational fluctuations take place, the enzyme–substrate complex is formed, where similar to the experimental conditions [S] is large enough to have always a substrate molecule in the vicinity of the enzyme; namely, [S] does not play a role in the dynamics of the off stage. Once the enzyme–substrate complex is formed the enzyme can react, transforming the substrate into a product, which terminates the off state. If we assume that the transformation of the substrate into a product is a fast process relative to the formation of the complex itself or its dissociation, then the appropriate kinetic scheme that underlies the studied enzymatic activity is the fluctuating enzyme model shown in Fig. 6A, where rate k_m can be still defined as a reaction rate of the enzymatic activity. The information extracted from the off ordered waiting times trajectory (the average number of successive fast events and the average time duration of a fast event) can be related to the average reaction rate of the fast conformations, 〈k〉_fast ≈ (8 ms)^-1, and the average fluctuation rate from slow to fast conformations, 〈γ〉_fast→slow ≈ (45 ms)^-1 (O.F., J.K., and A. Szabo, unpublished data).

The on-state time durations start when the product is formed and last until it escapes from the enzyme and its vicinity. If the formation of the product took place from conformation m in the off state, the escape process occurs with a reaction rate r_m, where we require r_m = κ for an exponential ϕ_on(t). We assume that conformational changes in the on state do not occur during occupying the on state, or, alternatively, the coupling rate values are small compared with κ (which is in fact the case if we consider 〈γ〉_fast→slow as an estimation of the fluctuating rate in the on state as well).

To relate ϕ_off(t) to the fluctuating enzyme model, we write the expression for ϕ_off(t) as, ϕ_off(t) = AΣ_mω_me^-λ_mt, where A is a normalization constant, the sum is taken over all possible substates, and ω_m and λ_m are the weights and relaxation rates, respectively. Because of the coupling between the off substates, the dependence of ω_m and λ_m on m involves all of the γ_m±1m's and the k_m's. The continuum representation of ϕ_off(t) for a large number of substates is given by

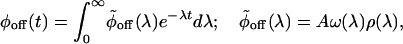[3]

where we introduce the density of rates, ρ(λ). Hence, 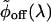is the inverse Laplace transform of ϕ_off(t) (34, 35) and serves as a generalized density of rates. Fig. 6B shows the broad monopeaked 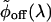obtained by numerically inverting the stretched exponential ϕ_off(t), with α = 0.15 and τ = 1.15 μs, blue curve, and α = 0.15 and τ = 2.3 μs, black curve. Both curves display a power law asymptotic decay pattern, 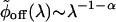, which is obtained by using the Tauberian theorem (36) for large enough λ values. In a recent article (12), a peaked distribution of reaction rates was extracted from single T4 Lysozyme TOC trajectories (≈50), lasting ≈20 s. In our studies, each of the trajectories was long-lasting (≈30 min) and consisted of contributions from the entire distribution, which leads to the nonexponential decay pattern of ϕ_off(t).

Concluding Remarks

Nonexponential behavior of biomolecules has been obtained in several systems (11, 32, 33). Here, we report on a direct observation on the single-molecule level of a stretched exponential off waiting time PDF in the enzymatic catalytic activity of lipase B from Candida antarctica, ϕ_off(t) ∼ e^-(t/τ)0.15 (τ ≈ 1 μs). Searching for the origin of the stretched behavior, we ruled out the possibility of an external source such as the substrate concentration. The oscillations in the function G[ϕ_off(t)] forced us to the conclusion that the off process is composed of a large number of subprocesses, which we interpreted as a spectrum of conformations, each of which contributes an exponential factor to the overall decay process. By confronting the experimental state-correlation function, C(t), with a theoretical state-correlation function for a TSSM process with the experimental ϕ_on(t) and ϕ_off(t), we concluded from the different behavior of these functions [in both cases 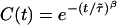with similar β values (=0.085) but with 3 orders of magnitude difference in the values of 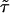] that the underlying mechanism cannot be described as a TSSM process and that correlations between events exist. Indeed, the trajectory of the off time durations exhibited local trends of bunched fast events. We were, thus, led to describe the observed enzymatic activity by the fluctuating enzyme model (Fig. 6A). In light of this model, average values for the coupling and reaction rates were estimated, 〈γ〉_fast→slow ≈ (45 ms)^-1 and 〈k〉_fast ≈ (8 ms)^-1, respectively.

The analysis presented here is related to two basic questions in the context of two-state single-molecule trajectories: (i) what is the maximal amount of information that can be extracted from two-state trajectories about the underlying kinetic schemes; and (ii) how should the information be extracted? The case of single lipase molecules provided an example for dealing with these questions. A detailed theoretical treatment of what can be learnt from two-state single molecule trajectories will be published elsewhere (O.F., J.K., and A. Szabo, unpublished work).