Inference on the Genetic Basis of Eye and Skin Color in an Admixed Population via Bayesian Linear Mixed Models

Abstract

Genetic association studies in admixed populations are underrepresented in the genomics literature, with a key concern for researchers being the adequate control of spurious associations due to population structure. Linear mixed models (LMMs) are well suited for genome-wide association studies (GWAS) because they account for both population stratification and cryptic relatedness and achieve increased statistical power by jointly modeling all genotyped markers. Additionally, Bayesian LMMs allow for more flexible assumptions about the underlying distribution of genetic effects, and can concurrently estimate the proportion of phenotypic variance explained by genetic markers. Using three recently published Bayesian LMMs, Bayes R, BSLMM, and BOLT-LMM, we investigate an existing data set on eye (n = 625) and skin (n = 684) color from Cape Verde, an island nation off West Africa that is home to individuals with a broad range of phenotypic values for eye and skin color due to the mix of West African and European ancestry. We use simulations to demonstrate the utility of Bayesian LMMs for mapping loci and studying the genetic architecture of quantitative traits in admixed populations. The Bayesian LMMs provide evidence for two new pigmentation loci: one for eye color (AHRR) and one for skin color (DDB1).

Variation in eye and skin color may be particularly apparent in admixed populations, especially those formed from ancestral populations with large differences in these phenotypes. Pigmentation is a diverse phenotype in humans, with most of the variation attributable to differences in the amount, type, and distribution of melanin: a broad term for a set of biopolymers synthesized by melanocytes (Jablonski and Chaplin 2000; Parra 2007). The genetic basis for human pigmentation diversity is yet to be fully understood, but evidence suggests that natural selection shaped the modern distribution of human pigmentation to be a balance between favoring dark skin near the equator to protect from folate deficiency and sunburn, and lighter skin at higher latitudes to allow for optimal vitamin D synthesis (Parra 2007). Genome-wide association studies (GWAS) provide an avenue to further understand the genetic mechanisms underlying this variation. However, GWAS have been predominantly performed in European populations, with other ancestral groups and admixed populations underrepresented (Need and Goldstein 2009; Bustamante et al. 2011). Aside from data availability, one key concern for GWAS in admixed populations is the control of spurious associations due to population structure. The large GWAS data sets currently being generated by the genomics community are likely to span multiple ancestral groups, and thus methods that can control for spurious associations in such data sets are of great interest.

There are many methods for correcting for population structure when performing GWAS, with genomic control (Devlin and Roeder 1999), regression control (Wang et al. 2005; Setakis et al. 2006), and principal component (PC) adjustment (Zhang et al. 2003; Price et al. 2006) being the most common approaches. These methods perform well for populations with simple population structure but may perform poorly when the relatedness structure is more complex or in the presence of cryptic relatedness (Zhao et al. 2007). Linear mixed models (LMMs) have been shown to be effective at controlling for population structure and cryptic relatedness in GWAS; however, they often only consider individual single nucleotide polymorphisms (SNPs) in isolation (Gianola et al. 2009; Vilhjálmsson and Nordborg 2013; Yang et al. 2014; Loh et al. 2015b). LMMs that jointly model marker effects may further increase power in structured populations by capturing the effect of the causal variant using multiple markers. Segura et al. (2012) proposed a multi-locus LMM approach that uses a stepwise selection algorithm to jointly capture weak effects, while Rakitsch et al. (2013) combined the Lasso (Tibshirani 1996) with the LMM to provide an efficient multi-locus method. Both methods observed higher power and a lower false discovery rate (FDR) than single-locus approaches for mapping. Extensions of the standard LMM, which assumes a single normal distribution on genetic effects, have been made from a Bayesian perspective to include alternative distributions on the genetic effects, and have been applied extensively in the plant and animal breeding literature (Meuwissen et al. 2001; Habier et al. 2011; Erbe et al. 2012; Zhou et al. 2013). Bayesian LMMs (BLMMs) are capable of modeling all markers jointly and have been shown to perform better in prediction than the standard LMM when the genetic architecture of a trait deviates from the infinitesimal model (Goddard et al. 2010; Moser et al. 2015). Recent implementations of BLMMs are capable of performing genome-wide analyses on a large number of individuals (Zhou et al. 2013; Moser et al. 2015).

We demonstrate the utility of BLMMs for gene discovery by applying them to eye and skin color phenotypes for individuals from Cape Verde, an island nation off West Africa that is home to individuals with large variation in eye and skin color due to the mix of West African and European ancestry. Beleza et al. (2013) performed GWAS on the Cape Verde data set, using principal component adjustment to correct for population structure (using the first three PCs). In addition, Beleza et al. (2013) carried out conditional analyses for the most significantly associated SNPs, linear regression adjusting for African ancestry and island of birth, and a mixed effect model implemented in the EMMAX software (Kang et al. 2010). All three methods used in Beleza et al. (2013) pointed to the same set of genetic loci found in the original PC-adjusted association analysis.

In this work, we apply three recently published BLMM methods – Bayes R (Erbe et al. 2012; Moser et al. 2015), Bayesian sparse LMM (BSLMM) (Zhou et al. 2013), and BOLT-LMM (Loh et al. 2015b) – to the unique Cape Verde data set. All three methods can perform gene discovery, variance component estimation, and prediction simultaneously, and assume different priors on the marker effects. This allows for a variation of the assumptions of the infinitesimal model, which is unlikely to hold for the eye and skin color phenotypes present. We explore the potential of BLMM approaches to yield improved power to detect associations in GWAS, particularly in cases where there is substantial confounding due to population structure or cryptic relatedness. Using real genotypes from the Cape Verde data set, we simulate both moderate and highly heritable phenotypes with genetic architectures that contain both small and large effects to demonstrate how BLMM methods can be adapted to identify new quantitative trait loci (QTL) from GWAS. We apply these methods to the Cape Verde data set and identify two additional loci that likely contribute to variation in eye and skin color.

Materials and Methods

Methods overview

The BLMM methods used in this study possess different implementations of a similar underlying model, i.e., the LMM with a finite mixture of normal distributions used to model the underlying distribution of marker effects. Bayes R (Erbe et al. 2012; Moser et al. 2015) and BSLMM (Zhou et al. 2013) estimate the effects of all markers jointly as random effects, and use Markov chain Monte Carlo (MCMC) to obtain approximate samples from their posterior distribution given the observed data. Methods that use multiple markers to jointly capture the causal QTL effect often lead to higher power and a lower FDR than single marker approaches (Segura et al. 2012; Rakitsch et al. 2013; Moser et al. 2015). Alternatively, BOLT-LMM (Loh et al. 2015b) uses a mixture of two Gaussian distributions to model the marker effects and uses a fast variational approximation to compute approximate phenotypic residuals, with each single marker then evaluated for association with the residuals via a retrospective score statistic. This method is more powerful than standard single marker regression (as are other similar LMM methods) and provides a bridge between Bayesian modeling and the frequentist association testing framework (Loh et al. 2015b). It is thus a good candidate for comparison with the fully Bayesian methods. Furthermore, BOLT-LMM differs from Bayes R and BSLMM in that associated evidence is assessed for each marker using a P-value, whereas Bayes R and BSLMM summarize the evidence of association via the posterior inclusion probability, which is the probability that the marker is associated with the trait given the data. For multiple-regression models (Bayes R and BSLMM), markers at a locus jointly capture the QTL effect and thus the association signal is best evaluated on genomic windows (1 Mb for example) (Fan et al. 2011; Fernando 2017). We utitlize a window-based method for discovering QTL that rests on the idea that the true associations are those that contribute the most to the total genetic variation irrespective of whether some proportion of this genetic variation is potentially due to confounding. We validate these methodological concepts through simulation and via application to the Cape Verde data set.

Cape Verde data set

The Cape Verde data set (Beleza et al. 2013) consists of 625 individuals with high-quality digital eye photographs and 684 individuals with skin reflectance measurements and genotypes. For eye color, Beleza et al. (2013) developed a new measure based on automated analysis of digital photographs that captures the full range of African-European eye color variation. For skin color, reflectance spectroscopy was used on the upper inner arm to calculate a modified melanin index. Genotype quality control was performed as per Beleza et al. (2013), but with a minor allele frequency (MAF) threshold of 0.02 resulting in 858,510 autosomal SNPs. Phenotypes were centered and scaled (by their SD) before regressing the phenotypes on sex and taking the residuals as the new phenotype. The distribution of the eye and skin phenotypes (standardized to mean 0 and variance 1) showed deviation from normality (Supplemental Material, Figure S1 in File S1). Thus, the continuous phenotypes for eye and skin color were transformed using a rank-based inverse normal transformation (Blom 1958).

To explore the level of admixture in the Cape Verde data set, we visualized the first two projected PCs [implemented in the software of Chen et al. (2016)] relative to the HapMap 3 (International HapMap 3 Consortium et al. 2010) European and African ancestry cohorts (Figure S2 in File S1). Furthermore, to investigate the relatedness of individuals in these data we summarized the diagonals and off diagonals of the genetic relationship matrix, which was estimated using genome-wide marker data in the GCTA software (Yang et al. 2011). For comparison, we also estimated the genetic relationship matrix of a random subset of 685 individuals from a homogeneous European population from the Atherosclerosis Risk in Communities (ARIC) Study (dbGaP accession number phs000090.v1.p1). A summary of the diagonals and off diagonals of the genetic relationship matrix for both populations shows much greater variance in the Cape Verde population than the European population (Figure S3 and Table S1 in File S1). The maximum value of the genetic relationship matrix off diagonals of the Cape Verde population is ∼0.25 suggesting that the population is not made up of solely unrelated individuals (Figure S3 in File S1).

Model statement

For each of the methods, the following linear model is used to relate phenotypes $y$ to genotypes $X$

$$y={\mathbf{1}}_n\mu +X\mathit{\beta }+\epsilon ,$$ (1)

where $y$ is a vector of phenotype values from n individuals, $X$ is an $n\times m$ matrix of genotypes measured for each individual, $\mathit{\beta }$ is a vector of m genetic effects to be estimated, ${\mathbf{1}}_n$ is a vector of size n of ones, μ represents the common phenotypic mean, and $\epsilon$ is a vector of size n from distribution $MVN\left(0,{\sigma }_e^{2}I\right),$ where $I$ is the identity matrix. The elements of $X$ are 0, 1, 2 encoded genotypes and represent the counts of the reference allele at each of m markers. Whether the columns of $X$ are centered and/or standardized depends on the method used, with Bayes R mean standardized and scaled to have variance 1, BSLMM mean centered only, and BOLT-LMM mean centered and standardized to have common variance (Loh et al. 2015b). Standardizing the columns of $X$ corresponds to making an assumption that rarer variants have larger effects than common variants (Zhou et al. 2013). To provide a baseline for comparison with the results generated by the BLMMs, associations between each SNP and the phenotypes (adjusted for sex) were assessed using the marginal regression model (i.e., standard GWAS). Similar to Beleza et al. (2013), the first 10 PCs were fitted as covariates to adjust for population stratification with the analyses performed using the PLINK 2 software (Chang et al. 2015).

Bayesian linear mixed models

Bayes R:

Erbe et al. (2012) were the first to present the Bayes R method, which uses a Bayesian hierarchical linear random regression model and poses the following four component mixture priors for each SNP effect in model (1):

$${\beta }_j\sim {\pi }_{1}N\left(0,0\times {\sigma }_g^2\right)+{\pi }_{2}N\left(0,{10}^{-4}\times {\sigma }_g^2\right)+{\pi }_{3}N\left(0,{10}^{-3}\times {\sigma }_g^2\right)+{\pi }_{4}N\left(0,{10}^{-2}\times {\sigma }_g^2\right),$$ (2)

where $j\in \left(1,\dots ,m\right)$ is an index over the SNPs, ${\sigma }_g^2$ is the additive genetic variance explained by SNPs, and ${\pi }_1$ is the proportion of SNPs that have no effect. In practice, the true distribution of genetic effects is not known and thus one of the strengths of this prior is its flexibility to approximate various underlying distributions. Depending on prior knowledge or cross-validation, the model can accommodate fewer or >4 components and larger variance classes (i.e., changing the multiplier of ${\sigma }_g^2$ for any of the mixture components ${10}^{-2}\to {10}^{-1}$ for instance). The model fits all SNPs simultaneously, which accounts for linkage disequilibrium (LD) between SNPs, and increases power to detect associations (as do other methods) (Erbe et al. 2012; Moser et al. 2015). The model also induces sparsity via the first component of the mixture, thus fitting with the hypothesis that not all markers are in LD with a causal variant. Moser et al. (2015) incorporated a hyper-parameter for the variance explained by genome-wide SNPs, ${\sigma }_g^2,$ which allows for the proportion of phenotypic variance explained by genotyped SNPs (PVE) to be estimated from the data, rather than fixing it prior to analysis as in Erbe et al. (2012).

BSLMM:

BSLMM (Zhou et al. 2013) summarizes the two ends of the spectrum with respect to the assumption of the distribution of genetic effects, where the LMM assumes every variant has an effect, and the sparse BLMM assumes that a very small proportion of variants have an effect. Zhou et al. (2013) highlight that the relative performance of BLMMs would vary depending on the true underlying genetic architecture of the phenotype. BSLMM is a hybrid approach that includes the LMM and sparse regression model as special cases and is capable of learning the genetic architecture from the data. Additionally, BSLMM makes estimation of this type tractable for reasonably large data sets using linear algebra tricks for LMMs. Bayes R and BSLMM report the posterior probability that a polymorphic site affects the trait conditional on the data, which is a very natural statistic to interpret in the context of QTL identification. For these methods, the posterior inclusion probability (PIP) summarizes the number of times a locus was present in the model.

Zhou et al. (2013) assume that ${\beta }_j$ from Equation (1) comes from a mixture of two normal distributions:

$${\beta }_j\sim \pi N\left(0,\left({\sigma }_a^2+{\sigma }_b^2\right)/\left(m\tau \right)\right)+\left(1-\pi \right)N\left(0,{\sigma }_b^2/\left(m\tau \right)\right);$$

where setting $\pi =0$ yields the LMM, and setting ${\sigma }_b=0$ yields the sparse regression model in which a subset of SNPs is assumed to have no effect (noninfinitesimal model), m is the number of genetic markers, and τ is the reciprocal of the residual variance. This model can be interpreted as all variants have at least a small effect, which are normally distributed with variance ${\sigma }_b^2/\left(m\tau \right),$ and some proportion π of variants that have an additional effect that is normally distributed with variance ${\sigma }_a^2/\left(m\tau \right).$

BOLT-LMM:

BOLT-LMM (Loh et al. 2015b) relaxes the assumptions of the infinitesimal model by using a mixture of two Gaussian distributions as the prior on ${\beta }_j$ in Equation (1), giving the model greater flexibility to accommodate SNPs of large effect while maintaining effective modeling of genome-wide effects (for example, ancestry). The noninfinitesimal component amounts to a generalization of the standard mixed model, which places a spike-and-slab mixture of two Gaussian priors on SNP effect sizes i.e.,

$${\beta }_j\sim \pi N\left(0,{\sigma }_1^2\right)+\left(1-\pi \right)N\left(0,{\sigma }_2^2\right),$$

where π is the mixing proportion and ${\sigma }_1^2$ and ${\sigma }_2^2$ the variances of the two Gaussians. This assumption gives the model greater flexibility to accommodate SNPs of large effect while modeling genome-wide effects. Loh et al. (2015b) note that it is important that the spike component have nonzero variance to capture genome-wide ancestry or relatedness effects. When testing SNPs for association, effects attributed to the random component, for all other chromosomes except that of the SNP being tested [also referred to as a leave one chromosome out (LOCO) approach (Yang et al. 2014)], are conditioned out from the phenotype and the final association is performed on the residuals of this conditioning step, which protects against confounding (Loh et al. 2015b). BOLT-LMM uses a variational approximation to fit Bayesian linear regressions for the Gaussian mixture priors rather than MCMC as in Bayes R and BSLMM. BOLT-LMM uses cross-validation to estimate hyper-parameters for the variational algorithm, rather than relying on variational approximate log-likelihoods, because it was found to be more robust to slackness of the variational approximation caused by LD (the variational approximation is a good approximation when the SNPs $X$ are independent; Carbonetto and Stephens 2012). BOLT-LMM could also be viewed as a hybrid methodology that applies a retrospective hypothesis test for association of the left-out SNPs with the residual phenotype. This is a key point of difference from Bayes R and BSLMM which report a PIP for each SNP, whereas BOLT-LMM retains the classical hypothesis test approach. Loh et al. (2015b) simulated phenotypes that included an ancestry effect and found that the BOLT-LMM chi-squared statistics were well calibrated in terms of ${\lambda }_{GC}$ and the mixed-model analysis achieved statistically significant gains in power over principal component analysis (PCA) across simulations. The genomic inflation factor ${\lambda }_{GC}$ is defined as the ratio of the median of the empirically observed distribution of the association test statistic to the expected median (from the ${\chi }_1^2$ distribution) (Devlin and Roeder 1999).

Implementation of BLMM methodology

For Bayes R [implemented in the software provided in Moser et al. (2015)], we assumed the prior in Equation (2) with a 5% largest class. Additional prior assumptions were made as per the default of the program provided in Moser et al. (2015). The 5% variance class was used because previous estimates of variance explained for large-effect loci from eye and skin color were of this order, as reported in Beleza et al. (2013). To monitor convergence of the MCMC chains, we ran two chains with 100,000 iterations and 20,000 burn iterations and another for 200,000 iterations with 40,000 burn in iterations, which included permuting the SNP order to improve mixing, and a thinning rate of 1 in every 10 iterations. We compared the results from the two chains, and investigated the agreement between the estimates of the PVE and the rank of the top regions for both eye and skin color. For BSLMM, we similarly ran a short and long chain, one with 1 million iterations with 100,000 burn in (program default) and a longer chain of 2 million iterations with 100,000 burn in. When implementing the BOLT-LMM software, an LD score table is required. The LD score table was generated for the Cape Verde data set using the available software (Bulik-Sullivan et al. 2015). This table was subsequently used when running the BOLT-LMM program.

Association inference from BLMMs

To make inferences about associated loci from Bayes R we follow the work of Fernando and Garrick (2013) and Fernando (2017), where the strength of association is tested for every nonoverlapping 1-Mb window. Fernando and Garrick (2013) outline that because BLMMs fit all markers simultaneously, markers that are in high LD are likely to jointly capture the association signal rather than attribute the signal to any one SNP within a locus. Therefore, inference from these methods is best made on genomic windows rather than on individual markers. To construct a posterior distribution for the proportion of genetic variance explained by markers in a genomic region we divide the genome into 1-Mb nonoverlapping regions. For each iteration t of the MCMC chain we calculate for each window $w\in \left(1,\dots ,W\right)$ the genetic variance ${\sigma }_{g_{\left(w\right)}}^{2\left(t\right)}=\mathrm{Var}\left(X_w{\mathit{\beta }}_w^t\right),$ where $X_w$ is the matrix of SNPs in the window and ${\mathit{\beta }}_w^t$ the estimated effects for the SNPs in the window. Additionally, for each iteration we calculate the total genetic variance as ${\sigma }_g^{2\left(t\right)}=\mathrm{Var}\left(X{\mathit{\beta }}^t\right).$ The ratio between the window variance and total genetic variance for each iteration t:

$$r_w^t=\frac{{\sigma }_{g_{\left(w\right)}}^{2\left(t\right)}}{{\sigma }_g^{2\left(t\right)}}$$

defines the proportion of the total genetic variance explained by the window. We form the posterior distribution for $r_w^t$ by calculating this value for each of t iterations in the MCMC chain. We compute the posterior probability that a window w explains $>1\text{\%}$ (for example) of the total genetic variation by calculating the ratio of the number of iterations that $r_w^t>0.01$ divided by the total number of MCMC iterations T, which is defined to be the window posterior probability of association [WPPA; Fernando and Garrick (2013)]. It can be shown that using a threshold of $\mathrm{WPPA}=\alpha$ to conclude that a locus is associated with the phenotype will result in controlling the proportion of false positives (PFP) to be $<1-\alpha$ (Fernando and Garrick 2013; Zeng 2015). The posterior probabilities contributing to these calculations require that the priors placed on the unknown variables in the model are identical to those used to generate these variables (Fernando and Garrick 2013). Unfortunately, this is unlikely to be the case, but as data size increases the posterior distributions will become increasingly independent of the priors used. Controlling the PFP has the added benefits of it being independent of the number of tests performed and does not require independence of tests (Fernando et al. 2004). Bayes R allows for the nonzero SNP effects for each iteration to be saved to file, which facilitates these calculations post analysis.

BSLMM does not report the genetic effect from each MCMC iteration and thus we cannot implement a similar method of inference to that of Bayes R. However, Guan and Stephens (2011) suggest calculating the posterior expected number of SNPs in a window by summing the estimated PIPs for all genetic variants in that region (denoted WPIP). We use this measure to summarize the results from BSLMM at the levels of regions and compare with the inference from the WPPA.

Loci associated with ancestry

To examine the degree of allelic differentiation across the ancestral gradient of SNPs in the Cape Verde data set, we used the method presented in Galinsky et al. (2016), which generalizes a previous method for detecting allele frequency differences between subpopulations to populations with fractional ancestry. The method uses the SNP weights from PCA to calculate a statistic that measures the differentiation of each SNP along the ancestral gradient. Galinsky et al. (2016) outline that the statistic is calculated as the dot product $D_j=y_j{v}_k,$ where $v_k$ is the kth eigenvector of the normalized genotype matrix and $y_j$ is the jth normalized SNP. As per Galinsky et al. (2016), the set of $D^2$ statistics for all of p SNPs has a ${\chi }_1^2$ distribution after appropriate rescaling, which allows for hypothesis testing for each SNP to be performed. Inference can then be made about which loci are highly differentiated along the ancestral gradient. It is proposed that if the top associations for eye and skin color do not lie in the set of lowest P-values after multiple testing correction, then this is further evidence that the set of loci detected is less likely to be spurious due to structure. Additionally, we use the set of statistics to rank the set of genotype SNPs for use in simulating phenotypes that are correlated with ancestry. For highly associated SNPs (eye and skin color) we only report $D^2$ statistic P-values for PC one as it captures most of the ancestral differences (Figure S2 in File S1). Estimation of the first 10 PCs of the genotype matrix was performed using the flashpca software (Abraham and Inouye 2014).

Simulation study

The Cape Verde data provide an opportunity to understand the performance of the BLMM methods relative to standard methods in an admixed sample. Specifically, we wanted to assess how BLMMs perform in terms of gene discovery and PVE estimation, under simulated genetic architectures that are similar to those hypothesized for eye and skin color. We used the simulations to infer the PIP that allows for confidence in making statements about whether a 1-Mb window around the causal variant is associated with the trait conditional on the data. Each of the simulation scenarios used the real genotype data (n = 685) from Cape Verde.

Simulation one:

We developed four simulation scenarios: (1) 90% PVE with effects attributed to SNPs at random; (2) 90% PVE with effects assigned to SNPs that are associated with ancestry; (3) 50% PVE with effects attributed to SNPs at random; and (4) 50% PVE with effects assigned to SNPs that are associated with ancestry. A list of ∼18,000 independent loci was generated for sampling using the PLINK 2 software and the independent pairwise option with an LD threshold of 0.1. In scenario one, 50 genetic effects were sampled from two normal distributions with five of the variants sampled such that they explained a total of 40% of the phenotypic variance. Another 45 variants were sampled to explain 50% of the phenotypic variance and thus each phenotype had a PVE of 0.9. The high PVE was chosen to reflect the eye and skin phenotypes in the Cape Verde data set. These simulated phenotypes were designed to be similar (in expectation) to that of eye and skin color in that there are a few large genetic effects along with many smaller effects. Fifty phenotypes were simulated with Bayes R, BSLMM, and BOLT-LMM run for each realization. Bayes R was run with a 5% largest variance class to model the simulated loci of large effect. Additionally, a single SNP association analysis (analyzed in PLINK 2) corrected for 10 PCs was run for gene discovery comparison and a PVE estimation benchmark was carried out using the widely used GREML approach (Yang et al. 2010) in the GCTA software (Yang et al. 2011).

Scenario two retained the same proportions of phenotypic variance for the randomly sampled 5 and 45 causal loci (and PVE of 0.9) but placed genetic effects on loci that were differentiated across the admixture gradient (as outlined in the section Loci associated with ancestry). It was hypothesized [and supported by results in Beleza et al. (2013)] that eye and skin color are correlated with ancestry; therefore, in order to simulate these traits more realistically we generated 50 phenotypes by randomly selecting 50 loci that were associated with the first PC (implicitly assuming that PC one is a good proxy for ancestry as demonstrated in Figure S2 in File S1). To generate the list of SNPs, we took the list of $D^2$ statistics and subsetted it to those loci that had P-values $<1\times {10}^{-2}$ but $>1\times {10}^{-3}$ ($\approx 11,000\mathrm{SNPs}$). This list includes SNPS that were differentiated across the ancestral gradient but were not the “most” differentiated. This decision was made by investigating the $D^2$ statistic P-values for the top loci found in Beleza et al. (2013), which showed that most of the top loci were differentiated but with P-values $>{10}^{-3}.$ This list was further filtered by LD to independent loci using the PLINK clumping procedure. The final list of SNPs consisted of ∼3500 PC-one-associated SNPs. Again Bayes R (5% largest variance class), BSLMM, and BOLT-LMM were run for each realization with a single SNP association analysis (run in PLINK) corrected for 10 PCs and PVE estimation in the GCTA software completed for comparison. Simulation Scenarios Three and Four were a repeat of the first two but with the 45 small-effect loci explaining 30% of the phenotypic variance, the five large-effect loci 20%, and a PVE value of 0.5. For both of these simulations Bayes R was run with a 1% largest variance class as the causal loci explained less variance.

Methods were assessed across simulation scenarios for their ability to identify genomic regions containing simulated causal SNPs. Two performance measures were used to summarize the results namely: the true positive rate (TPR) for detecting a 1-Mb window containing a simulated causal variant and the FDR for detecting a 1-Mb window containing a simulated causal variant. For the BOLT-LMM and PLINK association analyses, a 1-Mb window was deemed to be a true positive if it contained an SNP that passed genome-wide significance and was a member of the simulated windows that contained a causal SNP. For Bayes R and BSLMM, a 1-Mb window was deemed to be a true positive if it had a WPPA (of explaining >1% of the genetic variance) or WPIP greater than a threshold α and was one of the simulated windows that contained a causal SNP. For each method, the TPR was calculated as the number of true positive regions/number of simulated regions containing a causal SNP. The FDR was calculated as the (number of regions that passed the threshold − number of true positives)/number of regions that passed the threshold. These measures were summarized for each scenario for all methods with different α thresholds on WPPA and WPIP for Bayes R and BSLMM explored.

Furthermore, we investigated the control of the PFP for varying thresholds on the Bayes R WPPA. To achieve this, for each α threshold on the WPPA in the set $\left(0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.95\right)$ we calculated the observed PFP across the 50 replicates for each simulation scenario. A region was declared a false positive if it passed the α WPPA threshold but did not contain a simulated causal variant.

Simulation two:

In the second simulation we focused on investigating the PVE for large-effect loci and again summarized the ability of each method to estimate total PVE with an altered genetic architecture. This simulation investigated the hypothesis that confounding contributes less to loci that explain a substantial amount of the genetic variance. The sum of the contribution of only highly associated regions is but a portion of the total genetic variance because it ignores the contribution from loci that may explain genetic variance but do not show strong evidence for association. Therefore, it is hypothesized that the sum of the estimated PVE for highly associated regions should be a reasonable lower bound to the total PVE for a trait and should be relatively free of confounding. We test this hypothesis with simulation in order to guide the conclusions made about the contribution to PVE for the top loci detected for eye and skin color in the Cape Verde population.

The four scenarios in simulation two, were a repeat of simulation one in terms of PVE values and effect assignment to loci. However, for each of the four scenarios we place 1005 causal variants throughout the genome. For scenario one, five variants were chosen at random from independent SNPs and were fixed such that they each explained 10% of the phenotypic variance (total of 50%). This was done to limit variability as random sampling could lead to a few loci explaining much less or much more than 50%. The other 1000 variant effects were sampled from a normal distribution and, on average, explained a further 40% of the phenotypic variance. This number of small-effect variants was chosen to alter the genetic architecture from simulation one, and again avoid variability in the total PVE explained by these 1000 loci. Scenario two was similar to one, except loci were sampled at random from the set of PC-one-associated SNPs. Scenarios three and four had the same structure as one and two except a total PVE of 0.5 was simulated with the top five loci having a PVE of 0.3. Estimates of the PVE attributed to large-effect loci were calculated by summing the $2pq{\beta }^2/\mathrm{Var}\left(y\right)$ where p is the MAF of the causal locus, β the regression coefficient, and $y$ the phenotype vector. For Bayes R and BSLMM the estimate of PVE was calculated by summing the effects in a 1-Mb region around the simulated causal locus as these methods often spread effects or attribute the whole effect to an SNP in very high LD with the causal variant.

Data availability

Tables S7–S12 contain detailed results on detected loci for eye and skin color for the Bayes R, BSLMM, and BOLT-LMM methods and can be found in File S2. The following freely available programs were used to complete the analyses: BayesR (www.github.com/syntheke/bayesR), BOLT-LMM (www.hsph.harvard.edu/po-ru-loh/software/), GCTA (www.cnsgenomics.com/software/gcta/), GEMMA (http://www.xzlab.org/software.html), and PLINK (www.cog-genomics.org/plink2).

Results

Simulation study

Simulation one:

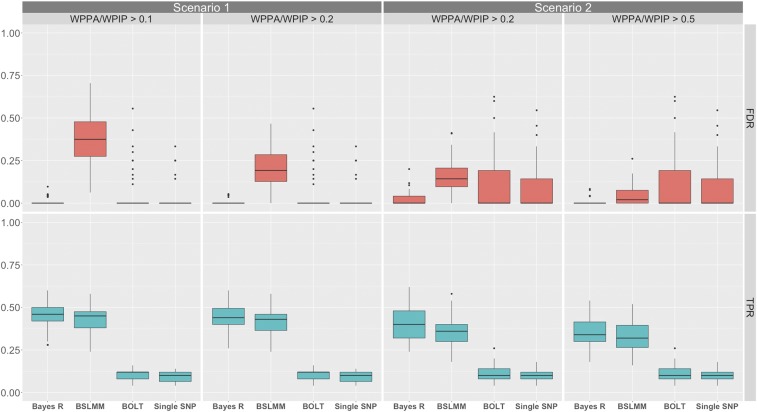
Bayes R and BSLMM performed substantially better (higher TPRs) than BOLT-LMM and single SNP analysis for more highly heritable traits and in the absence of confounding due to stratification (scenarios one and three, Figure 1 and Figure S4 in File S1), but persisted even in the presence of confounding (scenarios two and four, Figure 1 and Figure S4 in File S1). Thresholding on the WPPA controlled the proportion of false positives to be <($1-\alpha$) but appeared to be too stringent with a WPPA threshold of 0.5 leading to a PFP between 0.05 and 0.1 across simulation scenarios (Figure S5 in File S1). For each of the simulation scenarios an α threshold of 0.95 resulted in an approximate PFP of 1% and at 0.9 ∼2%. These results suggest that a WPPA and WPIP threshold of 0.5 is reasonable for concluding that a region has evidence that it is associated with the eye and skin color traits in these data. This conclusion rests on the assumption that pigmentation traits are moderately heritable and are driven by loci that are in part differentiated along the ancestral gradient in the Cape Verde population.

Figure 1.

Comparison of the performance of Bayes R, BSLMM, BOLT-LMM, and single SNP PC corrected association analysis (performed in PLINK) at identifying 1-Mb regions containing causal variants for simulation one, scenarios one and two, which had a simulated PVE equal to 0.9. Panels include method on the x-axis and rate on the y-axis with the true positive rate (TPR) for detecting a 1-Mb region containing a causal variant (cyan), and the false discovery rate (red) for each of the methods. For all panels BOLT-LMM and PLINK P-values are thresholded at the genome-wide significance level ($5\times {10}^{-8}$) and thus their rates remain fixed across panels. Scenario one (random allocated loci) shows results for Bayes R and BSLMM that have been thresholded on a WPPA or WPIP >0.1 and 0.2. Scenario two (loci associated with ancestry) shows results for Bayes R and BSLMM that have been thresholded on a WPPA and WPIP >0.2 and 0.5. For each scenario, the threshold on WPPA/WPIP was decreased from the initial value (left panel for each scenario) until the median FDR of at least one of either Bayes R of BSLMM was equal to that of BOLT-LMM and single SNP regression. An alternative threshold is also displayed so that the rate of decrease of the median FDR for the other method can be observed.

For estimates of PVE (Figure S6 in File S1), two general trends emerged. In the absence of confounding due to stratification (scenarios one and three), all four methods exhibited upward bias with regard to PVE estimation (more apparent in scenario three). However, in the presence of confounding due to stratification (scenarios two and four), all four methods overestimated PVE, consistent with what was originally described for BOLT-LMM (Loh et al. 2015a). Second, PVE estimates from BOLT-LMM and GCTA showed much more variance than that of Bayes R or BSLMM. Taken together, the results of simulation one suggest that applications of BLMM approaches in the Cape Verde population are most useful for gene discovery and identification of causal variants, as we describe below.

Simulation two:

Simulation two again suggests that BLMM/LMMs exhibit an upward bias (when simulated with genotypes from Cape Verde) with regard to PVE estimation especially in the presence of confounding due to stratification (Figure S7 in File S1). Potential reasons for the upward bias from the BLMMs across simulations are the inclusion of many small effects, as there exists a nonzero probability that any one SNP can be included in the model, and thus given the small sample size, the Bayesian methods include many small effects that cannot be set to 0 with certainty. This is likely to reflect overfitting given the large number of parameters relative to the sample size. This upward bias is hypothesized to be exacerbated when the effects are aligned with ancestry, as observed, due to markers capturing the population stratification. However, for these scenarios no individual noncausal SNP had a high inclusion probability or large effect across all iterations (i.e., posterior mean), and thus in each iteration there is a different set of null effects that sum to a nonzero heritability. These conclusions also apply to results from simulation one. For the five causal loci of large effect, the BLMMs have a small downward bias in the PVE when compared to estimates from PLINK (Figure S8 in File S1). However, the simulation shows that summing the proportion of phenotypic variance for regions surrounding the causal variant achieves a reasonable lower bound for the true PVE for large-effect loci and thus for the total PVE.

Loci associated with eye and skin color

For Bayes R, the rank of the top loci and WPPA, distributions of the genetic variance for the top regions, the posterior means of the PVE, and the number of loci in the largest variance class all remained stable for both eye and skin color when the results from the longer chain were compared with the shorter chain (Figures S9–S12 and Tables S2 and S3 in File S1). For BSLMM, we saw a similar stability in the rank and WPIP of the top loci for eye and skin color and the posterior mean of the PVE between the long and short chains (Figures S13 and S14 and Tables S4 and S5 in File S1). We therefore treat the results from the longer chains as a representative sample from the target distribution for each of the parameters of interest. Results from the Bayes R model are based on the longer chain run (200,000 iterations with 40,000 burn in), which includes 16,000 iterations after thinning (1 in 10). Similarly for BSLMM, posterior estimates were generated from the longer chain of 2 M iterations with 200,000 elements from the longer chain after thinning.

Eye color:

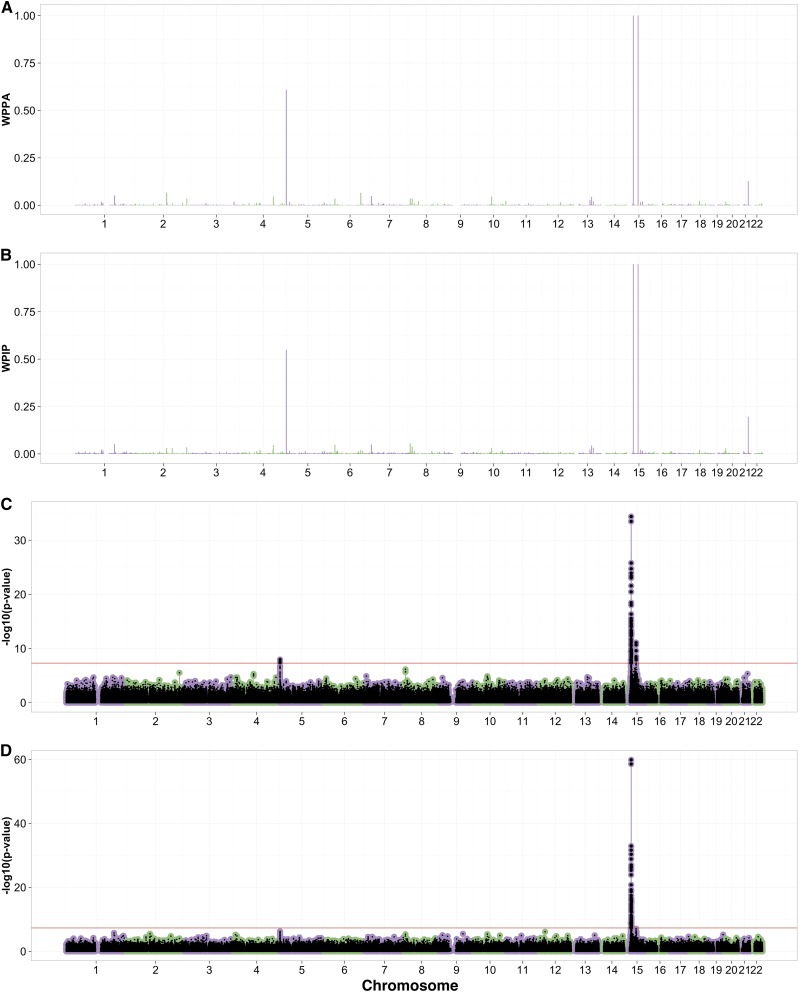
In the original analysis of the Cape Verde data set with a linear model and PC correction, two loci for eye color were identified, both on chromosome 15 and linked to the candidate genes SLC24A5 and HERC2/OCA2 with top SNPs rs2470102 and rs12913832, respectively. The three BLMM methods identified both of these loci and, in addition, revealed evidence for a new gene-dense locus on chromosome 5 (Figure 2 and Figure S15A in File S1 and Table 1). Bayes R and BSLMM showed very strong evidence for association for the SLC24A5 and HERC2/OCA2 gene regions with a WPPA = 1.0 and WPIP = 1.0 for both loci. The chromosome 5 region showed a WPPA of 0.61 and WPIP of 0.55 suggesting moderate evidence for association, with BOLT-LMM reporting the rs7736 SNP within this region as being genome-wide significant ($P-\text{value}=1.1\times {10}^{-8}$). Within the top regions, Bayes R and BSLMM reported large PIP values for the rs12913832 and rs1426654 SNPs (HERC2 and SLC24A5) (Table 1). The rs1426654 SNP has an LD $R^2$ of 0.99 with the rs2470102 SNP reported as the top association in Beleza et al. (2013). Within the chromosome 5 locus, the rs7736 SNP showed smaller PIPs of 0.06 and 0.05 for the top SNP (Table 1). The results from Bayes R and BSLMM show that there are many variants contributing to the regional association signal on chromosome 5 with smaller PIPs spread across many SNPs (Figure S15A in File S1 and Table S7 in File S2). Additionally, Bayes R and BSLMM show high PIPs for the SNP rs1635166 (0.67 and 0.90, respectively) suggesting that for the HERC2 locus there may be >1 causal SNP generating associations (Figure S15B in File S1). The LD $R^2$ of the rs1635166 SNP with rs12913832 is relatively small (0.25), further supporting this hypothesis (Table S6 in File S1). BOLT-LMM reported ${\lambda }_{GC}$ statistics of 0.99 for the infinitesimal statistics and 0.99 for the noninfinitesimal statistics (Figure S16 in File S1). The standard linear model analysis corrected for 10 PCs reported similar top loci to those of Beleza et al. (2013) (Figure 2D). The standard linear model analysis reported rs7736 ($5.7\times {10}^{-7}$) as the top SNP at the chromosome 5 locus.

Figure 2.

Manhattan plots from eye association analyses using Bayes R (A), BSLMM (B), BOLT-LMM (C), and a single SNP analysis with 10 PCs (D). Red lines in C and D indicate the genome-wide significance level.

Table 1. Summary of the top loci from Bayes R, BSLMM, and BOLT-LMM.

Locus	1-Mb region	WPPA	WPIP	Best SNP	BOLT-LMM P-value	Bayes R PIP	BSLMM PIP	$D^2$ statistic P-value	PVE
Eye
AHRR	chr5:68778:999418	0.61	0.55	rs7736	$1.1\times {10}^{-8}$	0.06	0.05	$2.5\times {10}^{-2}$	0.02 (0.00, 0.05)
HERC2	chr15:26001220:26998850	1.0	1.0	rs12913832	$4.2\times {10}^{-35}$	1.0	0.81	$7.8\times {10}^{-3}$	0.30 (0.23, 0.38)
SLC24A5	chr15:46004188-46999899	1.0	1.0	rs1426654	$8.3\times {10}^{-12}$	0.62	0.37	$4.2\times {10}^{-3}$	0.07 (0.04, 0.11)
Skin
SLC45A2	chr5:33000379-33999967	1.0	0.92	rs35395	$1.3\times {10}^{-10}$	0.72	0.44	$1.1\times {10}^{-2}$	0.05 (0.03, 0.08)
DDB1	chr11:60002783-60976798	0.91	0.86	rs2513329	$5.2\times {10}^{-7}$	0.32	0.13	$3.7\times {10}^{-4}$	0.03 (0.00, 0.06)
GRM5/TYR	chr11:88001883-88994234	0.96	1.0	rs10831496	$1.8\times {10}^{-10}$	0.08	0.06	$2.8\times {10}^{-2}$	0.03 (0.01, 0.06)
APBA2	chr15:27000239-27999050	1.0	0.98	rs4424881	$5.6\times {10}^{-10}$	0.17	0.03	$5.7\times {10}^{-4}$	0.05 (0.02, 0.08)
SLC24A5	chr15:46004188-46999899	1.0	1.0	rs1426654	$2.7\times {10}^{-25}$	1.0	0.56	$3.4\times {10}^{-3}$	0.16 (0.11, 0.20)

The WPPA and WPIP are reported for the stated 1-Mb regions with hg18 bp coordinates. For each region the best SNP refers to the SNP in the region with the smallest P-value from BOLT-LMM. For the eye color HERC2 locus the PIP for Bayes R is with reference to the SNP rs1129038, which has an LD $R^2$ of 0.98 with the rs12913832 SNP. For Bayes R the PIP for each SNP is that of being in the model, i.e., the sum of the PIP of being in any of the nonzero variance classes and for BSLMM the PIP corresponds to the SNP having an effect above the polygenic background. Rows containing bold gene names are potentially novel relative to those found by Beleza et al. (2013). The $D^2$ statistic P-values are those generated from the allelic differentiation along the ancestral gradient method and are for principal component one. The reported PVE is the posterior mean of the genetic variance for the 1-Mb region calculated from Bayes R in the WPPA procedure with the 95% credible interval in parentheses.

The degree of allelic differentiation across the ancestral gradient, summarized by the $D^2$ statistics, for the most highly associated SNPs showed P-values that did not pass genome-wide significance suggesting that these SNPs are not markedly differentiated across the first PC (Table 1). However, no SNP passed genome-wide significance for the allelic differentiation across the ancestral gradient analysis with the top SNP having an association P-value of $3.6\times {10}^{-6}.$ This shows that the associated SNPs for eye color are not the most differentiated across the ancestral gradient.

Each of the three BLMM methods showed moderate evidence for an association on chromosome 5 not reported in Beleza et al. (2013). The locus zoom plots showed a strong LD pattern extending across a region of several hundred kilobases that includes six genes of which one, AHRR (arylhydrocarbon receptor repressor), is a plausible candidate (Figure S15A in File S1). Originally recognized as a homolog of the arylhydrocarbon receptor (AhR) gene, AHRR encodes a bHLH-PAS protein that binds to the same response element as AhR but represses AhR signaling. AHRR is widely expressed, and in zebrafish embryos, morpholinos against an AHRR paralog, AHRRa, elicit changes in gene expression thought to reflect a role in eye development and function (Aluru et al. 2014).

Skin color:

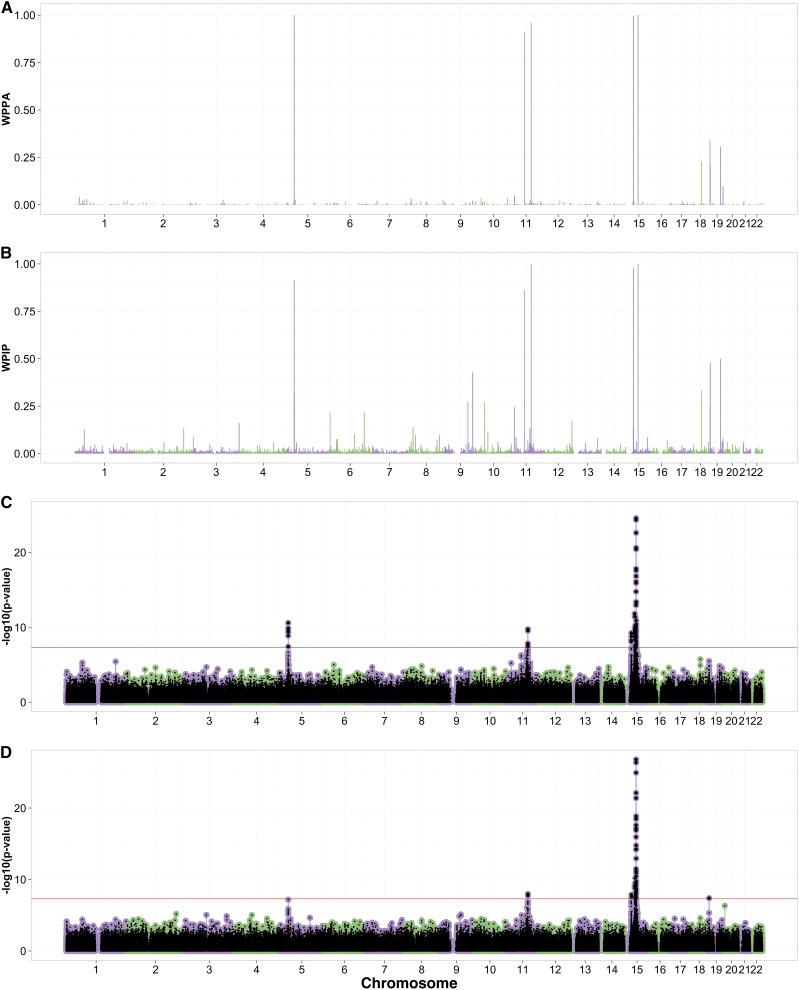
In the original GWAS, Beleza et al. (2013) reported four loci for skin color on chromosomes 5, 11, and 15 with candidate genes SLC45A2, GRM5/TYR, APBA2, and SLC24A5. Bayes R, BSLMM, and BOLT-LMM all reported these regions as showing evidence for association and, in addition, revealed evidence for a new region on chromosome 11. Bayes R and BSLMM reported WPPA and WPIP values >0.92 for the four loci identified in Beleza et al. (2013) with BOLT-LMM reporting SNPs passing the genome-wide significance for each of the regions (Figure 3 and Table 1). Among the genes present in the additional region on chromosome 11 recognized by the BLMM methods, the DDB1 gene is a plausible candidate for regulating variation in skin color (Figure S15C in File S1). DDB1 is involved in nucleotide excision repair following UV-induced DNA damage, and therefore could play a role in the tanning response and/or photosensitivity (Liu et al. 2000; Bekker-Jensen et al. 2010). Bayes R and BSLMM reported strong evidence for this locus with a WPPA = 0.91 and a WPIP = 0.86 that this region is associated with skin color. The SNP with the smallest P-value from BOLT-LMM (rs2513329) did not reach genome-wide significance (P-value = $5.2\times {10}^{-7}$). The Bayes R and BSLMM PIPs for the rs2513329 SNP (Table 1) in the DDB1 region were smaller than those for a second SNP located in the same region (rs10792312 PIP = 0.46 and 0.76), which has an LD $R^2$ of 1.0 with rs2513329 (Table S6 in File S1). Similar to the chromosome 5 locus for eye color, the GRM5/TYR locus showed many variants contributing to the regional association with no one variant showing a PIP >0.3 (Tables S10 and S11 in File S2).

Figure 3.

Manhattan plots from skin association analyses using Bayes R (A), BSLMM (B), BOLT-LMM (C), and linear model with 10 PCs (D). Red lines in C and D indicate the genome-wide significance level.

BOLT-LMM only reported the infinitesimal model statistics for skin color with a ${\lambda }_{GC}$ value of 1.04 (Figure S16 in File S1). The linear association analysis corrected for 10 PCs reported similar top loci to those by Beleza et al. (2013) (Figure 3D). The degree of allelic differentiation across the ancestral gradient analysis, summarized by the $D^2$ statistics, for the most highly associated SNPs showed allelic differentiation P-values that did not pass genome-wide, suggesting that these SNPs are not markedly differentiated across the first PC (Table 1).

Proportion of phenotypic variance explained by highly associated regions:

Given the evidence from the three models, three regions for eye color showed the most evidence for association. These were the AHRR gene region on chromosome 5, and the HERC2/OCA2 and SLC24A5 gene on chromosome 15. The distribution of the genetic variance was generated as a by-product of the WPPA calculation and thus from these analyses we calculated the posterior means for the PVE by dividing the estimated genetic variance for each region for each iteration t by the estimated phenotypic variance ${\sigma }_g^2+{\sigma }_e^2$ for each iteration. The three regions for eye color (AHRR, HERC2/OCA2, SLC24A5) explained 2.0% (0.0, 5.0), 30% (23, 38), and 7.0% (4.0, 11) of the phenotypic variance for eye color, respectively (intervals in parentheses indicate the 95% credible interval for these estimates calculated using quantiles). These three regions explained 39% (32, 46) of the phenotypic variance for eye color (Table 1).

For skin color, the five regions with the most evidence for association were SLC45A2, GRM5/TYR, APBA2, and SLC24A5, and the additional region of DDB1. These regions explained 5.0% (3.0, 8.0), 3.0% (1.0, 6.0), 5.0% (2.0, 8.0), 16% (11, 20), and 3.0% (0.0, 6.0) of the phenotypic variance, respectively (Table 1). The total proportion of genetic variation explained by the top five regions with evidence for association was 32% (26, 38).

Discussion

The use of BLMMs in the heavily admixed Cape Verde population has led to evidence for additional associations for eye and skin color when compared to those reported by Beleza et al. (2013). The results from the BLMMs are consistent with the top regions presented in Beleza et al. (2013), and avoid the choice of the number of PCs required to control for spurious associations (as do frequentist versions of the LMM) due to ancestral differences. The use of concordant evidence across the three BLMM methods, coupled with biological annotation, indicates a potential involvement of the AHRR gene region for eye color and the DDB1 gene region for skin color. The moderate WPPA and WPIP values for the AHRR gene locus were reinforced by a genome-wide significant result for the rs7736 SNP from BOLT-LMM. Given the high WPPA and WPIP for the locus in the DDB1 gene, and the central role in DNA repair post UV damage that the protein product of this gene encodes, we argue that this is statistically the most suggestive locus for an effect on skin color not detected by the PC-corrected linear model approach.

The results for eye and skin color are further supported by the simulations where for highly heritable traits, Bayes R and BSLMM retained higher TPRs for the same FDRs than the BOLT-LMM and standard GWAS methods (at a genome-wide significance threshold), which is likely derived from their ability to jointly capture the effect of a causal variant using multiple SNPs simultaneously (Guan and Stephens 2011; Segura et al. 2012; Moser et al. 2015). This loss in power was seen in the results for the chromosome five locus for eye color, where PC adjustment resulted in associations not being genome-wide significant relative to the BOLT-LMM results. This suggests that for discovery of new associations, BLMMs may be a potential improvement over currently implemented LMM methodology in structured populations. The results from simulation 1, scenarios 1 and 2 show that Bayes R has a higher median TPR and a lower median FDR than BSLMM for a given WPPA and WPIP threshold. This may be driven by the ability of Bayes R to better model the large genetic effects for these simulated traits, which are generated by the high PVE in these scenarios. This is further reinforced by the convergence of the median TPR and FDR for Bayes R and BSLMM in scenarios 3 and 4, which have a simulated PVE = 0.5. This suggests that for more polygenic traits, Bayes R and BSLMM are expected to perform equally well at mapping loci, a result observed in Moser et al. (2015). As BSLMM does not allow for the calculation of the WPPA statistics, the comparisons made between the median TPR and FDR across simulation scenarios are not optimal. It is difficult to evaluate how much of this difference is due to practical rather than fundamental (such as the prior distribution on the genetic effects) reasons. We also demonstrated that for each of the simulation scenarios that the PFP was controlled to be between 5 and 10% when a WPPA threshold of 0.5 was applied. This lends further evidence to the association results in the AHRR and DDB1 loci, which had a WPPA/WPIP of 0.6/0.55 and 0.91/0.86 respectively.

Previous estimates of PVE indicate that eye and skin color are highly heritable with estimates for both traits ranging between 0.7 and 0.9 (Bräuer and Chopra 1978; Byard 1981). One consequence of the definition of heritability is that it is a population-specific parameter, because both the variation in additive genetic factors (and nonadditive), as well as the environmental variance, are population specific (Visscher et al. 2008). For traits simulated using the Cape Verde genotypes, the median estimates of PVE from BSLMM/LMMs were upwardly biased and showed large variation, with medians hitting the boundary at unity in some scenarios. These results suggest that PVE estimation using BLMM/LMMs is unreliable for the Cape Verde data set. The LD score regression method (Bulik-Sullivan et al. 2015) is a recent development for distinguishing between inflated test statistics due to confounding bias and polygenicity. This method suggests one avenue for removing confounding from population structure from the heritability estimate but is yet to be extended to admixed populations (Bulik-Sullivan et al. 2015). Bayesian LMMs coupled with PC correction, or a generalized LD score regression, may be avenues for unbiased PVE estimation, which would require extensive simulations in a much larger data set with empirical data to validate. However, estimates of PVE from regions surrounding purported highly associated loci should provide a reasonable lower bound for the narrow-sense heritability as seen in simulation two. The results from the PVE for top associated loci are very similar to those reported for skin color in Beleza et al. (2013), which concluded that the four major loci contribute a total of 35% to skin color variation. Our results suggest that the PVE for the top five loci was 32% (26, 38) with the SLC24A5 locus contributing ∼16% and the DDB1 locus explaining an additional 3%. This highlights that although BLMMs and marginal linear regression both provide comparable estimates of PVE for an individual locus of large effect, the BLMMs allow for additional loci to be detected.

The posterior probability that a polymorphic site affects the trait conditional on the data is a very natural statistic to interpret in the context of QTL identification (Viallefont et al. 2001; Stephens and Balding 2009). For the Bayer R and BSLMM methods there may be a decrease in the posterior probability for individual markers at a locus due to the sharing of the effect across markers in LD. This leads to a decrease in power for any one of the SNPs as the PIP will be lower for each of them (0.5, for example, for a set of two markers in perfect LD and sharing a PIP of 1). Furthermore, the PIP for any one marker is dependent on the choice of prior, especially for small data sets, where the number of effects to be learned is much greater than the number of individuals contributing information. However, Guan and Stephens (2011) showed that when the genetic variance and the proportion of null effects, which have a large influence on the PIP, were fixed to a value substantially different from the true simulated value, the PIPs showed limited deviation from the truth. A further conclusion was that the rank and power were particularly insensitive to the choice of prior assumptions on the proportion of null effects and the genetic variance (Guan and Stephens 2011). Evidence for this is observed in this study, where the rank of the top regions for Bayes R and BSLMM, along with the WPPA and WPIP, are very similar given the large differences in modeling assumptions. Both the sharing of effects and the sensitivity to prior assumptions are mitigated by using a regional measure of association such as the WPPA, where uncertainty is averaged across the region. Alternatively, Wen (2015) derived Bayes factors for results generated from the LMM methodology, which could also be used as a primary statistical device for model comparison. It is important to point out that P-values convey a strength of evidence that depends on factors that affect power, which is not a concern for the posterior probability of association statistics provided by the Bayesian methods (Stephens and Balding 2009). We believe that the results of this paper suggest that Bayesian LMM-based methods coupled with a theoretically justified method for controlling the false-positive rate could be a very effective tool for mapping new genetic loci. However, more rigorous frameworks for prior choice and assessment of significance and uncertainty in genetic effects from Bayesian LMMs are needed, which is an interesting open question.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.193383/-/DC1.