Mathematical Constraints on F_ST: Biallelic Markers in Arbitrarily Many Populations

Abstract

${\mathit{F}}_{\mathrm{ST}}$ is one of the most widely used statistics in population genetics. Recent mathematical studies have identified constraints that challenge interpretations of $F_{\mathrm{ST}}$ as a measure with potential to range from 0 for genetically similar populations to 1 for divergent populations. We generalize results obtained for population pairs to arbitrarily many populations, characterizing the mathematical relationship between $F_{\mathrm{ST}},$ the frequency M of the more frequent allele at a polymorphic biallelic marker, and the number of subpopulations K. We show that for fixed K, $F_{\mathrm{ST}}$ has a peculiar constraint as a function of M, with a maximum of 1 only if $M=i/K,$ for integers i with $\lceil K/2\rceil \le i\le K-1.$ For fixed M, as K grows large, the range of $F_{\mathrm{ST}}$ becomes the closed or half-open unit interval. For fixed K, however, some $M<\left(K-1\right)/K$ always exists at which the upper bound on $F_{\mathrm{ST}}$ lies below $2\sqrt{2}-2\approx \mathrm{0.8284.}$ We use coalescent simulations to show that under weak migration, $F_{\mathrm{ST}}$ depends strongly on M when K is small, but not when K is large. Finally, examining data on human genetic variation, we use our results to explain the generally smaller $F_{\mathrm{ST}}$ values between pairs of continents relative to global $F_{\mathrm{ST}}$ values. We discuss implications for the interpretation and use of $F_{\mathrm{ST}}.$

GENETIC differentiation, in which individuals from the same subpopulation are more genetically similar than are individuals from different subpopulations, is a central concept in population genetics. It can arise from a large variety of processes, including from aspects of the physical environment such as geographic barriers, variable permeability to migrants, and spatially heterogeneous selection pressures, as well as from biotic phenomena such as assortative mating and self-fertilization. Genetic differentiation among populations is thus a pervasive feature of population-genetic variation.

To measure genetic differentiation, Wright (1951) introduced the fixation index $F_{\mathrm{ST}},$ defined as the “correlation between random gametes, drawn from the same subpopulation, relative to the total.” Many definitions of $F_{\mathrm{ST}}$ and related statistics have since been proposed (reviewed by Holsinger and Weir 2009). $F_{\mathrm{ST}}$ is often defined in terms of a ratio involving mean heterozygosity of a set of subpopulations, $H_{\mathrm{S}},$ and “total heterozygosity” of a population formed by pooling the alleles of the subpopulations, $H_{\mathrm{T}}$ (Nei 1973):

$$F_{\mathrm{ST}}=\frac{H_{\mathrm{T}}-H_{\mathrm{S}}}{H_{\mathrm{T}}}.$$ (1)

For a polymorphic biallelic marker whose more frequent allele has mean frequency M across K subpopulations, denoting by $p_k$ the frequency of the allele in subpopulation k, $H_{\mathrm{S}}=1-(1/K){\displaystyle {\sum }_{k=1}^K\left[p_k^2+{\left(1-p_k\right)}^2\right]}$ and $H_{\mathrm{T}}=1-\left[M^2+{\left(1-M\right)}^2\right].$

$F_{\mathrm{ST}}$ and related statistics have a wide range of applications. For example, $F_{\mathrm{ST}}$ is used as a descriptive statistic whose values are routinely reported in empirical population-genetic studies (Holsinger and Weir 2009). It is considered as a test statistic for spatially divergent selection, either acting on a locus (Lewontin and Krakauer 1973; Bonhomme et al. 2010) or, using comparisons to a corresponding phenotypic statistic $Q_{\mathrm{ST}},$ on a trait (Leinonen et al. 2013). $F_{\mathrm{ST}}$ is also used as a summary statistic for demographic inference, to measure gene flow between subpopulations (Slatkin 1985); or via approximate Bayesian computation, to estimate demographic parameters (Cornuet et al. 2008).

Applications of $F_{\mathrm{ST}}$ generally assume that values near 0 indicate that there are almost no genetic differences among subpopulations, and that values near 1 indicate that subpopulations are genetically different (Hartl and Clark 1997; Frankham et al. 2002; Holsinger and Weir 2009). Mathematical studies, however, have challenged the simplicity of this interpretation, commenting that the range of values that $F_{\mathrm{ST}}$ can take is considerably restricted by the allele frequency distribution (Table 1). Such studies have highlighted a direct relationship between allele frequencies and constraints on the range of $F_{\mathrm{ST}}$ through functions of the allele frequency distribution such as the mean heterozygosity across subpopulations, $H_{\mathrm{S}}.$ The maximal $F_{\mathrm{ST}}$ has been shown to decrease as a function of $H_{\mathrm{S}},$ both for an infinite (Hedrick 1999) and for a fixed finite number of subpopulations $K\ge 2$ (Long and Kittles 2003; Hedrick 2005). Consequently, if subpopulations differ in their alleles but separately have high heterozygosity, then $H_{\mathrm{S}}$ can be high and $F_{\mathrm{ST}}$ can be low; $F_{\mathrm{ST}}$ can be near 0 even if subpopulations are completely genetically different in the sense that no allele occurs in more than one subpopulation.

Table 1. Studies describing the mathematical constraints on F_ST.

Reference	Number of alleles	Number of subpopulations	Variable in terms of which constraints are reporteda
Hedrick (1999)	unspecified value $\ge 2$	$\mathrm{\infty }$	$H_{\mathrm{S}}$
Long and Kittles (2003)	unspecified value $\ge 2$	fixed finite value $\ge 2$	$H_{\mathrm{S}}$
Rosenberg et al. (2003)	2	2	δ
Hedrick (2005)	unspecified value $\ge 2$	fixed finite value $\ge 2$	$H_{\mathrm{S}}$
Maruki et al. (2012)	2	2	$H_{\mathrm{S}},$ M
Jakobsson et al. (2013)	unspecified value $\ge 2$	2	$H_{\mathrm{T}},$ M
Edge and Rosenberg (2014)	fixed finite value $\ge 2$	2	$H_{\mathrm{T}},$ M
This article	2	fixed finite value $\ge 2$	M

$H_{\mathrm{S}}$ and $H_{\mathrm{T}}$ denote the within-subpopulation and total heterozygosities, respectively. δ denotes the absolute difference in the frequency of a specific allele between two subpopulations, and M denotes the frequency of the most frequent allele.

^aInstead of heterozygosities $H_{\mathrm{S}}$ or $H_{\mathrm{T}},$ some studies consider homozygosities $J_{\mathrm{S}}=1-H_{\mathrm{S}}$ or $J_{\mathrm{T}}=1-J_{\mathrm{T}}.$

Detailed mathematical results have clarified the relationship between allele frequencies and $F_{\mathrm{ST}}$ in the case of $K=2$ subpopulations. Considering a biallelic marker, Maruki et al. (2012) evaluated the constraint on $F_{\mathrm{ST}}$ by the frequency M of the most frequent allele: the maximal $F_{\mathrm{ST}}$ decreases monotonically from 1 to 0 with increasing M, $1/2\le M<1.$ Jakobsson et al. (2013) extended this result to multiallelic markers with an unspecified number of distinct alleles, showing that the maximal $F_{\mathrm{ST}}$ increases from 0 to 1 as a function of M when $0<M<1/2,$ and decreases from 1 to 0 when $1/2\le M<1$ in the manner reported by Maruki et al. (2012). Edge and Rosenberg (2014) generalized these results to the case of a fixed finite number of alleles, showing that the maximal $F_{\mathrm{ST}}$ differs slightly from the unspecified case when the fixed number of distinct alleles is odd.

In this study, we characterize the relationship between $F_{\mathrm{ST}}$ and the frequency M of the most frequent allele, for a biallelic marker and an arbitrary number of subpopulations K. We derive the mathematical upper bound on $F_{\mathrm{ST}}$ in terms of M, extending the biallelic two-subpopulation result to arbitrary K. To assist in interpreting the bound, we simulate the joint distribution of $F_{\mathrm{ST}}$ and M in the island migration model, describing its properties as a function of the number of subpopulations and the migration rate. The K-population upper bound on $F_{\mathrm{ST}}$ as a function of M facilitates an explanation of counterintuitive aspects of global human genetic differentiation. We discuss the importance of the results for applications of $F_{\mathrm{ST}}$ more generally.

Mathematical Constraints

Model

Our goal is to derive the range of values $F_{\mathrm{ST}}$ can take, the lower and upper bounds on $F_{\mathrm{ST}},$ as a function of the frequency M of the most frequent allele for a biallelic marker when the number of subpopulations K is a fixed finite value ≥2. We consider a polymorphic locus with two alleles, A and a, in a setting with K subpopulations contributing equally to the total population. We denote the frequency of allele A in subpopulation k by $p_k.$ The frequency of allele a in subpopulation k is $1-p_k.$ Each allele frequency $p_k$ lies in the interval $\left[0,1\right].$

The mean frequency of allele A across the subpopulations is $M=\left(1/K\right){\displaystyle {\sum }_{k=1}^K{p}_k},$ and the mean frequency of allele a is $1-M.$ Without loss of generality, we assume that allele A is the more frequent allele in the total population, so that $M\ge 1/2\ge 1-M.$ Because by assumption the locus is polymorphic, $M\ne 1.$

We assume that the allele frequencies M and $p_k$ are parametric allele frequencies of the total population and subpopulations, and not estimated values computed from data.

F_ST as a function of M

Equation 1 expresses $F_{\mathrm{ST}}$ as a ratio involving within-subpopulation heterozygosity, $H_{\mathrm{S}},$ and total heterozygosity, $H_{\mathrm{T}}.$ We substitute $H_{\mathrm{S}}$ and $H_{\mathrm{T}}$ in Equation 1 with their respective expressions in terms of allele frequencies:

$$F_{\mathrm{ST}}=\frac{\frac{1}{K}{\displaystyle {\sum }_{k=1}^K\left[p_k^2+{\left(1-p_k\right)}^2\right]-\left[M^2+{\left(1-M\right)}^2\right]}}{1-\left[M^2+{\left(1-M\right)}^2\right]}.$$ (2)

Simplifying Equation 2 by noting that ${\displaystyle {\sum }_{k=1}^K{p}_k}=KM$ leads to:

$$F_{\mathrm{ST}}=\frac{\left(\frac{1}{K}{\displaystyle \sum _{k=1}^K{p}_k^2}\right)-M^2}{M\left(1-M\right)}.$$ (3)

For fixed M, we seek the vectors $\left(p_1,p_2,\dots ,p_K\right),$ with $p_k\in \left[0,1\right]$ and $\left(1/K\right){\displaystyle {\sum }_{k=1}^K{p}_k}=M,$ that minimize and maximize $F_{\mathrm{ST}}.$

We clarify here that in mathematical analysis of the relationship between $F_{\mathrm{ST}}$ and allele frequencies, we adopt an interpretation of $F_{\mathrm{ST}}$ as a “statistic” that describes a mathematical function of allele frequencies rather than as a “parameter” that describes coancestry of individuals in a population. Multiple interpretations of $F_{\mathrm{ST}}$ exist, giving rise to different expressions for computing it (e.g., Nei 1973; Nei and Chesser 1983; Weir and Cockerham 1984; Holsinger and Weir 2009). Our interest is in disentangling properties of the mathematical function by which true allele frequencies are used to compute $F_{\mathrm{ST}}$ from the population-genetic relationships among individuals and sampling phenomena that could be viewed as affecting the computation. As a result, it is natural to follow the statistic interpretation that has been used in earlier scenarios involving $F_{\mathrm{ST}}$ bounds in relation to allele frequencies viewed as parameters, rather than as estimates or outcomes of a stochastic process (Table 1), and in which such a disentanglement is possible. We return to this topic in the Discussion.

Lower bound

From Equation 3, for all $M\in \left[1/2,1\right),$ setting $p_k=M$ in all subpopulations k yields $F_{\mathrm{ST}}=0.$ The Cauchy–Schwarz inequality guarantees that $K{\displaystyle {\sum }_{k=1}^K{p}_k^2}\ge {\left({\displaystyle {\sum }_{k=1}^K{p}_k}\right)}^2,$ with equality if and only if $p_1=p_2=\dots =p_K.$ Hence, $K{\displaystyle {\sum }_{k=1}^K{p}_k^2}={\left({\displaystyle {\sum }_{k=1}^K{p}_k}\right)}^2,$ or by dividing both sides by $K^2$ to give $\left(1/K\right){\displaystyle {\sum }_{k=1}^K{p}_k^2}=M^2,$ requires $p_1=p_2=\dots =p_K=M.$ Examining Equation 3, $\left(p_1,p_2,\dots ,p_K\right)=\left(M,M,\dots ,M\right)$ is thus the only vector that yields $F_{\mathrm{ST}}=0.$ We can conclude that the lower bound on $F_{\mathrm{ST}}$ is equal to 0 irrespective of M, for any value of the number of subpopulations K.

Upper bound

To derive the upper bound on $F_{\mathrm{ST}}$ in terms of M, we must maximize $F_{\mathrm{ST}}$ in Equation 3, assuming that M and K are constant. Because all terms in Equation 3 depend only on M and K except the positive term ${\displaystyle {\sum }_{k=1}^K{p}_k^2}$ in the numerator, maximizing $F_{\mathrm{ST}}$ corresponds to maximizing ${\displaystyle {\sum }_{k=1}^K{p}_k^2}$ at fixed M and K.

Denote by $\lfloor x\rfloor$ the greatest integer less than or equal to x, and by $\left\{x\right\}=x-\lfloor x\rfloor$ the fractional part of x. Using a result from Rosenberg and Jakobsson (2008), Theorem 1 from Appendix A states that the maximum for ${\displaystyle {\sum }_{k=1}^K{p}_k^2}$ satisfies

$${\displaystyle \sum _{k=1}^K{p}_k^2}\le \lfloor KM\rfloor +{\left\{KM\right\}}^2,$$ (4)

with equality if and only if allele A has frequency 1 in $\lfloor KM\rfloor$ subpopulations, frequency $\left\{KM\right\}$ in a single subpopulation, and frequency 0 in all other subpopulations. Substituting Equation 4 into Equation 3, we obtain the upper bound for $F_{\mathrm{ST}}:$

$$F_{\mathrm{ST}}\le \frac{\lfloor KM\rfloor +{\left\{KM\right\}}^2-K{M}^2}{KM\left(1-M\right)}.$$ (5)

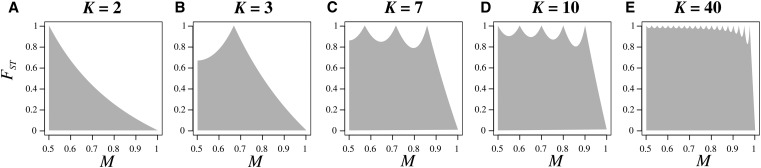
The upper bound on $F_{\mathrm{ST}}$ in terms of M has a piecewise structure, with changes in shape occurring when $KM$ is an integer.

For $i=\lfloor K/2\rfloor ,\lfloor K/2\rfloor +1,\dots ,K-1,$ define the interval $I_i$ by $\left[1/2,\left(i+1\right)/K\right)$ for $i=\lfloor K/2\rfloor$ in the case that K is odd and by $\left[i/K,\left(i+1\right)/K\right)$ for all other $\left(i,K\right).$ For $M\in I_i,$ $\lfloor KM\rfloor$ has a constant value i. Writing $x=KM-\lfloor KM\rfloor =KM-i$ so that $M=\left(i+x\right)/K,$ for each interval $I_i,$ the upper bound on $F_{\mathrm{ST}}$ is a smooth function:

$$Q_i\left(x\right)=\frac{K\left(i+x^2\right)-{\left(i+x\right)}^2}{\left(i+x\right)\left(K-i-x\right)},$$ (6)

where x lies in $\left[0,1\right)$ (or in $\left[1/2,1\right)$ for odd K and $i=\lfloor K/2\rfloor ),$ and i lies in $\left[\lfloor K/2\rfloor ,K-1\right].$

The conditions under which the upper bound is reached illuminate its interpretation. The maximum requires the most frequent allele to have frequency 1 or 0 in all except possibly one subpopulation, so that the locus is polymorphic in at most a single subpopulation. Thus, $F_{\mathrm{ST}}$ is maximal when fixation is achieved in as many subpopulations as possible.

Figure 1 shows the upper bound on $F_{\mathrm{ST}}$ in terms of M for various values of K. It has peaks at values $i/K,$ where it is possible for the allele to be fixed in all K subpopulations and for $F_{\mathrm{ST}}$ to reach a value of 1. Between $i/K$ and $\left(i+1\right)/K,$ the function reaches a local minimum, eventually decreasing to 0 as M approaches 1. The upper bound is not differentiable at the peaks, and it is smooth and strictly <1 between the peaks. If K is even, then the upper bound begins from a local maximum at $M=1/2;$ if K is odd, it begins from a local minimum at $M=1/2.$

Figure 1.

Bounds on $F_{\mathrm{ST}}$ as a function of the frequency of the most frequent allele, M, for different numbers of subpopulations K: (A) $K=2,$ (B) $K=3,$ (C) $K=7,$ (D) $K=10,$ and (E) $K=40.$ The shaded region represents the space between the upper and lower bounds on $F_{\mathrm{ST}}.$ The upper bound is computed from Equation 5; for each K, the lower bound is 0 for all values of M.

Properties of the upper bound

Local maxima:

We explore properties of the upper bound on $F_{\mathrm{ST}}$ as a function of M for fixed K by examining the local maxima and minima. The upper bound is equal to 1 on interval $I_i$ if and only if the numerator and denominator in Equation 6 are equal. Noting that $K\ge 2,$ this condition is equivalent to $x^2=x$ and hence, because $0\le x<1,$ $x=\left\{KM\right\}=0.$ Thus, on interval $I_i$ for M, the maximal $F_{\mathrm{ST}}$ is 1 if and only if $KM$ is an integer.

$KM$ has exactly $\lfloor K/2\rfloor$ integer values for $M\in \left[1/2,1\right).$ Consequently, given K, there are exactly $\lfloor K/2\rfloor$ maxima at which $F_{\mathrm{ST}}$ can equal 1, at $M=\left(K+1\right)/\left(2K\right),\left(K+3\right)/\left(2K\right),\dots ,\left(2K-2\right)/\left(2K\right)$ if K is odd and at $M=K/\left(2K\right),\left(K+2\right)/\left(2K\right),\dots ,\left(2K-2\right)/\left(2K\right)$ if K is even.

This analysis finds that $F_{\mathrm{ST}}$ is only unconstrained within the unit interval for a finite set of values of the frequency M of the most frequent allele. The size of this set increases with the number of subpopulations K.

Local minima:

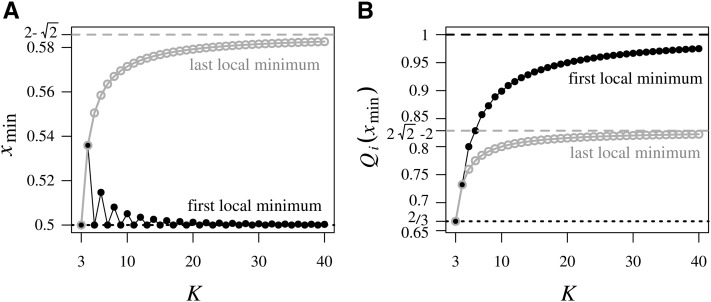
Equality of the upper bound at the right endpoint of each interval $I_i$ and the left endpoint of $I_{i+1}$ for each i from $\lfloor K/2\rfloor$ to $K-2$ demonstrates that the upper bound on $F_{\mathrm{ST}}$ is a continuous function of M. Consequently, local minima necessarily occur between the local maxima. If K is even, then the upper bound on $F_{\mathrm{ST}}$ has $K/2-1$ local minima, each inside an interval $I_i,$ $i=K/2,K/2+1,\dots ,K-2.$ If K is odd, then the upper bound has $\left(K-1\right)/2$ local minima, the first in interval $\left[1/2,\left(K+1\right)/\left(2K\right)\right),$ and each of the others in an interval $I_i,$ with $i=\left(K+1\right)/2,\left(K+3\right)/2,\dots ,K-2.$ Note that because we restrict attention to $M\in \left[1/2,1\right),$ we do not count the point at $M=1$ and $F_{\mathrm{ST}}=0$ as a local minimum.

Theorem 2 from Appendix B describes the relative positions of the local minima within intervals $I_i,$ as a function of the number of subpopulations K. From Proposition 1 of Appendix B, for fixed K, the relative position of the local minimum within interval $I_i$ increases with i; as a result, the leftmost dips in the upper bound (those near $M=1/2)$ are less tilted toward the right endpoints of their associated intervals than are the subsequent dips (nearer $M=1).$ The unique local minimum in interval $I_i$ lies either exactly at $M=\left[i+\left(1/2\right)\right]/K=1/2$ for the leftmost dip for odd K (Proposition 2), or slightly to the right of the midpoint $\left[i+\left(1/2\right)\right]/K$ of interval $I_i$ in other intervals, but no farther from the center than $M=\left(i+2-\sqrt{2}\right)/K\approx \left(i+0.5858\right)/K$ (Proposition 3; Figure B1).

The values of the upper bound on $F_{\mathrm{ST}}$ at the local minima as a function of i are computed in Appendix B (Equation B5) by substituting the positions M of the local minima into Equation 5. From Proposition 4 of Appendix B, for fixed K, the value of $F_{\mathrm{ST}}$ at the local minimum in interval $I_i$ decreases as i increases. The maximal $F_{\mathrm{ST}}$ among local minima increases as K increases (Proposition 5). The upper bound on $F_{\mathrm{ST}}$ at the local minimum closest to $M=1/2$ tends to 1 as $K\to \mathrm{\infty }$ (Proposition 5). The upper bound on $F_{\mathrm{ST}}$ at the local minimum closest to $M=1,$ however, is always smaller than $2\sqrt{2}-2\approx 0.8284$ (Proposition 6).

In conclusion, although $F_{\mathrm{ST}}$ is constrained below 1 for all values of M in the interior of intervals $I_i=\left[i/K,\left(i+1\right)/K\right),$ the constraint is reduced as $K\to \mathrm{\infty },$ and in the limit it even completely disappears in the interval $I_i$ closest to $M=1/2.$ Nevertheless, there always exists a value of $M<\left(K-1\right)/K$ for which the upper bound on $F_{\mathrm{ST}}$ is lower than $2\sqrt{2}-2\approx \mathrm{0.8284.}$

Mean range of possible F_ST values:

We now evaluate how strongly M constrains the range of $F_{\mathrm{ST}}$ as a function of K. Following similar computations for other settings where $F_{\mathrm{ST}}$ is considered in relation to a quantity that constrains it (Jakobsson et al. 2013; Edge and Rosenberg 2014), we compute the mean maximum $F_{\mathrm{ST}}$ across all possible M values. This quantity, denoted $A\left(K\right),$ is the area between the lower and upper bounds on $F_{\mathrm{ST}}$ divided by the length of the domain for M, or $1/2.$ $A\left(K\right)$ near 0 indicates a strong constraint.

Because the lower bound on $F_{\mathrm{ST}}$ is 0 for all M between $1/2$ and 1, $A\left(K\right)$ corresponds to the area under the upper bound on $F_{\mathrm{ST}}$ divided by $1/2,$ or twice the integral of Equation 5 between $1/2$ and 1:

$$A\left(K\right)=2{\displaystyle {\int }_{M=1/2}^1\frac{\lfloor KM\rfloor +{\left\{KM\right\}}^2-K{M}^2}{KM\left(1-M\right)}dM}.$$ (7)

The integral is computed in Appendix C. We obtain

$$A\left(K\right)=1-K+2\left(K+1\right)\ln K-\frac{4}{K}{\displaystyle \sum _{i=2}^{K}i\ln i}.$$ (8)

We also obtain an asymptotic approximation $\stackrel{\sim }{A}\left(K\right)\sim A\left(K\right)$ in Appendix C, where

$$\stackrel{\sim }{A}\left(K\right)=1-\frac{\ln K}{3K}-\frac{4\ln C}{K}.$$ (9)

Here, $C\approx 1.2824$ represents the Glaisher–Kinkelin constant.

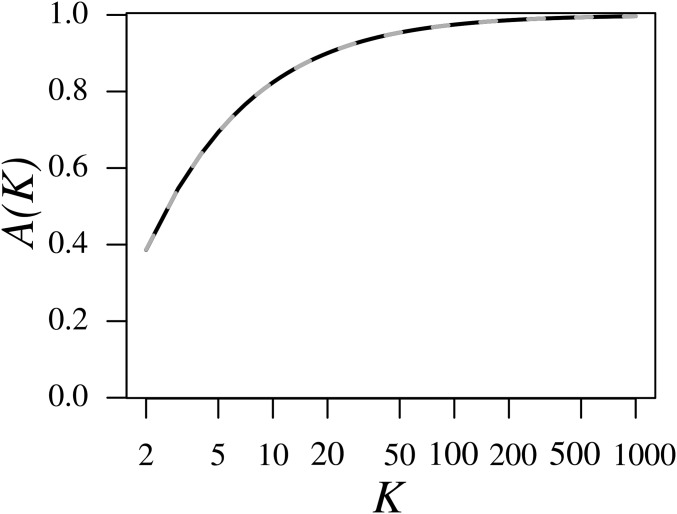
$A\left(2\right)=2\ln 2-1\approx 0.3863,$ in accord with the $K=2$ case of Jakobsson et al. (2013). Interestingly, the constraint on the mean range of $F_{\mathrm{ST}}$ disappears as $K\to \mathrm{\infty }.$ Indeed, from Equation 9, we immediately see that ${\lim }_{K\to \mathrm{\infty }}A\left(K\right)=1$ (Figure 2). As a mean of 1 indicates that $F_{\mathrm{ST}}$ ranges from 0 to 1 for all M (except possibly on a set of measure 0), for large K, the range of $F_{\mathrm{ST}}$ is approximately invariant with respect to M.

Figure 2.

The mean $A\left(K\right)$ of the upper bound on $F_{\mathrm{ST}}$ over the interval $M\in \left[1/2,1\right),$ as a function of the number of subpopulations K. $A\left(K\right)$ is computed from Equation 8 (black line). The approximation $\stackrel{\sim }{A}\left(K\right)$ is computed from Equation 9 (gray dashed line). A numerical computation of the relative error of the approximation as a function of K, $\left|A\left(K\right)-\stackrel{\sim }{A}\left(K\right)\right|/A\left(K\right),$ finds that the maximal error for $2\le K\le 1000$ is 0.00174, achieved when $K=2.$ The x-axis is plotted on a logarithmic scale.

The increase of $A\left(K\right)$ with K is monotonic (Theorem 3 of Appendix C). By numerically evaluating Equation 8, we find that although $A\left(2\right)\approx 0.3863,$ for $K\ge 7,$ $A\left(K\right)>0.75,$ and for $K\ge 46,$ $A\left(K\right)>\mathrm{0.95.}$ Nevertheless, although the mean of the upper bound on $F_{\mathrm{ST}}$ approaches 1, we have shown in Proposition 6 from Appendix B that for large K, values of M continue to exist at which the upper bound is constrained substantially below 1.

Evolutionary Processes and the Joint Distribution of M and $F_{\mathrm{ST}}$ for a Biallelic Marker and K Subpopulations

Thus far, we have described the mathematical constraint imposed on $F_{\mathrm{ST}}$ by M without respect to the frequency with which particular values of M arise in evolutionary scenarios. As an assessment of the bounds in evolutionary models can illuminate the settings in which they are most salient in population-genetic data analysis (Hedrick 2005; Whitlock 2011; Rousset 2013; Alcala et al. 2014; Wang 2015), we simulated the joint distribution of $F_{\mathrm{ST}}$ and M in three migration models, in each case relating the distribution to the mathematical bounds on $F_{\mathrm{ST}}.$ This analysis considers allele frequency distributions, and hence values of M and $F_{\mathrm{ST}},$ generated by evolutionary models.

Simulations

We simulated independent SNPs under the coalescent, using the software MS (Hudson 2002). We considered a population of total size $KN$ diploid individuals subdivided into K subpopulations of equal size N. At each generation, a proportion m of the individuals in a subpopulation originated from another subpopulation. Thus, the scaled migration rate is $4Nm,$ and it corresponds to twice the number of individuals in a subpopulation that originate elsewhere. We focus on the finite island model (Maruyama 1970; Wakeley 1998), in which migrants have the same probability $m/\left(K-1\right)$ to come from any specific other subpopulation. The finite rectangular and linear stepping-stone models generate similar results (Figures S1–S4 in File S1).

We examined three values of K (2, 7, 40) and three values of $4Nm$ (0.1, 1, 10). Note that in MS, time is scaled in units of $4N$ generations, so there is no need to specify the subpopulation sizes N. To obtain independent SNPs, we used the MS command “-s” to fix the number of segregating sites S to 1. For each parameter pair $\left(K,4Nm\right),$ we performed 100,000 replicate simulations, sampling 100 sequences per subpopulation in each replicate. $F_{\mathrm{ST}}$ values were computed from the parametric allele frequencies.

Fixing $S=1$ and accepting all coalescent genealogies entails an implicit assumption that all genealogies have equal potential to produce exactly one segregating site. We therefore also considered a different approach to generating SNPs, assuming an infinitely-many-sites model with a specified scaled mutation rate θ and discarding simulations leading to $S>1.$ We chose θ so that the expected number of segregating sites in a constant-sized population, or ${\displaystyle {\sum }_{i=1}^{KN-1}\theta /i},$ was 1. This approach produces similar results to the fixed-S simulation (Figure S5 in File S1).

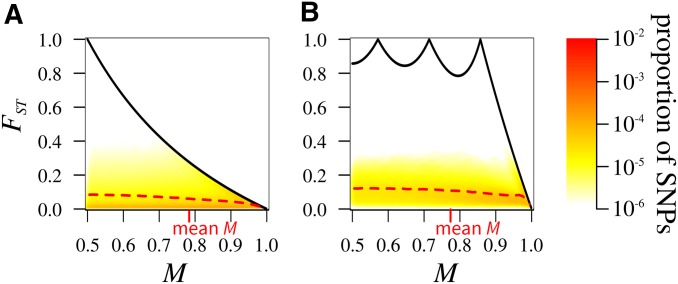
Weak migration

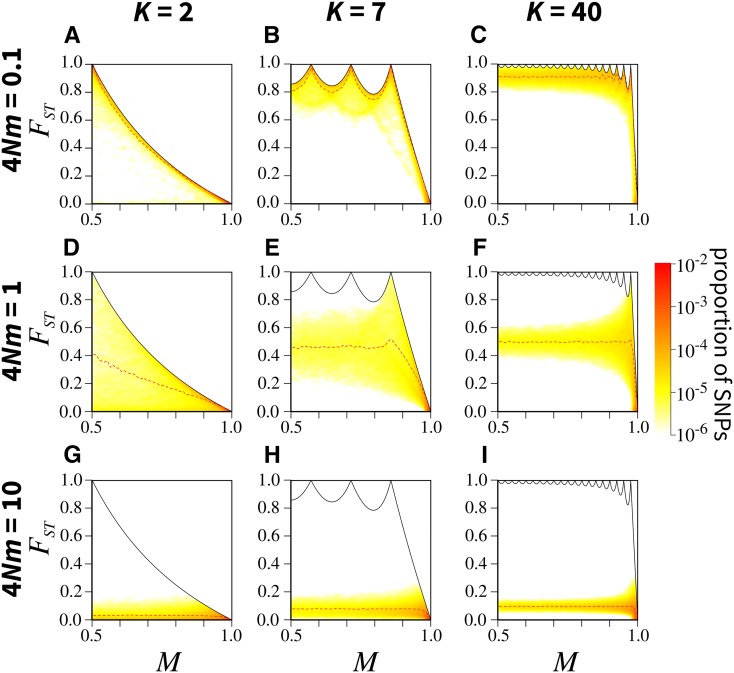
Under the island model with weak migration $\left(4Nm=0.1\right),$ the joint distribution of M and $F_{\mathrm{ST}}$ is highest near the upper bound on $F_{\mathrm{ST}}$ in terms of M, for all K (Figure 3, A–C). For $K=2,$ most SNPs have M near 0.5, representing fixation of the major allele in one subpopulation and absence in the other, and $F_{\mathrm{ST}}$ near 1 (Figure 3A). The mean $F_{\mathrm{ST}}$ in sliding windows for M closely follows the upper bound on $F_{\mathrm{ST}}.$ For $K=7,$ most SNPs have M near $4/7,$ $5/7,$ or $6/7,$ representing fixation of the major allele in four, five, or six subpopulations and absence in the others, and $F_{\mathrm{ST}}\approx 1$ (Figure 3B). The mean $F_{\mathrm{ST}}$ closely follows the upper bound. For $K=40,$ most SNPs either have M near $37/40,$ $38/40,$ or $39/40,$ and $F_{\mathrm{ST}}\approx 1,$ or $M<37/40$ and $F_{\mathrm{ST}}\approx 0.92$ (Figure 3C). The mean $F_{\mathrm{ST}}$ follows the upper bound for $M>37/40.$ For $M<37/40,$ it lies below the upper bound and does not possess its characteristic peaks.

Figure 3.

Joint density of the frequency M of the most frequent allele and $F_{\mathrm{ST}}$ in the island migration model, for different numbers of subpopulations K and scaled migration rates $4Nm$ (where N is the subpopulation size and m the migration rate): (A) $K=2,$ $4Nm=0.1;$ (B) $K=7,$ $4Nm=0.1;$ (C) $K=40,$ $4Nm=0.1;$ (D) $K=2,$ $4Nm=1;$ (E) $K=7,$ $4Nm=1;$ (F) $K=40,$ $4Nm=1;$ (G) $K=2,$ $4Nm=10;$ (H) $K=7,$ $4Nm=10;$ and (I) $K=40,$ $4Nm=10.$ The black solid line represents the upper bound on $F_{\mathrm{ST}}$ in terms of M (Equation 5); the red dashed line represents the mean $F_{\mathrm{ST}}$ in sliding windows of M of size 0.02 (plotted from 0.51 to 0.99). Colors represent the density of SNPs, estimated using a Gaussian kernel density estimate with a bandwidth of 0.007, with density set to 0 outside of the bounds. SNPs are simulated using coalescent software MS, assuming an island model of migration and conditioning on one segregating site. See Figure S5 in File S1 for an alternative algorithm for simulating SNPs. Each panel considers 100,000 replicate simulations, with 100 lineages sampled per subpopulation. Figures S2 and S3 in File S1 present similar results under finite rectangular and linear stepping-stone migration models.

We can interpret these patterns using the model of Wakeley (1999), which showed that when migration is infrequent compared to coalescence, coalescence follows two phases. In the scattering phase, lineages coalesce in each subpopulation, leading to a state with a single lineage per subpopulation. In the collecting phase, lineages from different subpopulations coalesce. As a result, considering K subpopulations with equal sample size n, when $4Nm\ll 1$, genealogies tend to have K long branches close to the root, each corresponding to a subpopulation and each leading to n shorter terminal branches. The long branches coalesce as pairs accumulate by migration in shared ancestral subpopulations. A random mutation on such a genealogy is likely to occur in one of two places. It can occur on a long branch during the collecting phase, in which case the derived allele will have frequency 1 in all subpopulations whose lineages descend from the branch, and 0 in the others. Alternatively, it can occur toward the terminal branches in the scattering phase, in which case the mutation will have frequency $p_k>0$ in one subpopulation and 0 in all others. These scenarios that are likely under weak migration, one allele fixed in some subpopulations or present only in one subpopulation, correspond closely to conditions under which the upper bound on $F_{\mathrm{ST}}$ is reached at fixed M. Thus, the properties of likely genealogies explain the proximity of $F_{\mathrm{ST}}$ to its upper bound.

Intermediate and strong migration

With intermediate migration $\left(4Nm=1\right),$ for all K, the joint density of M and $F_{\mathrm{ST}}$ is highest at lower values of $F_{\mathrm{ST}}$ than with $4Nm=0.1$ (Figure 3, D–F). For $K=2,$ most SNPs have $M>0.8$ and the mean $F_{\mathrm{ST}}$ is almost equidistant from the upper and lower bounds on $F_{\mathrm{ST}},$ nearing the upper bound as M increases (Figure 3D). For $K=7,$ most SNPs have $M>0.9;$ as was seen for $K=2,$ the mean $F_{\mathrm{ST}}$ is almost equidistant from the upper and lower bounds, moving toward the upper bound as M increases (Figure 3E). For $K=40,$ the pattern is similar, most SNPs having $M>0.95$ (Figure 3F).

Under intermediate migration, migration is sufficient that more mutations than in the weak-migration case generate polymorphism in multiple subpopulations. A random mutation is likely to occur on a branch that leads to many terminal branches from the same subpopulation, but also to branches from other subpopulations. Thus, the allele is likely to have intermediate frequency in multiple subpopulations. This setting does not generate the conditions under which the upper bound on $F_{\mathrm{ST}}$ is reached, so that except at the largest M, intermediate migration leads to values farther from the upper bound than in the weak-migration case. For large M, the rarer allele is likely to be only in one subpopulation, so that $F_{\mathrm{ST}}$ is nearer to the upper bound.

With strong migration $\left(4Nm=10\right),$ the joint density of M and $F_{\mathrm{ST}}$ nears the lower bound (Figure 3, G–I). For each K, most SNPs have $M>0.9$ and $F_{\mathrm{ST}}\approx 0,$ with the mean $F_{\mathrm{ST}}$ increasing somewhat as K increases. Under strong migration, because lineages can migrate between subpopulations quickly, they can also coalesce quickly, irrespective of their subpopulations of origin. As a result, a random mutation is likely to occur on a branch that leads to terminal branches in many subpopulations. The allele is expected to have comparable frequency in all subpopulations, so that $F_{\mathrm{ST}}$ is likely to be small. This scenario corresponds to the conditions under which the lower bound on $F_{\mathrm{ST}}$ is approached.

Proximity of the joint density of M and F_ST to the upper bound

To summarize features of the relationship of $F_{\mathrm{ST}}$ to the upper bound seen in Figure 3, we can quantify the proximity of the joint density of M and $F_{\mathrm{ST}}$ to the bounds on $F_{\mathrm{ST}}.$ For a set of Z loci, denote by $F_z$ and $M_z$ the values of $F_{\mathrm{ST}}$ and M at locus z. The mean $F_{\mathrm{ST}}$ for the set, or ${\overline{F}}_{\mathrm{ST}},$ is

$${\overline{F}}_{\mathrm{ST}}=\frac{1}{Z}{\displaystyle \sum _{z=1}^Z{F}_z}.$$ (10)

Using Equation 5, a corresponding mean maximum $F_{\mathrm{ST}}$ given the observed $M_z,$ $z=1,2,\dots ,Z,$ denoted ${\overline{F}}_{\max },$ is

$${\overline{F}}_{\text{m}ax}=\frac{1}{Z}{\displaystyle \sum _{z=1}^Z\frac{\lfloor K{M}_z\rfloor +{\left\{K{M}_z\right\}}^2-K{M}_z^2}{K{M}_z\left(1-M_z\right)}}.$$ (11)

The ratio ${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max }$ gives a sense of the proximity of the $F_{\mathrm{ST}}$ values to their upper bounds: it ranges from 0, when $F_{\mathrm{ST}}$ values at all SNPs equal their lower bounds, to 1, when $F_{\mathrm{ST}}$ values at all SNPs equal their upper bounds.

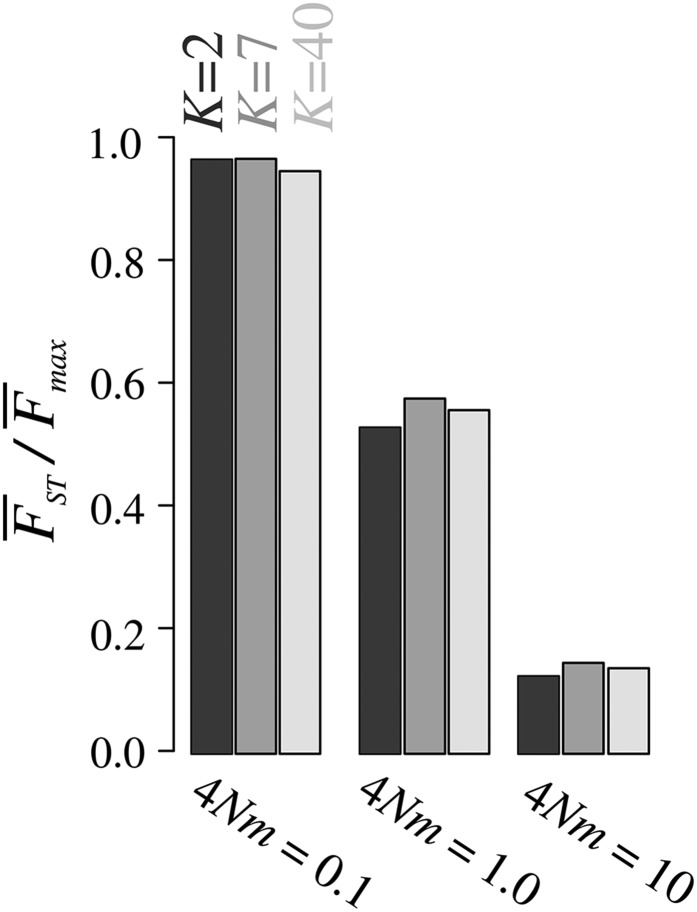
Figure 4 shows the ratio ${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max }$ under the island model for different values of K and $4Nm.$ For each value of the number of subpopulations, ${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max }$ decreases with $4Nm.$ This result summarizes the influence of the migration rate observed in Figure 3: $F_{\mathrm{ST}}$ values tend to be close to the upper bound under weak migration, and near the lower bound under strong migration. ${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max }$ is only minimally influenced by the number of subpopulations K (Figure 4). Even though the upper bound on $F_{\mathrm{ST}}$ in terms of M is strongly affected by K, the proximity of $F_{\mathrm{ST}}$ to the upper bound is similar across K values.

Figure 4.

${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max },$ the ratio of the mean $F_{\mathrm{ST}}$ to the mean maximal $F_{\mathrm{ST}}$ given the observed frequency M of the most frequent allele, as a function of the number of subpopulations K and the scaled migration rate $4Nm$ for the island migration model. Colors represent values of K. $F_{\mathrm{ST}}$ values are computed from coalescent simulations using MS for 10,000 independent SNPs and 100 lineages sampled per subpopulation. ${\overline{F}}_{max}$ is computed from Equation 11. Figure S4 in File S1 presents similar results under rectangular and linear stepping-stone migration models.

Application to Human Genomic Data

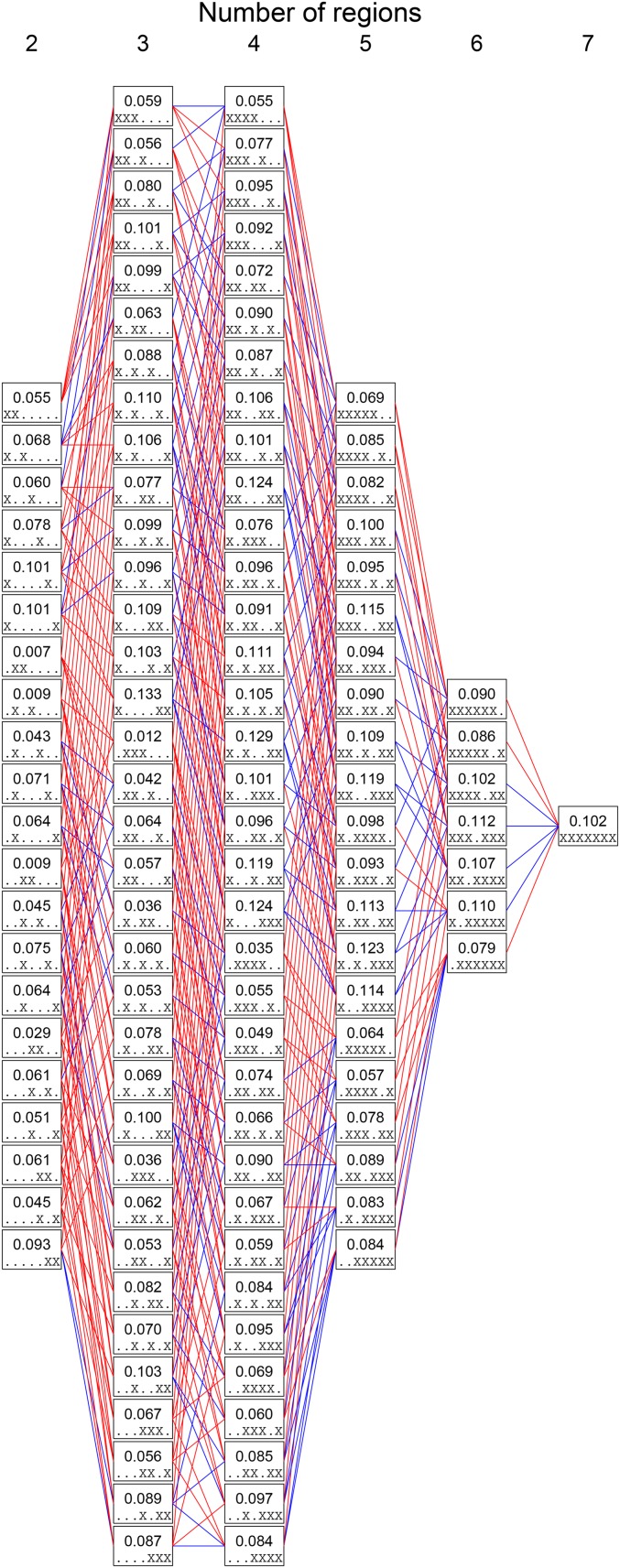
We now use our theoretical results to explain observed patterns of human genetic differentiation, and in particular, to explain the impact of the number of subpopulations. We examine data from Li et al. (2008) on 577,489 SNPs from 938 individuals of the Human Genome Diversity Panel (HGDP) (Cann et al. 2002), as compiled by Pemberton et al. (2012). We use the same division of the individuals into seven geographic regions that was examined by Li et al. (2008) (Africa, Middle East, Europe, Central and South Asia, East Asia, Oceania, and America). Previous studies of these individuals have used $F_{\mathrm{ST}}$ to compare differentiation in regions with different numbers of subpopulations sampled (Rosenberg et al. 2002; Ramachandran et al. 2004; Rosenberg 2011).

We computed the parametric allele frequencies for each region, averaging across regions to obtain the frequency M of the most frequent allele. We then computed $F_{\mathrm{ST}}$ for each SNP, averaging $F_{\mathrm{ST}}$ values across SNPs to obtain the overall $F_{\mathrm{ST}}$ for the full SNP set. To assess the impact of the number of subpopulations K on the relationship between M and $F_{\mathrm{ST}},$ we computed $F_{\mathrm{ST}}$ for all 120 sets of two or more geographic regions (Figure 5). The 21 pairwise $F_{\mathrm{ST}}$ values range from 0.007 (between Middle East and Europe) to 0.101 (Africa and America), with a mean of 0.057, SD of 0.027, and median of 0.061. $F_{\mathrm{ST}}$ is substantially larger for sets of three geographic regions. The smallest value is larger, 0.012 (Middle East, Europe, Central/South Asia); as is the largest value, 0.133 (Africa, Oceania, America); the mean of 0.076; and the median of 0.089. Among the $21\times 5=105$ ways of adding a third region to a pair of regions, 83 produce an increase in $F_{\mathrm{ST}}.$ For 17 sets of three regions, the value of $F_{\mathrm{ST}}$ exceeds that of each of its three component pairs.

Figure 5.

Mean $F_{\mathrm{ST}}$ values across loci for sets of geographic regions. Each box represents a particular combination of two, three, four, five, six, or all seven geographic regions. Within a box, the numerical value shown is $F_{\mathrm{ST}}$ among the regions. The regions considered are indicated by the pattern of “.” and “X” symbols within the box, with X indicating inclusion and “.” indicating exclusion. From left to right, the regions are Africa, Middle East, Europe, Central/South Asia, East Asia, Oceania, and America. Thus, for example, X...X.. indicates the subset {Africa, East Asia}. Lines are drawn between boxes that represent nested subsets. A line is colored red if the larger subset has a higher $F_{\mathrm{ST}}$ value, and blue if it has a lower $F_{\mathrm{ST}}.$ Computations rely on 577,489 SNPs from the HGDP.

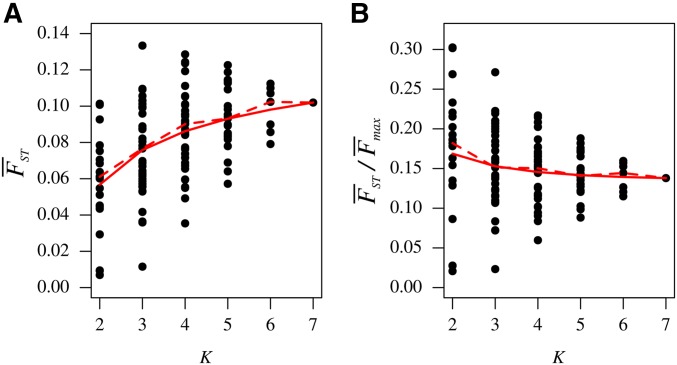
The pattern of increase of $F_{\mathrm{ST}}$ with the inclusion of additional subpopulations can be seen in Figure 6A, which plots the $F_{\mathrm{ST}}$ values from Figure 5 as a function of K. The magnitude of the increase is greatest from $K=2$ to $K=3,$ decreasing with increasing K. From $K=3$ to 4, 82 of 140 additions of a region increase $F_{\mathrm{ST}};$ 54 of 105 produce an increase from $K=4$ to 5; 21 of 42 from $K=5$ to 6; and 3 of 7 from $K=6$ to 7. The seven-region $F_{\mathrm{ST}}$ of 0.102 exceeds all the pairwise $F_{\mathrm{ST}}$ values.

Figure 6.

$F_{\mathrm{ST}}$ values for sets of geographic regions as a function of K, the number of regions considered. (A) ${\overline{F}}_{\mathrm{ST}}$ computed using Equation 10. (B) ${\overline{F}}_{\mathrm{ST}}/{\overline{F}}_{\max }$ computed using Equation 11. For each subset of populations, the value of $F_{\mathrm{ST}}$ is taken from Figure 5. The mean across subsets for a fixed K appears as a solid red line, and the median as a dashed red line.

The larger $F_{\mathrm{ST}}$ values with increasing K can be explained by the difference in constraints on $F_{\mathrm{ST}}$ in terms of M (Figure 7). For fixed M, as we saw in the increase of $A\left(K\right)$ with K (Figure 2), the permissible range of $F_{\mathrm{ST}}$ values is smaller on average for $F_{\mathrm{ST}}$ values computed among smaller sets of populations than among larger sets. For example, the maximal $F_{\mathrm{ST}}$ value at the mean M of 0.76 observed in pairwise comparisons is 0.33 for $K=2$ (black line in Figure 7A), while the maximal $F_{\mathrm{ST}}$ value at the mean M of 0.77 observed for the global comparison of seven regions is 0.86 for $K=7$ (Figure 7B). Given the stronger constraint in pairwise calculations, it is not unexpected that pairwise $F_{\mathrm{ST}}$ values would be smaller than the values computed with more regions, such as in the seven-region computation. Interestingly, the effect of K on $F_{\mathrm{ST}}$ is largely eliminated when $F_{\mathrm{ST}}$ values are normalized by their maxima (Figure 6B). The normalization, which takes both K and M into account, generates nearly constant means and medians of $F_{\mathrm{ST}}$ as functions of K, with higher values for $K=2.$

Figure 7.

Joint density of the frequency M of the most frequent allele and $F_{\mathrm{ST}}$ in human population-genetic data, considering 577,489 SNPs. (A) $F_{\mathrm{ST}}$ computed for pairs of geographic regions. The density is evaluated from the set of $F_{\mathrm{ST}}$ values for all 21 pairs of regions. (B) $F_{\mathrm{ST}}$ computed among $K=7$ geographic regions. The figure design follows Figure 3.

Data availability

MS commands for the coalescent simulations appear in File S2. See Li et al. (2008) for the human SNP data.

Discussion

We have evaluated the constraint imposed by the frequency M of the most frequent allele at a biallelic locus on the range of $F_{\mathrm{ST}},$ for arbitrarily many subpopulations. Although $F_{\mathrm{ST}}$ is unconstrained in the unit interval when $M=i/K$ for integers i satisfying $\lceil K/2\rceil \le i\le K-1,$ it is constrained below 1 for all other M. We have found that the number of subpopulations K has considerable impact on the range of $F_{\mathrm{ST}},$ with a weaker constraint on $F_{\mathrm{ST}}$ as K increases. As shown by Jakobsson et al. (2013) for $K=2,$ across possible values of M, $F_{\mathrm{ST}}$ is restricted to 38.63% of the possible space. For $K=100,$ however, $F_{\mathrm{ST}}$ can occupy 97.47% of the space. Although the mean over M values of the permissible interval for $F_{\mathrm{ST}}$ approaches the full unit interval as $K\to \mathrm{\infty },$ for any K, an allele frequency $M<\left(K-1\right)/K$ exists for which the maximal $F_{\mathrm{ST}}$ is lower than $2\sqrt{2}-2.$

Multiple studies have highlighted the relationship between $F_{\mathrm{ST}}$ and M in two subpopulations for biallelic markers (Rosenberg et al. 2003; Maruki et al. 2012) and, more generally, for an unspecified (Jakobsson et al. 2013) or specified number of alleles (Edge and Rosenberg 2014). We have extended these results to the case of biallelic markers in a specified but arbitrary number of subpopulations, comprehensively describing the relationship between $F_{\mathrm{ST}}$ and M for the biallelic case. The study is part of an increasing body of work characterizing the mathematical relationship of population-genetic statistics with quantities that constrain them (Hedrick 1999, 2005; Rosenberg and Jakobsson 2008; Reddy and Rosenberg 2012). As we have seen, such relationships contribute to understanding the behavior of the statistics in evolutionary models and to interpreting counterintuitive results in human population genetics.

Properties of F_ST in evolutionary models

Our work extends classical results about the impact of evolutionary processes on $F_{\mathrm{ST}}$ values. Wright (1951) showed that in an equilibrium population, $F_{\mathrm{ST}}$ is expected to be near 1 if migration is weak, and near 0 if migration is strong. On the basis of our simulations, we can more precisely formulate this proposition: considering a SNP at frequency M in an equilibrium population, $F_{\mathrm{ST}}$ is expected to be near its upper bound in terms of M if migration is weak and near 0 if migration is strong. This formulation of Wright’s proposition makes it possible to explain why SNPs subject to the same migration process can display a variety of $F_{\mathrm{ST}}$ patterns; indeed, under weak migration, we expect $F_{\mathrm{ST}}$ values to mirror the considerable variation in the upper bound on $F_{\mathrm{ST}}$ in terms of M.

Lower F_ST values in pairwise comparisons than in comparisons of more subpopulations

$F_{\mathrm{ST}}$ values have often been compared across computations with different numbers of subpopulations. Such comparisons appear frequently, for example, in studies of domesticated animals such as horses, pigs, and sheep (Cañon et al. 2000; Kim et al. 2005; Lawson Handley et al. 2007). In human populations, table 1 of the microsatellite study of Rosenberg et al. (2002) presents comparisons of $F_{\mathrm{ST}}$ values for scenarios with K ranging from 2 to 52. Table 3 of Rosenberg et al. (2006) compares $F_{\mathrm{ST}}$ values for microsatellites and biallelic indels in population sets with K ranging from 2 to 18. Major SNP studies have also compared $F_{\mathrm{ST}}$ values for scenarios with $K=2$ and $K=3$ groups (Hinds et al. 2005; International HapMap Consortium 2005).

Our results suggest that such comparisons between $F_{\mathrm{ST}}$ values with different K can hide an effect of the number of subpopulations, especially when some of the comparisons involve the most strongly constrained case of $K=2.$ For human data, we found that owing to a difference in the $F_{\mathrm{ST}}$ constraint for different K values, pairwise $F_{\mathrm{ST}}$ values between continental regions were consistently lower than $F_{\mathrm{ST}}$ values computed using three or more regions, and sets of three regions were identified for which the $F_{\mathrm{ST}}$ value exceeded the values for all three pairs of regions in the set. The effect of K might help illuminate why SNP-based pairwise human $F_{\mathrm{ST}}$ values (table S11 of 1000 Genomes Project Consortium 2012) are generally smaller than estimates that use all populations together (11.1% of genetic variance due to between-region or between-population differences; Li et al. 2008). We find that comparing $F_{\mathrm{ST}}$ values with different choices of K can generate as much difference—twofold—as comparing $F_{\mathrm{ST}}$ with different marker types (Holsinger and Weir 2009). This substantial impact of K on $F_{\mathrm{ST}}$ merits further attention.

Consequences for the use of F_ST as a test statistic

The effects of constraints on $F_{\mathrm{ST}}$ extend beyond the use of $F_{\mathrm{ST}}$ as a statistic for genetic differentiation. In F_ST-based genome scans for local adaptation, tracing to the work of Lewontin and Krakauer (1973), a hypothesis of spatially divergent selection at a candidate locus is evaluated by comparing $F_{\mathrm{ST}}$ at the locus with the $F_{\mathrm{ST}}$ distribution estimated from a set of putatively neutral loci. Under this test, $F_{\mathrm{ST}}$ values smaller or larger than expected by chance are interpreted as being under stabilizing or divergent selection, respectively. Modern versions of this approach compare $F_{\mathrm{ST}}$ values at single loci with the distribution across the genome (Beaumont and Nichols 1996; Akey et al. 2002; Foll and Gaggiotti 2008; Bonhomme et al. 2010; Günther and Coop 2013).

The constraints on $F_{\mathrm{ST}}$ in our work and the work of Jakobsson et al. (2013) and Edge and Rosenberg (2014) suggest that $F_{\mathrm{ST}}$ values strongly depend on the frequency of the most frequent allele. Consequently, we expect that $F_{\mathrm{ST}}$ outlier tests that do not explicitly take into account this constraint will result in a deficit of power at loci with high- and low-frequency alleles. Because pairwise $F_{\mathrm{ST}}$ and $F_{\mathrm{ST}}$ values in many populations have different constraints, we predict that the effect of the constraint on outlier tests relying on a single global $F_{\mathrm{ST}}$ (e.g., Beaumont and Nichols 1996; Foll and Gaggiotti 2008) will be smaller than in tests relying on pairwise $F_{\mathrm{ST}}$ (e.g., Günther and Coop 2013).

F_ST as a statistic or as a parameter

The perspective we used in obtaining $F_{\mathrm{ST}}$ bounds treats $F_{\mathrm{ST}}$ as a mathematical function of allele frequencies rather than as a population-genetic parameter. Thus, the starting point for our mathematical analysis (Equation 3) is that the allele frequencies are mathematical constants rather than random outcomes of an evolutionary process.

In the alternative perspective that $F_{\mathrm{ST}}$ is a parameter rather than a statistic, both the sample of alleles drawn from a set of subpopulations and the sample of subpopulations drawn from a larger collection of subpopulations are treated as random. An analysis of mathematical bounds analogous to our analysis of Equation 3 in terms of M would then investigate bounds on estimators of $F_{\mathrm{ST}},$ where the value of the estimator is bounded in terms of the largest sample allele frequency. In this perspective, the estimator of Weir and Cockerham (1984) for a biallelic locus $(\widehat{\theta };$ Weir 1996, p. 173), under an assumption of equal sample sizes in the K subpopulations and either haploid data or a random union of gametes in diploids, is

$$\widehat{\theta }=\frac{s^2-\frac{1}{2n-1}\left[\stackrel{\sim }{M}\left(1-\stackrel{\sim }{M}\right)-\frac{K-1}{K}{s}^2\right]}{\stackrel{\sim }{M}\left(1-\stackrel{\sim }{M}\right)+\frac{s^2}{K}}.$$ (12)

Here, $2n$ is the sample size per subpopulation (n diploid individuals or $2n$ haploids), $\stackrel{\sim }{M}$ is the mean sample frequency of the most frequent allele across subpopulations, and $s^2=\left[1/\left(K-1\right)\right]{\displaystyle {\sum }_{k=1}^K{\left({\stackrel{\sim }{p}}_k-\stackrel{\sim }{M}\right)}^2}$ is the empirical variance of the sample frequency ${\stackrel{\sim }{p}}_k$ of the most frequent allele across subpopulations.

Although Equation 12 has more terms than Equation 3, it can be shown that for fixed $\stackrel{\sim }{M}$ with $1/2\le \stackrel{\sim }{M}<1$ and fixed $K\ge 2$ and $2n\ge 2,$ $s^2$ and hence $\widehat{\theta }$ are minimized and maximized under corresponding conditions to those that minimize and maximize Equation 3. In particular, Theorem 1 applies to ${\left\{{\stackrel{\sim }{p}}_k\right\}}_{k=1}^K,$ with ${\displaystyle {\sum }_{k=1}^K{\stackrel{\sim }{p}}_k}=K\stackrel{\sim }{M}.$ We then expect that corresponding mathematical results to those seen for $F_{\mathrm{ST}}$ as computed in Equation 3 will hold for $\widehat{\theta }$ from Equation 12. Such computations indicate that our “statistic” perspective on $F_{\mathrm{ST}}$ generates mathematical results of interest to a “parameter” interpretation of $F_{\mathrm{ST}}.$

Conclusions

Many recent articles have noted that $F_{\mathrm{ST}}$ often behaves counterintuitively (Whitlock 2011; Alcala et al. 2014; Wang 2015), for example, indicating low differentiation in cases in which populations do not share any alleles (Balloux et al. 2000; Jost 2008) or suggesting less divergence among populations than is visible in clustering analyses (Tishkoff et al. 2009; Algee-Hewitt et al. 2016). It has thus become clear that observed $F_{\mathrm{ST}}$ patterns often trace to peculiar mathematical properties of F_ST—in particular its relationship to other statistics such as homozygosity or allele frequency—instead of to biological phenomena of interest. Our work here, extending approaches of Jakobsson et al. (2013) and Edge and Rosenberg (2014), seeks to characterize those properties, so that the influence of mathematical constraints on $F_{\mathrm{ST}}$ can be disentangled from biological phenomena.

One response to the dependence of $F_{\mathrm{ST}}$ on M may be to compute $F_{\mathrm{ST}}$ only when allele frequencies lie in a specific class, such as $M\le \mathrm{0.95.}$ Such choices can potentially avoid a misleading interpretation that a genetic differentiation measure is low in scenarios when minor alleles, though rare, are in fact private to single populations. We note, however, that the dependence of $F_{\mathrm{ST}}$ spans the full range of values of M, and exists for values of M both above and below a choice of cutoff. In addition, this dependence varies with the number of subpopulations K, so that use of the same cutoff could have a different effect on $F_{\mathrm{ST}}$ values in scenarios with different numbers of subpopulations.

In a potentially more informative approach, addressing the mathematical dependence of $F_{\mathrm{ST}}$ on the within-subpopulation mean heterozygosity $H_{\mathrm{S}},$ Wang (2015) has proposed plotting the joint distribution of $H_{\mathrm{S}}$ and $F_{\mathrm{ST}}$ to assess the correlation between the two statistics. Using the island model, Wang (2015) argued that when $H_{\mathrm{S}}$ and $F_{\mathrm{ST}}$ are uncorrelated, $F_{\mathrm{ST}}$ is expected to be more revealing about the demographic history of a species than when they are strongly correlated and $F_{\mathrm{ST}}$ merely reflects the within-subpopulation diversity. Our results suggest a related framework: studies can compare plots of the joint distribution of M and $F_{\mathrm{ST}}$ with the bounds on $F_{\mathrm{ST}}$ in terms of M. This framework, which examines constraints on $F_{\mathrm{ST}}$ in terms of allele frequencies in the total population, complements that of Wang (2015), which considers constraints in terms of subpopulation allele frequencies. Such analyses, considering $F_{\mathrm{ST}}$ together with additional measures of allele frequencies, are desirable in diverse scenarios for explaining counterintuitive $F_{\mathrm{ST}}$ phenomena, for avoiding overinterpretation of $F_{\mathrm{ST}}$ values, and for making sense of $F_{\mathrm{ST}}$ comparisons across settings that have a substantial difference in the nature of one or more underlying parameters.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.199141/-/DC1.

Appendix A: Demonstration of Equation 4

This appendix provides the derivation of the upper bound on ${\displaystyle {\sum }_{k=1}^K{p}_k^2}$ as a function of K and M.

Theorem 1. Suppose $\sigma >0$ and $K\ge \lfloor \sigma \rfloor +1$ are specified, where K is an integer. Considering all sequences ${\left\{p_k\right\}}_{k=1}^K$ with $p_k\in \left[0,1\right],$${\displaystyle {\sum }_{k=1}^K{p}_k}=\sigma ,$ and $k<\ell$ implies $p_k<p_{\ell },$${\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}{p}_k^2}$ is maximal if and only if $p_k=1$ for $1\le k\le \lfloor \sigma \rfloor ,$$p_{\lfloor \sigma \rfloor +1}=\sigma -\lfloor \sigma \rfloor ,$ and $p_k=0$ for $k>\lfloor \sigma \rfloor +1,$ and its maximum is ${\left(\sigma -\lfloor \sigma \rfloor \right)}^2+\lfloor \sigma \rfloor .$

Proof. This theorem is a special case of lemma 3 from Rosenberg and Jakobsson (2008), which states (changing notation for some of the variables to avoid confusion): “Suppose $A>0$ and $C>0$ and that $\lceil C/A\rceil$ is denoted L. Considering all sequences ${\left\{p_i\right\}}_{i=1}^{\mathrm{\infty }}$ with $p_i\in \left[0,A\right],$ ${\displaystyle {\sum }_{i=1}^{\mathrm{\infty }}{p}_i}=C,$ and $i<j$ implies $p_i\ge p_j,$ $H\left(p\right)={\displaystyle {\sum }_{i=1}^{\mathrm{\infty }}{p}_i^2}$ is maximal if and only if $p_i=A$ for $1\le i\le L-1,$ $p_L=C-\left(L-1\right)A,$ and $p_i=0$ for $i>L,$ and its maximum is $L\left(L-1\right)A^2-2C\left(L-1\right)A+C^2.$”

In our special case, we apply the lemma with $A=1$ and $C=\sigma .$ We also restrict consideration to sequences of finite rather than infinite length; however, our condition $K\ge \lfloor \sigma \rfloor +1$ for the number of terms in the sequence guarantees that the maximum in the case of infinite sequences, which requires $\lceil \sigma \rceil \le \lfloor \sigma \rfloor +1$ nonzero terms, is attainable with sequences of the finite length we consider. For convenience in numerical computations, we state our result using the floor function rather than the ceiling function, requiring some bookkeeping to obtain our corollary.

If σ is not an integer, then in lemma 3 of Rosenberg and Jakobsson (2008), $L=\lfloor \sigma \rfloor +1,$ and the maximum occurs with $p_1=p_2=\dots =p_{\lfloor \sigma \rfloor }=1,$ $p_{\lfloor \sigma \rfloor +1}=\sigma -\lfloor \sigma \rfloor ,$ and $p_k=0$ for $k>\lfloor \sigma \rfloor +1,$ equaling $L\left(L-1\right)A^2-2C\left(L-1\right)A+C^2=\left(\lfloor \sigma \rfloor +1\right)\lfloor \sigma \rfloor -2\sigma \lfloor \sigma \rfloor +{\sigma }^2.$

If σ is an integer, then $\lfloor \sigma \rfloor =\lceil \sigma \rceil =\sigma ,$ and the maximum occurs with $p_1=p_2=\dots =p_{\sigma }=1,$ $p_{\sigma +1}=\sigma -\lfloor \sigma \rfloor =0,$ and $p_k=0$ for $k>\sigma +1,$ equaling $L\left(L-1\right)A^2-2C\left(L-1\right)A+C^2=\lfloor \sigma \rfloor \left(\lfloor \sigma \rfloor -1\right)-2\sigma \left(\lfloor \sigma \rfloor -1\right)+{\sigma }^2.$

In both cases, the maximum simplifies to ${\left(\sigma -\lfloor \sigma \rfloor \right)}^2+\lfloor \sigma \rfloor ,$ noting that $\lfloor \sigma \rfloor =\lceil \sigma \rceil =\sigma$ in the latter case.□

In our application of the theorem in the main text, the definition of M gives ${\displaystyle {\sum }_{k=1}^K{p}_k}=KM,$ so that $KM$ plays the role of σ. We thus obtain that the maximal value of ${\displaystyle {\sum }_{k=1}^K{p}_k^2}$ for sequences ${\left\{p_k\right\}}_{k=1}^K$ with $p_k\in \left[0,1\right],$ $k<\ell$ implies $p_k<p_{\ell },$ and ${\displaystyle {\sum }_{k=1}^K{p}_k}=KM$ is ${\left(KM-\lfloor KM\rfloor \right)}^2+\lfloor KM\rfloor$ with equality if and only if $p_k=1$ for $1\le k\le \lfloor KM\rfloor ,$ $p_{\lfloor KM\rfloor +1}=\left\{KM\right\},$ and $p_k=0$ for $k>\lfloor KM\rfloor +1.$ Considering all sequences ${\left\{p_k\right\}}_{k=1}^K$ with $p_k\in \left[0,1\right]$ and not necessarily ordered such that $k<\ell$ implies $p_k<p_{\ell },$ the maximum is achieved when any $\lfloor KM\rfloor$ terms equal 1, one term is $\left\{KM\right\},$ and remaining terms are 0.

Appendix B: Local Minima of the Upper Bound on F_ST

This appendix derives the positions and values of the local minima in the upper bound on $F_{\mathrm{ST}}$ in terms of M (Equation 5).

Positions of the Local Minima

To derive the positions of the local minima of the upper bound on $F_{\mathrm{ST}}$ in terms of M, we study the function $Q_i\left(x\right)$ (Equation 6) on the interval $\left[0,1\right)$ for x, where $i=\lfloor KM\rfloor$ and $x=KM-i,$ so that $M=\left(i+x\right)/K.$ Recall that K and i are integers with $K\ge 2$ and i in $\left[\lfloor K/2\rfloor ,K-1\right].$ Note that $x<1$ ensures that $M<1,$ in accord with our assumption of a polymorphic locus.

Theorem 2. Consider fixed integers $K\ge 2$ and i in $\left[\lfloor K/2\rfloor ,K-1\right].$

1. $Q_i\left(x\right)$ has no local minimum on $\left[0,1\right)$ for $K=2$ or for $i=K-1.$

2. For $K\ge 3$ and i in $\left[\lfloor K/2\rfloor ,K-2\right],$ $Q_i\left(x\right)$ has a unique local minimum on the interval $\left[0,1\right)$ for x, with position denoted $x_{\min }.$

3. For odd $K\ge 3$ and $i=\left(K-1\right)/2,$ $x_{\min }=1/2.$

4. For all other $\left(K,i\right)$ with $K\ge 3$ and i in $\left[\lfloor K/2\rfloor ,K-2\right],$ $x_{\min }=\lambda \left(K,i\right),$ where

   $$\lambda \left(K,i\right)=\frac{i\left(K-i\right)-\sqrt{i\left(i+1\right)\left(K-i\right)\left(K-i-1\right)}}{2i-K+1}.$$ (B1)

Proof. We take the derivative of $Q_i\left(x\right):$

$$\frac{d{Q}_i\left(x\right)}{dx}=\frac{-K\left(2i-K+1\right)x^2+2iK\left(K-i\right)x-iK\left(K-i\right)}{{\left(i+x\right)}^2{\left(K-i-x\right)}^2}.$$ (B2)

As $1/2\le M=\left(i+x\right)/K<1,$ the denominator in Equation B2 is nonzero, and $d{Q}_i\left(x\right)/dx=0$ is equivalent to a quadratic equation in x:

$$-K\left(2i-K+1\right)x^2+2iK\left(K-i\right)x-iK\left(K-i\right)=0.$$ (B3)

If $i=\left(K-1\right)/2,$ then the quadratic term in Equation B3 vanishes and Equation B3 becomes a linear equation in x, with solution $x=1/2.$ That the solution is a local minimum follows from the continuity of $Q_i\left(x\right)$ on $\left[0,1\right)$ together with the fact that $Q_i\left(0\right)=Q_i\left(1\right)=1$ and $Q_i\left(x\right)<1$ for $0<x<1.$ Consequently, if K is odd, then the local minimum for $i=\left(K-1\right)/2$ occurs at $M=\left(i+x\right)/K=1/2,$ the lowest possible value of M. This establishes (iii).

Excluding $i=\left(K-1\right)/2$ for odd K, for all $i\in \left[\lfloor K/2\rfloor ,K-2\right]$ with $K\ge 3,$ Equation B3 has a unique solution in $\left[0,1\right);$ this solution has $x=\lambda \left(K,i\right)$ (Equation B1). The other root of Equation B3 exceeds 1. That $x=\lambda \left(K,i\right)$ represents a local minimum is again a consequence of the continuity of $Q_i\left(x\right)$ on $\left[0,1\right)$ together with $Q_i\left(0\right)=Q_i\left(1\right)=1$ and $Q_i\left(x\right)<1$ for $0<x<1.$ This establishes (ii) and (iv).

For the case of $i=K-1,$ Equation B3 has a double root at $x=1,$ outside the permissible domain for x, $\left[0,1\right).$ $Q_i\left(0\right)=1,$ $0\le Q_i\left(x\right)\le 1$ on $\left[0,1\right),$ and $Q_i\left(x\right)$ approaches 0 as $x\to 1.$ Consequently, $Q_i\left(x\right)$ has no local minimum for $i=K-1.$ For $K=2,$ $i=K-1$ is the only possible value of i, and $Q_i\left(x\right)$ has no local minimum. This establishes (i). □

Positions of the Local Minima for Fixed K as a Function of i

Having identified the locations of the local minima, we now explore how those locations change at fixed K with increasing i. For fixed $K\ge 3,$ we consider $x_{\min }$ from Theorem 2 as a function of i on the interval $\left[\lfloor K/2\rfloor ,K-2\right].$ It is convenient to define interval $I_{*},$ equaling $\left[K/2,K-2\right]$ for even K and $\left(\left(K-1\right)/2,K-2\right]$ for odd K.

Proposition 1. Consider a fixed integer $K\ge 3.$

1. The function $x_{\min }\left(i\right)$ increases as i increases from $\lfloor K/2\rfloor$ to $K-2.$

2. Its minimum is $x_{\min }\left[\left(K-1\right)/2\right]=1/2$ if K is odd, and $x_{\min }\left(K/2\right)=(K/4)\left(K-\sqrt{K^2-4}\right)$ if K is even.

3. Its maximum is $x_{\min }\left(1\right)=1/2$ for $K=3,$ and for $K>3$ it is

   $$x_{\min }\left(K-2\right)=\frac{2\left(K-2\right)-\sqrt{2\left(K-2\right)\left(K-1\right)}}{K-3}.$$ (B4)

Proof. By Theorem 2, for fixed $K\ge 3$ and $i\in I_{*},$ $x_{\min }\left(i\right)$ is given by Equation B1. Treating i as continuous, we take the derivative:

$$\frac{d{x}_{\min }\left(i\right)}{di}=\frac{\left[\left(K-i\right)\left(K-i-1\right)+i\left(i+1\right)\right]\left[2i\left(K-i-1\right)+K-1-2\sqrt{f\left(i\right)}\right]}{2{\left(2i-K+1\right)}^2\sqrt{f\left(i\right)}},$$

where $f\left(i\right)=i\left(i+1\right)\left(K-i\right)\left(K-i-1\right).$ Because all other terms of $d{x}_{\min }\left(i\right)/di$ are positive for i in $\left(\left(K-1\right)/2,K-2\right],$ $d{x}_{\min }\left(i\right)/di$ has the same sign as $2i\left(K-i-1\right)+K-1-2\sqrt{f\left(i\right)}.$

Rearranging terms, we have

$$\sqrt{f\left(i\right)}=\sqrt{{\left[i\left(K-i-1\right)+\frac{K-1}{2}\right]}^2-\frac{{\left(K-2i-1\right)}^2}{4}}.$$

Because $-{\left(K-2i-1\right)}^2/4<0$ for i in $\left(\left(K-1\right)/2,K-2\right],$ $\sqrt{f\left(i\right)}<\sqrt{{\left[i\left(K-i-1\right)+\left(K-1\right)/2\right]}^2}$ and $-2\sqrt{f\left(i\right)}>-2i\left(K-i-1\right)-K+1.$ Consequently, $2i\left(K-i-1\right)+K-1-2\sqrt{f\left(i\right)}>0$ for all i in $\left(\left(K-1\right)/2,K-2\right].$ Thus, $d{x}_{\min }\left(i\right)/di>0$ for all i in $I_{*},$ and $x_{\min }\left(i\right)$ increases with i in this interval.

For odd K and $i=\left(K-1\right)/2,$ Equation B1 gives ${\lim }_{i\to \left(K-1\right)/2^{+}}\lambda \left(K,i\right)=1/2.$ Thus, because $x_{\min }\left[\left(K-1\right)/2\right]=1/2$ by Theorem 2, $x_{\min }\left(i\right)$ is continuous at $\left(K-1\right)/2.$ The function $x_{\min }\left(i\right)$ therefore increases with i in the closed interval $\left[\lfloor K/2\rfloor ,K-2\right].$ This proves (i).

Because $x_{\min }\left(i\right)$ increases with i for all i in $\left[\lfloor K/2\rfloor ,K-2\right],$ $x_{\min }\left(i\right)$ is minimal when i is minimal. For odd K, the minimal value of i is $\left(K-1\right)/2.$ From Theorem 2, $x_{\min }\left[\left(K-1\right)/2\right]=1/2$ for all odd K. For even K, the minimal value of i is $K/2.$ From Theorem 2, $x_{\min }\left(K/2\right)=(K/4)\left(K-\sqrt{K^2-4}\right).$ This proves (ii).

Similarly, $x_{\min }\left(i\right)$ is maximal when i is maximal. From Theorem 2, the maximal value of i for which there exists a minimum of $Q_i\left(x\right)$ is $i=K-2,$ and the position of this local minimum is $x_{\min }\left(K-2\right)=\left[2\left(K-2\right)-\sqrt{2\left(K-2\right)\left(K-1\right)}\right]/\left(K-3\right).$ In particular, for $K=3,$ $\left(K-1\right)/2=K-2=1,$ so there is a unique local minimum at position $x_{\min }\left[\left(K-1\right)/2\right]=1/2.$ This proves (iii). □

Positions of the First and Last Local Minima as Functions of K

We now fix i and examine the effect of K on the local minimum at fixed i. We first focus on the interval closest to $M=1/2,$ the first local minimum of the upper bound on $F_{\mathrm{ST}}.$

Proposition 2. Consider integers $K\ge 3.$

1. For odd K, the relative position $x_{\min }\left[\left(K-1\right)/2\right]$ of the first local minimum does not depend on K and is $1/2.$

2. For even K, the relative position $x_{\min }\left(K/2\right)$ of the first local minimum decreases as $K\to \mathrm{\infty },$ tends to $1/2,$ and is bounded above by $4-2\sqrt{3}\approx \mathrm{0.5359.}$

Proof. For odd K, the interval closest to $M=1/2$ is $\left[1/2,1/2+1/\left(2K\right)\right).$ In this interval, from Proposition 1ii, the minimum occurs at $x_{\min }\left[\left(K-1\right)/2\right]=1/2$ irrespective of K. This proves (i).

For even K, the interval for M closest to $M=1/2$ is $\left[1/2,1/2+1/K\right).$ In this interval, from Proposition 1ii, the minimum has position $x_{\min }\left(K/2\right)=(K/4)\left(K-\sqrt{K^2-4}\right).$ The derivative of this function is

$$\frac{d{x}_{\min }\left(\frac{K}{2}\right)}{dK}=-\frac{{\left(K-\sqrt{K^2-4}\right)}^2}{4\sqrt{K^2-4}},$$

which is negative for all $K\ge 3.$ Thus, $x_{\min }\left(K/2\right)$ decreases with K for $K\ge 3.$ In addition, as $K\to \mathrm{\infty },$ $x_{\min }\left(K/2\right)\to 1/2.$ Because $x_{\min }\left(K/2\right)$ decreases with K, its maximum value is reached when K is minimal. The minimal even value of K is $K=4.$ Thus, $x_{\min }\left(K/2\right)\le x_{\min }\left(4/2\right)=4-2\sqrt{3}.$ This proves (ii). □

By Proposition 2, if K is large and even, then the first local minimum lies near the center of the interval $\left[1/2,1/2+1/K\right)$ for M.

Proposition 3. For integers $K\ge 3,$ the relative position $x_{\min }\left(K-2\right)$ of the last local minimum increases as $K\to \mathrm{\infty }$ and tends to $2-\sqrt{2}\approx \mathrm{0.5858.}$

Proof. From Theorem 2, for $K=3$ and $K=4,$ there is a single local minimum. Hence, from Proposition 2, the position of the last local minimum is $x_{\min }\left(1\right)=1/2$ for $K=3$ and $x_{\min }\left(2\right)=4-2\sqrt{3}\approx 0.5359$ for $K=4.$ The position of the last local minimum then increases from $K=3$ to $K=4.$

If $K>3,$ from Proposition 1iii, the position of the last local minimum follows Equation B4. We take the derivative

$$\frac{d{x}_{\min }\left(K-2\right)}{dK}=\frac{\left(3K-5\right)-2\sqrt{2\left(K-2\right)\left(K-1\right)}}{{\left(K-3\right)}^2\sqrt{2\left(K-2\right)\left(K-1\right)}}.$$

For $K>3,$ the denominator is positive and $d{x}_{\min }\left(K-2\right)/dK$ has the same sign as its numerator. Because for $K>3,$ ${\left(3K-5\right)}^2-8\left(K-2\right)\left(K-1\right)={\left(K-3\right)}^2>0,$ we have $3K-5>2\sqrt{2\left(K-2\right)\left(K-1\right)}$ and a positive numerator. Then $d{x}_{\text{min}}\left(K-2\right)/dK>0$ and $x_{\min }\left(K-2\right)$ increases for $K>3.$

From Equation B4, $x_{\min }\left(K-2\right)$ tends to $2-\sqrt{2}\approx 0.5858$ as $K\to \mathrm{\infty }.$ Thus, the last local minimum is not at the center of interval $I_{K-2};$ rather, it is nearer to the upper endpoint. Because $x_{\min }\left(K-2\right)$ increases with K, $x_{\min }\left(K-2\right)<{\lim }_{K\to \mathrm{\infty }}{x}_{\min }\left(K-2\right)$ and the last local maximum has position bounded above by $2-\sqrt{2}.$ □

As we have shown in Proposition 1i that for fixed K, as i increases from $\lfloor K/2\rfloor$ to $K-2,$ the relative position of the local minimum increases, this relative position is restricted in the interval $\left[x_{\min }\left(\lfloor K/2\rfloor \right),x_{\min }\left(K-2\right)\right].$ Further, because from Proposition 2, $x_{\min }\left[\left(K-1\right)/2\right]=1/2$ for odd K and $x_{\min }\left(K/2\right)>1/2$ for even K$,$ and from Proposition 3, $x_{\min }\left(K-2\right)<2-\sqrt{2},$ the relative positions of the local minima must be in the interval $\left[1/2,2-\sqrt{2}\right).$

Figure B1 illustrates as functions of K the relative positions of the first local minimum $(x_{\min }\left[\left(K-1\right)/2\right]$ for odd K and $x_{\min }\left(K/2\right)$ for even K$)$ and the last local minimum $\left(x_{\min }\left(K-2\right)\right).$ The restriction of these positions to the interval $\left[1/2,2-\sqrt{2}\right)$ is visible, with the first local minimum lying closer to the center of interval $\left[0,1\right)$ for x than the last local minimum. The decrease in the position of the first local minimum for even K alternating with values of $1/2$ for odd K (Proposition 2) and the increase in the position of the last local minimum (Proposition 3) are visible as well.

Values at the Local Minima

We obtain the value of the local minima of the upper bound on $F_{\mathrm{ST}}$ in each interval $I_i$ by substituting into Equation 6 the value of i for interval $I_i$ and its associated $x_{\min }\left(i\right)$ from Theorem 2. We obtain

$$Q_i\left[x_{\min }\left(i\right)\right]=\frac{K\left[i+x_{\min }{\left(i\right)}^2\right]-{\left[i+x_{\min }\left(i\right)\right]}^2}{\left[i+x_{\min }\left(i\right)\right]\left[K-i-x_{\min }\left(i\right)\right]}.$$ (B5)

Note that for odd K, although $\lambda \left(K,i\right)$ is undefined at $i=\left(K-1\right)/2,$ $x_{\min }\left(i\right)$ is continuous. Thus, $Q_i\left[x_{\min }\left(i\right)\right]$ is also defined and continuous for all $i\in \left[\lfloor K/2\rfloor ,K-2\right].$ We consider $Q_i$ as a function of i on this interval.

Proposition 4. For fixed $K\ge 3,$ the local minima $Q_i\left[x_{\min }\left(i\right)\right]$ decrease as i increases from $\lfloor K/2\rfloor$ to $K-2.$

Proof. We take the derivative $d{Q}_i\left[x_{\text{min}}\left(i\right)\right]/di$ for fixed K and $i\in I_{*}.$ From Equations B5 and B1,

$$\frac{d{Q}_i\left(x_{\min }\left(i\right)\right)}{di}=\frac{\sqrt{f\left(i\right)}K\left(2i-K+1\right)u\left(i\right)}{w{\left(i\right)}^2{\left[w\left(i\right)+K\left(2i-K+1\right)\right]}^2},$$

where $w\left(i\right)=\sqrt{f\left(i\right)}-i\left(i+1\right)$ and $u\left(i\right)=2\left(K^2-1\right)\sqrt{f\left(i\right)}+2\left(K^2+1\right)i^2-\left(K-1\right)\left(2i{K}^2+K^2-K+2i\right).$

For all $i\in I_{*},$ the denominator of the derivative is positive, as are $\sqrt{f\left(i\right)},$ K, and $2i-K+1.$ Hence, $d{Q}_i\left[x_{\min }\left(i\right)\right]/di$ has the same sign as $u\left(i\right).$

Because $f\left(i\right)$ decreases for $i\in \left[\left(K-1\right)/2,K-2\right],$ $\sqrt{f\left(i\right)}\ge \sqrt{f\left[\left(K-1\right)/2\right]}=\left(K^2-1\right)/4$ and $K^2-1-4\sqrt{f\left(i\right)}\ge 0.$ We factor $u\left(i\right):$

$$u\left(i\right)=2\left(K^2+1\right)\left[i-v\left(i\right)-\frac{K-1}{2}\right]\left[i+v\left(i\right)-\frac{K-1}{2}\right],$$

where $v\left(i\right)=\sqrt{\left(K^2-1\right)\left(K^2-1-4\sqrt{f\left(i\right)}\right)}/\left(2\sqrt{K^2+1}\right).$ Because $v\left(i\right)\ge 0,$ for all $i\ge \left(K-1\right)/2,$ $i+v\left(i\right)-\left(K-1\right)/2\ge 0.$ Thus, the sign of $u\left(i\right)$ is given by the sign of

$$i-v\left(i\right)-\frac{K-1}{2}=\frac{\left(2i-K+1\right)\sqrt{K^2+1}-\sqrt{\left(K^2-1\right)\left[K^2-1-4\sqrt{f\left(i\right)}\right]}}{2\sqrt{K^2+1}}.$$

For $i\in \left(\left(K-1\right)/2,K-2\right],$

$$\frac{K^2{\left(2i-K-1\right)}^4}{4{\left(K-1\right)}^2{\left(K+1\right)}^2}={\left[\frac{K^2-1}{4}-\frac{\left(K^2+1\right){\left[i-\frac{K-1}{2}\right]}^2}{K^2-1}\right]}^2-f\left(i\right)>0,$$

and hence,

$$-4\left|\frac{K^2-1}{4}-\frac{\left(K^2+1\right){\left[i-\left(K-1\right)/2\right]}^2}{K^2-1}\right|<-4\sqrt{f\left(i\right)}.$$ (B6)

The term ${\left[i-\left(K-1\right)/2\right]}^2$ increases as a function of i for $i\in \left[\left(K-1\right)/2,K-2\right].$ Hence, $\left(K^2-1\right)/4-\left\{\left(K^2+1\right){\left[i-\left(K-1\right)/2\right]}^2\right\}/\left(K^2-1\right)$ decreases with i. It is minimal at the largest value in the permissible domain for i, or $i=K-2,$ with minimum $\left[3K{\left(K-1\right)}^2-4\right]/\left[2\left(K-1\right)\left(K+1\right)\right].$ The denominator of this quantity is positive and the numerator increases with K. It is thus minimal for $K=3,$ at which $3K{\left(K-1\right)}^2-4=32>0.$ This proves that $\left[\left(K^2-1\right)/4\right]-\left\{\left(K^2+1\right){\left[i-\left(K-1\right)/2\right]}^2\right\}/\left(K^2-1\right)>0$ for $i\in [\left(K-1\right)/2,K-2].$

We can then remove the absolute value in Equation B6 and rearrange to obtain $\left(K^2+1\right){\left(2i-K+1\right)}^2<\left(K^2-1\right)\left[K^2-1-4\sqrt{f\left(i\right)}\right].$ Both sides of this inequality are positive for $i\in \left(\left(K-1\right)/2,K-2\right]$ and we can take the square root to obtain $\sqrt{K^2+1}\left(2i-K+1\right)<\sqrt{\left(K^2-1\right)\left[K^2-1-4\sqrt{f\left(i\right)}\right]}.$ Hence $i-v\left(i\right)-\left(K-1\right)/2<0$ for $i\in \left(\left(K-1\right)/2,K-2\right],$ $d{Q}_i\left[x_{\min }\left(i\right)\right]/di<0$ for $i\in I_{*},$ and the local minima $Q_i\left[x_{\min }\left(i\right)\right]$ decrease with i. □

Proposition 5. For $K=3,$ the first local minimum $Q_i\left[x_{\min }\left(i\right)\right]$ has value $2/3;$ for $K\ge 3,$ the first local minimum increases as a function of K and tends to 1 as $K\to \mathrm{\infty }.$

Proof. From Proposition 2i, for odd K, the first local minimum is reached for $i=\left(K-1\right)/2$ and $x=1/2,$ and the upper bound on $F_{\mathrm{ST}}$ is $Q_{\left(K-1\right)/2}\left(1/2\right)=1-\left(1/K\right).$ Thus, for $K=3,$ the first local minimum has value $Q_1\left(1/2\right)=2/3.$ For even K, the first local minimum is reached if $i=K/2$ and $x=x_{\min }\left(K/2\right),$ with upper bound on $F_{\mathrm{ST}}$ equal to

$$Q_{\frac{K}{2}}\left[x_{\min }\left(\frac{K}{2}\right)\right]=\frac{\left(K-2\right)\left[K\left(K+1\right)-\left(K+1\right)\sqrt{K^2-4}-2\right]}{\sqrt{K^2-4}\left(K-\sqrt{K^2-4}\right)}.$$ (B7)

Denote by ${\Delta }_1\left(K\right)=Q_{K/2}\left[x_{\min }\left(K/2\right)\right]-\left[1-1/\left(K-1\right)\right]$ the difference between the first local minimum for even K and the first local minimum for odd $K-1,$ and by ${\Delta }_2\left(K\right)=\left[1-1/\left(K+1\right)\right]-Q_{K/2}\left[x_{\min }\left(K/2\right)\right]$ the difference between the first local minimum for odd $K+1$ and the first local minimum for even K. To show that the first local minimum increases with K, we must show that for all even $K\ge 4,$ (i) ${\Delta }_1\left(K\right)>0,$ and (ii) ${\Delta }_2\left(K\right)>0.$

For (i), subtracting $1-\left[1/\left(K-1\right)\right]$ from Equation B7, we have

$${\Delta }_1\left(K\right)=\frac{\left(K-2\right)\left[\left(K+2\right)\left(K^2-K-1\right)-\sqrt{K^2-4}\left(K^2+K-1\right)\right]}{\left(K-1\right)\sqrt{K^2-4}\left(K-\sqrt{K^2-4}\right)}.$$

Because all other terms are positive for $K\ge 3,$ ${\Delta }_1\left(K\right)$ has the same sign as $\left(K+2\right)\left(K^2-K-1\right)-\sqrt{K^2-4}\left(K^2+K-1\right).$ Dividing by $\sqrt{K+2},$ this quantity in turn has the same sign as $\sqrt{K+2}\left(K^2-K-1\right)-\sqrt{K-2}\left(K^2+K-1\right).$ This last quantity is positive for $K\ge 4,$ as when we multiply it by the positive $\sqrt{K+2}\left(K^2-K-1\right)+\sqrt{K-2}\left(K^2+K-1\right),$ the result reduces simply to the number 4. This proves (i).

For (ii), subtracting Equation B7 from $1-1/\left(K+1\right),$ we have

$${\Delta }_2\left(K\right)=\frac{\left(K+2\right)\left[\sqrt{K^2-4}\left(K^2-K-1\right)-\left(K-2\right)\left(K^2+K-1\right)\right]}{\left(K+1\right)\sqrt{K^2-4}\left(K-\sqrt{K^2-4}\right)}.$$

Because all other terms are positive for $K\ge 3,$ ${\Delta }_2\left(K\right)$ has the same sign as $\sqrt{K^2-4}\left(K^2-K-1\right)-\left(K-2\right)\left(K^2+K-1\right).$ Dividing by $\sqrt{K-2},$ this quantity has the same sign as $\sqrt{K+2}\left(K^2-K-1\right)-\sqrt{K-2}\left(K^2+K-1\right),$ which was shown to be positive in the proof of (i). This demonstrates (ii).

From (i) and (ii), the value of the upper bound on $F_{\mathrm{ST}}$ at the first local minimum increases with K for all $K\ge 3.$ To see that the limiting value is 1 as $K\to \mathrm{\infty },$ we note that the subsequence of values $1-\left(1/K\right)$ at odd K tends to 1 as $K\to \mathrm{\infty }.$ As the sequence of values of the first local minimum with increasing K is monotonic and bounded above by 1, it is therefore convergent; as it has a subsequence converging to 1, the sequence converges to 1. □

Proposition 6. For $K=3,$ the last local minimum $Q_i\left[x_{\min }\left(i\right)\right]$ has value $2/3;$ for $K\ge 3,$ the last local minimum increases as a function of K and tends to $2\sqrt{2}-2$ as $K\to \mathrm{\infty }.$

Proof. From Proposition 5, for $K=3,$ the single local minimum has value $2/3.$ By Theorem 2, for $K>3,$ the last local minimum is reached when $i=K-2$ and $x=x_{\min }\left(K-2\right),$ in which case from Equations B5 and B1 the upper bound on $F_{\mathrm{ST}}$ is

$$Q_{K-2}\left[x_{\min }\left(K-2\right)\right]=\frac{2\left(K-2\right)\left[\sqrt{2}{\left(K-1\right)}^2-\sqrt{h\left(K\right)}\left(K+1\right)\right]}{\sqrt{h\left(K\right)}{\left(\sqrt{h\left(K\right)}-\sqrt{2}\right)}^2},$$ (B8)

where $h\left(K\right)=\left(K-2\right)\left(K-1\right).$

We examine the derivative of $Q_{K-2}\left[x_{\min }\left(K-2\right)\right]$ with respect to K. For $K\ge 3,$ $h\left(K\right)>0$ and

$$\frac{d{Q}_{K-2}\left[x_{\min }\left(K-2\right)\right]}{dK}=\frac{\alpha \left(K\right)\sqrt{2}}{\sqrt{h\left(K\right)}{\left(\sqrt{h\left(K\right)}-\sqrt{2}\right)}^4},$$

where $\alpha \left(K\right)=3K{\left(K-1\right)}^2-4-2\sqrt{2}\left(K-1\right)\left(K+1\right)\sqrt{h\left(K\right)}.$ For $K>3,$ the derivative has the same sign as $\alpha \left(K\right).$

We note that

$$\frac{{\left(K-3\right)}^4{K}^2}{8{\left(K-1\right)}^2{\left(K+1\right)}^2}={\left[\frac{3{\left(K-1\right)}^{2}K-4}{2\sqrt{2}\left(K-1\right)\left(K+1\right)}\right]}^2-h\left(K\right)\ge 0,$$

with equality only at $K=3.$ Because $3K{\left(K-1\right)}^2-4$ is positive for $K\ge 3,$ $\left[3K{\left(K-1\right)}^2-4\right]/\left[2\sqrt{2}\left(K-1\right)\left(K+1\right)\right]\ge \sqrt{h\left(K\right)},$ with equality only at $K=3.$ Thus, $\alpha \left(K\right)>0$ and $d{Q}_{K-2}\left[x_{\min }\left(K-2\right)\right]/dK>0$ for $K>3,$ and hence, the last local minimum increases with K.

For the limit as $K\to \mathrm{\infty },$ we take the limit of $Q_{K-2}\left[x_{\min }\left(K-2\right)\right]$ in Equation B8, obtaining $2\sqrt{2}-2\approx \mathrm{0.8284.}$ □

Appendix C: Computing the Mean Range of F_ST

This appendix provides the computation of the integral $A\left(K\right)$ (Equation 7) and its asymptotic approximation $\stackrel{\sim }{A}\left(K\right).$

Computing A(K)

To compute $A\left(K\right),$ we break the integral into a sum over intervals. If K is even, then we consider intervals $I_i=\left[i/K,\left(i+1\right)/K\right)$ with $i=K/2,\left(K/2\right)+1,\dots ,K-1.$ If K is odd, then we use intervals $I=\left[1/2,\left(K+1\right)/\left(2K\right)\right)$ and $I_i=\left[i/K,\left(i+1\right)/K\right)$ with $i=\left(K+1\right)/2,\left(K+3\right)/2,\dots ,K-1.$

By construction of $Q_i\left(x\right)$ (Equation 6), in each interval $I_i,$ the upper bound on $F_{\mathrm{ST}}$ is equal to $Q_i\left(x\right)$ with $x=\left\{KM\right\}.$ In the odd case, because $\left(K+1\right)/2$ is an integer, on interval $\left[1/2,\left(K+1\right)/\left(2K\right)\right),$ $\lfloor KM\rfloor$ has a constant value $\left(K-1\right)/2$ and $\left\{KM\right\}=KM-\left(K-1\right)/2,$ and the upper bound is equal to $Q_{\left(K-1\right)/2}\left(x\right).$ Making the substitution $x=KM-i,$ we obtain $dx=K\hspace{0.17em}dM$ and we can write Equation 7 in terms of $Q_i\left(x\right):$

$$A\left(K\right)=\{\begin{array}{ll}\frac{2}{K}{\displaystyle \sum _{i=\frac{K}{2}}^{K-1}{\displaystyle {\int }_0^1{Q}_i\left(x\right)dx}},\hfill & K\hspace{0.17em}\text{even}\hfill \\ \frac{2}{K}\left({\displaystyle {\int }_{\frac{1}{2}}^1{Q}_{\frac{K-1}{2}}\left(x\right)dx}+{\displaystyle \sum _{i=\frac{K+1}{2}}^{K-1}{\displaystyle {\int }_0^1{Q}_i\left(x\right)dx}}\right),\hfill & K\hspace{0.17em}\text{odd}.\hfill \end{array}$$ (C1)

We next use a partial fraction decomposition. For $\lfloor K/2\rfloor \le i\le K-2,$

$$Q_i\left(x\right)=1-K+\frac{i\left(i+1\right)}{i+x}+\frac{\left(K-i\right)\left(K-i-1\right)}{K-i-x},$$

$${\displaystyle {\int }_0^1{Q}_i\left(x\right)dx}=1-K+i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)+\left(K-i\right)\left(K-i-1\right)\ln \left(\frac{K-i}{K-i-1}\right).$$

For $i=K-1,$

$$Q_i\left(x\right)=1-K+\frac{i\left(i+1\right)}{i+x},$$

$${\displaystyle {\int }_0^1{Q}_{K-1}\left(x\right)dx}=1-K+\left(K-1\right)K\ln \left(\frac{K}{K-1}\right).$$

For $i=\left(K-1\right)/2,$

$${\displaystyle {\int }_{\frac{1}{2}}^1{Q}_{\frac{K-1}{2}}\left(x\right)dx}=\frac{1-K}{2}+\left(\frac{K-1}{2}\right)\left(\frac{K+1}{2}\right)\ln \left(\frac{K+1}{K-1}\right).$$

Thus, when K is even,

$$\begin{array}{c}A\left(K\right)=\frac{2}{K}{\displaystyle \sum _{i=\frac{K}{2}}^{K-1}{\displaystyle {\int }_0^1{Q}_i\left(x\right)dx}}\\ =-\frac{2}{K}{\displaystyle \sum _{i=\frac{K}{2}}^{K-1}\left(K-1\right)}+\frac{2}{K}{\displaystyle \sum _{i=\frac{K}{2}}^{K-1}\left[i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)\right]}\\ +\frac{2}{K}{\displaystyle \sum _{i=\frac{K}{2}}^{K-2}\left[\left(K-i\right)\left(K-i-1\right)\ln \left(\frac{K-i}{K-i-1}\right)\right]}\\ =1-K+\frac{2}{K}{\displaystyle \sum _{i=1}^{K-1}\left[i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)\right]}.\end{array}$$

When K is odd,

$$\begin{array}{c}A\left(K\right)=\frac{2}{K}{\displaystyle {\int }_{\frac{1}{2}}^1{Q}_{\frac{K-1}{2}}\left(x\right)dx}+\frac{2}{K}{\displaystyle \sum _{i=\frac{K+1}{2}}^{K-1}{\displaystyle {\int }_0^1{Q}_i\left(x\right)dx}}\\ =\frac{2}{K}\frac{1-K}{2}+\frac{2}{K}\left(\frac{K-1}{2}\right)\left(\frac{K+1}{2}\right)\ln \left(\frac{K+1}{K-1}\right)\\ -\frac{2}{K}{\displaystyle \sum _{i=\frac{K+1}{2}}^{K-1}\left(K-1\right)}+\frac{2}{K}{\displaystyle \sum _{i=\frac{K+1}{2}}^{K-1}\left[i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)\right]}\\ +\frac{2}{K}{\displaystyle \sum _{i=\frac{K+1}{2}}^{K-2}\left[\left(K-i\right)\left(K-i-1\right)\ln \left(\frac{K-i}{K-i-1}\right)\right]}\\ =1-K+\frac{2}{K}{\displaystyle \sum _{i=1}^{K-1}\left[i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)\right]}.\end{array}$$ (C2)

The expressions for $A\left(K\right)$ are equal for even and odd K. We can simplify further:

$$\begin{array}{c}{\displaystyle \sum _{i=1}^{K-1}i\left(i+1\right)\ln \left(\frac{i+1}{i}\right)}={\displaystyle \sum _{i=2}^K\left(i-1\right)i\ln i}-{\displaystyle \sum _{i=2}^{K-1}i\left(i+1\right)\ln i}\\ =K\left(K+1\right)\ln K-2{\displaystyle \sum _{i=2}^{K}i\ln i}.\end{array}$$ (C3)

Substituting the expression from Equation C3 into Equation C2 and simplifying, we obtain Equation 8.

Asymptotic Approximation for A(K) (Equation 9)

To asymptotically approximate $A\left(K\right),$ we first need a large-K approximation of ${\displaystyle {\sum }_{i=2}^{K}i\ln i}.$ Because ${\displaystyle {\sum }_{i=2}^{K}i\ln i}=\ln \left[H\left(K\right)\right],$ where $H\left(K\right)={\displaystyle {\prod }_{i=1}^K{i}^i}$ is the hyperfactorial function, we can use classical results about the asymptotic behavior of $H\left(K\right):$

$$\underset{K\to \mathrm{\infty }}{\lim }\frac{H\left(K\right)}{\exp \left(-\frac{K^2}{4}\right)K^{\frac{K^2}{2}+\frac{K}{2}+\frac{1}{12}}}=C,$$ (C4)

where C is the Glaisher–Kinkelin constant. Because the logarithm function is continuous at C, $\ln \left[H\left(K\right)\right]/\left[\exp \left(-K^2/4\right)K^{\left[\left(K^2/2\right)+\left(K/2\right)+\left(1/12\right)\right]}\right]$ has limit $\ln C$ as $K\to \mathrm{\infty }.$ Thus, if we write $f\left(K\right)\sim g\left(K\right)$ for two functions that satisfy ${\lim }_{K\to \mathrm{\infty }}\left[f\left(K\right)/g\left(K\right)\right]=1,$ then

$${\displaystyle \sum _{i=2}^{K}i\ln i}\sim -\frac{K^2}{4}+\left(\frac{K^2}{2}+\frac{K}{2}+\frac{1}{12}\right)\ln K+\ln C.$$ (C5)

Substituting the expression from Equation C5 into Equation 8, we obtain function $\stackrel{\sim }{A}\left(K\right)$ (Equation 9) and the relationship $\stackrel{\sim }{A}\left(K\right)\sim A\left(K\right).$

Monotonicity of Equation 8 in K

Theorem 3. $A\left(K\right)$ increases monotonically in K for $K\ge 2.$

Proof. We must show that $\Delta A\left(K\right)=A\left(K+1\right)-A\left(K\right)>0$ for all $K\ge 2.$ From the expression for $A\left(K\right)$ in Equation 8, we have:

$$\Delta A\left(K\right)=-1+2K\ln \left(1+\frac{1}{K}\right)-2\ln K+\frac{4{\displaystyle \sum _{i=2}^{K}i\ln i}}{K\left(K+1\right)}.$$ (C6)

To show that $\Delta A\left(K\right)>0,$ we find a lower bound for $\Delta A\left(K\right),$ denoted $D\left(K\right),$ and then show that $D\left(K\right)>0.$

We first find a lower bound for ${\displaystyle {\sum }_{i=2}^{K}i\ln i}.$ From the Euler–Maclaurin summation formula, we have

$${\displaystyle \sum _{i=2}^{K}i\ln i}=\left({\displaystyle {\int }_1^{K}x\ln x\hspace{0.17em}dx}\right)+\frac{K\ln K}{2}+{\displaystyle {\int }_1^K\left(\ln x+1\right)\left(x-\lfloor x\rfloor -\frac{1}{2}\right)dx}.$$

For all positive integers $i\ge 2,$

$${\displaystyle {\int }_{i-1}^i\left(\ln x+1\right)\left(x-\lfloor x\rfloor -\frac{1}{2}\right)dx}=\frac{1}{4}\left[2i-1-2i\left(i-1\right)\ln \left(\frac{i}{i-1}\right)\right].$$ (C7)

This integral can be seen to be positive from the equivalence for $i>1$ of $2i-1-2i\left(i-1\right)\ln \left(i/\left[i-1\right]\right)>0$ with $\exp \left[\left(2i-1\right)/\left[2i\left(i-1\right)\right]\right]>i/\left(i-1\right).$ This latter inequality follows from the inequality $\exp \left(x\right)>1+x+x^2/2$ for $x>0$ from the Taylor expansion of $e^x,$ noting that $1+\left(2i-1\right)/\left[2i\left(i-1\right)\right]+\left(1/2\right){\left[\left(2i-1\right)/[2i\left(i-1\right)\right]]}^2>i/\left(i-1\right).$

Consequently, as the integral in Equation C7 is positive for each $i\ge 2,$ ${\displaystyle {\int }_1^K\left(\ln x+1\right)\left[x-\lfloor x\rfloor -\left(1/2\right)\right]dx}>0,$ and

$$\begin{array}{c}{\displaystyle \sum _{i=1}^{K}i\ln i}>\left({\displaystyle {\int }_{i=1}^{K}x\ln x\hspace{0.17em}dx}\right)+\frac{K\ln K}{2}\\ =\frac{K\left(K+1\right)\ln K}{2}+\frac{1-K^2}{4}.\end{array}$$ (C8)

As a result, the following function is a lower bound for $\Delta A:$

$$\begin{array}{c}D\left(K\right)=-1+2K\ln \left(1+\frac{1}{K}\right)-2\ln K+\frac{4\left[\frac{K\left(K+1\right)\ln K}{2}+\frac{1-K^2}{4}\right]}{K\left(K+1\right)}\\ =-2+\frac{1}{K}+2K\ln \left(1+\frac{1}{K}\right).\end{array}$$

Dividing by $2K$ and substituting $u=1/K$ for $K>0,$ $D\left(K\right)>0$ if and only if $f\left(u\right)=\ln \left(1+u\right)-u+\left(u^2/2\right)>0$ for $u>0.$ It can be seen that this latter inequality holds by noting that $f\left(0\right)=0$ and $f^{\prime }\left(u\right)=\left[1/\left(1+u\right)\right]-1+u=u^2/\left(1+u\right)>0.$□

Figure B1.

The first and last local minima of $F_{\mathrm{ST}}$ as functions of the frequency M of the most frequent allele, for $K\ge 3$ subpopulations. (A) Relative positions within the interval $\left[i/K,\left(i+1\right)/K\right)$ of the first and last local minima, as functions of K. The position $x_{min}\left(i\right)$ of the local minimum in interval $I_i$ is computed from Equation B1. If K is odd, then this position is $x_{min}\left[\left(K-1\right)/2\right];$ if K is even, then it is $x_{min}\left(K/2\right).$ The position of the last local minimum is $x_{min}\left(K-2\right).$ Dashed lines indicate the smallest value for $x_{min}\left(i\right)$ of $1/2,$ and the limiting largest value of $2-\sqrt{2}.$ (B) The value of the upper bound on $F_{\mathrm{ST}}$ at the first and last local minima, as functions of K. These values are computed from Equation 5, taking $\lfloor KM\rfloor =i$ and $\left\{KM\right\}=x_{min}\left(i\right),$ with $x_{min}\left(i\right)$ as in part (A). Dashed lines indicate the limiting values of 1 and $2\sqrt{2}-2$ for the first and last local minima, respectively.