Significance
The mechanical properties of nucleic acids regulate multiple biological processes ranging from complex chromosome packing to replication of a plasmid. Single-molecule experiments have reported puzzling differences between the mechanical properties of double-stranded DNA (dsDNA) and double-stranded RNA (dsRNA) subjected to force and torque. This study investigates these differences using constant-force, all-atom, microsecond-long molecular dynamics. We provide a physical mechanism that explains the nonintuitive opposite twist-stretch response of these molecules based on the change of the interstrand distance with the stretching force. Changes in interstrand distance are ultimately related to differences in the chemical structure of dsDNA and dsRNA molecules. The methodology and results shown here open the field to explore larger forces to test experimental measurements, and to challenge the predictions given by our simulations.
Keywords: nucleic acid mechanical properties, twist-stretch coupling, DNA, RNA, molecular dynamics
Abstract
Multiple biological processes involve the stretching of nucleic acids (NAs). Stretching forces induce local changes in the molecule structure, inhibiting or promoting the binding of proteins, which ultimately affects their functionality. Understanding how a force induces changes in the structure of NAs at the atomic level is a challenge. Here, we use all-atom, microsecond-long molecular dynamics to simulate the structure of dsDNA and dsRNA subjected to stretching forces up to 20 pN. We determine all of the elastic constants of dsDNA and dsRNA and provide an explanation for three striking differences in the mechanical response of these two molecules: the threefold softer stretching constant obtained for dsRNA, the opposite twist-stretch coupling, and its nontrivial force dependence. The lower dsRNA stretching resistance is linked to its more open structure, whereas the opposite twist-stretch coupling of both molecules is due to the very different evolution of molecules’ interstrand distance with the stretching force. A reduction of this distance leads to overwinding in dsDNA. In contrast, dsRNA is not able to reduce its interstrand distance and can only elongate by unwinding. Interstrand distance is directly correlated with the slide base-pair parameter and its different behavior in dsDNA and dsRNA traced down to changes in the sugar pucker angle of these NAs.
In the past decades, particular effort has been devoted to unveil the complex mechanisms that drive the mechanical response of nucleic acids (NAs) (1–6). They occur in nature in two chemically different molecules, DNA and RNA, with both possessing the ability to form complementary double helices. In vivo, NAs are not typically found in their relaxed forms. Instead, in the biological processes in which they take part, proteins wrap (7), bend (8), stretch (9), and twist (10) double-stranded DNA (dsDNA) and double-stranded RNA (dsRNA) molecules (11). As a result of these mechanical stresses, NA structure and functionality are affected (12). Direct evidence of the interplay between mechanical stress and biological activity has been provided via single-molecule experiments (13, 14). Indeed, techniques such as optical and magnetic tweezers (1, 13, 14) have emerged as essential tools in the characterization of the mechanical properties of dsDNA (1) and, most recently, dsRNA (5, 6, 15).
Single-molecule experiments are performed on very long NA chains (thousands of base pairs), thus making it extremely challenging to access how the mechanical stress changes the NA structure locally (i.e., how it changes at the nanometer scale at which proteins operate). This limitation is especially important for the small forces (below 20 pN) at which most biological processes occur (16). The analysis of single-molecule force extension data with a continuum mechanics approach, the so-called elastic rod model (17, 18), reveals two particularly striking results: the threefold softer stretching response of dsRNA compared with dsDNA (6) and the opposite sign of the twist-stretch coupling (2, 3, 5, 19). Ad hoc model extensions, such as the addition of an outer helical wire (2), and several models at the base-pair level (5, 20) have been proposed to rationalize some of these results. However, no satisfactory explanation for the twist-stretch coupling difference between dsDNA and dsRNA at the continuum or coarse grain level has been found. A satisfactory explanation may involve differences in the atomic-scale structure that are beyond a continuum mechanics analysis (19, 21).
To investigate local NA structural changes induced by mechanical stress, one may resort to all-atom molecular dynamics (MD) simulations. MD can access the atomic detail of an NA structure (22–25) and provide information about the mechanical response of the chain as a whole (19, 23, 26–29). One common approach to address this problem is to determine the elastic parameters of a given NA chain through thermal fluctuations at the equilibrium of an unrestrained sequence (19, 30, 31). However, this approach cannot explore extensions corresponding to large force regimes. This limitation results in the incapability of understanding why dsDNA twist-stretch coupling changes with an applied force (2, 3, 32, 33). An alternative approach computes potential(s) of mean force (PMF) (26, 29, 34). Nevertheless, obtaining a PMF where a given reaction coordinate (e.g., elongation, twist) is sampled enough to ensure thermal equilibrium is reached at each point is a very demanding computational task. As a result, in most MD simulations reported so far, the PMF is computed from many short simulations (t ∼ 100 ns). Although they provide very useful insights about conformational changes arising from deformation, the statistical fluctuations of the observables are too large to provide an accurate quantitative prediction of NA mechanical parameters (29, 35).
Here, we overcome these limitations and provide a comprehensive characterization of the mechanical response of both dsDNA and dsRNA based on microsecond-long, all-atom MD simulations of these molecules under constant stretching forces in the range of 1–20 pN. From the response of the average elongation, the average twist, and the coupling of their fluctuations to the applied force, we determine all of the elastic constants of dsDNA and dsRNA without any prior assumption. Our data agree with general elastic values reported in the literature and reproduce the twist-stretch coupling force dependence measured in single-molecule experiments. A thorough analysis of our simulations provides a firm basis to explain the differences between both molecules. First, we develop the springiness hypothesis into a discrete model to understand the threefold softer stretching response of dsRNA. Second, we explain the opposite sign in the twist-stretch coupling of dsDNA and dsRNA by changes in their interstrand distance. Analysis of our data at the atomistic level allowed us to trace down this different behavior and the complex force dependence of the twist-stretch coupling to the response of the slide base-pair parameter, and its relation to the sugar pucker angle.
Results and Discussion
Determination of All NA Elastic Parameters from MD Simulations.
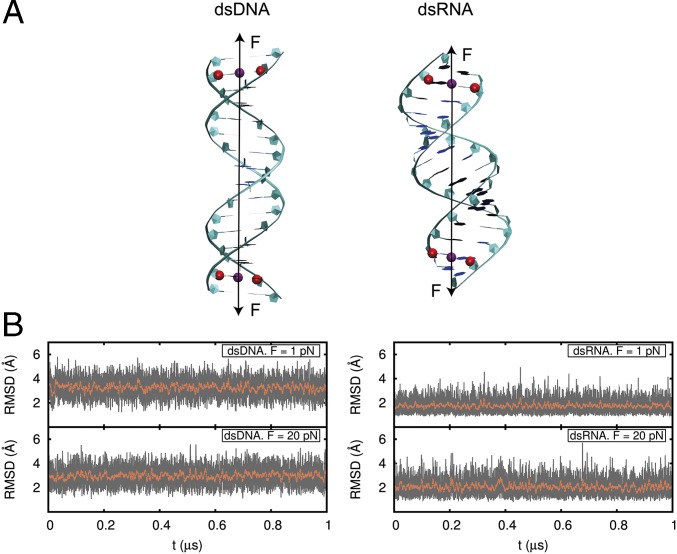
We performed all-atom MD simulations using the 16-mer dsDNA and dsRNA molecules used by Liebl et al. (19). Molecules were neutralized with 30 sodium counter-ions and placed in a cubic box with dimensions of ∼80 Å × 80 Å × 80 Å, which was then filled with explicit water molecules. Both NA molecules were stabilized at a pressure of 1 atm and a temperature of 300 K, and then subjected to a constant stretching force applied to the center of mass of the atoms belonging to the next to last base pairs of the sequences (Fig. 1A). The constant force protocol introduced here is given in SI Appendix. One microsecond-long MD simulations were performed for force = 1, 5, 10, 15, and 20 pN. Molecules remained close to the starting A and B forms during the simulation time at all forces (Fig. 1B and SI Appendix, Figs. S1 and S2). The MD trajectories were then analyzed with AmberTools and 3DNA software (36, 37).
Fig. 1.
dsDNA and dsRNA molecules under a constant stretching force. (A) dsDNA and dsRNA molecule starting configurations were B-form DNA and A-form RNA. For both molecules, the force (black arrow) was implemented to act on the centers of mass of the C1′ atoms of the second and 15th base pairs (red). Five simulations of t ≥ 1 μs each were run for each molecule at force moduli of 1, 5, 10, 15, and 20 pN. (B) Computed rmsd values for the heavy atoms of the 10 central base pairs of dsDNA and dsRNA with respect to their standard B- and A-forms at every frame (1,000 steps of 2 fs) of the simulation (gray) and averaged over a running window of 2,000 frames (red).
Our simulations were first analyzed with the elastic rod model (17, 18). Because bending fluctuations can be neglected on the length scale of the molecule (19) (SI Appendix), the energy of a stretched and twisted NA molecule subjected to a constant force may be written as:
| [1] |
where E is energy, F is force, is the equilibrium extension at zero force, is the elongation or deviation from , and is the change in helical twist from its unperturbed equilibrium value. The three constants , , and are the stretch modulus, the twist modulus, and the twist-stretch coupling constant, respectively. From Eq. 1, one can derive the elastic rod model constitutive equations for an NA molecule (2, 17):
| [2] |
| [3] |
| [4] |
where is the effective stretch modulus and values are obtained at equilibrium. To determine the NA elastic parameters , , and , it suffices to measure the force dependence of three observables [i.e., the average elongation , the average twist deformation , and how thermal fluctuations of the twist are coupled to fluctuations of the elongation ] (a detailed description is provided in SI Appendix).
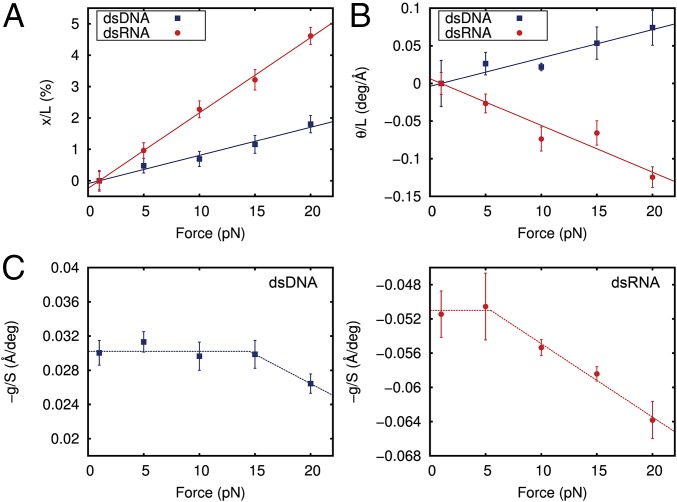
As predicted by the elastic rod model, and changed linearly with the applied force (Fig. 2 A and B), thus corroborating that the elongation and twist deformation are elastic in the range of forces used here. The slope of a linear fit to the extension data provided the twist unrestrained stretch modulus of the dsDNA and dsRNA molecules (Fig. 2A). For both molecules, was positive and the values provided by our simulations, = 1,120 ± 50 pN and = 416 ± 7 pN, were consistent with experimental results (Table 1) and reproduced the threefold softer behavior of dsRNA previously measured experimentally (6).
Fig. 2.
Determination of all of the parameters of the elastic rod model from MD data. (A) Relative change in extension of dsDNA (blue) and dsRNA (red) with respect to the extension at F = 1 pN and as a function of the applied force. The extension was computed as the mean value of the helical rises of the 10 central base pairs averaged over the last 0.8 μs (400,000 simulation frames) at each constant force. The linear fits have slopes of (89 ± 4) × 10−5 pN−1 and (240 ± 4) × 10−5 pN−1 for dsDNA and dsRNA, respectively. (B) Absolute change in the twisting angle of dsDNA and dsRNA with respect to the simulation data at F = 1 pN divided by the extension at F = 1 pN plotted as a function of the force. The twisting angle was computed as the mean of the helical twists of the 10 central base pairs averaged over all of the simulation frames. A linear fit was performed, yielding slopes of (3.8 ± 0.3) × 10−3 deg⋅Å−1⋅pN−1 and (−6.2 ± 0.6) × 10−3 deg⋅Å−1⋅pN−1 for dsDNA and dsRNA, respectively. deg, degrees. (C) Ratio −g/S was computed at each constant force simulation as the slope of the linear fit of the helical twist as a function of the helical rise (SI Appendix, Fig. S3). Dashed lines are a guide to the eye. Linear fits in A and B were constrained to pass through the origin point (1,0). Error bars were calculated as described in Materials and Methods.
Table 1.
Elastic constants determined from microsecond-long MD simulations of dsDNA and dsRNA and the constitutive equations of the elastic rod model
| Elastic parameter | dsDNA (this work) | dsDNA (exp. work) | dsDNA refs. | dsRNA (this work) | dsRNA (exp. work) | dsRNA refs. |
| , pN | 1,280 ± 70 | 1,450 to 1,750 | (32, 33) | 480 ± 11 | ||
| , pN | 1,120 ± 50 | 649 to 1,401 | (5, 6, 42–44) | 416 ± 7 | 350,500 | (5, 6) |
| , pN⋅nm2 | 303 ± 23 | 386 to 448 | (5, 45–47) | 310 ± 24 | 409 | (5) |
| , no units | −54 ± 3 | –17 to –39 | (2, 5, 32, 33, 41, 46) | 34 ± 1 | 11.5 | (5) |
The constitutive equations of the elastic rod model are shown in Eqs. 2–4. These equations allow us to compute all elastic parameters from the slopes of Fig. 2 A and B and from the helical rise-helical twist slopes computed for each force (SI Appendix, Fig. S3). Quoted errors represent deviations from the linear fits. Constants obtained in this work are compared with other experimental (exp.) work.
The torsional mechanical response of dsDNA and dsRNA (Fig. 2B) showed that as the force increases, DNA overwinds and RNA unwinds. Although counterintuitive, this behavior is in agreement with previous experimental and theoretical works (2, 3, 5, 19). The slope of a linear fit to the helical twist data provided a measurement of (Fig. 2B). Given that both and are positive, a negative slope leads to a positive value of (i.e., unwinding of dsRNA) and a positive slope leads to a negative value of (i.e., overwinding of dsDNA). The dsDNA and dsRNA showed twist rigidities of = 303 ± 23 pN⋅nm2 and = 310 ± 24 pN⋅nm2, which is in quantitative agreement with experimental measurements (Table 1).
Mining each of our 10 different microsecond MD trajectories following the methods reported by Liebl et al. (19), we were able to determine how the twist-stretch coupling changes with force (Fig. 2C and SI Appendix, Fig. S3). Our data lead to two remarkable observations. First, has a negative value for dsDNA and a positive value for dsRNA, providing independent confirmation of the opposite twist-stretch coupling of these molecules. Although these values compared reasonably with a previous theoretical work (19) (SI Appendix), they showed an overestimation in absolute values compared with experimental measurements (Table 1) as discussed further below. Second, the twist-stretch coupling for dsDNA and dsRNA changed with force. Although this dependence affected dsDNA for forces beyond 15 pN, in agreement with recent experimental results (32) (SI Appendix), changes in started at lower forces (5–10 pN). For instance, a change in force of 20 pN implied an increase of of ∼20% (i.e., it unwound more easily when stretched). The only experimental measurement of has been reported by Lipfert et al. (5), in the range of forces between 4 and 8 pN, where they found to be force-independent. According to our simulations, one should observe a small change of ∼4% in this range, which is clearly below the resolution of the reported experiments. To check how our measurements of and are affected by different salt concentrations (38), we have also computed the ratio at different forces for both molecules at 150 mM NaCl (SI Appendix, Fig. S4). We obtained very similar values at all forces with respect to neutralizing salt conditions (30 Na+ ions) with deviations below 10% (SI Appendix). Analysis of our data with the alternative software Curves+ (39) yielded very similar results (SI Appendix, Fig. S5).
In the following, we will take advantage of the atomistic detail of our simulations to dwell on the origin of the threefold softer stretching response of dsRNA compared with dsDNA, the opposite sign in their twist-stretch coupling, and its dependence with force.
Explaining the Striking Difference Between dsDNA and dsRNA Stretch Modulus.
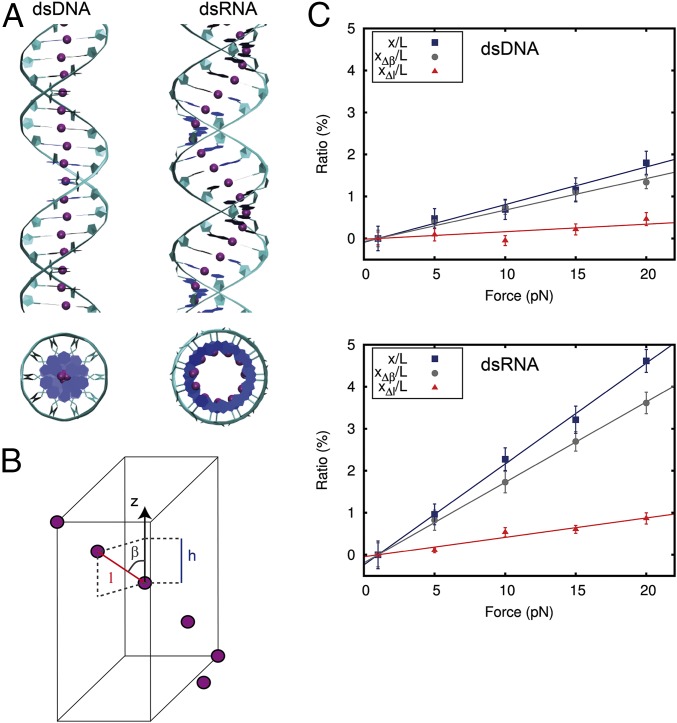
We developed a discrete model based on the springiness hypothesis proposed by Lipfert et al. (5) and Chou et al. (20). The springiness model considers a chain of segments that join the centers of all consecutive base pairs (Fig. 3A). If bending is neglected, the extension (h) of the molecule may be written as:
| [5] |
where is the length of the chain and represents the angle between the segments of the chain and the helical axis of the molecule, thus providing a measurement of the springiness of the system (Fig. 3B). Here, we propose that an increase in extension can be achieved by either decreasing or increasing (SI Appendix). Therefore, the elongation () is, at first order approximation, the sum of these two contributions:
| [6] |
We calculated and contributions for dsDNA and dsRNA for different forces and obtained a linear behavior (Fig. 3C). This linear response means that the change in extension can be modeled as two springs in a series, with elastic constants and . The inverse of the slopes of linear fits to the datasets , , and are, respectively, the elastic constants , , and (Fig. 3C). Note that can be also computed from , and , as
| [7] |
The values obtained for = 1,076 ± 68 pN and = 421 ± 15 pN from the springiness model were in good agreement with the ones calculated from Fig. 2A and Eq. 2, revealing that this simple model captures to a high precision the elastic stretching response of the NAs in this range of forces.
Fig. 3.
Discrete model explains the different stretching response of dsDNA and dsRNA. (A) Top and side views of dsDNA (Left) and dsRNA (Right) molecules. The model is based on the springiness hypothesis (5, 20), where purple beads represent consecutive base-pair centers and form a chain that runs around the helical axis of the molecules. This chain deviates from the helical axis significantly more for dsRNA than for dsDNA. (B) Each segment is characterized by the three parameters , , and , where is the distance to the next base-pair center, is the projection of on the helical axis, and is the angle defined by these two parameters. The extension can increase by either reducing (i.e., increasing ) and/or increasing . These values are denoted by and , respectively. At first-order approximation, the total change in extension can be written as (SI Appendix). (C) and contributions to the total relative change in extension (same data as in Fig. 2A) for dsDNA (Upper) and dsRNA (Lower). A linear fit constrained to pass through the origin point (1,0) was carried out for each dataset. From the slopes, we calculated = 1,330 ± 50 pN, = 522 ± 3 pN, = 5,600 ± 1,500 pN, and = 2,170 ± 140 pN. Error bars in C were calculated as described in Materials and Methods.
In a system of two springs in a series, the softer spring dominates the global elastic response. Our data show that when an NA is stretched under forces below 20 pN, the major contribution to the change in extension is the springy term, . In other words, the lengthening induced from separating the centers of the base pairs is much smaller than the contribution coming from deforming the chain. Although this result may be expected for dsRNA based on its more open structure, we show here that this claim also holds for dsDNA. This finding contrasts with the intuitive idea that dsDNA stretching should involve base-pair separation due to its nearly straight structure. In fact, a careful inspection of Fig. 3C shows that the contribution of to the extension is negligible up to 10 pN. Consequently, the qualitatively different stretching elastic response can be attributed to the approximately threefold larger of dsDNA with respect to dsRNA. At higher forces, as the molecule becomes completely straight (β→0), we expect a crossover of contributions to the relative extension, with becoming the dominant one.
The Physical Mechanism of the Opposite dsDNA and dsRNA Twist-Stretch Coupling Sign.
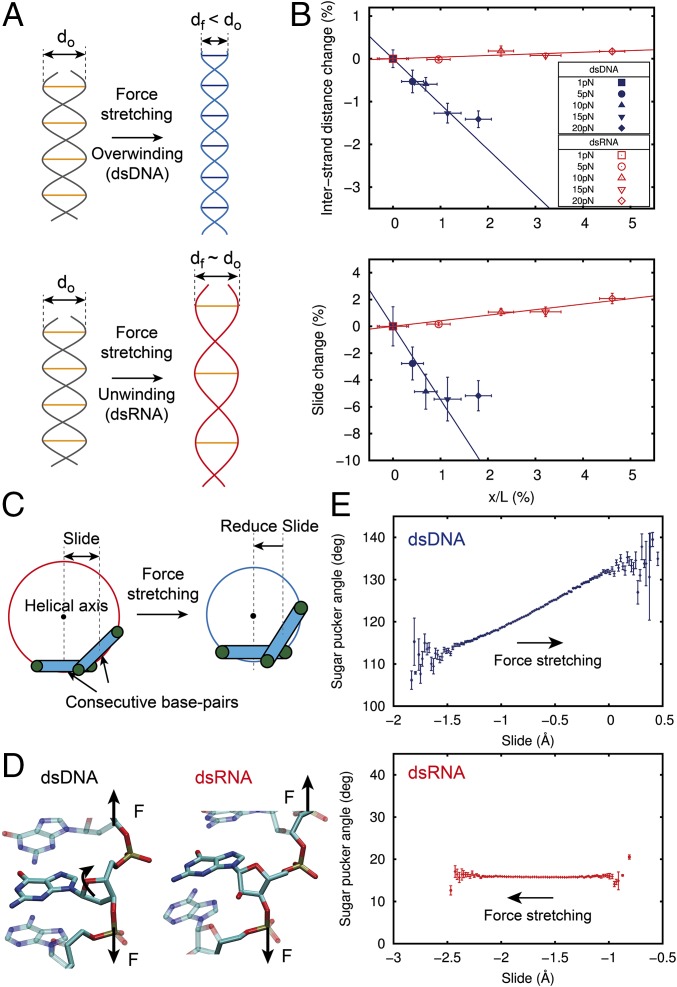
Experiments have reported an opposite twist-stretch coupling sign for dsDNA and dsRNA (5), resulting in overwinding of dsDNA and unwinding of dsRNA when the molecules are stretched. If we model the molecules as two strings wrapped around each other, our intuition tells us that they will unwind to extend (Fig. 4A). Although such is the case for dsRNA (g > 0), experiments have shown that such is not the case for dsDNA (g < 0) (2, 5). The counterintuitive nature of this result can be understood if we allow changes in separation of the two strands as previously suggested (2, 19). A fixed interstrand separation forces the molecule to unwind when stretched (the dsRNA case). If the distance between strands is allowed to shrink, then elongation can proceed by overwinding the molecule (the dsDNA case) (Fig. 4A).
Fig. 4.
Physical mechanism of the opposite sign of dsDNA and dsRNA twist-stretch coupling. (A, Upper) Double helical structure can overwind when stretched if the interstrand distance is allowed to shrink. (A, Lower) Alternatively, a fixed interstrand distance duplex will unwind when stretched. (B) Relative change of the interstrand distance (Upper) and slide (Lower) with respect to the F = 1 pN value, plotted against the relative increase in the extension induced by force (dsDNA, blue; dsRNA, red). Datasets were fitted to a linear function constrained to pass through the (0,0) point, excluding the value at F = 20 pN for dsDNA (main text). Error bars were calculated as described in Materials and Methods. (C) Cartoon illustrating the relationship between slide and interstrand distance upon stretching. A reduction of slide is accompanied by a reduction of the interstrand distance as it occurs with dsDNA (SI Appendix, Fig. S8). (D) Representation of two base-pair steps to highlight the different orientation of the sugar with respect to the phosphate backbone of dsDNA (Left) and dsRNA (Right). (E) Fluctuations in sugar pucker angle with respect to the slide parameter. The bin size is 0.02 Å. Data points are mean values with SEM.
A direct experimental measurement of the interstrand separation is very challenging because it would require knowledge of the microscopic details of the system. Our constant-force, microsecond-long simulations allowed us to look at the atomistic level and directly measure the force dependence of the interstrand separation. We measured this parameter as twice the mean distance from the P atoms to the helical axis. Interestingly, the evolution of this parameter with the force was very different for both molecules. Although the interstrand separation barely changed for dsRNA when stretched, this value experienced a significant decrease for dsDNA (Fig. 4B, Upper). This result supports the idea that overwinding or unwinding is coupled to the change in interstrand separation as suggested above. Alternative methods to calculate the interstrand distance (SI Appendix, Fig. S6) confirmed this result.
Inspection of the variation of all base-pair step parameters with the force showed a striking qualitative difference between dsDNA and dsRNA in the slide parameter (Fig. 4B, Lower and SI Appendix, Fig. S7). The slide parameter represents the displacement of two consecutive base pairs along the y axis (which defines the direction of the base pairing), and it is negative most of the time for both molecules (SI Appendix, Fig. S8A). For the sake of clarity, we consider a decrease of slide as a decrease of its absolute value, which corresponds to the approaching of consecutive base pairs. Importantly, the interstrand distance and the slide are strongly correlated (i.e., a decrease of slide leads to a decrease of interstrand distance) (Fig. 4C and SI Appendix, Fig. S8). For dsDNA, the slide decreased when stretched, whereas for dsRNA, it barely changed (Fig. 4B, Lower and SI Appendix, Fig. S9). Consequently dsDNA overwinding (i.e., interstrand distance reduction) can be explained in terms of the reduction of its slide parameter as it elongates (Fig. 4C). Note, however, that both the interstrand separation and slide of dsDNA deviated from the linear behavior at F = 20 pN (discussed in next section). On the contrary, dsRNA was not able to reduce its interstrand distance/slide; therefore, it can only elongate by unwinding.
The different behavior of the slide parameter of dsDNA and dsRNA can be traced down to the most fundamental difference between these two molecules. The connection of the nitrogenous bases to the phosphate backbone is done through a deoxyribose sugar in dsDNA and a ribose sugar in dsRNA. The additional oxygen atom of the ribose sugar results in a distinct orientation with respect to the backbone (40) (Fig. 4D). Moreover, application of force through the phosphate backbone is likely to affect the particular stereochemistry of the sugar. We measured the sugar pucker angle in our simulations and obtained a homogeneous population of C3′-endo (∼18°) for dsRNA and a more disperse population with an average value of ∼122° for dsDNA. From the fluctuations of the molecules, we observed that although the sugar pucker angle of dsDNA significantly changed with the slide, it remained constant around the C3′-endo configuration in dsRNA (Fig. 4E). This larger flexibility of the sugar pucker angle in dsDNA provides an additional degree of freedom to decrease the slide, allowing overwinding upon stretching. In the dsRNA case, the lack of this degree of freedom precludes reduction of the interstrand separation, resulting in unwinding.
A recent work has attributed the opposite twist-stretch coupling of dsDNA and dsRNA to an opposite change in the inclination parameter when the duplexes are overwound, arguing that the molecules elongate by decreasing this parameter (19). Although this hypothesis provides a very reasonable explanation of the opposite couplings in unrestrained simulations, we have observed that at ∼5 pN, inclination saturates for dsDNA; thus, the molecule no longer elongates by this mechanism (SI Appendix, Fig. S10). The mechanism proposed here, based on the slide, is substantially different from the mechanism proposed by Liebl et al. (19) and allowed us to trace down this counterintuitive behavior to the most fundamental difference between dsDNA and dsRNA (i.e., the extra hydroxyl group in dsRNA sugar).
dsDNA and dsRNA Twist-Stretch Coupling Dependence with Force.
Finally, to understand the dependence of with the force, we analyzed the fluctuations of the system. The values of the helical rise at each constant force simulation were discretized in bins of 0.02 Å, and the mean helical twist and slide were computed for each bin (Fig. 5 A and B and SI Appendix, Fig. S11). This representation revealed that the coupling between twisting and stretching defines a more complex scenario than a simple straight line, with regions where the molecule overwinds and others where it unwinds. It also emphasized the tight relation between the slide and the helical twist.
Fig. 5.
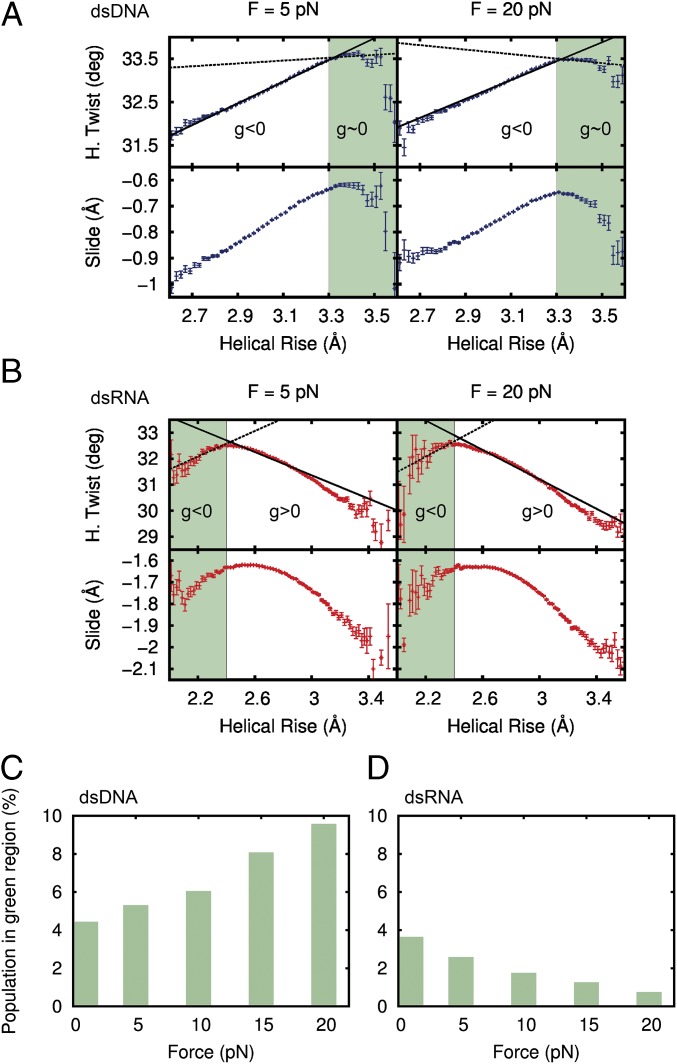
Coupling between twist and slide with helical rise as a function of the force. (A) Fluctuations in helical (H.) twist and slide plotted against helical rise at forces F = 5 pN and F = 20 pN for dsDNA. The helical rise was discretized in bins of 0.02 Å, and the mean value of the slide and the H. twist and helical rise were computed in each bin. Error bars are the SEM of each bin. The green region is defined as a helical rise >3.3 Å for dsDNA. The dashed line is the linear fit of the points in the green region, and the continuous line is the fit to all data points. (B) Fluctuations in H. twist and slide for dsRNA. The green region for dsRNA is defined as a helical rise <2.4 Å. (C) Population in the green region for dsDNA at different forces. (D) Population in the green region for dsRNA at different forces.
In the case of dsDNA, there were two clearly defined regions (Fig. 5A). For helical rise ≤3.3 Å, the molecule overwound when stretched ( < 0), in accordance with the negative sign previously found for (Fig. 2). For helical rise ≥3.3 Å (green region in Fig. 5A), DNA was no longer able to overwind (helical twist remained approximately constant) and the slope in this region was close to zero (dashed line in Fig. 5A, Upper). As a consequence, molecule excursions into this region lead to a reduction of the average value of (continuous line in Fig. 5A). A gradual effect can also be observed for intermediate forces (SI Appendix, Fig. S12). As the force increased, the green region became more and more populated (Fig. 5C), such that, at F = 20 pN, its population is large enough to induce a decrease in of 10% (Fig. 2). The observed flattening in mean slide at 20 pN (Fig. 4B, Lower) can also now be explained by the contribution of data points in the green region (Fig. 5A, Lower). The same argument applies to the fact that the interstrand distance barely changed at 20 pN (Fig. 4B, Upper). At higher forces, we predict an inversion in the trend of the slide, inducing an eventual increase in the interstrand separation and an inversion of the sign of . Furthermore, additional simulations at 30 pN confirmed the trend of decreasing observed at 20 pN. These results are in reasonable agreement with reported experimental measurements (SI Appendix, Fig. S13). This work provides a possible atomistic explanation for this experimentally observed effect (2, 3, 32, 33).
Similar reasoning can be applied to dsRNA (Fig. 5B). In this case, when the molecule explored the region with values of helical rise ≤2.4 Å (green region in Fig. 5B), it overwound when stretched ( < 0, dashed line in Fig. 5B, Upper), contrary to the average behavior of dsRNA. Data in the green region contributed to lower the average value of . As the force increases, this region gets depopulated (Fig. 5D), so that the value for dsRNA increases (Fig. 2C), facilitating the unwinding of the molecule. This transfer of population consolidates the positive value of , as opposed to the trend observed for dsDNA. Furthermore, the combined effect of the slope in the green regions, together with changes in their population, explains why the decrease in induced by the force observed in Fig. 2C could be detected at lower forces for dsRNA (F ∼ 5–10 pN) than for dsDNA (F ∼ 15–20 pN).
Values of the elastic parameters and obtained from our MD simulations were in good agreement with experimental data (Table 1). Regarding , values were in reasonable agreement with recent MD simulations performed at zero force (19), but systematically larger in absolute terms compared with the available experimental reports (2, 3, 5, 41). This discrepancy is not surprising, given that regions of helical rise ≥3.3 Å for dsDNA and ≤2.4 Å for dsRNA represent high-energy rarely visited states; however, as shown above, they contribute significantly to the value of . Therefore, it is likely that these higher energy states are not being sampled enough and their contribution to is being underestimated, yielding a higher absolute value for .
Our all-atom, microsecond-long MD simulations of dsDNA and dsRNA subjected to stretching forces up to 20 pN allowed us to characterize their mechanical response fully, extracting all of the elastic constants and providing an explanation of the striking differences found in single-molecule experiments. Furthermore, we showed how a hierarchical analysis from a continuum approach, through a discrete model, to an all-atom description paves the way to link the disparate behavior to structural differences in the arrangement of consecutive base pairs, and to the different sliding between base pairs upon stretching. Our work highlights MD simulations as a powerful tool to unveil the connection between forces and structure of NAs and, possibly, to gain insight into the associated changes in their biological functionality.
Materials and Methods
Simulation, data processing, and constant force protocol details are provided in SI Appendix. In brief, NA duplexes were built using NAB software (36). Energy minimization was carried out in 5,000 steps with restraints on the molecules, followed by an additional 5,000 steps of unrestrained energy minimization. The systems were heated up to 300 K and equilibrated for 20 ns in the NPT ensemble (constant number of particles, pressure, and temperature). Constant force simulations were then run for 1 μs. The first 200 ns were taken as a constant-force equilibration, and all measurements were performed during the last 800 ns. Following the method of Liebl et al. 19, only the 10 central base pairs were considered for analysis. Data analysis was carried out using Ambertools software. Errors were computed by splitting the data into five time windows of 160 ns and calculating the SEM considering the measurements in each window.
Supplementary Material
Acknowledgments
We thank C. L. Pastrana for fruitful discussions. We acknowledge the computer resources, technical expertise, and assistance provided by the Red Española de Supercomputación at the Minotauro Supercomputer (Barcelona Supercomputing Center). We also acknowledge the support provided by the computing facilities of the Extremadura Research Centre for Advanced Technologies-Center for Energy, Environment, and Technology (CETA-CIEMAT), funded by the European Regional Development Fund. CETA-CIEMAT belongs to CIEMAT and the Government of Spain. We thank the Spanish Ministry of Economy and Competitiveness (Projects CSD2010-00024, MAT2014-54484-P, and FIS2014-58328-P) for financial support. F.M.-H. received support from the European Research Council under the European Union’s Horizon 2020 Framework Programme for Research and Innovation (Grant 681299). A.M.-G. received support from the International PhD Program of “La Caixa-Severo Ochoa” as the recipient of a PhD fellowship.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1705642114/-/DCSupplemental.
References
- 1.Bustamante C, Bryant Z, Smith SB. Ten years of tension: Single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 2.Gore J, et al. DNA overwinds when stretched. Nature. 2006;442:836–839. doi: 10.1038/nature04974. [DOI] [PubMed] [Google Scholar]
- 3.Lionnet T, Joubaud S, Lavery R, Bensimon D, Croquette V. Wringing out DNA. Phys Rev Lett. 2006;96:178102. doi: 10.1103/PhysRevLett.96.178102. [DOI] [PubMed] [Google Scholar]
- 4.Kosikov KM, Gorin AA, Zhurkin VB, Olson WK. DNA stretching and compression: Large-scale simulations of double helical structures. J Mol Biol. 1999;289:1301–1326. doi: 10.1006/jmbi.1999.2798. [DOI] [PubMed] [Google Scholar]
- 5.Lipfert J, et al. Double-stranded RNA under force and torque: Similarities to and striking differences from double-stranded DNA. Proc Natl Acad Sci USA. 2014;111:15408–15413. doi: 10.1073/pnas.1407197111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Herrero-Galán E, et al. Mechanical identities of RNA and DNA double helices unveiled at the single-molecule level. J Am Chem Soc. 2013;135:122–131. doi: 10.1021/ja3054755. [DOI] [PubMed] [Google Scholar]
- 7.Cozzarelli NR, Cost GJ, Nöllmann M, Viard T, Stray JE. Giant proteins that move DNA: Bullies of the genomic playground. Nat Rev Mol Cell Biol. 2006;7:580–588. doi: 10.1038/nrm1982. [DOI] [PubMed] [Google Scholar]
- 8.Schleif R. DNA looping. Annu Rev Biochem. 1992;61:199–223. doi: 10.1146/annurev.bi.61.070192.001215. [DOI] [PubMed] [Google Scholar]
- 9.Conway AB, et al. Crystal structure of a Rad51 filament. Nat Struct Mol Biol. 2004;11:791–796. doi: 10.1038/nsmb795. [DOI] [PubMed] [Google Scholar]
- 10.Yeeles JT, van Aelst K, Dillingham MS, Moreno-Herrero F. Recombination hotspots and single-stranded DNA binding proteins couple DNA translocation to DNA unwinding by the AddAB helicase-nuclease. Mol Cell. 2011;42:806–816. doi: 10.1016/j.molcel.2011.04.012. [DOI] [PubMed] [Google Scholar]
- 11.Dulin D, et al. Backtracking behavior in viral RNA-dependent RNA polymerase provides the basis for a second initiation site. Nucleic Acids Res. 2015;43:10421–10429. doi: 10.1093/nar/gkv1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sinden RR. DNA Structure and Function. Academic; London: 1994. [Google Scholar]
- 13.De Vlaminck I, Dekker C. Recent advances in magnetic tweezers. Annu Rev Biophys. 2012;41:453–472. doi: 10.1146/annurev-biophys-122311-100544. [DOI] [PubMed] [Google Scholar]
- 14.Moffitt JR, Chemla YR, Smith SB, Bustamante C. Recent advances in optical tweezers. Annu Rev Biochem. 2008;77:205–228. doi: 10.1146/annurev.biochem.77.043007.090225. [DOI] [PubMed] [Google Scholar]
- 15.Abels JA, Moreno-Herrero F, van der Heijden T, Dekker C, Dekker NH. Single-molecule measurements of the persistence length of double-stranded RNA. Biophys J. 2005;88:2737–2744. doi: 10.1529/biophysj.104.052811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 17.Marko JF. Stretching must twist DNA. Europhys Lett. 1997;38:183–188. [Google Scholar]
- 18.Nelson P. Biological Physics. Freeman; New York: 2003. [Google Scholar]
- 19.Liebl K, Drsata T, Lankas F, Lipfert J, Zacharias M. Explaining the striking difference in twist-stretch coupling between DNA and RNA: A comparative molecular dynamics analysis. Nucleic Acids Res. 2015;43:10143–10156. doi: 10.1093/nar/gkv1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chou FC, Lipfert J, Das R. Blind predictions of DNA and RNA tweezers experiments with force and torque. PLOS Comput Biol. 2014;10:e1003756. doi: 10.1371/journal.pcbi.1003756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kriegel F, Ermann N, Lipfert J. Probing the mechanical properties, conformational changes, and interactions of nucleic acids with magnetic tweezers. J Struct Biol. 2017;197:26–36. doi: 10.1016/j.jsb.2016.06.022. [DOI] [PubMed] [Google Scholar]
- 22.Pérez A, Luque FJ, Orozco M. Dynamics of B-DNA on the microsecond time scale. J Am Chem Soc. 2007;129:14739–14745. doi: 10.1021/ja0753546. [DOI] [PubMed] [Google Scholar]
- 23.Pérez A, Luque FJ, Orozco M. Frontiers in molecular dynamics simulations of DNA. Acc Chem Res. 2012;45:196–205. doi: 10.1021/ar2001217. [DOI] [PubMed] [Google Scholar]
- 24.Dans PD, Pérez A, Faustino I, Lavery R, Orozco M. Exploring polymorphisms in B-DNA helical conformations. Nucleic Acids Res. 2012;40:10668–10678. doi: 10.1093/nar/gks884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Galindo-Murillo R, Roe DR, Cheatham TE., 3rd On the absence of intrahelical DNA dynamics on the μs to ms timescale. Nat Commun. 2014;5:5152. doi: 10.1038/ncomms6152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kannan S, Kohlhoff K, Zacharias M. B-DNA under stress: Over- and untwisting of DNA during molecular dynamics simulations. Biophys J. 2006;91:2956–2965. doi: 10.1529/biophysj.106.087163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Luan B, Aksimentiev A. Strain softening in stretched DNA. Phys Rev Lett. 2008;101:118101. doi: 10.1103/PhysRevLett.101.118101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mazur AK. Modeling DNA dynamics under steady deforming forces and torques. J Chem Theory Comput. 2009;5:2149–2157. doi: 10.1021/ct900124n. [DOI] [PubMed] [Google Scholar]
- 29.Rezác J, Hobza P, Harris SA. Stretched DNA investigated using molecular-dynamics and quantum-mechanical calculations. Biophys J. 2010;98:101–110. doi: 10.1016/j.bpj.2009.08.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lankas F, Sponer J, Langowski J, Cheatham TE., 3rd DNA basepair step deformability inferred from molecular dynamics simulations. Biophys J. 2003;85:2872–2883. doi: 10.1016/S0006-3495(03)74710-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lankas F, Sponer J, Hobza P, Langowski J. Sequence-dependent elastic properties of DNA. J Mol Biol. 2000;299:695–709. doi: 10.1006/jmbi.2000.3781. [DOI] [PubMed] [Google Scholar]
- 32.Gross P, et al. Quantifying how DNA stretches, melts and changes twist under tension. Nat Phys. 2011;7:731–736. [Google Scholar]
- 33.Broekmans OD, King GA, Stephens GJ, Wuite GJ. DNA twist stability changes with magnesium(2+) concentration. Phys Rev Lett. 2016;116:258102. doi: 10.1103/PhysRevLett.116.258102. [DOI] [PubMed] [Google Scholar]
- 34.Bongini L, Lombardi V, Bianco P. The transition mechanism of DNA overstretching: A microscopic view using molecular dynamics. J R Soc Interface. 2014;11:20140399. doi: 10.1098/rsif.2014.0399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Severin PM, Zou X, Gaub HE, Schulten K. Cytosine methylation alters DNA mechanical properties. Nucleic Acids Res. 2011;39:8740–8751. doi: 10.1093/nar/gkr578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Case DA, et al. Amber14. University of California; San Francisco: 2014. [Google Scholar]
- 37.Lu XJ, Olson WK. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chen AA, Marucho M, Baker NA, Pappu RV. Simulations of RNA interactions with monovalent ions. Methods Enzymol. 2009;469:411–432. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 39.Lavery R, Moakher M, Maddocks JH, Petkeviciute D, Zakrzewska K. Conformational analysis of nucleic acids revisited: Curves+ Nucleic Acids Res. 2009;37:5917–5929. doi: 10.1093/nar/gkp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vargason JM, Henderson K, Ho PS. A crystallographic map of the transition from B-DNA to A-DNA. Proc Natl Acad Sci USA. 2001;98:7265–7270. doi: 10.1073/pnas.121176898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lebel P, Basu A, Oberstrass FC, Tretter EM, Bryant Z. Gold rotor bead tracking for high-speed measurements of DNA twist, torque and extension. Nat Methods. 2014;11:456–462. doi: 10.1038/nmeth.2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wenner JR, Williams MC, Rouzina I, Bloomfield VA. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys J. 2002;82:3160–3169. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Baumann CG, Smith SB, Bloomfield VA, Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc Natl Acad Sci USA. 1997;94:6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 45.Bryant Z, et al. Structural transitions and elasticity from torque measurements on DNA. Nature. 2003;424:338–341. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 46.Sheinin MY, Wang MD. Twist-stretch coupling and phase transition during DNA supercoiling. Phys Chem Chem Phys. 2009;11:4800–4803. doi: 10.1039/b901646e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Moroz JD, Nelson P. Entropic elasticity of twist-storing polymers. Macromolecules. 1998;31:6333–6347. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.