Local thermal energy as a structural indicator in glasses

Significance

When liquids are cooled sufficiently fast, they fail to crystalize and form disordered solids—glasses. Understanding the physical properties of glasses remains a major challenge, in large part because of the lack of tools to characterize the emerging disordered structures and well-established structure–properties relations. In this work, we propose that fluctuational thermal energy reveals highly localized and soft structures in glasses. We show that the degree of softness of these “soft spots” follows a universal fat-tailed statistical distribution and relate it to the density of noncrystalline vibrational states. The softest spots are shown to predict the loci of irreversible plastic rearrangements in sheared glasses, thus offering a generic structure–properties approach to glassy materials.

Abstract

Identifying heterogeneous structures in glasses—such as localized soft spots—and understanding structure–dynamics relations in these systems remain major scientific challenges. Here, we derive an exact expression for the local thermal energy of interacting particles (the mean local potential energy change caused by thermal fluctuations) in glassy systems by a systematic low-temperature expansion. We show that the local thermal energy can attain anomalously large values, inversely related to the degree of softness of localized structures in a glass, determined by a coupling between internal stresses—an intrinsic signature of glassy frustration—anharmonicity and low-frequency vibrational modes. These anomalously large values follow a fat-tailed distribution, with a universal exponent related to the recently observed universal ${\omega }^4$ density of states of quasilocalized low-frequency vibrational modes. When the spatial thermal energy field—a “softness field”—is considered, this power law tail manifests itself by highly localized spots, which are significantly softer than their surroundings. These soft spots are shown to be susceptible to plastic rearrangements under external driving forces, having predictive powers that surpass those of the normal modes-based approach. These results offer a general, system/model-independent, physical/observable-based approach to identify structural properties of quiescent glasses and relate them to glassy dynamics.

Understanding the glassy state of matter remains one of the greatest challenges in condensed matter physics and materials science (1–5). In large part, the elusive nature of the glassy state is due to the absence of well-established tools and concepts to quantify the disordered structures characterizing glassy materials—in sharp contrast to their ordered crystalline counterparts—and because of the lack of understanding of the relations between glassy structures and dynamics. Over the years, many attempts have been made to identify physical quantities that can indicate underlying local structures within glassy materials (6–9). These indicators include, among others, free volume (10–12), internal stresses (13), local elastic moduli (14), local Debye–Waller factor (15), coarse-grained energy and density (16, 17), locally favored structures (18–20), short- and medium-range order (21–23), and various weighted sums over a system-dependent number of low-frequency normal modes (24–30).

These quantities measure some properties of quiescent glasses evaluated at or in the near vicinity of a mechanically (meta-)stable state of a glass (an inherent structure). Some of these indicators are purely structural in nature (i.e., they are obtained from the knowledge of particle positions alone), whereas others require in addition the knowledge of interparticle interactions. Recently, the local yield stress—the minimal local stress needed to trigger an irreversible plastic rearrangement—has been proposed as a structural indicator (31). It is required, however, to externally drive each local region in a glass to its nonlinear rearrangement threshold and hence, belongs to a different class of structural indicators compared with those previously mentioned. The utility of each of the proposed indicators is usually assessed by looking for correlations between the revealed structures—typically localized soft spots—and glassy dynamics, either thermally activated relaxation in the absence of external driving forces or localized irreversible plastic rearrangements under the application of global driving forces. In fact, a recent study established such structure–dynamics correlations by machine-learning techniques, leaving the precise physical nature of the underlying structural indicator unspecified (32, 33). These machine learning-based structural indicators also belong to a different class of structural indicators, because the training stage of the machine-learning algorithm requires knowledge of the plastic rearrangements themselves.

Some of the previously proposed structural indicators have revealed a certain degree of correlation between identified soft spots and dynamics, providing important evidence that preexisting localized structures in a glass significantly affect its dynamics. However, oftentimes, the physical foundations of the structural indicators remain unclear, and they are sometimes defined algorithmically but are not derived from well-established physical observables. Moreover, their statistical properties are not commonly addressed, the relations between them and other basic physical quantities are not established, and the fundamental reasons for them being particularly sensitive to underlying heterogeneous structures in glasses remain elusive.

Here, we propose a structural indicator of glassy “softness”—the local thermal energy (LTE)—which is a transparent physical observable derived by a systematic low-temperature expansion. We use the exact expression for the LTE of interacting particles to elucidate the underlying physical factors—most notably internal stresses, anharmonicity, and nonlinear coupling to low-frequency vibrational modes—that give rise to significant spatial heterogeneities of softness. We show that the LTE can attain anomalously large values directly related to particularly soft regions in a glass, which follow a fat-tailed distribution. The power law exponent characterizing this distribution is shown to be universal and directly related to the recently observed universal ${\omega }^4$ density of states of quasilocalized low-frequency vibrational modes (34, 35), constituting a link to a fundamental universal property of glassy systems. The LTE field, a “softness field,” thus exhibits highly localized spots, which are significantly softer than their surroundings. These soft spots are shown to be particularly susceptible to plastic rearrangements when the glass is being driven by external forces, having predictive powers that surpass those of the normal modes-based approach (24–27). As such, they can be identified with the long sought for glassy “flow defects,” the so-called shear transformation zones (STZ) (36, 37).

Physical Observables in the Low-Temperature Limit

Our starting point is the idea that the thermal average of local physical observables in a system equilibrated at a low temperature $T$ is expected to be sensitive to the system’s underlying structure (38). Therefore, we first aim at deriving an expression for the thermal average of a general physical observable $\mathcal{A}$, ${⟨\mathcal{A}⟩}_T$, in the low-temperature limit. The latter is given by ${⟨\mathcal{A}⟩}_T=\mathcal{Z}{(T)}^{-1}\int \mathcal{A}(\text{𝒙})\exp \left(-\mathcal{U}(\text{𝒙})/k_{B}T\right)d\text{𝒙}$, where the components of the vector x represent the deviations of the system’s degrees of freedom from a (possibly local) minimum of its energy $\mathcal{U}(\text{𝒙})$, $\mathcal{Z}(T)=\int \exp \left(-\mathcal{U}(\text{𝒙})/k_{B}T\right)d\text{𝒙}$ is the partition function, and $k_B$ is the Boltzmann constant. ${⟨\mathcal{A}⟩}_T$ can be systematically expanded to leading order in $T$, yielding (SI Appendix)

$$\frac{{⟨\mathcal{A}⟩}_T-{\mathcal{A}}^{(0)}}{\frac{1}{2}{k}_{B}T}\simeq \frac{{\partial }^2\mathcal{A}}{\partial \text{𝒙}\partial \text{𝒙}}:{\mathcal{𝓜}}^{-1}-\frac{\partial \mathcal{A}}{\partial \text{𝒙}}\cdot {\mathcal{𝓜}}^{-1}\cdot {\mathcal{𝓤}}^{‴}:{\mathcal{𝓜}}^{-1},$$ [1]

where $\mathcal{𝓜}\equiv {\partial }^2\mathcal{U}/\partial \text{𝒙}\partial \text{𝒙}$ is the dynamical matrix, ${\mathcal{𝓤}}^{‴}\equiv {\partial }^3\mathcal{U}/\partial \text{𝒙}\partial \text{𝒙}\partial \text{𝒙}$ is a third-order anharmonicity tensor, and ${\mathcal{A}}^{(0)}\equiv {lim}_{T\to 0}{⟨\mathcal{A}⟩}_T$. All derivatives are evaluated at the minimum of $\mathcal{U}$ (i.e., at $\text{𝒙}=\mathrm{𝟎}$). In obtaining Eq. 1, higher-order terms in $T$ were neglected. In the $T\to 0$ limit, these terms vanish, and the right-hand side (RHS) of Eq. 1 represents an intrinsic property of an inherent structure, independent of temperature.

To gain some understanding of the physics encapsulated in Eq. 1, let us briefly consider a few physical observables. Consider first the total energy $\mathcal{A}=\mathcal{U}(\text{𝒙})$ in the quadratic (harmonic) approximation. In this case, the first (harmonic) term on the RHS of Eq. 1 equals the number of degrees of freedom $N$, and the second (anharmonic) term vanishes because of mechanical equilibrium, $\partial \mathcal{U}/\partial \text{𝒙}=\mathbf{\hspace{0.17em}0}$. Consequently, we obtain ${⟨\mathcal{U}⟩}_T-{\mathcal{U}}^{(0)}=\frac{1}{2}N{k}_{B}T$, which is nothing but the equipartition theorem in the harmonic approximation (39). Consider then a system with energy $\mathcal{U}(X)$ that depends on a single (scalar) macroscopic degree of freedom $X$, representing changes in its linear dimension relative to a reference stable state $X=0$. In this case, the first (harmonic) term on the RHS of Eq. 1 vanishes, and we obtain ${⟨X⟩}_T\simeq -\frac{1}{2}{\mathcal{U}}^{‴}{({\mathcal{U}}^{″})}^{-2}{k}_{B}T+\mathcal{O}(T^2)$, where a prime denotes a derivative with respect to $X$. The latter expression describes linear thermal expansion, which is well-known to be an intrinsically anharmonic physical effect proportional to ${\mathcal{U}}^{‴}$ (39). These examples both show that Eq. 1 is fully consistent with well-established results (equipartition and thermal expansion) and highlight the anharmonic nature of the second term on the RHS of Eq. 1.

The examples presented above focused on macroscopic (global) scalar observables. Because our main interest is in spatial heterogeneity, we consider now microscopic (local) observables defined at the particles’ level. We thus focus on the microscopic generalization of ${⟨X⟩}_T$: the thermal displacement vector ${⟨\text{𝒙}⟩}_T$, which represents the variation of the mean positions of particles about the equilibrium state after thermal fluctuations are introduced. Using Eq. 1, the normalized thermal average of x in the $T\to 0$ limit takes the form

$$\mathcal{𝓧}\equiv \underset{T\to 0}{lim}\frac{{⟨\text{𝒙}⟩}_T}{\frac{1}{2}{k}_{B}T}=-{\mathcal{𝓜}}^{-1}\cdot {\mathcal{𝓤}}^{‴}:{\mathcal{𝓜}}^{-1}.$$ [2]

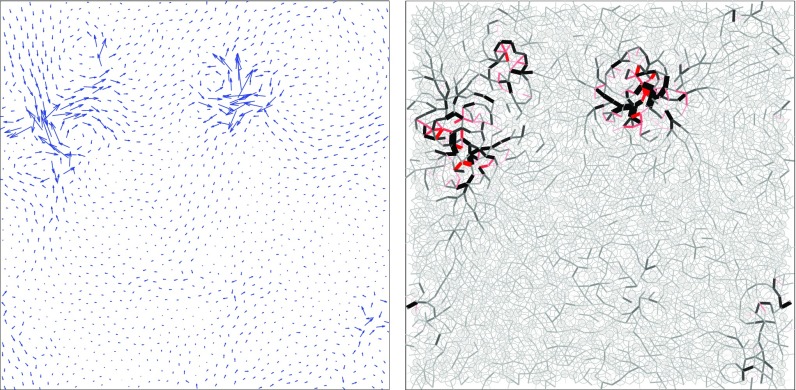
Note the analogy between Eq. 2—which features a quadratic (nonlinear) coupling between the anharmonicity tensor ${\mathcal{𝓤}}^{‴}$ and the inverse of the dynamical matrix ${\mathcal{𝓜}}^{-1}$—and the expression given above for ${⟨X⟩}_T$. The components of the normalized thermal displacement vector ${\mathcal{X}}_i$ in Eq. 2 should be distinguished from the local Debye–Waller factor $x_i^2$ (15), with thermal average according to Eq. 1 that is given by ${⟨x_i^2⟩}_T={({\mathcal{M}}^{-1})}_{ii}{k}_{B}T$ (no summation is implied). Although ${⟨x_i^2⟩}_T$ is completely given by the first term on RHS of Eq. 1, which involves a single contraction of the inverse of the dynamical matrix ${\mathcal{𝓜}}^{-1}$, ${\mathcal{X}}_i$ is completely given by the second term, which involves two contractions with ${\mathcal{𝓜}}^{-1}$. As will be shown below, this distinction makes a qualitative difference. Moreover, ${\mathcal{X}}_i$ is directly sensitive to anharmonicity, whereas ${⟨x_i^2⟩}_T$ is independent of it. $\mathcal{𝓧}$, plotted in Fig. 1 for a 2D model glass, is shown to exhibit significant spatial heterogeneity, suggesting that it is particularly sensitive to localized soft structures in glasses.

Fig. 1.

(Left) The normalized thermal displacement vector $\mathcal{𝓧}$, defined in Eq. 2, measured in a model glass in 2D (details are in the text) of $N=1,600$ particles. (Right) A spatial map of the normalized LTE ${\mathcal{E}}_{\alpha }$, defined in Eq. 3, for the same glass realization shown in Left. Line thickness and opacity represent the LTE, with red (black) representing negative (positive) LTE.

Local Thermal Energy

The normalized thermal displacement vector $\mathcal{𝓧}$, defined in Eq. 2 and shown to exhibit strong spatial heterogeneity in Fig. 1, contributes to the thermal average of any physical observable ${⟨\mathcal{A}⟩}_T$ that features $\partial \mathcal{A}/\partial \text{𝒙}\ne \mathbf{\hspace{0.17em}0}$ at $\text{𝒙}=\mathbf{\hspace{0.17em}0}$. It is important to emphasize the counterintuitive result that, for observables with $\partial \mathcal{A}/\partial \text{𝒙}\ne \mathbf{\hspace{0.17em}0}$, anharmonicity seems to be important at vanishingly small temperatures, independent of how well the harmonic approximation for the energy holds. Thus, on the face of it, the normalized thermal displacements $\mathcal{𝓧}$ could have been a good candidate for an indicator of softness of the underlying structure. However, we aim at proposing an observable that naturally “filters out” the regions of homogeneous, collective translation-like motion exhibited by the thermal displacements, further exposing localized soft structures that exhibit large gradients.

Our goal now is to identify a physical observable $\mathcal{A}$ that can potentially serve as a softness field (i.e., a local scalar that features a nonvanishing first spatial derivative and is particularly sensitive to gradients of $\mathcal{𝓧}$). Inspired by ref. 38, an observable that naturally suggests itself is the local potential energy ${\epsilon }_{\alpha }$, where $\alpha$ represents any pair of interacting particles, and $\mathcal{U}={\sum }_{\alpha }{\epsilon }_{\alpha }$. Using Eqs. 1 and 2, we then define

$${\mathcal{E}}_{\alpha }\equiv \underset{T\to 0}{lim}\frac{{⟨{\epsilon }_{\alpha }⟩}_T-{\epsilon }_{\alpha }^{(0)}}{\frac{1}{2}{k}_{B}T}=\frac{\partial {\text{𝒇}}_{\alpha }}{\partial \text{𝒙}}:{\mathcal{𝓜}}^{-1}+{\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧},$$ [3]

where ${\text{𝒇}}_{\alpha }\equiv \partial {\epsilon }_{\alpha }/\partial \text{𝒙}$ is the internal force vector acting between particles defining the interaction $\alpha$.

Mechanical equilibrium at particle $i$ implies that the sum of all of the forces acting on it vanishes. In systems with no internal frustration, internal forces/stresses do not exist, and this sum is trivially satisfied by having ${\text{𝒇}}_{\alpha }=\mathbf{\hspace{0.17em}0}$ for all $\alpha$s. In systems with internal frustration, however, internal forces/stresses generically emerge, ${\text{𝒇}}_{\alpha }\ne \mathbf{\hspace{0.17em}0}$. In the former case, the second term on the RHS of Eq. 3 vanishes. Such internal stress-free disordered systems were studied in ref. 38, where it was shown that, under these conditions, ${\mathcal{E}}_{\alpha }$ is universally bounded between zero and one. The bound on ${\mathcal{E}}_{\alpha }$ suggests that significant spatial heterogeneity in ${\mathcal{E}}_{\alpha }$ cannot emerge in internal stress-free systems.

An intrinsic signature of glassy systems is the existence of internal frustration (40) that leads to the emergence of internal forces/stresses, ${\text{𝒇}}_{\alpha }\ne \mathbf{\hspace{0.17em}0}$ (1). Consequently, we expect the ${\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧}$ term on the RHS of Eq. 3 to be generically nonzero for glasses. Because $\mathcal{𝓧}$ is already known to exhibit strongly localized structures, compared with Fig. 1, Left, we expect ${\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧}$ to expose localized regions with a very large concentration of the normalized LTE ${\mathcal{E}}_{\alpha }$. In fact, we expect the scalar product of ${\text{𝒇}}_{\alpha }$ with $\mathcal{𝓧}$ to amplify the spatial heterogeneity in $\mathcal{𝓧}$. To understand this amplification effect, note that ${\text{𝒇}}_{\alpha }$ is actually a force dipole composed of two forces acting along the line connecting the particles that define the interaction $\alpha$ in opposite directions. Therefore, ${\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧}$ is exactly the difference between the values of $\mathcal{𝓧}$ at the positions of the particles defining the interaction $\alpha$, projected along the line connecting them, multiplied by $|{\text{𝒇}}_{\alpha }|$. Consequently, regions of homogeneous thermal displacements are expected to feature small values of ${\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧}$, whereas heterogeneous regions—compared with Fig. 1, Left—are expected to feature much larger values.

To test these ideas, we plot in Fig. 1, Right the normalized LTE ${\mathcal{E}}_{\alpha }$ for the same glass realization shown in Fig. 1, Left. The result is striking: ${\mathcal{E}}_{\alpha }$ attains anomalously large values (both positive and negative) in localized regions where $\mathcal{𝓧}$ exhibits marked heterogeneity. This observation provides strong visual evidence, to be quantified below, that ${\mathcal{E}}_{\alpha }$ can be used to define a softness field that clearly identifies localized soft spots in glasses. Finally, note that ${\mathcal{E}}_{\alpha }$ can be also measured directly by tracking thermal fluctuations in low $T$ dynamics. Two examples obtained by finite $T$ molecular dynamics (MD) simulations are shown in Fig. 2, Inset, showing perfect agreement with the exact expression in Eq. 3.

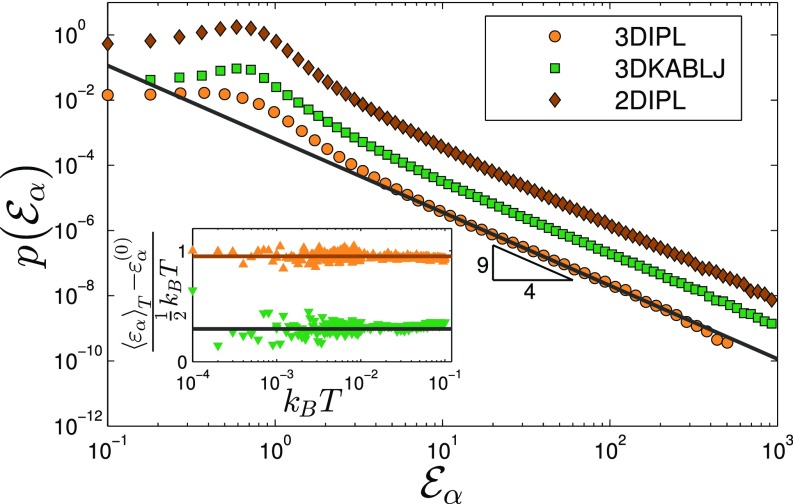
Fig. 2.

Distributions of LTE—$p({\mathcal{E}}_{\alpha })$—measured for three model glasses in 2D and 3D (details are in the text) shifted vertically for visibility. We find a universal form $p({\mathcal{E}}_{\alpha })\sim {\mathcal{E}}_{\alpha }^{-9/4}$ at large LTEs, independent of model or spatial dimension. (Inset) MD validation of Eq. 3 for two random interactions in a model glass. The continuous lines represent the exact expression for ${\mathcal{E}}_{\alpha }$.

Universal Anomalous Statistics

To quantify the degree of softness of soft spots revealed by ${\mathcal{E}}_{\alpha }$—compared with Fig. 1, Right—and its probability of occurrence, we focus next on the statistical properties of ${\mathcal{E}}_{\alpha }$. To this aim, we argue that the statistics of normalized thermal energies ${\mathcal{E}}_{\alpha }$ can be related to the density of vibrational frequencies $D(\omega )$. In particular, the form of Eqs. 2 and 3 suggests that soft vibrational modes (i.e., modes with small frequencies $\omega$) give rise to large values of ${\mathcal{E}}_{\alpha }$ because of the appearance of the inverse of the dynamical matrix ${\mathcal{𝓜}}^{-1}$. Recently, it has been observed that low-frequency vibrations in glassy materials appear in two qualitatively different species: one is ordinary long-wavelength plane waves, and the other is disorder-induced soft glassy modes. The former are spatially extended objects, whereas the latter are quasilocalized objects characterized by a disordered core and a power law tail (34). Moreover, long-wavelength plane waves follow a Debye density of states (DOS) $D_D(\omega )\sim {\omega }^{đ-1}$ in $đ$ dimensions, whereas soft glassy modes follow a universal DOS $D_G(\omega )\sim {\omega }^4$ (34, 35). We stress that our focus here is on generic glasses, which do not dwell near a jamming transition, where the physics is expected to change.

To proceed, note that ${\mathcal{E}}_{\alpha }$ in Eq. 3 has one contribution that involves a single contraction with ${\mathcal{𝓜}}^{-1}$ and another one that involves two contractions with ${\mathcal{𝓜}}^{-1}$; therefore, the latter is expected to dominate the former. Consequently, we write ${\mathcal{E}}_{\alpha }\sim {\text{𝒇}}_{\alpha }\cdot \mathcal{𝓧}$, with eigen decomposition that takes the form

$${\mathcal{E}}_{\alpha }\sim \sum _{i,j}\frac{({\text{𝒇}}_{\alpha }\cdot {𝚿}_i)c_{ijj}}{{\omega }_i^2{\omega }_j^2}\hspace{1em}\text{with}\hspace{1em}{c}_{ijj}\equiv {\mathcal{𝓤}}^{‴}\stackrel{.}{:}{𝚿}_i{𝚿}_j{𝚿}_j,$$ [4]

where $i,j$ run over all of the vibrational modes ${𝚿}_i$ defined by the eigenvalue equation $\mathcal{𝓜}\cdot {𝚿}_i={\omega }_i^2{𝚿}_i$.

We argue that low-frequency plane waves and quasilocalized soft glassy modes make qualitatively different contributions to the double sum in Eq. 4. In order to support this claim, we note that, similarly to the discussion about the dipolar nature of ${\text{𝒇}}_{\alpha }$ above, each contraction of ${\mathcal{𝓤}}^{‴}$ with a vibrational mode is proportional to the mode’s spatial derivative (compare with figure 3 in ref. 41). For low-frequency plane waves, each such derivative is proportional to the frequency $\omega$, whereas for quasilocalized soft glassy modes, the derivative is expected to attain a characteristic value that is nearly independent of frequency. Consequently, because $c_{ijj}\sim {\omega }^3$ and ${\text{𝒇}}_{\alpha }\cdot {𝚿}_i\sim \omega$ for plane waves (which we have numerically verified), we expect their contribution to be negligible compared with that of quasilocalized soft glassy modes, and hence, the above double sum is now understood to be dominated by the latter. Next, because different quasilocalized soft glassy modes are spatially well-separated, we expect $c_{ijj}$ for $i\ne j$ to be much smaller than $c_{iii}$, such that ${\mathcal{E}}_{\alpha }\sim {\sum }_i({\text{𝐟}}_{\alpha }\cdot {𝚿}_i)c_{iii}{\omega }_i^{-4}$. Finally, because the internal force ${\text{𝒇}}_{\alpha }$ is localized at the $\alpha$th interaction, only the glassy mode that is localized there will contribute to the sum, leading to

$${\mathcal{E}}_{\alpha }\sim {\omega }^{-4}.$$ [5]

Eq. 5, which is verified below, establishes an important relation between the LTE ${\mathcal{E}}_{\alpha }$ and the frequency of vibrational modes $\omega$. In fact, it constitutes a relation between ${\mathcal{E}}_{\alpha }$ and the local stiffness $\kappa \equiv {\omega }^2$, ${\mathcal{E}}_{\alpha }\sim {\kappa }^{-2}$, showing that particularly soft excitations, $\kappa \to 0$, correspond to anomalously large values of the LTE ${\mathcal{E}}_{\alpha }$. The predicted relation between local stiffness and LTE justifies the assertion that ${\mathcal{E}}_{\alpha }$ quantifies the degree of softness of glassy structures.

Using Eq. 5 and the universal relation $D_G(\omega )\sim {\omega }^4$, the probability distribution function $p({\mathcal{E}}_{\alpha })$ is obtained as

$$p({\mathcal{E}}_{\alpha })=D_G\left[\omega ({\mathcal{E}}_{\alpha })\right]\frac{d\omega ({\mathcal{E}}_{\alpha })}{d{\mathcal{E}}_{\alpha }}\sim {\mathcal{E}}_{\alpha }^{-1}{\mathcal{E}}_{\alpha }^{-5/4}\sim {\mathcal{E}}_{\alpha }^{-9/4}.$$ [6]

Note that, in the above discussion, we implicitly used the fact that the magnitude of the internal forces $|{\text{𝒇}}_{\alpha }|$ has a characteristic value as shown in SI Appendix. The prediction in Eq. 6 has far-reaching implications. First, it suggests that the physical observable ${\mathcal{E}}_{\alpha }$ (i.e., the LTE) effectively filters out the effect of low-frequency plane waves, which are known to obscure the origin of many glassy effects (41–43). In fact, when low-frequency plane waves coexist with quasilocalized soft glassy modes in the same frequency range, they hybridize, such that glassy modes acquire spatially extended background displacements and appear to lose their quasilocalized nature. The derivation leading to Eq. 6 assumed that ${\mathcal{E}}_{\alpha }$ is insensitive to hybridization and that the $D_G(\omega )\sim {\omega }^4$ distribution remains physically meaningful (i.e., it still characterizes the probability to find a soft localized structure in a glass) even in the presence of hybridization, when it cannot be directly probed by a harmonic normal modes analysis. Second, the prediction in Eq. 6 rationalizes the existence of anomalously soft localized spots in glassy materials and predicts its probability.

To test the prediction in Eq. 6 and its degree of universality, we performed extensive numerical simulations of different computer glass-forming models [(i) a binary system of point-like particles interacting via inverse power law purely repulsive pairwise potentials in 2D (2DIPL) and 3D (3DIPL) (34) and (ii) the canonical Kob–Andersen binary Lennard–Jones (3DKABLJ) system (44) in 3D (SI Appendix has details about models and methods)] to extract the statistics of ${\mathcal{E}}_{\alpha }$ according to Eq. 3. The results are summarized in Fig. 2. All of the glasses considered exhibit a power law tail with a universal exponent fully consistent with the theoretically predicted $-9/4$ exponent. These results lend strong support to the prediction in Eq. 6 and therefore, also implicitly, its underlying assumptions. The results presented in this section explain the physical origin of the sensitivity of ${\mathcal{E}}_{\alpha }$ to soft glassy structures, elucidate its anomalous statistical properties, and establish a relation between its statistical properties and the recently observed universal ${\omega }^4$ density of states of quasilocalized low-frequency vibrational modes (34), a fundamental property of glasses. Next, we would like to explore the possibility of defining mesoscopic soft spots based on ${\mathcal{E}}_{\alpha }$ and their predictive powers.

Softness Field and Predicting Plastic Rearrangements

The normalized LTE ${\mathcal{E}}_{\alpha }$ is microscopically defined for any interaction $\alpha$. In Fig. 3, Left, we present yet another example of the spatial map of ${\mathcal{E}}_{\alpha }$, here for a larger system compared with Fig. 1, Right. A continuous field can be naturally constructed by coarse-graining $|{\mathcal{E}}_{\alpha }|$ on a scale larger than the particles scale. We use $|{\mathcal{E}}_{\alpha }|$, because anomalously large negative and positive values of ${\mathcal{E}}_{\alpha }$ are strongly correlated in space. Coarse-graining is achieved by discretizing space into bins containing at least two bonds each, assigning a bin with softness obtained by averaging the values of $|{\mathcal{E}}_{\alpha }|$ of bonds belonging to it, and finally, averaging the bin’s value with the values of all bins in the first layer of neighboring bins (SI Appendix). Applying this procedure to Fig. 3, Left yields Fig. 3, Right, which we treat as a softness field. Our goal now is to test the predictive powers of this softness field in relation to glassy dynamics. The latter, either thermally activated relaxation in nondriven conditions or plastic rearrangements under external driving forces, entails crossing some activation barriers. Activation barriers revealed by soft localized vibrational modes ${𝚿}_i$ of frequency ${\omega }_i$ are small, of order ${\omega }_i^6/c_{iii}^2$ in the leading anharmonic expansion of the energy (45). Hence, we expect that regions that feature large values of $|{\mathcal{E}}_{\alpha }|$ will be particularly susceptible to plastic rearrangements.

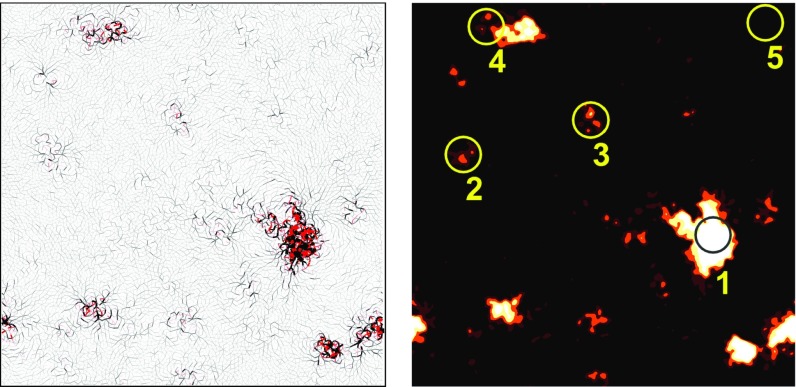
Fig. 3.

(Left) LTE field in a 2DIPL system of $N=10,000$, same as in Fig. 1. (Right) Coarse-grained softness field (in the text). Enumerated by occurrence order are the loci of plastic instabilities that occur upon application of quasistatic shear deformation.

To test the susceptibility of regions with large LTE to plastic rearrangements, we applied global quasistatic shear deformation in a certain direction under athermal conditions to each glass realization—such as the one shown in Fig. 3, Right—and measured the locations of the first few discrete irreversible plastic rearrangements as described in SI Appendix. The advantage of this $T=0$ protocol is that it allows one to uniquely and unquestionably identify the discrete irreversible plastic rearrangements. The locations of the first five discrete irreversible plastic rearrangements (events) were superimposed on the softness field in Fig. 3, Right. The first four plastic events overlap soft spots identified by the softness field, indicating a high degree of predictiveness of ${\mathcal{E}}_{\alpha }$.

To quantify the degree of predictiveness of the LTE ${\mathcal{E}}_{\alpha }$, we extracted the location of soft spots from the spatial distribution of ${\mathcal{E}}_{\alpha }$ (for example, the one shown in Fig. 3) as described in SI Appendix. In addition to its location, each soft spot is characterized by its degree of softness, representing the average value of $|{\mathcal{E}}_{\alpha }|$ in its near vicinity (SI Appendix). Because the fat-tailed distribution in Eq. 6 predicts very large variability in the degree of softness of different soft spots within a single glass realization and among different realizations, we define ${\mathrm{\Delta }}_{\mathcal{E}}$ of each soft spot as the maximal degree of softness in a given realization divided by the spot’s degree of softness. That way, we standardize the degree of softness, such that the softest spot in each realization has ${\mathrm{\Delta }}_{\mathcal{E}}=1$ and not as soft spots have ${\mathrm{\Delta }}_{\mathcal{E}}>1$. Then, each plastic event of ordinal number $n$ ($n=1$ for the first event, $n=2$ for the second, etc.) is associated with the soft spot that is closest to it in space (SI Appendix). We stress that the soft spots are extracted for the nonsheared system and are not updated between plastic events.

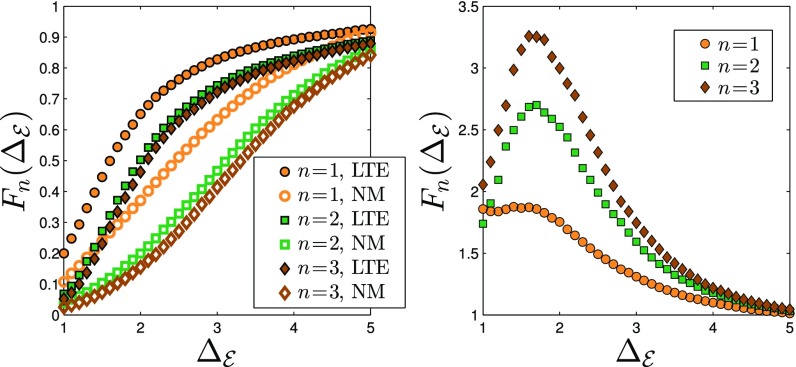
The cumulative distribution function $F_n({\mathrm{\Delta }}_{\mathcal{E}})$, quantifying the fraction of plastic events of ordinal number $n$ being closest to soft spots characterized by a value equal to or smaller than ${\mathrm{\Delta }}_{\mathcal{E}}$, is constructed by collecting data from 5,000 independent simulations of 2DIPL computer glasses. $F_n({\mathrm{\Delta }}_{\mathcal{E}})$ for $n=1,\mathrm{2,3}$ is shown in Fig. 4, Left, closed symbols. As expected, the smaller the $n$, the larger the predictive power. Moreover, it is observed that about $20\%$ of the first plastic events (i.e., $n=1$) are predicted by the softest spot in each realization and that nearly $70\%$ are predicted by soft spots with ${\mathrm{\Delta }}_{\mathcal{E}}\le 2$. To assess how good these predictive powers are, we need some reference case to compare with, which we consider next.

Fig. 4.

(Left) The cumulative distribution function $F_n({\mathrm{\Delta }}_{\mathcal{E}})$ quantifying the fraction of plastic events of ordinal numbers $n=1,\mathrm{2,3}$ being closest to soft spots characterized by a value equal to or smaller than ${\mathrm{\Delta }}_{\mathcal{E}}$ (closed symbols). The corresponding results based on the normal modes (NM) approach (details are in the text) are superimposed (open symbols). (Right) The ratio of $F_n({\mathrm{\Delta }}_{\mathcal{E}})$ for the two approaches, $\delta F_n({\mathrm{\Delta }}_{\mathcal{E}})$, is plotted for $n=1,\mathrm{2,3}$. It is clearly observed that the thermal energy-based approach significantly outperforms the NM-based approach.

Among the many structural indicators studied over the years (compare with the Introduction above), the normal modes-based approach (24–27) stands out according to the relatively high correlations between the structure and dynamics that it exhibits. The basic idea behind this approach is that, although a single low-lying normal mode ${𝚿}_i$ does not clearly exhibit localized structures, possibly because of hybridization, some weighted sum over a system-dependent number of normal modes does reveal such structures. We use this approach here to compare its predictions with the predictions obtained above based on the LTE. In particular, we follow ref. 15 and construct maps analogous to Fig. 3, Left and Fig. 1, Right by summing the norm squared of the components of low-lying normal modes ${𝚿}_i$ at each particle over the first $30$ nonzero modes (i.e., ${\sum }_{i=1}^{30}{|{𝚿}_i^{(j)}|}^2$) for every particle $j$. Here, ${𝚿}_i^{(j)}\equiv ({\mathrm{\Psi }}_{i,x}^{(j)},{\mathrm{\Psi }}_{i,y}^{(j)})$ are the components of the normal mode ${𝚿}_i$ at particle $j$, and $x,y$ are the axes directions in a global 2D Cartesian coordinate system.

After the normal modes maps are constructed (SI Appendix has more details), we apply to them the same procedure described above and calculate the cumulative distribution function $F_n({\mathrm{\Delta }}_{\mathcal{E}})$ based on them. The results are superimposed on the LTE results in Fig. 4, Left, open symbols. The comparison reveals that the thermal energy-based approach significantly outperforms the normal modes-based approach. The performance of both approaches is quantified in Fig. 4, Right, where we plot the ratio of $F_n({\mathrm{\Delta }}_{\mathcal{E}})$ for the two approaches for $n=1,\mathrm{2,3}$, $\delta F_n({\mathrm{\Delta }}_{\mathcal{E}})$, showing that the thermal energy-based approach outperforms the normal modes-based approach by up to a factor of $1.85$ for $n=1$ and up to a factor of $3.3$ for $n=3$.

We thus conclude that the LTE has predictive powers that surpass those of the normal modes-based approach. Can we also assess its predictive powers in absolute terms? To address this question, one should note that soft spots are expected to be anisotropic objects (41, 46) characterized by orientation and polarity and hence, feature variable coupling to shearing in various directions. That is, they are expected to be spin-like objects. Consequently, a spot that is very soft in a given direction may not undergo a rearrangement if the projection of the driving force on its soft direction is small. Hence, the optimal predictive power based on the degree of softness alone—a scalar measure—may be significantly smaller than unity. In particular, assuming a uniform/isotropic orientational distribution of equally soft spots, a naive estimation indicates that only $25\%$ of them will rearrange under shearing in a given direction. As a result, the $\sim 20\%$ predictive power of the softest soft in each realization, compared with Fig. 4, Left, closed symbols ($n=1$), may, in fact, be not so far from the optimal scalar predictiveness level. The optimal scalar predictiveness issue certainly deserves additional investigation.

Conclusion

We have shown that the low-temperature LTE ${\mathcal{E}}_{\alpha }$ is a physical observable that is particularly sensitive to localized soft structures in glasses. ${\mathcal{E}}_{\alpha }$ effectively filters out the contribution of long-wavelength plane waves; hence, it is dominated by soft glassy vibrational modes alone. This property allows one to establish a quantitative relation between the recently observed universal distribution of soft glassy vibrational modes, $D_G(\omega )\sim {\omega }^4$ in the limit of small frequencies $\omega$, and the distribution of the LTE, $p({\mathcal{E}}_{\alpha })\sim {\mathcal{E}}_{\alpha }^{-9/4}$ in the limit of large ${\mathcal{E}}_{\alpha }$. This universal anomalous, fat-tailed distribution of ${\mathcal{E}}_{\alpha }$ has been supported by extensive simulations on various computer glass-former in 2D and 3D.

Although the problems of coexistence and hybridization of long-wavelength plane waves and soft vibrational modes, which have hampered a direct observation of soft quasilocalized glassy modes and their statistical distribution for a long time, will be addressed elsewhere, we stress that our results have potentially important implications in this context. The universal fat-tailed distribution $p({\mathcal{E}}_{\alpha })\sim {\mathcal{E}}_{\alpha }^{-9/4}$ has been theoretically derived based on the DOS of soft quasilocalized vibrational modes $D_G(\omega )\sim {\omega }^4$. However, the LTE ${\mathcal{E}}_{\alpha }$ is a physical quantity that is defined without any explicit reference to soft quasilocalized vibrational modes or any harmonic normal modes analysis. Consequently, it should be valid in the thermodynamic limit where the harmonic normal modes analysis may not cleanly reveal soft quasilocalized vibrational modes or their ${\omega }^4$ DOS. As such, it suggests that the ${\omega }^4$ distribution has a physical meaning that goes beyond the eigenvalues of harmonic normal modes, where $\kappa ={\omega }^2$ is a generalized measure the stiffness of localized soft glassy structures (43).

The universal anomalous distribution of ${\mathcal{E}}_{\alpha }$ and its relation to the universal localized glassy modes DOS imply the existence of highly localized and soft structures in glassy materials. Consequently, ${\mathcal{E}}_{\alpha }$ forms a softness field that naturally reveals soft spots. These soft spots are expected to be characterized by particularly small activation barriers and hence, predict the loci of plastic rearrangements under shearing. As such, these soft spots are natural candidates for STZ (36, 37). The predictive powers of the LTE have been substantiated by extensive numerical simulations and have been shown to be superior to those of the normal modes-based structural indicator.

Our approach offers a general system/model-independent, physical/observable-based framework to identify structural properties of quiescent glasses and relate them to glassy dynamics. In particular, the identified field of soft spots and its time evolution under external driving forces should play a major role in theories of plasticity of amorphous materials, serving to define a population of STZ (37, 47–50). The predictive powers of our approach have been shown here for plastic rearrangements in athermal quasistatically driven systems. An important future challenge would be to test whether and to what extent these predictive powers persist at finite temperatures—possibly up to the glass transition region—and finite strain rates. It should also be tested against thermally activated relaxation in the absence of external driving forces. Finally, as mentioned above, an interesting direction would be to go beyond the scalar degree of softness measure by incorporating orientational information into a generalized structural indicator.