Abstract
Single-molecule measurements of DNA hybridization kinetics are mostly performed on a surface or inside a trap. Here we demonstrate a time-resolved, 3D single-molecule tracking (3D-SMT) method that allows us to follow a freely diffusing ssDNA molecule in solution for hundreds of milliseconds or even seconds and observe multiple annealing and melting events taking place on the same molecule. This is achieved by combining confocal-feedback 3D-SMT with time-domain fluorescence lifetime measurement, where fluorescence lifetime serves as the indicator of hybridization. With sub-diffraction-limit spatial resolution in molecular tracking and 15-ms temporal resolution in monitoring the change of reporter’s lifetime, we have demonstrated a full characterization of annealing rate (kon = 5.13×106 M−1s−1), melting rate (koff = 9.55 s−1), and association constant (Ka = 0.54 μM−1) of an 8-bp duplex model system diffusing at 4.8 μm2/s. As our method completely eliminates the photobleaching artifacts and diffusion interference, our kon and koff results well represent the real kinetics in solution. Our binding kinetics measurement can be carried out in a low signal-to-noise ratio condition (SNR ≈ 1.4) where ~130 recorded photons are sufficient for a lifetime estimation. Using a population-level analysis, we can characterize hybridization kinetics over a wide range (0.5–125 s−1), even beyond the reciprocals of the lifetime monitoring temporal resolution and the average track duration.
Graphical abstract
Accurate knowledge of nucleic acid (NA) hybridization kinetics in its natural context is critical for understanding the fundamental regulatory functions of small NAs. However, the current kinetics measurement techniques are not live cell compatible. Surface plasmon resonance1, 2 and ensemble fluorescence quenching3–5 are common techniques for annealing and melting kinetics measurements, but these methods require an externally imposed perturbation (such as rapid mixing4 or temperature jump6) followed by relaxation analysis, making them generally incompatible with live cell studies. In addition, not at the single-molecule level, these ensemble methods do not provide information about rare reaction intermediates7, minor reaction pathways8 or interaction hot spots9.
Recently, kinetics measurements have been carried out using single-molecule detection, which relies on either surface-based (e.g. DNA tethered to a surface10–13) or confinement-based schemes (e.g. DNA confined in a vesicle14 or electrokinetically trapped in a microfluidic device15) to enable long-time observation of single molecules. While these single-molecule methods have revealed kon and koff at equilibrium, there are concerns about artifacts from the surfaces and the confinements in the experiments16. For instance, the stability of surface-tethered duplexes can be affected by their electrostatic interactions with the surface17, 18 and the hydrophobicity of the surface19. The entropic effects on surface-tethered ssDNA (i.e. reduction in conformational freedom) can also influence duplex stability as single-stranded hairpin formation is favored on the surface20. Since these measurement conditions are not physiologically relevant, it is questionable whether those results faithfully reflect the true NA annealing and melting kinetics in solution. Therefore, a method that can directly probe the hybridization kinetics of freely diffusing NAs at the single-molecule level in solution is highly desired. Such a method will facilitate the kinetics studies of small NAs in their native conditions.
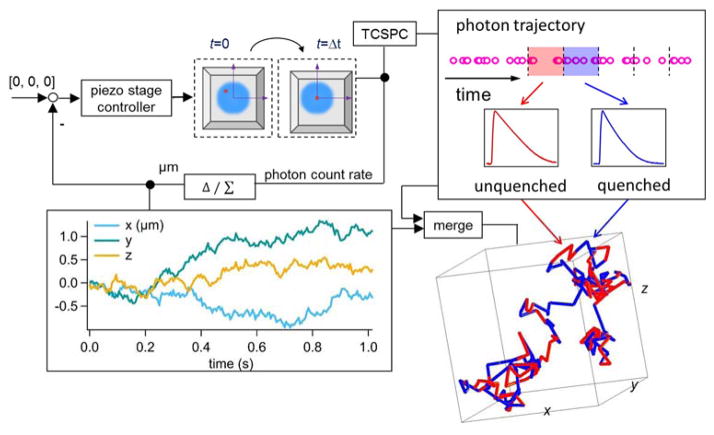
Here we demonstrate a time-resolved, 3D single-molecule tracking (3D-SMT) method that allows us to follow a freely diffusing ssDNA molecule in solution for hundreds of milliseconds to seconds and observe multiple annealing and melting events taking place on the same molecule. Without the need to tether the ssDNA molecule to a surface or to confine it in a trap, our technique is completely compatible with live cell studies. Confocal-feedback 3D-SMT microscopes (Supplemental Note S1) have been previously reported by us21–23 and others24, 25. In short, the 3D position of the molecule of interest is estimated by analyzing the fluorescence signals collected through four multimode optical fibers which serve as spatial filters (50-μm core diameter; each fiber is connected to a single-photon avalanche photodiode). These spatial filters are arranged in a way that the difference in signals collected by one pair of the optical fibers reveals the x position of the molecule, while the difference in signals collected by the other pair reveals the y position. As these two pairs of fibers are axially offset, the signal difference between the two pairs reveals the z position. Once the 3D position of the molecule is determined (at 5-ms temporal resolution), active feedback provided by an xyz piezo stage is employed to keep the molecule of interest at the center of the excitation focus (Fig. 1 top left). The 3D molecular trajectory is thus derived from the motion history of the xyz piezo stage.
Figure 1.
Schematic of our solution-based, spatiotemporally resolved single DNA annealing-melting kinetics measurement method. 3D single-molecule tracking is achieved by a confocal-feedback scheme (Top left). Active feedback provided by an xyz piezo stage is employed to keep the DNA molecule at the center of the excitation focus, where the motion history of the piezo stage represents the 3D trajectory of the tracked molecule (Bottom left). The time-tagged-time-resolved (TTTR) mode of the TCSPC module allows us to monitor the change of reporter’s fluorescence lifetime at 15-ms temporal resolution. In our DNA model system, the longer lifetime (from unquenched dye) represents the ssDNA state (red segment) while the shorter lifetime (from quenched dye) indicates the dsDNA state (blue segment) (Top right). The acquired single-molecule lifetime trace is mapped onto the molecule’s 3D trajectory, providing not only the temporal but also the spatial information of annealing-melting events that take place along this 1,015-ms trajectory (Bottom right).
Using a TCSPC (time-correlated single-photon counting) module, we can time tag the collected photons with 128-ps resolution and group them into consecutive time windows (Fig. 1 top right). After properly compensating the time delays among the four detection channels (Supplemental Note S2), a single fluorescent decay histogram can be built for each time window by accumulating photons collected in all four detectors. A maximum likelihood estimator26 is then used to fit the decay histogram, generating a representative fluorescence lifetime for each time window (Supplemental Note S3). In our experiments, ~130 recorded photons (SNR ≈ 1.4, Supplemental Note S4) are sufficient for a lifetime estimation. This leads to a temporal resolution of 15 ms in monitoring the lifetime of the tracked molecule (emission rate of a single ATTO633 is about 7–9 kHz under 100 μW excitation at 640 nm). The resulting single-molecule lifetime trace can be merged with the molecule’s 3D trajectory (Fig. 1 bottom left) to provide spatiotemporally resolved binding/unbinding kinetic information of the tracked molecule, as long as the binding/unbinding event is accompanied by a change in reporter’s lifetime.
Fig. 1 bottom right panel shows such a merged 3D trajectory – a 5′-ATTO633-labeled 8-nt ssDNA (reporter strand-1 in Table 1) freely diffusing in 70 wt % glycerol solution and transiently hybridizing with the complementary strands. The trajectory is color coded with two distinct fluorescence lifetimes. The longer lifetime (from unquenched ATTO633) corresponds to the ssDNA state, whereas the shorter lifetime (from quenched ATTO633) indicates the dsDNA state. Multiple annealing-melting events can be clearly observed along this merged 1-second trajectory.
Table 1.
Comparison of annealing and melting rates of two reporter strands at different Tris-HCl and glycerol concentration
| reporter | sequence (5′ to 3′) | Tris-HCl buffer | glycerol conc. | kon (106M−1s−1) | koff (s−1) |
|---|---|---|---|---|---|
| reporter strand-1 | ATTO633-TGGGCGGG | 20 mM | 70% | 5.13±0.40 | 9.55±0.64 |
| 4 mM | 70% | 3.63±0.66 | 21.60±0.40 | ||
| 20 mM | 80% | 0.45±0.05 | 10.99±2.0 | ||
|
| |||||
| reporter strand-2 | ATTO633-TGATTGTG | 20 mM | 70% | 5.65±0.56 | 15.71±1.98 |
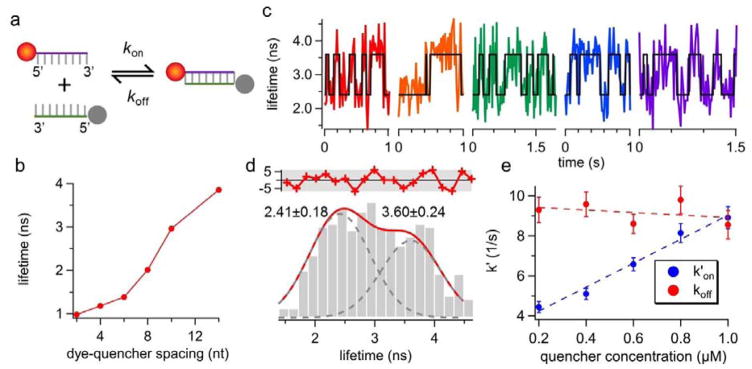
The goal of this work is to recover the annealing (kon) and melting (koff) rates of single DNA molecules from the fluorescence lifetime traces obtained in free solution. To enable tracking of one molecule at a time, the 5′-ATTO633-labeled reporter strand was kept at 50 pM throughout the experiments. The 5′-Iowa Black® FQ-labeled quencher strand, on the other hand, was added to the solution at a much higher concentration (0.2–1 μM). Iowa Black® FQ was selected as the dark quencher due to its absorption peak at 532 nm28, which only partially quenched ATTO633 (emission peak at 653 nm) at the donor-quencher separation distance of 8 bp (Fig. 2a). Before landing on the 8-bp duplex model system, we first characterized the quenching efficiency of ATTO633-Iowa Black® FQ pair at various donor-quencher separation distances (Fig. 2b and Supplemental Tables S1–S3). Our results indicated that 8 bp is an ideal donor-quencher separation distance for our FRET-based kinetics measurements, as at this distance reporter’s lifetime is ~50% reduced upon duplex formation. Because oxygen scavenging systems often lead to complex photophysics of dark quenchers (e.g. creating non-absorbing states of the quenchers) that induces donor blinking29, no oxygen scavenging system was used in our experiments. We observed no quencher-induced ATTO633 blinking (Supplemental Fig. S5). Since molecules with large diffusivities are difficult to track for a long time, we slowed down the diffusion of DNA by running the tracking experiments in 70 wt % glycerol solution.
Figure 2.
(a) The reaction scheme of the donor-quencher system. The reporter strand is a 5′-ATTO633-labeled 8-nt ssDNA. The quencher strand is a 5′-Iowa Black® FQ-labeled ssDNA that is complementary to the reporter. (b) The fluorescence lifetime of ATTO633 as a function of donor-quencher separation distance, measured from ensemble experiments. ATTO633’s lifetime drops from 4.16 ns (on ssDNA) to 2.01 ns (on dsDNA) when the dye-quencher distance is 8 bp. (c) Representative single-molecule lifetime traces of reporter strand-1 in 70 wt % glycerol solution at room temperature. The quencher strand concentration is 0.6 μM. Transient annealing and melting events are clearly manifested as the digital switch of fluorescence lifetime. (d) The lifetime histogram built from the lifetime traces in (c) also shows two states (3.60 ± 0.24 ns and 2.41 ± 0.18 ns, R2 = 0.87). The red curve in the upper panel shows the residuals from the two-peak Gaussian fit. (e) Apparent annealing (k′on) and melting (koff) rates extracted by ebFRET27. Dashed lines indicate linear fits. The annealing rate kon, which is the slope of the linear fit of k′on, is identified to be 5.13 ± 0.42 M−1s−1 whereas the melting rate koff is calculated to be 9.55 ± 0.64 s−1. Error bars represent standard deviations (SD) calculated from the SD of transition probabilities (Supplemental Note S6). R2 for kon fit is 0.98. The correlation coefficient between the quencher strand concentration and koff is −0.35, and the p-value for testing the null hypothesis that koff is independent of quencher concentration is 0.56 (≫0.05), indicating the null hypothesis is not rejected. Therefore, although koff is slightly reduced at higher concentration of the quencher strand (a linear fit between them also shows negative slope), the dependence of koff on quencher strand concentration is statistically insignificant.
Five representative lifetime traces of tracked single reporter strands are shown in Fig. 2c. The black lines indicate the binary-state (ssDNA or dsDNA) sequences identified by ebFRET27, a MATLAB library that analyzes single-molecule FRET time traces using hidden Markov model (HMM). Digital switching between two lifetimes is only seen in the presence of quencher strands (Supplemental Fig. S1). The lifetime histogram built from these traces can be well fitted by two Gaussian-distributed peaks centered at 2.41 and 3.60 ns, respectively (Fig. 2d). The 3.60 ns lifetime, presumably given by the unquenched ATTO633 on reporter strand-1 in the single-molecule measurement, is substantially shorter than the 4.16 ns lifetime of the same strand measured in 20 mM Tris-HCl pH 8.0 buffer at the ensemble level (Supplemental Table S1). Three factors may contribute to this discrepancy. First, difference in the refractive indices of the buffers can give distinct lifetime measurement results, as suggested by the Strickler Berg equation30, 31. Second, background fluorescence (lifetime < 600 ps) from Iowa Black® FQ can bias the fitted lifetime towards a smaller value. Third, as ensemble measurements require a stable duplex at room temperature, locked nucleic acids (LNA) are incorporated in the duplexes for the ensemble lifetime characterization (Supplemental Table S3). LNA-modified duplexes can have a different donor-quencher orientation factor as compared with their DNA counterparts, which can possibly explain why the ensemble and single-molecule measurements on the 8-bp duplexes give two distinct lifetime values (2.01 and 2.41 ns in Fig. 2b and 2d).
To find out the annealing (kon) and melting (koff) rates of single DNA molecules freely diffusing in solution, we conducted 3D-SMT of reporter strands at five different quencher strand concentrations (from 0.2 to 1 μM). As shown in Fig. 2e, the apparent annealing rate (k′on) recovered by ebFRET is proportional to the quencher strand concentration (k′on = kon · [quencher strand]), while the correlation of melting rate (koff) with the quencher strand concentration is statistically insignificant (p-value 0.56). This result reflects the fact that the DNA annealing process is essentially a pseudo first-order reaction (since the quencher strand concentration is at least 4,000-fold higher than that of the reporter strand), whereas the melting is a zero-order reaction. We have successfully characterized kon (5.13×106 M−1s−1), koff (9.55 s−1), and Ka (0.54 μM−1) of the 8-bp duplex model system diffusing at 4.8 μm2/s. It has been previously shown that kon measured in a 3D solution is 3 to 4-fold higher than that measured on a 2D lipid film32. As expected, our kinetics values are 1.5 to 3-fold higher than chose measured by surface-based single-molecule techniques10–12 (Supplemental Table S4).
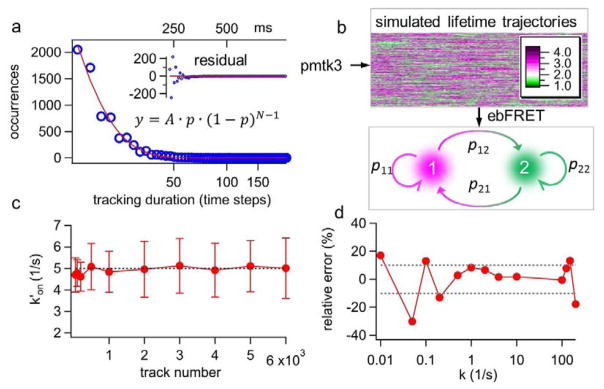
A major challenge in SMT-based DNA hybridization kinetics measurement lies in the fact that the track duration (i.e. how long we can follow a single molecule, which is limited by photostability of the reporter, diffusivity of the tracked molecule, and SNR in the detection) can be shorter than the average dwelling time of the molecule in a certain state. Under this condition, most of the acquired single-molecule lifetime traces show no state transitions. The information content of these short traces is found insufficient for the conventional HMM algorithms (e.g. Hammy33, vbFRET34, QuB35) to recover the transition rates between two states.
Here we show that the ebFRET algorithm provides an excellent solution to this challenge (Fig. 3 and Supplemental Note S5). The experimental track duration histogram can be modeled as a geometric distribution, showing the probability of 0.13 (p = 0.13) for losing track of a single molecule in the each 5-ms time step (Fig. 3a). Based on this experimentally derived probability (p = 0.13) and the preselected state transition rates (k′on = 5 s−1 and koff = 10 s−1), thousands of simulated lifetime traces were generated and fed to the ebFRET algorithm (Fig. 3b). Since ebFRET only generated a transition matrix, a conversion was carried out to turn the transition matrix (unitless) into the rates (s−1) (Supplemental Note S6). In this test, the estimated k′on was found to converge rapidly to the ground truth (5 s−1) and the relative error was found less than 4% when 500 traces or more were used for analysis. The koff result was similar (Supplemental Fig. S2). On the other hand, the estimated k′on from the vbFRET algorithm did not converge to the true value even when more than 1,000 traces were used for analysis (Supplemental Fig. S3).
Figure 3.
(a) The experimental track durations are found to follow a geometric distribution (y) with p = 0.13, where p is the probability of losing track of the molecule in each time step; N is the number of time steps before the molecule is lost; and A is the proportional constant. (b) Based on the experimentally derived p value and the preset annealing-melting rates, we generate thousands of simulated lifetime traces of various durations using the MATLAB toolkit pmtk3. The lifetime traces are then processed by ebFRET to obtain the transition matrix, and hence to calculate k′on and koff (Supplemental Note S6). (c) Apparent annealing rate k′on converges rapidly to the preset value (5 s−1) when the number of lifetime traces used for ebFRET analysis is growing. The error bars are calculated from the standard deviations of the transition matrix, which are also the output parameters from ebFRET. (d) 2,000 simulated lifetime traces produced over a wide range of rates (here k′on= koff = k) are processed by ebFRET. The relative error of estimated k over the broad range of preset k values (0.01–100 s−1) is shown.
In addition, ebFRET offers a broad dynamic range for rate estimation – ebFRET can recover k with less than 10% error when k is within 0.5–125 s−1 and 2,000 lifetime traces are used for analysis (Fig. 3d). The dynamic range for vbFRET analysis is an order of magnitude smaller (Supplemental Fig. S4). We emphasize that 2,000 traces are a practical number as they can be collected experimentally within one hour. Our simulation results prove that the integrated 3D-SMT and ebFRET method can discern kinetics (0.5–125 s−1) with average dwelling time shorter than the lifetime monitoring temporal resolution (15 ms) or longer than the average track duration (115 ms).
A number of buffer and strand conditions are known to affect the DNA annealing and melting rates, including salinity36, 37, osmolyte concentration38, and GC content. To further validate our method, we measured the kinetics of two model systems (GC content 87.5% vs. 37.5%) in buffers with different Tris-HCl and glycerol (an osmolyte) concentrations (Table 1). As expected, lowering the Tris-HCl concentration from 20 mM to 4 mM reduced the association constants Ka by 3.2 fold (from 0.54 to 0.17 μM−1), which can be attributed to the decreased kon and the increased koff in the low-salt buffer. Depending on the salt and glycerol concentration, glycerol can either stabilize39 or destabilize40–42 DNA duplexes. Here we show the significant reduction in duplex stability (a 13-fold reduction in Ka) when the glycerol concentration was increased from 70 to 80 wt %. Clearly a large decrease in kon (from 5.13 to 0.45×106 M−1s−1) was responsible for the reduced Ka. On the other hand, lowering GC content decreased the duplex stability mainly through an increase in koff, which is consistent with previous reports15.
Conclusion and Discussion
We have developed a single-molecule detection and analysis method that enables us to directly monitor individual DNA annealing and melting events occurring in the 3D space. By virtue of a population-level analysis, we can characterize DNA hybridization kinetics over a wide range, even beyond the reciprocals of the lifetime monitoring temporal resolution and the average track duration. In contrast to the traditional ensemble methods that rely on external perturbation and sequential relaxation analysis, our single-molecule approach can probe DNA kinetic properties at equilibrium. Although the transient binding rates can also be derived at equilibrium from fluorescence correlation spectroscopy (FCS, a pseudo single-molecule method)43, the reaction time constant ((kon + koff)−1) has to be quite different from the diffusion time constant in order for FCS to resolve the rate constants.
Previous single-molecule work has revealed that the transfer from a 3D solution to a 2D surface can substantially slow down the DNA hybridization kinetics, possibly due to the loss of freedom for surface-tethered DNA to explore its surroundings32. Therefore, compared with the surface-based detection schemes (Supplemental Table S4), our method is more suitable for examining DNA hybridization behavior in its native 3D environment. Additionally, in surface-based detection it is difficult to differentiate the event of reporter strand disassociation from surface from the event of reporter photobleaching, since both are shown as the disappearance of a bright spot in the TIRF image. On the contrary, in our method we record the annealing/melting event multiple times before the reporter bleaching finally occurs. Therefore, reporter bleaching does not bias our measurements.
While koff is generally thought to be independent of the complementary strand concentration12, 15, in our tracking-based kinetics measurement we have noticed that koff is actually negative correlated (although not statistically significant) with quencher strand concentrations (Fig. 2e). This can be explained by the fact that at high quencher strand concentrations, there are on average more than 100 quencher strands at any time in the confocal volume, ready to form duplex with the reporter strand. When a duplex dissociates, the liberated reporter strand can rehybridize with a nearby quencher strand so quickly that the earlier melting event is missed by our system. In other words, multiple annealing-melting-annealing events may merge into an apparently longer annealing event, leading to a smaller measured koff. To eliminate this artifact given by the high quencher strand concentration, an extrapolation of the koff linear fit down to the low quencher concentration region is used as the melting rate. A similar trend of decreasing koff at higher complementary strand concentrations has also been observed in surface-based detection11, but it could be due to a different reason.
At this moment, our system can only probe rapid rates (0.5–125 s−1) on the molecules diffusing at 4.8μm2/s. A homopolymer model12, 44 of DNA predicts that koff grows approximately exponentially with the duplex length. For a 10-bp DNA duplex, koff is about 0.11 s−1. This translates to a mean dwelling time of 9 s in the dsDNA state, much longer than our current average track duration. That is why we focus on the kinetics study of 8-bp duplex models in this report. However, by improving the tracking algorithm45 and enhancing reporter’s brightness and photostability, we can extend our capability to investigate the hybridization behaviors of the seed sequences (6–12 nt) on the small guided RNA46.
In this study, 3D tracking only serves the purpose to extend the observation window. The solution is homogenous and hence the spatial information (i.e. the dynamic information) of the annealing/melting kinetic processes does not provide any functional insight of the tracked molecule. However, inside live cells, the nucleic acid annealing and melting kinetics can be intracellular location dependent47. To observe kinetics in live cells, methods such as CellSqueeze48- and Streptolysin O49-based transient pore openings can be employed to deliver fluorescently labeled oligonucleotides into live cells. The fusion of spatial and temporal information on the nucleic acid’s kinetic and dynamic processes in complex biological environments can lead to new insight of regulatory functions of small nucleic acids. We emphasize that the investigation of kinetic properties of small nucleic acids in their native environments cannot be done by surface- or confinement-based single-molecule methods. Only 3D-SMT methods offer such an opportunity.
Supplementary Material
Acknowledgments
This work is supported by Texas 4000, Robert A. Welch Foundation (F-1833), National Institutes of Health (CA193038) and National Science Foundation (1611451). N. Jiang acknowledges financial support from Cancer Prevention and Research Institute of Texas (R1120), National Institutes of Health (AG040149), and Robert A. Welch Foundation (F-1785).
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/x0xx00000x
Notes and references
- 1.Thiel AJ, Frutos AG, Jordan CE, Corn RM, et al. In situ surface plasmon resonance imaging detection of DNA hybridization to oligonucleotide arrays on gold surfaces. Anal Chem. 1997;69:4948–4956. [Google Scholar]
- 2.Nelson BP, Grimsrud TE, Liles MR, Goodman RM, et al. Surface plasmon resonance imaging measurements of DNA and RNA hybridization adsorption onto DNA microarrays. Anal Chem. 2001;73:1–7. doi: 10.1021/ac0010431. [DOI] [PubMed] [Google Scholar]
- 3.Walter NG, Burke JM. Real-time monitoring of hairpin ribozyme kinetics through base-specific quenching of fluorescein-labeled substrates. RNA. 1997;3:392–404. [PMC free article] [PubMed] [Google Scholar]
- 4.Tsourkas A, Behlke MA, Rose SD, Bao G. Hybridization kinetics and thermodynamics of molecular beacons. Nucleic Acids Res. 2003;31:1319–1330. doi: 10.1093/nar/gkg212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang DY, Winfree E. Control of DNA strand displacement kinetics using toehold exchange. J Am Chem Soc. 2009;131:17303–17314. doi: 10.1021/ja906987s. [DOI] [PubMed] [Google Scholar]
- 6.Hilbers C, Haasnoot C, De Bruin S, Joordens J, et al. Hairpin formation in synthetic oligonucleotides. Biochimie. 1985;67:685–695. doi: 10.1016/s0300-9084(85)80156-5. [DOI] [PubMed] [Google Scholar]
- 7.Teramura Y, Ichinose J, Takagi H, Nishida K, et al. Single-molecule analysis of epidermal growth factor binding on the surface of living cells. EMBO J. 2006;25:4215–4222. doi: 10.1038/sj.emboj.7601308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ambrose WP, Goodwin PM, Jett JH, Van Orden A, et al. Single molecule fluorescence spectroscopy at ambient temperature. Chem Rev. 1999;99:2929–2956. doi: 10.1021/cr980132z. [DOI] [PubMed] [Google Scholar]
- 9.Liu Z, Legant WR, Chen B-C, Li L, et al. 3D imaging of Sox2 enhancer clusters in embryonic stem cells. Elife. 2014;3:e04236. doi: 10.7554/eLife.04236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dupuis NF, Holmstrom ED, Nesbitt DJ. Single-molecule kinetics reveal cation-promoted DNA duplex formation through ordering of single-stranded helices. Biophys J. 2013;105:756–766. doi: 10.1016/j.bpj.2013.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Peterson EM, Manhart MW, Harris JM. Single-Molecule Fluorescence Imaging of Interfacial DNA Hybridization Kinetics at Selective Capture Surfaces. Anal Chem. 2016;88:1345–1354. doi: 10.1021/acs.analchem.5b03832. [DOI] [PubMed] [Google Scholar]
- 12.Jungmann R, Steinhauer C, Scheible M, Kuzyk A, et al. Single-molecule kinetics and super-resolution microscopy by fluorescence imaging of transient binding on DNA origami. Nano Lett. 2010;10:4756–4761. doi: 10.1021/nl103427w. [DOI] [PubMed] [Google Scholar]
- 13.Johnson-Buck A, Su X, Giraldez MD, Zhao M, et al. Kinetic fingerprinting to identify and count single nucleic acids. Nat Biotechnol. 2015;33:730–732. doi: 10.1038/nbt.3246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cisse II, Kim H, Ha T. A rule of seven in Watson-Crick base-pairing of mismatched sequences. Nat Struct Mol Biol. 2012;19:623–627. doi: 10.1038/nsmb.2294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang Q, Moerner W. Single-molecule motions enable direct visualization of biomolecular interactions in solution. Nat Methods. 2014;11 doi: 10.1038/nmeth.2882. [DOI] [PubMed] [Google Scholar]
- 16.Peterson AW, Heaton RJ, Georgiadis RM. The effect of surface probe density on DNA hybridization. Nucleic Acids Res. 2001;29:5163–5168. doi: 10.1093/nar/29.24.5163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heaton RJ, Peterson AW, Georgiadis RM. Electrostatic surface plasmon resonance: direct electric field-induced hybridization and denaturation in monolayer nucleic acid films and label-free discrimination of base mismatches. Proc Natl Acad Sci USA. 2001;98:3701–3704. doi: 10.1073/pnas.071623998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wong IY, Melosh NA. Directed hybridization and melting of DNA linkers using counterion-screened electric fields. Nano Lett. 2009;9:3521–3526. doi: 10.1021/nl901710n. [DOI] [PubMed] [Google Scholar]
- 19.Kastantin M, Schwartz DK. DNA hairpin stabilization on a hydrophobic surface. Small. 2013;9:933–941. doi: 10.1002/smll.201202335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Watkins HM, Vallée-Bélisle A, Ricci F, Makarov DE, et al. Entropic and electrostatic effects on the folding free energy of a surface-attached biomolecule: an experimental and theoretical study. J Am Chem Soc. 2012;134:2120–2126. doi: 10.1021/ja208436p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu C, Perillo EP, Zhuang Q, Huynh KT, et al. 3D single-molecule tracking using one- and two-photon excitation microscopy. Proceedings of SPIE. 2014;8950:89501C. [Google Scholar]
- 22.Liu C, Zhuang Q, Yeh HC. Three Dimensional Single-Molecule Tracking with Confocal-Feedback Microscope. 9th Ieee International Conference on Nano/Micro Engineered and Molecular Systems (NEMS) 2014:481–484. [Google Scholar]
- 23.Liu C, Liu Y-L, Perillo EP, Dunn AK, et al. Single-molecule tracking and its application in biomolecular binding detection. IEEE Journal of Selected Topics in Quantum Electronics. 2016;22:6804013. doi: 10.1109/JSTQE.2016.2568160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wells NP, Lessard GA, Goodwin PM, Phipps ME, et al. Time-resolved three-dimensional molecular tracking in live cells. Nano Lett. 2010;10:4732–4737. doi: 10.1021/nl103247v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Welsher K, Yang H. Multi-resolution 3D visualization of the early stages of cellular uptake of peptide-coated nanoparticles. Nat Nanotechnol. 2014;9:198–203. doi: 10.1038/nnano.2014.12. [DOI] [PubMed] [Google Scholar]
- 26.Brand L, Eggeling C, Zander C, Drexhage KH, et al. Single-molecule identification of Coumarin-120 by time-resolved fluorescence detection: Comparison of one- and two-photon excitation in solution. Journal of Physical Chemistry A. 1997 Jun 12;101:4313–4321. [Google Scholar]
- 27.van de Meent J-W, Bronson JE, Wiggins CH, Gonzalez RL. Empirical Bayes methods enable advanced population-level analyses of single-molecule FRET experiments. Biophys J. 2014;106:1327–1337. doi: 10.1016/j.bpj.2013.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marras SA. Selection of fluorophore and quencher pairs for fluorescent nucleic acid hybridization probes. Fluorescent Energy Transfer Nucleic Acid Probes: Designs and Protocols. 2006:3–16. doi: 10.1385/1-59745-069-3:3. [DOI] [PubMed] [Google Scholar]
- 29.Holzmeister P, Wünsch B, Gietl A, Tinnefeld P. Single-molecule photophysics of dark quenchers as non-fluorescent FRET acceptors. Photochem Photobiol Sci. 2014;13:853–858. doi: 10.1039/c3pp50274k. [DOI] [PubMed] [Google Scholar]
- 30.Suhling K, Siegel J, Phillips D, French PM, et al. Imaging the environment of green fluorescent protein. Biophys J. 2002;83:3589–3595. doi: 10.1016/S0006-3495(02)75359-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tregidgo C, Levitt JA, Suhling K. Effect of refractive index on the fluorescence lifetime of green fluorescent protein. J Biomed Opt. 2008;13:031218-031218-8. doi: 10.1117/1.2937212. [DOI] [PubMed] [Google Scholar]
- 32.Hannestad JK, Brune R, Czolkos I, Jesorka A, et al. Kinetics of diffusion-mediated DNA hybridization in lipid monolayer films determined by single-molecule fluorescence spectroscopy. ACS Nano. 2012;7:308–315. doi: 10.1021/nn304010p. [DOI] [PubMed] [Google Scholar]
- 33.McKinney SA, Joo C, Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bronson JE, Fei J, Hofman JM, Gonzalez RL, et al. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.NicolaiI C, Sachs F. Solving ion channel kinetics with the QuB software. Biophysical Reviews and Letters. 2013;8:191–211. [Google Scholar]
- 36.Schildkraut C, Lifson S. Dependence of the melting temperature of DNA on salt concentration. Biopolymers. 1965;3:195–208. doi: 10.1002/bip.360030207. [DOI] [PubMed] [Google Scholar]
- 37.Tan Z-J, Chen S-J. Nucleic acid helix stability: effects of salt concentration, cation valence and size, and chain length. Biophys J. 2006;90:1175–1190. doi: 10.1529/biophysj.105.070904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Holmstrom ED, Dupuis NF, Nesbitt DJ. Kinetic and Thermodynamic Origins of Osmolyte-Influenced Nucleic Acid Folding. Journal of Physical Chemistry B. 2015 Mar 5;119:3687–3696. doi: 10.1021/jp512491n. [DOI] [PubMed] [Google Scholar]
- 39.Sorokin V, Gladchenko G, Valeev V, Sysa I, et al. Effect of salt and organic solvents on DNA thermal stability and structure. J Mol Struct. 1997;408:237–240. [Google Scholar]
- 40.Gu X-B, Nakano S-i, Sugimoto N. The effect of the structure of cosolutes on the DNA duplex formation. Nucleic Acids Symp Ser. 2006:205–206. doi: 10.1093/nass/nrl102. [DOI] [PubMed] [Google Scholar]
- 41.Bonner G, Klibanov AM. Structural stability of DNA in nonaqueous solvents. Biotechnol Bioeng. 2000;68:339–344. doi: 10.1002/(sici)1097-0290(20000505)68:3<339::aid-bit12>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 42.Fuller CW, Pisa-Williamson DA. DNA denaturation method. US5500339 A Patent. US Patent. 1996
- 43.Bonnet G, Krichevsky O, Libchaber A. Kinetics of conformational fluctuations in DNA hairpin-loops. Proc Natl Acad Sci USA. 1998;95:8602–8606. doi: 10.1073/pnas.95.15.8602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Anshelevich V, Vologodskii A, Lukashin A, Frank-Kamenetskii M. Slow relaxational processes in the melting of linear biopolymers: a theory and its application to nucleic acids. Biopolymers. 1984;23:39–58. doi: 10.1002/bip.360230105. [DOI] [PubMed] [Google Scholar]
- 45.Liu C, Liu Y-L, Perillo E, Jiang N, et al. Improving z-tracking accuracy in the two-photon single-particle tracking microscope. Appl Phys Lett. 2015;107:153701. doi: 10.1063/1.4932224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Künne T, Swarts DC, Brouns SJ. Planting the seed: target recognition of short guide RNAs. Trends Microbiol. 2014;22:74–83. doi: 10.1016/j.tim.2013.12.003. [DOI] [PubMed] [Google Scholar]
- 47.Schoen I, Krammer H, Braun D. Hybridization kinetics is different inside cells. Proc Natl Acad Sci USA. 2009;106:21649–21654. doi: 10.1073/pnas.0901313106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sharei A, Zoldan J, Adamo A, Sim WY, et al. A vector-free microfluidic platform for intracellular delivery. Proc Natl Acad Sci USA. 2013;110:2082–2087. doi: 10.1073/pnas.1218705110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Teng KW, Ishitsuka Y, Ren P, Youn Y, et al. Labeling proteins inside living cells using external fluorophores for microscopy. Elife. 2016;5:e20378. doi: 10.7554/eLife.20378. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.