Summary
In this paper, we first propose a Bayesian neighborhood selection method to estimate Gaussian Graphical Models (GGMs). We show the graph selection consistency of this method in the sense that the posterior probability of the true model converges to one. When there are multiple groups of data available, instead of estimating the networks independently for each group, joint estimation of the networks may utilize the shared information among groups and lead to improved estimation for each individual network. Our method is extended to jointly estimate GGMs in multiple groups of data with complex structures, including spatial data, temporal data and data with both spatial and temporal structures. Markov random field (MRF) models are used to efficiently incorporate the complex data structures. We develop and implement an efficient algorithm for statistical inference that enables parallel computing. Simulation studies suggest that our approach achieves better accuracy in network estimation compared with methods not incorporating spatial and temporal dependencies when there are shared structures among the networks, and that it performs comparably well otherwise. Finally, we illustrate our method using the human brain gene expression microarray dataset, where the expression levels of genes are measured in different brain regions across multiple time periods.
Keywords: Bayesian Variable Selection, Gaussian Graphical Model, Neighborhood Selection, Markov Random Field, Spatial and Temporal Data
1. Introduction
The analysis of biological networks, including protein-protein interaction networks (PPI), biological pathways, transcriptional regulatory networks and gene co-expression networks, has led to numerous advances in the understanding of the organization and functionality of biological systems (e.g., Kanehisa and Goto 2000; Shen-Orr et al. 2002; Rual et al. 2005; Zhang and Horvath 2005). The work presented in this paper was motivated from the analysis of the human brain gene expression microarray data, where the expression levels of genes were measured in numerous spatial loci, which represent different brain regions, during different time periods of brain development (Kang et al., 2011). Although these data offer rich information on the network information among genes, only naive methods have been used for network inference. For example, Kang et al. (2011) pooled all the data from different spatial regions and time periods to construct a single gene network. However, only a limited number of data points are available for a specific region and time period, making region- and time- specific inference challenging.
Our aim here is to develop sound statistical methods to characterize the changes in the networks across time periods and regions, as well as the common network edges that are shared. This is achieved through a joint modeling framework to infer individual graphs for each region in each time period, where the degrees of spatial and temporal similarity are learnt adaptively from the data. Our proposed joint modeling framework may better capture the edges that are shared among graphs, and also allow the graphs to differ across regions and time periods.
We represent the biological network with a graph G = (V, E) consisting of vertices V = {1, …, p} and edges E ⊂ V × V. In this paper, we focus on conditionally independent graphs, where (i, j) ∈ E if and only if node i and node j are not conditionally independent given all the other nodes. Gaussian graphical models (GGMs) have been proven among the best to infer conditionally independent graphs. In GGM, the p-dimensional X = (X1, …, Xp) is assumed to follow a multivariate Gaussian distribution . Denote Θ = Σ−1 the precision matrix. It can be shown that the conditional independence of Xi and Xj is equivalent to Θij ≠ 0: Xi ⫫ Xj | XV\{i,j} ⇔ Θij = 0. In GGM, estimating the conditional independence graph is equivalent to estimating the non-zero entries in Θ. Various approaches have been proposed to estimate the graph (Meinshausen and Bühlmann, 2006; Yuan and Lin, 2007; Friedman et al., 2008; Cai et al., 2011; Dobra et al., 2011; Wang et al., 2012; Orchard et al., 2013). Among these methods, Friedman et al. (2008) developed a fast and simple algorithm, named the graphical lasso (glasso), using a coordinate descent procedure for the lasso. They considered optimizing the penalized likelihood, with ℓ1 penalty on the precision matrix. As extensions of glasso, several approaches have been proposed to jointly estimate GGMs in multiple groups of data. Guo et al. (2011) expressed the elements of the precision matrix for each group as a product of binary common factors and group-specific values. They incorporated an ℓ1 penalty on the common factors, to encourage shared sparse structure, and another ℓ1 penalty on the group-specific values, to allow edges included in the shared structure to be set to zero for specific groups. Danaher et al. (2014) extended glasso more directly by extending the ℓ1 penalty for each precision matrix with additional penalty functions that encourage shared structure. They proposed two possible choices of penalty functions: 1. Fused lasso penalty that penalizes the difference of the precision matrices, which encourages common values among the precision matrices; 2. Group lasso penalty. Chun et al. (2014) proposed a class of non-convex penalties for more flexible joint sparsity constraints. As an alternative to the penalized methods, Peterson et al. (2014) proposed a Bayesian approach. They formulated the model in the G-Wishart prior framework and modeled the similarity of multiple graphs through a Markov Random Field (MRF) prior. However, their approach is only applicable when the graph size is small (∼ 20) and the number of groups is also small (∼ 5).
In this paper, we formulate the model in a Bayesian variable selection framework to estimate the graph structure (George and McCulloch, 1993, 1997). The precision matrix is estimated in a second step with the graph structure fixed (Hastie et al., 2009). Meinshausen and Bühlmann (2006) proposed a neighborhood selection procedure for estimating GGMs, where the neighborhood of node i was selected by regressing on all the other nodes. Intuitively, our approach is the Bayesian analog of the neighborhood selection procedure. Our framework is applicable to the estimation of both single graph and multiple graphs. For the joint estimation of multiple graphs, we incorporate the MRF model. Compared with Peterson et al. (2014), we use a different MRF model and a different inferential procedure. In small scale simulations (20 nodes), our method performed slightly worse than Peterson et al. (2014), but better than the other competing methods (Friedman et al., 2008; Guo et al., 2011; Danaher et al., 2014). One advantage of our approach is that it can naturally model complex data structures, such as spatial data, temporal data and data with both spatial and temporal structures. Another advantage is the computational efficiency. For the estimation of a single graph with 100 nodes (the typical size of biological pathways is around that range), the computational time on a laptop is ∼ 30 seconds for 1,000 iterations of Gibbs sampling, which is ∼ 3-folds faster than Bayesian Graphical Lasso, which implements a highly efficient block Gibbs sampler and is among the fastest algorithms for estimating GGMs in the Bayesian framework (Wang et al., 2012). For multiple graphs, the computational time increases roughly linear with the number of graphs. Our procedure also enables parallel computing and the computational time can be substantially reduced if multicore processors are available. For single graph estimation, we show the graph selection consistency of the proposed method in the sense that the posterior probability of the true model converges to one.
The rest of the paper is organized as follows. We introduce the Bayesian neighborhood selection procedure for single graph and the extension to multiple graphs in Section 2. The theoretical properties are presented in Section 3. The simulation results are demonstrated in Section 4 and the application to the human brain gene expression microarray dataset is presented in Section 5. We conclude the paper with a brief summary in Section 6.
2. Statistical Model and Methods
2.1 The Bayesian Neighborhood Selection Procedure
We first consider estimating the graph structure when there is only one group of data. Consider the p-dimensional multivariate normal random variable . We further assume that X is centered and . Let Θ = Σ−1 denote the precision matrix. Let the n × p matrix X = (X1, …, Xp) contain n independent observations of X. For A ⊆ {1, …, p}, define XA = (Xj, j ∈ A). Let Γi denote the subset of {1, …, p}, excluding the ith entry only. For any square matrix C, let denote the ith row, excluding the ith element in that row. Consider estimating the neighborhood of node i. It is well known that the following conditional distribution holds:
| (1) |
where I is the n × n identity matrix, Θii is a scalar and finding the neighborhood of Xi is equivalent to estimating the non-zero coefficients in the regression of Xi on . Let β and γ be matrices of dimension p × p, where and γ is the binary latent state matrix. The diagonal elements in β and γ are not assigned values. Conditioning on γij, βij is assumed to follow a normal mixture distribution (George and McCulloch, 1993, 1997):
where τi0/τi1 = δ and 0 < δ < 1. The prior on γij is Bernoulli: p(γij = 1) = 1 − p(γij = 0) = q. δ, τi1 and q are prefixed hyperparameters and are discussed in the Supplementary Materials. The off-diagonal entries in γ represent the presence or absence of the edges, which is the goal of our inference.
Let σ = (σ1, …, σp), where . The inverse gamma (IG) conjugate prior is assumed for :
In this paper, we assume that νi = 0 and the IG prior reduces to a flat prior (Li and Zhang, 2010).
For each node, we implement the Bayesian procedure to select the neighbors of that node. The graph selection consistency of our approach is shown in Section 3. Performing neighborhood selection is not equivalent to making inference on Θ (Dobra et al., 2004). Though is a conditional likelihood for Gaussian distribution, the function ∏i is not a Gaussian likelihood and it has the likelihood properties of a misspecified model with p regressions (Varin et al., 2011). We implement MCMC to estimate the posterior distributions and details for the algorithm are provided in the Supplementary Materials. In our approach, the symmetric constraint of the graph structure can be incorporated when sampling γ by assuming γij = γji for j ≠ i. Under the Gaussian assumption, the regression coefficients β are directly related to the corresponding entries in Θ and are also related to the partial correlation. The symmetry of Θ can be satisfied if we impose the constraint when sampling β. Without the constraint on β, the partial correlation may not be estimated coherently: the magnitudes and signs may be different between nodes i on j and nodes j on i. However, imposing the constraint will lead to substantial loss in computational efficiency since β have to be updated one at a time, instead of one row at a time. Moreover, our simulation results suggest that the two approaches are comparable for graph structure estimation, whether or not the constraint is imposed (data not shown). We do not impose the constraint on β in practice. Although most applications tend to focus more on the graph structure estimation, it may be desirable to obtain a symmetric positive definite estimate for Θ. To achieve this, we propose a two-step approach. First, we estimate the graph structure with Ĝ following the neighborhood selection approach. Second, we estimate Θ with the mode of the conditional likelihood p(X | Ĝ, Θ), where Θ is subjected to the constraint of Ĝ. The mode can be obtained with a fast iterative algorithm presented in Hastie et al. (2009). There are two limitations in the two-step approach. First, uncertainty of the graph structure in step 1 is not taken into account in step 2. Second, priors on the regression coefficients are part of the modeling framework in step 1, but not in step 2. Examples implementing the two-step procedure are provided in the Supplementary Materials.
2.2 Extension to mutiple graphs
When there is similarity shared among multiple graphs, jointly estimating multiple graphs can improve inference. We propose to jointly estimate multiple graphs by specifying a Markov Random Field (MRF) prior on the latent states. Our model can naturally incorporate complex data structures, such as spatial data, temporal data and data with both spatial and temporal structures. Consider jointly estimating multiple graphs for data with both spatial and temporal structures. Denote B the set of spatial loci and T the set of time points. Our proposed model can be naturally implemented when there is missing data, i.e. no data points taken in certain locus at certain time point. For now, we assume that there is no missing data. The latent states for the whole dataset are represented by a |B|×|T|×p×p array γ, where | | denotes the cardinality of a set. Let γbt·· denote the latent state matrix for locus b at time t. In the real data example, b is a categorical variable representing the brain region and t is a discrete variable that represents the time period during brain development. Same as that in Section 2.1, the diagonal entries in γbt·· are not assigned values.
Consider estimating the neighborhood of node i. Let γbtij denote the latent state for node j ∈ Γi in locus b at time t. Denote γ··ij = {γbtij : ∀b ∈ B, ∀t ∈ T}, and . Here contain all the pairs capturing spatial similarity and contain all the pairs capturing temporal dependency between adjacent time periods. We do not consider the direction of the pairs: (γijbt, γijb′t′) and (γijb′t′, γijbt) are the same. Let I1(·) and I0(·) represent the indicator functions of 1 and 0, respectively. The prior for γ··ij is specified by a pairwise interaction MRF model (Besag, 1986; Lin et al., 2015):
| (2) |
and conditional independence is assumed:
| (3) |
where Φ = {η1, ηs, ηt} are set to be the same for all i and j. η1 ∈ ℝ and when there is no interaction terms, 1/(1 + exp(−η1)) corresponds to q in the Bernoulli prior. ηs ∈ ℝ represents the magnitude of spatial similarity and ηt ∈ ℝ represents the magnitude of temporal similarity. In the simulation and real data example, η1 is prefixed, whereas ηs and ηt are estimated from the dataset. The priors on ηs and ηt are assumed to follow uniform distribution in [0, 2]. Sensitivity analyses on the choice of η1 and the priors on ηs and ηt are provided in the Supplementary Materials.
Let γ··ij/γbtij denote the subset of γ··ij excluding γbtij. Then we have:
| (4) |
where
In the MCMC for multiple graphs, the Metropolis-Hastings (MH) algorithm is implemented to update ηs and ηt. The normalizing constant in p(γ··ij | Φ) is generally not tractable as one has to sum over all 2|B|+|T| possible configurations of γ··ij. The likelihood ratio need in the MH step is approximated with the ratio of pseudolikelihoods (Besag, 1986) and the pseudolikelihood is calculated as: ∏b∈B ∏t∈T p(γbtij | γ··ij/γbtij, Φ). Comparison between using the ratio of pseudolikelihoods with the bridge sampler (Meng and Wong, 1996) is shown in the Supplementary Materials.
In the prior specification (2), we made the following assumptions: a) the spatial similarity does not change over time and b) the time periods are evenly spaced and can be represented by integer labels. The first assumption can be relaxed by allowing ηs to change over time. For the second assumption, ηt can be adjusted to a parametric function of the time interval. When there is only spatial or only temporal structure in the dataset, prior (2) can be adjusted by removing the summation over the corresponding pairs. The posterior probability-based false discovery rate (FDR) control (Newton et al., 2004) can be implemented to evaluate the marginal posterior probabilities (Supplementary Materials).
3. Theoretical Properties
We rewrite p as pn to represent a sequence pn that changes with n. Let 1 ≤ p* ≤ pn. Throughout, we assume that X satisfies the sparse Riesz condition (Zhang and Huang, 2008) with rank p*; that is, there exist some constants 0 < c1 < c2 < ∞ such that
for any A ⊆ {1, …, pn} with size |A| = p* and any nonzero vector .
Consider estimating the neighborhood for the ith node. We borrow some notations from Narisetty et al. (2014). For the simplicity of notation, let and . Write τi0, τi1 and q as τ0n, τ1n and qn, respectively, to represent sequences that change with n. We use a (pn − 1) × 1 binary vector ki to index an arbitrary model. The corresponding design matrix and parameter vector are denoted by and , respectively. Let ti represent the true neighborhood of node i.
Denote by λmax(·) and λmin(·) the largest and smallest eigenvalues of a matrix, respectively. For υ > 0, define
and
For K > 0, let
where |ki| denotes the size of the model ki and is the projection matrix onto the column space of .
For sequences an and bn, an ∼ bn means an/bn → c for some constant c > 0, an ≺ bn (or bn ≻ an) means an = o(bn), and (or ) means an = O(bn). We need the following conditions.
-
(A)
pn → ∞ and pn = O(nθ) for some θ > 0;
-
(B)
for some 0 ≤ α < 1 ∧ (1/θ);
-
(C)
and for some δ1 > 1 + α;
-
(D)
|ti| ≺ n/log pn and ;
-
(E)
there exist 1 + α < δ2 < δ1 and K > 1 + 8/(δ2 − 1 − α) such that, for some large C > 0, ;
-
(F)
p* ⩾ (K + 1)|ti|;
-
(G)and there exist some 0 < υ < δ2 and 0 < κ < 2(K − 1) such that
Theorem 1
Assume conditions (A)–(G). For some c > 0 and s > 1 we have, with probability at least , , where rn goes to 0 as the sample size increases to ∞.
To establish graph-selection consistency, we need slightly stronger conditions than (D)–(G). Let
-
(D′)
t* ≺ n/logpn and ;
-
(E′)
there exist 1 + α < δ2 < δ1 and K > 1 + 8/(δ2 − 1 − α) such that, for some large C > 0, ;
-
(F′)
p* ⩾ (K + 1)t*;
-
(G′)and there exist some 0 < υ < δ2 and 0 < κ < 2(K − 1) such that
Let denote the true graph structure and γ is the latent state matrix for all the nodes.
Theorem 2
Assume conditions (A)–(C) and (D′)–(G′). We have, as n → ∞, .
The proofs of Theorem 1 and 2 are provided in the Supplementary Materials. In the proof of Theorem 1, we borrowed the general framework and some ideas from Narisetty et al. (2014). The key difference in our proof is that (1) we need to simultaneously control the posterior probability for p regressions, while allowing p to diverge with the sample size; (2) we allow the true model size to diverge while Narisetty et al. (2014) assumed that it is fixed. Some prior specifications are also different. The maximum a posteriori (MAP) estimate is hard to achieve in practice as the searching space is too large: 2number of possible edges. Instead, we use the marginal posterior probability to select the edges. The consistency of joint posterior probability implies the consistency of marginal posterior probability.
4. Simulation examples
4.1 Joint estimation of multiple graphs
We first considered the simulation of three graphs. For all three graphs, p = 100 and n = 150. We first simulated the graph structure. We randomly selected 5% or 10% among all the possible edges and set them to be edges in graph 1. For graphs 2 and 3, we removed a portion (20% or 100%) of edges that were present in graph 1 and added back the same number of edges that were not present in graph 1. 20% represents the case that there is moderate shared structure. 100% represents the extreme case that there is little shared structure other than those shared by chance. For the entries in the precision matrices, we considered two settings: a) the upper-diagonal entries were sampled from uniform [−0.4, −0.1] ∪ [0.1, 0.4] independently and then set the matrix to be symmetric b) Same as that in a), except that for the shared edges, the corresponding entries were set to be the same. To make the precision matrix positive definite, we set the diagonal entry in a row to be the sum of absolute values of all the other entries in that row, plus 0.5.
The simulation results are presented in Figure 1. Our method (MRF) was compared with Guo’s method (Guo et al., 2011), JGL (Danaher et al., 2014) and graphical lasso (glasso) (Friedman et al., 2008). In glasso, the graphs are estimated independently. In JGL, there are two options, fused lasso (JGL-Fused) and group lasso (JGL-Group). For Guo’s method, glasso and JGL, we varied the sparsity parameter to generate the curves. For our method, we varied the threshold for the marginal posterior probabilities of γ to generate the curves. There are two tuning parameters in JGL, λ1 and λ2, where λ1 controls sparsity and λ2 controls the strength of sharing. We performed a grid search for λ2 in {0, 0.05, …, 0.5} and selected the best curve. In Figure 1, our method performed slightly better than Guo’s method. When there is little shared structure among graphs, our method performed slightly better than glasso, which is possibly due to the fact that we used a different modeling framework. When the entries were different for the shared edges, JGL-Fused did not perform well. However, when the entries were the same, JGL-Fused performed much better. The fused lasso penalty encourages entries in the precision matrix to be the same and JGL-Fused gains efficiency when the assumption is satisfied. We also performed simulations under high dimension settings (p < n) and simulations with a larger scale (p = 500). The results are similar and are shown in the Supplementary Materials. Moreover, we compared the methods for the detection of differential edges and shared edges in the graphs. We did not include JGL in the comparison as the similarity of the graphs is controlled with a tuning parameter. For the detection of shared edges, our method is better than Guo’s, and Guo’s method is better than glasso; for the detection of differential edges, our method is comparable to Guo’s, and glasso is slightly better than both methods. In addition, we compared our method with Peterson et al. (2014), a Bayesian approach using G-Wishart priors. Peterson’s method may not be applicable when p is moderately large or the number of graphs is more than a few (Supplementary Materials). We performed simulations with smaller scale and more replicates (p = 20, n = 100), where the setting is similar to that in Peterson et al. (2014). The results are shown in the Supplementary Materials. Our method performed slightly worse than Peterson’s method, but better than Guo’s method and JGL-Fused. Neighborhood selection methods may favor random graphs over graphs with hub structures. We also performed simulation for single graph, where the degree of nodes follows a power law distribution. Our method is comparable with glasso.
Figure 1.
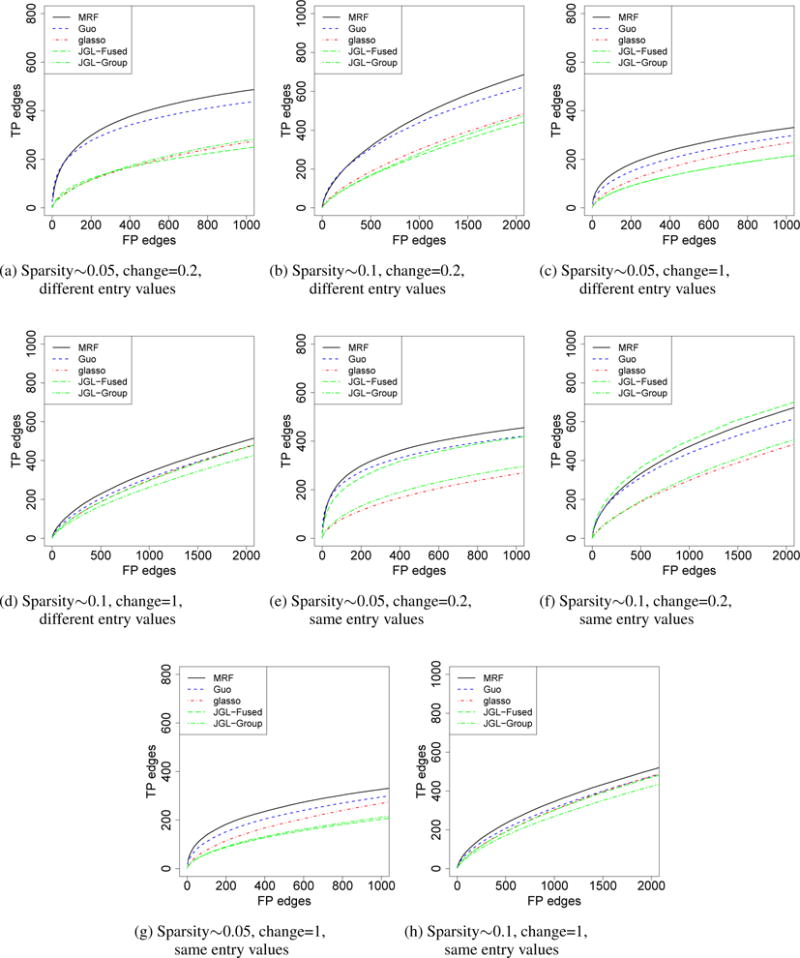
Comparisons of different models for the estimation of three graphs. For the shared edges, the corresponding entries in the precision matrices take the same (“same entry values”) or different (“different entry values”) non-zero values. The x-axis was truncated to be slightly larger than the total number of true positive edges. The curves represent the average of 100 independent runs.
4.2 Joint estimation of multiple graphs with temporal dependency
In this setting, we assumed that the graph structure evolved over time by Hidden Markov Model (HMM). We set p = 50. At time t = 1, we randomly selected 10% among all the possible edges and set them to be edges. At time t + 1, we removed 20% of the edges at time t and added back the same number of edges that were not present at time t. The entries in the precision matrix were set the same as that in a) in Section 4.1. We present the simulation results in Figure 2, varying n and |T|. We compared our method with Guo’s and JGL-Group, where the graphs were treated as parallel. Our method performed better than Guo’s method and JGL-Group in all three settings, and the difference was greater when either n or |T| increases. We did not include JGL-Fused in the comparison as the computational time for JGL-Fused increases substantially when the number of graphs is more than a few.
Figure 2.
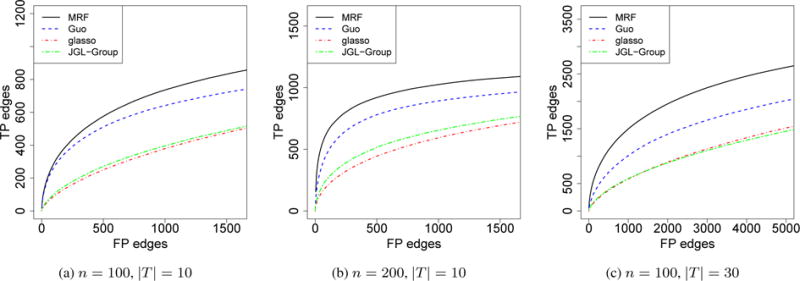
Comparisons of different models for the estimation of mutiple graphs with temporal dependency. The x-axis was truncated to be slightly larger than the total number of true positive edges. The curves represent the average of 100 independent runs.
4.3 Joint estimation of multiple graphs with both spatial and temporal dependency
We simulated graphs in |B| = 3 spatial loci and |T| = 10 time periods. We set p = 50, n = 100, and sparsity∼ 0.1. We first set the graphs in different loci at the same time point to be the same. The graph structure evolved over time by HMM similarly as that in Section 4.2, and 40% of the edges changed between adjacent time points. For all graphs, we then added some perturbations by removing a portion (10%, 20%, 50%) of edges and adding back the same number of edges. In each time period, the 3 graphs have similar degree of similarity with each other. The entries in the precision matrix were set the same as that in a) in Section 4.1. The simulation results are presented in Figure 3. Our method achieved better performance than all the other methods. We also compared the posterior distribution of ηs and ηt between real data and simulated data (Supplementary Materials). Based on ηs and ηt, the temporal dependency in the simulations is weaker than that in the real data; the simulations with 10% and 20% perturbations have stronger spatial dependency than that in the real data, and for the 50% one, it has similar degree of spatial similarity.
Figure 3.
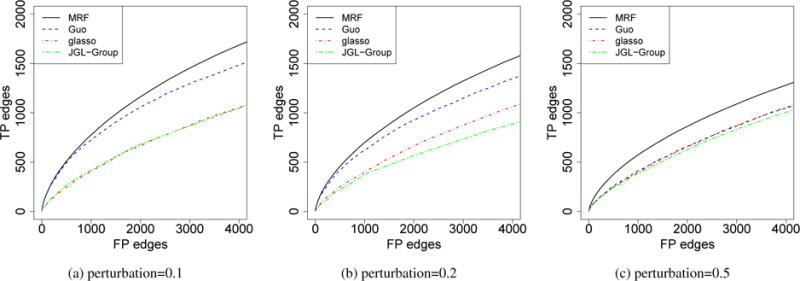
Comparisons of different models for the estimation of mutiple graphs with temporal and spatial dependency. The x-axis was truncated to be slightly larger than the total number of true positive edges. The curves represent the average of 100 independent runs.
4.4 Computational time
We evaluated the computational speed of our approach in the estimation of single GGM and multiple GGMs. For single GGM, we compared our method (B-NS) with Bayesian Graphical Lasso (B-GLASSO) (Wang et al., 2012) in Figure 4a. Our algorithm took 0.5 and 4.5 minutes to generate 1,000 iterations for p = 100 and p = 200, and B-GLASSO took 1.6 and 17.9 minutes. The performance of graph structure estimation is comparable (Supplementary Materials). We also evaluated the speed of our algorithm for the joint estimation of multiple graphs, where n and p were both fixed to 100. The CPU time was roughly linear as the number of graphs increased (Figure 4b). When multiple processors are available, parallel computing will result in substantial gain in computational speed (Figure 4). Our model enables parallel computing in two levels: 1. for single graph estimation, the rows in β can be updated in parallel (“rows parallel”); 2. for multiple graphs estimation, the matrix β for each graph can be updated in parallel (“graphs parallel”). “graphs parallel” requires more memory and tends to outperform “rows parallel” on data with a smaller scale. The computations presented in Figures 4a and 4b were implemented on a dual-core CPU 2.4 GHz laptop running OS X 10.9.5 using MATLAB 2014a. The other computations were performed on the Yale University Biomedical High Performance Computing Center. The computational cost of our algorithm is O(p3).
Figure 4.
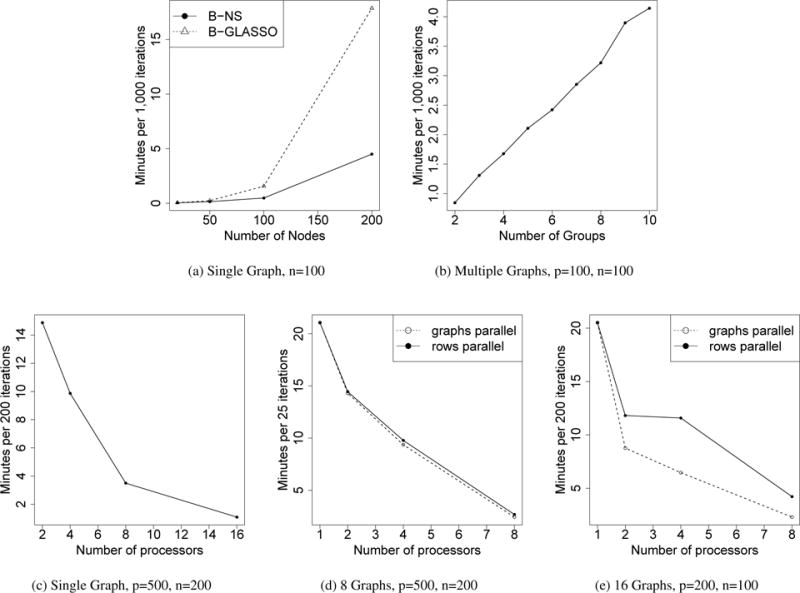
Comparing the running time. (a) Single graph with increasing number of nodes, we compared our method (B-NS) with Bayesian Graphical Lasso (B-GLASSO) (Wang et al., 2012); (b) Multiple graphs with increasing number of graphs; (c–e) we implemented parallel computing.
5. Application to the human brain gene expression dataset
Next we apply our method to the human brain gene expression microarray dataset (Kang et al., 2011). In the dataset, the expression levels of 17,568 genes were measured in 16 brain regions across 15 time periods. The time periods are not evenly spaced over time and each time period represents a distinct stage of brain development. The median number of biological replicates per time per region is 5. Because of the small sample size, we collapsed the 16 regions into two regions: neocortical regions (11 regions) and non-neocortical regions (5 regions). The neocortical regions are more similar with each other (Kang et al., 2011). We excluded the data from time periods 1 and 2 in our analysis because they represent very early stage of brain development, when most of the brain regions sampled in future time periods have not differentiated. We first studied the network of 7 high confidence genes associated Autism Spectrum Disorders (ASD): GRIN2B, DYRK1A, ANK2, TBR1, POGZ, CUL3, and SCN2A(Willsey et al., 2013). ASD is a neurodevelopment disorder that affects the brain and have an early onset in childhood. With a good understanding on the networks of the 7 ASD genes, we hope to gain insight into how these genes interact to yield clues on their roles in autism etiology. The posterior mean and standard deviation for ηs were 0.61 and 0.47, respectively. The posterior mean and standard deviation for ηt were 1.27 and 0.48, respectively. The estimated model parameters suggest strong temporal dependency of the network structure. The estimated graphs are shown in Figure 5, and in the Supplementary Materials.
Figure 5.
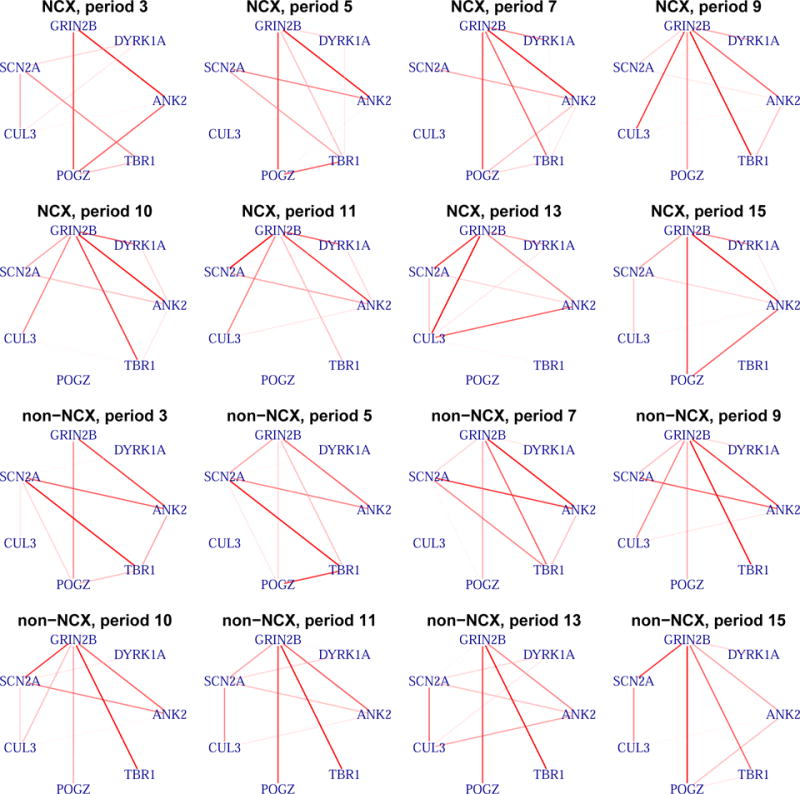
The estimated graphs for the ASD genes. Period 10 corresponds to early childhood (1 years ≤ age ≤ 6 years), which is the typical period of autism onset. Some periods are skipped and are shown in the Supplementary Materials. The rank of the marginal probabilities is represented by the color gradient of the edges. NCX: neocortical regions; non-NCX: non-neocortical regions.
Time period 10 corresponds to early childhood (1 years ≤ age ≤ 6 years), which is the typical period that patients show symptoms of autism. Of particular interest are the genes that are connected with TBR1, which is a transcription factor that may directly regulate the expression of numerous other genes. GRIN2B is a potential target of TBR1 (Bedogni et al., 2010) and Tbr1 has been shown to mediate the expression of Grin2b in adult mouse brain (Chuang et al., 2014). Interestingly, the edge between TBR1 and GRIN2B tends to be shared over time in the non-neocortical regions, but not in the neocortical regions: the edge inclusion probability tend to decrease after period 10 in the neocortical regions. Further biological experiments are required to validate the temporal dynamics of TBR1 and GRIN2B interaction. The marginal posterior probabilities of edge inclusion are compared between our approach (MRF) and the simpler approach not considering the data structure (B-NS) (Figure 6a). For a fair comparison, we set q = 1/(1 + exp(−η1)) in B-NS. Considering the data structure leads to a better separation of the marginal posterior probability.
Figure 6.
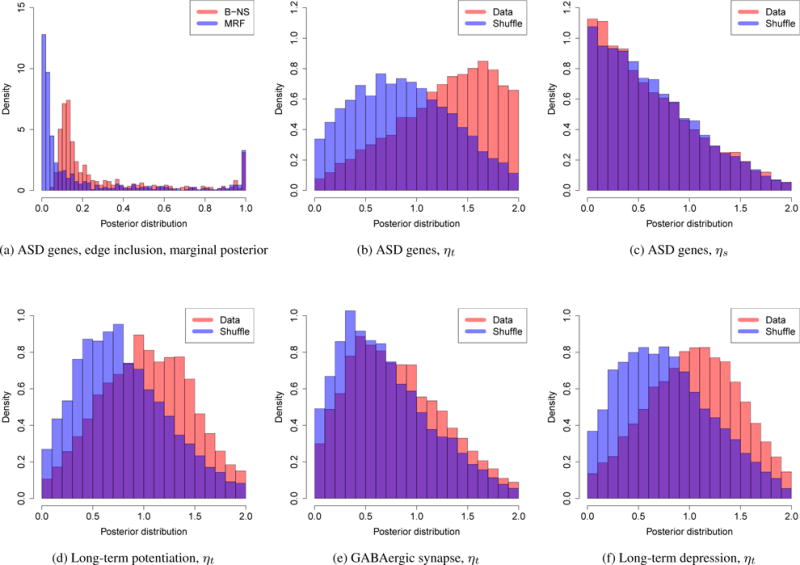
The posterior distributions. (a) The posterior distribution of the edge inclusion marginal probabilities, ASD genes; (b, c) The posterior distribution of the MRF model parameters, ASD genes; (d–f) The posterior distribution of ηt, the three pathways.
To demonstrate the temporal dependency, we shuffled the time periods and re-implemented our approach. ηt tends to be smaller in the shuffled data while ηs has similar posterior distribution (Figures 6b, and 6c). Collapsing the neocortical and non-neocortical regions, we implemented our approach on three manually curated biological pathways: long-term potentiation (65 genes), long-term depression (57 genes), and GABAergic synapse (86 genes). Long-term potentiation and long-term depression are associated with memory and learning; Gamma aminobutyric acid (GABA) is the most abundant inhibitory neurotransmitter in the mammalian central nervous system. When we shuffled the time periods, ηt tends to be smaller in long-term potentiation and long-term depression and it is slightly smaller for GABAergic synapse (Figures 6d, 6e, and 6f). Only in long-term potentiation, one gene is overlapped with the ASD gene set. The estimated graphs for the three pathways are shown in the Supplementary Materials. A large fraction of the top edges are shared in the adjacent periods (Supplementary Materials). Before birth, from period 6 to 7, the networks tend to rewire and the trend is similar in the three pathways (Supplementary Materials).
6. Conclusion
In this paper, we proposed a Bayesian neighborhood selection procedure to estimate Gaussian Graphical Models. Incorporating the Markov Random Field prior, our method was extended to jointly estimating multiple GGMs in data with complex structures. Compared with the non-Bayesian methods, there is no tuning parameter controlling the degree of structure sharing in our model. Instead, the parameters that represent similarity between graphs are learnt adaptively from the data. Simulation studies suggest that incorporating the complex data structure in the jointly modeling framework would benefit the estimation. For the human brain gene expression data, we applied our method on the autism genes and three biological pathways related to the nervous system. We identified some interesting connections in the networks of autism genes. We also demonstrated the graph selection consistency of our procedure for the estimation of single graph.
Supplementary Material
Acknowledgments
The authors thank Professor Forrest W. Crawford for the helpful discussions. This study was supported in part by the National Science Foundation grant DMS-1106738 and the National Institutes of Health grants R01 GM59507 and P01 CA154295. Tao Wang is supported by National Natural Science Foundation of China grant 11601326. Can Yang was supported in part by grant 61501389 from National Science Funding of China, grants 22302815 and 12316116 from the Hong Kong Research Grant Council, and grant FRG2/15-16/011 from Hong Kong Baptist University.
Footnotes
Supplementary Materials
Web Appendices and Figures, referenced in Section 2–5, are available with this paper at the Biometrics website on Wiley Online Library. The Matlab code is available at https://github.com/linzx06/Spatial-and-Temporal-GGM.
References
- Bedogni F, Hodge RD, Elsen GE, Nelson BR, Daza RA, Beyer RP, Bammler TK, Rubenstein JL, Hevner RF. Tbr1 regulates regional and laminar identity of postmitotic neurons in developing neocortex. Proceedings of the National Academy of Sciences. 2010;107:13129–13134. doi: 10.1073/pnas.1002285107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society. Series B (Methodological) 1986:259–302. [Google Scholar]
- Cai T, Liu W, Luo X. A constrained l1 minimization approach to sparse precision matrix estimation. Journal of the American Statistical Association. 2011;106:594–607. [Google Scholar]
- Chuang HC, Huang TN, Hsueh YP. Neuronal excitation upregulates tbr1, a high-confidence risk gene of autism, mediating grin2b expression in the adult brain. Frontiers in cellular neuroscience. 2014;8:280. doi: 10.3389/fncel.2014.00280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun H, Zhang X, Zhao H. Gene regulation network inference with joint sparse gaussian graphical models. Journal of Computational and Graphical Statistics. 2014:00–00. doi: 10.1080/10618600.2014.956876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danaher P, Wang P, Witten DM. The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2014;76:373–397. doi: 10.1111/rssb.12033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobra A, Hans C, Jones B, Nevins JR, Yao G, West M. Sparse graphical models for exploring gene expression data. Journal of Multivariate Analysis. 2004;90:196–212. [Google Scholar]
- Dobra A, Lenkoski A, Rodriguez A. Bayesian inference for general gaussian graphical models with application to multivariate lattice data. Journal of the American Statistical Association. 2011;106 doi: 10.1198/jasa.2011.tm10465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9:432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George EI, McCulloch RE. Variable selection via gibbs sampling. Journal of the American Statistical Association. 1993;88:881–889. [Google Scholar]
- George EI, McCulloch RE. Approaches for bayesian variable selection. Statistica sinica. 1997;7:339–373. [Google Scholar]
- Guo J, Levina E, Michailidis G, Zhu J. Joint estimation of multiple graphical models. Biometrika. 2011:asq060. doi: 10.1093/biomet/asq060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J, Hastie T, Friedman J, Tibshirani R. The elements of statistical learning. Vol. 2. Springer; 2009. [Google Scholar]
- Kanehisa M, Goto S. Kegg: kyoto encyclopedia of genes and genomes. Nucleic acids research. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HJ, Kawasawa YI, Cheng F, Zhu Y, Xu X, Li M, Sousa AM, Pletikos M, Meyer KA, Sedmak G, et al. Spatio-temporal transcriptome of the human brain. Nature. 2011;478:483–489. doi: 10.1038/nature10523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Zhang NR. Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. Journal of the American Statistical Association. 2010;105 [Google Scholar]
- Lin Z, Sanders SJ, Li M, Sestan N, Zhao H, et al. A markov random field-based approach to characterizing human brain development using spatial–temporal transcriptome data. The Annals of Applied Statistics. 2015;9:429–451. doi: 10.1214/14-AOAS802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso. The Annals of Statistics. 2006:1436–1462. [Google Scholar]
- Meng XL, Wong WH. Simulating ratios of normalizing constants via a simple identity: a theoretical exploration. Statistica Sinica. 1996:831–860. [Google Scholar]
- Narisetty NN, He X, et al. Bayesian variable selection with shrinking and diffusing priors. The Annals of Statistics. 2014;42:789–817. [Google Scholar]
- Newton MA, Noueiry A, Sarkar D, Ahlquist P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics. 2004;5:155–176. doi: 10.1093/biostatistics/5.2.155. [DOI] [PubMed] [Google Scholar]
- Orchard P, Agakov F, Storkey A. Bayesian inference in sparse gaussian graphical models. arXiv preprint. 2013 arXiv:1309.7311. [Google Scholar]
- Peterson C, Stingo F, Vannucci M. Journal of the American Statistical Association. 2014. Bayesian inference of multiple gaussian graphical models; pp. 00–00. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rual JF, Venkatesan K, Hao T, Hirozane-Kishikawa T, Dricot A, Li N, Berriz GF, Gibbons FD, Dreze M, Ayivi-Guedehoussou N, et al. Towards a proteome-scale map of the human protein–protein interaction network. Nature. 2005;437:1173–1178. doi: 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
- Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of escherichia coli. Nature genetics. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- Varin C, Reid N, Firth D. An overview of composite likelihood methods. Statistica Sinica. 2011:5–42. [Google Scholar]
- Wang H, et al. Bayesian graphical lasso models and efficient posterior computation. Bayesian Analysis. 2012;7:867–886. [Google Scholar]
- Willsey AJ, Sanders SJ, Li M, Dong S, Tebbenkamp AT, Muhle RA, Reilly SK, Lin L, Fertuzinhos S, Miller JA, et al. Coexpression networks implicate human midfetal deep cortical projection neurons in the pathogenesis of autism. Cell. 2013;155:997–1007. doi: 10.1016/j.cell.2013.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in the gaussian graphical model. Biometrika. 2007;94:19–35. [Google Scholar]
- Zhang B, Horvath S. A general framework for weighted gene co-expression network analysis. Statistical applications in genetics and molecular biology. 2005;4 doi: 10.2202/1544-6115.1128. [DOI] [PubMed] [Google Scholar]
- Zhang CH, Huang J. The sparsity and bias of the lasso selection in high-dimensional linear regression. The Annals of Statistics. 2008:1567–1594. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


