Abstract
Computer simulations can aid in understanding how collective materials properties emerge from interactions between simple constituents. Here, we introduce a coarse-grained model that enables simulation of networks of actin filaments, myosin motors, and cross-linking proteins at biologically relevant time and length scales. We demonstrate that the model qualitatively and quantitatively captures a suite of trends observed experimentally, including the statistics of filament fluctuations, and mechanical responses to shear, motor motilities, and network rearrangements. We use the simulation to predict the viscoelastic scaling behavior of cross-linked actin networks, characterize the trajectories of actin in a myosin motility assay, and develop order parameters to measure contractility of a simulated actin network. The model can thus serve as a platform for interpretation and design of cytoskeletal materials experiments, as well as for further development of simulations incorporating active elements.
Introduction
The actin cytoskeleton is a network of proteins that enables cells to control their shapes, exert forces internally and externally, and direct their movements. Globular actin proteins polymerize into polar filaments (F-actin) that are microns long and nanometers thick. Many different proteins bind to actin filaments; such proteins often have multiple binding sites that enable them to cross-link actin filaments into networks that can transmit force. Myosin proteins are composed of head, neck, and tail domains and aggregate via their tails to form minifilaments that can attach multiple heads to actin filaments (1). Each myosin head can bind to actin and harness the energy from ATP hydrolysis such that a minifilament can walk along an actin filament in a directed fashion—i.e., it is a motor. These dynamics have been extensively studied. It is well understood, for example, how they give rise to muscle contraction. In muscle cells, myosin II minifilaments bind to regularly arrayed antiparallel actin filaments and walk toward the barbed ends (2). In other types of cells lacking this level of network organization, however, the ways in which the elementary molecular dynamics (MD) act in concert to give rise to complex cytoskeletal behaviors remain poorly understood.
Addressing this issue requires a combination of experiment, physical theory, and accurate simulation. The last of these is our focus here—we present a nonequilibrium MD framework that can be used to efficiently explore the structural and dynamical state space of assemblies of semiflexible filaments, molecular motors, and cross-linkers. By allowing independent manipulation of parameters normally coupled in experiment, this computational model can guide our understanding of the relationship between the microscopic biochemical protein-protein interactions and the macroscopic mechanical functions of assemblies. Additionally, because the model simulates filaments, motors, and cross-linkers explicitly, we can elucidate microscopic mechanisms by studying its stochastic trajectories at levels of detail that are experimentally inaccessible. The fact that complex behaviors can emerge from simple interactions also allows simulations to be used to evaluate predictions from theory.
In this work we detail the model and demonstrate that it reproduces an array of known experimental results for actin filaments, assemblies of actin and cross-linkers (passive networks), and assemblies of actin and myosin (active networks). We go further to provide, to our knowledge, new experimentally testable predictions about these systems. For single polymers, we reproduce the spatiotemporal fluctuation statistics of actin filaments. For passively cross-linked networks, we reproduce known stress-strain relationships and predict the dependence of the shear modulus on cross-linker stiffness. For active networks, we reproduce velocity distributions of actin filaments in myosin motility assays and show how one can tune their dynamical properties by varying experimentally controllable parameters. In separate studies, we use the model to clarify microscopic mechanisms of actomyosin contractility and investigate how assemblies of actin filaments and cross-linkers can be tunably rearranged by myosin motors to form structures with distinct biophysical and mechanical functions (3). The collection of this benchmark suite is itself useful, as prior models (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) have focused on specific cytoskeletal features, making the tradeoffs needed to capture the selected behaviors unclear.
Indeed, our model builds on earlier studies, which we briefly review to make clear similarities and differences of the models (see also (15) for a list of cytoskeletal simulations). The most finely detailed simulations focus on the motion of a myosin minifilament with respect to a single actin filament. Erdmann and Schwarz (9) used Monte Carlo simulations to verify a master equation describing the attachment of a minifilament and, in turn, the duty ratio and force velocity curves as functions of the myosin assembly size. Stam et al. (16) used simulations to study force buildup on a single filament by a multiheaded motor and found distinct timescale regimes over which different biological motors could exert force and act as cross-linkers. These models of actin-myosin interactions are important for understanding the mechanics at the level of a single filament, and their results can be incorporated into larger network simulations.
A number of publications have dealt with understanding the rheological properties of cross-linked actin networks (4, 5, 6, 7). For example, to study the viscoelasticity of passive networks, Head et al. (5) distributed filaments randomly in 2D, cross-linked filament intersections to form a force-propagating network, sheared this network, and let it relax to an energy minimum. From this model, they were able to identify three elastic regimes that were characterized by the mean distance between cross-linkers and the temperature. Dasanayake et al. (8) extended this model to include a term in the potential energy that corresponded to myosin motor activity and observed the emergence of force chains that transmit stress throughout the network. These studies address questions about how forces propagate and how cross-linker densities alter mesh stiffness.
Other studies characterized network structure and contractility as functions of model parameters. Wang and Wolynes (10) considered a graph of cross-linkers (nodes) and rigid filaments (edges) in which motor activity was simulated via antisymmetric kicks along the filaments. They calculated a phase diagram for contractility as a function of cross-linker and motor densities. Such a simulation can provide qualitative insights into general principles of filament networks, but the model did not account for filament bending, and structures were sampled via a Monte Carlo scheme that was not calibrated to yield information about dynamics. Cyron et al. (17) used Brownian dynamics simulations to investigate structures that can form via mixtures of semiflexible filaments and cross-linkers and determined a phase diagram and phase transitions (18) between differently bundled actin networks that form as one varies cross-linker density and cross-linker-filament binding angle. Nédélec and Foethke (11) performed dynamic simulations of assemblies of semiflexible microtubules and kinesin motor proteins, which share features with assemblies of F-actin and myosin; they used their simulation package, CytoSim, to understand aster and network formation in microtubule assays and showed recently that the model can be adapted to treat actin networks (12). Gordon et al. (13), Kim (14), and most recently Popov et al. (15) similarly simulated dynamics of F-actin networks and included semiflexible filaments, motors, and cross-linkers. By varying motor and cross-linker concentrations, Gordon et al. (13) and Popov et al. (15) showed various structures that can emerge from assemblies of this type, and Kim et al. (7, 14) additionally quantified how these changes could affect force propagation within the network.
We have strived to include many of the best features of these preceding models in our model. We use the potential energy of Head et al. (5) for filament bending and stretching. However, in contrast to Head et al. (5) and Dasanayake et al. (8), which simply relax the network, we simulate the stochastic dynamics, including thermal fluctuations, cross-linkers and motors binding and unbinding, and the processive activity of myosin. The force propagation rules and motor force-velocity relation are similar to those of Nédélec and Foethke (11) and Gordon et al. (13), whereas the length and timescales simulated are on the order of those performed in Ennomani et al. (12) and Kim (14). We expand on these works by combining and documenting key elements in a single model, demonstrating that the model can quantitatively capture experimentally determined trends for cytoskeletal materials, and illustrating how the model can be used to study systems of current experimental interest.
Materials and Methods
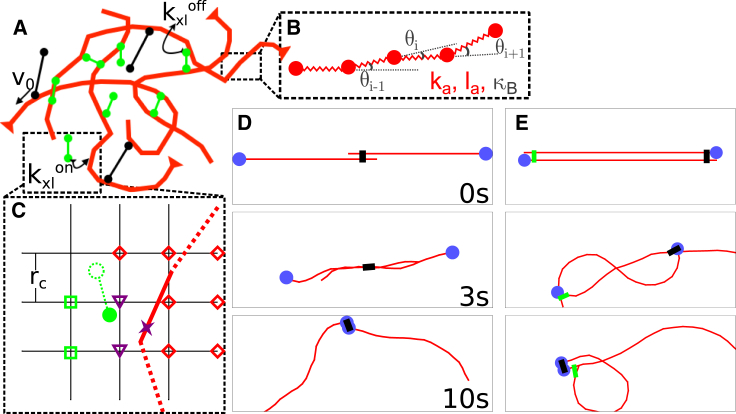
To access the time- and length scales relevant to cytoskeletal network reorganization, we treat actin filaments, myosin minifilaments, and cross-linkers as coarse-grained entities (Fig. 1 A). We model actin filaments as polar wormlike chains (WLCs) such that one end of the WLC represents the barbed end of an actin filament and the other represents the pointed end. We model cross-linkers as Hookean springs with ends that can bind and unbind from filaments. Thus, the connectivity of a network and, in turn, its capacity for force propagation varies during simulations. We model molecular motors similarly to cross-linkers except that each bound motor head can walk toward the filament barbed end with a load-dependent speed. The motors can slide filaments, translocate across filaments, and increase network connectivity. We simulate the system using Langevin dynamics in 2D because the in vitro experiments we wish to interpret are quasi-2D, and approximating the system as 2D allows us to treat larger systems for longer times. To account for the fact that a 3D system would have greater conformational freedom, we do not include steric interactions for our filaments, motors, and cross-linkers. This implementation of filaments, motors, and cross-linkers, which we detail below, allows for motor-driven filament sliding and filament buckling, as seen in Fig. 1, D–E. A complete list of model parameters, their values, and references is provided in Table 1.
Figure 1.
Overview of the model. See Materials and Methods for details. (A) Shown here is a schematic of a configuration of the model. Filaments are red, cross-linkers are green, and motors are black. (B) Shown here is an expanded view of the actin filament representation: a chain of beads connected by springs with spring constant ka, rest length la, and bending modulus κB, as detailed in Filaments. (C) Shown here is the process by which a cross-linker finds a filament to bind, as detailed in Cross-linkers. The solid red link is indexed to the grid points marked with either red diamonds or purple triangles, and the solid green motor head (circle) searches the grid points marked with either green squares or purple triangles for links to bind. The cross-linker head then stochastically binds to the nearest spot on the filament (see Supporting Materials and Methods and Fig. S1A) here marked with a purple x. (D) Shown here are successive images of two antiparallel 10 μm filaments (barbed ends marked by blue circles) interacting with one motor at the center. The motor binds to both filaments and slides them past each other. (E) This is similar to (D) but with a cross-linker that pins the top filament’s pointed end to the bottom filament’s barbed end. The motor, bound to both, walks toward the barbed end of the bottom filament and buckles the top filament. To see this figure in color, go online.
Table 1.
Parameter Values
| Symbol | Description (Units) (References) | Simulation |
|||
|---|---|---|---|---|---|
| Lp | Shear | Motility Assay | Network | ||
| Actin filaments | |||||
| Nf | number of filaments | 20 | 500 | 1 | 500 |
| NB | number of beads per filament | [21, 201] | 11 | [2, 26] | 11 |
| la | link rest length (μm) | [0.1, 1] | 1 | 1 | 1 |
| ka | stretching force constant (pN/μm) | [0.01, 1000] | 1000 | 1 | 1 |
| κB | bending modulus (pN μm2) (22) | [0.005, 800] | 0.068 | 0.068 | 0.068 |
| Myosin motors | |||||
| ρm | motor density (μm−2) | — | — | [0, 9] | 0.2 |
| lm | rest length (μm) (1) | — | — | 0.5 | 0.5 |
| km | stiffness (pN/μm) | — | — | 1 | 1 |
| maximum attachment rate (s−1) | — | — | [0.001, 2] | 1 | |
| maximum detachment rate (s−1) | — | — | 1 | 0.1 | |
| maximum detachment rate at barbed end (s−1) | — | — | 10 | 1 | |
| v0 | unloaded speed (μm/s) (31) | — | — | 1 | 1 |
| Fs | stall force of myosin (pN) (63) | — | — | 0.5 | 0.5 |
| Cross-linkers | |||||
| ρxl | cross-link density (μm−2) | — | 0.42 | — | 1 |
| lxl | rest length (Filamin) (μm) (64) | — | 0.150 | — | 0.150 |
| kxl | stiffness (pN/μm) | — | [0.1, 1000] | — | 1 |
| maximum attachment rate (s−1) | — | 1 | — | 1 | |
| maximum detachment rate (s−1) | — | 0.1 | — | 0.1 | |
| Environment | |||||
| Δt | dynamics timestep (s) | [10−6, 10−3] | 10−7 | 0.00005 | 0.00002 |
| Tf | total simulated time (s) | 2000 | 0.5 | 1000 | 400 |
| X, Y | length and width of assay (μm) | — | 75 | 50 | 50 |
| g | grid density (μm−1) | — | 2 | 2 | 2 |
| T | temperature (K) | 300 | 300 | 300 | 300 |
| ν | dynamic viscosity (Pa s) | 0.001 | 0.001 | 0.001 | 0.001 |
| Δγ | strain (%) (65) | — | 0.001 | — | — |
| trelax | time between sequential strains (s) | — | 0.001 | — | — |
Filaments
The WLC model for actin filaments is implemented as a chain of beads connected by N harmonic springs (links) and N−1 angular harmonic springs, as depicted in Fig. 1 B. The N linear springs penalize stretching and keep the filament’s average end-to-end length approximately constant. The N−1 angular springs penalize bending and determine the persistence length for a free filament. The filament configurations are governed by the potential energy Uf:
| (1) |
where is the position of the ith bead on a filament, θi is the angle between the ith and (i−1)th links, ka is the stretching force constant, κB is the bending modulus, and la is the equilibrium length of a link. In practice, Uf enters the simulation through its Cartesian spatial derivatives (i.e., the forces in Eq. 6). In this regard, it is important to note that linearized forms for the bending forces are employed in the literature for filaments whose length is constrained via Lagrange multipliers (11), but we found that it was necessary to use the full nonlinear force to obtain consistent estimates for the persistence length, Lp, for bead-spring-chain filaments (see Actin Filaments Exhibit Predicted Spatial and Temporal Fluctuations, below). We thus employ the full nonlinear Cartesian forces throughout this work, using the expressions in Appendix C of Allen and Tildesley (19) following the implementation in the LAMMPS MD Simulator (20).
The bending force constant is derived from the persistence length Lp such that κB = LpkBT, where kB is Boltzmann’s constant, and T is the temperature (21). Experimentally, Lp = 17 μm, so κB = 0.068 pN μm2 for T = 300 K (22). The elasticity per unit length measured for actin filaments with lengths on the order of a micron is 55 ± 15 pN/nm (23, 24). This implies that a reasonable value for the segment stretching force constant, ka, would be of this order of magnitude. However, simulating a network of such stiff filaments is computationally infeasible because the maximum timestep of a simulation is inversely proportional to the largest force constant in the simulation (25). Therefore, we set ka to a smaller value than estimated from experiment. We note that prevalent extensile behavior, which occurs when filaments interact with two populations of motors with opposite polarities (26), would necessitate using a more realistic ka. However, because ka ≫ κB/la3 still, upon compression, filaments prefer bending to stretching, and, as we show, the ability of our model to capture contractile network properties quantitatively is not compromised. Unless otherwise indicated, we use la = 1 μm, because it is the largest segment length that results in the expected spatial and temporal fluctuations for filaments (see Actin Filaments Exhibit Predicted Spatial and Temporal Fluctuations, below). We note that very high motor densities can cause filaments to buckle at length scales of ∼1 μm, and in these cases it would be necessary to use a smaller la to capture those effects (27).
Cross-linkers
There is a variety of different actin binding proteins that serve as cross-linkers in the cell cortex, including filamin, fascin, and α-actinin. Cross-linkers connect filaments dynamically and propagate force within the network. Thus, the cross-linkers in our model must be able to attach and detach from filaments with realistic kinetic rules and be compliant when bound. To this end, we model them as Hookean springs with stiffness kxl and rest length lxl. Like actin filaments, the Young’s modulus of most cross-linkers is significantly higher than would be reasonable to simulate; therefore, for network simulations without large external forces, we set kxl = ka so that the bending mode of actin filaments is significantly softer than the stretching mode of cross-linkers. The rest length lxl corresponds to the size of the cross-linker and therefore differs based on the particular actin binding protein one wishes to study.
The statistics of the bound (on) and unbound (off) states of each cross-linker are determined by a potential energy of the form
| (2) |
where is the position of head 1(2), I1(2) is 1 if head 1(2) is bound and zero otherwise, and () is the rate of binding (unbinding).
Owing to the form of Eq. 2 and the Monte Carlo rule for binding (below), it is inefficient for a cross-linker to attempt attachment to every filament link in the simulation box. Rather, we assign a cutoff distance such that if the distance between a cross-linker and a filament is greater than rc, the probability of attachment is zero. This implementation allows us to use the following neighbor list scheme, illustrated in Fig. 1 C, to determine cross-linker-filament attachment. A grid of lattice size of at least rc is drawn on the 2D plane of the simulation, and each filament link is indexed to the smallest rectangle of grid points that completely enclose it. In practice the lattice size is generally larger than rc due to memory constraints, and is denoted by the model parameter g, the number of grid points per μm in both the x and y directions. Because a cross-linker head cannot bind to a filament link that is farther away than rc, it suffices for a cross-linker head to only attempt attachment to the nearby filament links indexed to its four nearest grid points.
At each timestep of duration Δt, we enumerate the accessible filament links available to each unbound head. For each link, we determine the nearest point to the head’s present position and compute a Metropolis factor for moving to that point: (28). The head then binds to accessible filament link i with probability and stays unbound with probability (29).
At each timestep, we attempt to move each bound head to a position generated by reversing the displacement made upon binding, rotated to account for filament reorientation in the intervening time. This choice of allows us to satisfy detailed balance for binding and unbinding by accepting the unbinding transition with probability , as explained in Supporting Materials and Methods.
When both cross-linker heads are attached to filaments, the cross-linker is generally stretched or compressed. We propagate the tensile force stored in the cross-linker onto the filaments via the lever rule described in Gordon et al. (13) and Nédélec (30). Specifically, if the tensile force of a cross-linker head at position between filament beads i and i+1 is , then
| (3) |
are the forces on beads i and i+1, respectively, due to the cross-linker.
Motors
In this work, we focus on the motor protein myosin II. As mentioned above, tens of myosin II proteins aggregate into bipolar assemblies called “myosin minifilaments” (16). For both myosin minifilaments, and monomeric myosin, motility assay experiments have shown that, on average, bound myosin heads walk toward the barbed end of actin filaments at speeds in the range 0.2–4 μm/s (31, 32, 33, 34). Because myosin also functions to increase the local elasticity of networks where it is bound, we model a motor similarly to a cross-linker, in that it behaves like a Hookean spring with two heads, a stiffness km, and a rest length lm. The two heads of this spring do not correspond directly to individual myosin protein heads; rather, each of them represents tens of myosin molecules. Experimentally minifilaments have a very high Young’s modulus, and it is unlikely that their lengths change noticeably in cytoskeletal networks. As with the passive cross-linkers, we set km = ka so that filament bending is still the softest mode of deformation. The rest length was set to the average length of minifilaments, lm = 0.5 μm (1). Attachment and detachment kinetics, as well as force propagation rules for motors, are the same as for cross-linkers, subscripted with m instead of xl in Eqs. 2 and 3.
Unlike cross-linkers, motors move toward the barbed end of actin filaments to which they are bound at speeds that decrease with tensile force along the motor. Myosin motors have been observed to stop walking when the force on them exceeds the stall force, Fs ≈ 4 pN, and most do not step backward (35, 36). We model this behavior by giving each motor head a positive velocity in the direction of the barbed end of the filament to which it is attached; this velocity linearly decreases with the motor’s tension projected on the filament, i.e.,
| (4) |
where v0 is the unloaded motor speed, is the spring force on the motor, and is the tangent to the filament at the point where the motor is bound; points toward the pointed end of the filament. In the simulations below, we use a value of v0 = 1 μm/s, which is within range of experimental measurements, but we use a lower value of Fs ≈ 0.5 pN and truncate to a maximum value of 2v0, so that motors are not stretched to unphysical lengths as they walk.
If the length of a motor’s step is larger than the remaining length of filament, then the myosin moves to the barbed end of the filament. At the barbed end, it has speed v0 = 0, and detachment rate . We found that = 10 yielded reasonable results for motility assay and contractile network simulations. In experiments, where each myosin minifilament contains many myosins, a lower barbed-end affinity may arise from fewer of the minifilament’s myosins remaining attached to the actin filament. In the program, we treat cross-linkers and motors with equivalent objects, but set v0 = 0, and = for the cross-linkers.
Dynamics
We use overdamped Langevin dynamics to solve for the motion of filament beads, motors, and cross-linkers. The Langevin equation of motion for a spherical bead of mass m, radius R at position at time t, forced by in a medium with dynamic viscosity ν, is
| (5) |
where is a Brownian forcing term that introduces thermal energy, and we use the Stokes relation μ = (6πRν)−1 in the damping term. The fastest motions in this simulation are the filament bead fluctuations. Taking the bead radius to be 0.5 μm, the maximum speed to be (2kBT μ/Δt)1/2 = 200 μm/s and the dynamic viscosity to be ν = 0.001 Pa⋅s (corresponding to water), the Reynolds number is very low: Re ≈ 10−4. Hence, we treat the dynamics as overdamped and set m = 0 in Eq. 5. Furthermore, in the limit of small Δt, we may write . These two approximations allow us to rewrite Eq. 5 as
| (6) |
For the Brownian term, we use the form of Leimkuhler and Matthews (37):
| (7) |
where is a vector of IID random numbers drawn from the standard normal distribution. This numerical integrator minimizes deviations from canonical averages in harmonic systems; given that all the mechanical forces in our model are harmonic, we expect this choice to yield accurate statistics in this context as well. The value for Δt in Eq. 6 is most strongly dependent on the largest force constant in the simulation, ka, but also depends on other simulation parameters for both motors and cross-linkers, such as v0, kon, and koff. Table 1 can be used as a rough guide for how high one can set the value of Δt for a given set of input parameters; e.g., for a contracting network with ka = 1 pN/μm, v0 = 1 μm/s, = = = 1 s−1, = = 0.1 s−1, and = 10 s−1, a value of Δt = 2 × 10−5 s is just low enough to iteratively solve Eq. 6 without accumulating large errors.
Environment
In general we use periodic boundary conditions so as to limit finite-size effects. We implemented square boundaries to model closed systems, as well as Lees-Edwards boundaries for sheared simulations (19). The dimensions of the simulation box (Table 1) were chosen to be five times the contour length of filaments so as to be large enough to avoid artifacts due to the self-interaction of constituent components.
To ignore steric interactions, the fraction = Nfπ(D/2)2 L/V of Nf actin filaments (length L and diameter D) in a volume V must be lower than the critical volume fraction at which steric interactions yield an isotropic to nematic transition, which for long WLCs (D ≪ Lp and D ≪ L) is = 5.4 D/L (38, 39). For a network of 500 filaments of length L = 10 μm and diameter D = 0.01 μm, in a 50 × 50 × 0.1 μm3 plate, this condition is fulfilled, because = 0.0015 < = 0.0054. Although it is difficult to estimate the exact thickness of in vitro experimental actomyosin assays due to the complexity of their preparation, we estimate that they are not thinner than 0.1 μm (40). We have also ignored hydrodynamic interactions between filament beads; the restriction to low packing fraction obviates the need to incorporate anisotropic drag, so we take μ to be equivalent for both transverse and longitudinal motion (41).
Implementation
The model is implemented as an open source C++ package called Active Filament Network Simulation (AFINES) that is available for download at http://dinner-group.uchicago.edu/downloads.html. Installation instructions are available in the README file in the top directory of the AFINES package, and all information needed to reproduce the materials in this article are available in the subfolder “versatile_framework_paper”. To run a simulation, a user must compile the code into an executable (e.g., with the provided Makefile) and create an output directory. A user can set parameters using command line arguments or a file. For example, if the user has compiled the code into the executable “afines”, created the output directory “test”, and wants to run a simulation of 500 10-μm actin filaments (with la = 1 μm), interacting with 0.2 motors/μm2, and 1 cross-linker/μm2 (passive motors), in a cell that is 50 × 50 μm, for 100 s, he or she could write the following to the file my_config.cfg:
xrange=50 # system size in X
yrange=50 # system size in Y
npolymer=500 # number of actin filaments
nmonomer=11 # number of actin beads per filament
a_motor_density=0.2 # motor density;
p_motor_density=1 # cross-linker density
tf=100 # duration of simulation
dir=‘‘test’’ # output directory
and then run the code using the command
afines -c my_config.cfg
Alternatively, the user could bypass the configuration file and issue the following command:
afines --xrange 50 --yrange 50 --npolymer 500 --nmonomer 11 --a_motor_density 0.2 --p_motor_density 1 --tf 100 --dir test
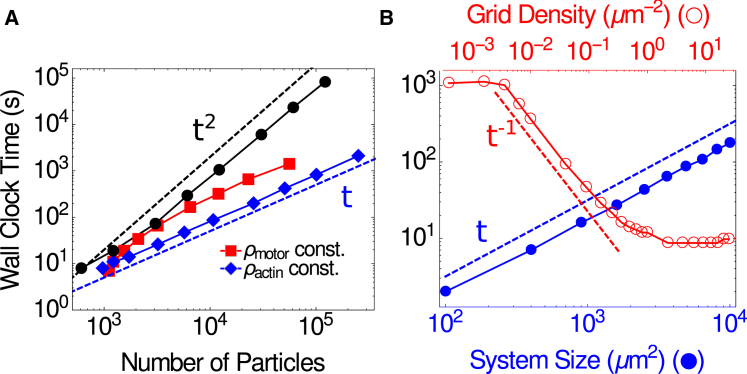
In this example, all other parameters were set to their default values (see the README file for full list of program parameters). With an executable compiled using g++ with the −O3 optimization flag and run on a model No. E5-2680 node (Intel, Santa Clara, CA) with 2 Gb of memory and a 2.7 GHz processor, this example required <1.5 days of wall-clock time. In general, the wall-clock time of the simulation scales linearly with system size (Fig. 2).
Figure 2.
Wall clock time for a 10,000-step simulation with step size Δt = 0.0001 s. (A) For a constant system size, run-time scales linearly or sublinearly as both filament density (red squares) and motor density (blue diamonds) are increased independently. If both are increased together (black circles), a quadratic scaling is approached for large numbers of particles. (B) (Blue filled) At constant motor, filament, and grid densities, run-time scales linearly with system size (i.e., the area of the simulation box, XY). (Red, open) At constant system size, run time decreases with increasing grid density, g2, and thereby the number of neighbor-list grid elements, g2XY, used to calculate motor-filament interactions. All benchmarks are for an Intel E5-2680 node with 2 Gb of memory and a 2.70 GHz processor. To see this figure in color, go online.
Results and Discussion
In this section, we numerically integrate the model to obtain stochastic trajectories and compare their statistics to known analytical results for semiflexible polymers and networks, as well as experimental observations. We also use the model to investigate these systems, including how the viscoelasticity of semiflexible polymer networks depends on cross-linker stiffness, and how the extent of directed motion in actin motility assays depends on filament and motor characteristics. Finally, we use the model to show how one can quantify contractility in a simulated actin network.
Actin filaments exhibit predicted spatial and temporal fluctuations
The persistence length of a semiflexible filament with bending modulus κB is expected to be Lp = κB/kBT. However, when simulating the dynamics, approximations can enter both the evaluation of the forces and the discretized numerical integration of the equations of motion. Because the persistence length is a measure of filament bending fluctuations, and not an input to the simulation, its dependence on simulation parameters must be determined numerically. As discussed in Filaments and further below, some care is required to obtain reliable estimates of Lp.
For a 2D filament it is possible to show analytically that if a small bend between links i and i − l of an N link chain results in a local change in free energy of (κB/2la)θi2, then
| (8) |
| (9) |
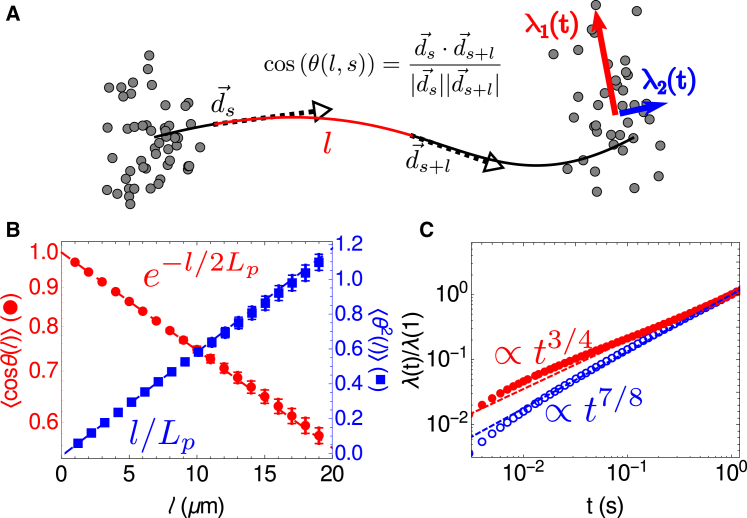
where θ(l) = θj − θi, l = la(j − i) (2 ≤ i < j ≤ N) (42). To test our WLC model against these predictions, we let 20 filaments of L = 20 μm and κB = 0.068 pNμm2 fluctuate at T = 300 K for Tf = 2000 s and measured the resulting filament configurations. The configurations saved were chosen to be 2 s apart, because the decorrelation time for θ(l) was at most 1.1 s (see Supporting Materials and Methods and Fig. S2 for details). The first 100 s of each simulation was disregarded as filaments had not yet equilibrated. For each of the 20 filaments, we evaluated 〈θ2(l)〉 and 〈cos(θ(l))〉 for each l ∈1,2,…,19 μm from its 1900 saved configurations. We show the average for each of these values over all filaments in Fig. 3 B, along with the expected behavior, given the input κB.
Figure 3.
Spatial and temporal fluctuations of the bead-spring WLC. (A) Shown here is a schematic of a filament and the order parameters that characterize its fluctuations. Spatial fluctuations are characterized by the angle between two tangent vectors and along the filament as a function of the contour length between them, l. Temporal fluctuations are characterized by the eigenvalues λ1,2(t) of the covariance matrix of filament endpoint positions as a function of time. The red arrow indicates the larger moment (λ1, measuring transverse fluctuations) whereas the blue arrow indicates the smaller moment (λ2, measuring longitudinal fluctuations). (B) Given here is the decorrelation of tangent vectors (red circles) and fluctuations in angles between links (blue squares) as a function of the arc length between them. For the N = 20 filaments analyzed, the red circles (blue squares) show the mean of 〈cos(θ(l))〉 (〈θ(l)2〉) and the error bars show their standard errors, , where σ is their SD. Dashed lines show expected behavior for κB = 0.068 pNμm2. (C) Given here are eigenvalues of covariance matrices for the positions of endpoints of filaments as a function of time. Red filled circles show λ1(t), which is expected to be proportional to t3/4 (red line) whereas blue open circles show λ2(t), which is expected to be proportional to t7/8 (blue line). SE is smaller than the size of the data points. To see this figure in color, go online.
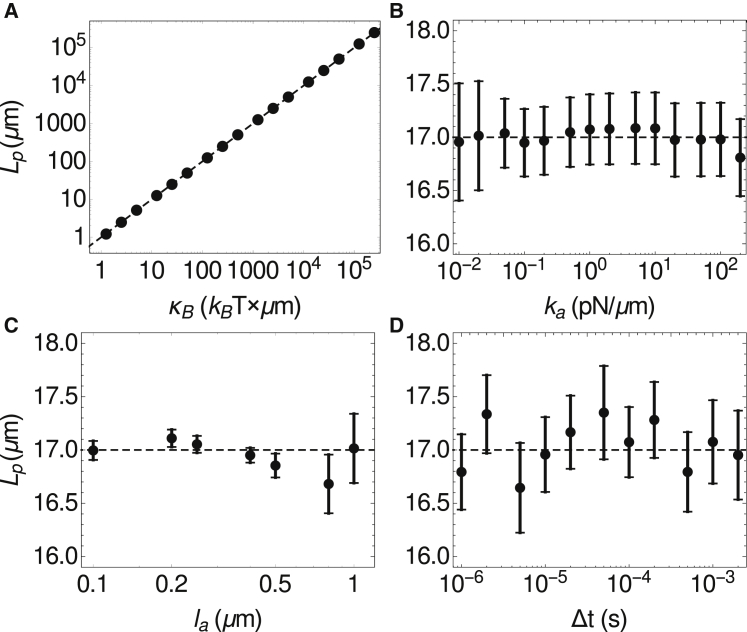
As alluded to above, the numerical integration can make the persistence length depend on simulation parameters in nonobvious ways. Consequently, we measured the sensitivity of Lp to independent variations of κB, la, and ka. The results shown in Fig. 4 are obtained from using the definition Lp = 1/(d〈θ2(l)〉/dl) (i.e., the inverse of the slope of the best fit line to the blue squares in Fig. 3 B). Fig. 4 A shows that in the range of κB ∈[1,105] μm × kBT, Lp determined from the simulation agrees well with the input bending modulus, and can be easily tuned to simulate filaments of varying rigidity. Fig. 4 B shows that for a wide range of link stiffnesses, Lp is independent of ka. We also tested the dependence of Lp on the link rest length, la. In thermal equilibrium, the variance of the link lengths is kBT/ka. Thus, to keep the fluctuations in the filament’s contour length L constant, one should set ka ∝ la−2. In practice, this scaling is computationally difficult to achieve when la < 0.3 μm because high ka requires a very small Δt in Eq. 6. We therefore used a less steep variation, ka = 1 pN/la, and show in Fig. 4 C that consistent values of Lp are obtained when la ∈[0.1,1] μm. We thus see that there is a range in which Lp is independent of the filament link parameters, ka and la, although high stiffness and low link length both require using a small timestep, and therefore limit the duration of the simulation. In Supporting Materials and Methods and Fig. S4, we measure the persistence length of fibers simulated using the simulation package CytoSim and obtain similar results.
Figure 4.
Dependence of the persistence length on the indicated parameters for numerically integrated semiflexible filaments. Error bars are , where σ is the SD of the values of Lp obtained from fitting a line to the first five data points of 〈θ2(l)〉 for each of the N = 20 filaments simulated. The dashed lines show the predicted persistence length, based on the input bending modulus κB. For (A)–(D), the default parameters are κB = 17 μm × kBT, ka = 1 pN/μm, and la = 1 μm. In (A)–(C), Δt ≥ 10−6 s, and the largest Δt that yielded stable integration was used. In (C), ka = 1 pN/la.
The statistics of temporal fluctuations are also known for semiflexible filaments. Fluctuations transverse to the filament orientation increase as 〈dr⊥2〉 ∝ t3/4, whereas longitudinal fluctuations increase as 〈dr||2〉 ∝ t7/8 (43). To determine if our simulations agreed with these theoretical scaling relations, we followed the procedure outlined in Everaers et al. (43) and generated N = 100 initial filament configurations of a 20-μm filament. This length was chosen because it satisfied the constraint provided in Everaers et al. (43) for the fluctuations of the two ends of the filament to be uncorrelated at long times (here t = 1 s); i.e., 20 μm > (tkBT/ν)1/8 (κB/kBT)5/8 = 7 μm. For each configuration we ran M = 1000 simulations of the filament diffusing freely for 1 s. We denote each of the M positions for each endpoint at each time by . For each of the clouds of points shown in Fig. 3 A, we calculated the moments, as the eigenvalues of the covariance matrix with elements for i, j ∈{x,y}. The larger eigenvalue λ1(t) corresponds to the transverse fluctuations (i.e., λ1(t) ∝ t3/4) whereas the smaller eigenvalue corresponds to the longitudinal fluctuations (λ2(t) ∝ t7/8). We show these results in Fig. 3 C. Each data point is the average over the 2NM eigenvalues for λ1(t) and λ2(t). As evident, the computed scaling relations are in good agreement with theoretically predicted behaviors.
Tunable elastic behavior of cross-linked filament networks
The mechanical properties of cross-linked F-actin have important ramifications for force generation and propagation within a cell. They are generally inferred from rheological measurements of in vitro networks (44, 45, 46, 47). In a typical experiment, actin and cross-linker proteins are mixed to form a cross-linked mesh and then sheared in a rheometer by a prestress, σ0. The prestressed network then undergoes a sinusoidal differential stress of magnitude dσ ≪ σ0. By measuring the resulting strain, one can calculate the differential elastic modulus G(σ0) = dσ/dγ. Results from such experiments indicate that, in contrast to a purely viscous fluid, cross-linked F-actin networks resist shear, and G increases nonlinearly with stress indicative of shear stiffening.
In experiments using a stiff cross-linker, such as scruin, the dependence of the differential modulus on high prestress is G ∝ σ03/2 (44, 47). Force-extension experiments with semiflexible filaments, in which one directly measures the force F required to extend a filament by a distance l, yield a remarkably similar relationship, dF/dl ∝ F3/2 (48, 49). As remarked in Gardel et al. (44), this suggests that the shear stiffening is a direct result of the nonlinear force-extension relationship of actin. Rheology studies using more compliant cross-linkers, such as filamin, have found a softer response, G ∝ σ0, indicating that a significant amount of stress is mediated through the cross-linkers, and not the filaments (46). These results suggest that the strain stiffening behavior of a cross-linked network can be tuned by varying the cross-linker stiffness.
To test this possibility and benchmark our simulations, we subjected passive networks composed of filaments and cross-linkers to shear. We initialized each simulation with N = 500 randomly oriented filaments of length 15 μm in a square box of area 75 × 75 μm. A 0.150-μm cross-link (corresponding to the length of filamin) was initially placed at each filament intersection. We performed 24 such simulations, each with a different cross-linker stiffness in the range 0.1–1000 pN/μm.
Simulating shear rheology experiments requires modifying the equations of motion and the boundary conditions to achieve a planar Couette flow. In general, planar Couette flow can be simulated via MD using Eq. 4.1 in Evans and Morriss (50):
| (10) |
where x and y are the Cartesian coordinates of a particle being sheared, Fint,x and Fint,y are the internal forces on those particles, and γ is the strain. Simultaneously, the upper and lower boundaries must be sheared by the total strain on the simulation box (19). Comparing Eq. 10 with Eq. 5, we substitute . In the overdamped limit, , so implementing Eq. 10 is equivalent to updating filament bead positions via Eq. 6, and shifting the horizontal position of a bead (xi) by
| (11) |
where and Y is the simulation cell height. The boundary conditions follow the Lees-Edwards convention (19).
Because moving the particles Δγ is equivalent to the addition of an external force on the system, it is necessary to let the network relax for a specified amount of time trelax after each shear event, before measuring the network’s internal energy. The magnitude of trelax depends on Δγ, which in turn depends on the chosen discretization of the strain and the timestep Δt. As shown in Supporting Materials and Methods and Fig. S3, we found that Δγ = 0.001, Δt = 10−7 s, and trelax = 0.001 s yielded a stable planar Couette flow, with high enough strains to observe strain stiffening. This protocol was performed for Tf = 0.5 s yielding a total strain of γ = ΔγTf/trelax = 0.5.
We measured the elastic behavior of the network for each cross-linker stiffness by calculating w, the strain energy density at each timestep:
| (12) |
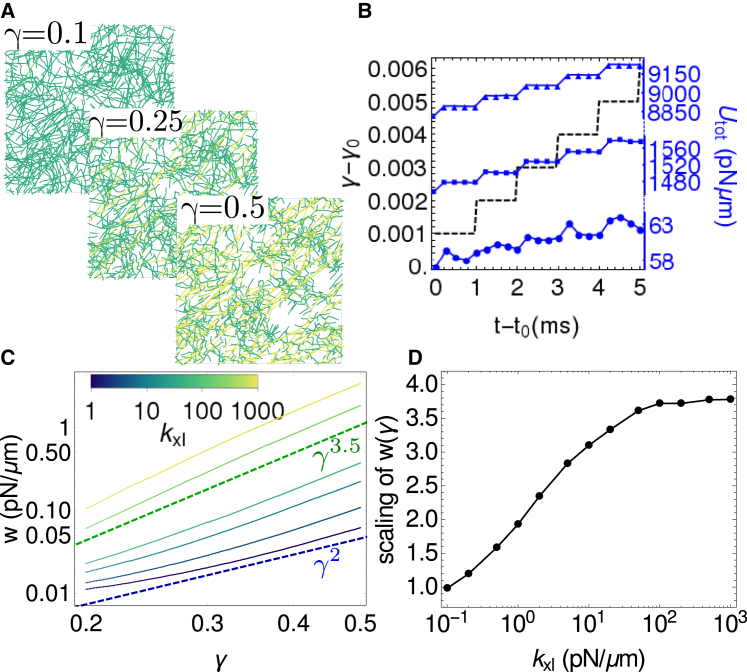
where Uf is the mechanical energy of individual filaments (Eq. 1) and Uxl is the mechanical energy of each cross-link (Eq. 2). By averaging over windows of size trelax, we determine w(γ). Fig. 5 shows the results of these calculations for various values of kxl. For extremely low kxl, the strain energy scaled linearly with strain, w ∝ γ, indicating that the network showed no resistance to shear: G = d2w/dγ2 = 0. For high kxl, we observe a neo-Hookean strain stiffening behavior, w ∝ γ4 (51). Thus, we can tune the material properties of cross-linked semiflexible networks from being liquidlike, with w ∝ γ, through the Hookean elastic regime of w ∝ γ2 up to the strain stiffening regimes of w ∝ γ3 and w ∝ γ3.5, as previously reported in experiments (44, 46). We show in Supporting Materials and Methods and Fig. S5 that the monotonic increase in scaling for low kxl corresponds to a regime where the strain energy is mostly stored in the cross-linkers, whereas the plateau at high kxl corresponds to a regime where the strain energy is mostly stored in filaments.
Figure 5.
Tunable elasticity of cross-linked networks. (A) Given here are snapshots of a strained network (ka = 1000 pN/μm, kxl = 20 pN/μm) at γ = 0.1, γ = 0.25, and γ = 0.5. Color indicates stretching energy on each link, with green (darkest) being the lowest and yellow (lightest) being the highest. For all snapshots, t = γ × 1 s. (B) Given here is the potential energy of the network as a function of time shown at different strains γ0 = 0.1 (circles), γ0 = 0.25 (squares), and γ0 = 0.4 (triangles), where t0 = γ0 × 1 s. The black dashed line shows the strain protocol. (C) Shown here is the strain energy density (w = U/XY) for various values of cross-linker stiffness kxl. The blue dashed line indicates expected behavior for a linearly elastic solid (w ∝ γ2) and the green dashed line indicates strain stiffening behavior of w ∝ γ3.5 as expected for semiflexible polymer networks (44, 47). (D) Given here is the power-law exponent of w(γ) as a function of cross-linker stiffness, evaluated by least squares fitting ln(w) as a function of ln(γ). To see this figure in color, go online.
Ensembles of motors interacting with individual filaments simulate actin motility assays
Whereas the attachment, detachment, and speed of an individual myosin motor is a model input (described in Cross-linkers and Motors, above), the collective action of many motors on a filament is an output that can be compared with actin motility assays (36, 52). In the canonical motility assay experiments, a layer of myosin is attached to a glass coverslip, and actin filaments are distributed on top of the layer of myosin motors. The fixed motors translocate the actin filaments. The speed of an actin filament has been reported to depend nonlinearly on the concentration of myosin and the concentration of ATP in the sample (32, 33). Thus, by allowing the filaments to interact with more motors, one can monotonically increase the filament speed to a constant value.
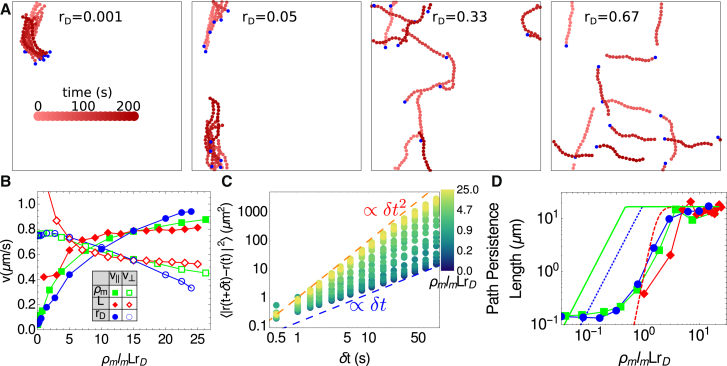
To explore the dynamics of such an assay, we randomly distributed motors on a 50 × 50-μm periodic simulation cell and tethered one head of each motor to its initial position. These model motors represent myosin minifilaments with dozens of heads, and therefore have a high default duty ratio (rD = 0.5), and rest length lm = 0.5 μm (1, 53). Filaments were then introduced in the simulation cell and allowed to interact with the free motor heads. The strength of motor-filament interactions was manipulated in three ways: by varying the motor concentration ρm, the filament contour length L, and the duty ratio rD = /( + ). Although L and rD are difficult to modulate experimentally in a well-controlled fashion, as they require the addition of other actin-binding proteins to the assay, they are predicted to impact the dynamics of actin by varying the number of myosin heads bound to an actin filament at any one time (33). Because they are both simple functions of the model’s parameters, we were able to test this hypothesis directly. We plot our simulation results in Fig. 6 as functions of the dimensionless control parameter = ρmlmLrD (where ρmlm is the linear motor density), which represents the average number of bound motor heads per filament.
Figure 6.
Nonlinear dependence of filament motility on motor-filament interaction probability. (A) Shown here is the trajectory of a filament for ρm = 4 μm−2 and L = 15 μm as a function of time for different values of the duty ratio, rD. Depth of color indicates time of the snapshot, as indicated by the scale. The blue circles mark the barbed ends. (B) Given here is the filament speed decomposed into longitudinal (filled symbols) and transverse (open symbols) components as a function of the dimensionless parameter = ρmlmLrD, by independently varying ρm (green squares), L (red diamonds), and rD (blue circles). The default parameters were ρm = 4 μm−2, L = 15 μm, and rD = 0.5. (C) Shown here is the mean squared displacement for various values of . The blue dashed line shows diffusive behavior and the orange dashed line shows ballistic behavior. (D) Given here is the path persistence length for simulations described in (B), evaluated via Eq. 9 over five replicates. The lines are theoretical predictions for these values using Eqs. 1–6 in Duke et al. (54). The red dashed line is for increasing L, the blue dotted line is for increasing rD, and the green solid line is for increasing ρm. To see this figure in color, go online.
Our findings are qualitatively similar to the previously reported experimental results and expand on them by collapsing the trends observed while varying ρm, L, and rD into a single effective parameter. At low , i.e., low motor density, filament length, or duty ratio, Fig. 6 B shows that transverse motion dominates over longitudinal motion as the filament is not propelled by motors faster than diffusion, and transverse filament fluctuations are larger than longitudinal fluctuations (consistent with Fig. 3 C). However, as increases, longitudinal motion dominates. Consistent with experimental results (31, 33), the longitudinal speed of the filament plateaus at v|| ≈ 1 μm/s, which is the input unloaded speed of a single motor. In Fig. 6 C, we plot the mean squared displacement of the filament, with angle brackets indicating an average over time t. We show that low yields diffusive behavior with 〈Δr2〉 ∝ δt, and high yields ballistic motion with 〈Δr2〉 ∝ δt2. We obtain similar results for motility assay behavior with a corresponding CytoSim simulation, as shown in Supporting Materials and Methods and Fig. S6.
An interesting outcome of these simulations is how the direction of a filament changes over time for varying . Specifically, we calculate the directional autocorrelation of a filament and, in turn, the persistence length of the path of the filament by applying Eq. 9 to the center of mass of the filament at frames separated by Δt = 1 s (Fig. 6 D). Scaling arguments suggest that the path’s persistence length depends strongly on motor density, duty ratio, and filament length (54). In the limit of high , the distance between motors that are bound to a filament is sufficiently short that the filament does not diffuse transversely; however, fluctuations in the filament configuration still allow directional decorrelation, and consequently the path’s persistence length is Lp. At low , the distance between bound motors is sufficiently large that rotational diffusion causes the filament’s path to be completely decorrelated, such that the path’s persistence length approaches zero. In Fig. 6 D, we show that the simulation agrees with theoretically predicted scaling laws at low and high (54). Our results delineate the values of at which there are crossovers between the predicted limiting regimes.
Molecular motors cause flexible, cross-linked networks to contract
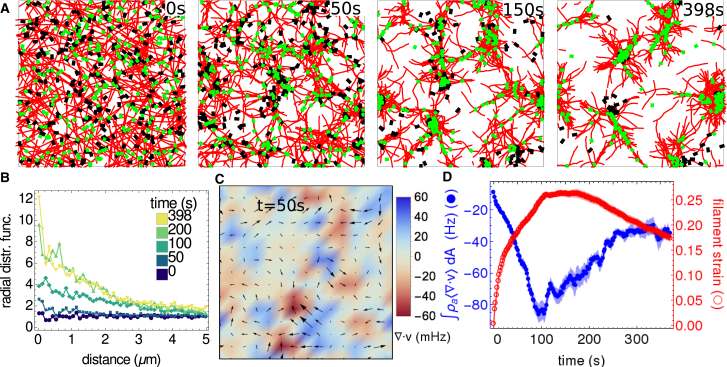
When motors, cross-linkers, and filaments are combined into a single assembly, simulated networks contract. The structure and dynamics of these networks exhibits a rich dependence on motor and cross-linker densities, binding/unbinding kinetics, and stiffness parameters. Here, we show one illustrative example to demonstrate that our model reproduces actomyosin contractility for a reasonable choice of parameters (Fig. 7 A). The network is initialized by randomly orienting 500 filaments, each 10 μm long, within a 50 × 50-μm simulation cell. We distribute 0.15-μm-long cross-linkers throughout the simulation cell at a density of 1 μm−2, and 0.5-μm-long motor oligomers at a density of 0.2 μm−2. As the simulation evolves, the actin density becomes more heterogenous as motors condense actin filaments into dense disordered aggregates. This density heterogeneity can be quantified by the radial distribution function of actin filaments, g(r) = P(r)/(2πrδρf), where P(r) is the probability that two filaments are separated by a distance r, δr = 0.1 μm is the spatial bin size, and ρf is the filament density. As shown by Fig. 7 B, g(r) ≈ 1 at t = 0 for all r as the actin filaments are homogeneously distributed. However, over time it becomes more peaked at lower separation distances between filaments, indicating filament aggregation.
Figure 7.
Contractility of a cross-linked filament network driven by motors. Filaments are red, motors are black, and cross-linkers are green. (A) Shown here are network configurations at t = 0, 50, 150, and 398 s. Although all filaments are shown, only 10% of cross-linkers and 50% of motors are shown for clarity. (B) Given here is the radial distribution function at frames corresponding to (A). (C) Shown here is the quantification of the motion at t = 500 s. Arrows (directions and sizes) indicate the filament-bead velocity field generated by the procedure in Supporting Materials and Methods. Colors map the corresponding divergence. (D) Shown here is the density weighted divergence (blue filled circles; dA = (1 μm)2) and the average filament strain (red open circles) of actin filaments for contractile networks. Dark lines for both curves shows the mean μ(t) of these results at each time t over N = 20 simulations. Shaded areas show the SE of the mean , where σ(t) is the SD. To see this figure in color, go online.
To measure the contractile activity of the network, we evaluate the divergence of its velocity field. This is done by calculating the velocity of each of the actin beads, followed by a grid-based interpolation of a velocity vector field from those values (black arrows in Fig. 7 C; interpolation scheme described in Supporting Materials and Methods). One can then evaluate the divergence of the interpolated field at every spatial location (color in Fig. 7 C). Because there is no flux of actin into the simulation box, the total divergence of the flow field is zero at all times (i.e., ). Therefore, we weight the divergence of each patch of the network by its local density and measure , where ρa = na/dA is the number density of actin beads and is the average actin divergence in the patch of size dA. As shown in Supporting Materials and Methods, this order parameter shows consistent behavior for small patches (dA ≤ (10 μm)2) and a range of step sizes (h ≤ 20 s) for the velocity calculation (see Eq. S6 in the Supporting Material). We also measure the average filament strain , in the network,
| (13) |
where is the position of the ith bead on an (N+1)-bead filament, and the bar denotes an average over all filaments. Fig. 7 D shows the results of measuring network divergence and filament strain from 20 simulations with the same parameter choices as in Fig. 7 A, but with different random number seeds. The divergence measurement (blue) shows that the network is contractile, because the density weighted divergence is negative, and its shape echoes the experimental results in Murrell and Gardel (55), where the magnitude of contractility decreases to a minimum before plateauing. The filament strain measurement (red) shows that as the network is contracting, individual filaments are buckling. This supports the notion that the mechanism behind contractility in disordered actomyosin networks is actin filament buckling (56, 57). We note that, whereas the parameterization of motors that we used for the motility assays yields contractile networks (Fig. S7), using a lower value of resulted in kinetics closer to those observed in experiment (55). This improvement with higher motor affinity may reflect differences in the number of participating motor heads in contractility and motility assays.
Conclusions
In this article, we have introduced an agent-based modeling framework that can accurately and efficiently simulate active networks of filaments, motors, and cross-linkers to aid in the interpretation and design of experiments on cytoskeletal materials and synthetic analogs. Although our focus here has been on selecting parameters that are representative of the actin cytoskeleton, we expect that this framework can be adapted to treating other active polymer assemblies as well, such as microtubule-kinesin-dynein networks. We demonstrated that the model gives rise to both qualitative and quantitative trends for structure and dynamics observed in experiments and provides experimentally testable predictions. Specifically, we reproduced the experimentally observed and theoretically described fluctuation statistics of actin filaments. We also captured strain stiffening scalings and predicted how network elasticity can potentially be tuned via cross-linker stiffness. We modeled sliding filament assays and determined specific system parameters that lead to the crossover from transversely diffusive to longitudinally processive motion first predicted in Duke et al. (54). In separate studies, we use our model to explore the phase space of various network structures and the dynamics that lead to them (3).
Although our model captures many experimental observations, we simplified certain features to limit both computational cost and model complexity. First, the structure of myosin minifilaments is significantly more complex than a two-headed spring. As mentioned, minifilaments have dozens of heads, which allows them to attach to more than two filaments simultaneously, significantly increasing local network elasticity (58) and enabling more complex motor dynamics (59). Second, filaments do not polymerize, depolymerize, or sever in the simulations; it is clear, however, that recycling of actin monomers, actin treadmilling and, to a lesser degree, filament severing, play important roles in contraction and shape formation (57, 60). Third, our simulations are restricted to 2D, without steric or hydrodynamic interactions. This can play a role in motility assays, for example, where at high actin densities, actin filaments organize into polar patterns with characteristic autocorrelation times (61). It would be valuable to make the model a progressively more faithful representation of reality in the future to better understand how each of these choices impacts the behavior of the model and in turn the implications for the associated physics.
Author Contributions
S.L.F., S.B., G.M.H., and A.R.D. designed the research. S.L.F. designed and implemented the software, and executed the calculations. S.B. provided a prototype program. S.L.F., S.B., G.M.H., and A.R.D. wrote the article.
Acknowledgments
We thank M. Gardel, J. Weare, C. Matthews, E. Thiede, F. Nédélec, F.C. Mackintosh, and M. Murrell for helpful conversations. We thank C. Tung, J. Harder, and S. Mallory for critical readings of the manuscript.
This research was supported in part by the University of Chicago Materials Research Science and Engineering Center (National Science Foundation grant 1420709). S.L.F. was supported by the Department of Defense through the NDSEG Program. G.M.H. was supported by an National Institutes of Health Ruth L. Kirschstein NRSA award (1F32GM113415-01). S.B. acknowledges support from the Institute for the Physics of Living Systems at the University College London.
Editor: Cecile Sykes.
Footnotes
Supporting Materials and Methods and seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30622-7.
Supporting Citations
Reference (62) appears in the Supporting Material.
Supporting Material
References
- 1.Niederman R., Pollard T.D. Human platelet myosin. II. In vitro assembly and structure of myosin filaments. J. Cell Biol. 1975;67:72–92. doi: 10.1083/jcb.67.1.72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huxley H.E. The mechanism of muscular contraction. Science. 1969;164:1356–1365. doi: 10.1126/science.164.3886.1356. [DOI] [PubMed] [Google Scholar]
- 3.Stam S., Freedman S.L., Gardel M.L. Filament rigidity and connectivity tune the deformation modes of active biopolymer networks. bioRxiv. 2017 doi: 10.1073/pnas.1708625114. http://biorxiv.org/content/early/2017/05/25/141796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.MacKintosh F.C., Käs J., Janmey P.A. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 5.Head D.A., Levine A.J., MacKintosh F.C. Distinct regimes of elastic response and deformation modes of cross-linked cytoskeletal and semiflexible polymer networks. Phys. Rev. E. 2003;68:061907. doi: 10.1103/PhysRevE.68.061907. [DOI] [PubMed] [Google Scholar]
- 6.Wilhelm J., Frey E. Elasticity of stiff polymer networks. Phys. Rev. Lett. 2003;91:108103. doi: 10.1103/PhysRevLett.91.108103. [DOI] [PubMed] [Google Scholar]
- 7.Kim T., Hwang W., Kamm R.D. Computational analysis of viscoelastic properties of cross-linked actin networks. PLOS Comput. Biol. 2009;5:e1000439. doi: 10.1371/journal.pcbi.1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dasanayake N.L., Michalski P.J., Carlsson A.E. General mechanism of actomyosin contractility. Phys. Rev. Lett. 2011;107:118101. doi: 10.1103/PhysRevLett.107.118101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Erdmann T., Schwarz U.S. Stochastic force generation by small ensembles of myosin II motors. Phys. Rev. Lett. 2012;108:188101. doi: 10.1103/PhysRevLett.108.188101. [DOI] [PubMed] [Google Scholar]
- 10.Wang S., Wolynes P.G. Active contractility in actomyosin networks. Proc. Natl. Acad. Sci. USA. 2012;109:6446–6451. doi: 10.1073/pnas.1204205109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nédélec F., Foethke D. Collective Langevin dynamics of flexible cytoskeletal fibers. New J. Phys. 2007;9:427. [Google Scholar]
- 12.Ennomani H., Letort G., Blanchoin L. Architecture and connectivity govern actin network contractility. Curr. Biol. 2016;26:616–626. doi: 10.1016/j.cub.2015.12.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gordon D., Bernheim-Groswasser A., Farago O. Hierarchical self-organization of cytoskeletal active networks. Phys. Biol. 2012;9:026005. doi: 10.1088/1478-3975/9/2/026005. [DOI] [PubMed] [Google Scholar]
- 14.Kim T. Determinants of contractile forces generated in disorganized actomyosin bundles. Biomech. Model. Mechanobiol. 2015;14:345–355. doi: 10.1007/s10237-014-0608-2. [DOI] [PubMed] [Google Scholar]
- 15.Popov K., Komianos J., Papoian G.A. MEDYAN: mechanochemical simulations of contraction and polarity alignment in actomyosin networks. PLOS Comput. Biol. 2016;12:e1004877. doi: 10.1371/journal.pcbi.1004877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stam S., Alberts J., Munro E. Isoforms confer characteristic force generation and mechanosensation by myosin II filaments. Biophys. J. 2015;108:1997–2006. doi: 10.1016/j.bpj.2015.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cyron C., Müller K., Bruinsma R. Equilibrium phase diagram of semi-flexible polymer networks with linkers. Europhys. Lett. 2013;102:38003. [Google Scholar]
- 18.Müller K.W., Cyron C.J., Wall W.A. Computational analysis of morphologies and phase transitions of cross-linked, semi-flexible polymer networks. P. R. Soc. A. 2015;471:20150332. [Google Scholar]
- 19.Allen M.P., Tildesley D.J. Oxford University Press; New York, NY: 1989. Computer Simulation of Liquids. [Google Scholar]
- 20.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 21.Rubinstein M., Colby R.H. Oxford University Press; Oxford, United Kingdom: 2003. Polymer Physics. [Google Scholar]
- 22.Ott A., Magnasco M., Libchaber A. Measurement of the persistence length of polymerized actin using fluorescence microscopy. Phys. Rev. E. 1993;48:R1642–R1645. doi: 10.1103/physreve.48.r1642. [DOI] [PubMed] [Google Scholar]
- 23.Kojima H., Ishijima A., Yanagida T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 1994;91:12962–12966. doi: 10.1073/pnas.91.26.12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Higuchi H., Yanagida T., Goldman Y.E. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys. J. 1995;69:1000–1010. doi: 10.1016/S0006-3495(95)79975-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Leimkuhler B., Matthews C. Springer; New York, NY: 2015. Molecular Dynamics: with Deterministic and Stochastic Numerical Methods. [Google Scholar]
- 26.Vale R.D., Malik F., Brown D. Directional instability of microtubule transport in the presence of kinesin and dynein, two opposite polarity motor proteins. J. Cell Biol. 1992;119:1589–1596. doi: 10.1083/jcb.119.6.1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bourdieu L., Duke T., Libchaber A. Spiral defects in motility assays: a measure of motor protein force. Phys. Rev. Lett. 1995;75:176–179. doi: 10.1103/PhysRevLett.75.176. [DOI] [PubMed] [Google Scholar]
- 28.Metropolis N., Rosenbluth A.W., Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 29.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 30.Nédélec F. Computer simulations reveal motor properties generating stable antiparallel microtubule interactions. J. Cell Biol. 2002;158:1005–1015. doi: 10.1083/jcb.200202051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kron S.J., Spudich J.A. Fluorescent actin filaments move on myosin fixed to a glass surface. Proc. Natl. Acad. Sci. USA. 1986;83:6272–6276. doi: 10.1073/pnas.83.17.6272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Umemoto S., Sellers J.R. Characterization of in vitro motility assays using smooth muscle and cytoplasmic myosins. J. Biol. Chem. 1990;265:14864–14869. [PubMed] [Google Scholar]
- 33.Harris D.E., Warshaw D.M. Smooth and skeletal muscle myosin both exhibit low duty cycles at zero load in vitro. J. Biol. Chem. 1993;268:14764–14768. [PubMed] [Google Scholar]
- 34.Finer J.T., Simmons R.M., Spudich J.A. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 35.Roux B. World Scientific; Singapore: 2011. Molecular Machines. [Google Scholar]
- 36.Riveline D., Ott A., Prost J. Acting on actin: the electric motility assay. Eur. Biophys. J. 1998;27:403–408. doi: 10.1007/s002490050147. [DOI] [PubMed] [Google Scholar]
- 37.Leimkuhler B., Matthews C. Robust and efficient configurational molecular sampling via Langevin dynamics. J. Chem. Phys. 2013;138:174102. doi: 10.1063/1.4802990. [DOI] [PubMed] [Google Scholar]
- 38.Prost J., De Gennes P.G. 2nd Ed. Oxford University Press; New York, NY: 1995. The Physics of Liquid Crystals, [Google Scholar]
- 39.Odijk T. Theory of lyotropic polymer liquid crystals. Macromolecules. 1986;19:2313–2329. [Google Scholar]
- 40.Murrell M., Thoresen T., Gardel M. Reconstitution of contractile actomyosin arrays. Methods Enzymol. 2014;540:265–282. doi: 10.1016/B978-0-12-397924-7.00015-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bird R.B., Armstrong R.C., Hassager O. Vol. 1. John Wiley; New York, NY: 1987. Dynamics of polymeric liquids. (Fluid Mechanics). [Google Scholar]
- 42.Frontali C., Dore E., Valdevit E. An absolute method for the determination of the persistence length of native DNA from electron micrographs. Biopolymers. 1979;18:1353–1373. doi: 10.1002/bip.1979.360180604. [DOI] [PubMed] [Google Scholar]
- 43.Everaers R., Jülicher F., Maggs A. Dynamic fluctuations of semiflexible filaments. Phys. Rev. Lett. 1999;82:3717. [Google Scholar]
- 44.Gardel M.L., Shin J.H., Weitz D.A. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 45.Koenderink G.H., Atakhorrami M., Schmidt C.F. High-frequency stress relaxation in semiflexible polymer solutions and networks. Phys. Rev. Lett. 2006;96:138307. doi: 10.1103/PhysRevLett.96.138307. [DOI] [PubMed] [Google Scholar]
- 46.Kasza K.E., Koenderink G.H., Weitz D.A. Nonlinear elasticity of stiff biopolymers connected by flexible linkers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:041928. doi: 10.1103/PhysRevE.79.041928. [DOI] [PubMed] [Google Scholar]
- 47.Lin Y.-C., Yao N.Y., Weitz D.A. Origins of elasticity in intermediate filament networks. Phys. Rev. Lett. 2010;104:058101. doi: 10.1103/PhysRevLett.104.058101. [DOI] [PubMed] [Google Scholar]
- 48.Bustamante C., Marko J.F., Smith S. Entropic elasticity of λ-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 49.Marko J.F., Siggia E.D. Stretching DNA. Macromolecules. 1995;28:8759–8770. [Google Scholar]
- 50.Evans D.J., Morriss G.P. Nonlinear-response theory for steady planar Couette flow. Phys. Rev. A. 1984;30:1528–1530. [Google Scholar]
- 51.Shokef Y., Safran S.A. Scaling laws for the response of nonlinear elastic media with implications for cell mechanics. Phys. Rev. Lett. 2012;108:178103. doi: 10.1103/PhysRevLett.108.178103. [DOI] [PubMed] [Google Scholar]
- 52.Walcott S., Warshaw D.M., Debold E.P. Mechanical coupling between myosin molecules causes differences between ensemble and single-molecule measurements. Biophys. J. 2012;103:501–510. doi: 10.1016/j.bpj.2012.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ideses Y., Sonn-Segev A., Bernheim-Groswasser A. Myosin II does it all: assembly, remodeling, and disassembly of actin networks are governed by myosin II activity. Soft Matter. 2013;9:7127–7137. [Google Scholar]
- 54.Duke T., Holy T.E., Leibler S. “Gliding assays” for motor proteins: a theoretical analysis. Phys. Rev. Lett. 1995;74:330–333. doi: 10.1103/PhysRevLett.74.330. [DOI] [PubMed] [Google Scholar]
- 55.Murrell M., Gardel M.L. Actomyosin sliding is attenuated in contractile biomimetic cortices. Mol. Biol. Cell. 2014;25:1845–1853. doi: 10.1091/mbc.E13-08-0450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Lenz M., Thoresen T., Dinner A.R. Contractile units in disordered actomyosin bundles arise from F-actin buckling. Phys. Rev. Lett. 2012;108:238107. doi: 10.1103/PhysRevLett.108.238107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Murrell M.P., Gardel M.L. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc. Natl. Acad. Sci. USA. 2012;109:20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Linsmeier I., Banerjee S., Murrell M.P. Disordered actomyosin networks are sufficient to produce cooperative and telescopic contractility. Nat. Commun. 2016;7:12615. doi: 10.1038/ncomms12615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Scholz M., Burov S., Dinner A.R. Cycling state that can lead to glassy dynamics in intracellular transport. Phys. Rev. X. 2016;6:011037. [Google Scholar]
- 60.Wilson C.A., Tsuchida M.A., Theriot J.A. Myosin II contributes to cell-scale actin network treadmilling through network disassembly. Nature. 2010;465:373–377. doi: 10.1038/nature08994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schaller V., Weber C., Bausch A.R. Polar patterns of driven filaments. Nature. 2010;467:73–77. doi: 10.1038/nature09312. [DOI] [PubMed] [Google Scholar]
- 62.Hetland, R. and J. Travers. 2001. SciPy: open source scientific tools for Python. RBF: radial basis functions for interpolation/smoothing scattered Nd data. https://www.scipy.org/.
- 63.Veigel C., Molloy J.E., Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat. Cell Biol. 2003;5:980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- 64.Ferrer J.M., Lee H., Lang M.J. Measuring molecular rupture forces between single actin filaments and actin-binding proteins. Proc. Natl. Acad. Sci. USA. 2008;105:9221–9226. doi: 10.1073/pnas.0706124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Stricker J., Falzone T., Gardel M.L. Mechanics of the F-actin cytoskeleton. J. Biomech. 2010;43:9–14. doi: 10.1016/j.jbiomech.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.