Transcriptome-wide noise controls lineage choice in mammalian progenitor cells

Abstract

Phenotypic cell-to-cell variability within clonal populations may be a manifestation of “gene expression noise”^1–6, or it may reflect stable phenotypic variants⁷. Such “non-genetic cell individuality”⁷ can arise from the slow fluctuations of protein levels⁸ in mammalian cells. These fluctuations produce persistent cell individuality, thereby rendering a clonal population heterogeneous. However, it remains unknown whether this heterogeneity may account for the stochasticity of cell fate decisions in stem cells. Here we show that in clonal populations of hematopoietic progenitor cells, spontaneous “outlier” cells with either extremely high or low expression levels of the stem cell marker Sca-1⁹ reconstitute the parental distribution of Sca-1 but do so only after more than one week. This slow relaxation is described by a Gaussian-Mixture Model (GMM) that incorporates noise-driven transitions between discrete subpopulations, suggesting hidden multi-stability within one cell type. Despite clonality, the Sca-1 outliers had distinct transcriptomes. Although their unique gene expression profiles eventually reversed to that of the median cells, revealing an attractor state, they lasted long enough to confer a greatly different proclivity for choosing either the erythroid or myeloid lineages. Preference in lineage choice was associated with elevated expression of lineage-specific transcription factors, such as a > 200-fold increase in GATA1¹⁰ among the erythroid-prone cells, or > 15-fold increased PU.1¹¹ expression among myeloid-prone cell. Thus, clonal heterogeneity of gene expression level is not due to independent noise in the expression of individual genes, but reflects metastable states of a slowly fluctuating transcriptome that is distinct in individual cells and may govern the reversible, stochastic priming of multipotent progenitor cells in cell fate decision.

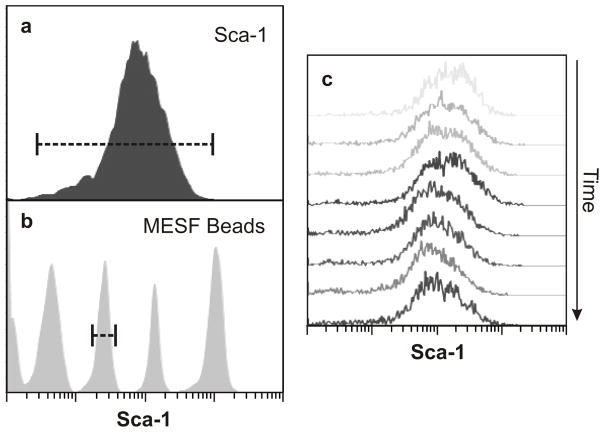
Cell-to-cell variability can be quantified by analyzing the dispersion of expression levels of a phenotypic marker within a cell population. Flow cytometric analysis of EML cells, a multipotent murine hematopoietic cell line¹², revealed an approximately 1000-fold range in the level of the constitutively expressed stem cell surface marker Sca-1 among individual cells within one newly-derived clonal cell population (Fig. 1a). The heterogeneity of Sca-1 expression in this clonal population was highly consistent between measurements (Fig. 1c) and could not be attributed to measurement noise (Fig. 1b). Moreover, cell-cycle dependent cell size variation contributed only 1% to the observed variability of Sca-1 levels per cell (Supplementary Discussion and Supplementary Fig. 1).

Figure 1. Robust clonal heterogeneity.

a, b, Heterogeneity in Sca-1 expression among clonal cells (a) was significantly larger than the resolution limit of flow cytometry approximated by measurement of reference MESF²⁴ beads (b). c, Stability of clonal heterogeneity in Sca-1 over 3 weeks.

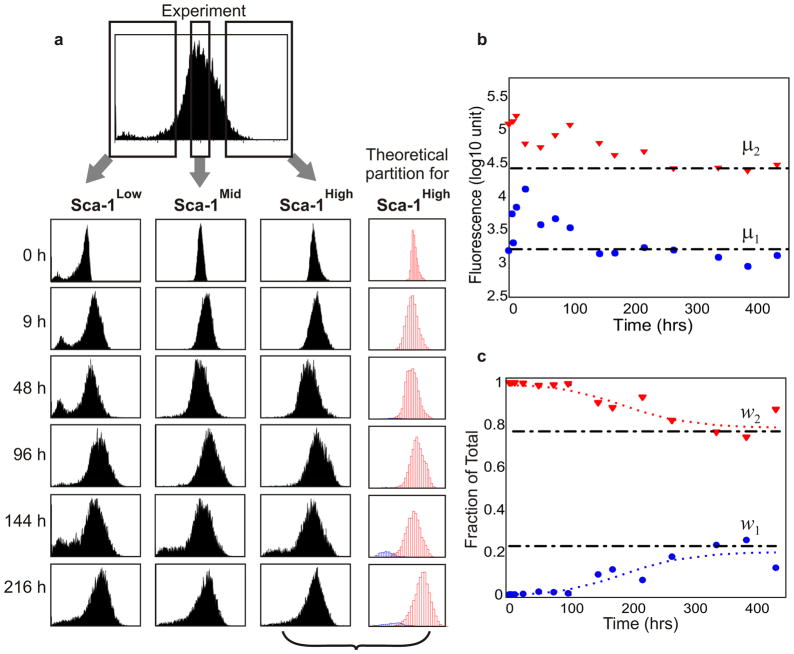
To characterize the dynamics by which population heterogeneity arises, cells with the highest, middle, and lowest ~15% Sca-1 expression level (denoted henceforth as Sca-1^Low, Sca-1^Mid, and Sca-1^High fractions) were isolated from one clonal population using fluorescence activated cell sorting (FACS). Cells were stripped free of the staining antibody immediately after isolation and cultured in standard growth medium. Within hours, all three fractions showed broadening of the narrow Sca-1 histograms obtained immediately after sorting (Fig. 2a) but more than 9 days elapsed before the three fractions regenerated Sca-1 histograms similar to that of the parental (unsorted) population (Fig. 2a). Therefore, the restoration of the wide range of Sca-1 surface expression levels is a slow process (requiring > 12 cell doublings) that is independent of initial Sca-1 expression-levels. Clonal heterogeneity was also regenerated from subclones derived from randomly selected individual cells that had varying initial mean Sca-1 levels (Supplementary Fig. 2).

Figure 2. Restoration of heterogeneity from sorted cell fractions.

a, Clonal cells with the highest (Sca-1^High), middle (Sca-1^Mid) and lowest (Sca-1^Low) 15% Sca-1 expression independently re-established the parental extent of clonal heterogeneity after 216 h in separate culture. As an example, each cell in the Sca-1^High experiment was theoretically partitioned into one of two GMM-subpopulations (blue and red). b, c, The temporal evolution of the means μ_1,2 (b) and weights w_1,2 (c) for the Sca-1^High GMM subpopulations 1 and 2. The evolution of the weights was fitted to a sigmoidal function (c, dotted curves). Black dotted dash lines, equilibrium values for μ_ı and w_i.

What drives the regeneration of the parental “bell-shaped” histogram from the three sorted population fractions (Fig. 2a)? Although a variety of mechanisms may in principle underlie this behavior (Supplementary Discussion and Supplementary Fig. 3 and 4), we consider here a general theoretical stochastic formulation. Because the genetic circuitry governing the expression of Sca-1 is poorly understood¹³, modeling the process explicitly with genetic circuits subjected to stochastic dynamics¹⁴ is not feasible. Instead, we took a phenomenological approach to determine the model class of stochastic processes which describes the observed behaviour. The simplest model is an elementary mean-reverting (Ornstein-Uhlenbeck, O-U) process¹⁵ that includes both noise-driven diffusion (capturing the generation of cell-cell variability) and a drift towards the deterministic equilibrium (representing relaxation to the parental distribution mean) (Supplementary Theoretical Methods). However, a simple O-U process describes the data only poorly, since it fails to recapitulate the growth of the long left tail (e.g., 100-fold range for the Sca-1^High fraction) in the histogram.

An alternative explanation is that the relaxation process is complicated by slow dynamics on a rugged potential landscape that consists of multiple quasi-discrete state transitions whose stochastic nature produces an additional source of variability¹⁶. Recent analysis of human myeloid progenitor cells has provided experimental evidence for the existence of multiple metastable states¹⁷, consistent with the dynamics of complex gene regulatory networks that control mammalian cell fates¹⁷. We thus extended the simple O-U model to include transitions between distinct states (virtual subpopulations) using a Gaussian-Mixture Model (GMM) as a first approximation to a multimodal system. As quantified by the Akaike Information Criterion (Supplementary Theoretical Methods), the data can be described by a minimal GMM model comprised of only two distinct states, each described as a Gaussian, the parameters of whichwere obtained from the observed histograms in the stationary phase (time ≥9 days).

Our GMM model allowed us to partition cells in every measured histogram (time point) into two “virtual subpopulations” (blue = subpopulation 1 and red = subpopulation 2 in Fig. 2a) based on the expression values of the individual cells, thus providing the time evolution of the mean μ_i and the relative abundance (weight) w_i for each subpopulation i =1, 2 (Fig. 2b and 2c and Supplementary Theoretical Methods). Interestingly, this theoretical description suggests that the asymmetric broadening of the truncated histograms, as partially reflected in the changes in μ for the two subpopulations (Fig. 2b), only accounts for a fraction of the restoration of the equilibrium heterogeneity. In contrast, stochastic transitions between the subpopulations, as reflected by the evolution of the weights w_i, played a dominant role in the later relaxation to equilibrium. Importantly, for the Sca-1^Mid and Sca-1^High fractions, changes in w_i were initially negligible until 96 h, at which point the w_i exhibited a steep change before eventually reaching a plateau (Fig. 2c).

In summary, our results suggest that the observed clonal population heterogeneity of protein expression is not simply the manifestation of noise around a single, deterministic equilibrium (attractor) state described by an O-U model. Instead it is likely the result of processes involving stochastic state transitions in a multi-stable system¹⁷, which may explain the slow regeneration of the parental heterogeneity.

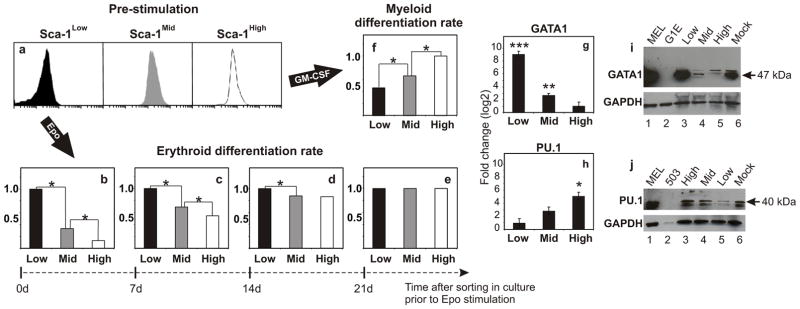
These results suggest that whole population averaging of the level of Sca-1 may not appropriately characterize its biological function. Instead, because of the slowness of relaxation to the mean values, momentary levels of Sca-1 within individual cells may reflect distinct, enduring functional states with different biological consequences. Thus, we asked whether clonal heterogeneity in Sca-1 expression correlates with heterogeneity of the differentiation potential of these cells. Indeed, among the secondary clones generated from the parental population, the rate of commitment to pro-erythrocytes in response to Erythropoietin (Epo) (Methods, and Supplementary Fig. 5) was inversely correlated to the baseline mean Sca-1 expression of each clone (Supplementary Fig. 6). Similarly, for the three sorted fractions (Fig. 3a), the relative erythroid differentiation rates were distinct, with Sca-1^Low cells differentiating the fastest, followed by Sca-1^Mid and Sca-1^High (Fig. 3b). Importantly, although the Sca-1^Low fraction differentiated into the erythroid lineage at a rate 7-fold higher than the Sca-1^High fraction (Fig 3b), the Sca-1^Low fraction was not composed of spontaneously and irreversibly pre-committed pro-erythrocytes. Instead, these cells were still undifferentiated as evidenced by expression of the stem cell marker c-kit, their normal proliferation capacity (Supplementary Fig. 7) and their ability to reconstitute the parental histogram (Fig. 2a).

Figure 3. Clonal heterogeneity governs differentiation potential.

a–f, Sca-1^Low (Low, black), Sca-1^Mid (Mid, grey), and Sca-1^High (High, white) fractions (a) stimulated by Epo (b) and GM-CSF (f) immediately after isolation showed variable differentiation rates into the erythroid and myeloid lineages, respectively. Upon 7, 14, and 21 days (d) of post-sort culture, Epo- treated cells showed convergence in both pre-stimulation, baseline Sca-1 expression (Fig. 2a) and relative differentiation rates (b–e). Asterisk, p < 0.001 (two-tailed normal-theory test). g, h, qRT-PCR analysis of GATA1 (g) and PU.1 (h) mRNA levels in Sca-1 sorted fractions. Means ± s.e.m. of triplicates shown; triple asterisk p < 10⁻⁵, double asterisk p < 0.0002, asterisk p < 0.003 (one-tail Student’s t-test). i, j, Western blot analysis of GATA1 (i) and PU.1 (j) protein levels in Sca-1 fractions (lanes 3–5) and mock-sorted cells (lane 6). MEL cell line (lane 1), positive control; G1E and 503 (lane 2) cell lines, negative controls for GATA1 and PU.1, respectively. GAPDH, loading control.

When we stimulated erythroid differentiation at later time points after sorting on 7, 14, and 21 days (as the Sca-1 histograms became more similar to each other while restoring the parental distribution), the difference in the erythroid differentiation rate between the Sca-1^Low versus Sca-1^High fractions was gradually lost (Fig. 3b–e). Surprisingly, despite the near complete convergence of the Sca-1 histograms at 7 days, variability in differentiation kinetics was consistently detectable beyond 14 days after sorting (Fig. 3d). This suggests that clonal heterogeneity in Sca-1 expression controls differentiation potential but constitutes only a one-dimensional projection of separate states in the high-dimensional space of gene expression levels¹⁷. To reveal additional dimensions, we looked for correlated heterogeneity in other proteins and investigated whether expression of the erythroid-fate determining transcription factor GATA1¹⁰ differed among the Sca-1 fractions. Real-time PCR revealed significantly higher GATA1 mRNA levels in the erythroid differentiation-prone Sca-1^Low progenitor cells (260-fold increase over Sca-1^High fraction), followed by the Sca-1^Mid (2.7-fold increase over Sca-1^High fraction) and Sca-1^High fractions (Fig. 3g), and these differences were paralleled by GATA1 protein levels (Fig. 3i). Importantly, GATA1 mRNA expression among the three sorted fractions at 5 and 14 days after sorting (Supplementary Fig. 8) mirrored the gradual loss of variability observed in the differentiation kinetics for the erythroid lineage (Fig. 3b–e).

GATA1 plays an antagonistic role in lineage determination with the myeloid-fate determining transcription factor PU.1, and these two transcription factors mutually inhibit each other to regulate the erythroid versus myeloid fate decision¹⁸. Thus, we hypothesized that cells that are least prone to erythroid differentiation and exhibit low GATA1 expression may have high PU.1 levels, and thus be predisposed to the myeloid lineage. Indeed, real-time PCR revealed the highest PU.1 mRNA levels among the Sca-1^High progenitor cells (17-fold increase over Sca-1^Low fraction), followed by the Sca-1^Mid (3.6-fold increase over Sca-1^Low fraction) and Sca-1^Low fractions (Fig. 3h). These differences were paralleled by PU.1 protein levels (Fig. 3j). Furthermore, myeloid differentiation rate was the highest among Sca-1^High cells, followed by Sca-1^Mid and Sca-1^Low (Fig. 3f) in response to GM-CSF and IL-3 (Methods and Supplementary Fig. 5). These results show that within a clonal population of multipotent progenitor cells, spontaneous non-genetic population heterogeneity primes the cells for different lineage choices.

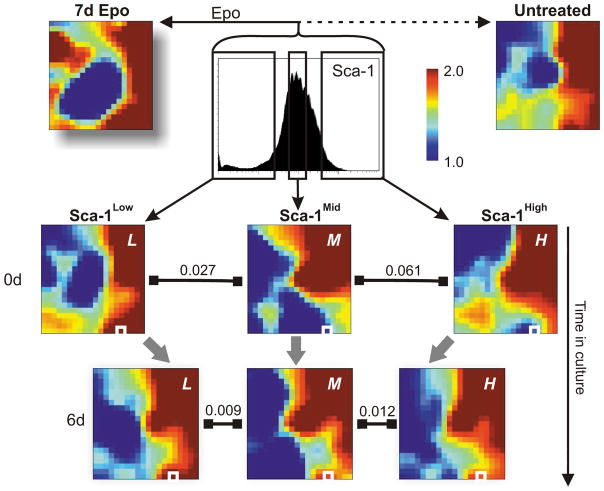
Since both GATA1 and PU.1 are pivotal lineage-specific transcription factors, we asked whether the dramatic up-regulation of GATA1 and associated down-regulation of PU.1 in the most erythroid-prone Sca-1^Low cells reflect a particular cellular state in terms of genome-wide gene expression. Microarray-based mRNA expression profiling on Sca-1^Low (L), Sca-1^Mid (M), and Sca-1^High (H) fractions immediately after sorting revealed that these three fractions differed considerably in their transcriptomes (Fig. 4). Replicate microarray measurements showed that the observed transcriptome differences could not be attributed solely to experimental error (Supplementary Fig. 9). Significance Analysis of Microarrays (SAM)¹⁹ revealed >3900 genes that were differentially expressed between the Sca-1^Low and Sca-1^High fractions at a stringent False Detection Rate (FDR) of 1.5%. The distinct global gene expression profiles of the three fractions converged to a common pattern within 6 days after sorting, a progression that can be quantified by the inter-sample distance metric D = 1-R, where R is the Pearson correlation coefficient. The distances between the three profiles decreased from D (L - M) _{0 days} = 0.027 to D (L - M) _{6 days} = 0.009 and from D (M - H)_{0 days} = 0.061 to D (M - H)_{6 day} =0.012 (Fig. 4 and Supplementary Table 1). Thus, the outlier populations reconstituted the traits of the parental population not only with respect to their distribution of Sca-1 expression (Fig. 2a) and differentiation rates (Fig. 3b–e), but also with respect to their gene expression profiles across thousands of genes. This global relaxation from both ends of the parental spectrum towards the center is predicted by the model in which a stable cell phenotype, such as the progenitor state here, is a high-dimensional attractor state²⁰. It also confirms that the Sca-1 outlier cells were not already irreversibly committed. Nevertheless, Sca-1^Low cells exhibited a transcriptome that was clearly more similar than the Sca-1^High cells to the maximally differentiated (unsorted) cells (Fig. 4) that were cultured in the presence of Epo for 7 days (D (L - 7d_Epo) = 0.079 versus D (H - 7d_Epo) = 0.158, Supplementary Table 1), a remarkable feat given the spontaneity and stochasticity of the process that generated these differentiation-prone outlier cells. In fact, with respect to 200 “differentiation marker genes” (Methods), only the Sca-1^Low cells were statistically similar to the Epo-treated cells (p < 3×10⁻¹⁴, pair-wise t-test), whereas the Sca-1^Mid (p >0.8) and Sca-1^High (p > 0.6) cells were not, further confirming the transcriptome similarity between the Sca-1^Low and Epo-treated cells, which may be related to their elevated GATA1 levels.

Figure 4. Clonal heterogeneity of Sca-1 expression reflects transcriptome-wide noise.

Self-organizing maps of global gene expression for a subset of 2997 genes visualized with the GEDI²³ program for Sca-1^Low (L), Sca-1^Mid (M), Sca-1^High (H) fractions at 0 and 6 days (d) after FACS isolation and for a differentiated erythroid culture (7d Epo) and an untreated (Untreated) control sample. Pixels in the same location within each GEDI map contain the same minicluster of genes. Color of pixels indicates centroid value of gene expression level for each minicluster in log10 units of signal. Dissimilarity between transcriptomes indicated above . GATA1-containing pixel boxed in white.

Our results demonstrate the robust nature of cell-to-cell variability that underlies the heterogeneity of gene expression in a clonal population of mammalian progenitor cells. While the source of the heterogeneity and the molecular mechanisms responsible for its slow restoration remain to be elucidated, our experiments and general theoretical considerations point to discrete transitions in a dynamical system exhibiting multistability as one source of this behavior. Independent of the specific mechanism, we show that biological function in metazoan cells is not necessarily determined by the ensemble average of a nominally homogenous cell population, and that outliers in a heterogeneous cell population do not simply represent irrelevant, short-lived phenotypic states caused by random fluctuations in the expression of a single gene. Instead, the departure from the average state is characterized by slowly fluctuating transcriptome-wide noise that has significant biological functionality in the priming of cell fate commitment. This finding helps unite two old dualisms: between plasticity and heterogeneity in explaining multipotency^21,22, and between instructive and selective regulation in explaining cell fate decisions¹⁸. Exploiting the spontaneous, transient yet enduring cell individuality in differentiation potential resulting from clonal heterogeneity also could be of practical value in attempts to steer lineage choice in stem cells for therapeutic applications.

Methods

Culture of EML cells, creation of single-cell derived subclones and differentiation into erythroid and myeloid cells

EML cells (gift from Keith Orford/David Scadden) were maintained in growth medium (GM) containing Iscove’s Modified Dulbecco’s Medium (IMDM) + 20% Horse Serum + 12–15% (v/v) BHK/MKL-conditioned medium (CM) + 1% glutamine/penicillin/streptomycin. To obtain single-cell derived subclones, cells were plated into 60 mm plates at 500–2000 cell/ml density in 1% methylcellulose (Methocult M3134) containing GM and incubated without disturbance for ten days. Individual well-demarcated colonies were hand-picked with Pasteur pipettes under microscopic guidance and transferred to liquid cultures in microwell plates. Typical subclones required ~18 days in culture to expand to a sufficiently large population for experiment. To differentiate EML cells into the erythroid lineage, previously reported differentiation protocol¹² was adapted. Briefly, on day 1, cells were cultured in GM + 10 ng/ml of mouse recombinant Erythropoietin (Sigma-Aldrich) at 250,000 cells/ml density. On day 3, cells are spun down and re-suspended into IMDM + 20% Horse Serum + 2% BHK/MKL – CM + 10 ng/ml of mouse recombinant Erythropoietin at 125,000 cells/ml density to give resulting erythroid cells a growth advantage. One day 6, an additional 10 ng/ml of Epo is added. Typically, seven days of Erythropoietin (Epo) treatment generated ~40–60% (of total) pro-erythrocytes that were benzidine stain positive and Sca-1/c-kit double negative (Supplementary Fig. 5). Benzidine staining was performed following reported protocol²⁵ and examined by microscopy after cytospin. To differentiate EML cells into myeloid cells, previously reported differentiation protocol¹² was adapted. Briefly, on day 1, cells were cultured in GM + 10 ng/ml of mouse recombinant IL-3 (Peprotech) + 10⁻⁵ M retinoic acid (Sigma-Aldrich) at 300,000 cells/ml density. On day 4, cells were thoroughly washed with PBS to remove remaining SCF from the growth medium and cultured in IMDM + 20% Horse Serum + 2% BHK/MKL – CM + 10 ng/ml of mouse recombinant granulocyte macrophage colony-stimulating factor (GM-CSF, R&D Systems) + 10⁻⁵ M retinoic acid (Sigma-Aldrich) at 200,000 cells/ml density. On day 6, an additional 10ng/ml of GM-CSF is added. After 7–9 days, differentiated myeloid cells dominate the culture and show Mac-1 and Gr-1 expression by flow cytometry.

Flow cytometry, Fluorescence Activated Cell Sorting (FACS), and Bead calibration

For direct cell surface protein immunostaining the antibodies Sca-1-PE (Caltag) and c-Kit-FITC (BD Pharmingen) antibodies were used at 1:1000 dilutions in ice-cold PBS + 1% fetal calf serum with (flow cytometry) or without (FACS) 0.01% NaN₃. Appropriate isotype control antibodies (BD Pharmingen) were used to establish background signal due to non-specific antibody binding. Propidium iodide (PI) staining was correlated with lower forward scatter (FSC) among EML cells (Supplementary Fig. 10). Thus, dead cells with positive PI staining were easily removed from all analysis by gating out the low FSC population. Flow cytometry was performed on a Becton Dickinson FACSCaliber analyzer and FACS with either a Becton Dickinson FACSAria or AriaSpecial Sorter UV laser system at the Dana Farber Cancer Institute Flow Cytometry Core. Computational data analysis was done with FlowJo 2.2.2. For cell sorting, input cell number ranged from 60 – 100 × 10⁶ cells. Cells were sorted into ice-cold medium for a maximal duration of 3 h. Gates for the lowest, middle, and highest Sca-1 expressors were set based on proportion of total population. For cells that were re-cultured after FACS, the staining antibody was removed following protocol as previously reported¹⁷. Quantum PE Molecules of Equivalent Soluble Fluorochrome (MESF) beads (Bangs Laboratories) were used to correct for the effect of day-to-day fluctuations in the flow cytometer, following the manufacturer’s instructions. Calibration curves were constructed using Matlab 7.2 (MathWorks) and used to convert obtained fluorescence data into absolute MESF units for the purpose of quantitative theoretical modeling.

Gene expression profiling with microarrays and data analysis

Gene expression profiling was performed at the Molecular Genetics Core facility at Childrens Hospital, Boston using MouseWG-6 v1.1 microbead chips (Illumina). Raw gene expression data was first subjected to Rank-Invariant Normalization using BeadStudio 3.0. Matlab 7.2 was used to filter the list of 46,628 genes based on two sets of criteria: 1) Detection p-value based on Illumina replicate gene probes: genes with detection p-values > 0.01 in all samples were called “absent” in all samples and thus removed (giving rise to Set 1, consisting of 14038 genes). Genes with differing detection call between the duplicate samples were also removed. 2) Fold-change: genes that did not show at least a 2-fold change compared to the Sca-1^Mid fraction in 4 out of the 12 total samples were also removed (resulting in Set 2: 2997 genes). Alternatively, the Significance Analysis of Microarrays¹⁹ algorithm was used to filter by fold change at a stringent False Detection Rate of 1.5% (resulting in Set 3: 3973 genes). Qualitative conclusions did not depend on the exact stringency of the filtering. After filtering, gene expression levels were transformed by log10 and subjected to clustering analyses. Gene Expression Dynamics Inspector (GEDI) maps for visual representation of global gene expression based on self-organizing maps (SOM) were generated using the program GEDI²³ (http://www.childrenshospital.org/research/ingber/GEDI/gedihome.htm). In GEDI, each “tile” within a “mosaic” represents a minicluster of genes with highly similar expression pattern across all the analyzed samples. The same genes are forced to the same mosaic position for all GEDI maps, hence allowing direct comparison of transcriptomes based on overall mosaic pattern. Color of tiles indicates the centroid value of gene expression level for each minicluster. Dissimilarity between samples was quantified by 1- R where R is the Pearson’s correlation coefficient calculated for all genes in a pair of samples. For statistically analysis of the similarity between the sorted fractions and the Epo-treated sample, a subset of ~200 “differentiation marker genes” were obtained from stringent SAM-analysis of the unsorted, untreated control and the unsorted, Epo-treated sample.