Combining experimental and simulation data of molecular processes via augmented Markov models

Significance

Structural biology is moving toward a paradigm characterized by data from a broad range of sources sensitive to multiple timescales and length scales. However, a major open problem remains: to devise an inference method that optimally combines all of this information into models amenable to human analysis. In this work, we make a significant step toward achieving this goal. We introduce a statistically rigorous method to merge information from molecular simulations and experimental data into augmented Markov models (AMMs). AMMs are easy-to-analyze atomistic descriptions of biomolecular structure and exchange kinetics. We show how AMMs may provide accurate descriptions of molecular dynamics probed by NMR spin relaxation and thereby provide a unique way to integrate analysis of experimental with simulation data.

Abstract

Accurate mechanistic description of structural changes in biomolecules is an increasingly important topic in structural and chemical biology. Markov models have emerged as a powerful way to approximate the molecular kinetics of large biomolecules while keeping full structural resolution in a divide-and-conquer fashion. However, the accuracy of these models is limited by that of the force fields used to generate the underlying molecular dynamics (MD) simulation data. Whereas the quality of classical MD force fields has improved significantly in recent years, remaining errors in the Boltzmann weights are still on the order of a few $kT$, which may lead to significant discrepancies when comparing to experimentally measured rates or state populations. Here we take the view that simulations using a sufficiently good force-field sample conformations that are valid but have inaccurate weights, yet these weights may be made accurate by incorporating experimental data a posteriori. To do so, we propose augmented Markov models (AMMs), an approach that combines concepts from probability theory and information theory to consistently treat systematic force-field error and statistical errors in simulation and experiment. Our results demonstrate that AMMs can reconcile conflicting results for protein mechanisms obtained by different force fields and correct for a wide range of stationary and dynamical observables even when only equilibrium measurements are incorporated into the estimation process. This approach constitutes a unique avenue to combine experiment and computation into integrative models of biomolecular structure and dynamics.

Atomistic molecular dynamics (MD) simulation is a popular tool to investigate mechanisms underlying biomolecular function, including ligand binding (1, 2) and allostery (3), whereas coarse-grained molecular models are often used when studying assembly and interactions of supramolecular systems (4, 5). With recent advances in massively paralleled computation, simulating thousands of short- to medium-length realizations of many biomolecular systems has become feasible (6, 7). Systematic analysis of such large sets of MD data in terms of Markov state models (MSMs) (8, 9) now enables the study of slow dynamic processes, including protein folding (10, 11), conformational transitions (12, 13), and quantitative comparison with experiments (14–16) otherwise affordable only on special-purpose supercomputers (17).

Whereas these technologies are closing the gap as to which macromolecular systems and timescales can be directly simulated, it is becoming increasingly evident that systematic errors in empirical models—force fields—limit our ability to predict experimental data quantitatively (18). Although force fields are undergoing continuous improvement, high accuracy needs to be balanced with computational efficiency. A viable approach is to aim at force fields that are good enough such that they can be reweighted or biased by experimental data and thus make them quantitatively predictive (19, 20).

Key to this approach is a consistent framework to integrate simulation and experimental data. Popular approaches include using available experimental data to bias the empirical models during simulation in an ad hoc fashion (21), using Bayesian (22–25) or maximum entropy (26–28) frameworks, or using a posteriori reweighting of the simulated ensembles (24, 29–31). Although these approaches generally improve agreement with experimental data, they have several technical issues (32) and a number of intrinsic limitations: Biased simulation strategies make it difficult to reuse simulation data if new experimental data become available. Existing reweighting techniques come at the cost of losing dynamic information in the unbiased simulation data. Both approaches currently require that the simulation ensemble can be sampled directly and do not make use of MSMs to sample long timescales. Further, most existing approaches do not clearly distinguish between systematic (force-field) error and statistical (sampling) error, which may result in unexpected behavior or involve user-specified weighting factors. Several Markov state model estimators have been developed that are conditioned on auxiliary data, especially microscopic quantities such as the stationary distribution or functions of the transition probability matrix (33–37). However, the direct augmentation of Markov state models with experimental data using a judicious treatment of force-field and sampling errors is still an open issue.

This work introduces augmented Markov models (AMMs). AMMs are MSMs that balance information from simulation and averaged experimental data during estimation. This balance is achieved by an information-theoretic treatment of systematic force-field errors and a probabilistic treatment of sampling and experimental errors. Using this approach, we show that AMMs more accurately recapitulate complementary stationary and dynamic experimental data than their MSM counterparts. AMMs are therefore a unique way to approach integrative structural biology, where information about the kinetics of conformational transitions is also accessible. This method moves the field closer to truly mechanistic data-driven models.

Theory

Augmented Markov Models.

MSMs describe the kinetics between a set of $n$ segments of configuration space in terms of a matrix $P=[p_{ij}]$, where $p_{ij}$ is the probability of transitioning to state $j$ at time $\tau$ after having being in state $i$. MSMs therefore approximate the system’s full phase-space dynamics by a discretization of space (via the $n$ Markov states) and time (lag time $\tau$) (9). The transition probability matrix is estimated through statistical inference based on transition counts, $c_{ij}$, observed in one or multiple independent MD trajectories (9). When modeling equilibrium dynamics, one typically enforces microscopic reversibility or detailed balance in the estimation procedure (34, 38, 39). Here, we present a way to combine statistics from MD trajectories and experimental data into a joint estimate of the matrix $P$.

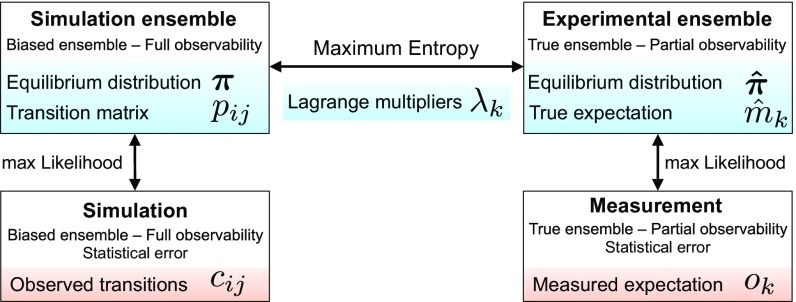
Simulations rarely match the in situ conditions of experiments exactly; however, even if they could, we would still expect systematic errors in the Boltzmann weights of the simulation’s molecular configurations due to inaccuracies of the force field. As a result, quantities computed from simulation and measured by experiment will differ even in the limit of extensive MD sampling. Specifically, the experimental state probability ${\widehat{\pi }}_i$ of the Markov state ${\mathrm{\Omega }}_i$ that affects measurable expectation values is ${\int }_{{\mathrm{\Omega }}_i}\widehat{\mu }(x)\mathrm{dx}$— where $\widehat{\mu }(x)$ is the “true” Boltzmann distribution of the system probed experimentally. In addition to this systematic difference, computing quantities from simulation data and measuring them by experiment are both subject to statistical error or noise. Here, we combine ideas from probability theory and information theory to account for the systematic and statistical errors and formulate an inference framework for AMMs that combines these two sources of data (Fig. 1).

Fig. 1.

Scheme illustrating AMMs. Unknown variables are shown in blue, and observed experimental and computational data are shown in orange.

Estimating AMMs from Simulation and Experimental Data.

Consider that we measure the expectation values of $K$ experimental observables ${ϵ}_k,k\in (1,\mathrm{\dots },K)$. Whereas these observables have noise-free expectations $({\widehat{m}}_1,\mathrm{\dots },{\widehat{m}}_K)$ according to the experimental Boltzmann ensemble, we assume that due to experimental noise our experiment measures expectation values $o_k$ that are normally distributed around the noise-free values ${\widehat{m}}_k$, as $o_k\sim \mathcal{N}({\widehat{m}}_k,{\sigma }_k)$, with experimental uncertainties ${\sigma }_k$.

Although we do not have direct access either to the true equilibrium distribution of the experimental ensemble $\widehat{𝝅}$ or to the noise-free expectations, ${\widehat{m}}_k$, we can connect them by means of the experimental observable. The expectation value of the $k$th spectroscopic observable in the $i$th Markov state can be written as a vector ${𝒆}_k=({(e_k)}_1,\mathrm{\dots },{(e_k)}_n)$ with elements

$${(e_k)}_i={\int }_{{\mathrm{\Omega }}_i}\frac{\widehat{\mu }(x)}{{\widehat{\pi }}_i}{ϵ}_k(x)\mathrm{d}x.$$

Here, ${ϵ}_k(x)$ is a scalar function that computes the experimental observable for a given molecular structure $x$ (a forward model). The noise-free expectations can then be written as ${\widehat{m}}_k=\widehat{𝝅}\cdot {𝒆}_{𝒌}$.

Now we can write an expression of the true experimental distribution $\widehat{𝝅}$ in terms of the biased simulation model distribution $𝝅$ and $k$ Lagrange multipliers ${\lambda }_v$. We reweigh the biased distribution with the principle of adding a minimal amount of additional information (maximum entropy), which can be achieved by minimizing the Kullback–Leibler divergence of $𝝅$ and $\widehat{𝝅}$ (SI Appendix, Theory):

$${\widehat{\pi }}_i=\frac{{\pi }_i\exp ({\sum }_v{\lambda }_v{(e_v)}_i)}{{\sum }_j{\pi }_j\exp ({\sum }_v{\lambda }_v{(e_v)}_j)}.$$ [1]

The Lagrange multipliers, ${\lambda }_k,$ are then obtained by enforcing the constraint of all measured values $o_k$ matching their corresponding expectations ${\widehat{m}}_k$.

Whereas Eq. 1 couples the experimental observations made in the ensemble $\widehat{𝝅}$ to the simulation data generated in the ensemble $𝝅$, both the experimental observations and the MD simulation data are subject to statistical errors. To account for these errors, we express the measured values and MD trajectory statistics by means of the following augmented Markov model likelihood:

$$L\propto \underset{simulation}{\underbrace{\prod _{i,j}{p}_{ij}^{c_{ij}}}}\underset{experiments}{\underbrace{\prod _k\exp \left(-w_k{({\widehat{m}}_k-o_k)}^2\right)}}.$$ [2]

Here, $c_{ij}$ counts the transitions between pairs of microstates (clusters) $i$ and $j$ at time-step $\tau$ sampled in the simulation(s), and $p_{ij}$ are the state-to-state transition probabilities subject to the detailed balance constraint with respect to the simulation’s equilibrium distribution $𝝅$. This first part is the well-known MSM likelihood (9). The second term is the probability to measure $k$ experimental expectation values given the noise-free expectations ${\widehat{m}}_k$ through a normal error model with variance ${\sigma }_k^2=\mathrm{\hspace{0.17em}1}/2w_k$. Thus, $w_k$ encodes the reliability (inverse uncertainty) of the $k$th experimental observation. An error model taking cross-correlations between the experimental observations into account may be used when such information is available (SI Appendix, Theory). Furthermore, the likelihood can be combined with a prior on the transition counts to enable Bayesian inference (SI Appendix, Theory), which was used to compute AMM uncertainties in the present article.

We can maximize Eq. 2 with respect to the unknown parameters $p_{ij}$ and ${\lambda }_k$ to obtain an AMM that balances simulation data with experimental observables. The algorithm involves alternating between rounds of updating the estimate of $𝝅$, the Lagrange multipliers ${\lambda }_v$, and $\widehat{𝝅}$, independently, while keeping all other unknowns fixed. Once these parameters have converged, the maximum-likelihood transition matrix $p_{ij}$ given $c_{ij}$ and constrained to the equilibrium distribution $\widehat{𝝅}$ is estimated using equations in section 4 of ref. 37. The estimation procedure is covered in more detail in SI Appendix, Theory. The AMM estimator is available in the PyEMMA software, version 2.5 (www.pyemma.org) (40).

Results

Rescuing Biased Relaxation Dynamics in a Protein-Folding Model.

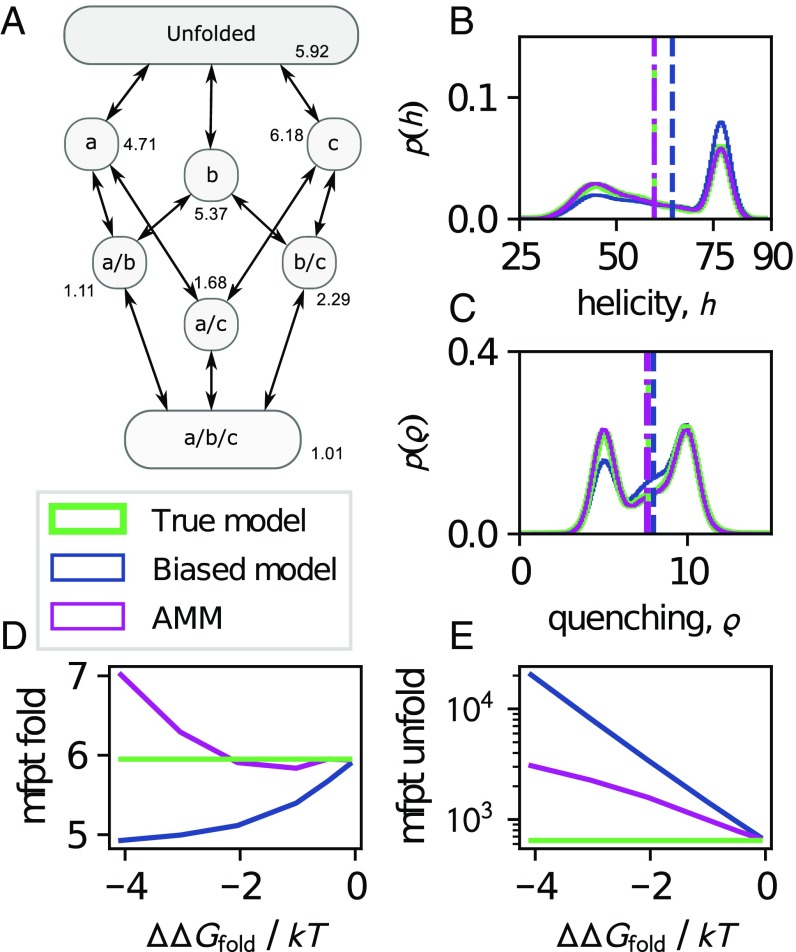
To illustrate the potential power of AMMs, we turn to an eight-state model of protein folding. The states represent different stages of folding of an idealized bundle of helices, a, b, and c, along multiple parallel folding pathways (Fig. 2A and Materials and Methods). For each state we assign a value to each of two observables: an average helicity, $h$, and the propensity of helix c to form an end-to-end contact, $\varrho$ (SI Appendix, Table S1). Consequently, given an equilibrium distribution of the states we can evaluate expectation values of these observables that may correspond to bulk circular dichroism and fluorescence quenching experiments, respectively. We generate a number of different variants of this model: a true reference model ($\mathrm{\Delta }{G}_{\text{fold}}=-4.92kT$) and six biased models where the enthalpic contributions to the free energy of each state are increased such that the $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}$ varies between $-0.095kT$ and $-4.07kT$, compared with the true model (SI Appendix, Table S1). As a result, the equilibrium distribution and kinetics of the biased models differ to an increasing degree from the true model.

Fig. 2.

Illustration of AMMs on a protein-folding model with true thermodynamics and kinetics shown in green. A representative biased simulation with $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}\approx -\mathrm{\hspace{0.17em}3}kT$ compared with the true model is shown in blue whereas the AMM-corrected values are shown in magenta. (A) Kinetic network topology. Each state is annotated by its true free energy in $kT$. (B and C) Equilibrium distributions (solid line) and expectation values (dashed/dashed-dotted lines) of helicity and fluorescence quenching observables. (D and E) Mean first passage times of folding and unfolding, respectively, of biased and AMM models as a function of the degree of bias, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{fold}}$ (Materials and Methods).

For each model, we generated numerous simulation trajectories (SI Appendix, SI Materials and Methods). Indeed, the obtained distributions of observables $h$ and $\varrho$ differ systematically between the biased models and the true model, also leading to a significant bias in the expectation value of $h$ (Fig. 2 B and C). Kinetic quantities such as the mean first passage times (mfpts) of unfolding and folding are also affected by the bias (Fig. 2 D and E). To recover from this bias, we combine the biased simulation data with an “experimental” measurement of the unbiased expectation values of $h$, using the AMM estimator outlined above. This case corresponds to a situation where we have good statistics in simulation and experiment and serves to illustrate the compensation of systematic errors. Furthermore, because the experimental restraint falls within the support of the helicity observable of all of the biased ensembles, the maximum of our likelihood may always fulfill the experimental constraint exactly (SI Appendix, Theory).

Although we restrain only the mean helicity to the true expectation value, the AMMs accurately recover the equilibrium distributions of both the helicity and the fluorescence quenching observables (Fig. 2 B and C) and improve agreement with dynamic observables such as mfpts (Fig. 2 D and E). Thus, when the stationary distribution of the simulation model, $𝝅$, is sufficiently close to the experimental ensemble $\widehat{𝝅}$, using AMMs may not only have improved thermodynamics but also improved kinetics compared with estimates using only simulation data.

Incorporating Experimental Data Increases the Similarity Between Protein Simulations in Different Force Fields.

Next, we estimate MSMs and AMMs of two previously published 1-ms trajectories of the native-state equilibrium fluctuations of ubiquitin, using the CHARMM22* (C22*) (42) and CHARMM-h (C-h) (43) force fields. Previous analyses of these simulations have shown that the stability of certain configurations is overestimated, either due to insufficient sampling or due to minor force-field inaccuracies (42, 43). Both force fields are among the state-of-the-art force fields for folded proteins and thus represent an interesting test case for AMMs. However, they are highly similar, differing only by a term to aid cooperativity of helix formation in C-h (44). Ubiquitin further serves as an ideal test system, as multiple sources of stationary and dynamic experimental data are readily available. These conditions put us in a a great position to thoroughly evaluate the presented methodology.

The simulations are embedded in a joint space of time-lagged independent components (TICs) (11, 45). TICs express slow order parameters in a system as linear combinations of a large number of input features or molecular descriptors. This space is then discretized into 256 nonoverlapping microstates, using $k$-means clustering (SI Appendix, SI Materials and Methods). Transition counts were determined for each trajectory independently and used as input for estimation of MSMs and AMMs. The MSMs were tested for convergence and self-consistency before we proceeded to estimation of AMMs (SI Appendix, Fig. S1). The AMMs used observables from NMR spectroscopy as experimental restraints: ${}^{\text{N}}\text{H}{-}^{\alpha }\text{H}$ ${}^{3}J$ couplings (46) and an extensive set of H–N residual dipolar couplings (RDCs) from 36 different alignment conditions (47–50).

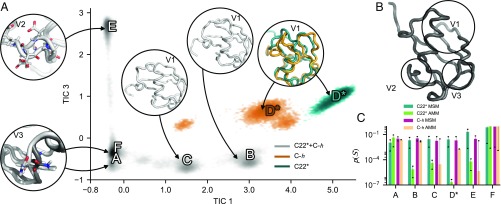
The two MD simulations have significant overlap in their densities in the TIC space. Yet there are regions that are sampled only in the C22* or only in the C-h simulation (Fig. 3A). This observation can be due to either insufficient sampling or the slightly different parameterizations of these force fields: The number of microstates visited in both trajectories is 188 or roughly 73% overlap in terms of states and 96% of the probability mass. We use the Jensen–Shannon divergence ($\mathcal{H}$, subscript and superscript are lower and upper bounds of a 95% CI, respectively) as a measure to compare the equilibrium distributions in microstates visited by both simulations in units of information entropy (nats) (SI Appendix, SI Materials and Methods). For the two MSMs we find $\mathcal{H}={\mathrm{\hspace{0.17em}0.115}}_{0.112}^{0.118}\text{nats}$. In comparison, the corresponding value for the AMMs is ${0.088}_{0.087}^{0.090}\text{nats}$. This result suggests that the AMMs are thermodynamically closer to each other than the corresponding MSMs. Comparing the MSM and the AMM for each of the two force fields reveals that C-h changes little (${0.026}_{0.024}^{0.028}\text{nats}$) compared with C22* (${0.112}_{0.108}^{0.115}\text{nats}$) when experimental data are included. In addition, the correlation times of AMMs are generally also closer to each other than in the corresponding MSMs, suggesting that the AMMs are kinetically closer to each other than the respective MSMs.

Fig. 3.

AMMs reconcile the equilibrium distributions simulated with different force fields. (A) Equilibrium density (log scale) sampled with C22* (teal) and C-h (orange) and both force fields (gray) as a function of the slowest and third-slowest TIC. A, Insets illustrate characteristic structural features in of metastable states $\mathcal{S}$  = A, B, C, D*, E, and F determined using Perron-cluster cluster analysis (41). All but one Inset illustrate more than one metastable state (A and F). In the case of the A/F Inset, F is shown in dark gray and A in light gray. For D* a representative structure from each of the force fields is shown, colored as the equilibrium densities. (B) Viewpoints (V1, V2, and V3) used in Insets shown in A. (C) Comparison of the equilibrium probability ($p(\mathcal{S})$) of metastable states in MSMs and AMMs. Sixty-eight percent CIs are shown as error bars.

AMMs Reconcile Stationary and Dynamic Experimental Data.

The estimated AMMs show an improved agreement with the ${}^{3}J$ coupling and RDC experimental data (SI Appendix, Figs. S2 and S3) used in the estimation process compared with the MSMs estimated from simulation data alone. The improvement in RDCs for the C-h AMM may seem insignificant when judged by the Q factor only; however, a detailed inspection of the most strongly enforced experimental data restraints (largest $|{\lambda }_v|$) reveals substantial changes in localized residues (SI Appendix, Fig. S4). The predicted ensemble averages of complementary data including cross-correlated relaxation (CCR) (51) and exact nuclear Overhauser enhancements (eNOEs) (52) show an on par agreement compared with their corresponding MSMs (SI Appendix, Table S2). This suggests that these experimental observables are largely insensitive to the changes in the equilibrium distributions in the AMMs relative to those in the MSMs and that we are not overrestraining when estimating the AMMs. Nevertheless the predictions of these experimental observables given by the MSMs and AMMs agree fairly well with their experimental values.

The slowest correlation times (${\tau }_1,\mathrm{\dots },{\tau }_4$) of both AMMs are significantly faster than in the corresponding MSMs estimated from simulation alone (SI Appendix, Table S2). Dielectric relaxation spectroscopy data of ubiquitin has identified a process with a timescale in the fast microsecond range (53), which indicates that the AMMs may be giving a more realistic kinetic description compared with the corresponding MSMs, although no kinetic data were used in the model generation.

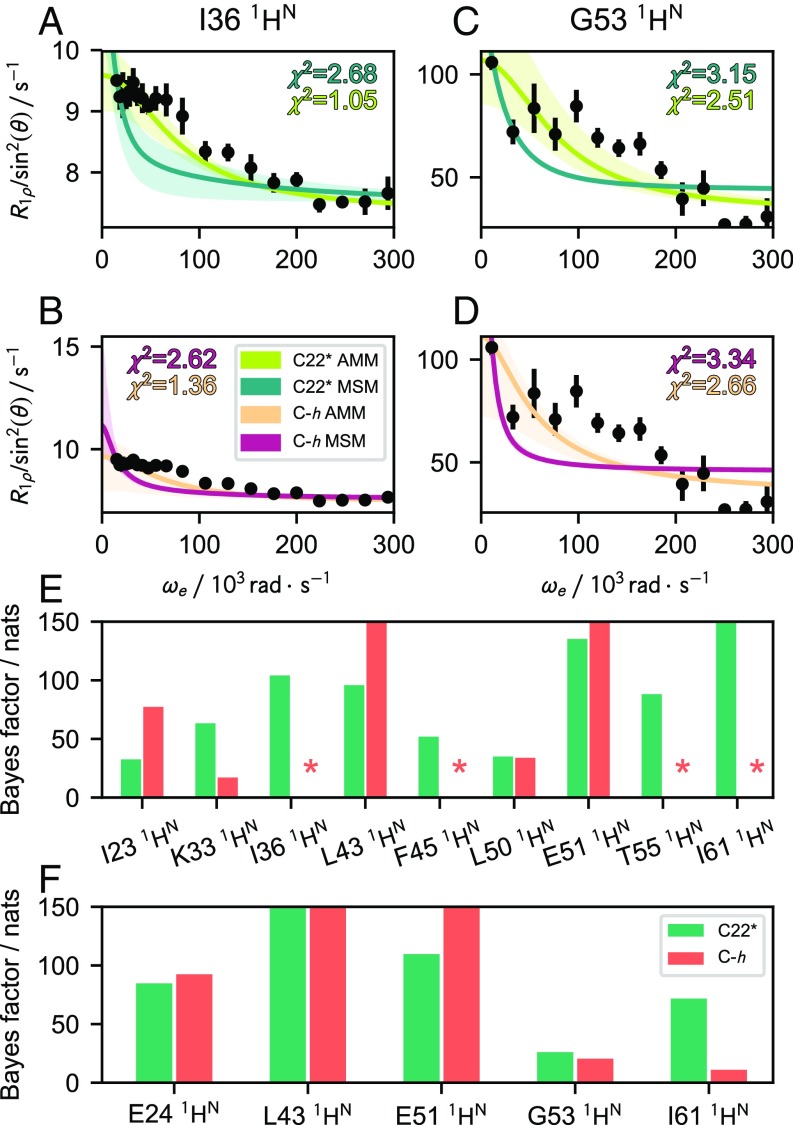
This finding prompted us to analyze the molecular kinetics of the AMMs and MSMs more quantitatively by comparing predictions of NMR spin-relaxation data (14) with recently reported experimental measurements (54). These data are sensitive to the correlation times of conformational transitions, the structures of the metastable configurations involved in the transitions, and their relative populations (55). As the data are resolved at the single-spin level, they provide a direct means to validate the altered dynamics seen in the AMMs at atomic resolution. We compare with data recorded at 292 K and 308 K (54) (SI Appendix, Figs. S5 and S6), both fairly close to the simulation temperature of 300 K. It is apparent that the AMMs improve the overall agreement with these data compared with the MSMs. We quantify this impression by computing ${\chi }^2$ values and Bayes factors—the latter testing whether the AMMs were significantly better than the corresponding MSMs within the model uncertainty. As an example, if the integrated posterior probability of a model is 100-fold larger than a competing model, the Bayes factor is 4.6 nats (Fig. 4 E and F and SI Appendix, SI Materials and Methods). AMMs have dramatically improved ${\chi }^2$ values compared with the MSMs in both the C-h (Fig. 4 B and D and SI Appendix, Fig. S5) and C22* (Fig. 4 A and C and SI Appendix, Fig. S6) force fields, although many ${\chi }^2$ values remain large. The Bayes factors also favor the AMMs, although four datasets at 292 K either favor the MSM or do not strongly support the AMM, when taken in isolation (Fig. 4 E and F). Still, as these improvements correlate with improved agreement with stationary experimental observables (RDCs and ${}^{3}J$ couplings), it suggests that estimation of AMMs may be a powerful way to mutually reconcile stationary and dynamic experimental observables with simulation data.

Fig. 4.

Comparison of $R_{1\rho }$ relaxation dispersion predicted from MSMs and AMMs (14) with experiments at 292 K and 308 K (54). (A and B) Representative spin-relaxation profiles from $R_{1\rho }$ of I36 ${}^1\text{H}^{\mathrm{N}}$ at 292 K of AMMs and MSMs in C22* (A) and C-h (B). (C and D) Representative spin-relaxation profiles from $R_{1\rho }$ of G53 ${}^1\text{H}^{\mathrm{N}}$ at 308 K of AMMs and MSMs in C22* (C) and C-h (D). Shaded area corresponds to a 95% CI. (E and F) Improvement of AMMs relative to MSMs in reproducing $R_{1\rho }$ spin-relaxation data at 292 K (E) and 308 K (F), measured by Bayes factors. y axes in E and F are truncated at (0, 150) for clarity. An asterisk (*) is shown for datasets where the AMM is not significantly better than the MSM (less than 4.6 nats).

Microscopic Differences in MSMs and AMMs.

Above we noted how integration of experimental data into the Markov model estimation procedure results in more similar models, compared with models trained on simulation data only. The latter observation opens the question of whether the underlying microscopic changes of the model also become more similar. To this end, we coarse grained the MSMs and AMMs into six metastable states, corresponding to density peaks in the equilibrium distribution (Fig. 3A). Five of these states consist of very similar molecular structures that overlap in the TIC projection between the two force fields. The F state is by far the most thermodynamically stable of these and closely resembles the configuration identified by X-ray and NMR structure determination. Metastable state A is very similar to F, but has a different backbone configuration in residues 58–62. The E state differs in its propensity to flip the configuration of residues 50–55. In states C and B one and two turns of the central $\alpha$-helix (residues 23–34) are unwound from the C-terminal end, respectively. Both of these states have an increased flexibility in the C-terminal loop following the helix. The D* states are distinct in the two force fields: K33 persistently interacts with solvent-exposed carbonyl oxygens in residues A28 and K29; this interaction is found in both force fields, yet the backbone configurations in residues 34–40 differ.

The probabilities of most of the metastable states change considerably in the AMMs relative to the corresponding MSMs (Fig. 3C). The combined population of the native-like states F and A increases in both cases, whereas the populations of all other metastable states are significantly reduced in the AMMs relative to the MSMs. This result mirrors the findings in SI Appendix, Fig. S4: The RDCs enforced the strongest in the AMMs are localized to residues 10–12, 30–40, and 45–55, which roughly correlates with the structural differences between states A and F and all of the others states. This illustrates how the same experimental restraints enforced in AMMs of different force fields roughly translate into consistent microscopic changes in the inferred AMMs, compared with their corresponding MSMs.

Conclusion

We present a method to combine simulation data generated using an empirical force field with unknown systematic errors and averaged, noisy, experimental data into kinetic models of molecular dynamics: AMMs. We show how this approach can accurately recover thermodynamics and kinetics in a protein-folding model subject to varying degrees of systematic error. In addition, we find the method improves the accuracy of models derived from atomistic molecular dynamics simulations. In particular, when including experimental data via AMMs, both thermodynamics and kinetics extracted from simulation data using two different molecular mechanics force fields become more alike, and their agreement with complementary experimental data, both stationary and dynamic, improves.

The presented method makes it possible to preserve dynamic information following integration of stationary experimental data. This account shows how the integration of stationary experimental data in such a framework may also improve the prediction of complementary dynamic observables. These two results open up the possibility of establishing more elaborate models for integrative structural biology where full thermodynamic and kinetic descriptions may be obtained. Future developments may allow for the integration of dynamic observables, such as relaxation rates or correlation functions, into AMMs by adopting a maximum caliber functional (56) or Bayesian methods (33, 34) to account for the systematic errors in these quantities.

Materials and Methods

Protein-Folding Model System.

Seven eight-state Markov models were constructed for the different free-energy potentials $F_i(\cdot )=Ui(S)-T\cdot S(S)$ (SI Appendix, Table S1). For each one, transition probabilities were obtained using kinetic Monte Carlo by row normalization of a matrix with ${\stackrel{\sim }{p}}_{ij}\propto {\mathrm{\Gamma }}_{i,j}\exp \left(-\beta [F(j)-F(i)]\right)$. The values ${\mathrm{\Gamma }}_{i,j}$ encode the topology shown in Fig. 2A, $\beta ={(kT)}^{-1}$, where k is Boltzmann’s constant and $T=\mathrm{\hspace{0.17em}300}\text{K}$ is the temperature. Further details on estimation, simulation, and analysis are given in SI Appendix, SI Materials and Methods.

AMMs and MSMs of Ubiquitin.

Estimation and validation were carried as outlined in Results above; further details are given in SI Appendix, SI Materials and Methods. Uncertainties were estimated using a Bayesian scheme (SI Appendix, Theory), and AMMs and MSMs were compared using Bayes factors and the Jensen–Shannon divergence (SI Appendix, SI Materials and Methods).