Abstract
We present a close electronic view of the protein–base interface for the N-terminal domain of the human protein U1A. Combining accurate mixed quantum mechanics/molecular mechanics techniques and protein structure prediction methods, we provide a detailed electronic structure description of the protein–RNA stacking interactions. Our analysis indicates the evolution of the protein structure optimizing the interaction between Asp-92 and the RNA bases. The results show a direct coupling of the C-terminal tail and Asp-92, providing a direct rationalization of the experimentally determined role of the C-terminal domain in RNA binding. Here, we propose a mechanism where a protein side chain, with a delocalized electronic pi system, assists in the nucleotide binding. The binding mechanism involves a short-range interaction of the side chain with the nucleotide base and an electronic long-range interaction through a sandwich-stacking motif. The structural motif of the binding mechanism is observed in similar protein–RNA interactions and in various protein-ATP-binding sites.
Keywords: ATP binding, quantum mechanics/molecular mechanics, stacking, aromatic
The mechanisms of protein-nucleotide association constitute a central intermolecular interaction. Such mechanisms, for example, regulate DNA, RNA, and NTP recognition and binding. As pointed out recently by Williamson (1), there is a large complexity of induced fit processes, requiring conformational change in the proteins, in the ligands, or in both. These dynamical processes, responsible for the induced affinity and specificity, are far from being understood. A common feature in ssDNA, RNA, and NTP binding is the direct interaction of the protein with the nucleotides' bases. Recent structural analyses have underlined the main features involved in these protein–base interactions (2, 3). These studies revealed the importance of van der Waal interactions, aromatic stacking interactions in particular, in the stabilization of the protein–base interaction.
The ribonucleoprotein domain, also known as the RNA-binding domain or the RNA-recognition motif, binds RNA by using extensive interactions through its characteristic four-stranded β-sheet structure (Fig. 1). Among the members of this motif, the N-terminal domain of the human protein U1A is the most studied (4–29). The isolated domain binds to a short RNA hairpin with high affinity and specificity. The importance of stacking interactions in RNA binding is confirmed by the aromatic nature of three of the most highly conserved residues in the RNA-recognition motif (30). Baranger and coworkers (11) recently obtained 5.5 kcal/mol destabilization of the protein–RNA complex when mutating Phe-56 to alanine. Subsequent studies by the same group indicated that stacking (hydrophobic) interactions are able to compensate for the loss of hydrogen-bonding-capable functional groups in the RNA bases (5). Recent kinetic data by Laird-Offringa and coworkers (6) supported a rapid initial association based on electrostatic interactions, followed by a subsequent locking step based on close-range interactions, proposing the stacking of Phe-56 with the base A11 as a possible source for the locking mechanism.
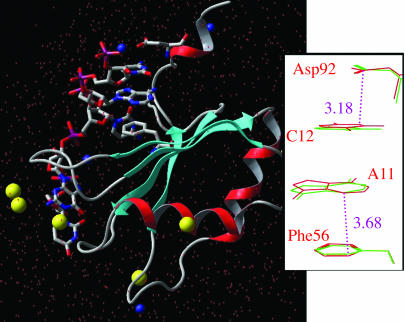
Fig. 1.
QM/MM model for the U1A protein–RNA interaction. The total system includes the full protein, bases from U8 to C12, a 14-Å sphere of solvated water, six Cl anions (yellow space fill) and four Na cations (blue space fill). The quantum region (in a stick representation) includes all bases, Phe-56, and Asp-92, for a total of 225 QM atoms. The system was minimized with the B3LYP DFT functional by using 6-31G* for Asp-92, C12, A11, and Phe-56, and for the remainder, we used 6-31G. The MM part uses the OPLS-AA MM force field. All oxygen atoms in the last2Åofthe solvent sphere were kept fixed. (Right) Shown is a magnified version of the Asp-92, C12, A11, and Phe-56 sandwich. The QM mechanical main distances for the Asp-92-C12 and Phe-56-A11 interactions are in Angstroms. A more detailed description of the methods and references to them can be found in a recent study on triosephosphate isomerase (38).
In the U1A-RNA-bound crystal (21) and NMR (8) structures, Asp-92, C12, A11, and Phe-56 are involved in a very interesting quadruple stacking sandwich, shown in Fig. 1. The aspartic residue links the protein–RNA interface with the C-terminal domain. The C-terminal tail has been the subject of several studies, indicating its importance for RNA binding stability and specificity (12, 14, 18, 22, 25–27). With a systematic truncation of the C-terminal tail, Hall (22) demonstrated a loss of 2 kcal/mol of binding free energy when terminating the C-terminal at the position 95. Subsequent deletion of more residues, including Asp-92 and Ile-93, which are involved in a direct interaction with the RNA, did not introduce further significant loss in affinity. Mutation of Lys-96 with alanine introduced only 0.7 kcal/mol difference in the binding free energy (14). Varani et al. (8) have recently shown that the C-terminal tail regulates the binding cooperativity of two U1A monomers with an RNA-regulatory region.
By using mixed quantum mechanics/molecular mechanics (QM/MM) methods combined with protein structure prediction algorithms, we are able to correlate the C-terminal tail truncation with Asp-92 dynamics and RNA binding. In the course of the study, we have identified a protein nucleotide-binding mechanism not only present in protein–RNA complexes but also in other biochemical systems. The mechanism involves a sandwich motif, as the one observed in Fig. 1, where the nucleotides' base(s) is/are trapped between an electronic delocalized conjugate group, such as ones found in the side chains of Glu, Asp, Arg, Gln, and Asn, and an aromatic group (mainly Tyr and Phe). The mechanism presents a short- and long-range component. The short-range component could be understood as a classical stacking interaction between the delocalized conjugate and the base. Meanwhile, the long-range component could be viewed, analogous to a DNA-charge transport, as the result of electronic resonance through a series of planar stacking, providing evidence for an electronic long-range interaction. This study constitutes the first close look, to our knowledge, at the electronic structure of the protein-RNA-recognition motif.
Methods
The present development of QM/MM techniques allows us to treat the protein–RNA interface at a high level of quantum theory, while describing the entire protein and solvation at a classical level. All QM/MM and QM calculations are carried out with the Schrödinger suite of programs (31, 32). The QM/MM system includes the U1A protein plus the bases U8, G9, C10, A11, and C12 from the crystallographic structure [Protein Data Bank (PDB) ID code 1URN] (21). The system is initially solvated in a box (with 15-Å minimum distance from the box edges to the protein/RNA surface) of simple point charge water molecules with six chlorine anions and four sodium cations. The solvent, hydrogen atoms, and missing side chains were initially equilibrated by a 40-ps molecular dynamics run at 300 K using periodic boundary conditions. The final QM/MM system is obtained by keeping all water molecules within 14 Å from any protein/RNA atom. The QM region includes all bases, Phe-56, and Asp-92, for a total of 225 QM atoms. The system was minimized with the B3LYP density functional (DFT) and the OPLS-AA MM force field (see the Fig. 1 legend for a more detailed description).
All protein conformational sampling is carried out with plop (33, 34), a program for protein modeling using all-atom energy functions and a surface generalized Born continuum solvation model. plop includes algorithms for multiscale truncated Newton minimization, side-chain optimization, and loop prediction.
Results and Discussion
Fig. 1 shows the optimized QM/MM structure. The all-heavy-atom rms deviation yields a difference of only 0.52 Å between both the experimental and the theoretical results. Fig. 1 Right indicates a detailed view of the interaction between Asp-92, C12, A11, and Phe-56, comparing the QM/MM-optimized results (red wire frame) with the initial crystal structure (green wire frame). Under the effects of the protein environment, a QM refinement of the RNA–protein interface clearly tightens the interaction between Asp-92 and C12. The C(Asp-92)-N(C12) distance (see also Fig. 2) decreases from an experimental value of 3.50 Å to a value of 3.18 Å. As seen in Fig. 1, the carboxylic group of the aspartic side chain slightly rotates, adopting a planar-stacking orientation with respect to the cytosine plane. The other protein–RNA contact in this particular sandwich, involving A11 and Phe-56, presents only minor differences when comparing the experimental and theoretical results, 3.64 and 3.68 Å, respectively. Thus, from the analysis of the crystal structure and the QM/MM refinement, the contact of Asp-92 with C12 appears to be a significantly strong interaction.
Fig. 2.
Energy associated with the Asp-92 side-chain dihedral from a QM-reduced system obtained directly from the QM/MM-minimized structure (Left; see Fig. 4 for a better view of the dihedral motion). The reduced system included all Asp-92 and the base of C12. The dihedral reaction coordinate has been studied by using 6-311+G* basis set and three different levels of QM theory: HF, DFT, and MP2. (Right Upper) Detail of the closed conformation showing stacking distances in angstroms. (Right Lower) The gas phase and QM/MM atomic charges for the main atomic interactions are shown. The charges, obtained by fitting to the quantum electrostatic potential surface, correspond to the closed conformation.
Short-Range Interactions. To understand and estimate the stabilization associated with Asp-92 stacking, we proceeded by building a small gas-phase model extracted directly from the QM/MM-minimized geometry. From this reduced model, a reaction coordinate along the aspartic dihedral side chain angle was built. The energy profile of this rotation is introduced in Fig. 2 Left. The rotation evolves the system from a closed configuration, where the aspartic side chain is parallel to the cytosine base pair (as seen in Figs. 1 and 2), to an open configuration, where the aspartic side chain is mainly exposed to the solvent in a perpendicular orientation with respect to the base pair. The closed conformation has a dihedral value of ≈60°, whereas the open state is located around dihedral values of 150°. As discussed below, the open and closed conformations are the two main energetically available states for the Asp-92 side chain.
As seen in Fig. 2, the energy profiles clearly indicate the presence of an energy minimum for the closed conformation, ≈2–3 kcal/mol. The energy stabilization is in good agreement at three different levels of quantum chemistry theory: Hartree–Fock (HF), DFT, and Møller–Plesset perturbation theory (MP2). Different studies have demonstrated the necessity of high-order electronic correlation quantum chemistry methods to describe the London dispersion energies responsible for the stacking stabilization in pyrimidine and benzene gas-phase dimer models (35–37). From the three quantum chemistry methods shown in Fig. 2, only the last one, MP2, could describe such stabilization, with HF and DFT having large qualitative differences. The semiquantitative agreement between the different methods shown in Fig. 2 indicates the electrostatic nature of this energy stabilization. The geometry and atomic charge analysis confirm this observation. There is a clear superposition of the three aspartates' carboxylic atoms on top of three particular cytosine atoms. This alignment introduces three complementary electrostatic interactions, as pointed out by the atomic charges on the table embedded in Fig. 2. The electrostatic alignment is reproduced both for the QM/MM scenario, where all of the protein (and solvent) is taken into account, and in the gas-phase environment, where the aspartic side chain and the cytosine base pair have been extracted from the QM/MM geometry. Furthermore, the analysis of the atomic charges along the dihedral reaction coordinate reveals a polarization of the carboxylate atoms, and, to a lesser degree, of the cytosine base pair, which increases the charge separation and enhances the electrostatic stabilization for the stacked closed conformation. By using a fixed-charge force field (2001OPLS-AA), the energy profile in Fig. 2 does not present any minima for the closed state, the potential exponentially decreasing toward the open state.
The reference energy (0 value) in the Fig. 2 energy profile is taken from the sum of both isolated moieties, which is equivalent to an infinite distance between the aspartic and cytosine. This result indicates that the stacking of the two molecules does not introduce any stabilization with respect to the isolated species. Thus, it appears as if the restricted motion of Asp-92 in the protein-RNA frame has been optimized to introduce a local stabilization.
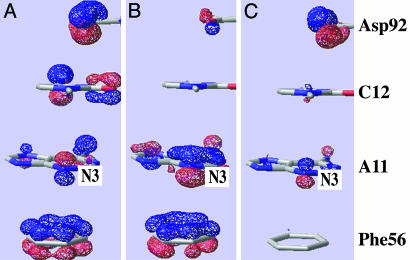
Long-Range Interaction. The analysis of the molecular orbitals for the minimized QM/MM structure revealed a possible long-range interaction within the protein–RNA sandwich. As seen in Fig. 3, some of the π-density molecular orbitals are delocalized among the different stacking elements of the protein–RNA interface. We want to emphasize that the molecular orbitals are obtained, considering the entire protein, 6 RNA bases, and an explicit water solvation box, for a total of 7,000 atoms with 225 atoms in the QM region. In particular, the orbital analysis indicates a large mixing of the aspartic conjugate π system with the adenosine and phenyl aromatic orbitals.
Fig. 3.
Occupied molecular orbitals involving π electronic density of Asp-92, C12, A11, and Phe-56. See text for more information concerning A–C.
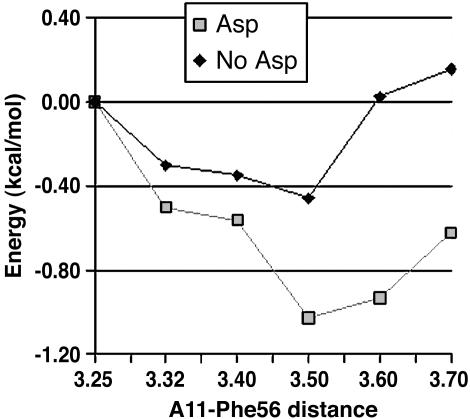
To test the possible long-range interactions, we proceeded by building a small quantum model, including the side chains of Asp-92 and Phe-56 and the bases of C12 and A11. The initial orbital analysis of such a reduced QM model has the aspartic π orbitals significant higher in energy than in the real QM/MM system. Thus, the partially solvated environment of the aspartic has stabilized its π orbitals to a resonance level with the aromatic orbitals of the other stacking moieties. To mimic this particular environment, we placed a sodium atom next to the aspartic side chain. At a distance of 2.79 Å from the carboxylic carbon in the bisection of the OCO angle, the QM/MM orbital delocalization is exactly reproduced. The stacking energy profile of A11-Phe-56 was then obtained in the presence and in the absence of the aspartic residue. The study involved MP2 (triple-ζ basis set) single-point calculations at the QM/MM geometries where the A11-Phe-56 distance was increased. Thus, the C12, A11, and Asp-92 (if applicable) are held fixed and only the phenyl side chain is displaced. Because the adenosine N3 lays almost on top of the center of the phenyl ring in both the experimental and QM/MM-minimized structures, this distance was chosen to increase and reduce the A11-Phe-56 reaction coordinate. As seen in Fig. 4, the energy profile clearly indicates that the presence of the aspartic residue (a mimic for the closed state in the protein) enhances the stacking between the two distant stacking moieties. Contrary to the short-range interaction exposed above, and in agreement with previous studies on aromatic stacking (36, 37), the energy profiles were qualitatively different for the different levels of quantum theory used. HF and DFT methods gave dissociative energy profiles, requiring an MP2 level of theory to reproduce a binding energy profile. Both HF and DFT gave no difference in the dissociative energy profile in presence/absence of Asp-92. Thus, the long-range interaction seems to be the result of perturbations on the electronic density affecting mainly the dispersion forces between the aromatic stacked moieties. As in the short-range interaction, a fixed-charge force field (2001OPLS) does not capture any difference in the A11-Phe-56 stacking with the presence/absence of Asp-92.
Fig. 4.
A11-Phe-56 binding-energy profile in the presence and absence of Asp-92. The energies were obtained with single-point MP2 calculations by using 6-311+G* [similar qualitative energy profiles were obtained with the 6-31G* and the cc-pvtz(-f) basis sets]. The distance of the adenine N3 to the Phe-56 ring center was used as the reaction coordinate, and the point at a distance of 3.25 Å was used as the energy reference.
Hence, it appears as if U1A has not only constrained the motion on Asp-92 to introduce a local stabilization in the interaction with C12 but has also exquisitely optimized its environment to adjust the carboxylic conjugate π orbitals to an energy level in resonance with the π orbitals of C12, A11, and Phe-56. Whereas recent calculations do not support the interpretation of stacking interaction based on molecular orbital theory (36), the orbital analysis in Fig. 3 suggests a qualitative explanation for the tighter A11-Phe-56 binding in presence of Asp-92. Fig. 3 A and B constitute a pair of bonding and antibonding molecular orbitals between the symmetric phenyl π 1 aromatic orbital and the adenosine N3 pz orbital. In the presence of Asp-92, the carboxylic π system mixes with the N3 pz orbital and decreases its contribution to the antibonding interaction between A11 and Phe-56. This interaction is shown in Fig. 3C, a molecular orbital contiguous to the antibonding orbital shown in Fig. 3B. In the open state, Asp-92 does not mix with N3 and the orbitals in Fig. 3 B and C are far apart and split into a pure antibonding system (with a larger N3 contribution) and a pure carboxylic π system. We have analyzed other similar motifs, described below, and found very similar molecular orbital interactions.
Correlation Between the C-Terminal Tail and Asp-92. The results presented indicate an active role of Asp-92 in stabilizing the protein–RNA binding by a direct interaction with C12 and by enhancing the Phe-56-A11 stacking. These stabilizations require Asp-92 to be in a closed conformation, where the carboxylate group of the aspartic residue stacks on top of the cytosine base pair. All of our attempts to sample Asp-92 resulted in only two main groups of conformations, corresponding to the open and closed state, being energetically accessible (we limited the exploration to a 20-kcal/mol window). The sampling was performed with a loop-sampling algorithm including Ser-91 and Leu-93, following the same protocol recently used in the loop sampling of triosephosphate isomerase (38). Recent NMR structures agree with the presence of only two main groups of Asp-92 side-chain conformations, corresponding to an open and a closed state (see, for example, figure 3a in ref. 17).
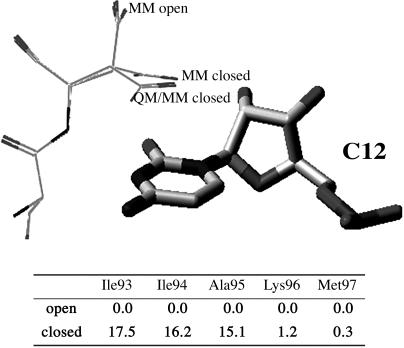
To explore the effects of the C-terminal tail on Asp-92, we have performed a series of conformational sampling where we systematically truncate the C-terminal tail, in a fashion similar to the experimental work by Hall (22). The results (Fig. 5) clearly indicate a large dependence of Asp-92 open/closed conformations on the length of the tail. Truncation below Lys-96 results in an open state largely more stable than the closed conformation. Fig. 5 also compares the open and closed conformations obtained by the protein-structure sampling, MM open and MM closed, with the QM/MM-minimized structure, QM/MM closed. We should keep in mind that this conformational sampling is based on a fixed atomic-charge force field, incapable of describing the electrostatic polarization observed on Asp-92-C12 stacking. This deficiency in the sampling is responsible for the differences observed in Fig. 5 between the MM closed and QM/MM closed conformations, the MM closed state resembling largely the crystal structure. Accordingly, we should correct the open/closed energy differences with ≈2–3 kcal/mol in favor of the closed state. Even with this correction, the population of the closed conformation is negligible when truncating below Lys-96. Furthermore, the sampling algorithms find substantially more open conformations when truncating the C-terminal chain below Lys-96. Thus, entropic contributions would further stabilize the open conformation. When considering the full C-terminal tail, there are only two main states accessible and one would expect only entropic solvent corrections that are included in our sampling algorithms by means of a continuum-solvent model. Hence, for those systems terminating in Ala-95 or below, Asp-92 is predominantly in an open state with the loss of its RNA-binding stabilization.
Fig. 5.
Example for the sampled Asp-92 open and closed conformations. (Upper) The sampled conformations are also compared with the QM/MM-optimized closed state. (Lower) Shown is the energy difference between the open and closed conformation for different levels of C terminus truncation. Protein sampling was performed with plop (33) and by using the QM/MM charges for the RNA fragment. Energy differences are in kcal/mol.
The addition of Lys-96 introduces an abrupt change in the stability of the open/closed conformations. The key component of this large energy change is the presence of the helix backbone hydrogen bond between Asp-92 and Lys-96. The open conformation introduces a strain in the backbone of Asp-92, which causes the hydrogen bond to increase in length significantly from 1.85 Å for the closed conformation to 3.21 Å for the open conformation. Thus, the presence of Lys-96, and following residues in the C-terminal tail, introduces an ordered α-helical structure stabilizing a closed conformation for Asp-92, which enhances the binding of the RNA. These results permit a straightforward rationalization of the different experimental results. They provide an explanation for the small experimental differences in the binding energy when truncating at residues 94, 93, and 92. Eliminating Asp-92 in a truncated tail (below Lys-96) does not introduce any further destabilization because Asp-92 is not in contact with the RNA bases. The nature of the closed conformation stabilization, a helix backbone hydrogen bond, explains the minor difference when mutating Lys-96 to alanine. When we substitute lysine with an alanine, we observe only a small change in the hydrogen bond, now 2.1 Å for the L96A-mutated species.
A key implication of these results is the possible role of the C-terminal in controlling the locking/unlocking mechanism proposed by Laird-Offringa and coworkers (6). The C-terminal domain could act as a signal receptor, activating the release of the RNA. As pointed out in the introduction, Varani et al. (8) have associated the cooperativity of two U1A proteins with contacts between the C-terminal tails. Furthermore, recent mutational and kinetic studies of RNA binding (I. A. Laird-Offringa, personal communication) support the notion that the quadruple stack is the last step in the RNA-binding mechanism, the locking step.
Analogous Protein-Base-Binding Motifs. Similar motifs can be found in many protein–RNA interactions. For example, a stack structure involving Arg-195, U6, and Tyr-131 is observed in the Sex-lethal protein of Drosophila melanogaster, PDB ID code 1B7F (39). Beside other protein-RNA structures, we find other biochemical binding processes with comparable protein-base sandwich motifs. A particularly interesting example is the role of arginines in different ATP-binding sites. Thornton and coworkers (2) have recently studied the molecular recognition and discrimination of guanine and adenine by means of empirical observations on high-resolution nonhomologous crystal structures. They observed that arginines often have their side chain stacked on top of the adenine (and not guanine), with no direct hydrogen bond between the two moieties. Recently, by using ab initio MP2 calculations, Biot et al. (40) and Mao et al. (41) have studied the stacking of arginine and adenine and analyze it in terms of cation-π interactions. Several ATP-dependent DNA helicases present a clear example of such sandwich structures between an arginine residue, the adenosine base, and a tyrosine aromatic side chain. Our results (K.W.B. and V.G., unpublished work) indicate that the arginine has a similar role to that of Asp-92 in U1A. Fig. 6 Left indicates the electrostatic alignment for the optimized QM/MM structure for RecQ (PDB ID code 1OYY) (42), a family of ATP-dependent helicases that is highly conserved from bacteria to humans. The alignment involves four nitrogens (negatively charged) and four hydrogens (positively charged). As in U1A, the short-range stacked-energy profile has a large electrostatic component. Interestingly, both U1A and RecQ present similar stacking geometries between the adenine base and the aromatic side chain, with the N3 atom lying on top of the center of the aromatic ring. In RecQ, the presence of the arginine induces a tighter binding (stacking) between the base and the tyrosine side chain, indicating the presence of long-range interactions as in the U1A quadruple stacking. The molecular orbital analysis, in Fig. 6 Right, indicates a mixing of the arginine π system with the base N3 pz orbital, which is analogous to U1A molecular orbitals.
Fig. 6.
Arginine/adenine short-range charge superposition (Left) and occupied molecular orbital illustrating the adenine and arginine π mixing (Right).
Sampling of the arginine side chain reveals an open conformation, more exposed to solution and facilitating the nucleotide entry and escape, in addition to the planar-stacked closed conformation. Our preliminary data indicate that the arginine responds to the different ATP and ADP dipole moments: ATP enhances the planar-stack structure by increasing the short-range electrostatic interaction, whereas ADP favors (with respect to ATP) the open conformation. Thus, the capping residue could be an important part of the specificity for ATP versus ADP.
Similar structures are also found with different capping residues. Amino-π interactions, where an amino side-chain stack on top of an aromatic group, have been shown to be favored in protein–protein interactions and in protein–base interactions (40, 43, 44). Gln 218, for example, presents a similar structure to the RecQ arginine in the hexameric ATPase P4 of dsRNA bacteriophage phi12 (45). A common feature in all these planar-stack capping residues is the presence of a delocalized π system capable of mixing with the nucleotide. The capping residues are partly exposed to solution that facilitates conformational changes between an open and closed state.
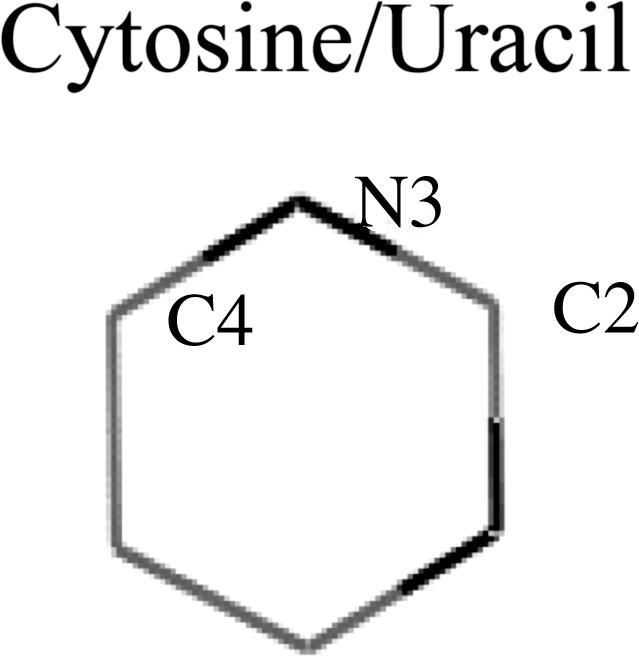
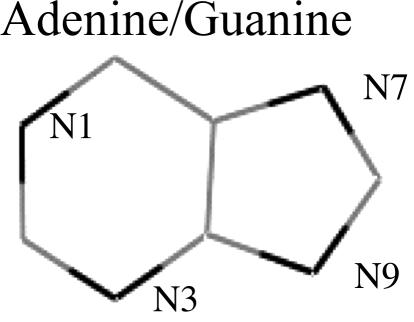
Specificity. An important aspect of the binding mechanism we propose here is the possible implications in specificity. Mutation of C12 introduces an ≈2 kcal/mol loss in binding affinity (22). Umezu et al. (23) observed that purified RecQ protein exhibited ATPase but no GTPase activity. Table 1 indicates the gas-phase atomic charges (electrostatic potential charges) for cytosine, uracil, adenine, and guanine. Table 1 shows the charge we used to calculate, with B3LYP, the DFT level by using the 6–311+G basis set and the charges directly obtained from the amber8 force field. The electrostatic alignment described here, in conjunction with the atomic charges in Table 1, indicate a substantially stronger short-range interaction for cytosine and adenine when compared with uracil and guanine. The increase in electrostatic interaction is observed when comparing the electrostatic alignment (using Fig. 2 or six schemes) for both our charges and the amber force field charges. This mechanism permits a straightforward explanation for the empirical observations of Thornton and coworkers (2): the large affinity for adenine versus guanine in the arginine stack structures. In the Asp-92-C12 case, for example, mutation of the cytosine could not only disrupt the binding stabilization but could also introduce some destabilization in the Asp-92/C-terminal interaction by forcing a different aspartic conformation.
Table 1. Electrostatic potential atomic charges for the main atoms involved in the short-range charge superposition.
The top two rows indicate our calculated gas-phase charges by using the B3LYP and 6-311+G* basis set. The bottom two rows are the amber8 force field charges (one of the most widely used force fields for DNA and RNA simulations).
In summary, we propose a mechanism for the binding of nucleotide bases. The protein traps the base by means of a sandwich with an aromatic side chain and a mobile capping residue with a small conjugated π system. The mechanism includes a short-range electrostatic stacking between the capping residue and a long-range electronic interaction through the sandwich motif. The present study provides a qualitative analysis of these interactions obtained by combining QM/MM techniques with QM model systems. Future studies will focus on a quantitative description of the binding mechanism, which is a difficult task because of the complexity of the systems and of their interactions. Of particular interest will be the possibilities of second-generation polarizable force fields in describing the binding mechanism. The presence of long-range electronic interactions, however, indicates the necessity of describing a many-body polarization effect, a non-trivial task. We have focused on the interaction of U1A with an RNA hairpin. The results, constituting a close look at the electronic structure of a real-sized model for a protein–RNA interaction, permit a straightforward rationalization of several experimental observations involving the role of the C-terminal domain in RNA binding.
Acknowledgments
We thank Professor Kathleen Hall for very helpful discussions. This work was supported by the startup funds from Washington University (St. Louis).
Author contributions: V.G. designed research; V.G. and K.W.B. performed research; V.G. and K.W.B. analyzed data; and V.G. wrote the paper.
Abbreviations: QM/MM, quantum mechanics/molecular mechanics; HF, Hartree–Fock; DFT, density functional; MP2, Møller–Plesset perturbation theory.
References
- 1.Williamson, J. R. (2000) Nat. Struct. Biol. 7, 834–837. [DOI] [PubMed] [Google Scholar]
- 2.Nobeli, I., Laskowski, R. A., Valdar, W. S. J. & Thornton, J. M. (2001) Nucleic Acids Res. 29, 4294–4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jones, S., Daley, D. T. A., Luscombe, N. M., Berman, H. M. & Thornton, J. M. (2001) Nucleic Acids Res. 29, 943–954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Showalter, S. A. & Hall, K. B. (2004) J. Mol. Biol. 335, 465–480. [DOI] [PubMed] [Google Scholar]
- 5.Tuite, J. B., Shiels, J. C. & Baranger, A. M. (2002) Nucleic Acids Res. 30, 5269–5275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Katsamba, P. S., Myszka, D. G. & Laird-Offringa, I. A. (2001) J. Biol. Chem. 276, 21476–21481. [DOI] [PubMed] [Google Scholar]
- 7.Blakaj, D. M., McConnell, K. J., Beveridge, D. L. & Baranger, A. M. (2001) J. Am. Chem. Soc. 123, 2548–2551. [DOI] [PubMed] [Google Scholar]
- 8.Varani, L., Gunderson, S. I., Mattaj, I. W., Kay, L. E., Neuhaus, D. & Varani, G. (2000) Nat. Struct. Biol. 7, 329–335. [DOI] [PubMed] [Google Scholar]
- 9.Mittermaier, A., Varani, L., Muhandiram, D. R., Kay, L. E. & Varani, G. (2000) J. Mol. Biol. 298, 163–163. [DOI] [PubMed] [Google Scholar]
- 10.Tang, Y. & Nilsson, L. (1999) Biophys. J. 77, 1284–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nolan, S. J., Shiels, J. C., Tuite, J. B., Cecere, K. L. & Baranger, A. M. (1999) J. Am. Chem. Soc. 121, 8951–8952. [Google Scholar]
- 12.Mittermaier, A., Varani, L., Muhandiram, D. R., Kay, L. E. & Varani, G. (1999) J. Mol. Biol. 294, 967–979. [DOI] [PubMed] [Google Scholar]
- 13.Kranz, J. K. & Hall, K. B. (1999) J. Mol. Biol. 285, 215–231. [DOI] [PubMed] [Google Scholar]
- 14.Kranz, J. K. & Hall, K. B. (1998) J. Mol. Biol. 275, 465–481. [DOI] [PubMed] [Google Scholar]
- 15.Howe, P. W. A., Allain, F. H. T., Varani, G. & Neuhaus, D. (1998) J. Biomol. NMR 11, 59–84. [DOI] [PubMed] [Google Scholar]
- 16.Zeng, Q. Y. & Hall, K. B. (1997) RNA 3, 303–314. [PMC free article] [PubMed] [Google Scholar]
- 17.Allain, F. H. T., Howe, P. W. A., Neuhaus, D. & Varani, G. (1997) EMBO J. 16, 5764–5774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kranz, J. K., Lu, J. R. & Hall, K. B. (1996) Protein Sci. 5, 1567–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Avis, J. M., Allain, F. H. T., Howe, P. W. A., Varani, G., Nagai, K. & Neuhaus, D. (1996) J. Mol. Biol. 257, 398–411. [DOI] [PubMed] [Google Scholar]
- 20.Stump, W. T. & Hall, K. B. (1995) RNA 1, 55–63. [PMC free article] [PubMed] [Google Scholar]
- 21.Oubridge, C., Ito, N., Evans, P. R., Teo, C. H. & Nagai, K. (1994) Nature 372, 432–438. [DOI] [PubMed] [Google Scholar]
- 22.Hall, K. B. (1994) Biochemistry 33, 10076–10088. [DOI] [PubMed] [Google Scholar]
- 23.Umezu, K., Nakayama, K. & Nakayama, H. (1990) Pro. Natl. Acad. Sci. USA 87, 5363–5367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hall, K. B. & Stump, W. T. (1992) Nucleic Acids Res. 20, 4283–4290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jessen, T., Oubridge, C., Teo, C., Pritchard, C. & Nagai, K. (1991) EMBO J. 10, 3447–3456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nagai, K., Oubridge, C., Jessen, T. H., Li, J. & Evans, P. R. (1990) Nature 348, 515–520. [DOI] [PubMed] [Google Scholar]
- 27.Scherly, D., Boelens, W., Vanvenrooij, W. J., Dathan, N. A., Hamm, J. & Mattaj, I. W. (1989) EMBO J. 8, 4163–4170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Reyes, C. M. & Kollman, P. A. (2000) J. Mol. Biol. 295, 1–6. [DOI] [PubMed] [Google Scholar]
- 29.Reyes, C. M. & Kollman, P. A. (1999) RNA 5, 235–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Birney, E., Kumar, S. & Krainer, A. (1993) Nucleic Acids. Res. 21, 5803–5816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.(2001) qsite (Schrödinger, Portland, OR).
- 32.(1991–2003) jaguar 5.5 (Schrödinger, Portland, OR).
- 33.Jacobson, M. P., Pincus, D. L., Rapp, C. S., Honig, B. & Friesner, R. A. (2004) Proteins 55, 351–367. [DOI] [PubMed] [Google Scholar]
- 34.Jacobson, M. P., Kaminski, G. A., Friesner, R. A. & Rapp, C. S. (2002) J. Phys. Chem. 106, 11673–11680. [Google Scholar]
- 35.Hobza, P. & Sponer, J. (2002) J. Am. Chem. Soc. 124, 11802–11808. [DOI] [PubMed] [Google Scholar]
- 36.Sponer, J. & Hobza, P. (2003) Collect. Czech. Chem. Commun. 68, 2231–2282. [Google Scholar]
- 37.Sinnokrot, M. O., Valeev, E. F. & Sherrill, C. D. (2002) J. Am. Chem. Soc. 124, 10887–10893. [DOI] [PubMed] [Google Scholar]
- 38.Guallar, V., Jacobson, M., McDermott, A. & Friesner, R. A. (2004) J. Mol. Biol. 337, 227–239. [DOI] [PubMed] [Google Scholar]
- 39.Handa, N., Nureki, O., Kurimoto, K., Kim, I., Sakamoto, H., Shimura, Y., Muto, Y. & Yokoyama, S. (1999) Nature 398, 579–585. [DOI] [PubMed] [Google Scholar]
- 40.Biot, C., Buisine, E. & Rooman, M. (2003) J. Am. Chem. Soc. 125, 13988–13994. [DOI] [PubMed] [Google Scholar]
- 41.Mao, L., Wang, Y., Liu, Y. & Hu, X. (2003) J. Am. Chem. Soc. 125, 14216–14217. [DOI] [PubMed] [Google Scholar]
- 42.Bernstein, D. A., Zittel, M. C. & Keck, J. L. (2003) EMBO J. 22, 4910–4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mitchell, J. B. O., Nandi, C. L., McDonald, I. K., Thornton, J. M. & Price, S. L. (1994) J. Mol. Biol. 239, 315–331. [DOI] [PubMed] [Google Scholar]
- 44.Mitchell, J. B. O., Nandi, C. L., Ali, S., McDonald, J. K., Thornton, J. M., Price, S. L. & Singh, J. (1993) Nature 366, 413. [Google Scholar]
- 45.Mancini, E. J., Kainov, D. E., Grimes, J. M., Tuma, R., Bamford, D. H. & Stuart, D. I. (2004) Cell 118, 743–755. [DOI] [PubMed] [Google Scholar]