Activation of pausing F₁ motor by external force

Abstract

A rotary motor F₁, a catalytic part of ATP synthase, makes a 120° step rotation driven by hydrolysis of one ATP, which consists of 80° and 40° substeps initiated by ATP binding and probably by ADP and/or P_i dissociation, respectively. During active rotations, F₁ spontaneously fails in ADP release and pauses after a 80° substep, which is called the ADP-inhibited form. In the present work, we found that, when pushed >+40° with magnetic tweezers, the pausing F₁ resumes its active rotation after releasing inhibitory ADP. The rate constant of the mechanical activation exponentially increased with the pushed angle, implying that F₁ weakens the affinity of its catalytic site for ADP as the angle goes forward. This finding explains not only its unidirectional nature of rotation, but also its physiological function in ATP synthesis; it would readily bind ADP from solution when rotated backward by an F_o motor in the ATP synthase. Furthermore, the mechanical work for the forced rotation was efficiently converted into work for expelling ADP from the catalytic site, supporting the tight coupling between the rotation and catalytic event.

The molecular rotary motor F₁-ATPase generates rotary torque driven by chemical energy liberated from ATP hydrolysis (1–4). In cells, F₁ constitutes the ATP synthase binding with its partner motor, F_o, which is embedded in a biomembrane and rotates its rotor ring driven by a proton flux down to the electrochemical potential across the membrane. F₁ and F_o are connected to each other through their rotor and stator parts, whereas their rotary directions are opposite. Thus, they push each other intramolecularly. Under physiological conditions where the proton-motive force is larger than the free energy obtained from ATP hydrolysis, F_o can generate a larger torque than F₁ and enforces F₁ to rotate in the reverse direction. Consequently, F₁ reverses its catalytic reaction to synthesize ATP from P_i and ADP. In contrast, when the free energy of ATP hydrolysis is larger, F₁ hydrolyzes ATP, inversely rotating F_o to pump protons in the opposite direction. Thus, F₁ is a reversible molecular machine for converting energy between the chemical potential of ATP and mechanical work of rotation. It has been proved that mechanically reversing F₁ molecules leads ATP synthesis (5). We recently revealed that the coupling efficiency of the mechanical ATP synthesis is very high with single-molecule manipulation and microfabrication techniques (6).

F₁ has a subunit composition of α₃β₃γε. Its minimum complex as ATPase is the α₃β₃γ subcomplex, which is referred to hereafter as F₁. Walker's group (7–9) solved F₁'s crystal structures to reveal that three α- and β-subunits are alternately arranged in a hexagonal cylinder in which the rotor subunit, γ, penetrates at the center. The catalytic site is located mainly on the β-subunit. Three β-subunits hydrolyze ATP in a cooperative manner to make a unidirectional rotation of the γ-subunit (10, 11). The kinetic model for its ATP hydrolysis coupled with the rotation was originally proposed by Boyer (12). The γ-rotation in F₁ hydrolyzing ATP was strongly supported by biochemical cross-linking (13) and a spectroscopic technique (14), and finally visualized at a single-molecule level (15). The direct observation of the rotation revealed F₁ makes a 120° stepping rotation upon each ATP hydrolysis (16). High-speed imaging of the F₁ rotation with no viscous load resolved the 120° step further, into 80° and 40° substeps (17). The kinetic analysis in these studies has made allowance for the idea that the 80° substep arises from ATP binding, and the 40° substep is triggered by ADP and/or P_i dissociation. Recently, it was demonstrated that ATP hydrolysis occurs between the 80° and 40° substeps by using a mutant F₁ that hydrolyzes ATP at an extremely slow rate (18).

In our previous work, we observed that the F₁ lapses into an inactive state during rotation and showed it to correspond to the ADP-inhibited form (19), which had been characterized by many biochemical studies (20, 21). The ADP-inhibited form is the state in which the F₁ fails to dissociate ADP to stop catalysis and rotation. The ADP-inhibited F₁ pauses after the 80° substep (19) in agreement with the idea that the 40° substep arises from the release of the product(s). The inactivation is a reversible process; the F₁ in pause spontaneously becomes active to rotate again. Recent single-molecule works showed that some other enzymes are also in equilibrium between catalytic active and inactive or less active forms (22, 23). If we identify the structural feature of an inactive enzyme and mechanically manipulate its conformation back to the catalytic active state, in principle, it is possible to activate the enzyme. However, there have been few experimental attempts to do so, one of which is a report by the Bustamante group (23) showing that the probability of the transcriptional pause of RNA polymerase is affected by external force directions. In the ATP synthase, F_o turns the F₁'s catalysis direction by rotating the γ-subunit; therefore, F₁ is expected to modulate kinetic parameters upon the forced rotation of the γ-subunit. In the present study, we found that the ADP-inhibited F₁ can be mechanically activated by pushing the rotor γ-subunit in the forward direction. An elaborate analysis of this phenomenon revealed that the mechanical stress on the γ-subunit opens the catalytic site to dissociate inhibitory ADP, and that the rate constant of ADP dissociation increases with the angle of the γ-subunit. These findings have important implications for the model of the F₁'s unidirectional rotation and its ATP synthesis in the ATP synthase.

Methods

Materials. A mutant α₃β₃γ subcomplex (α-C193S, β-His-10 at N terminus, γ-S107C/I210C) from a thermophilic Bacillus PS3 (referred to as F₁ unless otherwise specified) was expressed and purified as described (24). ATP, ADP, and phosphoenolpyruvate were purchased from Sigma. Pyruvate kinase and streptavidin-coated magnetic beads (0.73 μm) were purchased from Roche Diagnostics and Seradyn (Indianapolis), respectively.

Magnetic Tweezers. A schematic diagram of magnetic tweezers is shown in Fig. 1a. The tweezers comprise four electromagnets, each constructed of a soft iron core (10 × 10 × 40 mm) and a copper wire with 100 turns around the core. Each pair of tweezers was electrically connected in a series and separated by an interval of 15 mm. The two electromagnet pairs were crossed at each center space and positioned 10 mm above the microscope stage. The microscope stage and objective lens were constructed of antimagnetic materials to minimize the remanence magnetic field <0.2 G. The angle of the composite magnetic field was controlled by applying an electric current having sine components, to one pair (y axis) and cosine components, to the other (x axis), and the field intensity was controlled by changing the current amplitude. The magnetic field was measured with a gaussmeter (421 Gaussmeter, Lake Shore Cryotronics, Westerville, OH) to confirm that the magnetic tweezers generated ≈200 G at the center of the focal plane with a precision of 4% for the intensity and 5° for the angle.

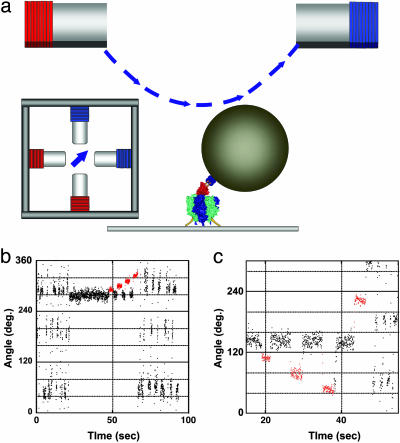
Fig. 1.

Mechanical activation of the ADP-inhibited F₁ with magnetic tweezers. (a) Side and top views of the manipulation system with magnetic tweezers. The ≈0.6-μm magnetic beads were attached to the γ-subunit in the F₁ immobilized on the slide glass. The magnetic tweezers were mounted on the microscope 10 mm above the specimen stage to generate a magnetic field parallel to the stage. (b) Time course of the mechanical activation by pushing in the forward direction. After a 120° stepping rotation that can be seen as an oscillating trace, the F₁ spontaneously lapsed into the ADP-inhibited form at 280°. The F₁ was stalled and released at +10°, +20°, +30°, and +40° from the angle for inhibition with magnetic tweezers. After a +40° stalling, the F₁ regained active rotation. Red areas indicate the manipulation time by using the magnetic tweezers. (c) Trial of the mechanical activation by pulling in the backward direction. The F₁ was not activated when stalled and released at –20°, –40°, and –80° with magnetic tweezers. To confirm that it was alive, it was activated by being pushed >+80°.

Rotational Assay. A flow cell was constructed from a bottom coverslip coated with Ni²⁺-NTA (5) and an uncoated top cover glass. F₁ of 1–2 nM in buffer A (50 mM Mops-KOH, pH 7.0/50 mM KCl/2 mM MgCl₂/10% BSA) was infused into the flow cell. After 2 min, the flow cell was washed with buffer A, and then the magnetic beads were infused. After 3 min, the unbound beads were washed out with buffer A, and then buffer A containing the indicated amount of Mg-ATP was infused. The rotating beads were observed as bright images (19). The images were videotaped and analyzed with custom software, see Movie 1, which is published as supporting information on the PNAS web site. For an ADP-free experiment, an ATP regenerating system (10.3 units/ml of pyruvate kinase, 1 mM phosphoenolpyruvate) was added to buffer A. In the experiments for examining the effect of ADP on mechanical activation, purified ADP was added to buffer A (5).

Mechanical Activation. The solution contained 200 nM ATP except for the indication, in which the F₁ shows 120° stepping rotation. When the F₁ lapsed into the ADP-inhibited form pausing at ≈80° (ADP inhibition position) from the ATP-waiting position (5), a manipulation with magnetic tweezers was performed as follows: the tweezers were activated to trap the magnetic bead(s) at the ADP-inhibition angle, and then the magnetic field was rotated to the desired angle within 0.4 s. After the indicated time (0.5–300 s), the external magnetic field was turned off to check whether the F₁ was activated. All procedures were controlled with a custom computer program (H.N.). Some magnetic beads of which the magnetic moment was not parallel to the microscope stage were inclined under an external magnetic field, and those beads were not analyzed. The image of the beads was videotaped with a charge-coupled device camera at 30 frames per s with 2-ms shutter speed (TAKEX Tokyo, FC300M) and was analyzed with a custom computer program (Ryohei Yasuda, Duke University, Durham, NC).

Results

Experimental System. The F₁ motor was immobilized on a glass plate through the α₃β₃ ring, and magnetic beads were attached to the γ-subunit (Fig. 1a). The rotation of the beads was videotaped at 30 frames per s in a bright field by using a charge-coupled device camera. To manipulate the F₁ motor, we developed magnetic tweezers consisting of two pairs of crossed electromagnets installed 10 mm above and parallel to the specimen stage of the microscope. The magnetic tweezers generate a magnetic field that is parallel to the stage. Its strength and orientation is controllable by changing the electric current on each electromagnet.

Observation of Mechanical Activation. The rotation of the F₁ was observed at 200 nM ATP, unless otherwise described, where F₁ rotates with a discrete 120° step, each initiated by ATP binding, which takes 0.3 s on average. As seen in our previous experiment, the F₁ motor spontaneously lapsed into the ADP-inhibited form to show a long pause (≈30 s) at an angle 80° forward from that for the ATP binding, that is, 40° backward from the next ATP binding angle. Hereafter, we define the origin angle, 0°, as the center angle for the ADP-inhibited form, plus as the rotary direction and minus as the opposite direction. The ADP-inhibited F₁ was manipulated with the magnetic tweezers to stall it at arbitrary angles, and then released from the tweezers. As seen in Fig. 1b, the F₁ was stalled for 3 s at +10°, +20°, +30°, and +40° and released each time. After it stalled at +10° to +30°, the F₁ still remained in its ADP-inhibited form, returning back to the original angle. On the other hand, the F₁ immediately restarted its rotation after being pushed to +40°. This finding means that the F₁ returned to its active form. This activation is discerned from the spontaneous recovery from the ADP-inhibited state. In the presence of 200 nM and 2 mM ATP, the average times for spontaneous activation without manipulation are 60 and 30 s, respectively, both of which are much longer than the standard manipulation time taken in the present experiment. In addition, it should be noted that any spontaneous activation did not occur after ADP-inhibited F₁ was stalled for several min at 0°, as described later. Therefore, any mechanical activation reported in this article was conducted by the manipulation.

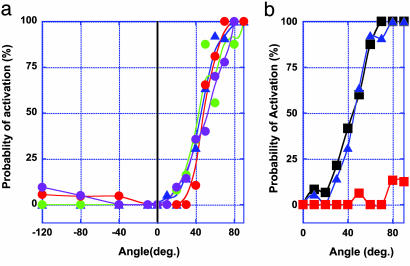
Angle Dependency of Mechanical Activation. The probability of mechanical activation within the 3-s stall was determined at each stall angle (Fig. 2a). In this case, it was defined as activation, when the F₁ motor rotated >+120° from 0° after it was released from the magnetic tweezers. Other cases were regarded as an activation failure. In most of the failure cases, the F₁ motor returned to 0° (Fig. 1b). When pushed >+40°, the activation probability sharply increased to reach up to nearly 100% at +70°. However, when pulled up to –120°, the F₁ motor mostly returned to 0° (Fig. 1c). Thus, both the rotary direction and angle amplitude were important for the mechanical activation. The activation probability was also determined in the presence of 1 mM ADP and/or 30 mM P_i. No major difference in the presence of ADP was found, except for the lower probability at 30° and 40°. Similar probabilities were also obtained at 2 mM ATP(Fig. 2b). These findings suggest that the mechanical activation is ascribable to the release of the inhibitory ADP, as opposed to the binding of the substrate/product from the solution. In previous biochemical experiments (24, 25), the ADP-inhibited F₁ was activated by ADP depletion, for example, through gel filtration. To verify this finding, the mechanical activation was examined at 20 mM ADP, where it was completely suppressed, thus confirming the above explanation (Fig. 2c). At 20 mM ADP is much higher than the previously reported K_d values for ADP (26, 27), probably because the affinity of ADP decreases with the rotary angle, as shown below. Therefore, much higher ADP was needed for the suppression of the mechanical activation >40°, whereas the γ-subunit in the biochemical experiments would mostly be 0°, maintaining a higher affinity to ADP. Indeed, 2 mM ADP was enough to inhibit the mechanical activation <30°, indicating that the K_d(ADP) for <30° is <2 mM. The K_d(ADP) between 40° and 60° was expected to lie between 2 and 20 mM.

Fig. 2.

Angle dependency of the probability of mechanical activation. (a) Probabilities of the mechanical activation were determined in the presence of 0.2 μM ATP (blue); 0.2 μM ATP, 30 mM P_i (green); 0.2 μM ATP, 1 mM ADP (red); and 0.2 μM ATP, 30 mM P_i, 1 mM ADP (purple). Each data point was determined from 17 observations on average. (b) Probabilities were determined in the presence of 0.2 μM ATP (blue), 2 mM ATP (black), and 33 μM ATP, 20 mM ADP (red). Each data point was determined from 15 observations on average.

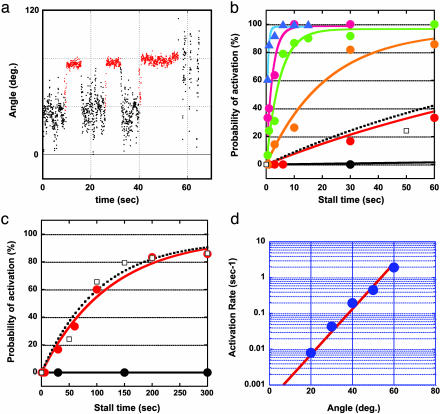
Time Course of Mechanical Activation. We examined how the mechanical activation depends on the stalling time. A typical time course of the experiment is shown in Fig. 3a, where the ADP-inhibited F₁ was stalled at 40° for 5, 5, and 15 s. Magnetic tweezers were turned off after each stalling to observe the activation. In this example, the F₁ was activated after 15 s of stalling. From these experiments, we obtained saturation curves for the activation probability, which exponentially increased with the stalling time (Fig. 3 b and c). These were well fitted with a single exponential equation that assumes a first-order reaction, ADP-inhibited form → activated form. Each fitting gave a rate constant for the mechanical activation, which exponentially increased with the rotary angle. Interestingly, the activation at 0° was too slow for this fitting, whereas the spontaneous activation occurred at the same rate as the mechanical activation at 20°. These results mean that the affinity of the inhibited F₁ to ADP at 0° is very high, and it decreases with the angle to accelerate ADP release. This finding is consistent with the observation that higher ADP was needed to suppress the activation in forward angles. Each fitting gave a saturation value of ≈100%, suggesting its irreversibility. To verify this idea, the following experiments were performed. The ADP-inhibited F₁ was stalled at >60° for 6 s to activate it, and it was rotated back to 0° to stall for 6 s to inactivate it, should it occur, and then it was released from the magnetic tweezers. In most of the cases (93%), released F₁ showed its active rotation (data not shown). Thus, it was confirmed that F₁ is not reversibly inactivated again in this condition. Once F₁ is activated by stripping inhibitory ADP, the reinactivation would need either ADP binding from the solution or production of ADP in catalysis.

Fig. 3.

Rate constant of the mechanical activation. (a) Time course of the mechanical activation with different stalling times. The ADP-inhibited F₁ was stalled and released at +40° after 5 s twice and after 15 s. (b) The probabilities of the mechanical activation by stalling at 0° (black), 20° (red), 30° (orange), 40° (green), 50° (purple), and 60° (blue) were plotted against the stalling time. Each data point was determined from 12 observations on average. (c) Shown is an expanded graph for probabilities of the spontaneous activation (□). (d) Rate constants (blue circles) were determined by fitting the curves in b and c with single exponential equations. The slope of linear fitted line (red) for these rates in semilogarithmic scale gives the angle dependency of the activation energy as –1.3 k_BT/10⁰.

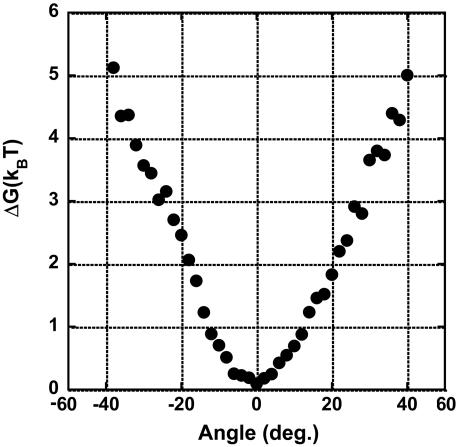
Activation Energy of Mechanical Activation. The rate constants of the mechanical activation, k_act, determined from Fig. 3 b and c, are plotted against stall angles (Fig. 3d). It was clearly shown that the rate increases exponentially with the angle. This finding means that the activation energy of the mechanical activation, G_a, given in the Arrehenius equation (1n k_act = 1nA – G_a/k_BT), decreases with the angle. The activation energy change was given as –1.3 k_BT/10° from the slope in Fig. 3d. This finding strongly suggests that, upon the mechanical energy input through the γ-subunit, the energy state of the inhibitory ADP binding shifts to a higher state, so that the activation energy becomes relatively lower. To determine the amount of energy transferred to the F₁ by the magnetic tweezers, the work for pushing the F₁ in the ADP-inhibited form was estimated. The Brownian motion of the magnetic beads attached to the F₁ in the ADP-inhibited form was observed for >30 s without applying magnetic field, and the probability density of angle was determined to calculate the potential shape according to the Boltzmann distribution law (Fig. 4). The determined potential >+20° had a linear slope, corresponding to the linear decrement of the activation energy of the mechanical activation. The energy increment of 1.5 k_BT per 10° coincides well with the activation energy decrement of 1.3 k_BT per 10°, suggesting that 85% of the mechanical energy input was transmitted to the catalytic site to weaken the binding energy of ADP. This finding is consistent with the tight coupling model between the catalytic reaction and the γ-rotation in the F₁ motor. The residual energy would remain stored as elastic energy for the other elements in our experimental system (for example, the γ-subunit itself, the α₃β₃ ring, His tag, or streptavidin).

Fig. 4.

The rotary potential of the ADP-inhibited form F₁. The probability density of the angle of the magnetic beads from the six molecules was transformed into potential according to the Boltzmann distribution law.

Angle Deviation Between the γ-Subunit and the Magnetic Beads. When the experimental system has highly flexible components such as the γ-subunit, the α₃β₃ ring, His tags, or streptavidin, the rotary angle of the magnetic beads could deviate by a large amount from the γ-angle. Even though the angle deviation was not definitely determined in the present work, some of our experimental data suggested that the deviation is probably not so large. First, the mechanical activation was observed when the magnetic beads were rotated >20°, suggesting that the γ-subunit certainly rotates against the α₃β₃ ring, which implies that the deviation is <20°. The rotary potential of the ADP-inhibited F₁ is also suggestive on this point. The determined potential comprises a loose spring-like potential within ±10° and linearly increasing potentials for over ±10°, which have slopes (= torque) of ≈35 pNnm for both sides. These values are consistent with the reported torque of ≈40 pNnm (16, 24, 28), implying that the potential >20° certainly reflects the interaction between the α₃β₃ ring and the γ-subunit. Thus, the angle deviation would be at most 20°. One of the most likely candidates for elastic components is the γ-subunit, because its protruding part from the α₃β₃ ring was twisted by 11° in the crystal structure of the mitochondrial F₁ modified by dicyclohexyl-carbodiimide (8, 9). Further studies on its elasticity remain to be done. It should be noted that the determined torque from the rotary potential is equal to the external torque by the magnetic tweezers because these two torque are equilibrated.

Backward Activation. Although the mechanical activation was not observed when the γ-subunit was pulled backward, up to –120°, preliminary experiments showed that the F₁ can be activated when pulled over by –160°. However, the results have been quite irregular so far. It is only certain that the activation probability was the highest in the presence of both ADP and P_i. A similar finding was reported by Vinogradov and colleagues (29, 30), that is, a submitochondrial particle containing the FoF₁-ATPase showed a higher ATP-hydrolysis activity after transient charging of the membrane potential. The most plausible explanation is that when F₁ is rotated in the ATP-synthetic direction in the presence of the ADP and P_i, the F₁ follows the ATP synthesis pathway to be efficiently activated.

Discussion

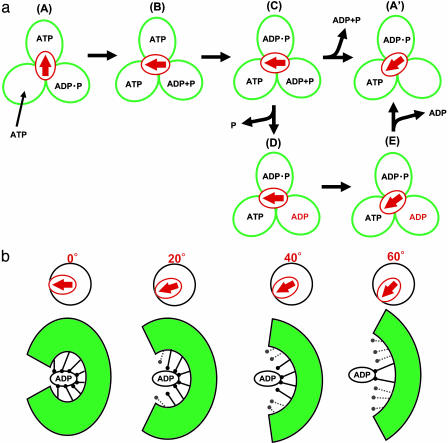
Mechanical Activation of Enzymes. The catalytically active F₁ spontaneously fails to dissociate ADP with some probability, and its rotation pauses at an angle after an 80° substep. This catalytically inactive state is called the ADP-inhibited form. In this study, we showed the mechanical activation of the F₁ motor in the ADP-inhibited form by pushing it with magnetic tweezers. When the ADP-inhibited F₁ was pushed >+40° with the magnetic tweezers, the F₁ regained its catalytic activity to restart the rotation, whereas it was not readily activated when pulled back. This mechanical activation was completely suppressed by ADP, but not by ATP and/or P_i. These findings showed that the mechanical activation is triggered by the dissociation of the inhibitory ADP. Also, in biochemical experiments, ADP removal is necessary for the activation of the ADP-inhibited F₁, for example, using gel filtration. The model for the mechanical activation in the catalysis and rotation scheme is shown in Fig. 5a. The scheme starts from the ATP-waiting state, A, where the β-subunit with an empty catalytic site waits for the ATP to bind, and the two are bound with ATP and ADP, respectively. This state approximately corresponds to the crystal structure of MF₁ solved in 1994, except for P_i binding in the model. Upon ATP binding to the empty β, the F₁ makes an 80° substep, which triggers the following catalytic reactions on the other βs, ATP hydrolysis (B → C) and ADP and/or P_i release (C → A′). When ADP releases from the F₁, the γ-subunit rotates 40° to reset the F₁ in a new ATP-waiting state, A′. With some probability, the F₁ in the state C releases phosphate and isomerizes to the ADP-inhibited form, state D. This scheme accords with a recent biochemical study using a mutant F₁ with an inserted tryptophan residue near the phosphate binding region, which showed that F₁ releases phosphate and then slowly isomerizes to the ADP-inhibited form (31). Even though the biochemical experiments were conducted in an unisite condition where the number of catalytic sites occupied with a nucleotide was one at most, it is assumed that a similar isomerization occurs in F₁ that operates in a multisite catalysis mode (32, 33) (here, the trisite model is used). When the γ-subunit of the ADP-inhibited F₁ (D) is rotated >40° with the magnetic tweezers, the mechanical stress on the F₁ changes the conformation of the β-subunit carrying the inhibitory ADP, enforcing the F₁ to strip the inhibitory ADP molecule. After releasing it, the F₁ returns to a new ATP-waiting state, A′, on the catalytic active pathway. This scheme explains our experimental data well; however, it should be noted that this scheme is provisional because the angle at which the active F₁ releases ADP and P_i has not been conclusively identified yet. Additionally, the mostly same model can be proposed standing on bisite mode in which site occupancy alternates between one and two.

Fig. 5.

The proposed model for conformational change around the catalytic site. (a) Reaction scheme in the catalysis and rotation model. Three green circles represent the catalytic state, and the red arrow indicates the angle of the γ-subunit. States D and E represent the ADP-inhibited form and forward-rotated form, respectively. (b) Schematic model of the conformational change around the catalytic site with the inhibitory ADP coupled with mechanical rotation. Upon forced rotation, the catalytic site progressively opens its conformation-breaking interactions with ADP.

Angle Dependency of ADP Affinity. The most important result obtained in the present study is that the angle of the γ-subunit determines the rate constant of the ADP dissociation from the β-subunit. The time course of the mechanical activation gave the rate constant of the ADP dissociation that exponentially increases with angles of the γ-subunit in the forward direction. This finding explains well the directed rotation coupled with ADP release. Similar findings on the kinesin motor have been reported by Uemura and Ishiwata (34). They determined the ratio of the ADP-bound kinesin to the nucleotide-free from the measurement of the unbinding force of the kinesin–microtuble complex to reveal that the direction of the external force determines the affinity of kinesin with ADP. Thus, the modulation of the ADP affinity in response to the external force would be a common feature for molecular motors to give rise to unidirectional motion.

This finding is very suggestive for the ATP synthesis reaction model, in which we assume similar angle dependency of the ADP dissociation rate for active F₁. For ATP hydrolysis, the F₁ motor has to dissociate ADP in the solution, whereas it also has to efficiently bind ADP from the aqueous solution for ATP synthesis. If the ADP binding/dissociation would occur merely at a specific angle, the F₁ would not manage these two reactions. However, when active F₁ has a similar angle dependency of ADP affinity, F₁ would readily catch ADP from the solution when the F_o motor pulls F₁ back. Thus, the angle dependency of ADP release accords with a property needed for F₁ to operate its physiological function of ATP synthesis.

Spontaneous Activation. The angle dependency of the activation implies that the ADP remains difficult to strip off until the γ-subunit is moved. It was actually observed that when the F₁ was clamped at 0°, the angle for the ADP-inhibited state, ADP did not dissociate even after 300 s. In contrast, when the F₁ motor was allowed to make the rotary Brownian motion without an external force, the F₁ was spontaneously activated at the same rate as the mechanical activation at 20°. This finding means that when the thermal energy occasionally pushes the γ-subunit >20°, the inhibited F₁ dissociates ADP to regain its activity. In this sense, the spontaneous activation is also a mechanical activation caused by the thermal energy. It would be also interesting to examine ADP release in the unisite catalysis from the same view point. In the unisite catalysis, ADP release is known to be very slow, whereas the ATP hydrolysis step and the following phosphate release are fast (31, 35). The F₁ is also in a kind of ADP-inhibited form, although it has a sole bound nucleotide. Therefore, similar mechanism could occur in the ADP release; F₁ waits for the thermal fluctuation to push forward to release the tightly bound ADP.

Structural Model of Mechanical Activation. As shown in Fig. 3d, the rate constant of the mechanical activation increased upon mechanical rotation of the γ-subunit, implying that the interaction between the bound ADP and the catalytic site on the β-subunit was weakened to accelerate ADP release. The analysis of the rate constants according to the Arrehenius equation suggested that the binding energy decreases in proportion to the rotary angle, by 1.3 k_BT per 10°. We discuss the structural features of the ADP-inhibited form and models to explain the mechanical activation below.

Structural studies on bovine mitochondrial F₁ (MF₁) by the Walker group (7–9) have revealed that the β-subunit can essentially use three types of conformation. The β-subunit with tightly bound ADP or ATP analog lifts the C-terminal domain up to the nucleotide binding domain enclosing the nucleotide in the crevice between the two domains. In contrast, the β-subunit without a nucleotide pulls down the C-terminal domain opening the catalytic site. Recently, an intermediate conformation was found, which weakly binds ADP in half-opened conformation. Thus, the F₁ closes the catalytic site upon ATP binding and opens its conformation after ADP release via the half-closed conformation. This conformational change is a typical induced-fit. The C-terminal domain has direct contact with the γ-subunit, thereby, this domain movement is thought to mechanically link the catalytic reactions and the γ-rotation. What are the structural features specific for the ADP-inhibited form? Considering that ADP binds tightly to the inhibited F₁, the ADP-inhibited β would be in the closed conformation (36). Further detailed structural features distinct from a catalytically active F₁ remain to be revealed. However, an interesting point is given by the recent crystal structures of MF₁ with dicyclohexyl carbodiimide (9) and complexes of ADP and beryllium fluoride (37). The catalytic site that corresponds to the ATP-binding site in other crystal structures does not bind ATP but does bind ADP. Because of the absence of the γ-phosphate, the side chain of the αR373, a catalytically crucial residue, is in a largely different conformation from other structures and forms a hydrogen bond to the 2′OH of the ribose of the ADP. Considering that isomerization to ADP inhibition occurs after phosphate release, it is possible that this structural rearrangement is a structural base of the ADP-inhibited form.

Kinetic analysis of the mechanical activation suggests that the mechanical forward rotation of the γ-subunit decreases the binding energy of ADP and the catalytic site. Therefore, we propose a simple structural model in which the mechanical forward rotation enforces the closed-β-subunit with the inhibited ADP to transform into the opened conformation, breaking the interactions between ADP and the catalytic site (Fig. 5b). When the interactions are unzipped sequentially with the forced rotation, it explains the linear drop of the ADP binding energy well. As an alternative model, a conformational rearrangement of a few amino acid residues, for example the αR373, which is decisive for the ADP inhibition, can be a trigger of mechanical activation. The analysis of the rotary Brownian motion showed that 85% of the energy given for forced rotation was transmitted to the catalytic site, supporting the tight mechanical linkage between the γ and the catalytic site. The structural model shown in Fig. 5b coincides well with progressive ATP-binding models proposed by Oster and Wang (38) and Cross (39) independently. These models explain well the efficient energy conversion and the reversibility of F₁-ATPase. In Oster and Wang's “binding-zipper” model, it is proposed that hydrogen bonds of ATP and the catalytic site are sequentially formed to drive the γ-rotation to explain the F₁'s constant torque against the rotary angle (38, 40). In the near future, the angle dependency of the affinity of F₁ with ATP also will be elucidated by using this method.

Conclusion

The F₁ catalyzes ATP synthesis when the F_o enforces it to rotate in the reverse direction. It means that catalytic parameters of F₁ can be modulated by rotating the γ-subunit. In this work, we successfully activated the ADP-inhibited F₁ molecules by rotating the γ-subunit with magnetic tweezers. From the analysis of this phenomenon, it was revealed that F₁ decreases its affinity to the inhibitory ADP with the γ-rotation by using external energy with high efficiency. Theses properties of F₁ well explain its unidirectional nature of rotation and physiological function: synthesis of ATP. The molecular mechanism regarding the manner in which F₁ tunes elementary chemical steps (ATP binding, ATP hydrolysis/synthesis, and P_i release) in response to an external torque would be challenged by this method.