Local conformational fluctuations can modulate the coupling between proton binding and global structural transitions in proteins

Abstract

Local conformational fluctuations in proteins can affect the coupling between ligand binding and global structural transitions. This finding was established by monitoring quantitatively how the population distribution in the ensemble of microstates of staphylococcal nuclease was affected by proton binding. Analysis of acid unfolding and proton-binding data with an ensemble-based model suggests that local fluctuations: (i) can be effective modulators of ligand-binding affinities, (ii) are important determinants of the cooperativity of ligand-driven global structural transitions, and (iii) are well represented thermodynamically as local unfolding processes. These studies illustrate how an ensemble-based description of proteins can be used to describe quantitatively the interdependence of local conformational fluctuations, ligand-binding processes, and global structural transitions. This level of understanding of the relationship between conformation, energy, and dynamics is required for a detailed mechanistic understanding of allostery, cooperativity, and other complex functional and regulatory properties of macromolecules.

The native states of proteins are conformationally heterogeneous (1–8). This characteristic is primarily the result of local structural fluctuations that are thought to contribute to stability and to function (9–11). As a consequence of these spontaneous conformational fluctuations, proteins in solution exist as ensembles of closely related, transient, and interconverting conformational microstates that, when averaged, describe the conformational state represented by the crystal structure. NMR spectroscopy can be used to study the very fast motions of proteins (9–11). Nevertheless, the probability and structural character of the full spectrum of microstates sampled by proteins is not yet known (12, 13). The sensitivity of the ensemble of microstates to changes in environmental conditions (i.e., pH, temperature, pressure, ligand binding, and concentrations of osmolytes and denaturants) is also not well understood, and neither is the manner in which local fluctuations are coupled to larger, more global structural transitions. Here, we introduce an ensemble-based description of proteins that accounts for the complex interplay between local conformational fluctuations, global stability, and ligand binding. This ensemble view of proteins can contribute innovative mechanistic insight into the evolution of enzymatic and regulatory functions of proteins.

To investigate the coupling between ligand binding, conformational fluctuations, and global stability, the proton-binding properties of staphylococcal nuclease (SNase) were studied. Proton-binding processes are particularly useful for this purpose because they are experimentally measurable and because the pK_a values of ionizable groups are exquisitely sensitive to their local microenvironments (14–27). Each proton-binding site acts as a site-specific probe of local conformation.

Proton-binding processes are also of special interest because many proteins have evolved to harness small differences in pH to trigger physiologically important conformational changes. The regulation of the oxygen affinity by hemoglobin (28), the activation of bacterial toxins (29), and key steps in the infectivity cycles of viruses as diverse as polio (30), influenza (31–33), and HIV (34) are examples of physiologically relevant processes in which function is regulated through proton-linked structural transitions. Understanding the relationship between local conformational fluctuations, ligand (i.e., H⁺) binding, and global structural transformations in these proteins is necessary to elucidate the physical basis of their function.

Molecular dynamics (MD) simulations and other all-atom approaches have been useful for describing the character and consequences of local conformational fluctuations (35–39), as well as providing significant functional insight (40). However, in the relatively short time scales that can be accessed routinely by MD methods, local backbone relaxations, and other slow relaxation events likely to be relevant to biological and equilibrium thermodynamic processes (12, 13) are not sampled sufficiently. The alternative approach that is described in this work focuses on the quantitative description of the instantaneous ensemble constituted by the different microstates populated by the native states of proteins in solution (41). If the structures of the different microstates can be sampled adequately, and a reliable energy function can be used to calculate the energy of each microstate, then a Boltzmann-weighted scheme (41) can be used to calculate global solution properties of the protein as a sum of contributions by individual microstates. Here, we show how this simple ensemble-based approach can be used to describe complex processes, such as the acid-driven unfolding of a protein. The ensemble-based approach enables a detailed description of the pH-driven shift in the character of the instantaneous ensemble wherein the coupling between ligand binding, local conformational fluctuations, and global structural transitions is described explicitly.

Methods

Generation of the Ensemble. The crystal structure of SNase (Protein Data Bank ID code 1STN; ref. 42) was used as a template to generate a model of the ensemble by using the corex algorithm described in refs. 41 and 43–46. In the corex calculations, the structure for each microstate is generated by treating local fluctuations as local folding-unfolding reactions that occur in an otherwise folded and native-like protein (Fig. 1A). In the present study, >10⁶ different conformational microstates were generated by systematically varying the number and location of fluctuating (locally unfolded) residues. The probability of each microstate (P_i) was estimated by using a structure-based calculation with a parameterized energy function that has been calibrated previously and tested extensively (47–55). This probability can be described by the Boltzmann relationship,

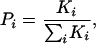[1]

where the statistical weight of each state (K_i) is determined by the relative Gibbs free energy of that state (K_i = e^–ΔGi/RT, where R is the gas constant and T is absolute temperature), and the summation is over all states in the ensemble.

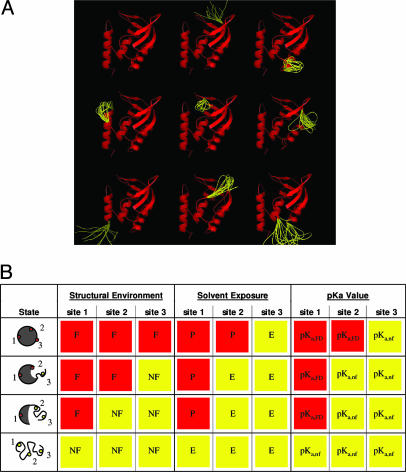
Fig. 1.

Schematic representation of the SNase ensemble calculated for thecorex/best algorithm. (A) Nine of the most probable conformational states (of ≈10⁶) of the SNase ensemble, modeled as described in ref. 47. Each microstate exhibits dual structural character and consists of a mixture of regions that are considered to be native-like (red) and regions that are treated thermodynamically as unfolded (yellow). Molecular diagrams in this figure were made by using the program pymol (65). (B) Ensemble model used to describe quantitatively the coupling between local unfolding energetics and the energetics of proton binding. Depicted are the proton titration properties of a hypothetical protein (gray circle) that has only three titratable groups (dots) and whose conformational ensemble contains only four microstates: a fully folded, two partially folded, and a fully unfolded state. Unfolded segments of the protein are depicted as randomly curved lines. The small dots represent the individual titratable groups of the protein: sites 1, 2, and 3. Each individual proton-binding site can reside in a folded (F) or an unfolded (NF) region, and they can be exposed to solvent (E) or protected from solvent (P). The pK_a value of each titratable group in each state was assigned according to the degree of solvent exposure of the titratable atoms. Groups that were protected from solvent were assigned the pK_a values calculated with Poisson–Boltzmann continuum electrostatics method (pK_a,FD). Groups that were exposed to solvent were assigned pK_a values identical to those observed in unfolded polypeptides (pK_a,nf).

pH Dependence of the Ensemble. To account for proton effects on the probability of each state generated by corex, we introduce the best (Biology using Ensemble-based Structural Thermodynamics) algorithm. In this algorithm, the statistical formula to calculate probability (Eq. 1) was expanded to account for proton-binding energies,

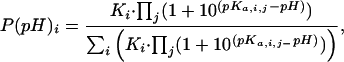[2]

where pK_a,i,j is the pK_a value of residue j in microstate i. For each microstate of the ensemble, each ionizable group can have one of two pK_a values: the pK_a value in the native conformation (pK_a,FD) or that of the unfolded state (pK_a,nf). For this reason, the distribution of microstates is pH-dependent. The set of rules summarized in Fig. 1B was used to assign pK_a values to each ionizable group in each of the different microstates of the ensemble. The set of pK_a,nf values used are those of model compounds in water (56, 57). The pK_a,FD values that were used were calculated by using the native-state structure and continuum electrostatic methods based on the numerical solution of the linearized Poisson–Boltzmann equation with the method of finite differences (58). The ionizable groups in the N- and C-terminal regions of the protein, which are not resolved in any known crystal structure of SN, were assigned pK_a,nf values.

Individual groups were assigned pK_a values based on the criteria of solvent accessibility. When the averaged solvent accessibility of the ionizable atoms of a titratable group was <31% (for Glu, Asp, Tyr, Lys, and Arg) or 45% (for His), these groups were assigned pK_a,FD values; all other groups were assigned pK_a,nf values. This cutoff maximized the agreement between the calculated and measured overall proton-binding curve of SNase (discussed below). Use of such a seemingly arbitrary cutoff was validated by the ability of the ensemble calculations thus performed to correctly identify the subset of ionizable groups that were shown experimentally to govern the acid unfolding reaction.

Proton Titration Properties of the Ensemble. In an ensemble-based calculation, any measurable solution property of a protein can be calculated as the probability-weighted sum of the individual contribution of all conformational states present in solution under a given set of conditions. In the case of proton titrations, the average degree of protonation at each pH, 〈Z〉, is calculated as the sum of the titrated protons, Z_i, in each microscopic state, 〈Z〉 = ∑_i (Z_i·P_i), where P_i is the pH-dependent probability of state i calculated with Eq. 2.

Results and Discussion

Modulation of the Ensemble by pH. To determine how the character of the ensemble of a protein is affected by changes in pH, the distribution of microstates in the ensemble of SNase was determined at different pH values. The effect of pH on the probability of the different microstates arises from the assignment of either pK_a,nf or pK_a,FD values to each ionizable group in the different microstates. This effect, in turn, depends on whether the titratable atom exists in a native-like or unfolded microenvironment.

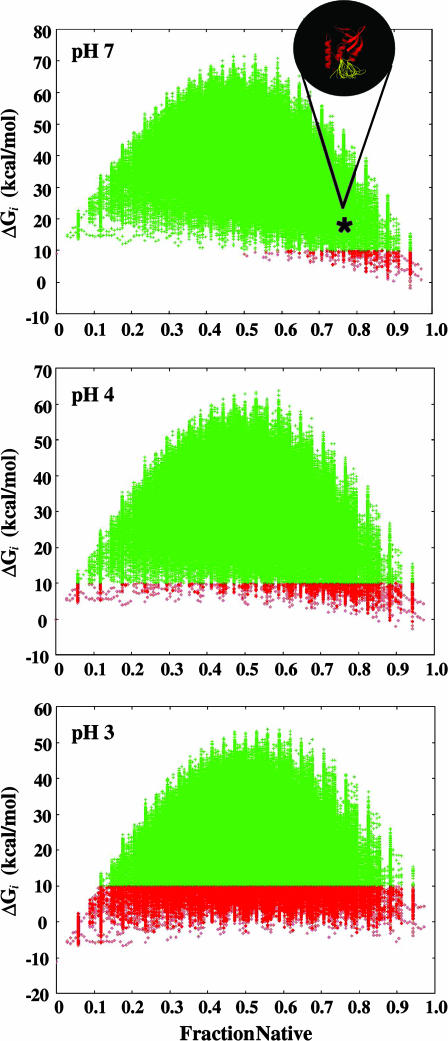
The pH sensitivity of the ensemble of microstates for SNase is shown in Fig. 2, where the free energies of the ≈10⁶ microstates are shown at three different pH values. Under conditions of low pH, the microstates with a higher affinity for protons (those with titratable groups with more normal pK_a values) are stabilized preferentially over the microstates with lower proton-binding affinity. However, at pH 7 the most probable (i.e., lowest energy) microstates in the ensemble are mostly native, with some locally unfolded sections (i.e., high degrees of fraction native; see Fig. 2). Interestingly, at pH 7 the SNase ensemble is populated mainly by microstates that have at least some fraction of the molecule unfolded (Figs. 2 and 3A). Although the stability of each of these partially unfolded states is predicted to be comparable to the stability of the fully folded state, the aggregate probability of these partially unfolded states actually dominates the conformational ensemble at neutral pH.

Fig. 2.

Relative stability (Gibbs free energy, ΔG) of each of the ≈10⁶ microstates plotted as a function of the fraction native (number of residues in folded segments/total number of residues) at three different pH values (pH 7, 4, and 3). Each point corresponds to a particular microstate, and the ΔG values were calculated relative the fully folded state (i.e., the stability of the fully folded state in the ensemble is 0 at all pH values). To highlight the changing character of the ensemble induced by pH, all states with ΔG of <10 kcal/mol are shown in red, and those states with ΔG of >10 kcal/mol are shown in green.

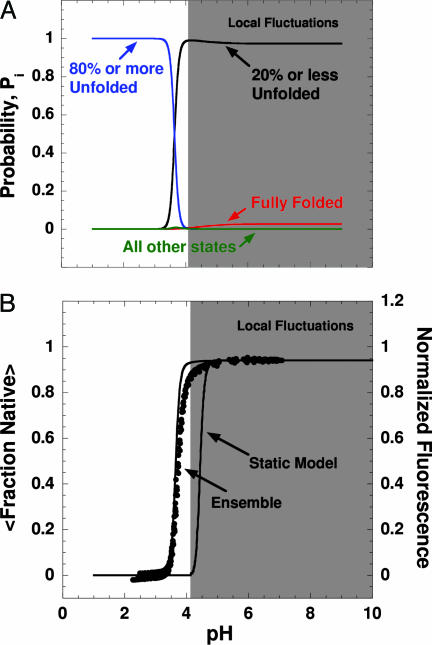
Fig. 3.

pH-induced modulation of the SNase ensemble. (A) Calculated pH dependence of the summed probability of all partially folded states in which 20% or fewer of the residues are unfolded (black), the summed probability of all states in which 80% or more of the residues are unfolded (blue), the probability of the fully folded state (red), and the summed probability of all other states of the ensemble (green). (B) Experimental acid unfolding of wild-type (WT) SNase monitored by pH titration of the intrinsic fluorescence of Trp-140 (24). The lines overlaid on the experimental data represent the ensemble-calculated pH-dependent unfolding of the protein. The relative extent of folding of the ensemble was calculated by 〈Fraction Native〉 = ∑_i Fraction Native_i·P(pH)_i. Also shown is the predicted acid unfolding transition based on pK_a values calculated with Poisson–Boltzmann electrostatics (58). Regions shaded gray in A and B indicate conditions wherein the conformational excursions are dominated by local fluctuations.

The pH sensitivity of the conformational character of the ensemble is of particular significance. States with a lower fraction native become favored as pH is decreased (Figs. 2 and 3A). However, this shift does not occur in a gradual, noncooperative fashion. Instead, as the pH is lowered from 7.0 to 4.0, the ensemble transforms in a highly cooperative fashion from one that is dominated by native-like microstates into one consisting of microstates that are largely unfolded (Fig. 3A). Under no conditions of pH are states with intermediate values of fraction native (i.e., 0.2 < x < 0.8) populated to a significant extent. Inspection of Fig. 3B reveals that the cooperativity (i.e., the steepness of the acid unfolding transition, which is related to the number of protons bound preferentially by the acid unfolded state relative to the native state) and the midpoint of the acid unfolding transition monitored experimentally by intrinsic fluorescence are reproduced quantitatively by the ensemble-based calculations.

Because the physical properties and the energy of each state in the ensemble is determined from a consistent set of principles (Fig. 1B and ref. 41), the predicted cooperativity is not an artifact imposed by a bias in the ensemble calculations. Instead, it indicates that, although the individual microscopic states and the associated proton-binding properties calculated with the ensemble method use simple principles, they nonetheless provide an accurate estimate of the average physical character as well as the average proton-binding properties of the dominant states in the native-state ensemble.

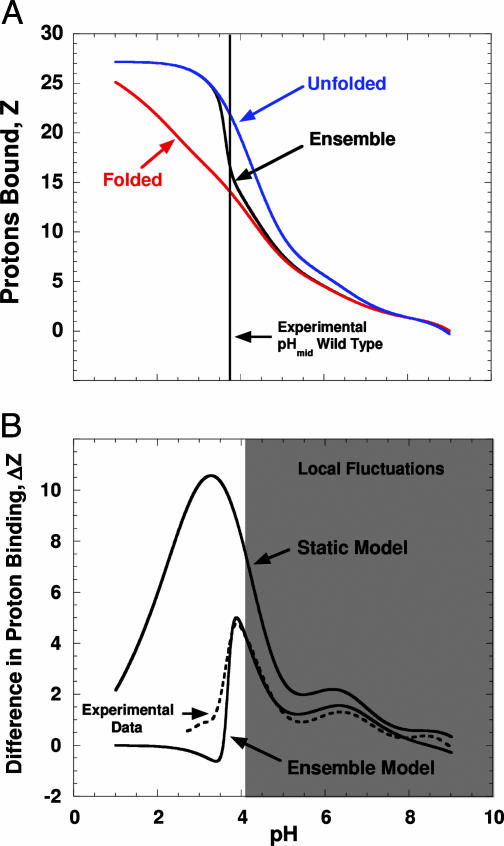
Coupling of Proton Binding to Local Fluctuations. The agreement between the proton-binding behavior calculated with the ensemble-based method and the behavior measured experimentally (Fig. 4) is consistent with a significant coupling between proton-binding reactions and local fluctuations. Note in Fig. 4A that in the neutral range of pH, the ensemble-averaged proton-binding properties of SNase resemble the binding properties of the fully folded state. At low pH, the ensemble-calculated proton titration properties correspond to those of a fully unfolded state. At intermediate pH values, however, the calculated proton titration curve of the pH-modulated ensemble is between the titration curves of the fully folded and the fully unfolded states (Fig. 4A). The proton titration properties of the pH-modulated ensemble monitor the same proton-linked global structural transition that is monitored experimentally (Fig. 3B). To appreciate the significance of the agreement between the experimentally determined number of protons bound upon acid unfolding and the value calculated with the ensemble-based approach (Fig. 4B), note that in contrast, the proton uptake upon acid unfolding that was calculated by using the pK_a values obtained from Finite Difference Poisson–Boltzmann (FDPB) methods applied to only the static crystal structure of the fully native state (58) significantly overestimates the number of protons that are bound upon acid unfolding (Fig. 4B), as well as the midpoint of the pH-induced structural transition (Fig. 3B).

Fig. 4.

Proton-binding properties of the SNase ensemble. (A) Calculated proton titration of the ensemble (black lines), the fully native state (red), and the fully unfolded state (blue) for SNase (solid lines). The proton-binding curves were all zeroed at pH 9.0 to facilitate comparison of the different curves. The vertical line describes the midpoint of the pH-induced transition measured experimentally (Fig. 3B). (B) Experimental and calculated preferential proton binding of the fully unfolded state relative to the fully native state and to the ensemble of SNase. The difference in proton binding between GdnHCl unfolded protein (measured in 6 M GdnHCl/100 mM KCl at 20°C) and native protein (100 mM KCl at 20°C) is shown by the dashed lines (24). The curve marked “Static Model” reflects the difference between proton binding of the fully unfolded state achieved in 6 M GdnHCl and the fully native state, calculated with the pK_a values obtained with continuum electrostatic methods (FDPB) applied to the x-ray structure (Protein Data Bank ID code 1STN). The curve marked “Ensemble Model” represents the difference in proton binding between the fully unfolded state and the ensemble. Gray shading is as described in Fig. 3.

Microscopic Origins of pH Sensitivity. According to the structure-based pK_a calculations with FDPB methods, 16 of the 17 structurally resolved carboxylic residues in SNase titrate with depressed pK_a values, owing to the existence of a large number of relatively weak, medium- to long-range Coulomb interactions between carboxylic residues and the many basic residues on the surface of SNase (C. A. Fitch, S.T.W., V.J.H., and B.G.-M.E., unpublished results). We note that this behavior is not a subtle feature of the FDPB calculation [i.e., even in calculations where the protein is treated artificially with the high dielectric constant of 80 for water, the pK_a values of nearly all Glu and Asp residues are depressed to some degree (C. A. Fitch, S. T. Whitten, and B.G.-M.E., unpublished results)]. Clearly, such a result is difficult to reconcile with the experimental proton-binding experiments (Fig. 4B), which indicate that a subset of the carboxylic residues must titrate with more normal pK_a values. The ensemble approach described here provides a means of explicitly considering the impact of conformational fluctuations on the titration behavior, and the resulting picture of the ensemble can be experimentally validated on a site-specific basis by determining the coupling between the titration of each residue and the global structural transition, as shown below.

According to the ensemble calculations, a subset of Glu and Asp groups titrates with normal pK_a values because they exist in regions of the protein that are predicted to be inherently unstable and therefore to be unfolded in many of the most probable microstates in the ensemble. A detailed inspection of the pH-dependent distribution of the conformational ensemble shows that 7 of the 17 carboxylic residues (Fig. 5A) titrate with normal pK_a values (i.e., above the midpoint of the acid unfolding transition). In the ensemble calculations, the titration of these seven groups is not coupled thermodynamically to the global structural transition; thus, the calculations reproduce the experimental proton uptake upon acid unfolding (Fig. 4B). Note that for the case of acid unfolding at a pH value close to the normal pH where carboxylic residues titrate, the results of the ensemble calculations are fully independent of the set of pK_a,FD values used, provided that they are depressed relative to the set of pK_a,nf values.

Fig. 5.

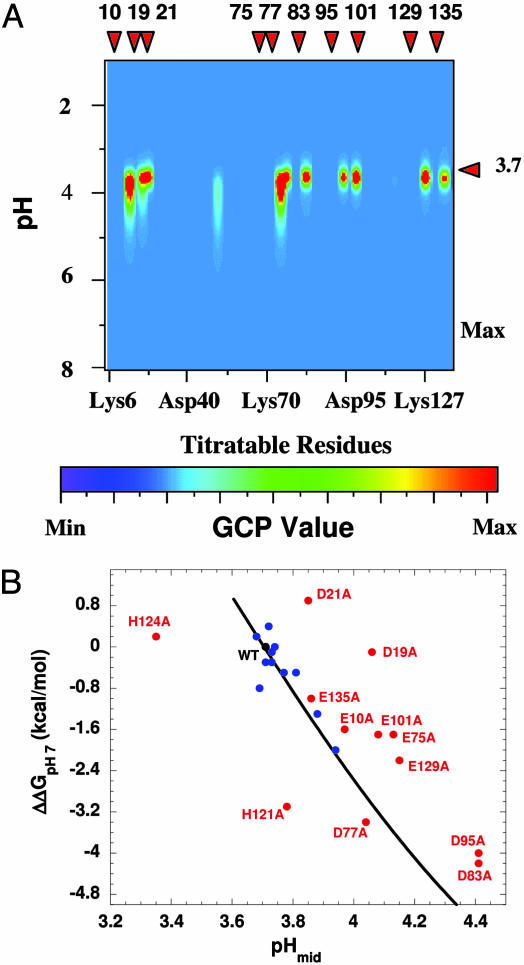
Microscopic origins of the pH-dependent stability of SNase. (A) Global coupling parameters (GCP) were used to identify coupling between proton binding and global conformational stability: GCP(pH)_j = |Z(pH)_f,j – 〈Z(pH)_j〉| × |Z(pH)_nf,j – 〈Z(pH)_j〉|. The values Z(pH)_f,j and Z(pH)_nf,j are the pH-dependent protonation states of residue j in the fully folded and fully unfolded states, respectively. 〈Z(pH)_j〉 is the ensemble-weighted value, equal to ∑_i Z(pH)_i,j·P(pH)_i. GCP of >0 identifies residues whose titration is affected by the pH-dependent redistribution of the conformational ensemble (i.e., their titration is coupled to the acid unfolding). GCP = 0 identifies residues whose titration is not affected by the pH-induced redistribution of the ensemble. The high GCP values are concentrated near pH_mid because they arise when the titration of a residue is coupled to the global shift in the equilibrium population of the ensemble. Only a subset of all ionizable residues (E10, D19, D21, E75, D77, D83, D95, E101, E129, and E135) show high GCP values. These residues are in folded segments in the majority of the highly probable states under native conditions, are predicted to govern the energetics of the acid-unfolding reaction, and are responsible for the cooperative character of this transition. (B) The effects of point mutations on the stability of SNase at pH 7 were measured by GdnHCl-induced unfolding (25). ΔΔG_pH7 describes the difference in stability between the WT protein and the Glu → Ala or Asp → Ala mutants. Also included in this plot are the four His → Ala point mutants. pH_mid refers to the pH at the midpoint of the acid-induced unfolding, monitored by intrinsic fluorescence (25). The black curve describes the expected dependence of pH_mid on global stability, calculated as ΔG(pH) =∫Δν(pH)_WT∂pH. For variants that fall on or close to the curve (blue), the substituted amino acid is not coupled to the global unfolding transition. For variants that do not fall on this line (red), titration at the substituted site is coupled to the global structural transition. Comparison of A and B indicates that the substitutions that fall away from the curve are also the ones that are calculated to contribute to ΔZ in the WT ensemble (see Fig. 4B) and thus determine the pH-dependent energetics of SNase.

To assess the validity of the predictions obtained with the ensemble-based calculations, it was necessary to identify experimentally the 10 residues that are predicted by the ensemble calculations to titrate concomitant with the global unfolding transition. Because SNase unfolds in the pH range where carboxylic residues normally titrate, it was not possible to identify these groups by monitoring their pK_a shifts with NMR spectroscopy. Instead, these groups were identified by measurement of the global unfolding properties of variants with single Glu → Ala and Asp → Ala substitutions. If local fluctuations allow a proton to be bound at pH values above the range of global unfolding (i.e., the pK_a value in the native ensemble becomes normal), then the substitution with Ala should not affect the global unfolding profile. Conversely, the unfolding profile should be affected when a group whose titration is coupled to the global unfolding is substituted with Ala. The results of the mutational experiments shown in Fig. 5B indicate that the subset of residues identified by the ensemble-based calculations as the residues that bind protons concomitant with unfolding (Fig. 5A) are indeed the sites where the Ala substitutions were found experimentally to affect the acid unfolding behavior. The ability of the ensemble-based calculation to accurately model the macroscopic proton uptake and acid unfolding transition, as well as to correctly identify those titratable residues that are responsible for the macroscopic behavior, validates the protocol used for the ensemble calculations, which includes the energy function, the representation of the microstates in the ensemble, and the seemingly arbitrary cutoff criteria used to assign pK_a values. The results also illustrate an important role of local fluctuations in modulating the proton-linked global structural transition in SNase.

Conclusions

Two important implications about the character of local fluctuations and their impact on protein stability and function emerge from these studies. First, the results are consistent with the notion that the native-state ensemble of a protein is populated primarily by states that display a dual character, with some regions being compact and thermodynamically native-like and other regions being highly solvated and displaying the thermodynamic signature of unfolded-like regions (Fig. 1 A). Interestingly, this dual character also has been observed in recent NMR spectroscopy studies that used cold denaturation to characterize structural features of the native-state ensemble (59). In fact, the ensemble calculations described here qualitatively reproduced both the structural and thermodynamic features of the cold denaturation process (59). The ability of this simple ensemble model to reproduce such seemingly disparate processes as ligand-linked conformational equilibria, hydrogen exchange, and cold denaturation suggests that these different processes, and presumably many other solution processes of proteins, are governed by properties of a common set of structural/thermodynamic building blocks.

Second, these results explain mechanistically the manner in which conformational fluctuations can affect the apparent coupling between ligand binding and global structural transitions. Wyman's theory of linked functions (60) explains rigorously and quantitatively how the preferential binding of ligands can affect the equilibrium between two macroscopic conformational states of a protein that bind ligands with different affinities (e.g., the T and R states of hemoglobin). Linkage theory, however, does not contribute mechanistic insight about how this coupling is established, nor about the role of all but the most large-scale conformational changes. The ensemble-based analyses described here demonstrate that the effects of ligands on the conformational equilibrium between two macroscopic thermodynamic states (i.e., the native and acid unfolded states; see Fig. 3A) also can be exerted by differences in binding properties between microscopic elements of the same macroscopic state. In effect, by regulating the binding properties within the macroscopic native state, the stability difference between the native and denatured states can be effectively modulated.

This result has particularly important implications for the design and evolution of proteins. It suggests that the ligand-sensitive equilibria of proteins can be fine-tuned simply by evolution of site-specific local stabilities within the protein. In the context described here, the evolution of the pH sensitivity of a macromolecule need not rely solely on the evolution of Coulomb, polar, or hydration interactions to modulate pK_a values. Apparently, pH sensitivity also can be achieved by tuning the local stability of the microenvironments surrounding ionizable residues, which is equivalent to tuning the dielectric response of the protein (ref. 61 and C. A. Fitch, S.T.W., V.J.H., and B.G.-M.E., unpublished results). In a more general sense, the evolution of allosterism and of cooperativity entails the evolution of a precise balance between the energetics of local fluctuations, ligand-binding affinities, and global stability (62).

Finally, we note that the parameterized energy function used in these ensemble-based calculations (41, 43, 47–55) is extremely simplified and provides only a coarse representation of the energy landscape accessible to each macroscopic state. It might seem paradoxical that such a simple representation of the energies of microstates could provide a unified phenomenological description of seemingly disparate equilibrium processes of proteins (43–46, 59, 63). We interpret the success of this simple approach as evidence of the following: (i) the observed properties of a protein are a manifestation of the energetic hierarchy of states in the ensemble, and (ii) that this hierarchy is a robust feature of each ensemble (i.e., not particularly sensitive to the precise features of the energy function) and therefore amenable to study with a coarse energetic description.

The success of the ensemble calculations suggests that many solution properties of proteins can be described quantitatively without having to go past the level of average properties of microstates and into the description of individual atoms and bonds. In this respect, the ensemble view of proteins constitutes a level of complexity intermediate between the unsophisticated treatment of proteins as strictly static structures and the daunting complexity of their treatment with explicit “all-atom” representations of each accessible conformation. Indeed, an especially appealing feature of the ensemble-based approach described in this study is that it offers a computationally tractable method of apparently sufficient resolution to study and unify disparate processes (46, 63), reconcile the role of conformational fluctuations in modulating functionally important processes (64), and understand proteins in terms of their elementary building blocks (59).