Abstract
Anatomically accurate and biophysically detailed bidomain models of the human heart have proven a powerful tool for gaining quantitative insight into the links between electrical sources in the myocardium and the concomitant current flow in the surrounding medium as they represent their relationship mechanistically based on first principles. Such models are increasingly considered as a clinical research tool with the perspective of being used, ultimately, as a complementary diagnostic modality. An important prerequisite in many clinical modeling applications is the ability of models to faithfully replicate potential maps and electrograms recorded from a given patient. However, while the personalization of electrophysiology models based on the gold standard bidomain formulation is in principle feasible, the associated computational expenses are significant, rendering their use incompatible with clinical time frames.
In this study we report on the development of a novel computationally efficient reaction-eikonal (R-E) model for modeling extracellular potential maps and electrograms. Using a biventricular human electrophysiology model, which incorporates a topologically realistic His–Purkinje system (HPS), we demonstrate by comparing against a high-resolution reaction–diffusion (R–D) bidomain model that the R-E model predicts extracellular potential fields, electrograms as well as ECGs at the body surface with high fidelity and offers vast computational savings greater than three orders of magnitude. Due to their efficiency R-E models are ideally suitable for forward simulations in clinical modeling studies which attempt to personalize electrophysiological model features.
Keywords: Cardiac electrophysiology, Bidomain model, Eikonal model, Electrical activation and repolarization
1. Introduction
The ability to monitor electrical activation and repolarization sequences in the human heart is of fundamental importance for understanding cardiac function under healthy conditions, and plays a pivotal role in the clinical diagnosis and treatment of cardiac diseases. These sequences – often visualized as isochronal maps on the heart built from recorded instants in time which indicate specific local events representative of depolarization or repolarization – are determined by the spatio-temporal distribution of the intrinsic bioelectric sources throughout the myocardium. These sources are the transmembrane currents which enter or leave a cell and thus alter the transmembrane voltages governing the dynamics of myocytes and also set up potential fields in the intra- and extracellular spaces.
A direct observation of bioelectric sources in vivo is currently not feasible. The clinical assessment of electrophysiological aspects of cardiac diseases relies almost exclusively upon the indirect observation of extracellular potentials. The time course of these potentials – referred to as electrograms – are recorded within the body, which acts as an extensive volume conductor. Thus they provide only a filtered non-unique view on the intrinsic sources, which can render their interpretation a challenging task. The degree of filtering depends largely on the distance of a recording electrode to the sources within the myocardial walls as well as conductivity and heterogeneities within the surrounding medium. Such electrogram recordings are ubiquitous in clinical electrophysiological examinations, be it by means of electrodes in implantable devices, with catheters during interventions or with electrical mapping systems which record electrograms synchronously at multiple sites to reconstruct spatio-temporal maps of the extracellular potential field.
A thorough understanding of the mechanisms underlying the genesis of extracellular potential fields within the human body and their relation to the electrical sources within the myocardium is therefore key for the sound construction of activation and repolarization maps, their interpretation and the therapeutic decisions based on it. In-silico computer models show high promise as a tool for gaining a better quantitative insight into the mechanisms which link cardiac sources to their signature in extracellular potential fields. Anatomically accurate and biophysically detailed bidomain models of the human heart and a surrounding torso are considered the gold standard for such forward electrophysiological modeling studies due to their ability to faithfully replicate organ-scale electrophysiology by representing both electrical sources and the concomitant current flow they induce in the interstitial and extracellular spaces. While such simulations have become feasible [46], the associated computational costs are significant due to the reaction–diffusion (R–D) nature of the bidomain model which imposes stability and accuracy constraints on spatio-temporal discretization schemes. Theses costs are considered a limiting factor, effectively restricting the use of such models to highly specialized research software which is able to efficiently exploit current high performance computing (HPC) infrastructure to keep simulations tractable [37,35,48].
Virtually all scenarios considering the clinical application of in-silico models critically depend on the ability of personalizing models to provide complementary input for diagnosis [38], disease stratification [2], therapy optimization, planning and outcome prediction in a patient-specific manner. Such applications require a substantial number of forward simulations as these are integrated in an optimization loop where often sizable parameters spaces must be explored to iteratively re-parameterize models until a sufficiently close match with clinical data is achieved. Typically, in such scenarios the use of R-D models is punitively expensive and thus not easily reconcilable with the constraints imposed by clinical workflows. Computationally cheaper models which yield electrograms of the same or at least of comparable electrophysiological fidelity are therefore sought after as a fundamental key technology for leveraging in-silico modeling in the clinic.
Significant computational savings can be achieved if the spatio-temporal evolution of cardiac sources within the myocardium can be represented accurately using coarser mesh resolutions. The eikonal model [17,31] has become a popular choice in applications where maps of cardiac activation and repolarization are to be modeled [41,28,60]. In this study we further advance this idea by investigating the appropriateness of a reaction-eikonal (R-E) source model for computing electrograms and ECGs which offers the computational advantages of the eikonal model while preserving the full biophysical details of a computationally costly reaction–diffusion (R–D) model. Coupling is achieved by triggering the reaction model through the injection of physiologically motivated stimulus currents in a modified monodomain or pseudo-bidomain model at the instants of depolarization wavefront arrival times as provided by the eikonal model [17,31] These trigger currents raise the transmembrane voltage following the foot of a propagated action potential in the same way as in a full-blown bidomain R-D model. Particular emphasis was put on the coupling of biophysically detailed reaction terms to eikonal-based activation as to ascertain that upstroke and early repolarization phase of the action potential remained unaffected and that repolarization gradients were adequately preserved.
Using a biventricular human electrophysiology model, which also incorporates a topologically realistic His–Purkinje system (HPS), we demonstrate by comparing against a high-resolution R-D bidomain model that the R-E model predicts extracellular potential maps and electrograms in the vicinity of myocardial surfaces as well as ECGs at the body surface with high fidelity at a vastly reduced computational expense. Computational savings greater than three orders of magnitude could be achieved without any appreciable deviations or any reduction in biophysical detail as compared to a full-blown R-D bidomain model. The achieved computational savings stem mainly from relaxed spatial resolution constraints as the R-E models yield converged activation patterns at coarser spatial resolutions. Due to their efficiency, R-E models are ideally suitable for forward simulations in clinical modeling studies which attempt to replicate electrophysiological recordings in the clinic or to efficiently personalize electrophysiological model features.
2. Methods
2.1. Bidomain model
The bidomain equations state that transmembrane currents, Im, that enter intracellular and extracellular spaces by crossing the cell membrane, represent sources for intracellular, Φi, and extracellular, Φe, potentials and are given by
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where Vm = Φi − Φe is the transmembrane voltage and {σi, σe} are the intracellular and extracellular conductivity tensors, respectively. The symmetric positive semi-definite 3 × 3 tensors are defined using scalar conductivities (gl(x), gt(x), gn(x)) associated to (l(x), t(x), n(x)), respectively the longitudinal, transversal and normal fiber directions:
| (6) |
β is the bidomain membrane surface-to-volume ratio, Iei and Ieb are extracellular stimuli applied in the interstitial space or the bath, respectively, Is is a transmembrane stimulus current, Cm is the membrane capacitance per unit area, and Iion is the membrane ionic current density which depends on Vm and a set of state variables, η.
At the tissue-bath interface that is, the interface between interstitial space of the myocardium Ω and the blood pool or the surrounding torso Ωb, continuity of Φe and the normal component of the extracellular current
| (7) |
| (8) |
is enforced. The intracellular space Ω is sealed which is approximated by imposing no flux boundary conditions on Φi,
| (9) |
At the boundaries formed by the surrounding medium, i.e. either the body surface or the boundary of a bath δΩb, no flux boundary conditions for Φe are imposed.
| (10) |
Equations (1)–(5) can be recast and solved in the elliptic-parabolic form given by
| (11) |
| (12) |
The full bidomain model thus provides the most physiologically-realistic representation of cardiac bioelectric activity at the organ scale, yielding Vm and Φe at every point in space and time, as well as implicitly accounting for the effects of bath-loading upon wavefront dynamics through representation of a surrounding conductive media such as blood pool or torso.
2.2. Pseudo-bidomain model
A pseudo-bidomain model approximates a full-blown bidomain model with high accuracy, but at a fraction of the computational costs. The derivation of the pseudo-bidomain model was reported in detail elsewhere [7,6]. Briefly, assuming that the intra- and extracellular domains are both anisotropic, but to the same degree, that is, σe = λσi holds with λ being a scalar, the bidomain equations can be reduced to the monodomain equation [39] by inserting this relation into Eqs. (1) & (2). This yields
| (13) |
where σm is the harmonic mean conductivity tensor or the effective bulk conductivity, which leads to an accurate match in conduction velocities between bidomain and monodomain model along the tissue’s principal eigenaxes [18].
As shown previously [7], bath-loading effects as observed in bidomain models are closely reproduced with monodomain models if the conductivity tensor σm in Eq. (13) is represented by where the * signifies either b in the tissue bulk or s along the surfaces. In the tissue bulk the eigenvalues of are given as
| (14) |
where ζ = l|t|n are the eigendirections of the tissue along the cardiac fiber direction (ζ = l), transverse (ζ = t) to the fibers within a sheet, and along a sheet normal direction (ζ = n). In the myocardial tissue close to the tissue-bath interface a thin augmentation layer is defined within which it is assumed that extracellular conductivity is rather governed by the bath conductivity σb than the interstitial conductivity σe thus the conductivity tensor in the augmentation layer is given by
| (15) |
As shown previously [7], this augmented monodomain approach faithfully accounts for bath-loading whilst, as it is computationally just a monodomain model, only representing Vm(x, t). Using Vm(x, t) as computed with an augmented monodomain as a right hand side of Eq. (11), allows the computation of extracellular potential fields Φe(x, t) within both interstitial Ω as well as bath domain Ωb, respectively. This coupling of an augmented monodomain model with the elliptic portion of the bidomain model in Eq. (11) is referred to as pseudo-bidomain model as it predicts the same activation sequence as a bidomain model, albeit at a much cheaper computational cost, and provides realistic extracellular potential fields in a bounded medium surrounding the heart. The computational complexity of the pseudo-bidomain model is only marginally higher than a monodomain model as the elliptic equation (11) is solved infrequently at those instances which correspond to a specified temporal output granularity. A detailed account on the limitations of the pseudo-bidomain approach has been reported elsewhere [7,6].
2.3. Spatio-temporal discretization
A Galerkin finite element approach using linear tetrahedral elements was used for spatial discretization of the domains Ω and Ωb [50]. The HPS was discretized in space using cubic-hermite line elements [62]. Elliptic (11) and parabolic portions (12) of the bidomain equations are decoupled and solved sequentially [63]. Temporal discretization relied upon elliptic-parabolic decoupling and operator splitting of diffusion and reaction terms. That is, first the elliptic system (11) is solved, then an operator splitting approach is employed to subsequently solve the parabolic system [56,47,57]. This allows us to treat reaction and diffusion terms separately. The reaction term represented by the ODE system (4) is solved using an accelerated Rush–Larsen technique, see [43], and the diffusion problem is solved using a Crank–Nicolson scheme. Using tk = kΔt yields the following linear system of equations to obtain ∈ ℝN × ℝN × ℝN such that
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
where
| (21) |
| (22) |
| (23) |
with being fast acting gating variables solved for by evaluating an analytical solution, τ and are functions of the rate coefficients which govern channel gating kinetics, and are slower acting states, integrated with a forward Euler method [43]. From this construction and we conclude that the matrices (21)–(23) are symmetric and positive semi-definite. The CG method is therefore applicable to solve the linear systems of equations (16) and (20).
2.4. Linear solvers
All linear solvers used in this study were implemented in the publicly available numerical package Parallel Toolbox (pt) [33,23]. The cardiac bidomain equations were solved in parallel using the Cardiac Arrhythmia Research Package (CARP) [61] as an outer framework which was interfaced with the pt library. Technical aspects have been described elsewhere [35]. CARP makes use of the MPI based library PETSc [4] as the basic infrastructure for handling parallel matrices and vectors. Parallel partitioning of unstructured grids relies upon the graph based domain decomposition ParMetis [29,30].
Details on the methods employed for solving the bidomain equations in parallel have been reported previously [42,63,35]. Briefly, the elliptic portion of the bidomain equations is solved using the algebraic multigrid preconditioner ptAMG [33] with an iterative CG solver method (ptAMG-PCG). The parabolic portion of the bidomain equation is solved using an ω-Jacobi preconditioner, also in combination with the iterative CG solver (ωJ-PCG), using an ω of 2/3 and two iterations per CG iteration [35]. In bidomain simulations no extracellular grounding electrode was used. Our solver enforced the average extracellular potential to be zero by employing a rank-one stabilization.
2.5. Eikonal model
In the early nineties, the eikonal model has been proposed as an efficient way of computing arrival times of depolarization wavefronts in the myocardium, and its potential limitations have been studied extensively [17,31,14]. Wavefront arrival times based on the eikonal model have also been used to prescribe the spatio-temporal evolution of the transmembrane voltage to predict extracellular potentials and electrograms [13,15,16].
In the eikonal model, wavefront arrival times ta in the myocardium Ω are described based on a spatially heterogeneous orthotropic velocity function encoded as V (x) and initial activations t0 at locations Γ. The eikonal equation is of the form
| (24) |
where Ω is the myocardium and ta is a positive function describing the wavefront arrival time at location x. The symmetric positive definite 3 × 3 tensor V (x) holds the squared velocities (vl(x), vt(x), vn(x)) associated to (l(x), t(x), n(x)), respectively the longitudinal, transversal and normal fiber directions:
| (25) |
This definition is analogous to that of the conductivity tensor in (6), and since V (x) and σi(x) are based on the same fibers (l, t, n) it follows that the velocities (vl, vt, vn) and the conductivities (gl, gt, gn) in (6) must be proportionally coupled. Fitting conductivity to a desired conduction velocity at a given spatial discretization is a non-trivial task and has been discussed in detail in [19].
It is important to note, that in the intended application of using the eikonal model as a fast forward approach for model personalization, {V, σi, σe} must be identified. For the sake of presenting the methodology, we prescribe constant conduction velocities and rule-based heterogeneous fiber and sheet directions in the intracellular domain.
The eikonal equation is solved using a custom implementation of the Fast Iterative Algorithm [21] with further additions to facilitate the incorporation of a His–Purkinje System (HPS) and its coupling to the myocardium through Purkinje-ventricular junctions (PVJ), similar to an implementation reported in [41].
A finite-element-based tetrahedral tessellation was used to spatially discretize the domain Ω and line elements were used for discretizing the HPS. A PVJ is therefore represented as a vertex where a line element connects to a tetrahedron. Asymmetric delays in impulse transduction between PS and myocardium were taken into account with 10 ms and 3 ms in anterograde and retrograde direction, respectively [27,10].
2.6. Reaction-eikonal model
Using an eikonal model ta(x) can be computed efficiently with sufficient accuracy at a lower spatial resolution and, thus, lower computational cost as compared to R-D models, which demand higher spatial resolutions due to numerical accuracy constraints [36]. This motivates a reaction-eikonal (R-E) model, where the propagation of depolarization wavefronts is mediated by eikonal-based activation maps and not by diffusion. Depolarization at site x is initiated at time ta(x) by a prescribed stimulus current, Ifoot, which is designed to depolarize the local membrane at x above the activation threshold of the sodium current. The time course of Ifoot(t) is chosen to depolarize the membrane following the same foot of an action potential, Vm,foot, as otherwise mediated by diffusion in a R-D model. That is, the foot current in time is given by
| (26) |
and in space by
| (27) |
A detailed rationale on the design of Ifoot(t) is given in Appendix A. In the R-E model the current Ifoot is either added as an additional stimulus current or is used to replace the diffusion term, which yields these two scenarios
| (28) |
or
| (29) |
In the latter formulation the contributions of the diffusion operator towards changing the local transmembrane voltage Vm(x, t) are fully ignored. Note that {Φi|Vm} suggests that either Φi or Vm needs to be inserted, respectively if the bidomain or pseudo-bidomain model is used. This omission is computationally enormously beneficial as the problem of solving the R-E system is reduced to purely local pointwise operations. However, since diffusion plays an important role in smoothing out gradients in Vm during repolarization the total neglect of diffusion may potentially distort the signature of repolarization in electrograms and the ECG to an unacceptable degree. To evaluate the accuracy of these two strategies – referred to as R-E+ or R-E− model which considers or ignores diffusion, respectively – relative to a bidomain R-D model the following models were investigated:
R-E− Diffusion is neglected, thus we solve
| (30) |
R-E+ Diffusion is taken into account. In order to avoid excess stimulation and distortions of the supra-threshold upstroke phase, an additional threshold condition was applied to Ifoot:
| (31) |
where Vth is chosen with a given margin of safety above the intrinsic excitation threshold of the cellular dynamics model used. Therefore, Ifoot(x, t) guarantees a latest time of activation, but activation can happen earlier due to diffusion currents. The equation we solve is then
| (32) |
Both R-E+ and R-E− model were compared to R-D model results to quantify deviations during depolarization and repolarization and to gauge the suitability of these models for predicting potential fields Φe(x, t) and electrograms.
2.7. Evaluation benchmarks
The ability of the R-E model to produce accurate activation and repolarization sequences as well as the fidelity of computed electrograms in the near field close to the electrical sources in the myocardium and in the far field at the body surface was evaluated. The evaluation was based on comparing R-E model predictions against gold standard high resolution bidomain R-D models which served as a reference.
2.7.1. Benchmark setups
Two setups of different complexity were considered, a geometrically simplified geometry of a transmural wedge preparation (dimensions: 25 × 25 × 5 mm) and a human biventricular (BiV) geometry equipped with a topologically realistic model of the His–Purkinje system (HPS). Both geometries were immersed in a conductive bath with a conductivity of σ = 1.0 S/m. Fiber architecture was incorporated assuming a linear rotation of fiber angles from −60° at the epicardium to +60° at the endocardium. Tetrahedral finite element meshes were used to discretize the geometries at different spatial resolutions, dx = 100, 200 and 400 μm for the wedge setup and average discretizations of dx = 220, 440 and 880 μm for the BiV setup. Details on the construction of the BiV benchmark setup were reported previously [3,20].
The Ten-Tusscher (TNNP) model [59] was used to describe cellular dynamics of ventricular myocytes. The TNNP model accounts for differences in the transient outward and slow delayed rectifier currents that make up the intrinsic electrophysiological heterogeneity in endocardial, midmyocardial, and epicardial regions [1]. In the human BiV setup, the ventricular wall consisted of 30% endocardium, 45% midmyocardium and 25% epicardium. In addition to transmural heterogeneity, apicobasal heterogeneity is also known to exist in the heart [58]. In the BiV setup apicobasal heterogeneity was accounted for via an alteration of the slow delayed rectifier potassium current IKs. In humans, action potential duration is longer at the base than at the apex [58]. To incorporate these characteristics into the benchmark setup, the ventricles were divided into base, mid, and apex regions where IKs was rescaled by factors of 1.0, 1.25 and 1.5, respectively [32]. Cellular dynamics in the HPS was described by the Stewart et al. model of a human Purkinje cell [55].
Assuming rotational isotropy of conduction velocities, the scalar conductivities used to compute the conductivity tensors {σi, σe} were chosen close to experimental measurements [49] for the wedge as gil = 0.16069, gel = 0.625, git = 0.04258 and get = 0.236, and for the BiV setup as gil = 0.23415, gel = 0.22, git = 0.08603 and get = 0.13, which resulted in conduction velocities of 0.6 m/s and 0.3 m/s in longitudinal and transverse direction, respectively. Note that subscripts i and e refer to intracellular and extracellular domains, respectively, and l and t to a longitudinal and transversal directions, respectively. These velocities were prescribed for all spatial resolutions. The conductivity of the surrounding bath medium and the blood pool in the BiV, σb, was chosen as 1 S/m. The membrane surface-to-volume ratio was chosen as β = 1/1400 cm−1 and the membrane capacitance as Cm = 1 μF/cm2.
2.7.2. Activation and repolarization sequences
Reference solutions were computed with the highest resolution meshes (100 μm and 220 μm for wedge and BiV setups, respectively) using both bidomain and pseudo-bidomain R-D models to be compared then against pseudo-bidomain R-E models. In the wedge benchmark, R-E models were solved over the same range of mesh resolutions as the R-D model. If not otherwise noted, in the BiV case resolutions of dx = 220 μm and dx = 880 μm were used for R-D and R-E models, respectively.
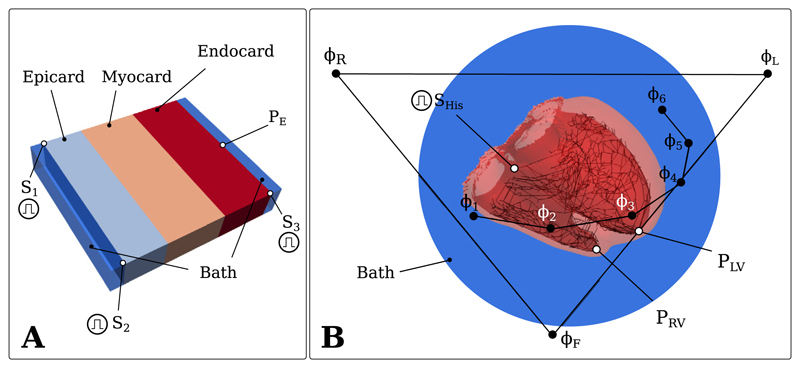
Wavefront propagation in the wedge setup was initiated at the S1 and S3 stimuli at time t = 0 ms and at the S2 stimulus at time t = 5 ms. In the BiV benchmark, propagation was initiated at time t = 0 by stimulating the His bundle (Fig. 1).
Fig. 1.
A) The wedge geometry with the stimuli S1, S2, S3 and the sensing electrode with PE. B) The human BiV geometry with the His stimulus SHis, the right-ventricular and left-ventricular sensing electrodes PRV and PLV and the ECG electrodes ΦL, ΦR, ΦF, Φ1, Φ2, Φ3, Φ4, Φ5, Φ6.
Metrics used for assessing the quality of the R-E approximation during the activation phase were based on the relative deviations between activation maps ta,R–D and ta,R–E
| (33) |
as well as temporal features of the upstroke phase of the action potential such as differences in shape between Vm,R–D and Vm,R–E and rate of rise, V̇m,R–D and V̇m,R–E. Activation maps ta,R–D were constructed by using the instant of maximum upstroke velocity, V̇max, as a marker of local activation [54]. For gauging the fidelity of the R-E models in reproducing repolarization gradients, the spatial distribution of Vm(x, t) over transmural cross section of the wedge experiment and the absolute deviations of Vm(x, tr50) between the R-E models and the R-D model
| (34) |
at tr50 the time instances of 50% repolarization, were compared.
2.7.3. Electrograms and ECGs
Subsequent to the evaluation of the R-E model’s ability to faithfully represent activation maps ta(x) and electrical source fields Vm(x, t), its potential to provide accurate predictions of extracellular potential fields Φe(x, t), endocardial/epicardial electrograms as well as ECGs were analyzed. Electrograms, as measured with endocardial contact mapping systems, recorded in the vicinity of the endocardium, and non-contact mapping systems, recorded in the blood pool, were simulated in both the simplified wedge benchmark and the anatomically accurate BiV benchmark. The same activation and repolarization sequence simulations were repeated with the R-D and R-E models, using a pseudo-bidomain model as an electrical source representation [7], to compute extracellular potentials Φe,R–D and Φe,R–E, respectively. The absolute deviations of Φe between the R-E models and the R-D model, at time instances of activation and repolarization, were compared.
| (35) |
Further, electrogram traces were compared at the recording sites PE in the wedge and PLV and PRV in the BiV benchmark (Fig. 1).
In addition to comparing electrograms recorded in the near field close to the myocardial sources, ECG recordings were simulated in the BiV benchmark to quantify differences between high resolution R-D model and lower resolution R-E model with regard to extracellular potentials Φe in the far field. A simplified ECG model was used based on the assumption of the heart being immersed in an unbounded conductive medium. In this case unipolar extracellular potentials can be recovered by using the integral solution to Poisson’s equation
| (36) |
where Φe are the potentials at a given field point, xf, Im is the source density at a given source point, xs, and rsf = ||xs − xf|| is the distance between source and field point [6,44].
Nine unipolar electrograms {ΦL, ΦR, ΦF, Φ1, Φ2, Φ3, Φ4, Φ5, Φ6} were recovered from leads located at the approximated clinical standard electrode positions {xL, xR, xF, x1, x2, x3, x4, x5, x6} at the torso surface (Fig. 1). Following [34], a twelve lead clinical standard ECG was derived then including the three Einthoven leads {VI, VII, VIII}, the augmented Goldberger leads {VaVL, VaVR, VaVF}, and the Wilson leads {V1, V2, V3, V4, V5, V6}.
2.7.4. Computational costs
Execution times for running R-D, R-E+ and R-E− model were recorded and broken down into the costs of solving eikonal equation (24), parabolic PDE (12), elliptic PDE (11), the set of ODE’s forming the reaction term (4) and of solving Eq. (36) to compute a body surface ECG.
3. Results
3.1. Activation sequence
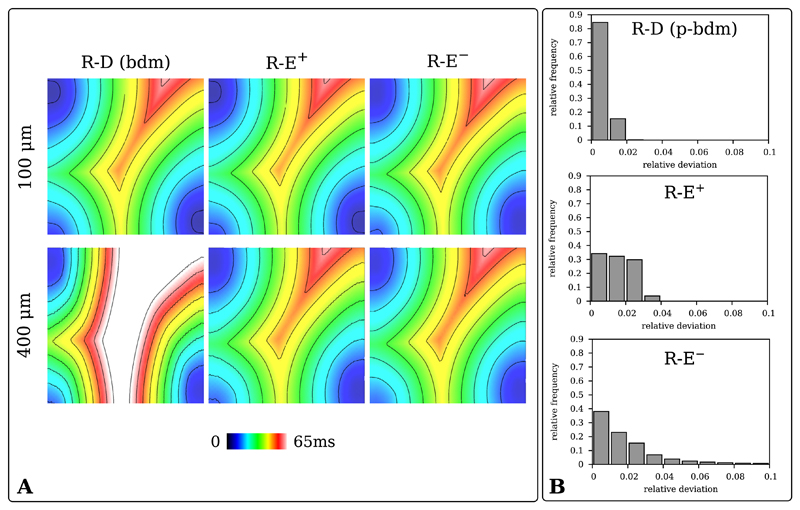
The ability of the R-E model to approximate activation sequences as computed with a high resolution R-D model was gauged by comparing activation maps ta(x). If not noted otherwise, a full bidomain formulation is used for the R-D model and a pseudo-bidomain formulation for the R-E models. A comparison of the maps ta,R-D(x), ta,R-E+(x) and ta,R-E−(x) at dx = 100 μm and dx = 400 μm is shown in Fig. 2A. In contrast to the R-D models, the R-E models do not show any variability in conduction velocity at lower spatial resolutions. Comparing the activation maps at dx = 400 μm with the 100 μm bidomain R-D reference solution reveals that conduction velocity of the R-D models are appreciably slower when reducing spatial resolution from 100 μm to 400 μm [36] whereas this effect was not witnessed with the R-E models.
Fig. 2.
A) Activation maps of R-D bidomain (R-D (bdm)), R-E+ and R-E− models for the 100 μm and 400 μm wedge benchmarks. B) Histograms of the relative difference in activation time from the R-D model for the pseudo-bidomain (R-D (p-bdm)), R-E+ and R-E− models.
Fig. 2B highlights differences in activation patterns, by displaying the histograms of the relative deviation (33) between the gold-standard bidomain R-D model and the pseudo-bidomain R-D, R-E+ and R-E− models. As previously demonstrated [7], with 85% of the activation times showing a deviation below 1%, the pseudo-bidomain R-D based activation sequence matches very closely the activation sequence based on the computationally substantially more expensive bidomain model. Also for the R-E models differences were small, with 95% of the R-E+ activation times having a deviation below 3% and almost 80% of the R-E− activations deviating less than 3%.
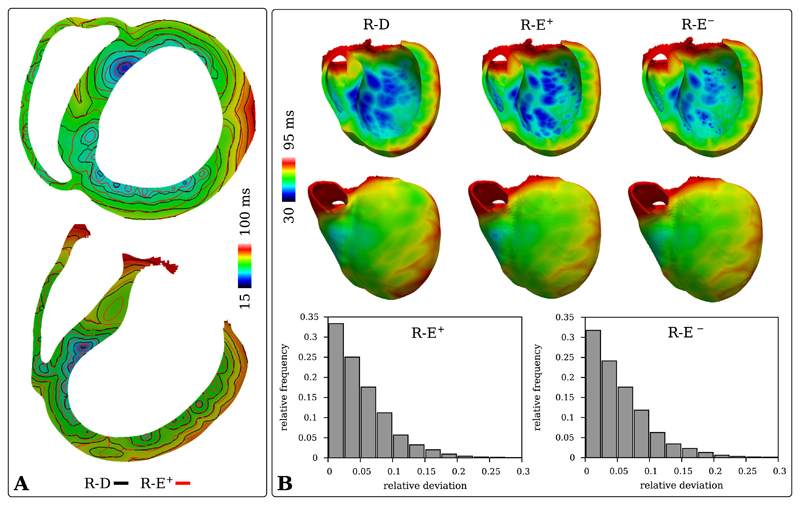
In the human BiV benchmark, a complex HPS initiated ventricular activation sequence was simulated with a R-D bidomain model and a R-E pseudo-bidomain model. The HPS initiated propagation at the ventricular endocardium at numerous PVJs, leading to a large number of depolarization wavefronts which increasingly amalgamated when traversing the myocardial wall in a transmural direction. A close match in shape and locations of the PVJs between the 220 μm and 880 μm BiV discretizations proved to be key in order to match transmural activation shapes. This was not the case at all PVJ locations, as can be seen in Fig. 3A. Still, a good overall agreement of the conduction velocity between the 220 μm R-D simulation and the 880 μm R-E simulations was observed, as a close activation match (75% of activations deviating less than 7.5%) could be maintained over the relatively large spatial distances in the human heart (Fig. 3B).
Fig. 3.
Comparison of activation patterns in the human BiV benchmark with HPS computed with R-D and R-E models at mesh resolutions of 220 μm and 880 μm, respectively. A) Isochronal maps computed from the activation maps obtained with the high resolution R-D model and the lower resolution R-E+ model. B) Upper panels show activation maps ta,R-D, ta,R-E+ and ta,R-E− at the posterior endocardium and anterior epicardium as well as over the transmural cross sections. Lower panels show relative deviation histograms of ta,R-E+ and ta,R-E− w.r.t. ta,R-D.
3.2. Coupling of eikonal model with reaction terms
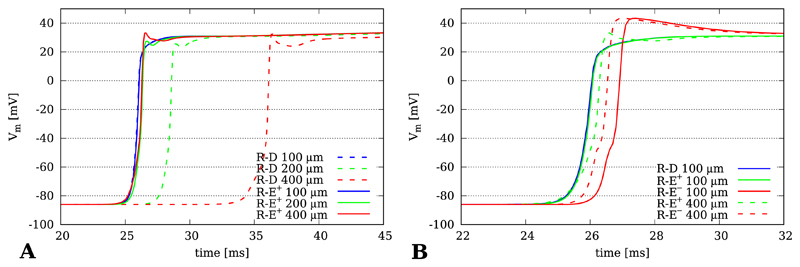
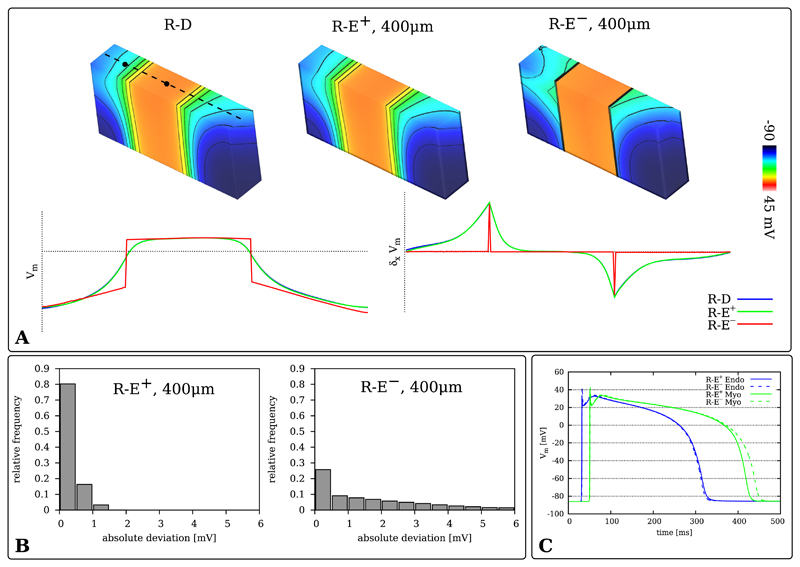
The effect of coupling the eikonal-triggered current, Ifoot(x, t), upon the foot, upstroke and early repolarization of propagated action potentials is illustrated in Fig. 4. Action potential propagation was simulated with R-D, R-E+ and R-E− at grids of varying resolutions dx = 100 μm, 200 μm and 400 μm. The time course of the upstroke of the action potential was recorded at location PE (Fig. 1A). Time traces obtained with the R-D model feature the known artifacts of reduced conduction velocity with coarser spatial discretization [36] (Fig. 4A). Moreover, at the coarsest resolution of dx = 400 μm additional bumps appeared during the upstroke phase of the action potential due to the inaccurate representation of gradients at coarser spatial resolutions. Minor delays were also witnessed with the R-E+ model, albeit to a much lesser degree, however diffusion-mediated bumps during the upstroke phase appeared as well the same way as in the R-D model. At the finer resolutions of 100 and 200 μm the time course of foot and upstroke of the action potential coincided very closely (Fig. 4B). The effect of ignoring diffusion in the R-E− model is highlighted in Fig. 4B. In this case the upstroke is slightly precipitated and the overshoot is overestimated.
Fig. 4.
Time traces Vm(t) taken from location PE at the endocardium of the wedge model. A) Comparison between R-D and R-E+ model for spatial resolutions of dx = 100 μm, 200 μm and 400 μm. B) Comparison between gold standard R-D model with R-E+ and R-E− model. Ignoring diffusion tends to accelerate upstroke velocity and to enhance the overshoot of the action potential.
3.3. Repolarization sequence
Gradients in transmembrane voltage during repolarization are the sources of extracellularly recorded repolarization signals such as the T-wave in the ECG. The fidelity of the R-E models in replicating these gradients were analyzed at tr50 = 305 ms the instant of ≈ 50% repolarization at the center of the wedge preparation (Fig. 5A).
Fig. 5.
A) Differences in transmembrane voltage distribution Vm(xmid, tr50) along a transmural line (dashed line) at tr50 = 305 ms, the instant of 50% repolarization, at the center of the cross section between R-D (100 μm) and the R-E models (400 μm). Vm and its normalized spatial derivative across the center line of the cross section are displayed as graphs. B) Histograms of the absolute deviation of Vm from the R-D model for the R-E+ and R-E− models at 400 μm spatial resolution. C) Time traces of action potentials taken along a central transmural line at positions located at the center of endocardial and myocardial layer (the black circles on the dashed center lines in panel A) for R-E+ and R-E− models. R-D traces are not shown as they are not discernible from the R-E+ case.
As displayed in Fig. 5B, no significant differences were detected between R-D and R-E+ models in the potential map across the center line of the cross section Vm(xmid, tr50) as well as in the absolute deviation metric (34), as the consideration of the diffusion term in the R-E+ model smoothed out intrinsic repolarization gradients exactly the same way as in the R-D model. This was not the case with the R-E− model which neglects diffusion and thus preserves intrinsic gradients. This led to a significant overestimation of spatial gradients across adjacent zones of differing intrinsic action potential duration relative to the R-D model and also altered temporal dynamics of repolarization noticeably (Fig. 5C).
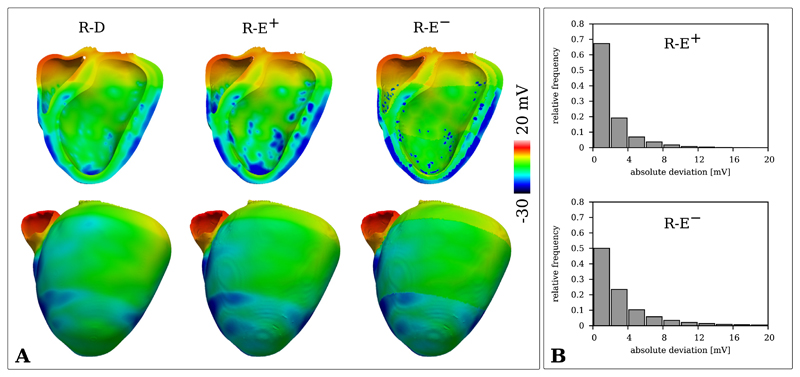
Similar observations were made in the BiV benchmark where repolarization patterns were compared between the high resolution R-D and the lower resolution R-E models. Fig. 6 illustrates differences in repolarization of R-E+ and R-E− relative to the R-D model. The most significant differences appeared in the vicinity of PVJs. Due to the discrete coupling method used, the lower resolution R-E experiments featured larger tissue volumes at lower potential levels around PVJs as compared to the high resolution R-D experiment. As in the wedge experiment, the R-E− model significantly overestimated repolarization gradients around the transitional zones between regions of different intrinsic action potential durations. Quantitatively, the absolute deviation of the R-E models was small, with around 70% of potential values deviating less than 2 mV in the case of R-E+ and 4 mV in the case of R-E−.
Fig. 6.
A) Distribution of Vm of the R-D (dx = 220 μm) and R-E (dx = 880 μm) BiV models during repolarization at t = 330 ms. B) Histograms of the absolute difference between R-D and R-E models of the potential distributions presented in A.
3.4. Electrograms and ECG
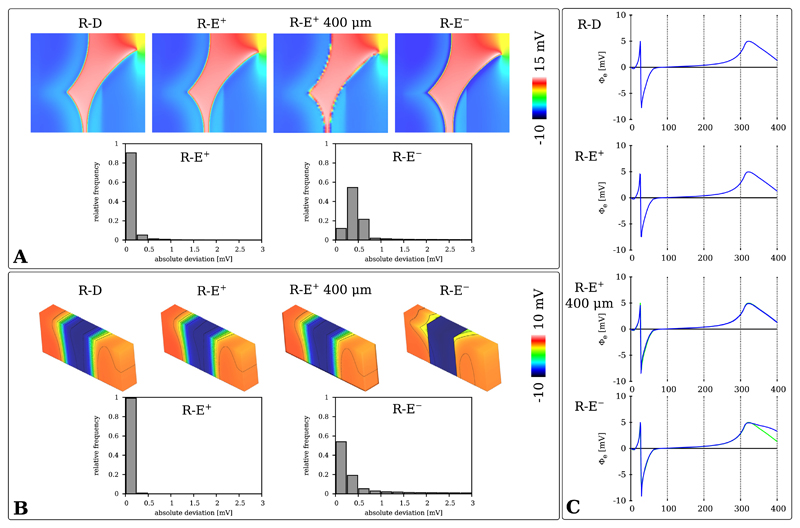
Extracellular potential fields Φe(x, t) were computed with R-D, R-E+ and R-E− pseudo-bidomain models in both wedge and BiV setup. Φe(x, t) in the wedge benchmark was visualized during wavefront propagation at td = 40 ms, the time instance where the activation fronts of S2 and S3 are almost colliding (Fig. 7A), as well as during repolarization at td = 320 ms (Fig. 7B). Unipolar electrograms recorded at electrode location PE are shown in Fig. 7C. All models approximated the depolarization phase of the electrogram with sufficient accuracy which resulted in very similar potential fields Φe(x, t). 90% of R-E+ potential values deviated less than 0.25 mV and 95% of R-E− values deviated less than 0.75 mV. During repolarization, a quantitatively similar accuracy of the R-E models could be observed. Still, the overestimation of spatial gradients of Vm in the R-E− source model due to the absence of diffusion translated into an overestimation of gradients in Φe. This is particularly apparent in the late repolarization phase in the electrogram shown in the R-E− panel of Fig. 7C). In contrast, the R-E+ model yielded electrograms which were virtually indiscernible from those provided by the reference R-D model (compare R-D and R-E+ panel in Fig. 7C). This was also the case when using coarser resolutions (compare R-E+ and R-E+ 400 μm panels in Fig. 7C).
Fig. 7.
Distribution map and absolute deviation histograms of Φe(x) during A) depolarization at td = 40 ms and during B) repolarization at tr = 320 ms in the wedge benchmark. C) Comparison of electrograms Φe(PE, t).
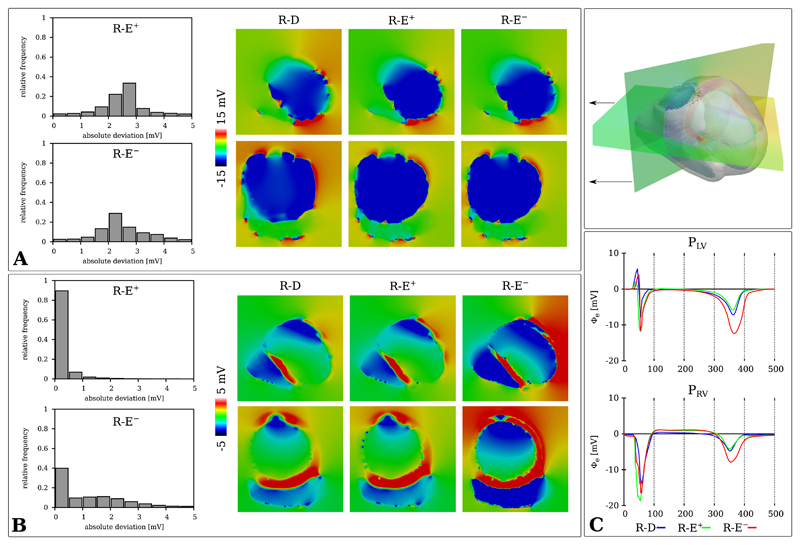
Analogously, the distribution of Φe(x) for the human BiV benchmark was compared during activation at td = 60 ms and repolarization at tr = 390 ms between R-D and R-E models. Minor deviations in potential maps Φe(x, td) during depolarization were apparent between R-D and the R-E models (Fig. 8A). In regions of more pronounced mismatch in the activation map 3A an analogous mismatch was witnessed in Φe(x, td). Quantitatively, most potential deviations were in the range of 1 to 3 mV. The repolarization potentials maps Φe(x, tr) showed excellent agreement between R-D and R-E+ model and noticeable deviations for the R-E− model (Fig. 8B). Similarly, this was apparent with electrograms computed at the recording sites PLV and PRV (Fig. 8C).
Fig. 8.
Potential distribution and absolute deviation histograms of Φe(x, t) during A) depolarization t = 60 ms and B) repolarization t = 390 ms for the R-D (220 μm) and R-E (880 μm) models. C) Electrograms recorded at locations PLV and PRV.
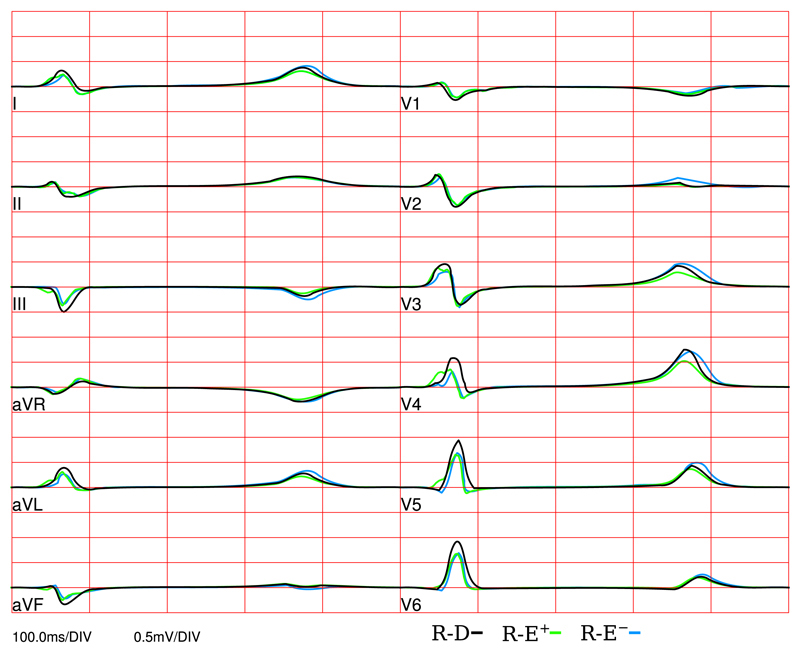
A standard clinical ECG was simulated with R-D, R-E+ and R-E− model using the lead system illustrated in Fig. 1. ECG traces of all three models are shown in Fig. 9. For the depolarization phase, the high resolution R-D model and the low resolution R-E models matched well, with the biggest deviation being at the V4 lead. However, during repolarization the R-E− model showed significant deviations at multiple leads.
Fig. 9.
Clinical standard ECG leads computed with R-D, R-E+ and R-E− models.
3.5. Computational costs
Table 1 summarizes the timings recorded for the human BiV benchmark. Execution times incurred for solving the eikonal equation (24) and forward ECG model (36) were insignificant, amounting only to a fraction of the overall setup time and as such there were not explicitly listed. For instance, computing the activation map ta(x) for the R-E simulations with the 880 μm human BiV model took only ≈7 seconds. The gold standard R-D simulation with a resolution of dx = 220 μm required over three orders of magnitude more CPU time as compared to the R-E+ simulation at a resolution of dx = 880 μm.
Table 1.
Execution time, Texec, in seconds for R-D and R-E human BiV simulation runs, broken down into compute time dedicated to solving elliptic PDE (Ell.), parabolic PDE (Par.) and set of ODEs. The degrees of freedom (d.o.f.) comprising the linear systems to be solved for the 220 μm and 880 μm models, the number of cores, Nc, as well as the used CPU time, TCPU, are given.
| # d.o.f. | # Nc | Ell. | Par. | ODEs | Texec | TCPU | ||
|---|---|---|---|---|---|---|---|---|
| R-D | 220 μm | 46,920,304 | 1,024 | 72,227 | 2,593 | 735 | 75,555 | 7.8 · 107 |
| R-E+ | 880 μm | 1,909,531 | 24 | 854 | 476 | 252 | 1,582 | 3.8 · 104 |
| R-E− | 880 μm | 1,909,531 | 24 | 867 | 1 | 270 | 1,138 | 2.7 · 104 |
4. Discussion
In this study we describe novel methodology for modeling intracardiac electrograms and ECGs in human organ scale models in a computationally efficient manner. A key requirement for modeling electrograms with a high degree of physiological fidelity is a biophysically accurate representation of bioelectric sources in the heart. The cardiac bidomain model or equivalent computationally cheaper variants [7,45] are considered to provide the most accurate source representation at mesoscopic (ensembles of cells large enough for homogenization) up to the macroscopic size scales (larger tissue patches up to the organ scale). However, the reaction–diffusion nature of these models imposes accuracy and stability constraints on numerical solution schemes which demand high spatio-temporal resolutions to resolve the fast transients and steep gradients driving the propagation of depolarization wavefronts, rendering bidomain simulations of human hearts computationally vastly expensive [37,45].
Eikonal equation have been shown to be an accurate approach for computing activation and repolarization sequences in the heart [17,31,14] The plain eikonal equation neglects curvature effects, but can be solved very efficiently [53,21]. To compute electrograms in the interstitial space, within the cavities, at endocardial or epicardial surfaces or at the body surface eikonal-based arrival times of depolarization wavefronts must be coupled to a source model to represent the biophysical quantities such as Vm, Im or Φi [13,15,16]. To achieve this coupling between instants of activation ta as provided by an eikonal model with reaction terms describing the electrical sources in a R-E model in a physiologically accurate way, a set of conditions must be fulfilled for a R-E model to be as universally applicable as possible as an efficient surrogate for a computationally expensive R-D bidomain model. First and most importantly, the difference in electrical activation sequence between R-D and R-E model must be sufficiently small, as activation governs the spatio-temporal behavior of depolarization wavefronts which in turn governs the depolarization complex in electrograms and the ECG. Secondly, the coupling of instants of activations with the reaction term should not distort the upstroke phase, particularly the late positively polarized phase, as any distortions there may interfere with the early repolarization phase of the action potential and, thus, alter the spike and dome morphology and influence important cellular signaling processes governing Ca2+ handling and excitation–contraction coupling [52,24]. Thirdly, during repolarization electrotonic currents act to smooth out the intrinsic heterogeneity of cellular dynamics between different regions in the heart. These interactions are not captured by local computation of reaction terms with eikonal-based activation times. However, the accurate representation of repolarization gradients is delicate as these directly influence the morphology of the repolarization signal in electrograms and the T-wave in the ECG. The developed R-E modeling methodology satisfies all of these requirements.
We demonstrate by comparing against a high resolution R-D bidomain simulation in both a simplified wedge benchmark as well as in a human BiV benchmark that i) activation sequences between R-D and R-E model are matched very closely; ii) the upstroke and overall morphology of the action potential remain unaffected by the R-E approach; and, iii) the repolarization patterns between R-D and R-E models agreed sufficiently well. These features combined yield electrograms and ECG of high physiological fidelity which can be computed with significantly reduced computational expenses as compared to a R-D model. These savings are largely attributable to the ability of the R-E model to accurately represent activation sequences with coarser computational meshes. Overall, these features render the R-E model a highly suitable approach for various modeling applications such as investigating the physics of pacing and sensing or for being used as a forward model in the patient-specific personalization of clinical electrophysiology models. In addition, as all biophysical details of the reaction model are fully preserved, the R-E model is highly suitable as an efficient driver for coupled electro-mechanical simulations which use biophysically detailed coupling between electrophysiology and myofilament model [3].
4.1. Coupling of eikonal model with reaction terms
Eikonal-based activation times must be coupled to a source model to represent the bioelectric sources which generate extracellular potential fields. In general this requires a trigger at time ta at location x to initiate an action potential. The method is based on the mathematical description of the foot of a propagated action potential for which we provide the theoretical underpinnings in Appendix A. Our method provides a generic mechanism for coupling any model of cellular dynamics with an eikonal-based triggering instant ta while avoiding any alterations of cellular dynamics due to the coupling terms. This is achieved by using a physiology-based current, Ifoot, which drives the local membrane up to the threshold of sodium channel opening. Characteristic artifacts as they are typically seen in action potential waveforms stimulated with non-physiological currents, are avoided. Specifically, we demonstrate that i) the foot of the action potentials remains essentially unaffected (Fig. 4); ii) upstroke velocity and the action potential morphology of the positively polarized phase of the upstroke were virtually identical between R-D and R-E+ model. Preserving the morphology of the positively polarized phase of the upstroke and the early repolarization phase as in the R-D model is of pivotal importance as the action potential morphology during these phases may not only strongly influence the internal state variables of a myocyte model [24], but also alter the J-wave in electrogram recordings [65,22]. Most importantly, the early repolarization phase sets the plateau voltage level of the action potential, affects action potential duration and intracellular Ca2+ concentration and therefore impacts Ca2+ handling and excitation–contraction coupling. While the overall action potential morphology may still be comparable, intracellular signaling may be significantly impaired. Similar considerations apply to numerical discretization artifacts which affect the late upstroke phases. For instance, numerical schemes were reported geared towards facilitating the use of coarser spatio-temporal discretizations [64]. Depending on a chosen discretization, action potential morphologies converged towards reference solutions computed with fine spatio-temporal resolutions, but featured striking oscillations during early repolarization. Such significant deviations for the intrinsic morphology during early repolarization are unacceptable in biophysically detailed modeling studies due to the marked impact upon cellular signaling. In the case of the R-E− model alterations in upstroke waveform were noticed. Due to the absence of diffusion the waveform of the late phase of the upstroke resembles the upstroke observed in an isolated myocyte and thus upstroke velocity is faster and the overshoot is more pronounced. Depending on the specific applications such minor deviations may be acceptable or not.
4.2. Activation sequence
The electrical activation sequence ta(x) tracks the spatio-temporal patterns of depolarization wavefronts over the myocardium. These patterns represent the bioelectric sources which drive the extracellular potential fields and shape the depolarization complexes in extracellular potential recordings. An accurate description of bioelectric sources relies therefore upon an accurate representation of the activation sequence and the computation of extracellular potential fields in turn relies upon an accurate source model. The location of wavefronts and their spatial profile is directly reflected in the depolarization complexes of electrograms. An accurate source model is therefore key for modeling electrograms with the best possible fidelity, particularly if finer details of electrograms recorded in closer vicinity to the sources at endocardial or epicardial surfaces are under investigation.
As illustrated in Figs. 2, the R-E model is able to replicate the activation sequence computed with a R-D model at high spatial resolution with high fidelity at lower resolutions at a fraction of the computational costs. However, as shown in Fig. 3, differences in the representation of PVJs at different spatial resolutions may induce some degree of mismatch between high resolution R-D and low-resolution R-E activation patterns. This is to be blamed largely on the discrete coupling approach and uncertainties in the impulse transduction between the HPS and the ventricular myocardium [62].
As evidenced in Fig. 2A, conduction velocity v in the R-D model decreases with decreasing spatial resolution [36,18]. At very coarse resolution, where the spatial extent of the depolarization wavefront Δζ along a given direction of propagation ζ is at the same order of magnitude as the chosen spatial discretization dx, severe distortions of wavefront profiles or even artificial conduction blocks may occur [12]. This is particularly critical under conditions of slow or decremental conduction where Δζ may drop well below the length scale of a myocyte. The R-E model is not prone to any resolution-related artefacts such as slowing of wavefront velocities or artificial conduction blocks, as can be witnessed in Fig. 2. This is at last the case withing certain bounds of spatial resolution and cannot be extended to arbitrary coarse meshes as an overly aggressive reduction in spatial resolution will inevitably reduce geometric fidelity and also fail to capture curvature and rotation of fiber and sheet arrangements. The coupling of eikonal-based activation times with reaction terms as implemented in our R-E model ensures that tissue at location x is activated in the latest at time t ≤ ta(x). A marginally earlier activation is possible in the R-E+ case since the combined effect of diffusion and the eikonal-triggered current Ifoot may precipitate the foot of the action potential such that the threshold of excitation is surpassed earlier than prescribed by the eikonal-based activation time ta.
4.2.1. Wavefront curvature and bath loading effects
Subtle differences in activation sequence between R-E and R-D model are expected since the eikonal model used for driving wavefront spread in the coupled R-E model does not capture all physical effects of the R-D model. In particular, there are three major phenomena impacting the activation sequence that are not accounted for by the R-E model: i) The eikonal model does not account for boundary effects. Wave front propagation accelerates when approaching a sealed end since more charge is available for depolarizing the local membrane as no charge is needed for charging downstream tissue [54]. Further, in the R-E− case, where diffusion is not considered, no normal current flux boundary conditions are imposed and as a consequence, activation isochrones do not meet the boundary at a right angle. Further, minor differences are also expected at sites where propagation is initiated. Relative to uniform conduction observed in tissue areas further away than 5 space constants from any tissue boundary, conduction velocity is slower [54]. ii) Unlike the eikonal-curvature model [31] the plain eikonal model [17] used in this study does not account for conduction slowing and acceleration due to changes in source-sink ratio of wavefronts of concave or convex curvature [11]. Thus wavefronts travel at the prescribed velocity along the eigenaxes of the tissue as if the wavefront was planar. iii) Finally, the R-E model does not capture wavefront acceleration effects due to bath loading [26,5,7,6]. Due to the higher conductivity of the surrounding medium relative to the interstitial conductivity, the conductivity of the extracellular current path at the tissue-bath interface is higher, which translates into a higher conduction velocity in superficial tissue layers [7]. Depending on factors such as the direction of wavefront propagation, the spatial variation in orthotropy due to fiber and sheet arrangement [25] and the ratio of conductivities between bath and interstitial space [7] wavefront profiles may be significantly altered by bath loading effects with a noticeable impact on electrogram signals. Accounting for bath loading with R-E models can be implemented by assigning faster conduction velocity within a thin tissue layer adjacent to the tissue-bath interface, but the accuracy of such an approach was not evaluated in this study.
Activation sequences as shown in Fig. 2 suggest that the impact of bath loading upon wavefront profiles was very minor, despite the use of those conductivity values which were shown to provoke the largest bath loading effect among all the measured interstitial conductivity values reported in the literature [49,51]. Due to the numerous confounding factors the results presented in this study are not sufficiently complete to support a more general claim that bath loading effects do not impact wavefront profiles under all circumstances of physiological relevance. As we have shown previously [8], striking bath loading effects on transmural wavefront profiles are observed for planar wavefronts propagating in an apicobasal direction in absence of fiber rotation. However, in mammalian hearts where fiber rotation is always present and wavefronts move predominantly in a transmural direction, bath loading effects are largely attenuated with the impact of fiber rotation on wavefront profiles dominating over bath loading effects.
4.2.2. Purkinje-ventricular junctions
The endocardial terminals of the HPS – the Purkinje-ventricular junction (PVJ) – play a key role in the initiation of the ventricular activation sequence. There are two major differences in the representation of PVJ between the R-D and R-E simulations: i) While the topology of the HPS and the locations of the PVJs were exactly identical between the R-D and the R-E models, the transduction of the electrical activation from the HPS into the ventricles is mediated by different mechanisms. In the R-E models, each PVJ was connected to a single location at the endocardial surface and anterograde and retrograde transduction delays were precisely prescribed. This is not the case with the R-D model where transduction delays are influenced by the electrotonic load on either side of the junctions and by differences in electrophysiological properties [10]. ii) The mechanism used to transfer diffusion currents between HPS and cardiac tissue is the same between the R-D and R-E+ models. This mechanism does not enforce the volumetric shape of the PVJs to be consistent across different spatial discretizations. As a consequence, the PVJs are represented by different volumetric shapes at different spatial resolutions. This induces differences between the R-D and the R-E models at both activation and repolarization phases, which were not witnessed in the wedge experiments as the HPS was not represented there.
4.3. Repolarization sequence
The repolarization sequence, tr(x), is determined by the activation sequence ta(x) and the intrinsic action potential duration APD(x). APD(x) is modulated by electrotonic currents which act to precipitate or delay repolarization (see Fig. 5). Compared to the duration of the action potential upstroke which lasts only ≈ 1 ms, repolarization is a much slower process lasting for several tens of ms. This translates into a much larger spatial extent of the waveback compared to the spatial extent of the wavefront. The constraints on spatial discretization during repolarization are therefore much more relaxed, facilitating the accurate representation of the spatio-temporal dynamics of wavebacks with much coarser resolutions. Numerical approximation errors are of lesser concern during this phase and as such the exact same discretization schemes can be used in both the R-D and the R-E+ models. Consequently, aside from minor discrepancies introduced by deviations in activation, the repolarization phase is virtually identical between the R-E+ and R-D models (compare R-D and R-E+ panels in Fig. 5). This is not the case for the R-E− model though. As the R-E− does not take into account diffusion intrinsic cellular differences in APD(x) are fully preserved, leading to sharp transitions between regions of different cellular dynamics. These sharp transitions act as artificial sources which noticeably influence the repolarization complex in electrograms (Fig. 7 and Fig. 8). However, it is worth noting that the scenario considered in here with sharp transitions in intrinsic properties of cellular dynamics can be considered an extreme case. Gradients in ion channel properties exist in healthy hearts and are exacerbated in disease, but properties vary spatially in a smoother less abrupt fashion [9]. Thus this distinct disadvantage of the R-E− model is likely to play a less prominent role in cases with physiologically more realistic gradients in ion channels. Further, minor differences in repolarization behavior were also observed over the endocardia. These can be attributed to differences in modeling the physics of coupling the HPS with the myocardium via PVJs which is not identical between R-D and R-E models, as elucidated above in Sec. 4.2.2.
4.4. Electrograms and ECG
In general, extracellular potential maps Φe(x) of the R-D model were accurately replicated with both R-E models which was also reflected in a close agreement of the depolarization complexes in the electrograms. This was also the case during repolarization, but only for the R-E+ model. The R-E− ignores diffusion and thus intrinsic heterogeneities in action potential waveforms were preserved. This introduced artificial sources which led to more severe differences in Φe(x) and noticeable distortions of the repolarization complexes in the electrograms.
Similar conclusions can be drawn with regard to modeling a clinical 12-lead ECG. Differences in depolarization complexes were marginal between the R-E+ and R-E− models. With respect to the R-D model, smaller QRS amplitudes were observed in several leads, but QRS duration was accurately reproduced. T-waves were virtually indiscernible between R-D and R-E+ model in 10 of 12 leads, but significant differences appeared in the R-E− based ECG traces in 6 leads.
While many salient features of the clinical standard ECGs were replicated by our model such as the progression of R magnitude and the reduction in S magnitude in the unipolar Wilson leads, other features such as concordant T-waves in the Einthoven leads or a Q-wave in lead I were not. Replicating all known ECG features for a regular sinus activation driven activation and repolarization sequence would require modifications of the generic Purkinje system as well as a more detailed modeling of repolarization gradients [32]. However, as the focus of this study was to demonstrate the suitability of the R-E model for replicating extracellular potential fields as produced with the gold standard bidomain model, a detailed reproduction of all known ECG features was beyond the scope.
4.5. Computational costs
The computational savings of the R-E models stem mainly from the reduced spatial resolution. Further significant reductions in execution times are possible by reducing temporal resolution as well, but this has not been fully explored in this study. R-E models impose significantly weaker constraints upon spatial discretization, h, compared to the R-D model [36,12]. Artificial h-dependent alterations in conduction velocity and depolarization wave forms are remedied as the coupling of eikonal-based activation maps ta(x) with reaction terms ensures accurately timed onsets of depolarization, even when using a coarser h. Since accuracy and stability constraints play a much less critical role during the repolarization phases as spatial distribution of potentials are smooth and the rates of change with time are more than two orders of magnitude slower than during depolarization, temporal resolution dt can be reduced with R-E models. In the case of the R-E− model, the choice of dt is only governed by the stability constraints imposed by the ODE integrator and the desired accuracy. With R-E− models in absence of diffusion (see Sec. 2.6) even precomputed time-shifted action potentials can be used as reaction terms. In this scenario the entire system of equations is free of time derivatives thus allowing to solve the system only at the desired temporal output granularity and to reduce the solving of the system of ODEs to a simple table look-up. In the R-E− model all computations are entirely local without any need for communication which furnishes this approach with extremely parallel scalability. The R-E+ model is computationally more costly than the R-E− models, but in return allows to represent repolarization as accurately as the R-D bidomain model. This renders the R-E+ model an ideal driver for electro-mechanical simulations in which the coupling between electrophysiology and deformation model shall be represented with full biophysical detail.
Further reductions in h and thus in computational costs may be possible depending on a particular application. With anatomically accurate models such as the human BiV model used in this study the choice of h in the R-E models is dictated by the demands of resolving anatomical features, parameter heterogeneities as well as solution fields with sufficient accuracy. With coarser h the quality of representing potential fields Φe(x) is noticeably diminished leading to jagged and noisy electrograms which cannot be used for further analysis without appropriate filtering (not shown). In our view a choice of h ≤ 1 mm is most suitable for R-E models and can be considered a balanced trade-off between compute cost and accuracy.
4.6. Limitations
Due to its efficiency, the presented R-E model can be used as a fast forward model for a wide range of applications. Application scenarios are the modeling of action potential propagation and the electric fields linked with it. Due to the design based on using the current Ifoot, this also includes models with electrophysiological heterogeneities in terms of resting potential. As discussed in section 4.2.1, a minor limitation of the R-E model in our implementation, is the use of a plain eikonal model to drive activation as opposed to a more advanced eikonal-curvature model. A major limitation of the R-E model in its current form, is its unsuitability for studying conduction block mechanisms or reentrant activation patterns. Any application to problems that involve the formation or maintenance of reentrant activation patterns are therefore precluded.
5. Conclusions
This study presents novel methodology for the efficient computation of electrograms and ECGs in human whole heart simulations. Using the coupled R-E model activation and repolarization sequences and the extracellular potential fields they are generating can be computed with reduced spatio-temporal resolution and, thus, significantly reduced computational costs without compromising on accuracy and electrophysiological fidelity. Extracellular potential maps and electrograms predicted by the R-E model matched very closely – within the margins of uncertainty of such models – with those predicted by the gold standard bidomain R-D model. Computational savings of three orders of magnitude could be achieved. Due to their efficiency R-E models are ideally suitable for forward simulations in clinical modeling studies which attempt to replicate electrophysiological recordings in the clinic or to efficiently personalize electrophysiological model features.
Supplementary Material
Acknowledgments
☆ This research was supported by the grants F3210-N18 and I2760-B30 from the Austrian Science Fund (FWF) and the EU grant CardioProof 611232. Fernando O. Campos acknowledges financial support from CNPq - Brazil. We acknowledge PRACE for awarding us access to resource SuperMUC based in Germany at LRZ (grant CAMEL), and the Vienna Scientific Cluster VSC3. Further support was received from ERACoSysMed administered through ANR-15-CMED-0003-01 and Agence National de Recherche grants ANR-13-MONU-0004-02 and ANR-10-IAHU-04.
References
- [1].Antzelevitch C, Fish J. Electrical heterogeneity within the ventricular wall. Basic Res Cardiol. 2001;96:517–527. doi: 10.1007/s003950170002. [DOI] [PubMed] [Google Scholar]
- [2].Arevalo HJ, Vadakkumpadan F, Guallar E, Jebb A, Malamas P, Wu KC, Trayanova NA. Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat Commun. 2016;7:11437. doi: 10.1038/ncomms11437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Augustin CM, Neic A, Liebmann M, Prassl AJ, Niederer SA, Haase G, Plank G. Anatomically accurate high resolution modeling of human whole heart electromechanics: a strongly scalable algebraic multigrid solver method for nonlinear deformation. J Comput Phys. 2016;305:622–646. doi: 10.1016/j.jcp.2015.10.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Balay S, Buschelman K, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H. PETSc Users Manual, Tech Rep ANL-95/11 – Revision 3.0.0. Argonne Nat. Lab; 2008. [Google Scholar]
- [5].Bernus O, Vigmond E. Asymptotic wave propagation in excitable media. Phys Rev E. 2015;92(1):010901. doi: 10.1103/PhysRevE.92.010901. [DOI] [PubMed] [Google Scholar]
- [6].Bishop MJ, Plank G. Bidomain ECG simulations using an augmented monodomain model for the cardiac source. IEEE Trans Biomed Eng. 2011;58(8):2297–2307. doi: 10.1109/TBME.2011.2148718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Bishop MJ, Plank G. Representing cardiac bidomain bath-loading effects by an augmented monodomain approach: application to complex ventricular models. IEEE Trans Biomed Eng. 2011;58(4):1066–1075. doi: 10.1109/TBME.2010.2096425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bishop MJ, Vigmond E, Plank G. Cardiac bidomain bath-loading effects during arrhythmias: interaction with anatomical heterogeneity. Biophys J. 2011;101:2871–2881. doi: 10.1016/j.bpj.2011.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Boukens B, Sulkin M, Gloschat C, Ng F, Vigmond E, Efimov I. Transmural apd gradient synchronizes repolarization in the human left ventricular wall. Cardiovasc Res. 2015;108(1):188–196. doi: 10.1093/cvr/cvv202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Boyle PM, Deo M, Plank G, Vigmond EJ. Purkinje-mediated effects in the response of quiescent ventricles to defibrillation shocks. Ann Biomed Eng. 2010;38(2):456–468. doi: 10.1007/s10439-009-9829-4. [DOI] [PubMed] [Google Scholar]
- [11].Cabo C, Pertsov A, Baxter W, Davidenko J, Gray R, Jalife J. Wave-front curvature as a cause of slow conduction and block in isolated cardiac muscle. Circ Res. 1994;75(6):1014–1028. doi: 10.1161/01.res.75.6.1014. [DOI] [PubMed] [Google Scholar]
- [12].Clayton RH, Bernus O, Cherry EM, Dierckx H, Fenton FH, Mirabella L, Panfilov AV, Sachse FB, Seemann G, Zhang H. Models of cardiac tissue electrophysiology: progress, challenges and open questions. Prog Biophys Mol Biol. 2011;104:22–48. doi: 10.1016/j.pbiomolbio.2010.05.008. [DOI] [PubMed] [Google Scholar]
- [13].Franzone P Colli, Guerri L. Spreading of excitation in 3-d models of the anisotropic cardiac tissue. I. Validation of the eikonal model. Math Biosci. 1993;113(2):145–209. doi: 10.1016/0025-5564(93)90001-q. [DOI] [PubMed] [Google Scholar]
- [14].Franzone P Colli, Guerri L, Pennacchio M, Taccardi B. Spread of excitation in 3-d models of the anisotropic cardiac tissue. II. Effects of fiber architecture and ventricular geometry. Math Biosci. 1998;147(2):131–171. doi: 10.1016/s0025-5564(97)00093-x. [DOI] [PubMed] [Google Scholar]
- [15].Franzone P Colli, Guerri L, Pennacchio M, Taccardi B. Spread of excitation in 3-d models of the anisotropic cardiac tissue. III. Effects of ventricular geometry and fiber structure on the potential distribution. Math Biosci. 1998;151(1):51–98. doi: 10.1016/s0025-5564(98)10004-4. [DOI] [PubMed] [Google Scholar]
- [16].Franzone P Colli, Guerri L, Pennacchio M, Taccardi B. Anisotropic mechanisms for multiphasic unipolar electrograms: simulation studies and experimental recordings. Ann Biomed Eng. 2000;28(11):1326–1342. doi: 10.1114/1.1327595. [DOI] [PubMed] [Google Scholar]
- [17].Franzone P Colli, Guerri L, Rovida S. Wavefront propagation in an activation model of the anisotropic cardiac tissue: asymptotic analysis and numerical simulations. J Math Biol. 1990;28(2):121–176. doi: 10.1007/BF00163143. [DOI] [PubMed] [Google Scholar]
- [18].Costa C, Hoetzl E, Rocha B, Prassl A, Plank G. Automatic parameterization strategy for cardiac electrophysiology simulations. Comput Cardiol. 2013;40:373–376. [PMC free article] [PubMed] [Google Scholar]
- [19].Costa CM, Hoetzl E, Rocha BM, Prassl AJ, Plank G. Automatic parameterization strategy for cardiac electrophysiology simulations. Computing in Cardiology Conference, CinC; 2013; IEEE; 2013. pp. 373–376. [PMC free article] [PubMed] [Google Scholar]
- [20].Crozier A, Augustin CM, Neic A, Prassl AJ, Holler M, Fastl TE, Hennemuth A, Bredies K, Kuehne T, Bishop MJ, Niederer SA, et al. Image-based personalization of cardiac anatomy for coupled electromechanical modeling. Ann Biomed Eng. 2016;44(1):58–70. doi: 10.1007/s10439-015-1474-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Fu Z, Kirby RM, Whitaker RT. A fast iterative method for solving the eikonal equation on tetrahedral domains. SIAM J Sci Comput. 2013;35(5):C473–C494. doi: 10.1137/120881956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Gima K, Rudy Y. Ionic current basis of electrocardiographic waveforms: a model study. Circ Res. 2002;90:889–896. doi: 10.1161/01.res.0000016960.61087.86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Haase G, Liebmann M, Douglas CC, Plank G. A parallel algebraic multigrid solver on graphics processing units. In: Zhang W, Chen Z, Douglas CC, Tong W, HPCA (China), editors. Lecture Notes in Computer Science. Vol. 5938. Springer; 2009. pp. 38–47. Revised Selected Papers. [Google Scholar]
- [24].He Q, Feng Y, Wang Y. Transient outward potassium channel: a heart failure mediator. Heart Fail Rev. 2015;20(3):349–362. doi: 10.1007/s10741-015-9474-y. [DOI] [PubMed] [Google Scholar]
- [25].Helm PA, Tseng HJ, Younes L, McVeigh ER, Winslow RL. Ex vivo 3d diffusion tensor imaging and quantification of cardiac laminar structure. Magn Reson Med. 2005;54:850–859. doi: 10.1002/mrm.20622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Henriquez CS, Muzikant AL, Smoak CK. Anisotropy, fiber curvature, and bath loading effects on activation in thin and thick cardiac tissue preparations: simulations in a three-dimensional bidomain model. J Cardiovasc Electrophysiol. 1996;7:424–444. doi: 10.1111/j.1540-8167.1996.tb00548.x. [DOI] [PubMed] [Google Scholar]
- [27].Huelsing D, Spitzer K, Cordeiro J, Pollard A. Conduction between isolated rabbit Purkinje and ventricular myocytes coupled by a variable resistance. Am J Physiol. 1998;274:H1163–H1173. doi: 10.1152/ajpheart.1998.274.4.H1163. [DOI] [PubMed] [Google Scholar]
- [28].Jacquemet V. An eikonal-diffusion solver and its application to the interpolation and the simulation of reentrant cardiac activations. Comput Methods Programs Biomed. 2012;108(2):548–558. doi: 10.1016/j.cmpb.2011.05.003. [DOI] [PubMed] [Google Scholar]
- [29].Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J Sci Comput. 1998;20(1):359–392. (electronic) [Google Scholar]
- [30].Karypis G, Schloegel K, Kumar V. Parmetis: parallel graph partitioning and sparse matrix ordering library. Version 1.0. Dept. of Computer Science, University of Minnesota; 1997. [Google Scholar]
- [31].Keener JP. An eikonal-curvature equation for action potential propagation in myocardium. J Math Biol. 1991;29(7):629–651. doi: 10.1007/BF00163916. [DOI] [PubMed] [Google Scholar]
- [32].Keller DUJ, Weiss DL, Dossel O, Seemann G. Influence of IKs heterogeneities on the genesis of the T-wave: a computational evaluation. IEEE Trans Biomed Eng. 2012;59(2):311–322. doi: 10.1109/TBME.2011.2168397. [DOI] [PubMed] [Google Scholar]
- [33].Liebmann M. Efficient PDE solvers on modern hardware with applications in medical and technical sciences. PhD in natural sciences; Institute of Mathematics and Scientific Computing–Karl Franzens University Graz: 2009. [Google Scholar]
- [34].Malmivuo J, Plonsey R. Bioelectromagnetism – Principles and Applications of Bioelectric and Biomagnetic Fields. Oxford University Press; 1995. [Google Scholar]
- [35].Neic A, Liebmann M, Hoetzl E, Mitchell L, Vigmond EJ, Haase G, Plank G. Accelerating cardiac bidomain simulations using graphics processing units. IEEE Trans Biomed Eng. 2012;59(8):2281–2290. doi: 10.1109/TBME.2012.2202661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Niederer SA, Kerfoot E, Benson AP, Bernabeu MO, Bernus O, Bradley C, Cherry EM, Clayton R, Fenton FH, Garny A, Heidenreich E, et al. Verification of cardiac tissue electrophysiology simulators using an n-version benchmark. Philos A Trans Math Phys Eng Sci. 2011;369(1954):4331–4351. doi: 10.1098/rsta.2011.0139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Niederer SA, Mitchell L, Smith N, Plank G. Simulating human cardiac electrophysiology on clinical time-scales. Front Physiol. 2011;2:14. doi: 10.3389/fphys.2011.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Niederer SA, Plank G, Chinchapatnam P, Ginks M, Lamata P, Rhode KS, Rinaldi CA, Razavi R, Smith NP. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc Res. 2011;89(2):336–343. doi: 10.1093/cvr/cvq318. [DOI] [PubMed] [Google Scholar]
- [39].Nielsen BF, Ruud TS, Lines GT, Tveito A. Optimal monodomain approximations of the bidomain equations. Appl Math Comput. 2007;184:276–290. [Google Scholar]
- [40].Paes de Carvalho AP, Hoffman BF, Langan WB. Two components of the cardiac action potential. Nature. 1966;211(5052):938–940. doi: 10.1038/211938a0. [DOI] [PubMed] [Google Scholar]
- [41].Pashaei A, Romero D, Sebastian R, Camara O, Frangi AF. Fast multiscale modeling of cardiac electrophysiology including Purkinje system. IEEE Trans Biomed Eng. 2011;58(10):2956–2960. doi: 10.1109/TBME.2011.2162841. [DOI] [PubMed] [Google Scholar]
- [42].Plank G, Liebmann M, Weber dos Santos R, Vigmond EJ, Haase G. Algebraic multigrid preconditioner for the cardiac bidomain model. IEEE Trans Biomed Eng. 2007;54(4):585–596. doi: 10.1109/TBME.2006.889181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Plank G, Zhou L, Greenstein JL, Cortassa S, Winslow RL, O’Rourke B, Trayanova NA. From mitochondrial ion channels to arrhythmias in the heart: computational techniques to bridge the spatio-temporal scales. Philos Trans R Soc Math Phys Eng Sci. 2008;366(1879):3381–3409. doi: 10.1098/rsta.2008.0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Plonsey R. Bioelectric sources arising in excitable fibers (alza lecture) Ann Biomed Eng. 1988;16:519–546. doi: 10.1007/BF02368014. [DOI] [PubMed] [Google Scholar]
- [45].Potse M, Dubé B, Richer J, Vinet A, Gulrajani RM. A comparison of monodomain and bidomain reaction–diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng. 2006;53:2425–2435. doi: 10.1109/TBME.2006.880875. [DOI] [PubMed] [Google Scholar]
- [46].Potse M, Krause D, Kroon W, Murzilli R, Muzzarelli S, Regoli F, Caiani E, Prinzen FW, Krause R, Auricchio A. Patient-specific modelling of cardiac electrophysiology in heart-failure patients. Europace. 2014;16(4):iv56–iv61. doi: 10.1093/europace/euu257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Qu Z, Garfinkel A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans Biomed Eng. 1999;46(9):1166–1168. doi: 10.1109/10.784149. [DOI] [PubMed] [Google Scholar]
- [48].Richards DF, Glosli JN, Draeger EW, Mirin AA, Chan B, Fattebert JL, Krauss WD, Oppelstrup T, Butler CJ, Gunnels JA, Gurev V, et al. Towards real-time simulation of cardiac electrophysiology in a human heart at high resolution. Comput Methods Biomech Biomed Eng. 2013;16(7):802–805. doi: 10.1080/10255842.2013.795556. [DOI] [PubMed] [Google Scholar]
- [49].Roberts DE, Scher AM. Effect of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ Res. 1982;50:342–351. doi: 10.1161/01.res.50.3.342. [DOI] [PubMed] [Google Scholar]
- [50].Rocha BM, Kickinger F, Prassl AJ, Haase G, Vigmond EJ, dos Santos RW, Zaglmayr S, Plank G. A macro finite-element formulation for cardiac electrophysiology simulations using hybrid unstructured grids. IEEE Trans Biomed Eng. 2011;58(4):1055–1065. doi: 10.1109/TBME.2010.2064167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Roth BJ. Electrical conductivity values used with the bidomain model of cardiac tissue. IEEE Trans Biomed Eng. 1997;44(4):326–328. doi: 10.1109/10.563303. [DOI] [PubMed] [Google Scholar]
- [52].Sah R, Ramirez R, Kaprielian R, Backx P. Alterations in action potential profile enhance excitation – contraction coupling in rat cardiac myocytes. J Physiol. 2001;533(1):201–214. doi: 10.1111/j.1469-7793.2001.0201b.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Sermesant M, Coudière Y, Moreau-Villèger V, Rhode KS, Hill DLG, Razavi RS. A fast-marching approach to cardiac electrophysiology simulation for XMR interventional imaging. Medical Image Computing and Computer-Assisted Intervention, MICCAI, Lecture Notes in Computer Science. 2005;3750:607–615. doi: 10.1007/11566489_75. [DOI] [PubMed] [Google Scholar]
- [54].Spach MS, Kootsey JM. Relating the sodium current and conductance to the shape of transmembrane and extracellular potentials by simulation: effects of propagation boundaries. IEEE Trans Biomed Eng. 1985;32(10):743–755. doi: 10.1109/TBME.1985.325489. [DOI] [PubMed] [Google Scholar]
- [55].Stewart P, Aslanidi OV, Noble D, Noble PJ, Boyett MR, Zhang H. Mathematical models of the electrical action potential of Purkinje fibre cells. Philos A Trans Math Phys Eng Sci. 2009;367(1896):2225–2255. doi: 10.1098/rsta.2008.0283. [DOI] [PubMed] [Google Scholar]
- [56].Strang G. On the construction and comparision of difference scheme. SIAM J Numer Anal. 1968;5:506–517. [Google Scholar]
- [57].Sundnes J, Lines GT, Tveito A. An operator splitting method for solving the bidomain equations coupled to a volume conductor model for the torso. Math Biosci. 2005;194(2):233–248. doi: 10.1016/j.mbs.2005.01.001. [DOI] [PubMed] [Google Scholar]
- [58].Szentadrassy N, Banyasz T, Biro T, Szabo G, Toth BI, Magyar J, Lazar J, Varro A, Kovacs L, Nanasi PP. Apico-basal inhomogeneity in distribution of ion channels in canine and human ventricular myocardium. Cardiovasc Res. 2005;65:851–860. doi: 10.1016/j.cardiores.2004.11.022. [DOI] [PubMed] [Google Scholar]
- [59].ten Tusscher KHWJ, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol, Heart Circ Physiol. 2006;291(3):H1088–H1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- [60].Vergara C, Lange M, Palamara S, Lassila T, Frangi A, Quarteroni A. A coupled 3d–1d numerical monodomain solver for cardiac electrical activation in the myocardium with detailed Purkinje network. J Comput Phys. 2016;308:218–238. [Google Scholar]
- [61].Vigmond E, Hughes M, Plank G, Leon L. Computational tools for modeling electrical activity in cardiac tissue. J Electrocardiol. 2003;36:69–74. doi: 10.1016/j.jelectrocard.2003.09.017. [DOI] [PubMed] [Google Scholar]
- [62].Vigmond EJ, Clements C. Construction of a computer model to investigate sawtooth effects in the Purkinje system. IEEE Trans Biomed Eng. 2007;54(3):389–399. doi: 10.1109/TBME.2006.888817. [DOI] [PubMed] [Google Scholar]
- [63].Vigmond EJ, Weber dos Santos R, Prassl AJ, Deo M, Plank G. Solvers for the cardiac bidomain equations. Prog Biophys Mol Biol. 2008;96(1–3):3–18. doi: 10.1016/j.pbiomolbio.2007.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Whiteley J. An efficient numerical technique for the solution of the monodomain and bidomain equations. IEEE Trans Biomed Eng. 2006;53(11):2139–2147. doi: 10.1109/TBME.2006.879425. [DOI] [PubMed] [Google Scholar]
- [65].Yan GX, Antzelevitch C. Cellular basis for the electrocardiographic J wave. Circulation. 1996;93(2):372–379. doi: 10.1161/01.cir.93.2.372. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.