Homology-dependent methylation in primate repetitive DNA

Abstract

In mammals, several studies have suggested that levels of methylation are higher in repetitive DNA than in nonrepetitive DNA, possibly reflecting a genome-wide defense mechanism against deleterious effects associated with transposable elements (TEs). To analyze the determinants of methylation patterns in primate repetitive DNA, we took advantage of the fact that the methylation rate in the germ line is reflected by the transition rate at CpG sites. We assessed the variability of CpG substitution rates in nonrepetitive DNA and in various TE and retropseudogene families. We show that, unlike other substitution rates, the rate of transition at CpG sites is significantly (37%) higher in repetitive DNA than in nonrepetitive DNA. Moreover, this rate of CpG transition varies according to the number of repeats, their length, and their level of divergence from the ancestral sequence (up to 2.7 times higher in long, lowly divergent TEs compared with unique sequences). This observation strongly suggests the existence of a homology-dependent methylation (HDM) mechanism in mammalian genomes. We propose that HDM is a direct consequence of interfering RNA-induced transcriptional gene silencing.

Transposable element (TE) activity within genomes may have numerous deleterious consequences, such as their insertions into genes or regulatory elements, or genomic disorders resulting from ectopic recombination between homologous TE copies (1). Thus, specific mechanisms that limit such deleterious effects within genomes are expected to have arisen. Indeed, Selker et al. (2) discovered in Neurospora crassa a defense mechanism against TEs associated with DNA methylation [namely, RIP (Repeat Induced Point mutations)]. DNA methylation in the genome of N. crassa is exclusively confined to repeated sequences (3, 4) and causes their inactivation in no more than one generation (reviewed in ref. 3). Although this mechanism is not entirely understood, DNA methylation is triggered by the existence of two or more homologous DNA sequences longer than a few hundred base pairs (3). The immediate inactivation of methylated sequences in N. crassa is a result of massive C-to-T mutational events due to the deamination of methylated cytosines into thymines, which is likely to be induced by the methylase itself (5, 6). Another example indicating that DNA methylation controls the potential deleterious effects of TEs comes from plants: Only TEs exhibit high methylation levels, which prevents their expression (7, 8). In mammals, several lines of experimental and theoretical evidence suggest the existence of a specific methylation pattern in TEs (9–14). For instance, TEs in Mus musculus retain their methylated state during early embryonic stages, whereas nonrepetitive DNA becomes non-methylated (14). In the same species, Yates et al. (12) demonstrated that tandem B1 elements can induce strong de novo DNA methylation. In humans, Chesnokov and Schmid (11) discovered that Alu elements in the germ line escape DNA methylation by binding with a sperm protein, contrarily to those in the somatic lineage (10). Finally, Liang et al. (13) reported in mouse embryonic stem cells that the methylation maintenance of TEs involved a specific cooperativity between two types of DNA methyltransferases, suggesting specific methylation mechanisms and patterns. In apparent contradiction, Rabinowicz et al. (8) reported no differential levels of methylation in mammals between exons and TEs by using a PCR-based technique. However, the technique they used to detect DNA methylation is qualitative rather than quantitative, and hence it is possible that they failed to measure quantitative differences in methylation levels. It is also possible to determine indirectly the pattern of germ-line methylation by analyzing the level of CpG depletion. Indeed, mammalian DNA methylation is limited to the cytosine of 5′-CpG-3′ (hereafter denoted as CpG) doublets, leading to a 10-fold increase of their transition rate due to the passive deamination of methylated cytosines into thymines (5). Kricker et al. (9) used this approach on a small data set of human DNA sequences (comprising <100 sequences, including TEs, genes, and pseudogenes). They observed a stronger CpG depletion in repetitive sequences and concluded that a RIP-like mechanism had evolved in mammals to accelerate the inactivation of repeated sequences. All of these results suggest specific methylation levels in mammalian TEs compared with those of nonrepetitive DNA. Strong DNA methylation in TEs may be under selection for counteracting deleterious effects associated with their activity by diminishing their expression, reducing the frequency of ectopic recombination, and/or by accelerating their inactivation by mutation (1, 9, 15). Here, our aim is to analyze the variability of DNA methylation in primate repetitive DNA throughout the germ line. We took advantage of the fact that the degree of germ-line methylation is reflected by the transition rate at CpG sites. We directly derived the recent substitution pattern in 16.0 megabases of orthologous DNA sequences from primates (human, chimpanzee, and baboon) and analyzed the variability of CpG transition rates in noncoding nonrepetitive DNA and in various TE families. TEs exhibit a high CpG transition rate (37% higher than nonrepetitive DNA), which varies widely with their size and divergence from the ancestral copy, whereas other rates remained comparable with those of nonrepetitive DNA. Such patterns are most likely attributable to homology-dependent methylation (HDM) in primate TEs. Analyses in young primate pseudogenes show higher methylation levels in families with numerous copies compared with single-copy families, consistent with the HDM model. We then discuss the consequences of high CpG transition rates in repetitive DNA on various studies in the field of molecular evolution, the possible molecular mechanisms accounting for HDM in primates, and HDM potential effects on fitness.

Methods

Primate Triple Alignments. To construct genomic human/chimpanzee/baboon alignments, we retrieved large (≥20 kb) chimpanzee and baboon (Pan and Papio species) DNA sequences (291 and 233, respectively) from GenBank (release 135, April 2003). We conducted a similarity search against human chromosomes (Ensembl, release 12.31) by using megablast to roughly map chimpanzee and baboon sequences on their orthologous loci. We then used human/chimpanzee and human/baboon pairwise alignments computed by mga (16) to generate an accurate mapping, which enabled us to identify potential triple alignments. Finally, the alignments were generated by using clustalw and comprised a total of 16.0 megabases of orthologous sites distributed on 17 human chromosomes. More details on the methodology are provided in the supporting information of ref. 17. The alignments are available from the authors upon request.

Sequence Annotation. TEs were detected in primate triple alignments by repeatmasker (A. F. A. Smit and P. Green, unpublished data) using the Repbase Update reference library (38). The output provided an estimate of the TEs' size and divergence from the ancestral copy. CpG islands and exons as defined by Ensembl (release 12.31) were excluded from the analysis.

Site and Substitution Inference. Substitution data relative to primate triple alignments were inferred in human and chimpanzee lineages by using unweighted parsimony on informative sites, with the baboon as the outgroup. It is known that because of multiple substitutions, parsimony may be misleading. Given the evolutionary distances considered here, only hypermutable CpG dinucleotides are expected to generate homoplasy. We therefore considered three classes of sites: (i) sites expected to have never been part of a CpG doublet since the last common ancestor of the three species (non-CpG sites), (ii) sites for which the ancestral human/chimpanzee state was most certainly part of a CpG (CpG sites), and (iii) other sites not belonging to either of the two former categories. We defined non-CpG sites as sites immediately preceded and followed by an identical nucleotide in the three species, excluding C in 5′ and G in 3′. We defined CpG sites as the middle base of the following human/chimpanzee/baboon patterns: XNG/XCG/XCG or XCG/XNG/XCG, with X denoting any nucleotide except C to avoid overlapping CpGs. Indeed, the ancestral human/chimpanzee state is quite likely to have been a C, because it seems by far the most parsimonious scenario. We also considered the sites fitting the complementary pattern as CpG sites.

Substitution Rate Inference. In what follows, we use the notation XX̄ → YȲ to refer to a substitution from X to Y or its complementary (i.e., from X̄ to Ȳ). Substitution rates in primate triple alignments were estimated simply by dividing the number of observed changes by the number of inferred ancestral sites. In non-CpG sites, we inferred by parsimony six rates (pooling together complementary rates): four transversion rates (AT → TA, GC → CG, AT → CG, and CG → AT) and two transition rates (GC → AT and AT → GC). In CpG sites, three rates were estimated: two transversion rates (GC → CG and CG → AT) and one transition rate (GC → AT). For better rate estimates, we pooled together substitutions in human and chimpanzee lineages.

Validation of Site and Substitution Rate Inferences. Concerning site and substitution rate inferences relative to primate triple alignments, simulations in ref. 17 revealed that (i) sites that we defined as non-CpG sites truly evolved without being part of a CpG, (ii) sites that we defined as CpG sites were truly part of an ancestral CpG before the human/chimpanzee split, and (iii) all substitution rates relative to these two categories were accurately estimated (rate estimation errors ≤ 3%).

Pseudogene Triple Alignments. To study the substitution pattern in recent retropseudogenes, we built triple DNA alignments including the pseudogene and its functional human paralogous coding sequence (CDS) and using the corresponding mouse orthologous CDS as an outgroup. A total of 5,961 human processed pseudogenes and their paralogous functional CDSs were extracted from the Hoppsigen database (18) (http://pbil.univ-lyon1.fr/databases/hoppsigen.html). Only lowly divergent pseudogenes (i.e., presenting a divergence of <10% with their paralogous functional gene) were retained for this analysis. The mouse orthologous genes were extracted by using hovergen (19), and triple alignments were computed by using clustalw. We then selected two sets of pseudogenes: (i) those belonging to families with only one processed pseudogene (denoted as rare pseudogenes) and (ii) those belonging to families with >10 lowly divergent processed pseudogenes (denoted as numerous pseudogenes). Finally, 193 alignments were kept, 124 with rare pseudogenes and 69 with numerous pseudogenes. The pseudogene alignments are available from the authors upon request.

Pseudogene Site and Substitution Rate Inferences. We defined CpG and non-CpG sites as above, excluding sites on third codon positions to avoid potential biases due to saturation. The substitution rates in pseudogenes were estimated as for those in primate triple alignments. We had to use the third codon position to infer CpG and non-CpG sites on first or second codon position. However, the relatively low overall pseudogene divergence to their paralogous functional coding sequence (<10%) and the restrictive definition of CpG and non-CpG classes made site and substitution rate inferences reliable (rate estimation errors ≤ 5%).

Pseudogene Substitution Rate Comparisons. It is not possible to directly compare the rate of substitution measured in different pseudogenes, because they do not have the same age. We therefore computed relative substitution rates. Notably, we measured the relative rate of transition at CpG sites (i.e., the ratio of GC → AT transition at CpG sites to GC → AT transition at non-CpG sites). We compared these ratios in families of rare and numerous pseudogenes. To test the significance of these differences, we used a Monte Carlo approach. Given the same number of sites, we simulated the substitution data (10,000 replicates) in rare and numerous pseudogenes by using estimates of the two substitution rates relative to the ratio under consideration. Such estimates were computed by pooling site and substitution data in rare and numerous pseudogenes (i.e., under the null hypothesis that the pseudogene category had no effect on substitution rates). The frequency of the simulations that displayed a difference between the two ratios greater than that observed provided an estimate of the P value.

Results

Substitution Rate Inference in Primate TEs. To analyze TE substitution rate variability in the human and chimpanzee lineages, we aligned 16.0 megabases of orthologous noncoding DNA sequences from human, chimpanzee, and baboon (see Methods). The triple alignments were located on 17 human chromosomes. As previously reported (17), the average rate of divergence (excluding indels) between human and chimpanzee is 1.1%, and the average rate of divergence between baboon and human or chimpanzee is 5.7%. We then searched our alignments for CpG and non-CpG sites for which substitution rates could be reliably inferred by parsimony (referred to as CpG and non-CpG substitution rate, respectively). The whole data set included 54,371 non-CpG substitutions and 8,618 CpG substitutions among 8,202,418 non-CpG sites and 147,739 CpG sites. We computed by parsimony six and three substitution rates in non-CpG sites and CpG sites, respectively, for various categories of DNA sequences [nonrepetitive, long interspersed elements (LINEs), short interspersed elements (SINEs), LTRs, and DNA transposons], pooling substitution data in human and chimpanzee lineages. A summary of the substitution data for each of these features is given in Table 1.

Table 1. Summary of the alignments and substitution data.

	No. of sites		No. of substitutions
Sequence	Non-CpG	CpG	Non-CpG	CpG
SINE	994,321	39,355	7,235	2,594
LINE	1,363,688	11,500	9,995	803
LTR	421,422	6,077	3,203	446
DNA transposon	259,076	3,043	1,816	202
Nonrepetitive DNA	5,163,911	87,764	35,325	4,573

No. of sites, no. of orthologous bases in a triple alignment; no. of substitutions, no. of informative substitutions.

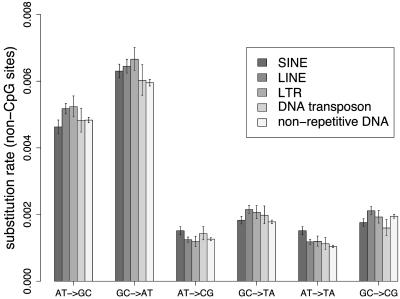
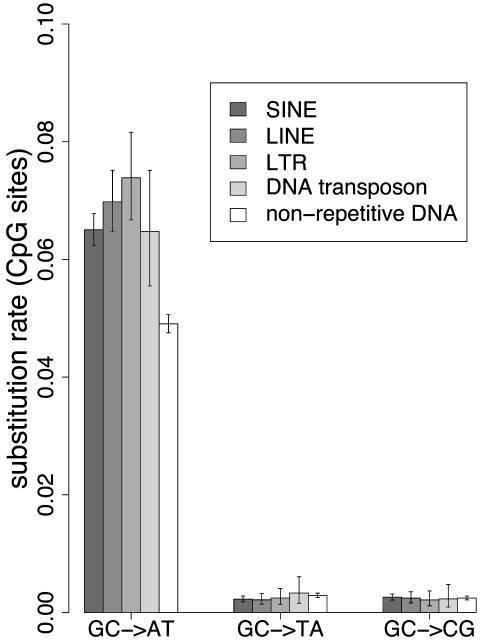
Substitution Rate Variability in TEs. Rates of substitution at non-CpG and CpG sites were estimated in nonrepetitive DNA and in various TE families (Figs. 1 and 2, respectively). Overall, rates of substitution at non-CpG sites are similar in TEs and nonrepetitive DNA (Fig. 1). The only noteworthy observation at non-CpG sites was a small increase in the substitution rate in TEs compared with that of nonrepetitive DNA (an 8.0% increase on average, with a maximum of 21.2% for the AT → TA transversion rate). The GC → TA transversion rate was higher in CpG sites than non-CpG sites (×1.5) in nonrepetitive DNA but did not significantly differ between TEs and nonrepetitive DNA CpG sites (4.8 ± 0.6 × 10^–3 substitutions per site versus 5.4 ± 0.5 × 10^–3 substitutions per site, respectively; P = 0.179). The most striking observation is that the rate of transition at CpG sites was very different in TEs compared with nonrepetitive DNA. The ratio (CpG GC → AT transition rate)/(non-CpG GC → AT transition rate) was 8.3, 10.3, 10.3, 11.7, and 12.5 for nonrepetitive DNA, SINEs, DNA transposons, LINEs, and LTRs, respectively. The CpG transition rate was significantly higher in each TE family compared with that in nonrepetitive DNA, and a mean increase of 37% was observed when comparing the CpG transition rate in all of the TEs with that in nonrepetitive DNA (6.7 ± 0.2 × 10^–2 substitutions per site versus 4.9 ± 0.04 × 10^–2 substitutions per site, respectively; P = 1.62 × 10^–36).

Fig. 1.

Non-CpG substitution rate in nonrepetitive DNA and TEs. Substitution rate is the number of substitutions per non-CpG site since human–chimpanzee divergence. Confidence intervals at the 5% level are displayed. Complementary substitutions were pooled together. We used the notation XX̄ → YȲ to describe complementary substitutions (i.e., X̄ → Y + X̄ → Ȳ). For example, AT → GC = A → G + T → C.

Fig. 2.

CpG substitution rate in nonrepetitive DNA and TEs. Substitution rate is the number of substitutions per CpG site since human–chimpanzee divergence. (See legend of Fig. 1.)

CpG Substitution Rate and Regional Factors. Patterns of substitution vary along mammalian chromosomes, notably according to large-scale variations in GC content (the isochores) and to the rate of recombination (17, 20). These regional variations of substitution patterns have an impact on both TEs (21) and nonrepetitive DNA (17). But, interestingly, these variations apparently do not affect the rate of substitution at CpG sites. Indeed, whereas LINEs and SINEs have an opposite distribution along the genome [SINEs are more frequent in GC-rich isochores, whereas LINEs are more frequent in GC-poor isochores (22)], they both show a similar increase in CpG transition rate compared with nonrepetitive sequences (Fig. 2). Moreover, we found no significant relationship between the rate of CpG transitions in nonrepetitive DNA and the GC content of isochores or the rate of recombination (see Supporting Text and Figs. 7 and 8, which are published as supporting information on the PNAS web site), suggesting that CpG substitution rate variations were not influenced by regional factors.

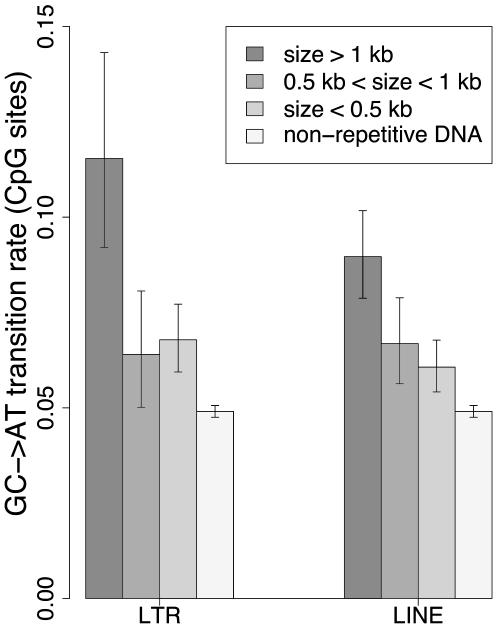
CpG Transition Rate and Size of TEs. We analyzed the rate of CpG transition in LINEs and LTR elements according to their size. We classified these TEs into three size groups: <500 bp, between 500 bp and 1 kb, and >1 kb (these values were chosen to have similar sample sizes in each group). As shown in Fig. 3, the CpG transition rate increased with the size of LINE and LTR elements. Remarkably, the CpG transition rate in LINEs > 1kb was significantly higher than that of those < 1 kb (9.0 ± 1.2 × 10^–2 substitutions per site versus 6.2 ± 0.6 × 10^–2 substitutions per site, respectively; P = 2.5 × 10^–5). A similar trend was observed in LTR elements (11.5 ± 2.8 × 10^–2 substitutions per site for LTRs > 1 kb versus 6.7 ± 0.7 × 10^–2 substitutions per site for LTRs < 1 kb; P = 5.4 × 10^–5). SINE elements displayed very little size variation, and hence it was not possible to investigate the impact of their size on CpG transition rates. DNA transposons were excluded from the analysis because of the paucity of substitution data.

Fig. 3.

CpG transition rate and size of TEs. GC → AT transition rate is the number of G → A + C → T transitions per CpG site since human–chimpanzee divergence. size, TE size. Confidence intervals at the 5% level are displayed.

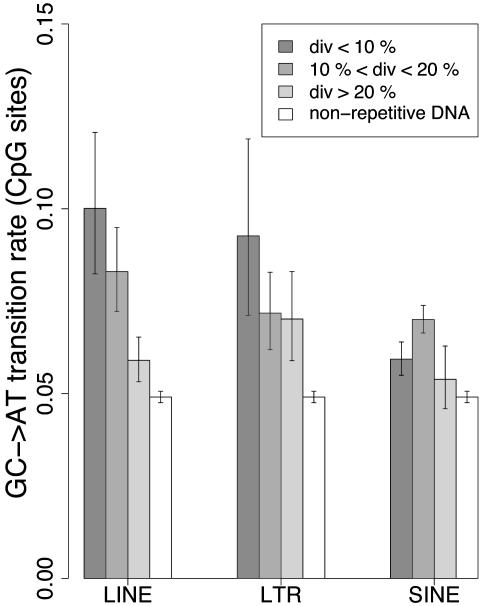
CpG Transition Rate and Divergence of TEs. We also investigated whether the CpG transition rate in TEs was correlated with their divergence from their ancestral copy. We classified LINEs, SINEs, and LTRs into three divergence groups: <10%, between 10% and 20%, and >20%. Again, such values were chosen so as to obtain groups with similar sample sizes. As shown in Fig. 4, the rate of CpG transition generally decreased with increasing divergence. The CpG transition rate in LINE elements clearly decreased with respect to their divergence (P = 1.1 × 10^–6). LTR elements with divergence < 10% exhibited a higher CpG transition rate than other LTRs, although this trend was marginally significant (9.3 ± 2.6 × 10^–2 substitutions per site versus 7.1 ± 0.8 × 10^–2 substitutions per site, respectively; P = 0.088). Interestingly, CpG transition rates were significantly higher in SINEs of intermediate divergence (between 10% and 20%) compared with those of other SINEs (7.0 ± 0.4 × 10^–2 substitutions per site versus 5.8 ± 0.4 × 10^–2 substitutions per site, respectively; P = 7.1 × 10^–5). DNA transposons were excluded from the analysis because of the paucity of substitution data.

Fig. 4.

CpG transition rate and divergence of TEs. div, TE divergence from its ancestral copy expressed as a percentage. (See legend of Fig. 3.)

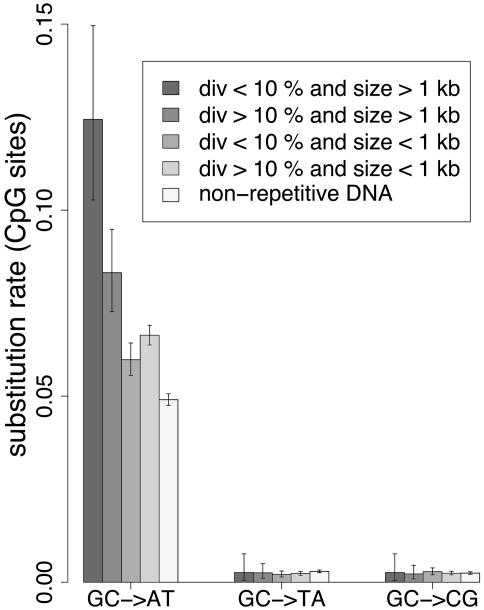
Variations in CpG Substitution Rate with Size and Divergence. The size and divergence of TEs are not independent parameters: Over time, TEs accumulate both base substitutions and deletions, and hence TE size is negatively correlated with TE divergence. To disentangle the relative contribution of the two parameters, we analyzed the CpG substitution rate variations as a function of size and divergence simultaneously. To have enough substitution data in each class of TE size and divergence, we pooled data from LTRs and LINEs. The CpG substitution rates as a function of both size and divergence are shown in Fig. 5. Consistent with Fig. 2, the transversion rates showed very little variation with no particular trend, whereas the CpG transition rates varied widely according to the TE size and divergence. For short TEs (<1 kb), the CpG transition rate exhibited very little variation with divergence (from 6.0 × 10^–2 substitutions per site with divergence < 10% to 6.6 × 10^–2 substitutions per site with divergence > 10%). In long TEs (>1 kb), the CpG transition rate varied markedly with divergence (from 8.3 × 10^–2 substitutions per site with divergence > 10% to 12.4 × 10^–2 substitutions per site with divergence < 10%). Thus, both TE size and divergence are correlated with the CpG transition rate. However, precisely exploring CpG transition rate variations with TE size and divergence will require more data.

Fig. 5.

CpG substitution rate as a function of size and divergence of TEs. Substitution rate is the number of substitutions per CpG site since human–chimpanzee divergence. size, TE size; div, TE divergence from its ancestral copy expressed as a percentage. (See legend of Fig. 1.)

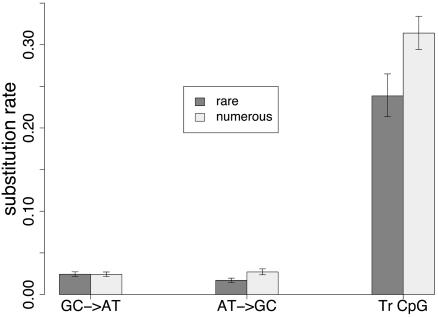
Analysis of Substitution Rates in Processed Pseudogenes. We have shown that the rate of transition at CpG sites is higher in TEs than in nonrepetitive DNA. To test whether this phenomenon is specific to TEs or common to all repeated sequences, we analyzed the substitution pattern in recent processed pseudogenes. For this purpose, we built triple alignments including one human retropseudogene, its cognate functional gene, and the orthologous functional gene in mouse (used as an outgroup). Substitution rates were inferred as for TEs, except that third codon positions were excluded because of possible problems of saturation for the comparison with the outgroup (see Methods). We compared the rates of substitution in two data sets of processed pseudogenes (see Table 2): (i) those belonging to families with only one pseudogene (denoted as rare pseudogenes) and (ii) those belonging to families with >10 recent pseudogenes (denoted as numerous pseudogenes). Transition rates in rare and numerous pseudogenes are shown in Fig. 6 (note that transversion rates were not presented because there were not enough substitutions for an accurate estimation). The rate of transition at CpG sites is higher in numerous pseudogenes than in rare pseudogenes. However, because the age of these pseudogenes is unknown, it is not possible to compare directly their rate of substitution (see Methods). We therefore computed the relative rate of transition at CpG sites [i.e., the ratio (CpG GC → AT transition rate)/(non-CpG GC → AT transition rate)]. These two rates shared the same nature and differ only by their CpG context. This ratio was significantly greater in numerous pseudogenes than in rare pseudogenes (13.00 versus 9.78; P = 0.0072). Thus, the increase of the GC → AT transition rate, due to CpG context effect, was higher for numerous pseudogenes than for rare pseudogenes.

Table 2. Summary of processed pseudogene data.

		No. of sites		GC content
Family size	Mean length	Non-CpG	CpG	Pseudogene	Coding sequence
1	946	23,132	1,090	0.369	0.499
>10	956	20,190	2,118	0.513	0.557

Family size, no. of processed pseudogenes in a family; mean length, mean base no. in an alignment; no. of sites, no. of sites for which the substitution pattern could be safely derived.

Fig. 6.

Non-CpG and CpG transition rate in processed pseudogenes. Substitution rate is the number of substitutions per site in processed pseudogenes. “Tr CpG” denotes transition rate in CpG sites. Other rates are relative to non-CpG sites. rare, rare pseudogenes; numerous, numerous pseudogenes. Transversion rates were not presented because there were not enough substitutions for an accurate estimation. (See legend of Fig. 1.)

Discussion

HDM in Primate Repetitive DNA. In this study, we compared the pattern of substitution in TEs and nonrepetitive DNA in primates. Our most striking observation is that the transition rate at CpG sites is significantly higher (by ≈37%) in TEs than in nonrepetitive DNA and shows considerable variations among TEs. Such variations cannot be explained by the influence of regional factors such as local GC content or local recombination rate (Figs. 7 and 8). This effect is specific to transition at CpG sites: Substitution rates at non-CpG sites and transversion rates at CpG sites are similar in TEs and nonrepetitive DNA (see Figs. 7 and 8). These fluctuations in the CpG transition rate at CpG sites are therefore most likely attributable to different levels of methylation in the germ line. Thus, our results support the idea that the methylation level in primates is significantly higher (by ≈37%) in TEs than in nonrepetitive DNA. Remarkably, the rate of CpG transitions increases with TE size and decreases with their level of divergence from the ancestral TE (Figs. 3, 4, 5), except for SINE elements, whose substitution pattern is discussed below (see Fig. 4). Again, this effect is specific to transition at CpG sites (see Supporting Text; see also Figs. 9–11, which are published as supporting information on the PNAS web site). In particular, long (>1 kb) LINEs and LTRs with a divergence < 10% exhibit a 2.7-fold rate increase in their CpG transition rate compared with nonrepetitive DNA. Together, these results indicate that the level of DNA methylation in the primate germ line increases substantially in long, lowly divergent repeated sequences. This observation supports the existence of a HDM mechanism in mammals. If so, all kinds of repeated sequences should be affected. Moreover, the level of DNA methylation should increase with the number of copies dispatched throughout the genome. To test these predictions, we analyzed substitution rates in retropseudogenes that belong to families with either a single copy or numerous copies. The increase of the GC → AT transition rate in CpG sites compared with that in non-CpG sites was significantly higher in numerous pseudogenes (×13.00) than in single pseudogenes (×9.78). This result indicates a higher methylation level in large retropseudogene families, in agreement with the HDM model.

Methylation Pattern in SINE Elements. In apparent contradiction with the HDM model, SINEs display a lower degree of methylation in copies with low divergence (<10%) compared with copies of intermediate divergence (10–20%). The result of Chesnokov and Schmid (11) provides an attractive explanation for the relatively low methylation level in SINEs. Indeed, these authors demonstrated that Alu elements (the main components of the SINE family) are protected from methylation in the human germ line because they bind with a sperm protein. As Alu elements diverge, their ability to bind the sperm protein is probably reduced, and they become more methylated. Thus, the peculiar methylation pattern in SINEs is most likely due to the fact that lowly divergent Alus are protected from methylation in the germ line.

TEs as Markers of Neutral Evolution. Numerous studies in the field of molecular evolution rely on the assumption that the substitution pattern observed in TEs is a good marker of the evolution of neutral sequences (21, 23, 24). Some used TEs as markers of genome-wide neutral evolutionary rate and interpreted lower divergence rates in nonrepetitive DNA as a sign of natural selection (23, 24). Simulations (data not shown) show that the difference of CpG transition rates in TEs compared with nonrepetitive DNA has a weak impact on the overall sequence divergence, suggesting that the analyses in refs. 23 and 24 are not affected by high CpG transition rates in TEs. Arndt et al. (21) studied the substitution rates of various TE subfamilies reflecting ≈250 million years of evolutionary time. They observed a 4-fold increase in the CpG transition rate 90 million years ago and interpreted this increase as evidence of a genome-wide change in the CpG transition rate that would have occurred at the time of mammalian radiation (21). Here, we have shown that the present pattern of CpG transition (since human–chimpanzee divergence) is different in nonrepetitive DNA and in TEs and also varies according to the age of TEs (Fig. 4). Our results, therefore, indicate that the evolution of the methylation pattern in TEs does not perfectly reflect the evolution of methylation in the whole genome. However, this bias is probably not strong enough to change the conclusion of Arndt et al. (21). Indeed, our analyses show that the relative transition rate at CpG sites (i.e., the ratio of the GC → AT transition rate in CpG sites over the GC → AT transition rate in non-CpG sites) varies presently from 8.3 in nonrepetitive DNA to 21.0 in long, lowly divergent TEs, whereas the analyses of Arndt et al. (21) indicate that 90 million years ago, this ratio was only 1.52. Thus, there was clearly a strong change in the rate of transition at CpG sites during mammalian evolution.

Molecular Mechanisms Accounting for HDM. Which molecular mechanism could be responsible for the HDM of genomic sequences in mammals? Various mechanisms involving DNA–DNA, RNA–DNA, and/or RNA–RNA pairing can be proposed (25). One model involving DNA–DNA pairing has been elaborated from the methylation patterns observed in plant and fungi (26). It assumes a genome-wide scanning for homologous sequences using DNA–DNA pairing, the detection of which would trigger their methylation (25, 26). DNA–DNA pairing is a well established genomic feature involved in recombination processes, for instance. However, to our knowledge, no experimental work provided evidence for DNA–DNA pairing as a potential starting point for a molecular pathway involving DNA methylation. Thus, the model appears valid but lacks experimental support. Another interesting hypothesis is that HDM could result from RNA interference: homologous repeats that are transcribed could interact at the RNA level, triggering RNA-induced transcriptional gene silencing (TGS). The TGS mechanism can be summarized as follows: Two fragments of transcribed RNAs that can pair with one another trigger a molecular pathway, leading to the methylation of DNA sequences that are homologous to the interacting RNA fragments (27–29). There are two reasons why we favor this model of HDM mediated by RNA interference. First, although most of the TE copies present in mammalian genomes are defective, many of them are transcribed. Indeed, TEs are very frequent in mammalian genomes, not only in intergenic regions, but also in introns and UTRs of protein-coding genes (22, 30) and within noncoding transcription units (31). In other words, all TE families include many copies that are transcribed when their host gene is expressed (22). Moreover, these TEs inserted within genes are found in both orientations relative to the transcription of the host gene (22, 30, 31). Hence, all TE families include some copies that are transcribed in opposite orientation and thus that can potentially lead to the formation of dsRNA. Secondly, it has been recently demonstrated that dsRNA does induce TGS through methylation in primates (29, 32, 33). Given these two observations, it is expected that TEs should be subject to methylation through this process of RNA interference. It is important to note that this mechanism can also account for the DNA methylation of nontranscribed copies of TEs. Indeed, if in a given TE family some sequences are transcribed and form dsRNAs, the TGS mechanism should lead to DNA methylation of all homologous TE copies in the genome, including the nontranscribed ones. We therefore believe that in genomes with a TGS mechanism featuring DNA methylation, HDM should come as a natural consequence. This model is consistent with numerous studies proclaiming TGS as a key process influencing DNA methylation in a broad range of organisms such as fungi, plant, and metazoa (27–29, 34–36).

HDM and Natural Selection. Here, we provide evidence for the existence of HDM in primates. The increase in TE CpG transition rates are not sufficiently high to cause substantial variations in their inactivation speed by mutation, which suggests that HDM is not selected for rapid inactivation of repetitive DNA. Alternatively, effects of HDM on fitness could be the control of repetitive DNA expression and/or the diminution of ectopic recombination between similar copies. It is also important to point out that HDM might also affect the pattern of bona fide gene expression (32, 33, 37). Thus, it seems likely that besides its role as a defense mechanism against TEs, HDM has been recruited during evolution for regulating the expression of genes and therefore could turn out to be a potent tool for gene expression regulation.