Comparative evolutionary genetics of spontaneous mutations affecting fitness in rhabditid nematodes

Abstract

Deleterious mutations are of fundamental importance to all aspects of organismal biology. Evolutionary geneticists have expended tremendous effort to estimate the genome-wide rate of mutation and the effects of new mutations on fitness, but the degree to which genomic mutational properties vary within and between taxa is largely unknown, particularly in multicellular organisms. Beginning with two highly inbred strains from each of three species in the nematode family Rhabditidae (Caenorhabditis briggsae, Caenorhabditis elegans, and Oscheius myriophila), we allowed mutations to accumulate in the relative absence of natural selection for 200 generations. We document significant variation in the rate of decay of fitness because of new mutations between strains and between species. Estimates of the per-generation mutational decay of fitness were very consistent within strains between assays 100 generations apart. Rate of mutational decay in fitness was positively associated with genomic mutation rate and negatively associated with average mutational effect. These results provide unambiguous experimental evidence for substantial variation in genome-wide properties of mutation both within and between species and reinforce conclusions from previous experiments that the cumulative effects on fitness of new mutations can differ markedly among related taxa.

Few topics in evolutionary biology have generated as much controversy in recent years as spontaneous mutation, considered at the level of the entire genome (1–4). It is widely accepted that the great majority of new mutations are either neutral or deleterious (refs. 1 and 5–7; also see refs. 3 and 8–13), and the importance of deleterious mutations to a wide variety of biological processes and phenomena is well appreciated (7). The source of the controversy stems from uncertainty in the rate at which new mutations accrue in the genome and the distribution of effects of those mutations on fitness.

Beginning in the early 1960s, Mukai, Ohnishi, and their colleagues (14–18) conducted several large mutation accumulation (MA) experiments with Drosophila melanogaster that were designed to estimate the rate and average effect of new mutations on fitness. By the early 1970s, the results seemed clear: averaged over experiments, egg-to-adult viability declined rapidly, on the order of 1% per genome per generation, with the implication that the diploid genomic mutation rate (U) was on the order of 0.6 per generation or greater and the average homozygous effect on fitness of a new mutation (2ā) was ≈0.05 or less. The typical newborn fly was thus expected to harbor one new mutation that could be expected to reduce its viability by ≈5% when homozygous.

Several additional lines of evidence supported the results from the early fly MA experiments. First, the considerable inbreeding depression in Drosophila implied either a high rate of deleterious mutation or considerable overdominance, for which there was little evidence (ref. 19, chapter 10; also see ref. 20). Second, it was well established that the rate of new lethal mutations in D. melanogaster was ≈0.02 per genome per generation (21, 22), and it was considered likely that the overall rate of deleterious mutations that are not lethal would be greater than the rate of lethal mutations. Third, the standing genetic variation observed in Drosophila was broadly consistent with the high rate of mutation inferred from Mukai's experiments (23–25). The evidence seemed compelling, and given the difficulty of acquiring the data, the “classical” Mukai-Ohnishi results essentially took on the status of gospel for a generation of evolutionary biologists.

In the mid-1990s, motivated in large part by the “deterministic mutation” theory of the evolution of sex (26), there was a resurgence of interest in genomic mutational properties with conflicting results. Several new MA experiments with Drosophila resulted in a decline in mean fitness (and U) an order of magnitude less than the classical result (27–29), although other experiments produced results fairly consistent with the classical values (22, 30, 31). Some reanalysis of Mukai's data resulted in a much smaller U and a much larger ā than Mukai's own calculations (32–34), although others did not (31, 35); the apparent steep decline in viability was variously attributed to adaptation of control populations or the increasing ability over the course of experiments of observers to identify the “curly” wing mutants that served as markers. Extrapolation of estimates of molecular mutation rates in flies to the entire genome were interpreted as implying a much lower genomic mutation rate than the classical values, although those interpretations are rife with assumptions, and similar analyses applied to mammals imply a considerably higher mutation rate than the classical fly rate (1, 36). Finally, two MA experiments with the N2 strain of the nematode Caenorhabditis elegans (37–39) and two MA experiments with different strains of the annual plant Arabidopsis thaliana (40, 41) resulted in much slower declines in fitness than the classical fly studies with U concomitantly lower by about an order of magnitude. Drake et al. (6) suggested that the apparent difference in mutation rates between flies and worms/Arabidopsis could potentially be adaptive, arising from differences in mating system; C. elegans and Arabidopsis are largely self-fertilizing, whereas Drosophila is not. However, if the classical fly experiments greatly overestimated the genomic mutation rate, explanations that invoke adaptive differences in mutation rate between selfing and outcrossing taxa are unnecessary.

By 1999, there was such uncertainty about genomic mutational properties that an influential review of the field referred to “the riddle of deleterious mutation” (1). In our opinion, there are three possible explanations for the so-called riddle. First, the classical interpretation of the fly data may be largely correct. If so, the much slower mutational decay in fitness of C. elegans and Arabidopsis argues that there is real variation among taxa in mutational properties, which in turn argues that the rate, and perhaps the average effect, of new mutations is an evolved property. However, this explanation also implies that estimates of mutational decline in several recent Drosophila experiments must be atypically low.

Alternatively, it may be that both the classical fly experiments and the recent fly experiments that appear to refute them are correct and that there is considerable variation in mutational properties even within D. melanogaster. Fry (35) has argued that the mutational decline in Ohnishi's (18) experiment is much lower than in Mukai's (14, 42) experiment and that even within Mukai's study, a subset of lines may have a much higher mutation rate than others. Fry concluded that the most likely explanation for the discrepancy between fly studies is genetic variation in mutation rate between strains of flies, but the evidence is circumstantial. Whether such variation could result from adaptive evolution is uncertain. “Mutator” strains are known to evolve in experimental populations of bacteria and yeast (43), particularly under conditions of environmental stress. There is considerable debate about whether the stress-induced increase in mutation rate in microorganisms is adaptive (44–46), although there is evidence that it is (47). However, it is not clear that the evolutionary dynamics of mutators in microorganisms with extremely large population sizes are relevant to the evolution of multicellular organisms whose population sizes must be smaller by many orders of magnitude (48). Mutator alleles are not expected to fix by positive selection in sexual taxa because recombination will break up the linkage disequilibrium between the mutator allele and the beneficial mutations it generates (49–51). However, it has been demonstrated that transposable element (TE) activity varies among strains of numerous organisms, including Drosophila (52) and C. elegans (53) and crosses involving balancer stocks of Drosophila, such as those used by Mukai, often show increased TE activity (1). The strains of C. elegans and Arabidopsis for which we have MA data have little TE activity (40, 53, 54), which could account for the difference between those species and the classical fly studies.

The third possibility is that the variation in mutational properties represents the error variance inherent in empirical biology as a result of different labs, protocols, observers, etc. We emphasize, however, that there are likely to be underlying biological phenomena of interest buried in the “error” variance as we have defined it. For example, mutational properties have been shown to depend on the environment in which individuals are assayed. Flies raised under “stressful” conditions show larger mutational declines in fitness than do experiments with flies raised in “benign” conditions (30), and the same appears to be true for C. elegans (39) and yeast (55). It may be that much of the variation between experiments in Drosophila is not a main effect of source genotype but rather a genotype-by-environment interaction such that either the fraction of mutations that are deleterious or the magnitude of their effects (or both) depend on the environmental context.

To begin to resolve the uncertainty regarding the nature of spontaneous mutations, we initiated a comparative MA experiment by using two strains from each of three species of Rhabditid nematodes, chosen on the basis of their similar life histories. Our goal is to characterize the extent of genetic variation in the mutational process within and among species. If mutational properties do not differ substantially among strains, it would imply that they have been conserved over at least 100 million years of evolution and is consistent with the idea the mutation rate has been optimized over the course of evolution (6). Conversely, the existence of significant genetic variation in the mutational process, at any hierarchical level, does not rule out the possibility that the mutation rate is optimized, but it obviously argues against the existence of a globally conserved optimal mutation rate. Ascertaining the causes of genetic variation would require further investigation. Here, we report results after ≈200 generations of MA.

Materials and Methods

Systematics and Natural History of Nematode Strains. We chose two species in the genus Caenorhabditis, C. elegans and C. briggsae, and the confamilial species Oscheius myriophila. All are androdioecious hermaphrodites; androdioecy appears to have evolved independently in these three species (56). Hermaphrodites can only outcross to males (57), which are rare in laboratory cultures of all three species (≈0.1% in most strains of C. elegans). Generation time of all three species at 20°C is ≈3.5 days, and fecundity is similar in all species.

C. elegans is divided into two clades that are divided by a deep node (58). From one clade we chose the N2 strain; from the other we chose the PB306 strain. We chose the HK104 and PB800 strains of C. briggsae and the EM435 and DF5020 strains of O. myriophila. C. briggsae and C. elegans are believed to have diverged at least 50 million years ago (59), with Caenorhabditis and Oscheius having diverged well before then. Collection information on all strains is available from the Caenorhabditis Genetics Center.

Mutation Accumulation. MA protocols have been outlined in detail in ref. 38. The principle is simple: many replicate lines of a highly inbred stock population are allowed to evolve in the relative absence of natural selection, thereby allowing deleterious mutations to accumulate. Descendent populations are then compared with the ancestral control stock. If the average effect of new mutations is not zero, the mean phenotype will change over time. Because different lines accumulate different mutations, the variance among lines will increase over time, even if the average mutational effect tends to zero. In sexual diploids, the change in the mean phenotype is the product of the gametic mutation rate, U/2, where U is the diploid genomic mutation rate and the average homozygous effect of a mutation, 2ā (ref. 19, p. 341). With certain assumptions (see below), the per-generation change in mean phenotype (R_m) and the per-generation change in the among-line component of variance (V_b) can be used to calculate U and ā.

We began by inbreeding each strain for six generations by self-fertilization of a single hermaphrodite. After the sixth generation of inbreeding, populations were allowed to expand to a larger size, and worms were frozen by using standard methods (57). Frozen worms were thawed and allowed to reexpand to a large population size. From this ancestral source population, 100 replicate lines from each strain were started from a single worm in March 2001. All lines were kept at 20°C in the same incubator and propagated by transferring a single immature worm at four-day intervals. At each transfer, the prior three generations were kept as backups, the first generation at 20°C and the second and third at 10°C. If a worm failed to reproduce, it was replaced with a single worm from the preceding generation. If a worm was slow to reproduce (unhatched eggs or visibly gravid), it was held over for the four-day interval without going to the backup. Lines that were held over thus had fewer generations of reproduction than those that were not held over. We refer to G_max as (total time in days)/4, the maximum number of generations a line could have been through. Backups were usually taken from the same generation as the dead or missing worm.

The probability of fixation of a new mutation is a function of its selection coefficient s and the effective population size N_e; mutations with a selection coefficient s < 1/4N_e are expected to accumulate at the neutral rate (60). With single hermaphrodites, N_e = 1, so mutations that reduce fitness by <25% will be invisible to selection.

Fitness Assays. Fitness was assayed twice, at G_max = 100 generations (G100) and again at G_max = 200 generations (G200); both assays were done in two blocks. The protocol for assaying fitness follows that of Vassilieva and Lynch (38, 39). We describe the assay for G100; the G200 assay was similar, except as noted. Worm husbandry (e.g., incubator conditions and seeded plates) was as in the MA phase of the experiment. At G100, all surviving MA lines were frozen. At the beginning of the first block, 34 randomly chosen MA lines from each strain were thawed (except O. myriophila EM435, of which many MA lines did not survive freezing). Similarly, a sample of the control population was thawed, and 20 worms were chosen to begin replicate lines and allowed to reproduce. From each of the 34 MA and 20 control lines, 5 replicates were started from a single worm and transferred by single-worm descent for three generations (P1–P3). Plates were assigned a random number, and after the first generation, were identified only by the random number and handled in random numerical order. If a worm failed to reproduce at the P1 or P2 generation, we started the plate again at the previous generation. A single newly hatched offspring (labeled R1) was collected from each P3 parent and put on a fresh plate. On the third day of an R1 worm's life, it was removed and placed on a fresh seeded plate and transferred to a new plate daily for the next three days. The plate from which the R1 worm was removed was incubated overnight at 20°C to allow eggs to hatch and then were stored at 4°C for subsequent counting. In most cases, reproduction after the third day of reproduction was negligible. Upon completion of the assay, plates were stained with 0.075% toluidine blue, and worms were counted under a dissecting microscope at ×20 magnification.

The protocol for the second G100 assay block was the same as for the first block except we used 15 control lines per strain instead of 20, we did not replace worms that failed to reproduce, and the EM435 strain was included. We used a different set of MA lines in block 2 than in block 1 (e.g., MA lines 1–34 in block 1 and MA lines 35–67 in block 2). Thus, for each strain/treatment group, “line” is nested within block rather than crossed with block.

The G200 assay was identical to block 1 of the G100 assay except that EM435 was included. We attempted to use the same lines in the G200 assay that we used in G100. A few lines went extinct between G100 and G200 and several lines used in G100 did not thaw in G200, so the sets of lines were mostly but not completely congruent in the two assays (see Table 2, which is published as supporting information on the PNAS web site).

Data Analysis. Replicates that made it to the R1 generation were scored as “present” in the assay; individuals that were present that produced offspring were said to have “survived.” “Productivity” was calculated as the lifetime reproduction of all worms that survived. Total fitness (W̄) was calculated as the lifetime reproduction of all worms present at R1. We report results for W̄; results for Productivity were very similar and are available in Table 3, which is published as supporting information on the PNAS web site.

For a given species and strain, each observation was formulated as a mixed model as in ref. 41. For the tth generation (t = 0, 100, or 200), the ith MA line, and jth observation of that line, the model is y_tij = R_m × t + block effect + m_i + error_tij. The random effects associated with the ith MA line, m_i, are assumed to be normally distributed. The three generations of data for a given species and strain are treated as three separate traits in a multivariate maximum likelihood variance component analysis where the error covariances are zero as are the mutational variances and covariances associated with generation 0 (the control lines) (41). The (mutational) covariance between generations 100 and 200 is expected to be equal to the generation 100 mutational variance (61), although these parameters are not constrained to be equal (Tables 4 and 5, which are published as supporting information on the PNAS web site). In no case did the generation 0 among-line variance differ significantly from zero (data not shown). The per-generation change in mean trait value (R_m) was estimated within the analysis as the generalized linear regression coefficient of trait value on generation number. The per-generation increase in the among-line variance (V_b) was estimated as 2V_M, where V_M is the per-generation input of genetic variance from new mutations (41).

We also report the per-generation change in the mean scaled as a fraction of the control mean ΔM = R_m/z₀. To determine confidence limits on ΔM, bootstrap means were calculated for each treatment (MA and control) for each assay block at each generation (100 and 200) by resampling lines within each block with replacement, calculating the block mean and taking the mean of the two blocks as a pseudoestimate of the treatment mean; a pseudoestimate of ΔM was then calculated as (z̄₀ – z̄_t)/tz̄₀. The resampling protocol accounts for variation both within and among blocks within an assay. One thousand pseudo-values of ΔM were generated; the standard deviation of the bootstrap distribution is an approximate standard error (62).

Hypotheses were tested by using likelihood ratio tests. We first tested the hypothesis that R_m did not differ among all strains. We then tested the hypotheses that R_m did not differ between species and between strains within each species. To accomplish this test, we obtained the profile of the likelihood function under the null hypothesis of equal R_m by calculating the log likelihood for each strain at a given R_m and summing these values over the (independent) strains. This process was repeated for R_m values ranging from 0 to –0.5 in 0.01 decrements. The maximum of this likelihood profile was taken as the log likelihood of the H0. To obtain the maximum of the likelihood under the alternative hypothesis of R_m differing among strains, we summed the maximum likelihood for the separate unconstrained single-strain analyses. To calculate the reported P values for comparisons across strains, the maximum profile likelihood (null hypothesis) was compared with the sum of the separate MLEs (alternative hypothesis), and twice this difference was compared with the χ²⁽ⁿ⁾ distribution, where n is one fewer than the number of datasets being added together for the comparison, (n = 5 for testing the hypothesis that R_m did not differ among all strains and n = 1 for testing if R_m did not differ within a species). The 95% confidence intervals for separate data sets are the intervals on the single strain likelihood profiles where the difference between the likelihood and the maximum is <1.95.

Rate and Average Effect of New Mutations. The diploid genomic mutation rate, U_min, and the average effect of a new mutation, ā_max, were calculated for each strain by using the method of Bateman (63) and Mukai (14) (see ref. 19, pp. 341–343). A lower-bound estimate of the genomic mutation rate is

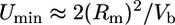[1]

and an upper-bound estimate of the average effect of a new mutation is

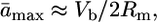[2]

which we divide by the control mean phenotype z₀ (the mean of the G100 and G200 estimates of the control mean) to express the average effect as a proportional reduction in mean phenotype. Homozygotes are expected to have mean fitness reduced by 2ā and heterozygotes by 2āh, where h is the average dominance and h = 0.5 denotes additivity (19). Approximate standard errors were calculated by using the Delta method (19, 38) and the standard errors for R_m and V_b. Results are presented in Tables 1 and 3.

Table 1. Total fitness (± SEM) for strains in generations 100 and 200.

	DF (O. myriophila)		EM (O. myriophila)		N2 (C. elegans)		PB306 (C. elegans)		HK (C. briggsae)		PB800 (C. briggsae)
	100	200	100	200	100	200	100	200	100	200	100	200
W̄control	152.6 ± 3.2	159.0 ± 8.0	96.5 ± 10.2	112.6 ± 10.7	197.5 ± 64.8	220.1 ± 8.4	166.7 ± 21.1	180.6 ± 0.76	58.2 ± 32.1	99.6 ± 13.0	152.3 ± 34.2	208.2 ± 3.6
W̄MA	127.0 ± 6.9	120.9 ± 14.3	112.6 ± 5.7	108.4 ± 9.9	170.9 ± 47.3	178.3 ± 9.3	141.6 ± 7.6	137.2 ± 8.8	40.1 ± 13.6	37.0 ± 10.1	111.3 ± 29.8	108.2 ± 9.9
ΔM (×10-3)	-1.653 ± 1.003	-1.202 ± 0.259	1.807 ± 1.405	-0.012 ± 0.092	-1.237 ± 0.479	-0.940 ± 0.367	-1.455 ± 0.626	-1.193 ± 0.254	-2.516 ± 1.743	-3.149 ± 0.259	-2.711 ± 0.312	-2.403 ± 0.194
RM	-0.186 ± 0.037		0.004 ± 0.042		-0.219 ± 0.043		-0.210 ± 0.040		-0.298 ± 0.030		-0.447 ± 0.043
Vb	12.68 ± 2.45		6.82 ± 2.13		11.54 ± 2.64		13.30 ± 2.74		2.39 ± 0.92		16.02 ± 3.08
UMIN	0.0055 ± 0.0045		—		0.0083 ± 0.0068		0.0066 ± 0.0052		0.074 ± 0.041		0.025 ± 0.011
āMAX	-0.219		—		-0.126		-0.182		-0.051		-0.099

W̄ and ΔM are calculated from the data at each assay. R_m, V_b, U_min, and ā_max are estimated from the full data set. See text for details of calculations.

The Bateman–Mukai method depends on the unrealistic assumption that mutational effects are constant; the degree to which it is violated will influence the extent of the bias in the estimates of U and ā. The sampling covariance between U_min and ā_max is negative, which is intuitively obvious because the change in the trait mean is simply the number of mutations multiplied by their average effect. To underestimate the number of mutations (U) means that their effects (ā) must be exaggerated or vice versa. Negative sampling covariance between mutation rate and effect is not limited to the Bateman–Mukai method; rather, it is an inherent property of the exercise. Likelihood methods (10, 37, 39) suffer from the same limitation, although they need not have a directional bias.

Results and Discussion

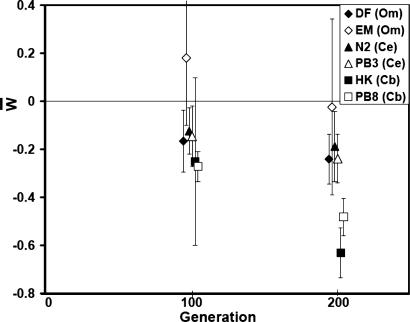
Our primary motivation is comparative biology, and from that standpoint the results are clear: there is substantial genetic variation in the mutational process at all hierarchical levels (Table 1). The per-generation change in the mean (R_m) differed among all strains (P « 0.0001), among species (P « 0.0001), and between strains of O. myriophila (P < 0.001) and C. briggsae (P < 0.005); only the two strains of C. elegans did not differ (P > 0.87). That result is not an artifact of scaling: when the mean change was scaled as a fraction of the ancestral (control) mean (ΔM) the two strains of C. briggsae declined in fitness about twice as fast as either C. elegans or O. myriophila (Fig. 1 and Table 1).

Fig. 1.

Plot of total fitness (W̄) of MA lines, scaled to the control mean, against number of generations of mutation accumulation. Error bars represent ± 2 SEM; see Methods and Materials for details. Diamonds are O. myriophila, triangles are C. elegans, and squares are C. briggsae. Ancestral control fitness is represented at generation 0.

The consistency of the results between assays 100 generations apart is noteworthy, especially considering the variation observed among generations in many previous MA experiments with both C. elegans and Drosophila. The most easily interpreted summary statistic is ΔM, the percent change in the trait mean per generation, and for every strain except EM435, the point estimate of ΔM was very consistent between generations 100 and 200. The rank order in ΔM among strains was essentially the same at G100 and G200 (Fig. 1).

Interestingly, fitness in the EM435 strain did not decline across 200 generations of MA. There are several possible explanations for the anomalous behavior of EM435, including cross-generation environmental effects, residual genetic variation in the controls, and/or compensatory mutations. There was no evidence for residual variation in the controls. A previous experiment with mutationally degraded lines of the N2 strain revealed a nontrivial rate of compensatory mutations (11), so it is possible that the lack of mutational degradation of the EM435 strain represents a balance between deleterious and compensatory mutations in a genotype already suffering from substantial mutation load.

Averaged over all strains at both assays, the Bateman–Mukai estimates of U_min and ā_max are consistent with previous estimates from the N2 strain of C. elegans (37–39). U_min is on the order of 1% to a few percent, and the average effects of new mutations are large compared with the classical Drosophila results, on the order of 10–20% (i.e., a homozygous effect 2ā of 20–40%). Point estimates of U_min for both strains of C. briggsae are severalfold greater than those of C. elegans; estimates of ā_max are concomitantly smaller for C. briggsae than for C. elegans (Tables 1 and 3). Because ΔM is twice as large for the two strains of C. briggsae as it is for the two C. elegans, it is intuitively reasonable that the genomic mutation rate in C. briggsae might be twice as high. It is not intuitive that the decline in fitness in C. briggsae might be greater because the average effects of new mutations are smaller. However, mutations of smaller effect are more likely to fix. Averaged over strains and assays, 2ā_max for W̄ for the two strains of C. elegans was ≈0.25, approximately the upper limit for neutral dynamics (4N_es < 1) if our total fitness is a good estimate of fitness. It is possible that different distributions of mutational effects between taxa might produce the observed pattern of change in trait means. Our estimates of the genomic mutation rate, U_min, are remarkably similar to the estimates of the deleterious mutation rate (U_d ≈ 0.02 per generation) for C. elegans and C. briggsae from synonymous nucleotide substitutions between taxa (64). In contrast, the estimated genomic deleterious mutation rate from sequencing directly accumulated mutations in the N2 strain is U_d ≈ 0.48 (65).

The difference between the two strains of C. briggsae and those of C. elegans deserves comment. Obviously, any conclusion about “species-specific” properties based on a sample size of two genotypes per species is speculative. We speculate that the observed difference in ΔM between the two species may reflect an underlying G × E interaction. The protocols used in this study were optimized for C. elegans. There is evidence (M. Ailion, unpublished data) that the thermal niches of C. briggsae and C. elegans differ. Our assays were conducted at 20°C, considered the optimum for C. elegans; 25°C is near the upper limit of C. elegans thermal tolerance but close to the optimum for C. briggsae. Because MA lines are compared with a control, any environmental effects are necessarily genotype-by-environment interactions, not main effects of the environment.

Assuming the mutation rate remains constant, nonlinear change in the trait mean over time is the signature of epistasis. If the curvature is concave downward, epistasis is said to be “synergistic,” multiplicative epistasis results in exponential decay (log-linearity) and upward concavity is the signature of “diminishing returns” epistasis (15, 16, 66). Although no individual strain exhibits significant curvature for W̄, point estimates of ΔM are smaller in G200 than in G100 (concave upward) for four of the five strains that exhibit a significant change in the mean; HK104 is the only exception. However, because the average homozygous effects of new mutations appear to be at the threshold of effective neutrality (at least in C. elegans), if epistasis was synergistic, mutations that would be selectively neutral in an unloaded genetic background could have effects on fitness that were statistically deleterious in a loaded background and would fail to accumulate. Alternatively, extinction of heavily loaded lines between generation 100 and 200 or failure to recover from freezing at G200 could result in an artificially small value of ΔM at G200 compared with that at G100. With the exception of DF5020, for which 9 of the 62 lines present in the G100 assay were not in the G200 assay, almost all of the lines included in the assay at G100 also were in the G200 assay (Table 2). The difference in ΔM between G100 and G200 was greatest for DF5020 (Tables 1 and 2), so it is possible that the estimate of ΔM at G200 for that strain is a slight underestimate. There is no evidence for epistasis, but we consider the potential epistatic effects of mutations in these lines to be an unresolved issue.

The HK104 strain is of additional interest because the controls consistently exhibited much lower productivity and survival than the other strains (Tables 1 and 3). HK104 also experienced the most rapid decline in fitness relative to the control mean (ΔM) and had the largest estimated U_min. The line with the lowest initial fitness experiencing the most rapid subsequent decline suggests that the deleterious mutation rate may be an increasing function of itself. If so, that result has important implications, inasmuch as the evolutionary consequences of deleterious mutations will differ depending on whether the mutation rate is fitness-dependent (67). Our results are merely suggestive, but the relationship between current and future mutation rate warrants careful empirical investigation.

Conclusions

The riddle of deleterious mutation must now be rephrased as: “Why is there genetic variation in genomic mutational properties?” All strains were assayed at the same time in the same environment, thus differences due to effects of the environment are necessarily G × E effects. Our results confirm the recent suggestion by Fry (35) that “the” mutation rate (and other mutational properties) may be genotype-specific. In particular, we argue that the Drosophila MA data should be taken at face value: some strains of D. melanogaster may, in fact, have much higher mutation rates than others. The next task is to determine the underlying genetic, genomic, and evolutionary causes of variation in genomic mutational properties.