Modeling Restricted Mean Survival Time under General Censoring Mechanisms

Abstract

Restricted mean survival time (RMST) is often of great clinical interest in practice. Several existing methods involve explicitly projecting out patient-specific survival curves using parameters estimated through Cox regression. However, it would often be preferable to directly model the restricted mean for convenience and to yield more directly interpretable covariate effects. We propose generalized estimating equation methods to model RMST as a function of baseline covariates. The proposed methods avoid potentially problematic distributional assumptions pertaining to restricted survival time. Unlike existing methods, we allow censoring to depend on both baseline and time-dependent factors. Large sample properties of the proposed estimators are derived and simulation studies are conducted to assess their finite sample performance. We apply the proposed methods to model RMST in the absence of liver transplantation among end-stage liver disease (ESLD) patients. This analysis requires accommodation for dependent censoring since pre-transplant mortality is dependently censored by the receipt of a liver transplant.

1 Introduction

The Cox proportional hazards model (Cox 1972, 1975) is the strong default for analyzing time to event data with covariate adjustment. A key motivation for the hazard ratio (HR) is its connection to the ordering of the survival functions, under the assumption of proportional hazards. However, when there are departures from proportional hazards, this connection is lost and it is then difficult to interpret the HR. A HR estimated by ignoring the non-proportionality will be a poorly specified mixture of the survival distribution and censoring distribution (Gillen and Emerson 2007), such that the resulting inference may then differ for studies with identical survival time distributions but different censoring patterns. In the presence of non-proportionality, alternatives to the HR include the ‘average effect’ (Xu and O’Quigley 2000), or applying a ‘stopped Cox model’ (Van Houwelingen 2007; Van Houwelingen and Putter 2015).

Covariate effects that are cumulative in nature are often of greater interest than instantaneous effects, especially in the presence of non-proportionality (Schaubel and Wei 2011). In particular, the contrast in restricted mean survival time (RMST) is a useful alternative. The RMST is defined as the average survival time up to a fixed point L and can be written as the area under the survival curve on [0, L]. RMST is an easily interpretable and clinically relevant measure for summarizing the mortality over a fixed follow-up time period of interest. Most existing methods estimate RMST indirectly through hazard regression (e.g., Zucker 1998; Chen and Tsiatis 2001; Zhang and Schaubel 2011). These approaches start by estimating the regression parameters and baseline hazard from a Cox model, calculating the cumulative baseline hazard, transforming it to obtain the survival function and, finally, integrating the survival function to obtain the RMST. Such indirect RMST estimation is inconvenient and computationally cumbersome, even for obtaining a point estimate, let alone its corresponding asymptotic standard error. Hence, it may be preferable to directly model RMST itself (Andersen et al. 2004; Tian et al. 2014).

The majority of existing methods for directly modeling RMST require assumptions regarding the censoring mechanism, which are often untenable. Censoring may result from multiple sources in an observational study. The simplest type would be covariate-independent censoring, which occurs independently of the death time and all the covariates. When this is the only type of censoring present, one can conduct regression analysis of RMST using imputed event times based on pseudo-observation methods (Andersen et al. 2004), or one can construct estimating equations for RMST based on Inverse Probability of Censoring Weighting (IPCW; Robins and Rotnitzky 1992; Robins 1993; Robins and Finkelstein 2000) as in Tian et al. (2014). However, in observational studies, censoring will often depend on the covariate vector. Censoring can depend on baseline covariates, but be conditionally independent of the event time given such covariates; this is referred to as covariate-dependent censoring. For example, it is common to have staggered entry in an observational study with a fixed calendar period, such that subjects who enter later would have a different censoring distribution than those who enter earlier; e.g., registration date on the wait-list for a liver transplant. Since mortality is often subject to calendar time trends, covariate-dependent censoring would be expected to be a frequent occurrence in observational studies. Andersen and Perme (2010) and Binder et al. (2014) conducted simulation studies to examine the bias and efficiency of the pseudo-observations approach for competing risks, in the presence of covariate dependent censoring. A third type of censoring is dependent censoring, which is often correlated with the event time through a mutual association with time varying covariates. Covariate-dependent and dependent censoring have been overcome in many applications by IPCW. Through pseudo-observations, Xiang and Murray (2012) modeled a standard linear regression of restricted survival time on the logarithm scale and handled dependent censoring through IPCW. Specifically, we connect the RMST and covariate vector through a user-specified link function, while Xiang and Murray (2012) model log restricted survival time through linear regression. In addition, being based on a pseudo-observation approach, their work has no systematic procedure for evaluating the asymptotic properties. To our knowledge, there is no existing method to directly model RMST in the presence of dependent censoring, or even covariate-dependent censoring.

The setting which motivated the proposed methods involves mortality in the absence of liver transplantation among End-Stage Liver Disease (ESLD) patients. Since the number of patients in need of liver transplantation is much greater than the number of available deceased-donor livers, medically suitable ESLD patients are placed on a wait-list. Priority for transplantation is then determined by medical urgency, as quantified by the Model for End-Stage Liver Disease (MELD) score. This score is calculated using bounded versions of serum bilirubin, serum creatinine, international normalized ratio for prothrombin time (INR) and dialysis status (Kamath et al. 2001; Wiesner et al. 2003). The MELD score has been shown to be strongly predictive of pre-transplant survival among chronic ESLD patients (Wiesner et al. 2001). For a given ESLD patient, the MELD score is updated frequently, such that MELD constitutes a time-varying covariate. Since wait-listed patients are sequenced on the wait-list in decreasing order of current MELD score, MELD is strongly associated with transplant rate. As the organ assignment is correlated with pre-transplant mortality through its mutual association with time varying MELD score, dependent censoring occurs through the receipt of a liver transplant, which precludes the observation of pre-transplant death. We are interested in the effect on pre-transplant mortality of prognostic factors observed at the time of wait-listing, as such information would be useful to hepatologists and transplant surgeons for counseling patients.

We propose semi-parametric regression methods for directly modeling RMST given baseline covariates in the presence of both covariate-dependent and dependent censoring. The proposed methods can be used to evaluate the cumulative effect of baseline covariates and to quantify treatment effects in terms of contrasts in RMST. Our proposed methods do not require any distributional assumption on the death variates and, analogous to generalized linear models, allow for different link functions.

The contribution of our proposed work, compared to Tian et al. (2014), is that the latter requires that censoring does not depend on the covariate vector. Although random censoring may be a reasonable assumption in clinical trials, it will often fail in observational studies. Our methods not only allow for covariate-dependent censoring, but also allow for dependent censoring (e.g., dependence between the death and censoring times not captured by the covariates used in the death model). In Tian et al. (2014), the weight function is the inverse of the Kaplan-Meier estimator. In the methods we propose, we distinguish between covariate dependent and dependent censoring; in particular, a double inverse weight is required and estimated through separate Cox models for the two types of censoring.

The remainder of this article is organized as follows. In Section 2, we formulate the data structure, define the necessary assumptions and then describe the proposed methods. Asymptotic properties are given in Section 3. In Section 4, we conduct simulation studies to evaluate the accuracy of the proposed procedures in finite samples. In Section 5, we apply our methods to the motivating ESLD data to determine the effect on pre-transplant mortality of several clinically meaningful variables. We conclude this paper with a brief discussion in Section 6. Derivation of the asymptotic properties and additional results for ESLD data analysis are provided in the Supplementary Materials.

2 Proposed Methods

We begin with the necessary notation. Let D_i be the treatment-free survival time for subject i from a cohort of sample size n. We consider two types of censoring. One potential censoring time, denoted as C_i, is independent of D_i conditional on the baseline covariates; this type of censoring includes loss to follow-up or administrative censoring on the day the database closes. The other potential censoring, denoted as T_i, is not conditionally independent of D_i given baseline covariates; one example would be treatment time, which may dependently censor pre-treatment mortality. The observation time for subject i is X_i = D_i ∧ T_i ∧ C_i, where a ∧ b = min{a, b}; and the indicators for at risk status, pre-transplant death, dependent and independent censoring are denoted by R_i(t) = I(X_i ≥ t), ${\Delta }_i^D=I(D_i\le T_i\wedge C_i)$, ${\Delta }_i^T=I(T_i<D_i\wedge C_i)$ and ${\Delta }_i^C=I(C_i<D_i\wedge T_i)$ respectively. We denote the covariates predicting D_i, T_i and C_i by ${\mathit{Z}}_i^D(t)$, ${\mathit{Z}}_i^T(t)$ and ${\mathit{Z}}_i^C$ respectively. Although we have defined these notations to accommodate time varying covariates, some elements of each may be time constant; e.g., gender or race. In some practical studies, the investigators might want to use the same covariate set for censoring and death time; however, we will distinguish these covariate sets for the purpose of generality. Stacking these covariates together and removing any redundancy, we obtain Z_i(t) and the corresponding covariate history as ${\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)=\{{\mathit{Z}}_i(u):0\le u<t\}$. Our observed data are then given by {X_i, ${\Delta }_i^D$, ${\Delta }_i^T$, ${\Delta }_i^C$, $\stackrel{\mathbf{\sim }}{\mathit{Z}}(X_i)$ : i = 1, …, n}.

Let L be a pre-specified time point of interest, before the maximum follow-up time τ = max{X_i : i = 1, …, n}. Denote the restricted observation time as Y_i = X_i ∧ L and its corresponding indicator Δ_i = I(D_i ∧ L ≤ T_i ∧ C_i). We are interested in the average survival time up to L and will model this measure through baseline covariates ${\mathit{Z}}_i^D(0)$:

$${\mu }_i(L):=E\left\{D_i\wedge L|{\mathit{Z}}_i^D(0)\right\}.$$

Analogous to a generalized linear model, we assume a direct relationship between this RMST and baseline covariates as follows:

$$g[{\mu }_i(L)]\equiv g\left[E\left\{D_i\wedge L|{\mathit{Z}}_i^D(0)\right\}\right]={{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0),$$ (1)

where g is a strictly monotone link function with a continuous derivative within an open neighborhood ${ℬ}_D$ of β_D. Examples of link functions include g(x) = x (identity link), g(x) = log(x) (log link) and g(x) = log(x/(L − x)) (logistic link). We choose to model the impact of baseline covariates for many reasons. First, our intention is to develop a model useful for application at the start of follow-up. For example, modeling (1) such modeling could be used in counseling ESLD patients regarding their prognosis in the absence of liver transplantation, given the information observed at the time of wait-list registration. Second, RMST predictions based on time-dependent covariates are difficult to interpret, at least for internal time varying factors (Kalbfleisch and Prentice, 2002). The role of Z_i(t) depends on the model being considered. In model (1), only baseline values are used and we average over the time-varying process. However, time-dependent values are needed to accommodate dependent censoring, as explained in the paragraphs below.

The choice of L requires careful thought. One would normally choose a time point of clinical relevance or, at least, of particular interest to the investigators, respecting the bound at the maximum follow-up time. If too small an L value is selected, D ∧ L = L for most subjects, leading to a largely uninformative analysis. Conversely, if too large an L value is selected, Ŝ(L) ≈ 0. Setting L too large or too small will generally result in attenuated covariate effects. The choice of link function also requires some consideration. The identity link is usually the most interesting because of its straightforward interpretation. However, it has the problem of unbounded predicted values. From this perspective, the logistic link may be a better choice, at least for the purposes of prediction. In addition, practitioners can conduct sensitivity analyses and model diagnostic procedures to test the performance of different link functions, as we demonstrate in Section 5.

Note that we do not make any assumption about the error structure, in the interest of flexibility and robustness. Although it might be difficult to envision an arbitrarily truncated variate having a well-behaved distribution, it is reasonable to assume that the corresponding mean has a convenient form. Framing the model in terms of g[E(D_i ∧ L)] instead of E[g(D_i ∧ L)] is very important in our settings. For example, if $\log \{E(D_i\wedge L)\}={{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)$, the parameters in β_D can be interpreted as the multiplicative effect on RMST per unit increase in the corresponding covariate. This is quite different from the model assumption $E\{\log (D_i\wedge L)\}={{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)$, where β_D equals the average change in logarithm of restricted survival time per unit increase in ${\mathit{Z}}_i^D(0)$. The latter interpretation is much less intuitive, since back-transforming is invalid in the light of Jensen’s Inequality.

We now derive the estimating equation for the parameter of interest, β_D. In absence of censoring, based on (1), β_D could be estimated via the following estimating equation:

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathit{Z}}_i^D(0)\left[D_i\wedge L-g^{-1}\left\{{\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^D(0)\right\}\right]}=\mathbf{0}.$$ (2)

Although connected to generalized linear models, (2) is more accurately interpreted as a generalized estimating equation due to the absence of distributional assumptions on D_i ∧ L.

However, we will not observe D_i for all patients due to the occurrence of censoring. Instead we may observe either independent censoring time C_i or treatment time T_i. Provided that a rich set of variables is included in Z_i(0), we assume that C_i is conditionally independent of D_i, given the baseline covariate vector. Such an assumption is not assumed to hold for T_i; however, we can assume that the dependence of T_i and D_i occurs through (and only through) the time varying process ${\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)$. That is, conditional on ${\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)$, we assume “no unmeasured confounders”, which can be formulated as follows:

$$\begin{array}{l}\underset{h\to 0}{\lim }\frac{P\{X_i\in [t,t+h),{\Delta }_i^T=1|X_i\ge t,{\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t),D_i\}}{h}\\ =\underset{h\to 0}{\lim }\frac{P\{X_i\in [t,t+h),{\Delta }_i^T=1|X_i\ge t,{\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)\}}{h}.\end{array}$$

This essentially assumes that the hazard of being censored by T_i at t depends only on the observed covariate history up to t and not additionally on future data. For example, based on the current liver allocation system, the receipt of a deceased-donor transplant depends only on the patient’s current prognostic factors, and not the future disease pathology.

Denote the hazard functions for C_i and T_i at time t as ${\mathrm{\lambda }}_i^C(t)$ and ${\mathrm{\lambda }}_i^T(t)$, respectively; i.e.,

$$\begin{array}{l}{\mathrm{\lambda }}_i^C(t)=\underset{h\to 0}{\lim }\frac{P\{X_i\in [t,t+h),{\Delta }_i^C=1|X_i\ge t,{\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)\}}{h},\\ {\mathrm{\lambda }}_i^T(t)=\underset{h\to 0}{\lim }\frac{P\{X_i\in [t,t+h),{\Delta }_i^T=1|X_i\ge t,{\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(t)\}}{h},\end{array}$$

with corresponding cumulative hazards, ${\Lambda }_i^C(t)={\displaystyle {\int }_0^t{\mathrm{\lambda }}_i^C(u)du}$ and ${\Lambda }_i^T(t)={\displaystyle {\int }_0^t{\mathrm{\lambda }}_i^T(u)du}$. Although $E({\mathit{Z}}_i^D(0)[Y_i-g^{-1}\{{{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}])\ne \mathbf{0}$ in the presence of censoring, we can show that under our assumption the IPCW weighted expectation is still zero; i.e., $E({\mathit{Z}}_i^D(0)W_i(Y_i){\Delta }_i[Y_i-g^{-1}\{{{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}])=\mathbf{0}$, where $W_i(t)=W_i^T(t)W_i^C(t)$, $W_i^T(t)=\exp \{{\Lambda }_i^T(t)\}$ and $W_i^C(t)=\exp \{{\Lambda }_i^C(t)\}$. Therefore, the following equation is unbiased for β_D:

$${\mathit{\Phi }}^{\ast }(\mathit{\beta })=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathit{Z}}_i^D}(0)W_i(Y_i){\Delta }_i\left[Y_i-g^{-1}\left\{{{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\right\}\right]=\mathbf{0},$$ (3)

provided that the weight function $W_i(t)=\exp \{{\Lambda }_i^T(t)\}\exp \{{\Lambda }_i^C(t)\}$ is known. However, ${\Lambda }_i^T(t)$ and ${\Lambda }_i^C(t)$ are rarely known in practice and therefore must be estimated from the observed data. For this purpose, we assume Cox models for ${\mathrm{\lambda }}_i^T(t)$ and ${\mathrm{\lambda }}_i^C(t)$. Cox regression is a natural choice for modeling censoring times since it is a well established approach, especially in the context of IPCW. Besides its computational convenience, Cox regression can flexibly accommodate both time constant and time varying covariates. We assume the following Cox models, for T_i through time-dependent covariates ${\mathit{Z}}_i^T(t)$, and for C_i based on covariates ${\mathit{Z}}_i^C$:

$$\begin{array}{l}{\mathrm{\lambda }}_i^T(t)={\mathrm{\lambda }}_0^T(t)\exp \left\{{{\mathit{\beta }}^{\mathbf{\prime }}}_T{\mathit{Z}}_i^T(t)\right\}.\\ {\mathrm{\lambda }}_i^C(t)={\mathrm{\lambda }}_0^C(t)\exp \left({{\mathit{\beta }}^{\mathbf{\prime }}}_C{\mathit{Z}}_i^C\right).\end{array}$$

Using partial likelihood (Cox 1975) and the Breslow estimator (Breslow 1972), we can estimate ${\widehat{\Lambda }}_0^T(t)$ and ${\widehat{\mathit{\beta }}}_T$ from data $\{X_i,{\Delta }_i^T,{\mathit{Z}}_i^T(t):t\in [0,X_i),i=1,\dots ,n\}$, and ${\widehat{\Lambda }}_0^T(t)$ and ${\widehat{\mathit{\beta }}}_C$ from data $\{X_i,{\Delta }_i^C,{\mathit{Z}}_i^C:i=1,\dots ,n\}$ respectively. Plugging ${\widehat{\Lambda }}_i^T(t)$, ${\widehat{\mathit{\beta }}}_T$, ${\widehat{\Lambda }}_i^C(t)$, ${\widehat{\mathit{\beta }}}_C$ into (3), we obtain the following estimating equation,

$$\mathit{\Phi }(\mathit{\beta })=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathit{Z}}_i^D(0){\widehat{W}}_i(Y_i){\Delta }_i\left[Y_i-g^{-1}\left\{{{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\right\}\right]}=\mathbf{0},$$ (4)

where ${\widehat{W}}_i(t)={\widehat{W}}_i^T(t){\widehat{W}}_i^C(t)$, ${\widehat{W}}_i^T(t)=\exp \{{\widehat{\Lambda }}_i^T(t)\}$ and ${\widehat{W}}_i^C(t)=\exp \{{\widehat{\Lambda }}_i^C(t)\}$. The solution to (4) provides for consistent estimation of β_D, with its asymptotic properties discussed in Section 3. The use of a double inverse weight has some similarity to Schaubel and Wei (2011). However, unlike the methods we propose, the first weight in Schaubel and Wei (2011) is derived from Inverse Probability of Treatment Weighting (IPTW) and serves to balance treatment-specific covariate distributions.

3 Asymptotic Properties

Before presenting the asymptotic properties of our proposed estimators, we specify the following regularity conditions (a)–(g) for i = 1, …, n.

1. $\{X_i,{\Delta }_i^T,{\Delta }_i^C,{\stackrel{\mathbf{\sim }}{\mathit{Z}}}_i(X_i)\}$ are independently and identically distributed.

2. P(R_i(t) = 1) > 0 for t ∈ (0, τ].

3. $|Z_{ik}(0)|+{\displaystyle {\int }_0^{\tau }d|Z_{ik}(t)|<M_Z}<\infty$ for i = 1,…,n, where Z_ik(0);Z_ik(t) are the kth components of Z_i(0) and Z_i(t), respectively.

4. ${\Lambda }_i^T(\tau )<\infty$, ${\Lambda }_i^C(\tau )<\infty$ and ${\Lambda }_i^T(t)$, ${\Lambda }_i^C(t)$ are absolutely continuous for t ∈ (0; τ ].

5. There exist neighborhoods ${ℬ}_T$ of β_T and ${ℬ}_C$ of β_C such that for k = 0; 1; 2,

   $$\begin{array}{r}\underset{t\in (0,\tau ],\mathit{\beta }\in {ℬ}_T}{\sup }\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n\exp \left\{{\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^T(t)\right\}}{R}_i(t){\mathit{Z}}_i^T{(t)}^{\otimes k}-{\mathit{r}}_T^{(k)}(t;\mathit{\beta })\Vert \stackrel{p}{\to }0,\\ \underset{t\in (0,\tau ],\mathit{\beta }\in {ℬ}_C}{\sup }\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n\exp \left({\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^C\right)}{R}_i(t){\mathit{Z}}_i^{C\otimes k}-{\mathit{r}}_C^{(k)}(t;\mathit{\beta })\Vert \stackrel{p}{\to }0,\end{array}$$

   where υ^⊗0 = 1, υ^⊗1 = υ, υ^⊗2 = υ′υ and

   $$\begin{array}{l}{\mathit{r}}_T^{(k)}(t;\mathit{\beta })=E\left[\exp \left\{{\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^T(t)\right\}{R}_i(t){\mathit{Z}}_i^T{(t)}^{\otimes k}\right],\\ {\mathit{r}}_C^{(k)}(t;\mathit{\beta })=E\left\{\exp \left({\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^C\right)R_i(t){\mathit{Z}}_i^{C\otimes k}\right\}.\end{array}$$

6. Define h(x) = ∂g⁻¹(x)/∂x, where h exists and is continuous in an open neighborhood ${ℬ}_D$ of β_D.

7. The matrices A(β_D), Ω_T (β_T), Ω_C(β_C) are each positive definite, where

   $$\begin{array}{l}\mathit{A}(\mathit{\beta })=E\left[{\mathit{Z}}_i^D{(0)}^{\otimes 2}h\left\{{{\mathit{\beta }}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\right\}\right],\\ {\mathit{\Omega }}_T(\mathit{\beta })=E\left[{\displaystyle {\int }_0^{\tau }\left\{\frac{{\mathit{r}}_T^{(2)}(t;\mathit{\beta })}{r_T^{(0)}(t;\mathit{\beta })}-{\overline{\mathit{z}}}_T{(t;\mathit{\beta })}^{\otimes 2}\right\}d{N}_i^T(t)}\right],\\ {\mathit{\Omega }}_C(\mathit{\beta })=E\left[{\displaystyle {\int }_0^{\tau }\left\{\frac{{\mathit{r}}_C^{(2)}(t;\mathit{\beta })}{r_C^{(0)}(t;\mathit{\beta })}-{\overline{\mathit{z}}}_C{(t;\mathit{\beta })}^{\otimes 2}\right\}d{N}_i^C(t)}\right],\end{array}$$

   and

   $$\begin{array}{l}{\overline{\mathit{z}}}_T(t;\mathit{\beta })=\frac{{\mathit{r}}_T^{(1)}(t;\mathit{\beta })}{r_T^{(0)}(t;\mathit{\beta })},\\ {\overline{\mathit{z}}}_C(t;\mathit{\beta })=\frac{{\mathit{r}}_C^{(1)}(t;\mathit{\beta })}{r_C^{(0)}(t;\mathit{\beta })}.\end{array}$$

Condition (a) can be relaxed at the expense of additional technical development. Condition (b) is needed for the purpose of identifiability. Conditions (c)–(f) ensure the convergence of several stochastic integrals used in the proofs. The matrices A(β_D), Ω_T (β_T), Ω_C(β_C) in condition (g) are at least non-negative definite and will be positive definite under any non-redundant specification of the respective covariate vectors. Our main asymptotic results are summarized in Theorems 1 and 2 below, with the proofs presented in Web Appendix A.

Theorem 1

Under regularity conditions (a)–(g), as n → ∞, $\sqrt{n}\mathit{\Phi }({\mathit{\beta }}_D)$ converges to a zero-mean Normal with variance B(β_D) = E{B_i(β_D)^⊗2}, for any subject i = 1, …, n,

$$\begin{array}{l}{\mathit{B}}_i(\mathit{\beta })={\mathit{\epsilon }}_i(\mathit{\beta })+{\mathit{K}}_T(\mathit{\beta }){\mathit{\Omega }}_T{({\mathit{\beta }}_T)}^{-1}{\mathit{U}}_i^T({\mathit{\beta }}_T)+{\mathit{K}}_C(\mathit{\beta }){\mathit{\Omega }}_C{({\beta }_C)}^{-1}{\mathit{U}}_i^C({\mathit{\beta }}_C)\\ +{\displaystyle {\int }_0^{\tau }{\mathit{H}}_T(u;\mathit{\beta })}{r}_T^{(0)}{(u;{\mathit{\beta }}_T)}^{-1}d{M}_i^T(u)+{\displaystyle {\int }_0^{\tau }{\mathit{H}}_C(u;\mathit{\beta })}{r}_C^{(0)}{(u;{\mathit{\beta }}_C)}^{-1}d{M}_i^C(u),\end{array}$$

where we define

$$\begin{array}{l}{\mathit{\epsilon }}_i(\mathit{\beta })={\Delta }_i{W}_i(Y_i)[Y_i-g^{-1}\{{\mathit{\beta }}^{\mathbf{\prime }}{\mathit{Z}}_i^D(0)\}]{\mathit{Z}}_i^D(0),\\ {\mathit{U}}_i^T(t)={\displaystyle {\int }_0^t\{{\mathit{Z}}_i^T(u)-{\overline{\mathit{z}}}_T(u;{\mathit{\beta }}_T)\}}d{M}_i^T(u),\\ {\mathit{U}}_i^C(t)={\displaystyle {\int }_0^t\{{\mathit{Z}}_i^C-{\overline{\mathit{z}}}_C(u;{\mathit{\beta }}_C)\}}d{M}_i^C(u),\\ {\mathit{K}}_T(\mathit{\beta })=E\{{\mathit{\epsilon }}_i(\mathit{\beta }){\mathit{D}}_i^T{(Y_i)}^{\prime }\},\\ {\mathit{K}}_C(\mathit{\beta })=E\{{\mathit{\epsilon }}_i(\mathit{\beta }){\mathit{D}}_i^C{(Y_i)}^{\prime }\},\\ {\mathit{H}}_T(u;\mathit{\beta })=E[{\mathit{\epsilon }}_i(\mathit{\beta })\exp \{{{\mathit{\beta }}^{\mathbf{\prime }}}_T{\mathit{Z}}_i^T(u)\}{R}_i(u)],\\ {\mathit{H}}_C(u;\mathit{\beta })=E\{{\mathit{\epsilon }}_i(\mathit{\beta })\exp ({{\mathit{\beta }}^{\mathbf{\prime }}}_C{\mathit{Z}}_i^C)R_i(u)\},\\ {\mathit{D}}_i^T(t)={\displaystyle {\int }_0^t\{{\mathit{Z}}_i^T(u)-{\overline{\mathit{z}}}_T(u;{\mathit{\beta }}_T)\}d{\Lambda }_i^T(u),}\\ {\mathit{D}}_i^C(t)={\displaystyle {\int }_0^t\{{\mathit{Z}}_i^C(u)-{\overline{\mathit{z}}}_C(u;{\mathit{\beta }}_C)\}d{\Lambda }_i^C(u),}\end{array}$$

with Ω_T (β), Ω_C(β) defined in Condition (g).

Here we use the usual counting process notations, where $N_i^T(t)=I(X_i\le t,{\Delta }_i^T=1)$ and $N_i^C(t)=I(X_i\le t,{\Delta }_i^C=1)$ are observed counting processes for T_i and C_i respectively, with $d{M}_i^T(t)=d{N}_i^T(t)-R_i(t)d{\Lambda }_i^T(t)$ and $d{M}_i^C(t)=d{N}_i^C(t)-R_i(t)d{\Lambda }_i^C(t)$ being the corresponding zero mean processes. The proof utilizes various results derived in Zhang and Schaubel (2011), primarily the asymptotic expression of the empirical weight in terms of the true weight. The main purpose of Theorem 1 is to set up Theorem 2.

Theorem 2

Under regularity conditions (a)–(g), as n → ∞, ${\widehat{\mathit{\beta }}}_D$ converges in probability to β_D and $\sqrt{n}({\widehat{\mathit{\beta }}}_D-{\mathit{\beta }}_D)$ converges to a zero-mean Normal with variance A(β_D)⁻¹B(β_D)A(β_D)⁻¹ with A(β) defined in condition (g) and B(β) defined in Theorem 1.

The proof of consistency of ${\widehat{\mathit{\beta }}}_D$ follows primarily from the Inverse Function Theorem (Foutz 1977) while the proof of asymptotic normality follows through the combination of various Taylor series expansions and the Cramér-Wold Theorem.

We propose two versions of asymptotic standard error (ASE) estimators for our proposed estimator ${\widehat{\mathit{\beta }}}_D$. The first ASE is derived from (3) and, as such, treats the IPCW weights as known:

$${\text{ASE}}_1=\sqrt{\frac{1}{n}\text{Diag}[\widehat{\mathit{A}}{({\mathit{\beta }}_D)}^{-1}{\widehat{\mathit{B}}}^{\ast }({\mathit{\beta }}_D)\widehat{\mathit{A}}{({\mathit{\beta }}_D)}^{-1}]},$$

where ${\widehat{\mathit{B}}}^{\ast }(\mathit{\beta })=\widehat{E}\{{\mathit{\epsilon }}_i{(\mathit{\beta })}^{\otimes 2}\}$. The second ASE is based on (4) and derived in Theorem 2:

$${\text{ASE}}_2=\sqrt{\frac{1}{n}\text{Diag}[\widehat{\mathit{A}}{({\beta }_D)}^{-1}\widehat{\mathit{B}}({\mathit{\beta }}_D)\widehat{\mathit{A}}{({\mathit{\beta }}_D)}^{-1}]},$$

where $\widehat{\mathit{B}}(\mathit{\beta })=\widehat{E}\{{\mathit{B}}_i{(\mathit{\beta })}^{\otimes 2}\}$. These two ASEs can be obtained by plugging all the undetermined terms with their respective estimators. More detail about the calculation procedures is provided in Web Appendix B. These two versions of sandwich ASEs share the same second derivative matrix, A(β), but differ with two different middle matrices. The first version, ASE₁, which results from the weight function being known as opposed to estimated, treats the weights as fixed and therefore its middle matrix involves ε_i only. The second version, ASE₂, contains several extra terms in its middle matrix, in order to account for the variation due to estimating the weights. Although ASE₂ should be closer to the truth, it adds the complexity of middle matrix and is usually more complicated to calculate in practice than ASE₁. In contrast, ASE₁ can be easily computed with built-in commands from many statistical software packages (e.g., SAS, R) and therefore serves as a useful approximation of ASE₂. We evaluate the performance of both ASE₁ and ASE₂ through simulations presented in the next section.

4 Simulation Study

We conducted simulations to evaluate the performance of the proposed methods in finite samples. Two different percentages of right censoring were considered, moderate and heavy censoring. For each simulated subject i = 1, …, n, two baseline covariates Z_i1, Z_i2 were generated from Bernoulli(0.5) distributions. The death time, D_i, was generated from D_i = g⁻¹ (α₀ + α₁Z_i1 + α₂Z_i2)+ε_1i, where ε_1i ~ Uniform(−σ, σ), α = [α₀, α₁, α₂]′ and σ were chosen in accordance with the particular link function. More specifically, α = [5.5, 0.25, 0.25]′ was tested for the linear link, and α = [−0.63, .08, .08]′ was tested and for log link. This death generator was used to induce the same mean structure for D_i and D_i ∧ L, as the mean structure of the former, g{E(D_i|Z_i1, Z_i2)} = α₀ + α₁Z_i1 + α₂Z_i2, is similar to that of the latter,

$$g\{E(D_i\wedge L|Z_{i1},Z_{i2})\}={\beta }_{D0}+{\beta }_{D1}{Z}_{i1}+{\beta }_{D2}{Z}_{i2}+{\beta }_{D3}{Z}_{i1}{Z}_{i2}.$$ (5)

Because the above model (5) is saturated, due to an extra interaction term Z_i1Z_i2, the true values of β_D = [β_D0, β_D1, β_D2, β_D3]′ can be determined computationally and are calculated using Monte Carlo methods with size 10 million. We set L = 10 to yield a reasonable range of P (D > L). We evaluated the linear and log links, since they would be the most popular choices in practice.

We generated the independent censoring time C_i from a Cox model with the following hazard,

$${\mathrm{\lambda }}_i^C(t)={\mathrm{\lambda }}_0^C\exp ({\beta }_{C1}{Z}_{i1}),$$ (6)

where ${\mathrm{\lambda }}_0^C$ ranged from 1/36 to 1/21 and β_C1 ranged from −log(3) to log(2). We generated a time-dependent covariate which was correlated with death time D_i and treatment time T_i even after conditioning on baseline covariates Z_i1, Z_i2. First, let V_i = −V₀ log{(ε_i1 + σ)/(2σ)} + ε_i2, where V₀ is a constant ranging from 40 to 100 and ε_i2 ~ Uniform(0, 1). Then define a time-dependent variable V_i(t) = I(t ≤ V_i). Thus V_i(t) is still correlated with D_i, through ε_i1, even after conditioning on Z_i1, Z_i2. Treatment time T_i was generated from a Cox model with the following hazard,

$${\mathrm{\lambda }}_i^T(t)={\mathrm{\lambda }}_0^T\exp \{{\beta }_{T1}{Z}_{i2}+{\beta }_{T2}{V}_i(t)\},$$ (7)

where ${\mathrm{\lambda }}_0^T$ ranged from 1/35 to 1/18, β_T1 ranged from −log(4) to log(3) and β_T2 ranged from log(2) to log(3). Therefore T_i is correlated with D_i conditional on Z_i1, Z_i2, through a mutual unobserved variable ε_i1.

We present results for samples sizes n = 250 and n = 500, under moderate and heavy censoring. For the linear link, P (D > 10) ≈ 11%, approximately 10% C_i and 21% T_i are observed in the moderate censoring scenario, and 15% C_i and 36% T_i are observed in the heavy censoring scenario. For the log link, P (D > 10) ≈ 10%, approximately 8% C_i and 24% T_i are observed in the moderate censoring scenario, with 15% C_i and 35% T_i observed in the heavy censoring scenario. As displayed in Tables 1 and 2, the estimates for β_D are approximately unbiased, with the magnitudes of any bias generally decreasing with increasing sample size. The calculated ASE₁s and ASE₂s are very close to their corresponding empirical standard deviations (ESD), and therefore their empirical coverage probabilities CP₁ and CP₂ are close to 95%. The implications from our simulation studies are that, in moderate samples, the proposed methods result in unbiased estimation, and that the easily computed ASE₁ is a useful approximation to the more complicated ASE₂. In our real-data application presented in Section 5, the sample size far exceeds 1,000, which would render finite-sample bias in ASE₁ much less of an issue than in our simulation studies.

Table 1.

Simulation results: g(x) = x

Scenario	N	βD	True	BIAS	ESD	ASE1	CP1(%)	ASE2	CP2(%)
Moderate Censoring	250	β0	5.452	−0.008	0.505	0.519	94	0.515	94
		β1	0.23	−0.037	0.714	0.72	95	0.735	96
		β2	0.227	0.008	0.67	0.686	95	0.711	96
		β3	−0.014	0.033	0.928	0.947	95	0.99	96
	500	β0	5.452	0.002	0.346	0.368	96	0.364	96
		β1	0.23	−0.016	0.503	0.508	95	0.519	95
		β2	0.227	−0.018	0.469	0.487	96	0.505	96
		β3	−0.014	0.012	0.674	0.671	95	0.701	97
Heavy Censoring	250	β0	5.452	−0.006	0.467	0.486	96	0.577	98
		β1	0.23	−0.042	0.704	0.725	95	0.858	98
		β2	0.227	−0.037	0.821	0.83	95	0.991	98
		β3	−0.014	−0.021	1.271	1.249	94	1.493	96
	500	β0	5.452	0.01	0.328	0.345	96	0.398	98
		β1	0.23	−0.024	0.512	0.512	94	0.589	96
		β2	0.227	−0.043	0.591	0.594	95	0.694	97
		β3	−0.014	−0.017	0.924	0.887	93	1.039	97

Table 2.

Simulation results: g(x) = log(x)

Scenario	N	βD	True	BIAS	ESD	ASE1	CP1(%)	ASE2	CP2(%)
Moderate Censoring	250	β0	−0.634	−0.008	0.104	0.104	95	0.102	94
		β1	0.075	−0.007	0.143	0.139	95	0.142	96
		β2	0.074	0.005	0.13	0.129	95	0.133	96
		β3	−0.004	0.008	0.173	0.172	95	0.179	95
	500	β0	−0.634	−0.004	0.068	0.073	97	0.072	96
		β1	0.075	−0.001	0.095	0.097	96	0.099	96
		β2	0.074	−0.001	0.088	0.091	96	0.094	97
		β3	−0.004	0.001	0.12	0.121	96	0.126	97
Heavy Censoring	250	β0	−0.634	−0.013	0.124	0.125	94	0.125	95
		β1	0.075	−0.01	0.183	0.171	94	0.177	94
		β2	0.074	0.007	0.157	0.157	95	0.167	96
		β3	−0.004	0.01	0.222	0.212	95	0.227	96
	500	β0	−0.634	−0.008	0.083	0.089	96	0.088	96
		β1	0.075	0.001	0.121	0.12	95	0.124	95
		β2	0.074	0.001	0.109	0.111	95	0.118	97
		β3	−0.004	0.001	0.151	0.15	95	0.159	96

Mis-specification of the censoring model is a common issue in IPCW methods, in which case bias will generally exist in the estimation of the mortality model parameters. To evaluate how much bias is introduced by such mis-specification, we conducted additional numerical studies. In particular, we considered 3 different types of mis-specification:

1. Model for independent censoring, C, is mis-specified: add a covariate, Z_i2, to the censoring hazard ${\mathrm{\lambda }}_i^C(t)$; i.e., Z_i2 was added to the generator, but not the model for C_i being fitted.

2. Model for dependent censoring, T, is mis-specified: add a covariate, Z_i1, to censoring hazard ${\mathrm{\lambda }}_i^T(t)$, but not to the T_i model being fitted.

3. Models are mis-specified for both C and T simultaneously, per (i) and (ii) above.

Figure 1 displays the bias for sample size N = 250 calculated with 1, 000 replications for the 4 scenarios in Table 1 and 2, after introducing mis-specification (i)–(iii). In general, bias exists when the censoring model is not correctly specified, and is more pronounced when both types of censoring are incorrectly modeled.

Fig. 1.

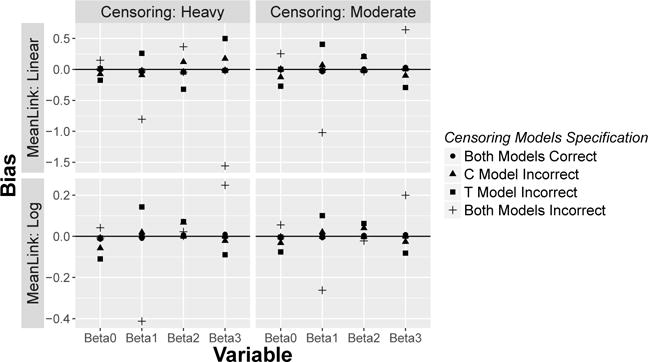
Bias of [β_D0, β_D1, β_D2, β_D3]′ when censoring models are mis-specified

An interesting comparison is between our methods and those proposed by Tian et al. (2014). Methods of Tian et al. (2014) were developed in the context of covariate-independent censoring and, thus, proposed IPCW weights based on Kaplan-Meier estimators. When the censoring mechanism is more complicated than independent censoring (i.e., in presence of either covariate-dependent or dependent censoring), then our methods should perform better than Tian’s methods. We illustrated this phenomenon with additional simulations; specifically, we ran the simulation studies in Table 1 and 2 again, applied Tian et al. (2014), and then plotted the resulting bias along with the bias from our methods. As shown in Fig 2, Tian et al. (2014) has quite severe bias for N = 250 cases, with similar results obtained for the N = 500 case. This is expected, since we are testing Tian et al. (2014) outside the set-up for which the methods were developed.

Fig. 2.

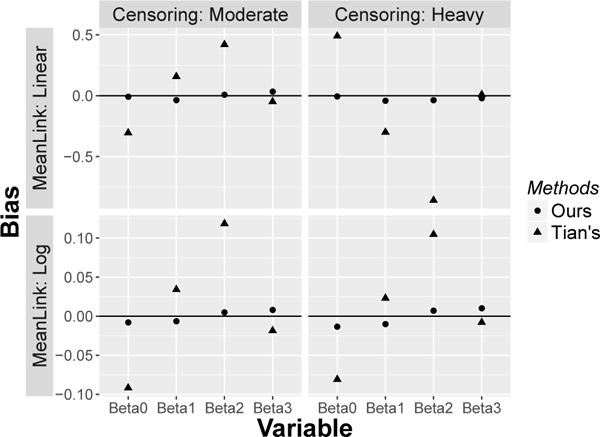
Bias comparison between our and Tian’s methods in presence of dependent censoring

In presence of only covariate-independent censoring, both our methods and those of Tian et al. (2014) should apply. In evaluating our methods, we blindly added non-predictive covariates into the censoring model, in order to assess the degree of efficiency loss. We generated death time with D_i = g⁻¹ (5.25 + 0.5Z_i1 + 0.5Z_i2) + ε_1i, where Z_i1, Z_i2 ~ Bernoulli(0.5) and ε_1i ~ Uniform(−5.25, 5.25). We chose L = 9 and introduced a simple censoring pattern (Exponential, rate 0.05). Approximately 79% D’s are observed, with P (D > L) ≈ 19%. In Table 3, Bias₁ and ESD₁ are bias and empirical standard deviation (ESD) calculated by our methods with futile covariates Z_i1, Z_i2 in the censoring model, and Bias₂ and ESD₂ are calculated using Tian et al. (2014) with a correctly specified non-parametric censoring model. The last column is Empirical Relative Efficiency (ERE) between Tian et al. (2014) and our methods, computed as the ratio of mean square error. Examining various replicates, the estimated regression coefficients for the C model tends to be very close to 0, with large p values. In practice, users would feel inclined to drop them from the model, due to their negligible effect on C. Since these non-zero censoring coefficients are actually 0, our methods have a little bit greater bias than Tian et al. (2014). Regarding efficiency, our methods exhibited approximately the same efficiency as Tian et al. (2014), despite including the two irrelevant covariates in the C model.

Table 3.

Efficiency comparison between our and Tian’s methods in presence of only covariate-independent censoring: g(x) = x

N	βD	True	Bias1	Bias2	ESD1	ESD2	ERE
250	β0	5.148	0.023	< 0.001	0.344	0.351	0.963
	β1	0.406	−0.017	−0.002	0.404	0.401	1.012
	β2	0.403	−0.009	0.005	0.403	0.402	1.004
500	β0	5.148	0.012	0.001	0.244	0.25	0.953
	β1	0.406	−0.007	< 0.001	0.286	0.286	1.003
	β2	0.403	−0.009	−0.002	0.286	0.286	1.002

5 Analysis of Liver Disease Data

We applied the proposed methods to directly estimate RMST among End-Stage Liver Disease (ESLD) patients. Of interest was survival in the absence of liver transplantation. We obtained data from the Scientific Registry of Transplant Recipients (SRTR). The SRTR data system includes data on all donors, wait-listed candidates, and transplant recipients in the U.S., as submitted by the members of the Organ Procurement and Transplantation Network (OPTN), and has been described elsewhere. The Health Resources and Services Administration (HRSA), U.S. Department of Health and Human Services provides oversight to the activities of the OPTN and SRTR contractors.

The study population consisted of all chronic ESLD patients initially wait-listed for deceased-donor liver transplantation in U.S. at age ≥ 18 between January 1, 2005 and December 31, 2012. For each patient, the time origin (t = 0) is the date of wait-listing, with each patient followed from that date until earliest of death, receipt of a liver transplant, loss to follow-up, or the end of the observation period on 12/31/2012. Independent censoring occurs through loss to follow-up, administrative censoring, or receipt of a living-donor liver transplant. Note that living-donor transplantation is usually carried out with a liver segment donated by a family member or a close friend, such that the process is not systematically influenced by MELD score trajectory conditional on baseline covariates. As described in Section 1, dependent censoring occurs through the receipt of a deceased-donor transplant, which is correlated with pre-transplant mortality through its mutual association with time varying MELD score. A total of n =55,651 patients were included in our study population. Among them, 13,640 (25%) died before receipt of a transplant, 23,335 (42%) received a liver transplant, and 18,676 (34%) were independently censored.

We constructed our independent censoring model and pre-transplant mortality model using baseline covariates historically reported to be important prognostic factors, including age, gender, race, blood type, United Network for Organ Sharing (UNOS) Region, calendar year of listing, underlying diagnosis, body mass index (BMI), dialysis, sodium, hospitalization status and MELD score at listing (t = 0). The liver transplant hazard model incorporated additional time-dependent covariates, including MELD score, dialysis, sodium, ascites and encephalopathy. UNOS has established 11 geographic Regions for administrative purposes. The availability of deceased-donor organs and the distribution of mortality is quite different across these 11 Regions. This therefore suggests the necessity of adjusting for UNOS Region in both our censoring and mortality models:

$${\mathrm{\lambda }}_{ij}^T(t)=A_i(t){\mathrm{\lambda }}_{0j}^T(t)\exp \left\{{{\mathit{\beta }}^{\mathbf{\prime }}}_T{\mathit{Z}}_i^T(t)\right\},$$ (8)

$${\mathrm{\lambda }}_{ij}^C(t)={\mathrm{\lambda }}_{0j}^C(t)\exp \left({{\mathit{\beta }}^{\mathbf{\prime }}}_C{\mathit{Z}}_i^C\right),$$ (9)

where the subscript j = 1, 2, …, 11 stands for UNOS Region, while the indicator A_i(t) records whether the patient is active and not removed from the wait-list at time t. Patients generally start follow-up as active, such that A_i(0) = 1, but may be made temporarily inactive due to illness (A_i(t) = 0), in which case the patient retains his/her position on the wait-list but cannot receive deceased-donor liver offers. A patient whose health condition declines to the point where liver transplantation is considered futile may be permanently removed from the wait-list (A_i(u) = 0 for any time point u after the time of removal). Therefore A_i(t) serves as a time varying at-risk indicator for transplantation. Subintervals during which a given patient is in-active make no contribution to the fitting of model (8). We then compute cumulative hazard functions as ${\widehat{\Lambda }}_{ij}^C(t)=\exp \{-{\displaystyle {\int }_0^t\exp ({{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_C{\mathit{Z}}_i^C)d{\widehat{\Lambda }}_{0j}^C(u)}\}$ and ${\widehat{\Lambda }}_{ij}^T(t)=\exp [-{\displaystyle {\int }_0^t{A}_i(u)\exp \{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_T{\mathit{Z}}_i^T(u)\}d{\widehat{\Lambda }}_{0j}^T}(u)]$ and obtain the IPCW weight as ${\widehat{W}}_{ij}(t)=\exp \{{\widehat{\Lambda }}_{ij}^C(t)\}\exp \{{\widehat{\Lambda }}_{ij}^T(t)\}$. Since more than 99% of the estimated IPCW weights are below 10, we cap the weights by 10 in order to reduce variance.

We modeled restricted mean survival time at L = 1, L = 3, L = 5 years post wait-list registration, which are reasonable time windows in the ESLD setting. Overall crude survival probabilities are approximately 79%, 62% and 51% for the 3 time windows respectively. We present the parameter estimates for the pre-transplant mortality model using three link functions, including linear, log and logistic. As shown in Table 4, the covariate effects demonstrate the same trends across the different link functions. The average pre-transplant survival time out of the next 3 years is estimated as approximately 33, 35.8, and 33 months using the three link functions respectively, for a ‘reference’ patient; i.e., a white male wait-listed at age 50, registered in Region 5 (the Region with the largest population) during year 2005, diagnosed as none of the listed types, not hospitalized, not on dialysis, with blood Type O, BMI between 20 and 25, sodium level at 130 mmol/l and MELD score 6 (the minimum possible value). For another patient with the same profile but a different MELD score (e.g., MELD=30), the average pre-transplant survival time out of the next 3 years is estimated as approximately 11.6, 9.8, and 7.5 months respectively. This discrepancy in predicted RMST underscores the importance of the MELD score. The linear link does not always result in fitted RMST values within an admissible range (0, L]. This could perhaps be remedied by transforming various covariates, or by simply bounding estimated RMST. The remaining parameter estimates for the 1- and 5-year windows are provided in Web Appendix E.

Table 4.

Estimated covariate effects on RMST in the absence of liver transplantation (L = 36 months)

	Linear			Log			Logistic
${\mathit{Z}}_i^D(0)$	${\widehat{\mathit{\beta }}}_D$	ASE1	p	${\widehat{\mathit{\beta }}}_D$	ASE1	p	${\widehat{\mathit{\beta }}}_D$	ASE1	p
Intercept	32.95	0.5	< 0.01	3.57	0.02	0.8	2.42	0.08	< 0.01
Year-2005	−1.02	0.05	< 0.01	−0.04	< 0.01	< 0.01	−0.16	0.01	< 0.01
Age-50 (Years)	−0.2	0.01	< 0.01	−0.01	< 0.01	< 0.01	−0.04	< 0.01	< 0.01
Sodium-130 (mmol/l)	0.47	0.02	< 0.01	0.02	< 0.01	< 0.01	0.08	< 0.01	< 0.01
MELD Score-6	−0.89	0.02	< 0.01	−0.05	< 0.01	< 0.01	−0.16	< 0.01	< 0.01
UNOS Region	Reference Group: 5
1	−1.52	0.49	< 0.01	−0.06	0.02	< 0.01	−0.27	0.07	< 0.01
2	−1.35	0.38	< 0.01	−0.06	0.01	< 0.01	−0.22	0.06	< 0.01
3	−3.26	0.43	< 0.01	−0.11	0.02	< 0.01	−0.49	0.07	< 0.01
4	0.23	0.34	0.5	0.02	0.01	0.09	0.04	0.06	0.46
6	−0.97	0.54	0.07	< 0.01	0.02	0.95	−0.12	0.09	0.21
7	−0.59	0.42	0.16	−0.02	0.02	0.32	−0.1	0.07	0.14
8	−0.9	0.42	0.03	< 0.01	0.02	0.94	−0.13	0.07	0.06
9	−1.41	0.36	< 0.01	−0.07	0.01	< 0.01	−0.21	0.06	< 0.01
10	−2.24	0.48	< 0.01	−0.09	0.02	< 0.01	−0.39	0.07	< 0.01
11	−2.75	0.44	< 0.01	−0.1	0.02	< 0.01	−0.44	0.07	< 0.01
Gender	Reference Group: Male
Female	0.49	0.22	0.02	< 0.01	0.01	0.95	0.06	0.03	0.1
Race	Reference Group: White
Black	0.34	0.41	0.41	0.02	0.02	0.23	0.06	0.06	0.31
Hispanic	0.23	0.27	0.4	0.01	0.01	0.21	0.04	0.05	0.33
Asian	1.76	0.55	< 0.01	0.05	0.02	0.01	0.33	0.11	< 0.01
Others	−0.57	0.89	0.52	−0.01	0.04	0.74	−0.11	0.15	0.48
Blood Type	Reference Group: O
A	−0.08	0.21	0.72	−0.01	0.01	0.26	−0.02	0.03	0.63
B	−0.02	0.36	0.95	−0.01	0.01	0.59	< 0.01	0.06	0.97
AB	−0.59	0.78	0.44	−0.05	0.03	0.08	−0.19	0.11	0.1
Diagnosis	Reference Group: No or Yes
Hepatitis C	−1.33	0.33	< 0.01	−0.04	0.01	< 0.01	−0.26	0.05	< 0.01
Noncholestatic	0.76	0.33	0.02	0.06	0.01	< 0.01	0.12	0.05	0.02
Cholestatic	−1.26	0.45	0.01	−0.05	0.02	< 0.01	−0.28	0.07	< 0.01
Acute Hepatic Necrosis	2.27	0.81	0.01	0.06	0.03	0.04	0.56	0.18	< 0.01
Metastatic Disease	−2.95	0.66	< 0.01	−0.11	0.03	< 0.01	−0.53	0.11	< 0.01
Malignant Neoplasm	−7.24	0.37	< 0.01	−0.43	0.02	< 0.01	−1.23	0.06	< 0.01
BMI	Reference Group: (20, 25]
(0, 20]	−2.05	0.47	< 0.01	−0.07	0.02	< 0.01	−0.28	0.07	< 0.01
(25, 30]	0.02	0.27	0.95	0.01	0.01	0.25	−0.01	0.04	0.8
> 30	−0.09	0.27	0.74	< 0.01	0.01	0.98	−0.02	0.04	0.57
Hospitalized	Reference Group: Not Hospitalized
ICU	−1.83	0.65	< 0.01	−0.54	0.08	< 0.01	−0.82	0.14	< 0.01
not ICU	−2.41	0.42	< 0.01	−0.33	0.04	< 0.01	−0.49	0.08	< 0.01
Dialysis	Reference Group: No or Yes
Yes	1.69	0.54	< 0.01	0.13	0.04	< 0.01	0.49	0.09	< 0.01

An offset of L = 36 months is applied for log link.

Figure 3 plots fitted RMST values (L = 3 years) by MELD score (ranging from 6 to 40; i.e., for all possible MELD scores), for the above-described reference patient. For all the three link functions, RMST decreases strongly with increasing MELD score, as anticipated. The fitted values based on all the three links result in fitted values which tail off at higher MELD scores. Among the three link functions, the linear link may be most appealing in terms of its straightforward interpretation. For example, for per unit increase in a patient’s MELD score, the average survival time (capped at 3 years) will decrease approximately 0.9 months; for a 5-year increase in age at wait-listing, 3-year RMST decreases by approximately 1 month. Analogous trends are also observed in the models using the other two link functions. We will further compare the model adequacy using different link functions in terms of discrimination ability and prediction accuracy.

Fig. 3.

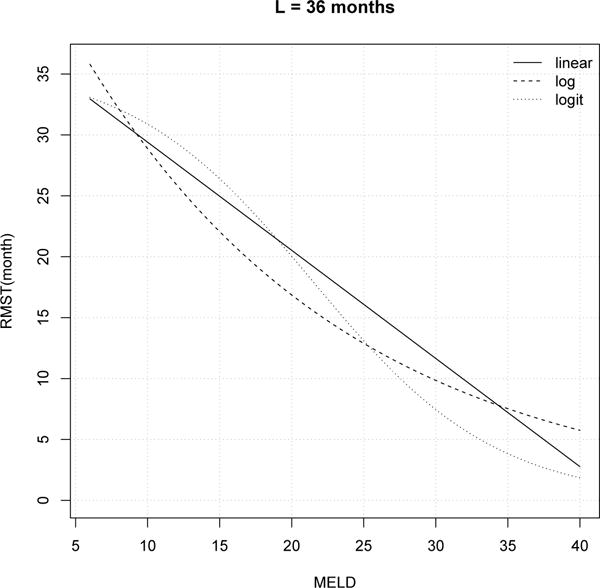
Fitted RMST (L = 36 months) by MELD score for a reference patient: white, male, age=50, Region=5, year=2005, not hospitalized, not on dialysis, blood Type=O, BMI ∈ (20, 25], sodium=130

To evaluate each model’s discrimination ability, we compute the Index of Concordance (IOC), also known as the C statistic (Harrell et al. 1996; Heagerty and Zheng 2005; Uno et al. 2011), denoted by:

$$\text{IOC}=\frac{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\Delta }_i{\widehat{W}}_i(Y_i){\widehat{W}}_j(Y_i)I\left[Y_i<Y_j,g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}<g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_j^D(0)\}\right]}}}{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\Delta }_i{\widehat{W}}_i(Y_i){\widehat{W}}_j(Y_i)I(Y_i<Y_j)}}}.$$

This statistic converges to a censoring distribution free quantity, $P({{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)<{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_j^D(0)|D_i\wedge L<D_j\wedge L)$, measuring the agreement of predictions with observed failure order. Quantities frequently used to evaluate model prediction accuracy include the mean absolute deviation (MAD) and mean squared deviation (MSD) (see Davison and Hinkley 1997; Tian et al. 2007), formulated as:

$$\begin{array}{l}\text{MAD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\Delta }_i{\widehat{W}}_i(Y_i)\left|[Y_i-g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}\right|},\\ \text{MSD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\Delta }_i{\widehat{W}}_i(Y_i){\left[Y_i-g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}\right]}^2},\end{array}$$

which converge to $E|D_i\wedge L-g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}|$ and $E{[D_i\wedge L-g^{-1}\{{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}}_D{\mathit{Z}}_i^D(0)\}]}^2$ respectively, quantifying the “distance” between predicted and observed outcomes. Proof sketches of the convergence of IOC, MAD and MSD are provided in Web Appendix C.

In Table 5, we calculate these three statistics for the 9 models (3 link functions, with 3 values of L) through 2-fold cross validation. Specifically, we split our data by randomly selecting half of patients (n =27,825) into a “training” set (to which the models are fitted), and using the remaining half (n =27,826) as the “validation” set (to which the discrimination and predictive accuracy measures are applied). For L = 1, IOC=0.82 for all three link functions. For L = 3 and L = 5, IOC is largest for the log link, although not by a wide margin. As L increases, the IOCs decrease, for all link functions; this makes sense intuitively since covariate measurements at times more distant in the past should correspond to reduced discrimination. In terms of both MAD and MSD, the logistic link has the best prediction accuracy by a fair margin.

Table 5.

Index of Concordance (IOC), Mean Absolute Deviation (MAD) and Mean Squared Deviation (MSD): Comparison of link functions by L (years)

Measure	L	Linear	Log	Logistic
IOC	1	0.82	0.82	0.82
	3	0.77	0.78	0.77
	5	0.72	0.75	0.74
MAD	1	1.52	1.67	1.36
	3	5.08	5.05	4.58
	5	7.19	6.56	6.06
MSD	1	6.66	6.97	6.42
	3	70.10	69.51	66.02
	5	153.25	145.78	139.75

6 Discussion

We have proposed methods to model restricted mean survival time as a function of baseline covariates, using techniques that are valid under a wide variety of censoring mechanisms. RMST is often of inherent interest to investigators, especially in settings where cumulative covariate effects are appealing. RMST is also an attractive alternative when the proportional hazards assumption does not hold. We have constructed double IPCW weights to simultaneously account for independent and dependent censoring. This general setup is frequently necessary in applications, and failing to account for either type of censoring may result in biased estimation of the mortality model. In studies with only one type of censoring, one would need to calculate the corresponding IPCW weight and set the other to 1. In the interests of flexibility and robustness, our proposed approach does not assume a model for the death time D∧L but for its mean E(D ∧ L). This, however, sacrifices some efficiency in settings wherein a (correctly specified) parametric model is assumed.

Stemming from our current work are several interesting directions worth exploring in the future. One is to consider ‘residual’ RMST (Grand and Putter 2015); i.e. conditional RMST given that the patients is still alive at a later time point after being wait-listed. This could be achieved by applying our methods to landmark analysis, which incorporates time-varying covariates in the mortality model. For instance, results from this landmark analysis should be of interest to patients (already wait-listed for a period of time) who want to know the effect of MELD on residual survival time. It would also be interesting to contrast RMST to the analogous number, expectancy of life lost before time L, which is the area under the curve of cumulative incidence functions rather than marginal survival functions. Andersen (2013) has discussed decomposition of number of life years lost using pseudo-observations in the context of competing risk. Assuming the absence of time-varying covariates (as needed in Andersen 2013) and the use of a simple linear link, we expect the estimated covariate effects from modeling number of life years lost would remain the same magnitude but change the sign, and the intercept would change to L subtracted by the intercept in RMST model. Furthermore, one recent paper by Zhao et al. (2016) proposed to infer RMST curves as a function of L. Following this direction, extension of our methods to RMST curves might be worth further consideration.

We have applied our proposed method to ESLD data to study pre-transplant mortality. Such data requires consideration not only of independent censoring, but also of dependent censoring, where the receipt of a transplant precludes observation of wait-list mortality. This is the first paper to directly estimate RMST in the ESLD setting. The R code to implement our methods is available upon request to the first author.