Computational tools help improve protein stability but with a solubility tradeoff

Abstract

Accurately predicting changes in protein stability upon amino acid substitution is a much sought after goal. Destabilizing mutations are often implicated in disease, whereas stabilizing mutations are of great value for industrial and therapeutic biotechnology. Increasing protein stability is an especially challenging task, with random substitution yielding stabilizing mutations in only ∼2% of cases. To overcome this bottleneck, computational tools that aim to predict the effect of mutations have been developed; however, achieving accuracy and consistency remains challenging. Here, we combined 11 freely available tools into a meta-predictor (meieringlab.uwaterloo.ca/stabilitypredict/). Validation against ∼600 experimental mutations indicated that our meta-predictor has improved performance over any of the individual tools. The meta-predictor was then used to recommend 10 mutations in a previously designed protein of moderate thermodynamic stability, ThreeFoil. Experimental characterization showed that four mutations increased protein stability and could be amplified through ThreeFoil's structural symmetry to yield several multiple mutants with >2-kcal/mol stabilization. By avoiding residues within functional ties, we could maintain ThreeFoil's glycan-binding capacity. Despite successfully achieving substantial stabilization, however, almost all mutations decreased protein solubility, the most common cause of protein design failure. Examination of the 600-mutation data set revealed that stabilizing mutations on the protein surface tend to increase hydrophobicity and that the individual tools favor this approach to gain stability. Thus, whereas currently available tools can increase protein stability and combining them into a meta-predictor yields enhanced reliability, improvements to the potentials/force fields underlying these tools are needed to avoid gaining protein stability at the cost of solubility.

Introduction

Most natural proteins have modest thermodynamic stability, limiting their development as effective biocatalysts, biosensors, and therapeutics (1). Generally, increasing stability tends to increase protein production yields (2, 3), lengthen shelf-life (4–6), and improve survival under challenging solution conditions (pH, proteases, cosolvents, etc.). Increased stability also allows the use of elevated reaction temperatures, improving reaction rates and reducing unwanted bacterial growth in industrial reactions (7). Increased stability may also decrease local and/or global unfolding rates, thereby reducing the formation of aggregates and, consequently, immunogenicity (4–6, 8). Despite its great significance, the reliable engineering of protein stability via sequence changes is still a challenging and often laborious task (9). Various experimental methods, including directed evolution (10) and deep sequencing (11, 12), are commonly used to improve protein stability in practice, but these are time-consuming and costly (13).

To allow simple and cost-effective protein engineering, numerous computational tools have been developed to predict the effect of mutations on stability. These tools are readily employed by both experts and non-experts due to simple inputs (a PDB² structure) and output (a predicted change in stability). Some tools, like EGAD (14), rely on physical force fields that seek to recapitulate the forces felt by a solvated protein. Others, such as PoPMuSiC (15), use statistical potentials, based on the probability of particular amino acids or atoms being in contact in known structures. Combining some elements of each of the above with empirical terms (such as an explicit term for hydrogen bonding) is often referred to as an empirical potential, employed by well-established tools, such as FoldX (16) and Rosetta (17). Still others, like IMutant3 (18), utilize a set of specific features, such as change in hydrophobicity or size, in conjunction with machine learning techniques. To date, however, only a few of these tools (FoldX (16), Rosetta-ddG (17), and PoPMuSiC (15)) have been employed to improve protein stability experimentally through the use of point mutations (19–31), whereas many have only been tested on existing mutation data sets. Entirely sequence-based approaches, such as consensus design and ancestral reconstruction, have also been applied to the protein engineering problem. Whereas these methods often generate sequences with high stability, functional specificity may be sacrificed (32). Making specific consensus mutations, rather than changing the entire sequence, has also proven to be effective (9). However, the size and quality of the multiple sequence alignments needed for this method can vary considerably from one target to another, and too much or too little diversity can be detrimental (33). Thus, choosing a particular tool when undertaking protein engineering to enhance protein stability can be fraught.

To decrease reliance on any one tool and increase the chance of success when using computational methods, which remains notably low (9, 34, 35), we combined diverse tools into a single meta-predictor. Meta-predictors have performed well in related predictions, such as covalent protein modification (36), protein–ligand binding (37), protein–protein interfaces (38), disordered regions of proteins (39, 40), and protein aggregation (41), where the combination of tools with differing and perhaps complementary strengths and weaknesses may allow retention of strengths while ameliorating weaknesses. We show that this stability meta-predictor performs better than any single tool when tested against a large set of experimental mutations from the Protherm database (42). In addition, we tested the meta-predictor by using it to predict mutations to stabilize a previously designed protein, ThreeFoil, which has moderate thermodynamic stability (43), as is often the case in initial design iterations and generally limits further development of protein function (44, 45). Experimental characterization of 10 of the top predicted stabilizing mutations resulted in four stabilizing mutations that combine to yield a substantial improvement in stability. However, the mutation predicted to be the most stabilizing was experimentally the most destabilizing. Moreover, the highly stabilized multiple mutants lost considerable solubility due to increases in surface hydrophobicity. Critically, analysis of the Protherm database and individual prediction tools shows that increased surface hydrophobicity is a common and significant caveat to enhancing stability. Thus, we find that, although increasing accuracy and accounting for solubility warrant further attention, meta-prediction offers an effective, inexpensive, and extensible way to model and improve protein stability, which may be valuable for a great diversity of applications.

Results

Meta-prediction of stability change

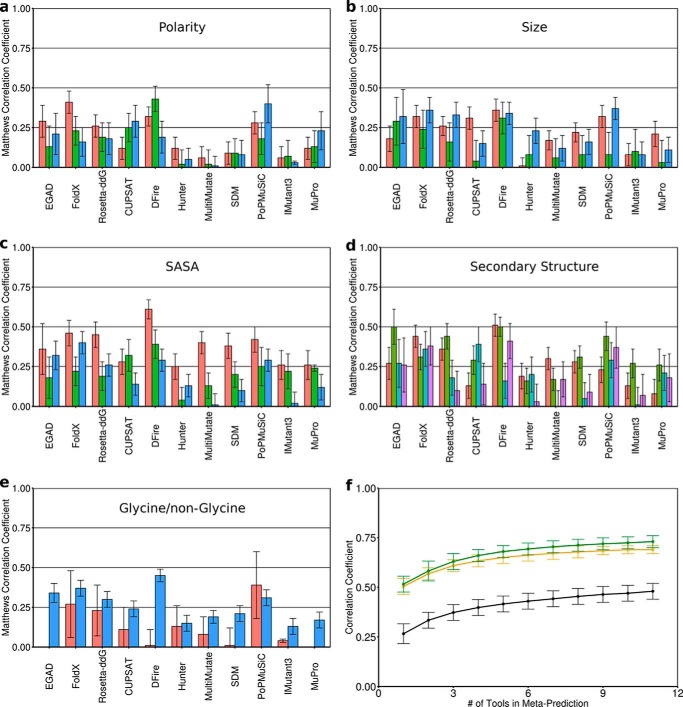
There are numerous freely available and easy-to-use tools for predicting the change in protein stability upon point mutation. These include FoldX (16), Rosetta-ddG (17), PoPMuSiC (15), EGAD (14), IMutant3 (18), CUPSAT (46), SDM (47), Hunter (48), MuPro (49), MultiMutate (50), and DFire (51). Examining the individual performance of each of these 11 stability prediction tools against a data set of 605 mutations (supplemental Table S1) from the Protherm database (42), which had not been used in their training or parameterization, revealed significant differences between tools, depending on the type of mutation (e.g. solvent-exposed versus buried) (Fig. 1, a–e).

Figure 1.

Building the meta-predictor. The performance of each tool as measured by MCC (96) is shown for different classifications of point mutations. a, polarity: decreased (red), similar (green), increased (blue). b, size: smaller (red), similar (green), larger (blue). c, solvent-accessible surface area of the WT residue: buried (red), partially exposed (green), exposed (blue). d, secondary structure of the backbone at the mutated position: helical (red), strand (green), turn (cyan), unstructured (purple). e, whether the mutation is to/from a glycine (red) or non-glycine (cyan). f, the more tools that were combined in the meta-predictor, the better the average performance, shown for MCC (black), ρ (orange), and R (green). Error bars (a–e), S.D. from 1000 analyses using 50% of the mutation data set. Individual predictors are grouped based on methodology: physical force field (EGAD), empirical potentials (FoldX and Rosetta), statistical potentials without machine learning (CUPSAT, DFire, Hunter, MultiMutate, and SDM), statistical potentials with machine learning (PoPMuSiC), and feature-based with machine learning (IMutant3 and MuPro).

Notably, there are many cases where specific tools are particularly well or poorly suited to certain types of mutations. For instance, tools using physical or empirical potentials (EGAD, FoldX, and Rosetta-ddG) appear to more accurately predict mutations that increase hydrophobicity than those that reduce it or leave it essentially unaltered (Fig. 1a, red versus green and blue bars). By contrast, many of the tools using statistical potentials (CUPSAT, SDM, PoPMuSiC, and MuPro) show the opposite trend (Fig. 1a). Interestingly, whereas all tools are better at predicting changes to buried residues compared with partially buried or exposed residues (Fig. 1c, red versus green and blue bars), some tools (EGAD, FoldX, Rosetta-ddG, DFire, and PoPMuSiC) do fairly well overall, whereas others like MultiMutate and IMutant3 are not reliable for surface-exposed residues (Fig. 1c, blue bars).

To utilize all of these tools to maximum effect, a meta-predictor was constructed such that the weight given to the prediction from any particular tool was based on that tool's performance against similar types of mutations from the training set of 605 mutations (see “Experimental procedures”). Cross-validation (see “Experimental procedures”) showed that the meta-predictor has improved performance as more individual tools are incorporated (Fig. 1f). The performance of the meta-predictor was superior to any individual tool based on numerous statistical measures, including correlation coefficients, precision, accuracy, and error (Fig. 2 and Table 1). Thus, combining any number of stability prediction tools weighted according to their individual performance is a useful and extensible strategy for improving performance and may be valuable for many applications, such as predicting stability changes for disease-causing mutations and identifying mutations to stabilize a protein of biotechnological importance. A web-server for the meta-predictor can be found at meieringlab.uwaterloo.ca/stabilitypredict/.³

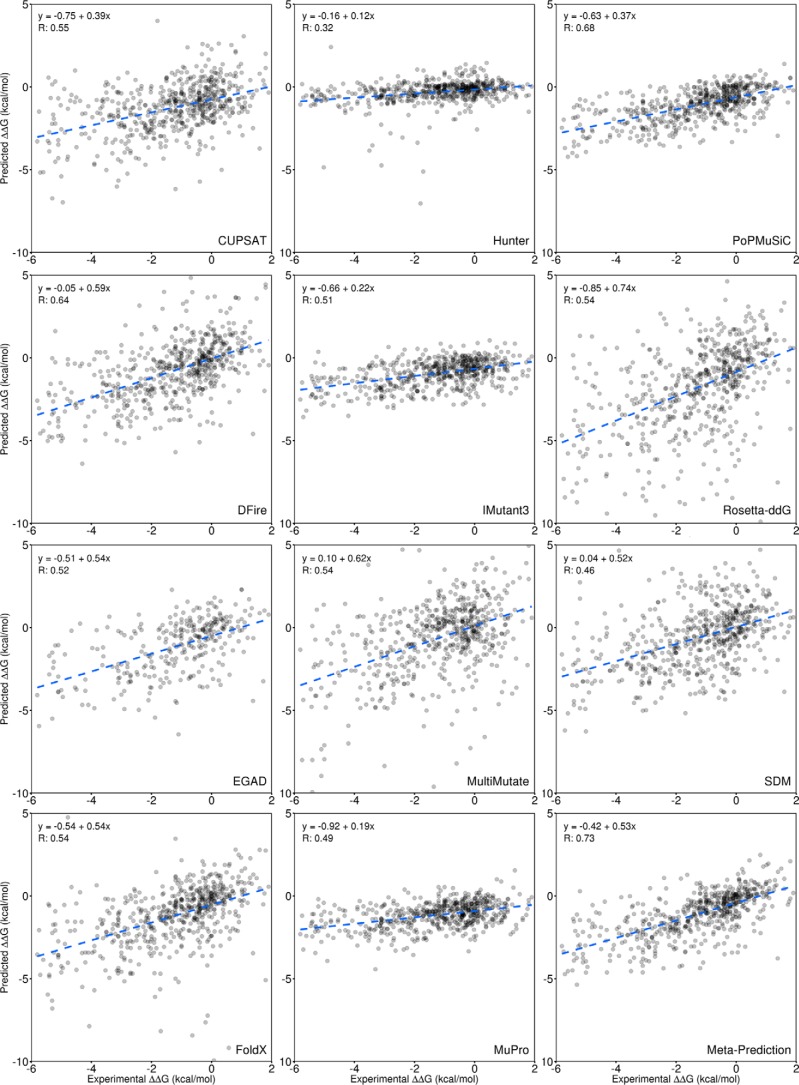
Figure 2.

Comparison of individual tools with the meta-predictor. The predicted ΔΔG for a point mutation is compared with the experimentally determined value for 605 mutations from the Protherm database (42). This comparison is performed for each of the individual prediction tools and the meta-predictor (bottom right). The equations for the linear fit are given as well as the Pearson (R) correlation coefficient based on the mean of 1000 samples of 50% of the data, as shown in Table 1.

Table 1.

Comparison of individual tools with the meta-predictor

Each tool was tested on a data set of 605 mutations covering protein structural classes of α, β, and mixed. Performance was measured using correlation coefficients (MCC and Pearson R) as well as precision (the percentage of mutations predicted to stabilize that do so experimentally), accuracy (the percentage of mutations correctly classified as stabilizing or destabilizing), and S.E. For MCC, precision, and accuracy, mutations predicted or experimentally determined to have an effect <0.2 kcal/mol were not included, thus eliminating a significant source of noise due to uncertainty in small ΔΔG values. Reported values are the mean from 1000 tests using a randomly selected 50% of the data set. For the meta-predictor, this allowed cross-validation by training the weights using 50% of the data set while testing on the remaining 50%. The best result for each metric (shown in boldface type) was obtained using the meta-predictor.

Tool	MCC	R	Precision	Accuracy	S.E.
			%	%	kcal/mol
EGAD	0.34	0.52	50	74	1.61
FoldX	0.38	0.54	52	78	1.78
Rosetta-ddG	0.32	0.54	46	75	2.34
CUPSAT	0.24	0.55	44	75	1.77
DFire	0.43	0.64	49	76	1.84
Hunter	0.16	0.32	34	68	1.89
MultiMutate	0.19	0.54	32	62	2.34
SDM	0.26	0.46	37	68	1.96
PoPMuSiC	0.33	0.68	59	79	1.32
IMutant3	0.14	0.51	41	75	1.52
MuPro	0.18	0.49	57	78	1.52
Meta-predictor	0.48	0.73	63	82	1.29

Improving ThreeFoil stability

In an effort to improve the thermodynamic stability of ThreeFoil (which is ∼6 kcal/mol) (43), the meta-predictor was used to predict the change in thermodynamic stability (ΔΔG) for all point mutations (excluding cysteine) to each of ThreeFoil's 141 residues, excluding 21 residues probably involved in carbohydrate or sodium binding function (supplemental Fig. S1). Because ThreeFoil possesses 3-fold sequence and structural symmetry, the predicted ΔΔG values were averaged across symmetric positions. Thus, small structural variations between symmetric positions can provide an ensemble-like representation, improving prediction accuracy (52). The outcome was a total of 720 predictions, 83 (12%) of which were expected to be stabilizing. At some positions there were multiple predicted stabilizing mutations; these may be unidentified functional sites (53–55) or areas where the initial design was poor (56). To test diverse positions, only the most stabilizing mutation at each residue was considered. An exception was the selection of two mutations at Glu-66, a completely solvent-exposed position for which 10 of the 18 possible substitutions were predicted to stabilize and where poor agreement between Rosetta and consensus design was observed during the initial development of ThreeFoil (56). In total, 10 point mutations predicted to stabilize were tested experimentally (Fig. 3a). These mutations were made in ThreeFoil's second symmetric subdomain, and the effect of each mutation was determined using kinetic unfolding and folding measurements (Fig. 3b, Table 2, and supplemental Fig. S2).

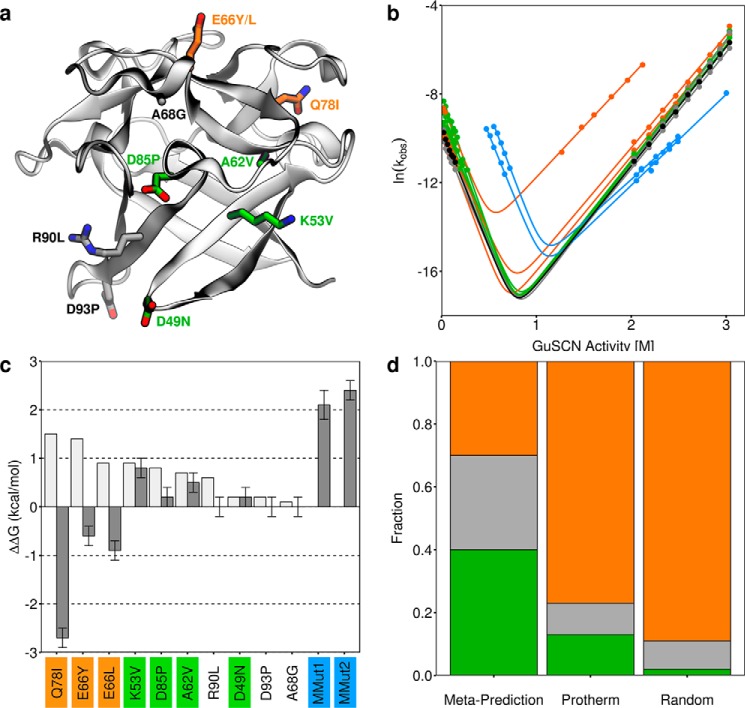
Figure 3.

Experimental characterization of mutations to ThreeFoil. a, ThreeFoil's structure with sites of mutation shown as sticks. Stabilizing mutations are shown in green, destabilizing mutations in orange, and neutral in gray. b, folding and unfolding kinetics of ThreeFoil and mutants. The same colors are used as in a, with wild type shown in black and the highly stabilized multiple mutants in blue. Solid lines, fits of the data to a two-state unfolding model using Equation 3. c, predicted (light gray) and experimentally determined (dark gray) change in thermodynamic stability for ThreeFoil mutants, ΔΔG_{U − F}. Positive values indicate increased stability, calculated using folding and unfolding rate constants in the absence of denaturant (see “Experimental procedures” and Table 2). d, fractions of mutations that are stabilizing (green, ΔΔG_{U − F} ≥ 0.2 kcal/mol), neutral (gray, 0.2 kcal/mol > ΔΔG_{U − F} > −0.2 kcal/mol), or destabilizing (orange, ΔΔG_{U − F} ≤ −0.2 kcal/mol) determined for ThreeFoil mutants designed using the meta-predictor, the Protherm database, and random mutagenesis (from deep sequencing studies (12, 57–59); see supplemental Table S2). Error bars, uncertainty from linear fit using Origin 5 software.

Table 2.

Kinetic parameters of ThreeFoil mutants

Equations for determining kinetic values are given under “Experimental procedures.” Single mutants are listed in order of experimental stability changes, with mutations confirmed to stabilize experimentally (ΔΔG_{U − F} ≥ 0.2 kcal/mol) listed in boldface type. MMut1, K6V/K53V/K100V, A15V/A62V/A109V, D38P/D85P/D132P; and MMut2, MMut1 plus D2/49/96N. Error estimates from the data fit used Origin version 5.

Mutant	ln (kf)	ln(ku)	mf	mu	Cmid	ΔΔGU − F
			kcal mol−1 m−1	kcal mol−1 m−1	m	kcal/mol
WT	−9.57 ± 0.06	−22.0 ± 0.2	−6.22 ± 0.33	3.20 ± 0.05	0.79 ± 0.02	0
K53V	−8.07 ± 0.05	−21.9 ± 0.3	−7.10 ± 0.24	3.24 ± 0.08	0.80 ± 0.03	0.8 ± 0.2
A62V	−8.66 ± 0.05	−22.0 ± 0.3	−6.78 ± 0.28	3.25 ± 0.07	0.79 ± 0.03	0.5 ± 0.2
D85P	−9.14 ± 0.06	−21.9 ± 0.3	−5.97 ± 0.33	3.19 ± 0.07	0.83 ± 0.03	0.2 ± 0.2
D49N	−9.07 ± 0.03	−21.9 ± 0.1	−6.37 ± 0.17	3.23 ± 0.03	0.80 ± 0.02	0.2 ± 0.2
A68G	−9.59 ± 0.05	−22.1 ± 0.2	−6.12 ± 0.29	3.28 ± 0.04	0.79 ± 0.02	0.0 ± 0.2
R90L	−9.99 ± 0.05	−22.4 ± 0.2	−5.78 ± 0.29	3.34 ± 0.04	0.81 ± 0.02	0.0 ± 0.2
D93P	−9.45 ± 0.06	−21.9 ± 0.2	−6.26 ± 0.36	3.13 ± 0.05	0.79 ± 0.03	0.0 ± 0.2
E66Y	−9.73 ± 0.07	−21.2 ± 0.3	−6.76 ± 0.38	3.09 ± 0.06	0.69 ± 0.03	−0.6 ± 0.2
E66L	−9.58 ± 0.06	−20.6 ± 0.2	−5.60 ± 0.31	3.02 ± 0.05	0.76 ± 0.02	−0.9 ± 0.2
Q78Ia	−8.40 ± 0.13	−16.3 ± 0.1	−6.22 ± 0.33	2.70 ± 0.03	0.52 ± 0.03	−2.7 ± 0.2
MMut1	−4.50 ± 0.3	−20.4 ± 0.3	−6.34 ± 0.31	2.46 ± 0.07	1.08 ± 0.05	2.1 ± 0.3
MMut2	−3.15 ± 0.17	−19.6 ± 0.2	−6.75 ± 0.16	2.32 ± 0.06	1.08 ± 0.03	2.4 ± 0.2

^a Only a single point was determined on the refolding branch for Q78I due to aggregation at intermediate denaturant concentrations. The m_f from WT was used to estimate ln(k_f), and values affected by this approximation are given in italic type.

The experimental effects of the mutations on stability were mixed (Fig. 3c). Four mutations (K53V, A62V, D85P, and D49N) increased the folding rate, stabilizing ThreeFoil by 0.8, 0.5, 0.2, and 0.2 kcal/mol, respectively (Table 2 and Fig. 3 (green mutations)). Three mutations (A68G, R90L, and D93P) had no significant effect on stability, although in the case of A68G and D93P, the predicted effect was also small (Table 2). The remaining three mutations (E66Y, E66L, and Q78I), which had been predicted to be the most stabilizing, resulted in faster unfolding and stability losses of 0.6, 0.9, and 2.7 kcal/mol, respectively. Consistent with mutations being, by design, outside ThreeFoil's carbohydrate binding sites, none of the stabilizing mutations affected carbohydrate binding affinity (supplemental Fig. S3). Predictions of the individual tools differed considerably, and no single tool was reliable (supplemental Fig. S4). Overall, the 40% success rate of the meta-predictor compares favorably with an expected rate of ∼2% for random mutagenesis (based on recent deep sequencing experiments; supplemental Table S2 (12, 57–59)).

Taking advantage of symmetry

By using the most stabilizing mutations and not only combining them, but repeating them in all three symmetric subdomains (Fig. 4), ThreeFoil's symmetry was leveraged to achieve substantial stabilization. Two multiple mutants were made, the first (MMut1) incorporating K53V, A62V, and D85P at all symmetric sites, and the second (MMut2) adding D49N at each symmetric site. Both multiple mutants stabilize the protein by >2 kcal/mol and increase the denaturation midpoint as a result of greatly increased refolding rates (Fig. 3 (b and c), blue mutants). For instance, whereas the wild-type has a refolding half-life in the absence of denaturant of several hours, the multiple mutants have refolding half-lives of 1 min or less under the same conditions. Although the stabilization and improvement in refolding rates represent a marked improvement, both multiple mutants are considerably less soluble (0.1–0.2 mg/ml) than the original protein (>20 mg/ml) (Table 3). Given the nature of the individual mutations (K6V/K53V/K100V and D38P/D85P/D132P replace charged and exposed side chains with hydrophobic ones, A15V/A62V/A109V increases the size of a hydrophobic side chain, and D2N/D49N/D96N replaces a charged and exposed side chain with a polar one), these results highlight a potential problem wherein selecting for the singular characteristic of improved stability has given the unintended outcome of lower solubility, probably due to increased surface hydrophobicity.

Figure 4.

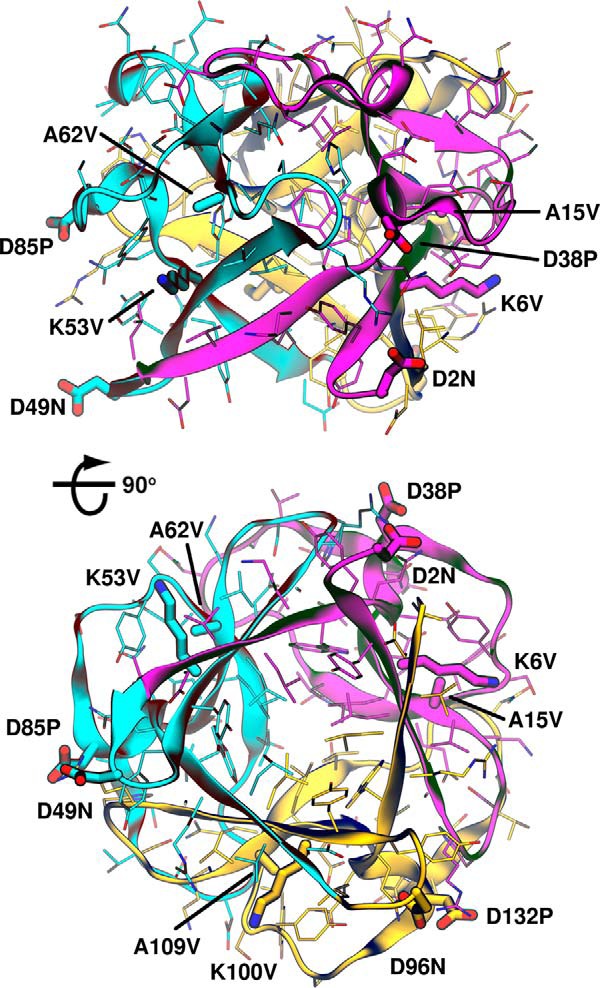
Taking advantage of symmetry to improve stability. ThreeFoil structure (PDB entry 3PG0) is shown from a side view, perpendicular to the 3-fold axis of symmetry (top) and rotated 90° to look along the axis of symmetry toward the capping β-hairpin triplets (bottom). The first, second, and third subdomains are shown in magenta, cyan, and yellow, respectively. Sites of mutations used for MMut1 (K6V/K53V/K100V, A15V/A62V/A109V, and D38P/D85P/D132P) and MMut2 (same as MMut1 plus D2N/D49N/D96N) are shown as thick sticks.

Table 3.

Experimental and predicted solubility of ThreeFoil variants

Values for each solubility prediction tool were normalized to be 1.0 for WT. In cases where the tool's output is a lower value when solubility is decreased, the score is simply normalized as Mut_score /WT_score. In cases where the tool's output is a higher value when solubility is decreased, the normalized score is (1/Mut_score)/(1/WT_score) (alternatively, WT_score/Mut_score). Thus, all predictions of reduced solubility relative to WT have scores < 1.0. The following output values were used from each tool: Aggrescan3D (99), total score; CamSol (100), intrinsic solubility; PASTA (101), number of amyloid-forming regions; TANGO (102), Agg parameter; ZipperDB (103), number of amyloid-prone regions; Zyggregator (104), intrinsic aggregation propensity. Hydrophobicity is defined by the change in side chain solvation free energy, as determined by Wimley et al. (65).

Mutant	Solubility	Aggrescan3D	CamSol	PASTA	TANGO	ZipperDB	Zyggregator	Hydrophobicity
	mg/ml
WT	23.8	1.00	1.00	1.00	1.00	1.00	1.00	1.00
K53V	22.5	0.97	0.78	0.98	0.01	0.94	1.08	0.95
A62V	21.1	1.00	0.98	1.00	1.00	0.88	0.99	0.98
D85P	16.9	0.96	0.99	1.00	0.99	1.00	0.92	0.94
D49N	25.0	0.98	0.99	1.00	1.00	0.94	0.91	0.95
A68G	21.9	1.00	1.01	1.00	1.00	1.00	1.00	1.01
R90L	16.8	0.92	0.87	1.00	0.42	1.00	1.08	0.95
D93P	21.2	0.93	0.98	1.00	1.00	1.00	0.92	0.94
E66Y	19.9	0.95	0.98	1.00	1.00	1.00	0.90	0.93
E66L	17.0	0.96	0.99	1.00	1.00	1.00	0.90	0.92
Q78I	1.4	1.00	0.96	0.91	0.02	1.00	0.99	0.97
MMut1	0.2	0.79	0.28	0.86	0.00	0.63	1.01	0.72
MMut2	0.1	0.76	0.15	0.86	0.01	0.58	0.73	0.65
R		0.71	0.75	0.93	0.75	0.69	0.30	0.75
ρ		0.60	0.63	0.58	0.64	0.20	0.15	0.59

Stabilizing mutations tend to increase surface hydrophobicity

Whereas protein function often relies on having at least some stability (maintenance of the native form of the protein), it is also crucial to have enough solubility (protein available in solution) to perform that function adequately. Examining the source of reduced solubility of the multiple mutants, and minor reduction in solubility of the single mutants, reveals critical problems with the potentials/force fields underlying current protein stabilization tools.

A diverse set of factors that may contribute to reduced protein solubility have been recognized, from specific structural features like exposed hydrophobic patches (60) and regions with high propensity to form amyloid-like structures (61) to overall properties, such as net charge (62) and amino acid content (63, 64). Many solubility prediction tools exist that take these factors into account. Applying six tools available online showed they successfully predicted the greatly reduced solubility of the multiple mutants but could not discriminate well the differences in solubility between the single mutants (Table 3). Notably, however, simply accounting for the change in hydrophobicity of the mutation (measured by change in solvation free energy of the side chains) (65) gave an equally good prediction of the multiple mutants' poor behavior, as measured by both linear and rank correlation coefficients (Table 3). Indeed, 9 of the 10 mutations are to more hydrophobic residues, and this apparent preference for hydrophobic mutations, even on the protein surface, suggested a potential general problem with computational prediction.

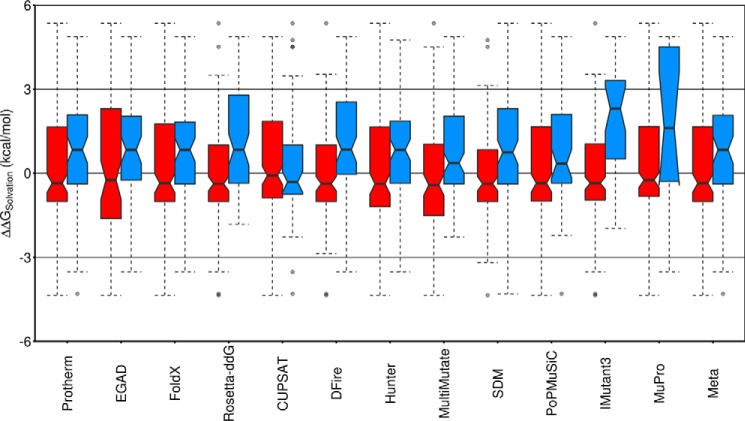
Whereas a few experimental studies have suggested that increasing hydrophobicity at the protein surface improves stability (66–70), and the favoring of increased hydrophobicity has been reported for a few computational tools (14, 71, 72), our analysis indicates that this is, in fact, a widespread phenomenon. Examining the Protherm data set shows that stabilizing mutations on the protein surface are often observed when making substitutions to more hydrophobic residues, whereas destabilizing mutations tend to be substitutions to more hydrophilic residues (Fig. 5, Protherm). Critically, we find that 10 of the 11 individual tools have a bias toward recommending hydrophobic mutations on the protein surface as stabilizing. Overall, this results in predicted stabilizing mutations increasing solvation free energy by 0.84 kcal/mol on average (Fig. 5), similar to mutating alanine to valine (65). Although the tools may be recapitulating a real tendency for hydrophobic surface mutations to stabilize, the fact that protein design attempts most frequently fail because of poor solubility (73) makes this a critical concern for protein engineering and design.

Figure 5.

Stabilizing mutations on the protein surface favor increasing hydrophobicity. The changes in side chain solvation free energy, ΔΔG_solvation (kcal/mol) (65) for all 229 solvent-exposed mutations in the Protherm-derived data set (positive ΔΔG_solvation indicates a mutation to a more hydrophobic residue with reduced solubility in water (65)) are shown as box plots. Red boxes, mutations predicted to destabilize (ΔΔG_{U − F} ≤ −0.2 kcal/mol); blue boxes, mutations predicted to stabilize (ΔΔG_{U − F} ≥ 0.2 kcal/mol). For the Protherm-derived data set (far left), red indicates mutations experimentally determined to destabilize, and blue indicates mutations experimentally determined to stabilize relative to the wild-type protein. The notched region around the median (horizontal line) of each box represents the 95% confidence interval for the median, indicating that for Protherm and the majority of the predictors, mutations on the protein surface that increase stability tend to be to more hydrophobic amino acids, whereas mutations that decrease stability tend to be to more hydrophilic amino acids (CUPSAT is the singular exception). The colored region of each box includes the middle 50% of the data, with dashed whiskers showing 1.5 times the interquartile range above and below the middle 50% (the interquartile range is the difference between the top and bottom of the colored region, or the difference between the 25th and 75th percentiles). Outliers (mutations outside the whiskers) are shown as semitransparent single points.

Prediction tools underestimate the importance of buried polar groups

In addition to favoring hydrophobic mutations on the protein surface, the individual tools and meta-predictor may underestimate the importance of buried polar groups. This is suggested by the failure of the Q78I mutation, predicted to stabilize by seven of the individual tools (CUPSAT, DFire, FoldX, MultiMutate, PoPMuSiC, Rosetta-ddG, and SDM, with the remaining predicting essentially no change) (supplemental Fig. S4) and estimated by the meta-predictor to give ∼1.5 kcal/mol of stability, yet resulting in much faster unfolding than WT, and a loss of ∼3 kcal/mol of stability (Fig. 3, b and c). A single buried hydrogen bond has been estimated to contribute ∼1 kcal/mol to protein stability (74). Because Gln-78 makes three buried hydrogen bonds (one side chain–side chain and two side chain–backbone) (Fig. 6), the loss of ∼3 kcal/mol of stability may be accounted for by the loss of these specific interactions. Whereas buried hydrophobic groups (e.g. -CH₂−) may contribute a similar ∼1 kcal/mol to stability (74), isoleucine has only 1 additional -CH₂− group compared with glutamine, suggesting that the buried hydrogen bonds were either undervalued or unrecognized by most of the prediction tools. In the case of physical or empirical force fields, this could arise from solvation terms or parameterization that penalizes the burial of polar or charged residues (75), whereas statistical potentials may inherently undervalue certain interactions (76–78). Here, the mutation of a buried polar sidechain to a hydrophobic one illustrates the dramatic failure that results when computational methods either do not recognize the presence of buried hydrogen bonds or inaccurately predict their contribution to protein stability.

Figure 6.

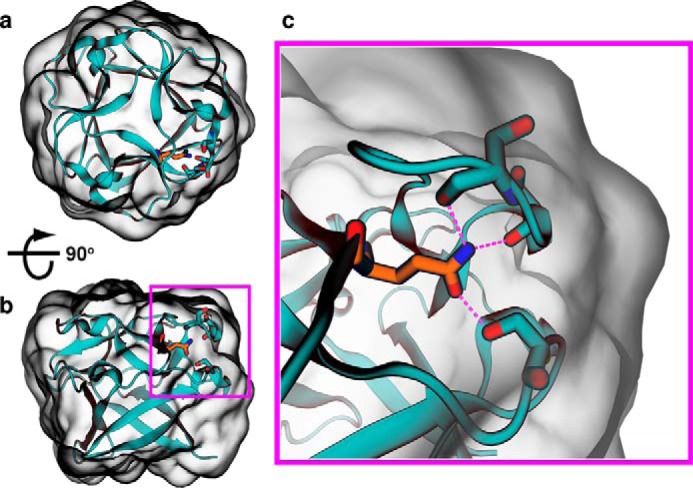
Thermodynamic contributions of buried hydrogen bonds are poorly predicted. In ThreeFoil, the wild-type glutamine at position 78 is completely buried from solvent yet forms three hydrogen bonds. a and b, views of the entire protein are shown with a 90° rotation to illustrate the buried nature and position of Gln-78. c, enlarged view illustrating hydrogen bonds. Two hydrogen bonds are with backbone oxygens, and one is with the oxygen of a serine side chain. Bonds to the glutamine's nitrogen involve the backbone oxygens from serines 22 and 24, whereas the single bond to the glutamine's oxygen involves the side chain oxygen of serine 59. Hydrogen bonds are shown as magenta dashed lines; Gln-78 is shown as orange sticks; and Ser-22, Ser-24, and Ser-59 are shown as cyan sticks.

Discussion

Stabilizing mutations give multiple desirable attributes to proteins: enhanced capacity for directed evolution and design of novel functions (44, 45), increased resistance to high temperature and harsh solution conditions (7, 9), and reduced immunogenicity caused by local or global unfolding and subsequent aggregation (4–6, 8). The meta-prediction approach used here, which incorporated 11 diverse computational tools for predicting ΔΔG upon mutation, was better than any single tool at predicting the effects of more than 600 experimentally characterized point mutations. The meta-predictor also successfully identified stabilizing mutations to a previously designed protein, ThreeFoil. Most mutations to ThreeFoil resulted in stability changes close to the predicted values (Fig. 3), with a success rate of 40%, comparing favorably with other studies (23, 24, 26, 27, 30). Moreover, the stabilizing single mutations could be combined to yield highly stabilized multiple mutants. Because the meta-predictor weighs the contribution of each tool according to its performance on different mutation types (increased size, decreased polarity, etc.), it is readily extensible, allowing for future improvements using complementary or improved individual tools.

The experimental results are also notable because functional residues, which are often sources of instability and easy targets for improvement, were excluded (53–55). Indeed, binding function was maintained upon mutation. The amplification of stability (>2 kcal/mol) gained by leveraging the sequence and structural symmetry of ThreeFoil (56), demonstrates the tractability of engineering using symmetric (79) or repeat protein scaffolds (80, 81), both of which are abundant in nature (82).

Although the stabilization offered by the multiple mutants is substantial, there was a considerable loss in solubility, probably resulting from increases in surface hydrophobicity. All but 1 of the 10 tested mutations either introduced a hydrophobic amino acid or changed a charged residue to a polar one, and the majority of these changes occurred on the protein surface. Although it may seem counterintuitive that hydrophobic mutations at solvent-exposed positions would stabilize, it may be that even on the protein surface, hydrophobic side chains can bury relatively more surface area when in the native rather than the denatured state (67). Here, an analysis of more than 200 experimentally characterized point mutations on protein surfaces reveals that when computational tools attempt to improve protein stability, they often rely on the stabilizing effect of hydrophobic mutations at the cost of solubility. Even the tools that are the most widely used and/or perform the best (high correlation coefficients and/or low error) fall into this trap, such as Rosetta, FoldX, DFire, and PoPMuSiC. Although protein solubility may be generally improved by introducing a high density of similarly charged residues on the protein surface, this leads to decreases in stability (62). However, specifically designing optimized networks of surface electrostatics using a small number of mutations has been shown to improve both stability and foldability, illustrating that stability and solubility tradeoffs are not mandatory (83).

The tendency of the prediction tools to favor hydrophobic mutations is not limited to the protein surface. Mutation of a buried glutamine (Gln-78) to isoleucine was predicted to be the most stabilizing, with the majority of individual tools predicting considerable stabilization and the remainder predicting a nearly neutral effect. Mutations to valine, leucine, and methionine at the same position were also predicted to stabilize. Surprisingly, the Q78I mutation was the most destabilizing mutation tested, dramatically accelerating unfolding. The results for Gln-78 point to an imbalance in force field terms (75) or systematic errors and biases in statistical potentials (76–78); properly recognizing the key role of buried polar side-chains that can hydrogen-bond (84–86) is key to future improvements in prediction reliability.

Accurate and reliable prediction of point mutations is critical to protein design and engineering. Because destabilizing mutations, particularly buried ones, often have larger effects than stabilizing ones (87), even a single incorrectly predicted mutation, like Q78I here, can jeopardize the stability of the entire protein and counteract a larger number of stabilizing mutations. Thus, getting the details right when predicting changes in stability will allow confident engineering of multiple mutants without testing individual mutations and result in reliable success during de novo design (9, 34, 35). For design targets with homologous sequences, incorporating information from multiple-sequence alignments may improve reliability (31, 79, 88–90). However, the availability of such sequences, and thus the benefit of their use, will differ from one target to another. Furthermore, choosing the appropriate level of sequence diversity can be challenging (33). Predictions may also be improved by accounting for backbone flexibility, either by building this directly into the tool itself (17) or through multistate design, which could improve the accuracy of existing predictors, although at the cost of additional computational resources (91). Further improvements in the reliability of meta-prediction approaches may be gained by incorporating these additional tools and methods.

In summary, the meta-prediction approach presented here combines individual predictors to improve performance, as demonstrated in testing against a large data set of experimentally characterized mutations and by finding new stabilizing mutations to a previously designed protein while retaining its function. This approach, wherein the weight given to any one tool's prediction is proportional to its performance on similar types of mutations, is extensible to future tools and offers a simple method to gain additional reliability when improving protein stability. Critically, however, the protein engineering tools used here have a marked tendency to improve protein stability by mutating residues on a protein's surface to more hydrophobic side chains, which commonly results in a loss of solubility. This loss of solubility is a key issue that must be resolved for protein engineering to be employed widely and reliably, with a transformative impact on biotechnology.

Experimental procedures

Stability prediction by individual tools

The following individual tools were used for ΔΔG predictions: CUPSAT (web server: cupsat.tu-bs.de/)³ (46), DFIRE2 (stand-alone executable, version 1.1; wild-type and mutant structures were generated using SCWRL4 (92)) (51), EGAD (stand-alone library) (14), FoldX (stand-alone executable, version 3.0) (16), Hunter (stand-alone executable) (48), IMutant3 (stand-alone executable, version 3.0.7) (18), MultiMutate (stand-alone executable) (50), MuPro (stand-alone executable, version 1.1) (49), PoPMuSiC (web server, version 2.0; currently only version 2.1 is available) (15), Rosetta-ddG (stand-alone executable (ddg_monomer) using protocol 16, which incorporates backbone flexibility, Rosetta version 3.5) (17), and SDM (web server: mordred.bioc.cam.ac.uk/∼sdm/sdm.php)³ (47). For predictions of point mutations to ThreeFoil, the PDB structure 3PG0 was used. For predictions of mutations in the Protherm database (42), the structure associated with the particular entry in the database was used and reduced to the residues indicated in the database (i.e. for multidomain proteins). For prediction tools requiring temperature or pH as part of the input, a temperature of 27 °C was used and a pH of 8.1 for consistency with experimental conditions used in testing ThreeFoil. Note that values of the change in free energy for the mutants is based on the convention of measuring the difference in free energy changes from folded to unfolded,

$$\Delta \Delta G_{U-F}=\Delta G_{U-F\left(\text{mut}\right)}-\Delta G_{U-F\left(\text{WT}\right)}$$ (Eq. 1)

where ΔG_{U − F} = G_U − G_F.

Thus, positive ΔΔG_{U − F} values represent increased stability (output from individual tools is converted to this convention).

Curation of the Protherm database

We searched the Protherm database (42) for unique point mutations with experimentally measured ΔΔG values where the temperature and pH of the experiment was between 20 and 30 °C and between 5 and 9, respectively. Additionally, most of the prediction tools cannot account for co-factors or prosthetic groups, so proteins with such groups were also removed. This left 1663 point mutations in total. Testing the prediction tools against mutations used for their training or parameterization may give misleading results. To avoid this, we removed all 1058 mutations used in the training or parameterization of any of the tools, leaving 605 mutations to 60 proteins, including all major structural classes (results of testing against the 1058 removed mutations are given as supplemental Table S3).

A known problem with the Protherm database is entry of ΔΔG values with the wrong sign (42). To correct such entries, we manually reviewed the publications reporting the 605 mutations. In addition to fixing numerous cases where the sign was entered incorrectly, we found several cases where the value reported in the publication was in kJ/mol but had been entered in kcal/mol. A table summarizing the 605 curated mutations is included as supplemental Table S1. As above, we use ΔΔG_{U − F}, with positive values indicating increased stability.

Building the meta-predictor

For the 605-mutation data set (supplemental Table S1), predictions were made using each of the 11 tools. Mutations were then categorized based on five criteria: 1) change in polarity as measured by ΔG of solvation (less, the same, more); 2) change in size (smaller, the same, larger); 3) solvent-accessible surface area of the wild-type residue (buried, partially exposed, fully exposed); 4) secondary structure at the site of mutation (α, β, turn, unstructured); and 5) whether the mutation was to or from glycine (because performance on mutations involving glycine tended to differ most dramatically from other amino acids).

Measures of solvation free energy were taken from the work of Wimley et al. (65), with a difference of >0.1 kcal/mol (ΔΔG_solvation) required to consider the mutation more or less polar. Measures of size were taken from the work of Darby and Creighton (93), and a difference of at least 19 ų (approximately the size of a CH₃ group) was considered larger or smaller. Exposure of the WT residues was calculated using VMD (www.ks.uiuc.edu/Research/vmd/)³ (94), by dividing the solvent-accessible surface area of the amino acid in the PDB structure by that of the fully exposed amino acid. Ranges for the ratios were as follows: buried, ≤0.05; partially buried, 0.05–0.20; exposed, ≥0.20. The secondary structure was calculated using DSSP (95).

Predictions from each tool were weighted by the Matthews correlation coefficient (96) (MCC) for each type of mutation (Fig. 1). The MCC values were determined through cross-validation, in which the data set of 605 mutations was split into halves, with one half used to determine MCC values as weights and the other half used to test overall performance (Fig. 1f); this was repeated 1000 times. Final reported performance values are an average of those 1000 tests (Fig. 1f and Table 1), and the scatter plot in Fig. 2 shows the average value for each mutation when it was not used to train the weights. Overall, the meta-predictor score was calculated as follows,

$$\Delta \Delta G_{\text{meta}}=\frac{{\displaystyle {\sum }_i^{\text{tools}}{\displaystyle {\sum }_j^{\text{types}}{w}_{i,j}}\times \Delta \Delta G_{{\text{tool}}_i}}}{{\displaystyle {\sum }_i^{\text{tools}}{\displaystyle {\sum }_j^{\text{types}}{w}_{i,j}}}}$$ (Eq. 2)

where w_i,j is the weight for the ith tool on the jth mutation type.

Weights for each tool and each type of mutation are given in supplemental Table S4. In the case of the work presented here, all 11 tools were used, but as shown in Fig. 1, benefit can still be derived from combining a subset of those tools if not all are readily available. The web-server for the meta-predictor (meieringlab.uwaterloo.ca/stabilitypredict/) does not include the PoPMuSiC predictor, but it can be used individually from the authors' website (dezyme.com).

Meta-prediction of ThreeFoil point mutations

The ΔΔG of point mutations to ThreeFoil were predicted with each of the 11 tools and then combined into a meta-ΔΔG as above (see Equation 1). To preserve function, we excluded 18 residues in the three symmetric carbohydrate-binding sites (Asp-17/64/111, Ile-30/77/124, Tyr-32/79/126, Ser-35/82/129, Asn-39/86/133, and Gln-40/87/134) and three residues (Asn-28/75/122) in the single sodium-binding site, 21 residues in total. This left 120 residues to test. ThreeFoil is well-behaved in solution, and to preserve this, we chose to avoid incorporation of cysteine, which could cause aberrant cross-linking and aggregation (ThreeFoil has no cysteine residues). Given the remaining set of 18 natural amino acids (not including the WT amino acid) and 120 positions, we tested a total of 2160 mutations with each tool (except for EGAD, which cannot predict mutations to or from glycine or proline (14)).

Because ThreeFoil has a 3-fold symmetric sequence and structure, we reasoned that the quality of the predictions could be improved by averaging the results across symmetric positions, because the mutation impact ought to be very similar at each position. Experimental testing of point mutations was performed using the symmetric position in the second/middle subdomain module.

Expression and purification of ThreeFoil mutants

ThreeFoil was expressed from a pET-28a plasmid (Novagen) in BL21 DE3 Escherichia coli cells, as described previously (43, 56). Expression was induced with 1 mm isopropyl 1-thio-β-d-galactopyranoside, and cells were harvested after 24 h at 37 °C. Inclusion bodies were solubilized in buffered urea (6 m urea, 100 mm sodium phosphate, 10 mm Tris, pH 8.1), bound to a nickel-nitrilotriacetic acid column, and eluted with the same buffer as above but at pH 4.5. The protein was then refolded by dialysis (1:10, 10 times) in lyophilization buffer in 50 mm ammonium acetate and lyophilized.

Kinetic analysis of ThreeFoil mutants

All measurements were performed at 27 °C. Folding and unfolding were monitored by fluorescence using a SpectraMax M5 plate reader (Molecular Devices) with excitation at 274 nm and emission at 317 nm. Fluorescence was measured from the bottom of 96-well UV Star® (Greiner Bio-One) black-well plates with clear, UV-transparent bottoms and the top sealed with HD Clear sealing tape (Hampton Research) to prevent evaporation. To folded or unfolded protein (10 mg/ml ThreeFoil (∼550 μm) in standard buffer (50 mm Tris, 150 mm NaCl, pH 8.1) with or without 4 m GuSCN), varying concentrations of GuSCN in standard buffer were added, such that the final volume in each well was 250 μl at a protein concentration of 3.3 μm. For mutants with much reduced solubility under folded conditions (Q78I, MMut1, and MMut2), the final concentration was kept at 3.3 μm, but the initial stock was of lower concentration; thus, the range of denaturant concentrations that could be explored was less.

The shortest experiments ran for 30 min, whereas the longest ran for 4 days, and the interval for taking plate readings (10 s to 30 min) was chosen such that each run would have ∼200 measurements. Each kinetic trace was fit to a single exponential equation,

$$S=B+C{e}^{-kt}$$ (Eq. 3)

where S is the fluorescence signal, B is the offset, C is the amplitude, k is the rate constant, and t is the time in seconds. The chevron of observed rate constants, k_obs, as a function of denaturant activity, A, was fit to the equation for a two-state transition between folded (f) and unfolded (u) states of the protein (97),

$$\ln \left(k_{\text{obs}}\right)=\ln \left(e^{f+m_{f}A}+e^{u+m_{u}A}\right)$$ (Eq. 4)

where m_fand m_u are the linear denaturant dependence of folding and unfolding, respectively, and f = ln(k_f^H2O) and u = ln(k_u^H2O) are the natural logarithms of the respective folding and unfolding rate constants in water (measured in s⁻¹). The denaturant activity, A, was calculated as by Cota and Clarke (98),

$$A=\left[\text{GuSCN}\right]\times \left(C_{0.5}/\left(C_{0.5}+\left[\text{GuSCN}\right]\right)\right)$$ (Eq. 5)

where C_0.5 is the [GuSCN] at half activity, equal to 6.47 m. The Gibbs free energy of unfolding, also referred to as the thermodynamic stability of the protein, was calculated from the ratio of the folding and unfolding rate constants in the absence of denaturant,

$$\Delta G_{U-F}=-RT\ln \left(k_u^{{\text{H}}_2\text{O}}/k_f^{{\text{H}}_2\text{O}}\right)$$ (Eq. 6)

where R is the universal gas constant, and T, the temperature, is 300 K.

Solubility measurements and predictions

A saturated protein solution was obtained by adding 250 μl of buffer (150 mm NaCl, 50 mm Tris, pH 8.1) to 10 mg of lyophilized protein. After incubating for 2 h at room temperature, the sample was centrifuged at 13,300 × g for 10 min to pellet undissolved protein. The protein concentration of the supernatant was measured spectrophotometrically after a 1:20 dilution in buffer, using a molar absorption coefficient of 33,600 μl mol⁻¹ cm⁻¹ (56).

Prediction of mutant solubility was performed using the web servers for Aggrescan3D (99) (biocomp.chem.uw.edu.pl/A3D/),³CamSol (100), PASTA (101) (protein.bio.unipd.it/pasta2/),³ TANGO (102) (tango.crg.es/),³ ZipperDB (103) (services.mbi.ucla.edu/zipperdb/intro),³ and Zyggregator (104). The hydrophobicity scale for side chains based on solvation free energy was taken from Table 2 of Wimley et al. (65). All values were normalized such that the WT score was 1 and predictions of reduced solubility would score lower than 1. For predictors that represent reduced solubility as lower scores, this was done by dividing the WT and mutant scores by the WT score. For predictors that represent reduced solubility as higher scores (i.e. higher aggregation propensity), this was done by dividing the inverse of each score by the inverse of the WT score.

Author contributions

A. B. and E. M. M. conceived of and coordinated the study and wrote the paper. A. B. and Z. J. designed, performed, and analyzed the computational predictions/modeling and wet laboratory experiments. A. B. and K. T. curated and analyzed the Protherm database. All authors reviewed the results and approved the final version of the manuscript.