cOSPREY: A Cloud-Based Distributed Algorithm for Large-Scale Computational Protein Design

Abstract

Finding the global minimum energy conformation (GMEC) of a huge combinatorial search space is the key challenge in computational protein design (CPD) problems. Traditional algorithms lack a scalable and efficient distributed design scheme, preventing researchers from taking full advantage of current cloud infrastructures. We design cloud OSPREY (cOSPREY), an extension to a widely used protein design software OSPREY, to allow the original design framework to scale to the commercial cloud infrastructures. We propose several novel designs to integrate both algorithm and system optimizations, such as GMEC-specific pruning, state search partitioning, asynchronous algorithm state sharing, and fault tolerance. We evaluate cOSPREY on three different cloud platforms using different technologies and show that it can solve a number of large-scale protein design problems that have not been possible with previous approaches.

1. Introduction

Recently computational protein design (CPD) has become an important tool for protein engineering (Alvizo et al., 2007). The effectiveness of CPD has been successfully demonstrated in a wide range of applications, such as peptide synthesis (Ottl et al., 1996), drug design (Gorczynski et al., 2007), enzyme synthesis (Chen et al., 2009; Stevens et al., 2006), drug resistance prediction (Frey et al., 2010; Reeve et al., 2015), and protein–protein interaction design (Roberts et al., 2012; Gorczynski et al., 2007). Specifically, in the structure-based computational protein design (SCPD) problem, the goal is to predict a list of amino acid sequences that fold to specific target protein structures with novel biological functions. More precisely, under the assumption of a rigid backbone and given the predefined energy function, the input backbone structural template and a set of all possible discrete side-chain conformations (aka rotamers), the goal of SCPD is to find the globally optimal solution, also called the global minimum energy conformation (GMEC), that minimizes the energy function. A comprehensive introduction to the protein design topic can be found in Donald, (2011).

The SCPD problem is NP-hard (Pierce and Winfree, 2002; Chazelle et al., 2004). There exist many heuristic approaches to compute approximate solutions, such as Monte Carlo, simulated annealing and genetic algorithms (Street and Mayo, 1999; Kuhlman and Baker, 2000; Marvin and Hellinga, 2001), which unfortunately provide no guarantees on finding the globally optimal solution.

On the other hand, researchers have developed numerous combinatorial search-based methods to find the optimal GMEC solution. A popular optimization strategy is to first prune the exponential conformational space as much as possible, and then search over the remaining conformational space to find the optimal solution. Typical examples include integer linear programming (Kingsford et al., 2005), branch-and-bound search (Hong and Lozano-Pérez, 2006; Hong et al., 2009), tree decomposition (Xu and Berger, 2006), and/or branch-and-bound (Marinescu and Dechter, 2009; Zhou et al., 2015), the cost function network (Traoré et al., 2013), and dead-end elimination (DEE) followed by A* search (Gainza et al., 2013; Zhou et al., 2014). Despite the optimality guarantee, most of these algorithms only run on a single machine, limiting their scalability to solve large-scale problems.

Among these approaches, OSPREY (open source protein redesign for you) (Gainza et al., 2013) is a software package that has been widely used to solve numerous biomedically important protein engineering cases (Georgiev et al., 2012; Donald, 2011) and is well recognized by the protein design community (Rudicell et al., 2014; Zhao et al., 2015; Georgiev et al., 2014). In this work, we focus on scaling OSPREY to a large cloud computing infrastructure, so that it can solve larger SCPD problems. Cloud computing infrastructure, compared to traditional high-performance clusters, offers lower per-machine performance and reliability, but comes with larger volume and lower price (hence with much better scalability). With the reduction of computational cost, it becomes attractive to improve OSPREY to fully exploit the massive parallelism of the cloud-based distributed systems.

Compared to molecular dynamics (MD) simulations or other heuristic methods, it is generally more difficult to distribute combinatorial search algorithms to multiple machines, because these algorithms often require the synchronization of global states to guide the search process, for example, the global bounds in the branch-and-bound (BnB) algorithm and the priority queue in the A* algorithm. The synchronous communication design like the message-passing interface (MPI) used in OSPREY makes the state distribution inefficient on a cloud platform. Distributed computational frameworks such as MapReduce (Dean and Ghemawat, 2008) introduce a promising programming model for data-intensive applications by providing automatic task partitioning, scheduling, asynchronous communication, and fault tolerance. Researchers have built distributed combinatorial search systems, such as DryadOpt (Budiu et al., 2011) and BranchReduce (Brachreduce) but these framworks exclude important optimizations, especially GMEC-specific heuristics such as DEE, and thus are not efficient enough for solving the large-scale protein design problem.

We present cOSPREY, a new distributed extension to OSPREY under the branch-and-bound (BnB) search framework, to scale up the size of the protein design problems that can be solved by the provable search algorithms on the cloud platforms. With a combination of algorithm and system optimizations, cOSPREY not only guarantees to find the optimal GMEC solution but also takes full advantage of the massive parallism available in the current cloud systems.

On the algorithm side, we propose several new combinatorial optimization strategies to accelerate the traditional BnB search for protein design. We embed a dead-end elimination (DEE)-based pruning scheme (see section 2.2) into each branch step to remove a large fraction of infeasible conformational space without losing the global optimality guarantee. We also apply several optimization techniques to improve the tightness of both lower and upper bounds in BnB search. On the system side, we design a low overhead synchronization scheme to keep track of the global states of the algorithm.

We conduct experiments on a private 64-server cloud infrastructure, as well as two virtualized cloud computing systems including Amazon's Elastic Computing Cloud (EC2) and an OpenStack-based cloud. We show that by coupling elegant algorithm optimizations with novel system design strategies, we can achieve significant improvement of protein design performance over traditional search algorithms. Our new design approach can solve protein design cases that have never been possible with previously reported exact algorithms. Also, cOSPREY is data-compatible with OSPREY, and thus researchers can easily migrate to cOSPREY and take advantage of the massive scalability of the cloud. We demonstrate such a migration using a real design case from recent literature.

We have made the following contributions in this article:

• 1. A new extension to the widely used OSPREY software, cOSPREY, that fully exploits the massive parallelism in cloud computing while being data-compatible with the existing software.

• 2. A number of algorithm and system optimizations targeting the protein design problem, including DEE-based pruning, linear programming-based lower bound estimation, local search-based upper bound computation, and low-overhead global state synchronization.

• 3. A comprehensive and practical evaluation of cOSPREY on three different cloud technologies and demonstration of its applications in solving large-scale protein design problems.

2. Methods

2.1. Background

To find the optimal solution to the structure-based computational protein design (SCPD) problem, we often need to search over a huge conformational space. As in most popular provable methods, we first apply dead-end elimination (DEE) as a prefiltering algorithm to prune the rotamers that are provably not part of the GMEC, significantly reducing the conformational space. Then we exploit the distributed computation over a large-scale cloud platform to search over the remaining rotamer combinatorial space to find the GMEC solution.

Problem formulation. Let us consider an SCPD problem with n mutable residues, in which the total energy E_total of a rotamer sequence 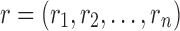is defined as follows:

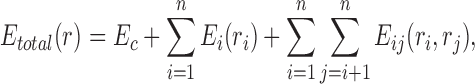where 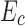is the constant energy of the backbone, 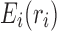is the self-energy of rotamer r_i at residue position i, and 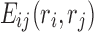is the pairwise interaction energy between rotamers 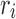and .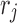

The goal of the SCPD problem is to find the optimal rotamer sequence 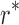that minimizes the total energy function, which is

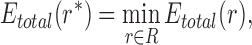where 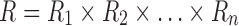is the whole rotamer combinatorial space, and 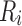is the set of all possible rotamers at residue position i. The optimal solution 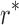is also called the global minimum energy conformation (GMEC).

Branch-and-bound. The branch-and-bound (BnB) algorithm is a widely used search algorithm for solving various combinatorial optimization problems. This algorithm constantly divides the conformational space into several smaller subspaces (branching step) and then computes the bounds (including upper and lower bound) for each subspace (bounding step). After that, those subspaces that are impossible to contain the optimal solution (in which the lower bound is larger than the known best upper bound) are safely pruned. To be more specific, let us consider the SCPD problem on conformational space S. The BnB algorithm includes the following two main steps:

The branching step: The conformational space 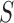is split into two or more subspaces 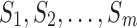such that 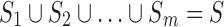and 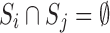for all .

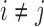The bounding step: The lower bound and the upper bound of each subspace S_i are computed, which are denoted by LB(S_i) and UB(S_i), respectively. Let GUB = min_1≤i≤m UB(S_i) be the minimum upper bound. Then we can safely prune the subspace S_i if LB(S_i) > GUB, since there will be always an element in other subspaces that has a lower energy value than all elements in S_i.

We recursively perform the aforementioned combination of the branching and bounding steps until the conformational subspace only contains a single element.

2.2. Algorithm optimization

2.2.1. A dead-end elimination (DEE)-based branch pruning scheme

The dead-end elimination (DEE) algorithm (Desmet et al., 1992) is an efficient method that has been popularly used in protein design to eliminate infeasible rotamers. For two different rotamers r_i and r_i′ at residue position i, if Equation (1) is satisfied, rotamer r_i is provably not part of the optimal solution, and thus can be safely eliminated. DEE can significantly reduce the solution space (i.e., the rotamer combinatorial space).

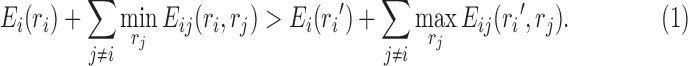A more powerful DEE criterion proposed by Goldstein (1994) is

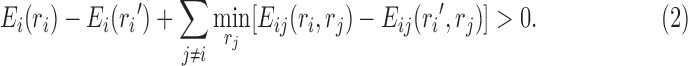We extend the Goldstein DEE criterion in Equation (2), and use the extended version to further reduce the solution space by pruning infeasible conformational space. The following theorem states the criterion of our dead-end elimination-based branch pruning scheme, and its proof can be found in appendix Section 5.1.

Theorem 1 (dead-end elimination-based branch pruning). Let s = (r₁,r₂,…,r_k) represent a conformational space in which the first k residue positions have been determined. If Equation (3) is satisfied for some pair (i,r_i′), where 1 ≤ i ≤ k and r_i′∈ R_i, then the conformational space s can be safely pruned.

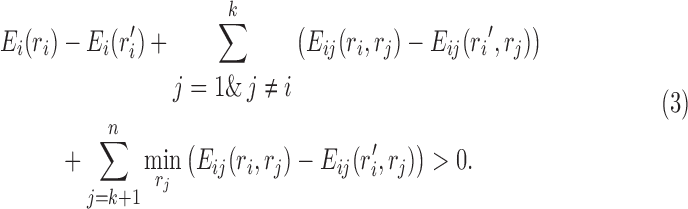Through the above pruning criterion, we can prune a large fraction of infeasible conformational space and thus greatly improve the efficiency of our branch-and-bound search process. Our dead-end elimination-based branch pruning (DEE-based pruning) differs from other DEE algorithms: the traditional DEE or split-DEE pruning algorithm (Desmet et al., 1992; Georgiev et al., 2006; Gainza et al., 2013; Hallen et al., 2013), eliminates the infeasible rotamers, whereas our DEE-based pruning algorithm prunes those conformational spaces that do not contain the optimal solution.

2.2.2. Lower bound

Suppose that the rotamers of the first k residue positions have been determined. We can easily compute a simple admissible lower bound of the energy function by considering the best possible rotamer assignment in each of the undetermined residues (Gainza et al., 2013), which is

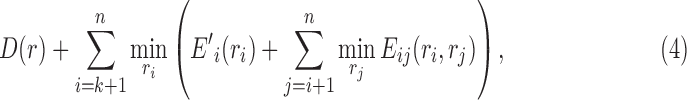where 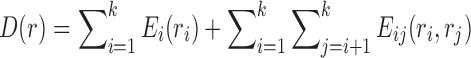is the assigned energy term for the rotamer sequence 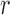after fixing the rotamers of the first k positions, and 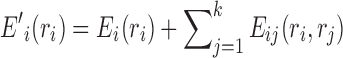This lower bound is not tight enough though, and we provide a much tighter one using linear programming techniques here.

Observing the admissible lower bound in Equation (4), if we split 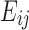into two terms and 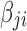, such that 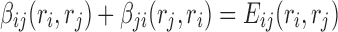for all 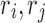, the lower bound becomes

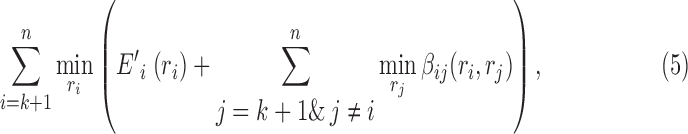where we leave out the constant term D(r) of the determined rotamer sequence r. We can easily find that Equation (5) has different values for different splitting terms 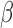, thus we can improve the lower bound using the following linear programming:

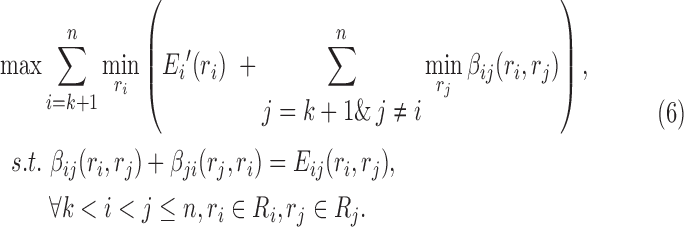The above optimization problem is a convex dual of MAPLPR (maximum a posteriori linear programming relaxation). We can obtain optimal value of β using the convergent message passing algorithm (Globerson and Jaakkola, 2008). This type of message-passing solution to the dual of the linear programming lower bound has been used for protein design in Roberts et al. (2015).

2.2.3. Upper bound

For each conformational space in our BnB search, we apply a local search strategy to compute a relatively good solution in current conformational space and then use it to derive the upper bound. Researchers have proposed several meta-heuristic methods, such as Monte-Carlo, with simulated annealing (Kuhlman and Baker, 2000; Voigt et al., 2000) and genetic algorithms (Raha et al., 2000), to compute the local minimum of the protein design problem. We apply these local search methods (e.g., simulated annealing) to compute the best possible upper bound in the current conformational space. Note that these meta-heuristic methods do not provide any theoretical guarantee of finding the globally optimal solution, while our BnB algorithm can find the GMEC solution. The upper bound derived from the local minimum solution computed by these heuristic approaches may provide a tighter upper bound at the early stage of the algorithm, which can increase the fraction of pruned conformational space in our BnB search, and thus improve the efficiency of computing the globally optimal solution.

2.3. Optimizations for the cloud infrastructure

2.3.1. Branching as a Map function

We implement cOSPREY on top of the Hadoop MapReduce framework (White, 2009). MapReduce takes a divide-and-conquer approach. During the Map step, the programmers can exploit the intrinsic independence of the input, partition the entire input into multiple shards (or partitions), and then have each shard processed on a different mapper machine by running the user-defined Map function. In the Reduce step, the system processes all data with the same key using a user-defined Reduce function.

We implement the branching step as a Map function, as described in Algorithm 1. The input to the Map function, ConformationalSpace, represents the current conformational space, which contains two parts: the global state GUB that stores the best upper bound found so far by the algorithm, and a vector of size n to keep track of whether a mutable residue position has been searched or not.

Algorithm 1:

Branching step as a Map Function

1: function Map(null,ConformationalSpace)

2: S ← ConformationalSpace

3: (S1,S2,…,Sm) ← Branch(S)

4: fori ← 1 tomdo

5:  GUB ← min(GUB,UpperBound(Si))

6: end for

7: result ← ∅

8: fori ← 1 tomdo

9:  if LowerBound(Si) < GUBthen

10:   result ← result ∪{Si}

11:  end if

12: end for

13: returnresult

14: end function

Algorithm 1 first selects an undetermined residue position and expands it to a set of new subspaces. As mentioned in section 2.2, the algorithm first applies the DEE-based pruning and then updates the lower and upper bounds of the expanded subspaces to further prune the infeasible branches. Also, it computes a new GUB based on the current best upper bound. The Map function outputs a set of expanded subspaces S₁,S₂,…,S_m for the next iteration until there is nothing to expand.

2.3.2. Synchronizing GUB globally

Despite its name, the GUB variable in Algorithm 1 is local to a specific Map instance only. We still need to inform all Map instances about the current best GUB. It is nontrivial as communication between a large number of machines is slow and expensive, especially when servers can fail. We design an efficient approach to synchronize the global state of GUB. We add a global state server (GSS) onto the Hadoop framework to help distribute the GUB value. The GSS is simply a server holding the best GUB. Each Map task synchronizes the GUB with the GSS during its execution. As the globally best GUB is only an extra optimization to the algorithm, which does not affect the correctness, we can allow each Map task to synchronize with GSS in a best-effort fashion: the query may fail or receive a timeout or error, but the execution continues. The best-effort approach makes GSS both efficient and fault-tolerant. Appendix Section 5.2 provides a detailed description of the implementation.

3. Experiments and Results

We evaluated cOSPREY on three clusters representing three typical commodity cloud computing infrastructures: a 64-server physical cluster with 768 CPU cores, Amazon's Elastic Computing Cloud (EC2) servers, as well as a cloud based on Openstack (openstack), a popular open-source cloud software. Appendix Section 5.3.1 provides more details on the experiment setup.

3.1. Benchmark tests

In this section, we showed cOSPREY performance using the same set of 30 protein design cases obtained from OSPREY 2.1 beta that have been widely used in protein design as a benchmark (Rudicell et al., 2014; Georgiev et al., 2014; Georgiev et al., 2012; Roberts et al., 2012; Frey et al., 2010; Zhou et al., 2015). In these benchmark tests, cOSPREY solved all the cases, including eight that the state-of-the-art single-machine algorithms failed on. In our largest test case, cOSPREY searched 114 million states, which is far above the computing capacity of any single machine. We also provide the results of the detailed performance evaluation results in appendix Sections 5.3.2 and 5.3.3.

We first ran our algorithm on the benchmark design cases on a 64-server physical cluster, and then compared the performance of cOSPREY with the state-of-the-art GMEC algorithms that attempt to find the optimal solutions. Specifically, we compared cOSPREY with the traditional DEE/A* algorithm (Gainza et al., 2013) included in the OSPREY software package and the and/or branch-and-bound (AOBB) algorithm (Zhou et al., 2015).

Table 1 shows the performance comparison of cOSPREY, DEE/A*, and AOBB. In all the design cases, the underlying residue interaction graphs was considered complete, meaning there was an interaction between every pair of rotamers at different residue positions. Note that the AOBB running time is different from the results reported in the original article (Zhou et al., 2015). This is because the original AOBB results did not include initialization time, which contained the computation of the minibucket heuristic table and the initial bound in branch-and-bound search. To make a fair comparison, we also included the loading time in all three cases.

Table 1.

Performance Comparison of DEE/A^*, AOBB, and cOSPREY

				Running Time
PDB	n	d	Space size	DEE/A*	AOBB	cOSPREY
2COV	13	24	1.15 × 1010	<1s	16s	1m 48s
3DNZ	12	54	5.11 × 1012	8s	1m 20s	2m 25s
3FGV	10	134	6.45 × 1012	<1s	1m 21s	2m 7s
1LNI	15	233	2.98 × 1013	M	1m 34s	2m 30s
1MWQ	14	301	9.28 × 1013	M	50s	2m 57s
1ZZK	12	102	3.45 × 1015	M	29s	2m 25s
2HS1	14	135	6.36 × 1016	M	1m 22s	3m 39s
2O9S	14	187	3.53 × 1017	M	1m 38s	2m 48s
1IQZ	15	145	7.12 × 1017	30m 25s	1m 31s	2m 57s
2FHZ	15	163	1.83 × 1018	57m 56s	1m 48s	3m 12s
1L9L	15	130	5.23 × 1018	M	1m 37s	3m 53s
1TUK	14	107	1.73 × 1019	M	1m 38s	3m 41s
1M1Q	71	18	2.33 × 1019	M	T	5m 52s
1UCR	11	348	6.69 × 1019	M	1m 42s	3m 22s
1UCS	14	166	1.10 × 1020	M	1m 41s	2m 45s
2WJ5	15	81	1.48 × 1020	M	13m 52s	3m 4s
3G36	47	11	4.28 × 1020	M	T	5m 27s
3I2Z	14	212	4.62 × 1020	M	T	3m 43s
2R2Z	12	272	7.48 × 1020	M	1m 43s	3m 40s
3FIL	14	311	2.62 × 1021	M	1m 58s	4m 28s
1OAI	14	232	3.28 × 1021	M	1m 46s	4m 13s
3G21	15	170	4.59 × 1021	M	1m 30s	3m 31s
2RH2	10	418	1.18 × 1022	M	T	5m 45s
1PSR	14	157	1.94 × 1022	M	1m 32s	3m 57s
2BWF	12	147	5.54 × 1022	M	26m 5s	4m 3s
1R6J	13	167	3.42 × 1025	M	2m 25s	4m 32s
1T8K	75	21	2.83 × 1043	M	T	26m 57s
3JTZ	71	24	1.95 × 1045	M	T	34m 44s
1I27	69	29	6.69 × 1045	M	T	14m 36s
1XMK	74	24	2.66 × 1048	M	T	119m 25s

Here, n and d represent the number of mutable residues and the maximum number of rotamers respectively, and space size is the size of the conformational space after DEE pruning. We show the running time of the three algorithms, including DEE/A^*, AOBB and cOSPREY. “M” indicates that the run has exceeded the memory size of 8 GB, and “T” indicates that the program has exceeded the running time of 8 hours.

cOSPREY solved all 30 design cases, while DEE/A* and AOBB only solved 5 and 22, respectively. Existing single-machine algorithms are limited by memory space to hold the large conformational space. In contrast, cOSPREY stores the intermediate expanded conformations to disks and compensates the slow data transmission in disks with massive parallelism from the cloud system.

In many small design cases, cOSPREY was slower because the setup cost, including the distributed executable program files and job scheduling. The data compatibility with OSPREY allows us to use the traditional single-node implementation for small design cases and easily scale to cOSPREY for large-scale problems without modifying the input data files.

Finally, we want to note that the AOBB article (Zhou et al., 2015) presented six cases (1I27, 1M1Q, 1T8K, 1XMK, 3G36, 3JTZ) with approximate results, as it failed to find the optimal solutions in a reasonable amount of time. AOBB has a threshold parameter λ (which was set to 0.04 in Zhou et al., 2015) to heuristically limit the residue interactions, providing a tradeoff between precision and running time. Disabling such an approximation, AOBB failed to find the globally optimal solutions after 8 hours. On the other hand, cOSPREY successfully found the GMEC solutions, and the results were indeed better than AOBB's approximation.

As in OSPREY, which can find the best k solutions, cOSPREY can also find all suboptimal solutions in which the energies are larger than the minimum by at most δ, where δ is a threshold parameter that can be set by the user.

3.2. Cloud-friendly features

Fault tolerance. We demonstrated the fault tolerance of cOSPREY using an extreme case in which we killed 32 out of the 64 servers. Using the 1T8K case as an example, we found that although the execution time increased from 26 min 57 sec to 41 min 35 sec, about 15 minutes longer, cOSPREY still got the correct optimal result. The fault tolerance was an intrinsic product from both MapReduce framework and the asynchronous communication designs. The fault tolerance is the key feature that allows cOSPREY to run on low-cost but unreliable cloud infrastructures.

Running on virtualized cloud infrastructures. We evaluated cOSPREY on both Amazon EC2 and a private Openstack-based cloud (open stack). In particular, we used Amazon's Elastic MapReduce (Amazon EMR) as the cloud framework (Amazon Elastic MapReduce). In addition, we set up our own virtualized Hadoop cluster on the Openstack environment. Table 2 summarizes the performance results on both EC2 and our Openstack platforms. Comparing to the physical cluster (section 3.1), the EC2 and Openstack frameworks showed relatively lower and less predictable performance. However, as we have pointed out, we can use a large number of commercial cloud servers on demand with relatively low cost. For example, the 11 nodes we used on EC2 (flavor m3.xlarge) costed $4.402 per hour to run in total, translating to only a couple of dollars per design case. If we take advantage of the less reliable spot instances, the cost can further go down to $1.639 per hour, making the cloud-based design approach economically attractive.

Table 2.

cOSPREY Performance on Virtualized Cloud Infrastructures

		Running time
PDB	Space size	Amazon EC2	Openstack
1T8K	2.83 × 1043	291m 45s	124m 42s
2RH2	1.18 × 1022	11m 40s	20m 35s
1M1Q	2.33 × 1019	22m 12s	20m 08s
3I2Z	4.62 × 1020	8m 40s	16m 17s
1R6J	3.42 × 1025	11m 26s	10m 52s
3G36	4.28 × 1020	21m 37s	20m 45s

3.3. A case study of empirical protein design

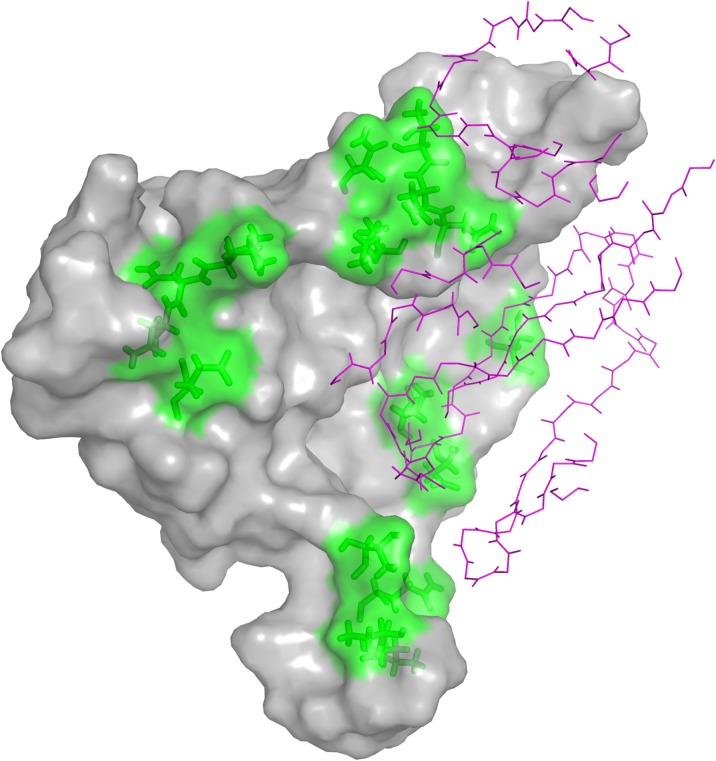
As a case study, we looked into the empirical redesign of the complex of HIV surface protein gp120 with the antibody protein NIH45-46 [PDB ID: 3U7Y (Ron et al., 2011)]. A similar study on a related antibody with experimental results can be found in Rudicell et al. (2014). Redesigning the gp120 surface to bind to a specific type of antibody with high binding affinity is important for constructing effective molecular probes for extracting such antibodies from sera, which is thus useful in vaccine immunogen design (Hallen et al., 2015; Georgiev et al., 2012). As in Hallen et al. (2015), we considered 16 mutable residues on the gp120 surface in our design, which include five key residues that directly interact with NIH45-46, and 11 other residues around the binding pocket (Fig. 1).

FIG. 1.

Mutable residues on the gp120 surface in complex with the antibody NIH45-46 [PDB ID: 3U7Y (Ron et al., 2011)]. The protein gp120 is visualized as gray surface, while the heavy and light chains of the antibody NIH45-46 are shown with magenta lines. The mutable residues on the gp120 surface are shown in green.

We used 69 machines on our Openstack cloud to perform this redesign task, in which we only considered a rigid backbone and discrete rotamers. Our program cOSPREY only took 10 minutes to compute the globally optimal solution. For the final results, we outputted the top 12 conformations whose energies were within 0.06 kcal/mol from the minimum. Among these top 12 conformations, 7 (including the top solution) have the same amino acid sequence, while the remaining 5 solutions had only one single mutation relative to the top sequence. These high clusterings of conformations in the top design solutions agreed with a previous redesign study of the gp120 surface against the antibody NIH45-46 (Hallen et al., 2015), in which a compact representation of the continuous energy landscape was used in the design. As stated in Hallen et al. (2015), the above result was consistent with the fact that the complex between NIH45-46 and gp120 was produced through the extensive affinity maturation of the antibody.

4. Conclusion and Future Work

cOSPREY combines the wide applicability of OSPREY with the massive scalability of commodity cloud-computing infrastructures. The tight coupling of specific optimizations in the branch-and-bound algorithm and system-level design choices is the key feature of cOSPREY. The algorithm applied several advance techniques, such as embedding a DEE-based pruning scheme into each branch step and tightening the lower bound using linear programming to significantly reduce the search space. Also, our asynchronous and algorithm-specific sharing of the global state also brings compelling performance gain. Based on tests on one physical and two virtualized cloud infrastructures, we have demonstrated that cOSPREY runs efficiently on most commercial cloud platforms and solves protein design cases that cannot be addressed using the current single-machine techniques.

We consider the following future work. First, we are planning to extend cOSPREY to support the SCPD problems with continuous side-chain and backbone flexibility (Hallen et al., 2013). Second, we will improve our algorithm to solve the problem with sparse energy functions (Jou et al., 2015) more effectively. Third, we will implement a multitenant service where researchers can transparently “overflow” the CPD computation from the single-node version of OSPREY on demand.

5. Appendix

5.1. Proof of theorem 1

Proof. Let 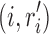be a pair satisfying Equation (3) in section 2.2.1. To prove the theorem, we show that for every rotamer sequence 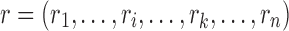in conformational space s, if we replace 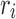with 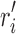, the new rotamer sequence 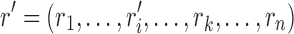will have lower energy value than r. This is because

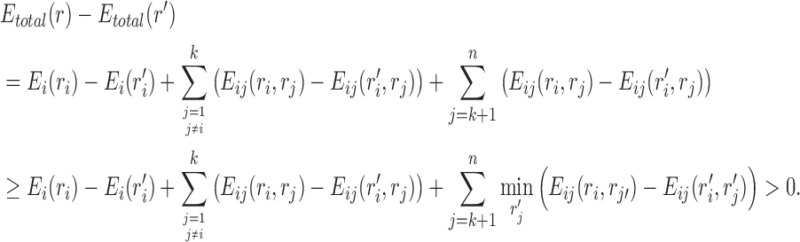Thus, the rotamer sequence 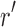has a lower energy value, which means that for any rotamer sequence in the conformational space s, there always exists another rotamer sequence that has a lower energy. Therefore, we can safely prune the conformational space s.

5.2. Global state synchronization

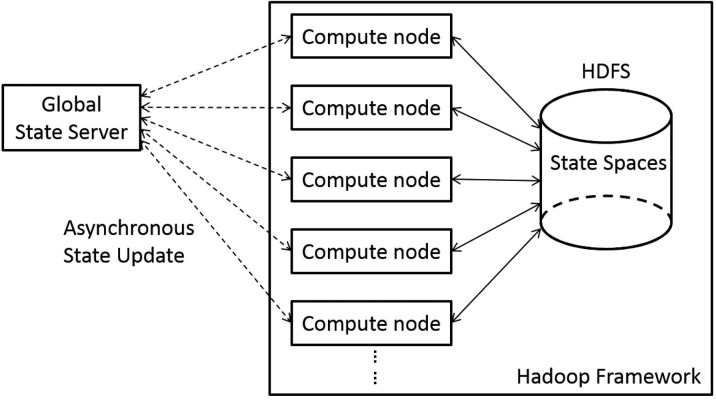
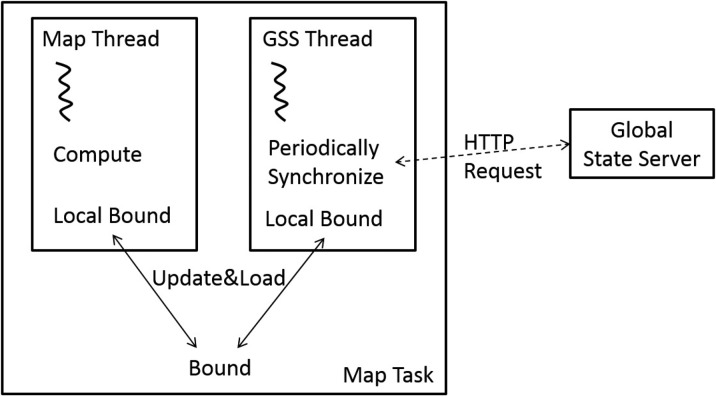
We propose an innovative approach that uses a global state server (GSS) to distribute the GUB. The GSS is simply a web server holding the best GUB. Figure 2 illustrates the system architecture after adding the GSS. Each Map task communicates with the GSS to synchronize its own local GUB with the global best GUB periodically during the Map execution. To scale the GSS and handle server failures efficiently, we relax the consistency requirement. In other words, each Map task queries the GSS in a best-effort fashion, as described in section 2.3. We use a separate and completely independent thread to perform the query, so that the Map computation continues even if the GUB update fails. The CPU and networking cost of the GUB-synchronizing thread is negligible, compared to that of the computation thread. Figure 3 shows details of an independent GUB-syncing thread added to the Map tasks.

FIG. 2.

System architecture of the global state server approach. In the Hadoop Framework, compute nodes start map tasks, perform computations, and communicate with a distributed file system to store conformational spaces. Outside this framework runs the global state server. Compute nodes communicate with the state server to maintain the global minimum upper bound and update the bound asychronously.

FIG. 3.

A map task runs two threads. One thread runs the Map function, while the other synchronizes with GSS periodically.

The GSS approach allows a thread to receive the up-to-date GUB from the current iteration. We can also completely eliminate the Reduce step to save resources. Of course, the GSS requires some changes to the MapReduce architecture, breaking the independent Map assumption. Moreover, the GUB may never be shared if the GSS remains dead for an extended period of time. Despite these problems, the GSS approach still works, as using an out-of-date global best GUB does not affect the correctness of our algorithm. We believe such a best-effort approach is a viable system-level optimization.

5.3. Computational experiments

5.3.1. Details on experiment setup

In our first cloud with physical machines, the cluster had 64 compute servers and one extra manage server. Each server node had two Intel Xeon E5-2620 (6-core with hyper-threading, 2GHz) processors and 128 GB RAM. The cOSPREY algorithm did not use the entire 128 GB RAM. With 12 Map tasks running on each node, cOSPREY used less than 10% of the memory. Each node had three 3TB disks running the Hadoop file system. These nodes were interconnected with 1 Gbps ethernet. All nodes ran commodity CentOS 6.5. Our system was implemented in Java 7 on top of Apache Hadoop 1.2.1. The state server was implemented using the Ruby on Rails framework and ran on the same server configuration. If not specifically mentioned, experiments were performed on this cluster.

We also used two commercial cloud infrastructures that were based on virtualization technology. Visualization improves the sharing of physical computation resources and manageability, and thus lowers the overall computation cost. First, we used the Amazon EC2 platform, probably the most widely used public cloud computing infrastructure. We had a cluster of 11 virtual machines running hadoop 1.0.3. Each virtual machine had four virtual CPUs and 15 GB RAM. Also, we used an OpenStack-based platform. Openstack is a popular open source cloud management system. We also ran 11 virtual machines with 4 vCPUs and 8 GB RAM on each machine.

5.3.2. Effectiveness of the DEE-based pruning

The DEE-based pruning, as discussed in section 2.2, plays an important role in performance optimization. In this section we show more details of the effectiveness of DEE-based pruning using five cases from Table 1. We tested these five cases with DEE-based pruning disabled during the branching step, using DEE only at the beginning of the algorithm, as in other algorithms (such as AOBB or DEE/A*).

Table 3 shows the results. The DEE-based pruning can eliminate a significant fraction of conformational space in our algorithm. Without the DEE-based pruning, in the 1I27 case, the algorithm needed to search 5x more conformations, and in the other three cases (1T8K, 3JTZ, 1XMK), the algorithm failed to find the GMEC solution within 8 hours. Of course, in a very small case (2BWF), DEE-based pruning seemed to be overkill, as there were only 493 conformations to search.

Table 3.

cOSPREY vs. cOSPREY_D (cOSPREY Without DEE-based Pruning)

	cOSPREY		cOSPREYD
PDB	# of states	time	# of states	time
2BWF	493	4m 3s	493	3m 56s
1T8K	4,476,674	26m 57s	–	T
3JTZ	12,373,809	34m 44s	–	T
1I27	246,693	14m 36s	1,426,297	20m 56s
1XMK	113,935,129	119m 25s	–	T

Intuitively, the benefit of having DEE-based pruning is a chance to prune a huge fraction of conformational space, which may become the key to finding the global optimal solution. The cost of running DEE-based pruning adds a constant factor to the running time of the entire algorithm. We compensate the constant factor by using more machines. Thus, we believe the DEE-based pruning is a good design choice in cOSPREY.

5.3.3. Speed-up with the number of CPUs

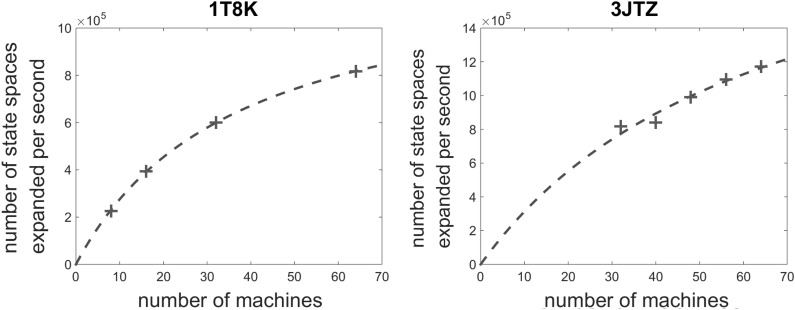
We evaluated the speedup of cOSPREY with the increasing number of compute nodes using two large design cases (1T8K and 3JTZ). Figure 4 shows the average number of conformational spaces expanded and searched per second, with the increasing number of servers.

FIG. 4.

cOSPREY speedup with the increasing number of nodes. Each “+” represents a single measurement.

In the 1T8K case, we found that the speedup was almost linear up to 16 servers (192 cores). Then we started to observe diminishing returns by adding more servers. The reduction of speedup was probably due to the setup overhead as discussed in section 3.1. Also the scalability was limited by the size of search space. If we partition a small search space into too many pieces, we will have very small shards. As the fixed overhead (e.g., reading the directories and locating the files) dominates in small file operations, thus the level of parallism is limited in small cases. Of course, in a small case, we do not really need that many machines.

Larger cases like 3JTZ showed better speedup. Figure 4 only shows the results with 32 to 64 servers, as it took too long to complete using fewer servers. Doubling the number of the servers from 32 to 64, we got approximately a 50% improvement on throughput, while 1T8K only improved about 30% at the same range. We believe that the larger design cases will benefit from cOSPREY's scalability even more.

Acknowledgments

Funding: This work is supported in part by the National Basic Research Program of China Grant 2011CBA00300, 2011CBA00301; the National Natural Science Foundation of China Grant 61033001, 61361136003, and 61472205; Google Faculty Award; and China's Youth 1000-Talent Program. This work is supported by a grant to B.R.D from the National Institutes of Health (R01 GM-78031).

Author Disclosure Statement

The authors declare that no competing financial interests exist.