Curvature and Rho activation differentially control the alignment of cells and stress fibers

Stress fibers, single cells, and densely packed cells align on gently curved surfaces and restructure upon Rho activation.

Abstract

In vivo, cells respond to a host of physical cues ranging from substrate stiffness to the organization of micro- and nanoscale fibrous networks. We show that macroscale substrates with radii of curvature from tens to hundreds of micrometers influence cell alignment. In a model system of fibroblasts, isolated cells aligned strongly in the axial direction on cylinders with radii similar to the cell length and more weakly on cylinders of much larger radius. Isolated vascular smooth muscle cells did not align as effectively as fibroblasts. However, both cell types aligned robustly in weak curvature fields when in confluent monolayers. We identified two distinct populations of stress fibers in both cell types: long, apical stress fibers that aligned axially and short, basal stress fibers that aligned circumferentially. Circumferential alignment of the basal stress fibers is in apparent disagreement with a long-standing hypothesis that energetic penalties for bending enforce axial alignment on cylinders. To explore this phenomenon, we manipulated stress fibers by activating Rho, a small guanosine triphosphatase that regulates stress fiber assembly. In response, apical stress fibers disassembled, whereas basal stress fibers thickened and aligned more strongly in the circumferential direction. By activating Rho in confluent monolayers of vascular smooth muscle cells, we recapitulated the circumferential alignment pattern of F-actin within these cells that is observed in cylindrical vessels in vivo. In agreement with recent theory, these results suggest that stress fiber bending penalties are overcome when stress fiber contractility is enhanced and motivate deeper study of the mechanics of these distinct stress fiber populations.

INTRODUCTION

The formation of spatial patterns in tissues is a long-standing problem in biology. Decades of research have focused on understanding how biochemical signaling and morphogen gradients establish cell patterns during development and tissue morphogenesis. Only recently have physical environmental factors such as extracellular matrix stiffness and externally applied forces been implicated in developmental and morphogenetic responses (1). Here, we aim to shed light on how the curvature of a cell’s environment influences the formation of patterns within tissues.

Geometric cues on the order of nanometers and micrometers are well known to affect a variety of cell behaviors. For example, nano- and microtopographical features influence cell alignment, cytoskeletal organization, migration, and the deposition of extracellular matrix proteins (2–7). Less is known about how larger geometric cues (that is, those on the order of a cell length scale) influence cell behaviors. When cultured on cylinders with radii less than or equal to the cell length scale, fibroblasts align their nuclei (8), cell bodies (9, 10), and stress fibers (SFs) (originally referred to as actin bundles) (11) in the axial direction. On cylinders with radii larger than cell length scales, this preferential orientation is lost (8, 10). It has been hypothesized that SFs and thus cell bodies align in the axial direction because this orientation minimizes the energetic costs associated with SF bending. Epithelial cells cultured on cylinders with small radii have SFs aligned in the circumferential direction, that is, the direction orthogonal to the SF alignment direction in fibroblasts (9, 11, 12). Thus, the mechanisms driving alignment cannot be simply explained by substrate geometry.

In vivo, endothelial cells create and experience complex curvature fields. By vasculogenesis or angiogenesis, endothelial cells establish curved blood vessels in developing and adult tissues (13–15). Different cell types, including pericytes and smooth muscle cells, interact with the curvature fields established by endothelial cells. Pericytes wrap extensions in the circumferential direction around small capillaries (16, 17). In larger vessels, vascular smooth muscle cells (VSMCs) align in the circumferential direction or in helical patterns within the cylindrical tissues (18). Cyclic strain, nano- and microtopographical features, and shear stresses are known to affect the alignment of VSMCs (19–24). Here, we aimed to understand if macroscale curvature, like that experienced by VSMCs in vivo, also influences cell alignment.

An additional physical cue that can influence the alignment of cells is the orientation of neighboring cells. In confluent monolayers of fibroblasts on planar surfaces, cells elongate and coalign with adjacent cells, resulting in domains of coalignment that are on the order of ~500 μm (25). The unique alignment pattern shown by these cells has been compared to the nematic order that emerges in physical systems such as liquid crystals (25–27). In these systems, tightly packed groupings of elongated elements are positioned randomly in space but are oriented in a common direction. VSMCs exhibit a similar pattern of order in blood vessels. Whether wrapped in the circumferential direction or in a helical pattern in cylindrical vessels, the smooth muscle cells are densely packed and aligned in a common direction with their neighbors (18, 28). Here, we addressed the question of whether the collective alignment effect that is observed in confluent monolayers on planar surfaces alters the ability of cells to sense curvature cues like those experienced by smooth muscle cells in vivo.

We initially aimed to understand how isolated mesenchymal cells align in response to curvature fields and found that isolated human VSMCs (hVSMCs) align in the axial direction on cylinders with radii equal to the cell length scale, although less strongly than mouse embryonic fibroblasts (MEFs). On larger cylinders, neither cell type aligned preferentially. However, when in confluent monolayers, both cell types showed a striking enhancement of alignment in the axial direction on large cylinders, indicating that being densely packed provided the cells with additional curvature sensing capabilities. To quantify this effect, we developed a number of techniques for evaluating cell morphology and alignment on curved surfaces that are more accurate than methods used in the past.

These methods also revealed that apical and basal SFs align in different patterns in a manner that depends on the curvature magnitude. On cylinders with small radii, long, apical SFs aligned with cell bodies in the axial direction, whereas basal SFs robustly wrapped cylinders in the circumferential direction. Activation of Rho, a small guanosine triphosphatase (GTPase) that plays a role in SF bundling (29, 30), nearly eliminated the apical SFs in hVSMCs and enriched the population of thick, basal SFs, ultimately recapitulating the F-actin alignment patterns observed in blood vessels in vivo.

RESULTS

A collective effect enhances the curvature alignment response of fibroblasts

To study how cells align in response to cell-scale curvature, we cultured MEFs on the exterior of glass capillary tubes. Cells were cultured sparsely on capillary tubes that had been functionalized with a mixture of unlabeled and Alexa Fluor 488–conjugated fibronectin. MEFs stained with phalloidin-TRITC (tetramethylrhodamine isothiocyanate) and the fibronectin-functionalized surface were imaged with a laser scanning confocal microscope. Image stacks were reconstructed to visualize the F-actin cytoskeleton and cell morphology on the cylinders (Fig. 1A). To evaluate the orientation of these cells, we first mapped the phalloidin channel to a common plane. Briefly, each image within the stack was transformed on the basis of its position from the top of the cylinder, effectively “unrolling” the surface of the cylinder onto a single plane that could be analyzed easily (Fig. 1B). This method generates a more accurate representation of cell morphology on the cylinder surface than a projection normal to the cylinder axis (8–11).

Fig. 1. Fibroblasts in confluent monolayers sense weaker curvature fields than isolated cells.

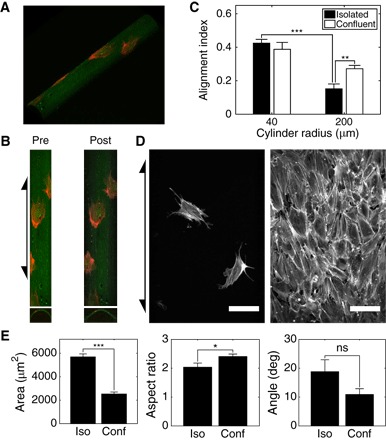
(A) Three-dimensional reconstruction of MEFs stained with phalloidin-TRITC (red) on cylinder (R_c = 40 μm) functionalized with Alexa Fluor 488–conjugated fibronectin (green). (B) Projection along the surface normal (premapping; left) and mapped image (postmapping; right) of surface in (A) and corresponding cross sections. (C) AIs of isolated and confluent monolayers of MEFs on cylinders with R_c = 40 and 200 μm. (D) Mapped images of isolated (left) and confluent monolayer (right) of MEFs on cylinders with R_c = 200 μm. Arrows indicate cylinder axis orientation. Scale bars, 100 μm. (E) Analysis of outlines of MEFs on cylinders with R_c = 200 μm. Area of outlined cells (left), ratio of major-to-minor axis length of ellipses fit to cell outlines (middle), and orientation angle of long axes of fit ellipses relative to cylinder long axis (right). Cells on at least seven independent cylinders were analyzed in each condition. Results are mean and SE. *P < 0.05, **P < 0.01, ***P < 0.001, Student’s t test. ns, not significant.

To quantify the extent of alignment and elongation of cells on cylinders, bounding rectangles (BRs) were drawn around each cell in a mapped image. For each cell, we then calculated an alignment index (AI) given by

$$\text{AI} = {\text{log}}_{10}\left(\frac{{\mathit{L}}_{\text{BR},\text{axial}}}{{\mathit{L}}_{\text{BR},\text{circumferential}}}\right)$$

where L_BR,axial and L_{BR,circumferential} are the length of the BR in the axial and circumferential directions, respectively. This is a measure of the alignment and elongation of cells centered around zero (8): Positive and negative values indicate alignment in the axial and circumferential directions, respectively, and the magnitude indicates the extent of elongation in the given direction. We found that isolated MEFs aligned and elongated in the direction parallel to the cylinder axis when cultured on small cylinders with radii of 40 μm, consistent with previous findings (Fig. 1C) (8, 9, 11). When cultured on large cylinders with radii of 200 μm, isolated cells aligned more weakly, confirming that these fibroblasts sense and align in response to curvature when the curvature length scale is near the cell length scale.

MEFs cultured in confluent monolayers on cylinders coaligned with adjacent cells, much like in nematic monolayers on planar surfaces (Fig. 1D and fig. S1) (25). Although a small number of monolayers wrapped the cylinders at oblique pitch angles, a large majority (>90%) of monolayers aligned in the axial direction and exhibited an enhanced (1.8-fold) AI on large cylinders (Fig. 1, C and D). This finding was surprising because two-dimensional equilibrium or active nematics are predicted to coalign but have no preferential orientation direction on cylinders. Because the geometry of the cylinder induces neither bend nor splay in the co-oriented cell monolayers and the isolated cells showed little preferential alignment, we expected to observe helical wrappings of the cylinders with various pitch angles. These results demonstrate that a collective effect enhances the ability of cells to align in response to weak curvature fields in a manner that deviates from predictions of traditional nematics.

To better discern the relative contributions of cell orientation and elongation captured in the AI metric, we outlined the phalloidin-stained cytoskeletons of mapped cells. Cell area was quantified directly from these cell outlines, and cell orientation angle and aspect ratio were quantified by fitting an ellipse to each cell outline. Despite cells in confluent monolayers being less than half as spread as isolated cells, they were more elongated, as indicated by the larger fit ellipse aspect ratio (Fig. 1E). The larger AI value for confluent monolayers compared to isolated cells shown in Fig. 1C is attributed to this increased aspect ratio because the cell orientation angles were not significantly different (Fig. 1E).

VSMCs align weakly in response to curvature

We next aimed to understand how macroscale curvature and cell density influence VSMCs to form alignment patterns. In cylindrical blood vessels in vivo, VSMCs are tightly packed and align circumferentially or in helical patterns (18, 28). We cultured hVSMCs on cylindrical substrates to determine whether curvature and dense packing were sufficient to recapitulate the circumferential alignment observed in vivo or would induce the axial alignment pattern seen in MEFs.

When cultured on cylinders with a radius of R_c = 40 μm, isolated hVSMCs aligned in the axial direction significantly more weakly than MEFs (Fig. 2A). Analysis of cell outlines revealed that the mean orientation angle of hVSMCs significantly deviated from the nearly axial orientation of MEFs (Fig. 2B) and that MEFs were not more elongated than hVSMCs (Fig. 2C). Thus, the difference in AI of hVSMCs compared to MEFs is likely due to differences in orientation angle and not elongation. It has been suggested that isolated fibroblasts align axially on cylindrical substrates to minimize the bending of actin SFs; because these elongated bundles of microfilaments have a finite bending energy, they are thought to be organized in the direction that minimizes their deformation (8). We noticed that the levels of F-actin, based on phalloidin staining, were lower in hVSMCs compared to MEFs (Fig. 2, D and E). With less F-actin organized into thick SFs, hVSMCs may have a lower energy penalty for deviating from the ideal axial alignment and thus a smaller AI than MEFs on small cylinders.

Fig. 2. VSMCs align weakly on cylinders when isolated.

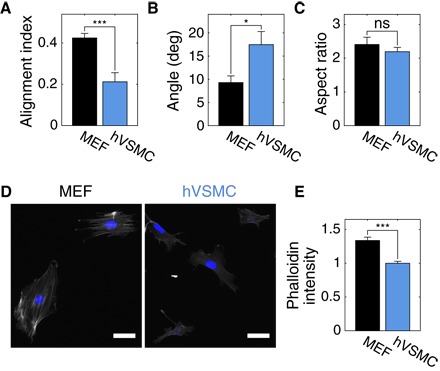
(A) Isolated hVSMCs have a smaller AI than isolated MEFs on cylinders with R_c = 40 μm; this is due to weaker axial alignment (B) and not a difference in elongation (C), as measured from the dimensions of ellipses fit to cell outlines. At least 16 cells were analyzed in each condition. Representative images of phalloidin-TRITC (gray) and 4′,6-diamidino-2-phenylindole (DAPI; blue) staining of MEFs and hVSMCs on coverslips (D) and corresponding phalloidin-TRITC intensities (E). Scale bars, 50 μm. At least 40 cells of each type in two independent experiments were analyzed. Results are mean and SE. *P < 0.05, ***P < 0.001, Student’s t test.

We observed the generation of nematic order in confluent monolayers of hVSMCs on planar plastic and glass, much like in MEFs (fig. S1); this coalignment pattern looked qualitatively similar to the ordering of VSMCs observed in vessels in vivo (18). On cylinders, confluent monolayers of hVSMCs had a nearly threefold larger AI value than isolated cells (Fig. 3, A and B). Despite their relatively poor alignment when isolated, hVSMCs in confluent monolayers had a 26% larger (P = 0.03) AI than MEFs in confluent monolayers. Analysis of cell outlines revealed that, much like MEFs, hVSMCs in confluent monolayers had smaller spread area and were significantly more elongated than isolated cells on large cylinders but were also oriented more strongly in the axial direction (Fig. 3, C to E).

Fig. 3. hVSMCs in confluent monolayers sense weaker curvature fields than isolated cells.

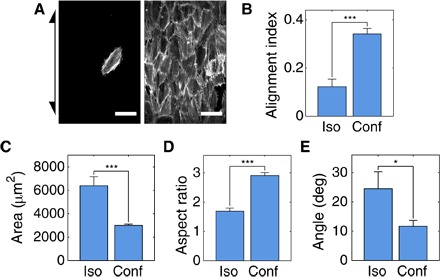
(A) Representative mapped images of isolated (left) and confluent monolayers (right) of hVSMCs on cylinders with R_c = 200 μm. Arrow indicates cylinder axis orientation. Scale bars, 100 μm. (B) AIs of isolated and confluent hVSMCs on cylinders with R_c = 200 μm. (C) Spread area of isolated hVSMCs and hVSMCs in confluent monolayers on cylinders with R_c = 200 μm. Aspect ratio (D) and orientation angle relative to cylinder axis (E) of ellipses fit to cell outlines on cylinders with R_c = 200 μm. Cells on at least eight independent cylinders were analyzed in each condition. Results are mean and SE. *P < 0.05, ***P < 0.001, Student’s t test.

Apical and basal SFs align in distinct patterns in response to curvature

To discern the response of SFs to these curvature fields, we studied their alignment patterns on small and large cylinders. Careful examination of the phalloidin-TRITC image stacks from a laser scanning confocal microscope revealed that two subpopulations of SFs aligned in distinct patterns in a curvature-dependent manner (Fig. 4, A to D). In both hVSMCs and MEFs (fig. S2), one population of SFs reached over the top of the nucleus. These apical SFs formed a perinuclear actin cap (31) and were aligned strongly in the axial direction on small cylinders (Fig. 4C) but more weakly on large cylinders (Fig. 4D). The longest SFs were apical in both cell types.

Fig. 4. Apical and basal SFs align in distinct patterns in response to curvature.

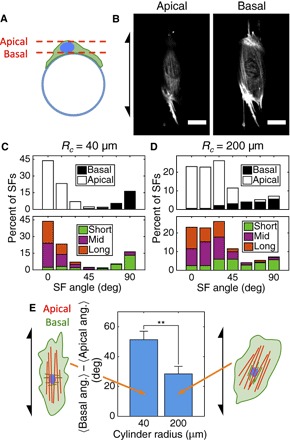
(A) Apical SFs sit above the nucleus, and basal SFs sit below the nucleus relative to the cylinder surface shown in cross section. (B) Representative images of an hVSMC on a cylinder with R_c = 40 μm stained with phalloidin-TRITC showing apical and basal SFs from a single confocal stack. Arrow indicates cylinder axis orientation. Scale bars, 30 μm. (C and D) Angle distribution plots showing the directions in which basal and apical SFs are oriented (top) on small and large cylinders. The bottom plots show the longest 30% (Long; 22.3 μm ≤ L_40μm ≤ 67.4 μm; 18.6 μm ≤ L_200μm ≤ 47.3 μm), shortest 30% (Short; L_40μm ≤ 12.1 μm; L_200μm ≤ 11.3 μm), and the remaining 40% (Mid) of SFs, where ${\mathit{L}}_{{\mathit{R}}_{\mathrm{c}}}$ denotes the length of SFs on cylinders with radius R_c. Axial and circumferential orientations are given by orientation angles of 0° and 90°, respectively. (E) Angle between the mean orientation of basal SFs and the mean orientation of apical SFs in cells on each substrate. At least 272 SFs in 10 cells were analyzed in each condition. Results are mean and SE. **P < 0.01, Student’s t test.

In the literature, SFs in epithelial cells and a small number of SFs in fibroblasts were observed to align in the circumferential direction on small cylinders (9, 11, 12). However, we observed circumferentially aligned SFs in both MEFs and hVSMCs and found that these SFs comprised a separate population that sits below the nucleus. On small cylinders, these basal SFs aligned nearly orthogonally to the apical SFs (Fig. 4C) and were significantly shorter than the apical SFs (Fig. 4C and fig. S3).

We further explored the distinct curvature-dependent alignments of these two SF populations by examining their relative orientations in individual cells. Within each cell, the average angle between apical and basal SFs increased with cylinder curvature (that is, decreased with cylinder radius) because apical SFs became more axially aligned and basal SFs became more circumferentially aligned (Fig. 4E).

Activation of Rho alters the sizes of SF populations in hVSMCs

Although the long, apical SFs aligned axially and agreed with the curvature alignment hypothesis based on bending energy described previously, the basal SFs appeared to directly contradict this hypothesis; these SFs aligned along the direction of maximum curvature and were thus bent as much as they could be on small cylinders. This observation suggests that curvature alignment of SFs is guided by more than just the SF bending energy. An alternative hypothesis suggests that the balance between SF bending energy and contractility determines the alignment pattern of SFs in response to curvature (32). If SF bending energy dominates, then SFs tend to align in the axial direction. If contractility instead dominates, then SFs tend to align along the circumferential direction.

To probe the relationship between SF bending energy, contractility, and curvature alignment, we activated Rho in both MEFs and hVSMCs with CN03. Rho is a small GTPase that is known to regulate SF formation and actomyosin contractility (29). CN03 constitutively activates Rho by blocking its GTPase activity and does not affect the activity of Rac or Cdc42 (33, 34). Cells on cylinders were treated for 6 hours to allow for cytoskeletal reorganization before fixation. Treated cells showed a strikingly different SF organization compared to control cells on a cylinder of intermediate size (R_c = 125 μm): The SFs were thicker, tightly packed, and almost exclusively aligned in the circumferential direction (Fig. 5A). Cylinders with R_c = 125 μm were used to study the restructuring of SFs aligned by curvature via activation of Rho (Figs. 5 and 6) for two reasons: At this radius, curvature is strong enough to drive SF alignment, and more cells are observable on each cylinder than on the smaller cylinders of R_c = 40 μm. The phalloidin signals in the control and treated cells appear to have similar intensities only because the laser intensity was reduced to make the SFs in treated cells visible; on coverslips, Rho-activated cells had a significantly brighter phalloidin-TRITC signal than control cells (fig. S4). Costaining with the nuclear dye DRAQ5 revealed that nearly all of the SFs were basal (Fig. 5, B to D).

Fig. 5. Activation of Rho alters the sizes of SF populations.

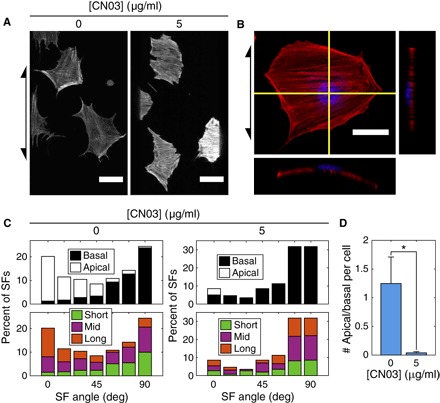
(A) Representative mapped phalloidin-TRITC images of hVSMCs on cylinders with R_c = 125 μm treated with CN03. Scale bars, 50 μm. (B) Z-projection and orthogonal slices of hVSMC on a cylinder with R_c = 125 μm treated with CN03. Red, phalloidin-TRITC; blue, DRAQ5. Scale bar, 30 μm. Arrows indicate cylinder axis orientation. (C) Angle distribution plots showing the directions in which basal and apical SFs are oriented (top) in control cells and cells treated with CN03. The bottom plots show the longest 30% (Long; 19.6 μm ≤ L_0μg/ml ≤ 50.7 μm; 18.1 μm ≤ L_5μg/ml ≤ 38.4 μm), shortest 30% (Short; L_0μg/ml ≤ 12.3 μm; L_5μg/ml ≤ 12.0 μm), and the remaining 40% (Mid) of SFs, where L_[CN03] denotes the length of SFs in cells treated with a concentration of CN03 equal to [CN03]. Axial and circumferential orientations are given by orientation angles of 0° and 90°, respectively. (D) Ratio of the number of apical-to-basal SFs per cell in isolated hVSMCs treated with CN03 on cylinders with R_c = 125 μm. At least 259 SFs in 11 cells were analyzed in each condition. Results are mean and SE. *P < 0.05, Student’s t test.

Fig. 6. Rho activation establishes F-actin alignment observed in vivo.

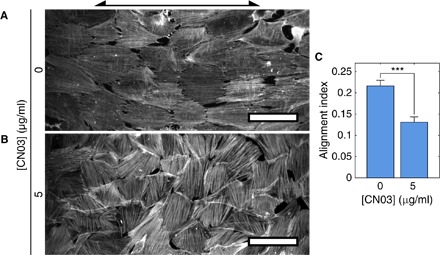
hVSMCs on cylinders with R_c = 125 μm were treated with CN03 [0 μg/ml (A) or 5 μg/ml (B)]. Arrow indicates cylinder axis orientation. Scale bars, 100 μm. (C) AIs of CN03-treated hVSMCs in confluent monolayers on cylinders with R_c = 125 μm. Cells on at least 13 independent cylinders were analyzed in each condition. Results are mean and SE. ***P < 0.001, Student’s t test.

The activation of Rho with CN03 had a robust and long-lasting effect on the organization of SFs. Treated hVSMCs had thick SFs oriented in the circumferential direction even 48 hours after washing away the activator (fig. S5). This persistent effect is likely due to the mechanism by which CN03 activates Rho: CN03 converts the glutamine residue in position 63 to glutamate (33, 34), a covalent modification that is unlikely to be reversed in the time scales examined.

To determine whether inhibition of the Rho pathway would reduce the thickness and curvature alignment of basal SFs, we inhibited ROCK, a kinase downstream of Rho that stimulates SF formation (35), using Y-27632. The inhibition of ROCK eliminated the apical population of SFs, much like the activation of Rho (fig. S6). A small number of circumferentially oriented, thin, basal SFs were the only SFs that remained in treated cells. This suggests that basal SFs are more stable and resistant to perturbations of the Rho/ROCK pathway than apical SFs.

F-actin in confluent monolayers of hVSMCs adopts an alignment pattern observed in vivo upon activation of Rho

Activation of Rho in confluent monolayers of hVSMCs induced the same shift in SF populations observed in isolated cells. Cells treated with CN03 had thick, bright, basal SFs oriented in the circumferential direction on intermediate-radius cylinders with R_c = 125 μm (Fig. 6, A and B). In blood vessels in vivo, phalloidin staining showed that F-actin is oriented in a similar circumferential orientation (28). Activation of Rho also caused the cells to be less elongated and aligned in the axial direction, as indicated by a reduction in the AI (Fig. 6C). Thus, by providing cells with a macroscale curvature cue and activating Rho, we recapitulated the circumferential F-actin alignment pattern observed in vessels in vivo and reduced axial cell alignment.

DISCUSSION

In addition to sensing chemical cues, mammalian cells have the ability to detect and respond to physical stimuli from their environment. Here, we explored how macroscale curvature acts as an external physical cue that guides changes in the alignment and morphology of isolated cells, populations of cells, and their actin cytoskeletons. We found that isolated VSMCs aligned more weakly than fibroblasts on cylindrical substrates. Although isolated cells had a weak pattern of alignment on cylinders with radii larger than the cell length scale, both MEFs and hVSMCs in confluent monolayers aligned prominently in the direction parallel to the cylinder axis. Long, apical SFs in isolated cells aligned in the axial direction on cylinders with radii equal to the cell length scale, whereas a subpopulation of short, basal SFs aligned in the orthogonal direction, wrapping cylinders around their circumferences. Upon activation of Rho, nearly all of the apical SFs vanished, whereas the basal SFs became thick and robustly aligned in the circumferential direction. By activating Rho in confluent monolayers of hVSMCs, we recapitulated the circumferential orientation of F-actin that is observed in blood vessels in vivo.

These results suggest that cell and SF response to curvature is more complex than previously appreciated. It was thought that SFs and, thus, cells themselves align on cylinders with radii smaller than the cell length scale because there is an energy penalty for bending the long SFs; when aligned along the cylinder axis, the SFs do not have to bend, and thus, axial alignment is preferred (8). Many of our results substantiate this hypothesis: (i) Many long SFs in isolated cells aligned axially on small cylinders, and (ii) the potentially weaker F-actin cytoskeletons in isolated hVSMCs caused them to align less strongly than MEFs.

While intriguing, this hypothesis is not supported by all results. For example, the SFs within epithelial cells (11) and a subpopulation of basal SFs in MEFs and hVSMCs align in the circumferential direction on small cylinders, which is the direction in which the SFs are most bent. We initially thought that activation of Rho in cells on large cylinders would cause SFs to become thicker and more resistant to bending; ultimately, this would lead to enhanced axial alignment of both SFs and cells on a surface that produced no preferential alignment of untreated cells. We observed the opposite trend: Thick SFs aligned in the circumferential direction. Thus, it is apparent that bending energy arguments are insufficient to explain SF alignment on their own and additional mechanisms are at play. Increases in SF stiffness are likely correlated with those in contractility in most cases. For example, addition of the protein phosphatase 1 and 2A inhibitor calyculin A increases both contractility and SF stiffness (36, 37). Biton and Safran (32) described a theoretical curvature alignment model, which suggested that SFs align in either the axial or circumferential direction based on the balance between SF bending energy and contractility. SFs were predicted to align circumferentially when contractility dominated over SF bending penalties. On the basis of this argument, it is possible that a transition from a bending-dominated regime to a contractility-dominated regime may have occurred in our Rho activation experiments. Perhaps, activation of Rho enhances contractility in hVSMCs more than it increases SF bending, resulting in the observed circumferential alignment. Although our data provide evidence in support of this theory, the model does not account for the presence and restructuring of two spatially separated populations of SFs that we observe in experiments. This raises the possibility that the mechanical properties and tensions within SFs may vary along the z axis within individual cells. Related mechanisms based on tension generated by VSMCs in collagen matrices uphold contractility as an important player in circumferential cell alignment (28, 38–40). We aim to continue exploring this hypothesis by measuring the SF mechanical properties and cell contractility upon activation of Rho.

More work is also required to understand the molecular basis for the generation of order in densely packed populations of mesenchymal cells. On planar surfaces, fibroblasts exhibit several hallmarks of active nematics, including long-range coalignment and the formation of topological defects (25–27). On cylinders, MEFs and hVSMCs coaligned, but their alignment patterns relative to the cylindrical substrates deviated from those predicted by theory of nematics. Nematic theory suggests that cells, the “nematogens” in this system, would wrap cylinders in helical patterns with various pitch angles because the isolated cells aligned in random directions on large cylinders. Because the cylinder would not induce any deformation of the two-dimensional nematic (that is, no bend or splay), no orientation angle would be preferable over another. Instead, cells in confluent monolayers aligned strongly in the axial direction on large cylinders, indicating that the mechanisms driving the alignment in cell monolayers are more complex than those governing equilibrium or molecular active nematics. We suspect that junctional proteins mediating cell-cell contact play an important role in establishing nematic order in confluent monolayers as well as in driving this noncanonical alignment pattern. Adherens junctions allow cells to exert forces on each other and influence the organization of the actin cytoskeleton (41, 42), perhaps altering SF mechanics such that bending penalties are increased and axial alignment is enhanced. Alternatively, cells in confluent monolayers may align in the axial direction more strongly than isolated cells because the monolayers may have a larger effective length scale due to the connection of SFs through cell-cell adhesions. That is, SFs in adjacent hVSMCs may connect to each other through adherens junctions (43, 44), ultimately creating a network of SFs that is more resistant to bending than the SFs in isolated cells. This is a focus of ongoing work.

The influence of curvature, contractility, and packing on pattern formation in inert materials is well appreciated (45, 46). Our work suggests that these factors also guide the alignment of cells that experience curvature fields in vivo. We found that VSMCs aligned in the direction orthogonal to the direction in which they align in blood vessels; in vivo, smooth muscle cells wrap around vessels in the circumferential direction or in helical patterns (18). The reason for this marked difference in alignment directions is not known. SF bending penalties have long been implicated in curvature alignment, but more recent theory suggests that contractility-generated tension can override these effects. Our Rho activation data in hVSMCs indicate that contractility is an important parameter in establishing the circumferential orientation of F-actin observed in blood vessels in vivo. These results suggest that an interplay between macroscale geometry, F-actin bending penalties, and cell-generated tension influences cell alignment both in vitro and in vivo.

MATERIALS AND METHODS

Cell culture, treatment, and staining

Spontaneously immortalized MEFs were cultured in Dulbecco’s modified Eagle’s medium (DMEM) containing 10% (v/v) fetal bovine serum (FBS), 2 mM l-glutamine, 2.5 μM Hepes, and gentamicin (50 μg/ml). Human aortic VSMCs purchased from the American Type Culture Collection were cultured in DMEM containing 10% (v/v) FBS, amino acid supplement, 1 mM sodium pyruvate, and gentamicin (50 μg/ml). Both cell types were maintained in 10% CO₂ at 37°C.

To activate Rho in isolated cell experiments, cells were first serum-starved with 1% FBS medium for ~24 hours, followed by ~24 hours with medium in which serum had been replaced by bovine serum albumin (1 mg/ml). For confluent monolayer experiments, cells were serum-starved with 1% FBS medium for ~24 hours, followed by ~24 hours with 0.2% FBS medium. Cells were then seeded on cylinders and allowed to adhere and spread on the substrates overnight before they were treated with CN03 (5 μg/ml) or an equivalent volume of water (vehicle) for 6 hours. This provided cells with a sufficient amount of time to reorganize their actin cytoskeletons in response to curvature. The same procedure was performed in the presence of 10 μM Y-27632 or an equivalent concentration of dimethyl sulfoxide (vehicle).

In the CN03 washout experiments, two substrates seeded with serum-starved cells were treated for 6 hours, as described above. After the 6-hour treatment, one of the substrates was fixed. This served as the posttreatment/prewash condition. The other substrate was washed thoroughly with fresh medium and was incubated for 48 hours. After the 48-hour incubation, this second substrate was fixed. This is the postwash condition.

Cells were fixed in 4% paraformaldehyde, permeabilized in 0.5% (v/v) Triton X-100, and stained with phalloidin-TRITC (ECM Biosciences) and DRAQ5 (Thermo Fisher Scientific) or DAPI. Bovine plasma fibronectin was labeled with Alexa Fluor 488 succinimidyl ester (Molecular Probes) in accordance with the manufacturer’s protocol.

Imaging

Stained cells were imaged using an upright Leica TCS SP5 laser scanning confocal microscope (University of Pennsylvania Bioengineering Microscopy Core). Cells on cylindrical substrates were imaged using a 25× water immersion objective. Imaging of phalloidin intensity was performed on a Nikon Eclipse 80i epifluorescence microscope.

Plotting

The MATLAB function tight_subplot written by P. Kumpulainen in 2010 was used to generate some of the plots in this article. This function is freely available through the file exchange at MathWorks.

Fabrication and use of cylinder substrates

Glass capillary tubes with outer radii of 40, 125, and 200 μm (VitroCom) were cut into ~8 mm lengths. A number of these lengths were placed across a ~10 mm × 5 mm hole in a circular slab of cured polydimethylsiloxane (PDMS) with a diameter of 25 mm and a thickness of 1 mm. The capillary tubes were fixed in place using liquid PDMS as an adhesive (fig. S7A). A second, 2-mm-thick PDMS slab with a ~10 mm × 10 mm hole was placed on the first slab so that the cylinders fit within the hole (fig. S7B). The entire construct was secured to the bottom of a 35-mm dish using PDMS as an adhesive (fig. S7C) and baked overnight at 65°C. Suspending the cylinders above the bottom of the dish allows cells to adhere to and migrate on the entire cylinder.

Before cells were seeded on the cylinders, the substrates were sonicated in 200-proof ethanol for 10 min and placed on a hot plate until dry. Once dry, the cylinders were submerged in 200 μl of a fibronectin solution containing one part labeled fibronectin and three parts unlabeled fibronectin with a final concentration of ~50 μg/ml. The cylinders were functionalized with fibronectin by incubating them in this solution for 30 min at 37°C. The cylinders were rinsed with phosphate-buffered saline and then medium before cells were seeded in the cylinder chamber. After the cells had attached and started spreading for 30 to 60 min in the incubator, additional medium was added to the dish to supply the cells with sufficient nutrients for the remaining culture period. Cells were cultured until the desired surface density was achieved and were then fixed and stained.

Mapping of confocal stacks

Examination of phalloidin-TRITC confocal stack projections normal to the cylinder axis distorted the analysis of cell and SF morphology and alignment; cells on the sides of the cylinder were tilted relative to the laser scanning direction and appeared smaller and more axially aligned than those near the top of the cylinder in these projections. To resolve this issue, we developed a custom MATLAB mapping algorithm to map the phalloidin-TRITC signal on the surface of the cylinders to a common plane. This method improved the visualization of cell morphology relative to the cylinder surface and facilitated image analysis.

To perform the mapping, a confocal stack was first rotated in the xy plane to ensure that the cylinder was aligned in the vertical direction. Then, each slice of the stack was transformed on the basis of the position of the cylinder at the given height from the top of the cylinder. A projection of this new stack of transformed, or “mapped,” images was used for the analysis of cell and SF morphology and orientation.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1700150/DC1

fig. S1. MEFs and hVSMCs coalign on planar surfaces.

fig. S2. Apical and basal SFs align in distinct patterns in MEFs in response to curvature.

fig. S3. Lengths of apical and basal SFs in hVSMCs on small and large cylinders.

fig. S4. Phalloidin intensity of isolated hVSMCs on coverslips treated with CN03.

fig. S5. F-actin organization is not recovered after CN03 washout.

fig. S6. Basal SFs remain after inhibition of ROCK.

fig. S7. Assembly of cylinder substrates.