Genome-scale architecture of small molecule regulatory networks and the fundamental trade-off between regulation and enzymatic activity

Summary

Metabolic flux is in part regulated by endogenous small molecules that modulate the catalytic activity of an enzyme, e.g. allosteric inhibition. In contrast to transcriptional regulation of enzymes, technical difficulties have hindered the production of a genome-scale atlas of small molecule/enzyme regulatory interactions. Here, we develop a framework leveraging the vast, but fragmented, biochemical literature to reconstruct and analyze the small molecule regulatory network (SMRN) of the model organism Escherichia coli, including the primary metabolite regulators and enzyme targets. Using metabolic control analysis, we prove a fundamental trade-off between regulation and enzymatic activity, and combine it with metabolomic measurements and the SMRN to make inferences on the sensitivity of enzymes to their regulators. Generalizing the analysis to other organisms, we identify highly conserved regulatory interactions across evolutionarily divergent species, further emphasizing a critical role for small molecule interactions in the maintenance of metabolic homeostasis. 2

Graphical Abstract

Introduction

Despite nearly a century of accumulated experimental data on the identity, biophysical nature, and structural basis of small molecule regulation of enzymes, there has been little progress in elucidating at genome-scale the regulation of enzymes by small molecules. Such interactions, e.g. allosteric regulation or competitive inhibition, play an essential role in homeostasis and in fast adaptations to abrupt environmental changes. For instance, feedback inhibition of amino-acid biosynthesis pathways by end-products preserves anabolic resources when sufficient levels of amino acids are available (Stryer et al., 2002). In contrast, the ultrasensitive feed-forward activation of PEP carboxylase by fructose bisphosphate in glycolysis enables Escherichia coli to rapidly import glucose following periods of carbon starvation (Xu et al., 2012a).

Recently, it has been established that properly accounting for the activation/inhibition of enzymes by endogenous small molecules can lead to metabolic models that explain experimental data better (Chandra et al., 2011; Hackett et al., 2016; Khodayari and Maranas, 2016; Link et al., 2013; Xu et al., 2012a), facilitate engineering of novel metabolic pathways (Chen et al., 2015; He et al., 2016), and improve our understanding of metabolic phenomena in health and disease (Christofk et al., 2008). So far, high-throughput experimental assays for discovering small molecule regulatory interactions have been technically limited (Feng et al., 2014; Li et al., 2013; Nikolaev et al., 2016; Orsak et al., 2012; Reinhard et al., 2015; Savitski et al., 2014), while hybrid approaches that integrate experimental data with computational models are not scalable and typically focus on central carbon metabolism (Hackett et al., 2016; Link et al., 2014, 2013; Schueler-Furman and Wodak, 2016).

An alternative strategy for studying small molecule regulation is to leverage the vast record of biochemical studies to informatically reconstruct a small molecule regulatory network (SMRN) (Alam et al., 2017). Such an approach would produce a network of interactions between enzymes and metabolites/small molecules (terms we will use interchangeably) that mirrors the native interactions of metabolites as substrates for enzymes, and could be naturally integrated with genome-scale metabolic models (GSMMs, e.g. BIGG models (King et al., 2016)), which are in wide use today. An informatic approach would likely cover a larger swath of metabolism, including peripheral and rarely-studied pathways, by aggregating experimental data from many reports. Furthermore, reports of small molecule/enzyme regulation from separate publications could provide additional, independent evidence for such an interaction. Finally, an informatically reconstructed SMRN would also offer a window to distilling how the critical regulatory components of the cell, i.e. the regulating metabolites and the regulated enzymes, fit into the broader hierarchy of processes controlling metabolic flux, from thermodynamics to transcriptional regulation.

Here, we report a computational framework for investigating small molecule regulation across the complete metabolism of an organism. Using E. coli as a model, we assemble a genome-scale SMRN by mining the BRENDA (Chang et al., 2015, 2009) and BioCyc (Caspi et al., 2016) databases. The resulting atlas of small molecule regulation captures widespread inhibition and activation of metabolic enzymes by endogenous metabolites. Overlaying this network onto a genome-scale metabolic model of E. coli enables a direct comparison between the topology of metabolism and its regulatory scaffolding. Integrating the SMRN with experimentally determined metabolite concentrations and binding affinities exposes how cells balance between the dual roles of small molecules (i.e. as substrates or inhibitors) as well as their condition-dependent contribution to metabolic flux regulation. Finally, by a natural extension of our approach, we compare the incidence of small molecule regulatory interactions across phylogenetic taxa spanning all kingdoms of life, revealing a handful of canonical regulatory interactions that permeate the metabolism of widely divergent species.

Results

Assembling a Small Molecule Regulatory Network (SMRN)

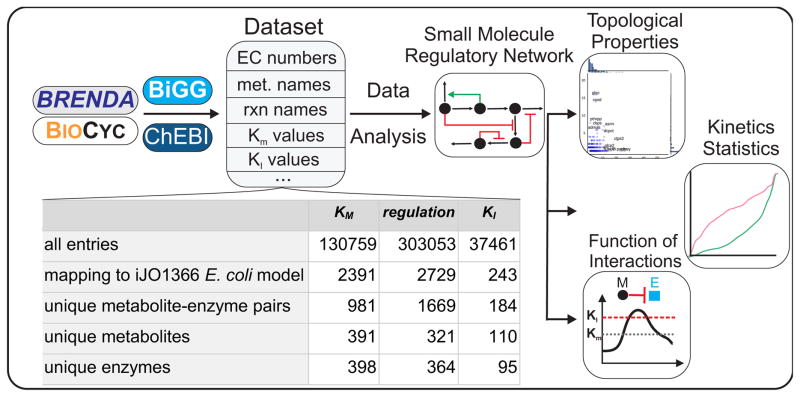
In contrast to the proliferation (Orth et al., 2011; Thiele et al., 2009) and automated reconstruction (Henry et al., 2010) of genome-scale metabolic models, no analogous computational pipeline is available for the analysis of enzyme regulation by small molecules. Here, we describe a pipeline for mining existing data on small molecule regulation from public repositories, and computational tools for integrating it with a curated, genome-scale metabolic model (Figure 1).

Figure 1. Framework for reconstruction and analysis of the small molecule regulatory network (SMRN).

The BRENDA and BioCyc databases were mined for each reaction taking place in E. coli. The identified entries (including data on EC numbers, enzyme names, activating or inhibiting small molecule – enzyme interactions, metabolite names, K_m and K_I values) were stored and then matched by EC number to reactions in the most recent genome-scale reconstruction of E. coli, iJO1366. This dataset was searched and analyzed for regulatory small molecules, yielding a comprehensive Small Molecule Regulatory Network (SMRN). The SMRN was used as the primary resource for the remainder of the analysis. We analyzed the topological properties of the SMRN, evaluated the similarities and differences in the kinetic properties of reactions and interactions, and used published metabolite concentration data in order to evaluate the functional role of inhibitory small molecule/enzyme interactions.

Our general approach relies on the BRENDA and BioCyc databases for data concerning the inhibition or activation of enzymes by small molecules in a particular organism. To facilitate comparison across species, information in these databases is organized along Enzyme Commission (EC) numbers, which functionally classify enzymes according to the reaction they catalyze. Thus, for every EC number, we obtained a list of possible regulating small molecules, the type of interaction (activation vs. inhibition), and the interaction constant (K_I), if available. In addition to gathering data on the presence of a small molecule interaction, we also compiled available information on the Michaelis-Menten constants for the substrates of each metabolic reaction. The computational pipeline is freely available for download at http://github.com/eladnoor/smallmolecule-regulation.

Because of its well-defined genome, highly curated metabolic network, and heavily studied metabolism, we decided to focus on the model bacterium Escherichia coli. The assembled data described above was mapped onto a genome scale metabolic reconstruction of E. coli (Orth et al., 2011), producing a small molecule regulatory network (SMRN, Table S1). Importantly, our computational framework can be extended with minimal effort to reconstruct and analyze the SMRN of other organisms besides E. coli, provided that a genome scale metabolic model is available and that there is sufficient data in the BRENDA and BioCyc databases.

Landscape of Interactions in the E. coli SMRN

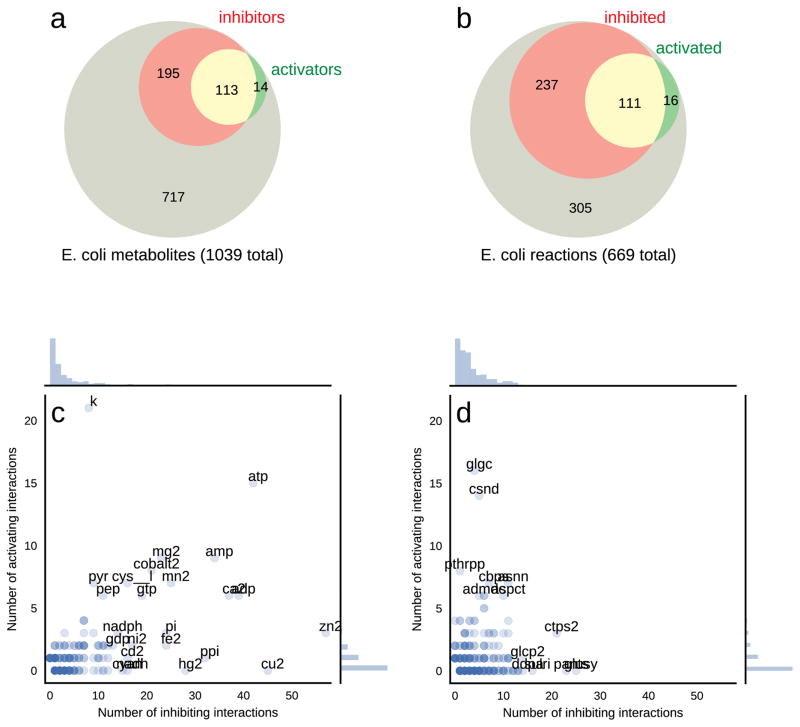
The computationally reconstructed E. coli SMRN contains 1669 unique interactions between 321 unique endogenous metabolites and 364 unique enzymes (EC numbers) (Table S1, Figure S1). The vast majority (83%) of these interactions are inhibitory. Out of the ~700 unique EC numbers in the E. coli model, about half are regulated by at least one native metabolite in E. coli. Similarly, ~320 distinct native metabolites (out of the total ~1000) regulate at least one enzyme (Figure 2a, b). Figure 1 provides a tally of interactions and kinetic constants recovered from the BRENDA and BioCyc databases. We additionally found that 325 of the 1669 interactions in the SMRN are supported by 2 or more independent literature references, which may be treated in the future as an informatic surrogate for the likelihood that the interaction is functionally relevant in vivo.

Figure 2. Overview of small molecule interactions from BRENDA.

Statistics of the computationally reconstructed E. coli SMRN, covering (a) the proportions of 1039 E. coli metabolites which are inhibitors, activators, or both, and (b) of 669 E. coli enzymatic reactions which are inhibited, activated, or both. (c)–(d) Scatter plots depicting the number of activating and inhibiting interactions each metabolite (c) and each reaction (d) participates in.

Certain metabolites and EC numbers participated in exceptionally high numbers of regulatory interactions (Figure 2c, d). In particular, the cofactors ATP, AMP, ADP, PI, PPI, NADPH, and GTP together with the metabolites cysteine, pyruvate, and phosphoenolpyruvate (PEP) were the most frequent metabolite regulators, participating in at least 15 interactions (both inhibitory and activating). Notably, ATP was found to regulate 57 different reactions, reflecting its important role as a global reporter of the energetic status of the cell (Atkinson, 1968). Although not strictly molecules, metal ions were found to comprise a significant fraction of the group of small molecule regulators. Interestingly, potassium was the most frequently reported activator, likely reflecting the ability of monovalent cations to activate a broad group of enzymes (Page and Di Cera, 2006). Divalent cations, on the other hand, are among the most recurrent inhibitors, with zinc having more than 50 reported interactions and copper, calcium, manganese, mercury, iron, and magnesium each reported to inhibit more than 20 different reactions.

Small molecules can regulate enzymes for which they are not native substrates or products, potentially as a mechanism for long-distance signaling between metabolic pathways with direct connection via their reactants. Therefore, we investigated the distance covered by small molecule regulation (i.e. the shortest graph-distance between each regulatory metabolite and its targeted enzyme), using the genome-scale stoichiometric network of E. coli as a scaffold. As described in the Methods, this distance corresponds to the number of reactions a metabolite must traverse in order to reach a target enzyme. We found that enzymes are typically regulated by metabolites that are in their close vicinity. Specifically, 17% of inhibitory interactions are also reactants of the corresponding enzyme, 25% are only one enzymatic step away, and 35% are two steps away. Activating interactions tend to have slightly longer range interactions with only 8% of activators regulating enzymes that utilize them as substrates (Figure S1).

To obtain specific insight on how small molecule–enzyme interactions operate across different metabolic pathways, we used the genome-scale E. coli metabolic model (Orth et al., 2010) to classify each reaction according to functional metabolic subsystems. We found that most interactions in the E. coli SMRN seem to target seven main subsystems/pathways: cofactor biosynthesis, alternate carbon metabolism, nucleotide salvage pathway, arginine/proline metabolism, nucleotide biosynthesis, cell envelope biosynthesis, and glycolysis/gluconeogenesis (Figure S2). Interestingly, some canonically high-flux pathways (e.g. the TCA cycle and the pentose phosphate pathway) were regulated by comparatively few metabolites. It is possible that such pathways are sparsely regulated by small molecules because they are mostly regulated transcriptionally, as has been recently suggested for TCA cycle genes (Chubukov et al., 2013; Gerosa et al., 2015).

Further mining of this rich dataset revealed pathway-specific preferences for the regulatory targets of certain small molecules. In particular, PEP, citrate, and AMP each activated 3 or more reactions in the glycolysis/gluconeogenesis pathway, suggesting that these three metabolites act as critical sensors controlling the overall rate and direction of glucose metabolism. Similarly, a group of nucleoside triphosphates, deoxynucleoside triphosphates, and adenosine appear to specifically inhibit enzymes in three pathways related to nucleotide metabolism (nucleotide salvage, purine/pyrimidine biosynthesis, and prosthetic group biosynthesis), perhaps reflecting a negative feedback loop for the maintenance of adequate levels of various nucleotides (Figure S2).

Design Principles in the Regulation of Central Carbon Metabolism

Central carbon metabolism, encompassing glycolysis, the pentose phosphate pathway, and the TCA cycle, provides all the energetic and biosynthetic precursors for the cell, and is known to be highly transcriptionally, post-translationally, and allosterically regulated (Chubukov et al., 2014). The central metabolism of E. coli is also one of the few parts of metabolism where in vivo evidence is available to support the functional role of small molecule regulation, e.g. in order to induce flux reversal (Link et al., 2013). In silico efforts to model the response of central metabolism to nutrient perturbations, combined with experimental data, have highlighted the fact that our understanding of the intricate regulation of central metabolism is incomplete (Gerosa et al., 2015; Hackett et al., 2016; Kochanowski et al., 2013; Link et al., 2013; Xu et al., 2012a).

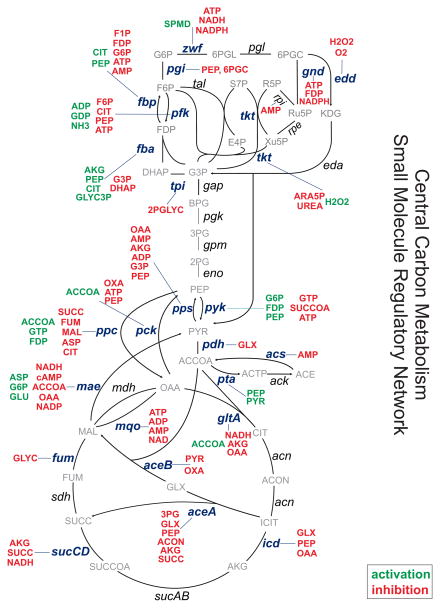
The majority of enzymes in E. coli’s central carbon metabolism are regulated (Figure 3, Figure S3), and interact with more small molecules than average in the SMRN (Figure S1), reflecting the heavy research attention these pathways have historically attracted. Interestingly, some of the enzymes in central metabolism are very heavily regulated - specifically those in upper glycolysis (e.g. fbpase, pfk, and fba), terminal glycolysis (pck, ppc, pps, and pyk), and the branching reactions of the TCA cycle (mae, aceA, and icd). Conversely, some metabolites seem to have a more central role in certain regions of central metabolism; PEP, for instance, regulates six reactions in glycolysis (pfk, pgi, fbpase, fba, pps, pyk).

Figure 3. Small Molecule Regulatory Network of E. coli Central Carbon Metabolism.

Depiction of the small molecule regulatory interactions in the central carbon metabolism of E. coli. Red metabolites are inhibitors, green metabolites are activators of the indicated reactions. Another view of this SMRN is given in Figure S3, showing clearly which reactions are inhibited, activated, or both.

A glance at the structure of small molecule regulation in E. coli’s central metabolism strongly suggests that the distribution of regulatory interactions is non-random, and has likely been shaped by evolution. What are the pressures selecting for regulatory interactions in E. coli’s SMRN? In this regard, the theoretical and experimental literature has proposed a variety of thermodynamic and economic arguments to explain patterns of SMR interactions in central carbon metabolism. Below, we evaluate the consistency of each hypothesis with data from the E. coli SMRN.

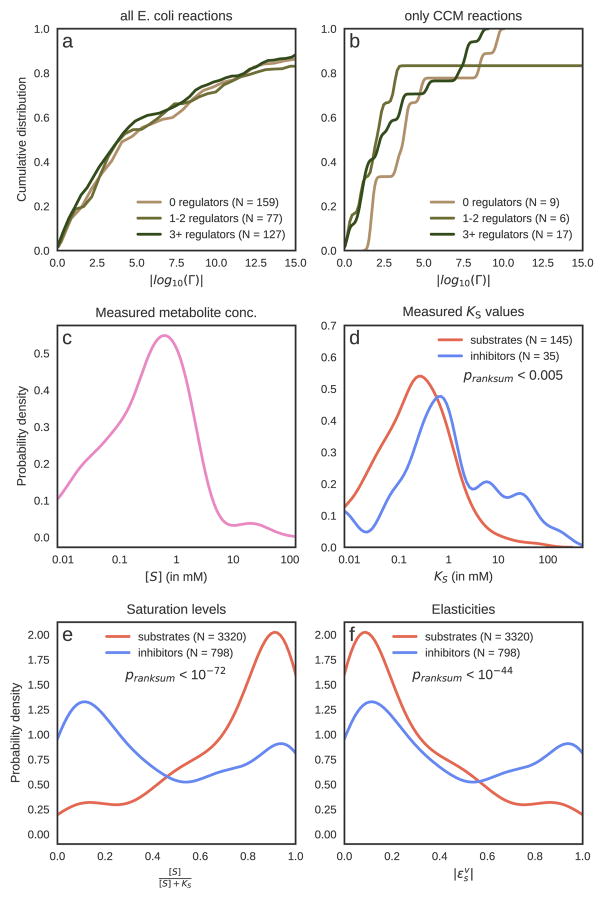
One frequently cited hypothesis is that small molecule regulation is concentrated in those reactions exhibiting a large drop in free energy (Stryer et al., 2002). To evaluate this possibility, we acquired thermodynamic data for most metabolic reactions using the component contribution method (Noor et al., 2013). Using reactions’ ΔG^o together with reaction stoichiometry and standard physiological metabolite concentrations of substrates or products, we calculated a reversibility index (denoted Γ) quantifying the extent to which each reaction is thermodynamically reversible (Noor et al., 2012). Using two complementary methods, we did not find the distributions of Γ values for regulated/unregulated reactions in central carbon metabolism to be statistically different (p-value < 0.3, Mann-Whitney U test; p-value 0.1, Gene Set Enrichment Analysis; Figure 4b). The same result was observed when repeating the analysis on all available reactions in E. coli (p-value < 0.5, Mann-Whitney U test; p-value 0.25, Gene Set Enrichment Analysis; Figure 4a and supplementary material - Table S4). While many irreversible reactions in CCM were indeed regulated by small molecules, a similar proportion of reversible reactions were also regulated. In particular, we found reactions like 6-phosphogluconolactonase in the PP pathway (EC 3.1.1.31, ln(Γ)=9.6), that do not have any reported small molecule interactions yet exhibit a large drop in free energy. Similarly, many reversible reactions have several regulators, as in the case of succinyl-CoA synthetase (EC 6.2.1.5, ln(Γ)=0.22), which is inhibited by NADH and alpha-ketoglutarate or glucose-6-phosphate isomerase (EC 5.3.1.9, ln(Γ)=1.02) which is inhibited by PEP and 6PGC. Taken together, our data does not support the hypothesis that thermodynamically irreversible reactions are more likely to be regulated by a small molecule.

Figure 4. Thermodynamics, saturation, and elasticity of small molecule regulatory interactions in E. coli.

(a)–(b) Comparison of reversibility indices (Γ) (Noor et al., 2012) between regulated and unregulated reactions. |log₁₀(Γ)| reflects how much freedom the reactants’ concentrations need for reversing the flux. For instance, a reaction whose |log₁₀(Γ)| > 3 would require a concentration range of at least 1:10³ (e.g. 30 uM to 30 mM) in order to reverse its direction. Physiological constraints typically limit this range to 10³–10⁴. (a) shows the cumulative distribution of |log₁₀(Γ)| for all reactions in the E. coli model for which an equilibrium constant could be computed using component contributions (Noor et al., 2013). This means that 60%–70% of reactions are reversible, with virtually no regard to whether they are regulated or not. The difference between the distribution of |log₁₀(Γ)| for regulated and unregulated reactions is not significant (Mann-Whitney U test p-value = 0.5). In (b), we focus only on reactions in central carbon metabolism, where the difference is not significant either (p-value = 0.3). (c) The distribution of measured metabolite concentrations, where the peak value is slightly below ~1 mM. (d) The histograms of K_M and K_I values are significantly different (Mann-Whitney U test p-value < 0.005). For a more detailed comparison on a single-metabolite basis, see Figure S6. (e) Conversion of measured binding constants to saturation levels using measurements of metabolite concentrations across 13 conditions further highlights the difference between substrates (K_M values) and inhibitors (K_I values) (Mann-Whitney U test p-value < 10⁻⁷²). When comparing the distributions of scaled elasticities (f) we find that inhibitors have significantly higher values (p-value < 10⁻⁴⁴), and seem to have a bimodal distribution which is split exactly at 0.5. Note that the absolute elasticity value for inhibitors is exactly equal to the saturation, therefore the blue histogram is the same in (e) and (f). For substrates, however, the elasticity is equal to 1 minus the saturation, so the red histogram in (f) is the mirror image of the one in (e).

A second hypothesis is that cells use small molecule regulation to conserve precious metabolic resources by preventing futile cycling. We observe several examples of interactions in the E. coli SMRN supporting this possibility. For example, fbpase and pfk catalyze opposing reactions, and their simultaneous operation leads to futile cycling (Daldal and Fraenkel, 1983). Two metabolites (citrate and PEP) serve as activators for fbpase and as inhibitors for pfk, thus curbing this futile cycle (Figure 3). A similar regulatory architecture can be found in the regulation of the four reactions metabolizing PEP: acetyl-CoA is an activator of pck but an inhibitor of the reverse reaction catalyzed by ppc. Similarly, PEP itself activates pyruvate kinase but inhibits the reverse reaction PEP synthase. Moving beyond anecdotal observations, we used a genome scale metabolic model (iJO1366 (Orth and Palsson, 2012)) to detect reactions that can lead to futile cycling. We identified 58 non-overlapping futile cycles, the majority of which comprise only two reactions. Combining this information with the SMRN, we find no statistically significant overrepresentation of small molecule regulation in reactions that take part in futile cycling (see Supplementary Text). Our finding here needs careful interpretation: the fact that futile cycle reactions are not more likely to be regulated does not necessarily mean that conservation of resources is not important for fitness. For example, it might be that many futile cycles are not regulated because they are in the periphery of metabolism and do not carry high flux, thus making their lack of regulation not very costly for the cell. Or perhaps, most of these futile cycles are avoided by preventing the co-expression of all cycle enzymes simultaneously. Indeed, the fact that fbpase and pfk are often co-expressed in E. coli might be a rare case due to the importance of glycolysis and the need for rapid adaptation of its flux direction.

Besides the prevention of futile cycles, conservation of resources can be also achieved by avoiding wasteful biosynthetic overproduction. This could be implemented by control of supply and demand of amino acids or nucleotides. In particular, SMR interactions can prevent large fluctuations/instability in the concentrations of biosynthetic end-products via feedback inhibition. It is, therefore, often hypothesized that allosteric regulation of the branching reactions from central metabolism leading to amino acid biosynthesis may achieve accurate supply/demand control (Hofmeyr and Rohwer, 2011; Hofmeyr and Cornish-Bowden, 2000) and thus prevent unnecessary waste. Interactions in the E. coli SMRN are consistent with this hypothesis: analysis of the SMRN reveals that 16 out of the 20 amino acids regulate their own biosynthesis using a negative feedback loop - i.e. by inhibiting the first enzyme of their biosynthetic pathway (Figure S4). The remaining non-feedback-inhibitory amino acids (glycine, alanine, aspartate, and glutamate) are 4 of the 5 cheapest ones in terms of the energetic investment required to produce them (Akashi and Gojobori, 2002; Link et al., 2015).

In summary, we find that one of the common (thermodynamic) hypotheses regarding the incidence of small molecule regulation is not supported by data from the E. coli SMRN, and find only anecdotal evidence for an enrichment of regulation in futile cycles. We do, however, find compelling support for an economic role of SMR interactions via feedback inhibition of biosynthesis pathways, at least for 16 out of the 20 amino acids. The four exceptions to this rule, however, might prove to be interesting cases where having a regulatory interaction is more costly than the benefit it provides to the cell. In the following sections, we elaborate on this cost, and quantify it using metabolic control analysis.

How is a Metabolite’s Role as Regulator and Substrate Balanced?

Small molecule metabolites serve two fundamentally distinct roles in the cell: one, as substrates for metabolic reactions, and another, as regulatory molecules affecting the activity of enzymes and transcription factors (Gerosa and Sauer, 2011). How does the cell balance between these two responsibilities, especially in bacteria that have no intracellular compartments that could offer spatial separation (Alam et al., 2017)? More specifically, are the cellular concentrations of these metabolites and the affinities of their interactions with the different enzymes in E. coli tuned such that they can inhibit some reactions while efficiently serving as substrates for others? To address this question, we gathered all reported Michaelis-Menten constants (K_M) and inhibitory half-saturation constants (K_I) (activation constants were not available in BRENDA). We decided to use these K_M and K_I values as approximate indicators of a small molecule’s “metabolic operating point” and “regulatory operating point”, respectively.

We first evaluated whether K_M and K_I values were quantitatively similar to each other (K_A values, or binding constants associated with activating interactions, were not available in BRENDA and were thus excluded). As reported by others (Park et al., 2016), in general, K_I values tend to be higher than K_M values (Figure 4d, Mann-Whitney U test p-value < 0.005). A more informative approach to evaluating differences in K_M and K_I values is by a direct comparison with physiological metabolite concentrations. For example, if a metabolite’s concentration is much higher than all of its associated K_M and K_I values, then all interactions related to this metabolite are approximately fully saturated, and any differences between K_M and K_I are not physiologically meaningful. Here, we quantify the level of saturation using the formula $\frac{s}{s+K_S}$, where K_S is a binding constant (either K_M or K_I) and S is the concentration of the substrate or inhibitor. For a substrate, the saturation represents the relative activity of an enzyme compared to a case where S is very high and the enzyme is fully activated (assuming all other parameters are kept constant and the reaction obeys irreversible, mono-substrate kinetics). We use this definition to identify physiologically relevant differences between substrate and inhibitor affinities.

To apply the notion of saturation to our data, we obtained previously published metabolite concentrations in exponentially growing E. coli cultures on 13 different carbon sources (Kochanowski et al., 2017). For each unique binding constant/metabolite concentration pair, we calculated the saturation level (332 enzyme-inhibitor-condition triplets and 798 enzyme-substrate-condition triplets, Figure 4e). A comparison between substrate and inhibitor saturation levels yielded a significant difference in the saturation of inhibitor and substrate binding sites (Mann-Whitney U test p-value < 10⁻⁷²). This suggests that at physiologically relevant concentrations of metabolites, the majority of substrate binding sites are at or near saturation, while inhibitor sites are occupied but largely far from being saturated, as was reported in the past (Bennett et al., 2009; Park et al., 2016).

Quantifying the metabolic response to small molecules across different conditions and the tradeoff between regulation and enzymatic activity

The results presented in Figure 4e indicate that approximately one third of the inhibitory interactions involved metabolites whose concentrations were higher than the associated K_I (saturation level at least 0.5). This suggests that many enzymes are operating below their maximal catalytic potential. Why would metabolic enzymes be poised at such a point, well below maximal activity? As we show below and in the Supplementary Text, one possible explanation is a fundamental tradeoff enzymes face: in order to be responsive to the abundance of metabolite regulators, enzymes must sacrifice some of their catalytic activity. Put another way, there is an inherent cost associated with small molecule regulation: to effectively regulate enzyme activity, an inhibitor must be at sufficiently high concentration. Using theoretical arguments from metabolic control analysis (MCA), we prove that this trade-off between activity and regulation is valid for a general class of kinetic rate laws (e.g. competitive, noncompetitive, and uncompetitive inhibition), applying both to inhibitors and activators (see Supplementary Text).

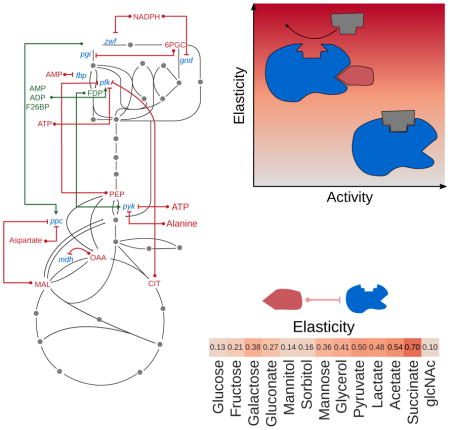
The relevant quantity in MCA which leads to the finding above is the scaled elasticity ε_s^v, which quantifies how fluctuations in the concentration of a metabolite S affect the flux through reaction v. For substrates of reactions described by irreversible Michaelis-Menten kinetics, the scaled elasticity is given by ${{\epsilon }_s}^v=\frac{\partial v}{\partial s}·\frac{s}{v}=1-\frac{s}{s+K_M}$, i.e. it is maximized (equal to 1) when the substrate binding site is unsaturated (S ≪ K_M). In this regime, a fluctuation in the concentration of substrate leads to a linearly proportional change in the flux of the enzyme (for an isolated enzyme, like in an in vitro assay). On the other hand, the elasticity of non-cooperative, non-competitive inhibitors I is described by ${{\epsilon }_I}^v=\frac{\partial v}{\partial I}·\frac{I}{v}=-\frac{I}{I+K_I}$ (see Figure S5). Counter-intuitively, this means that a reaction is most sensitive to an inhibitor I when I is at high concentration and the enzyme is strongly inhibited (I ≫ K_I). Conversely, when the inhibitor concentration is low, its elasticity approaches zero and the flux cannot respond to changes in I. Therefore, substrates and inhibitors are subject to opposite quantitative relationships describing their potential to regulate reactions (Figure 5a). Therefore, the saturation level has two complementary consequences: first, it affects the elasticity (how sensitive the reaction rate is to changes of the regulator level), and second, it determines the necessary amount of enzyme (because enzyme that is not used at its full capacity needs to be compensated by higher enzyme levels).

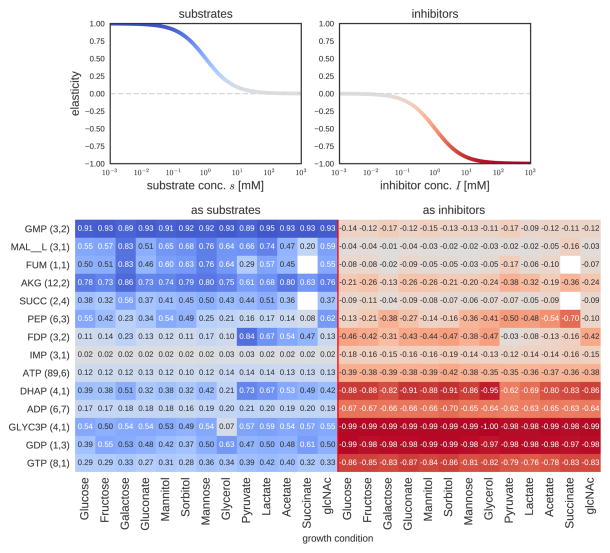
Figure 5. Functional role of small molecule-enzyme interactions in central metabolism.

(a) The opposing relationship between elasticity and concentration for a prototypical substrate or inhibitor. In general, substrates have high elasticity at low concentrations, while inhibitors have high elasticity at high concentrations. (b) A heatmap of the median values of each metabolite’s elasticity values across all enzymes that utilize it as a substrate (left-hand side) and across all enzymes inhibited by it (right-hand side). The different columns correspond to different growth conditions (batch growth on minimal media with single carbon sources, samples in mid-exponential phase). Saturation levels were calculated using the formula [S]/([S] + K_S), where K_S is either the Michaelis-Menten coefficient (K_M) or the inhibition constant (K_I) and in turn elasticities were calculated as described in main text. The numbers next to each metabolite in parentheses count the number of different K_M or K_I values, respectively, that a metabolite has in our database (for different reactions). If a metabolite has more than one K_M or K_I value (i.e. for more than one enzyme), the median of all elasticities is shown. For more details, see Figure S5 and tables S5–S8.

Thus, an alternative way of examining the difference between K_M and K_I data is by translating estimates of saturation into elasticities (which we treat as proxies for the metabolic response coefficient, see Discussion and Supplementary Text). To simplify the calculation and avoid dependencies between multiple parameters and metabolite concentrations, we assume that all reactions follow irreversible Michaelis-Menten kinetics and all inhibitors are non-competitive. A detailed examination of elasticities across the 13 different growth conditions, further reveals the regulatory contribution of a set of central metabolites as substrates and inhibitors (Figures 4f and 5, Tables S5–S8). Interestingly, metabolites like IMP, ATP and ADP have very low elasticities as substrates (since they are typically at saturating levels), whereas others (GMP, AKG) have high substrate elasticities spanning from 0.7 to 0.9. As inhibitors, many metabolites are poised between elasticities of 0.2–0.5, whereas some metabolites (e.g. GDP, ADP) have high elasticities across all conditions. A higher elasticity could increase the flux response to changes in these metabolites, which is supported by prior work e.g. it has been reported that ADP strongly regulates PRPP synthase (prpps, EC 2.7.6.1) as a form of biosynthetic feedback inhibition (Willemoes et al., 2000), as well as fructose-1-phosphate kinase (fruk, EC 2.7.1.56) as a mediator of end-product inhibition (Buschmeier et al., 1985).

Notably, the elasticity of several highly connected metabolites in the SMRN (i.e. PEP and FDP) changes substantially between environmental conditions. FDP has high elasticities when cells grow in a glycolytic mode (e.g. growth on glucose, fructose, mannitol), consistent with the proposed role of FDP as a flux sensor in glycolytic conditions (Kochanowski et al., 2013). Interestingly, PEP as an inhibitor has high (absolute) elasticities on gluconeogenic carbon sources (e.g. pyruvate, acetate, succinate), operating anti-symmetrically to FDP. This regulatory design is critical for adaptation to environmental conditions, for example for the control of the flux through phosphofructokinase (pfk), which PEP is known to inhibit (Fenton and Reinhart, 2009). This inhibition is not needed though when cells grow on glycolytic carbon sources like glucose. Interestingly, we find that on glycolytic carbons that can only support a slow growth rate, PEP has still high elasticities (e.g. −0.38 and −0.36 for pfk when cells grow on galactose or mannose respectively).

Small Molecule Regulation Across Kingdoms of Life

While some central pathways of metabolism are nearly ubiquitous, whole-cell metabolism varies substantially between different organisms. At the coarsest resolution, some phylogenetic taxa (e.g. bacteria and plants) can fix inorganic carbon, while others (e.g. animals) cannot. On the other hand, the architecture of central carbon metabolism is broadly conserved across all kingdoms of life (Peregrín-Alvarez et al., 2009; Peregrin-Alvarez et al., 2003). However, there is little understanding of the extent to which small molecule regulatory interactions are conserved across evolutionarily distant taxa. Therefore, we analyzed all available data on small molecule activators and inhibitors available in the BRENDA database, stratifying by the species in which the interaction was reported. We mined this data for recurrence of a regulatory interaction between a small molecule and EC number across different species. We then focused on analyzing interactions which were: (1) evident in at least 10 different species, and (2) supported by at least 10 different reports in the literature. A full list describing the 253 such interactions is available as Supplementary Material - Table S3.

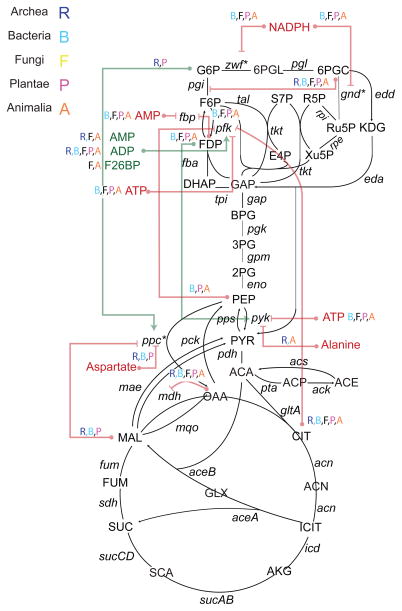
Because of the high interest in modeling and understanding of flux through central carbon metabolism, we focused our efforts on understanding recurrent regulatory interactions in this pathway (Figure 6). After excluding small ions and non-endogenous metabolites, we identified 18 small molecule regulatory interactions evident broadly across several phylogenetic taxa, which converged on the regulation of a small number of enzymes: four nodes in glycolysis, phosphofructokinase (6 recurrent regulators), fructose bisphosphatase (2 recurrent regulators), PEP carboxylase (3 recurrent regulators) and pyruvate kinase (3 recurrent regulators. Surprisingly, we found few conserved interactions in the TCA cycle, glyoxylate shunt and the non oxidative branch of the PP pathway. In line with its role as a committing step in glycolysis, phosphofructokinase was subject to negative feedback control by two metabolites far downstream in glucose catabolism, citrate and PEP, as well as regulation by energy-related cofactors ATP, ADP, and AMP. In contrast, pyruvate kinase was negatively regulated by ATP, but also subject to feedforward activation by FDP (fructose-1,6 diphosphate). The counter-intuitive activation of pyruvate kinase by FDP has been shown (Xu et al., 2012b) to be important for the rapid response of yeast to changes in environmental glucose levels, by driving accumulation of PEP for future phosphorylation of glucose in glucose-depleted conditions. Similarly, the inhibition of phosphofructokinase by PEP has also been shown to be of critical importance in dynamic perturbations in E. coli (Link et al., 2013)

Figure 6. Small molecule regulation across kingdoms of life.

The BRENDA database was mined for all reports of small molecule regulatory interactions across all species. These interactions were aggregated by unique metabolite-reaction pairs. For each interaction evident in at least 10 different organisms and supported by evidence from at least 10 different published studies, followed by manual curation of the results. We identified the broad phylogenetic taxon within which the interaction was present. Nearly all conserved interactions are inhibitory, with a two exceptions: the activation of PFK by three metabolites, AMP, ADP, and fructose-2,6-bisphosphate, and the activation of PEP carboxylase by G6P. 16

Interestingly, several of the recurrent regulatory interactions we identified were evident in only a subset of phylogenetic taxa. In some cases, this was due to the absence of the enzyme in a taxon (e.g. PEP carboxylase is only present in archaea, bacteria, and plants, and the pentose phosphate pathway is not present in archaea). In other cases, small molecule regulation was simply different across taxa, with potentially interesting implications. For example, pyruvate kinase was inhibited by L-alanine in fungi and animals, but not in other species. In humans, this differential regulation plays a role in disease: the inhibition of one splice isoform of pyruvate kinase (PKM2) by L-alanine (but not the other, PKM1) contributes to the cancer-associated shift to aerobic glycolysis by promoting the shunting of glucose-derived carbon into biosynthetic pathways (Morgan et al., 2013).

Discussion

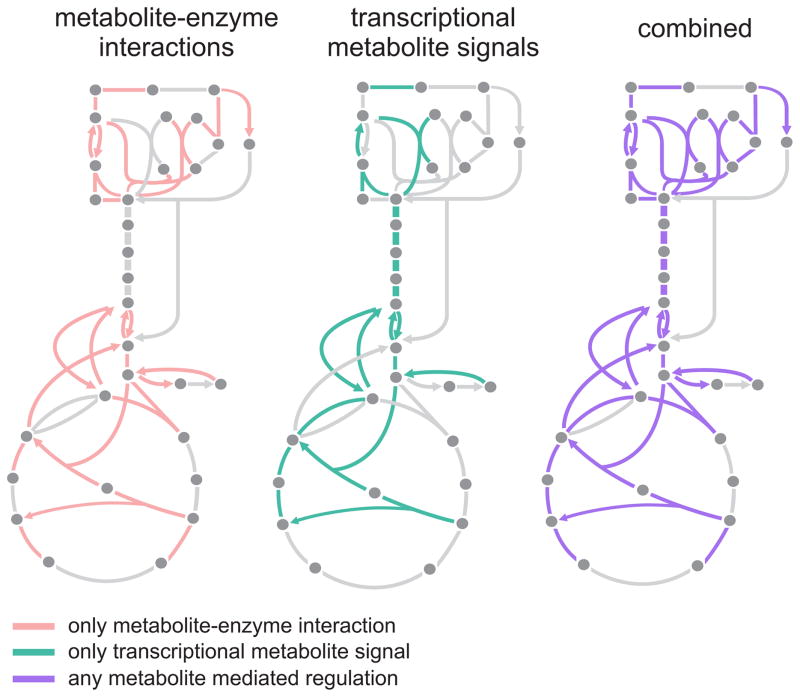
The regulatory action of small molecules on enzymes and other proteins ensures robust operation of metabolism upon dynamic changes. For central carbon metabolism, metabolites can directly (acting as effectors) or indirectly (acting as signals to transcription factors) regulate the flux of almost all enzymatic reactions (Figure 7). While our understanding of transcriptional and post-translational regulation of metabolism has benefited from advances in sequencing and mass spectrometric technologies, experimental challenges have hindered similar breakthroughs in our understanding of regulation of enzyme activity by small molecule metabolites (Lindsley and Rutter, 2006). Our approach here has been to leverage the fragmented wealth of published biochemical data to generate an atlas of small molecule regulation informatically, i.e. without performing additional laboratory experiments. Our findings illustrate the dual architecture of small molecule regulation and the underlying metabolic network, allow us to test a common hypothesis about the connection between regulation and thermodynamics, and to compare between metabolite concentrations and their respective binding affinities to target enzymes.

Figure 7. Combined architecture of direct small molecule and indirect transcriptional regulation via endogenous metabolites in E. coli.

A map of the reactions in central carbon metabolism that are regulated directly or indirectly by metabolite(s). On the left are reactions which are reported to have at least one metabolite - enzyme interaction. Middle diagram indicates reactions which are indirectly regulated by metabolites via transcription: in each case, the reaction is regulated by transcription factors that are recipients of metabolic signals (i.e. Cra-FDP, Crp-cAMP), as reported in (Kochanowski et al., 2017). Some reactions, e.g. those in intermediate glycolysis, are regulated exclusively by transcription. Map on the right overlays small-molecule and transcriptional regulation.

Here, we report a resource of experimentally evaluated interactions between endogenous metabolites and enzymes. Importantly, the computational framework we developed is freely available (http://github.com/eladnoor/small-molecule-regulation) and can be readily applied to reconstruct the SMRN of an arbitrary organism of choice, given a suitable genome-scale metabolic model and adequate data in BRENDA/BioCyc. Such a resource may guide future implementations of kinetic models and also guide experiments designed to identify novel and functionally relevant in vivo metabolite-protein interactions. Most implementations of kinetic models so far do not account for all known small-molecule enzyme interactions, but rather a subset of them (Khodayari and Maranas, 2016; Millard et al., 2017). Using our SMRN, such kinetic models could be expanded to include all relevant interactions, allowing for systems-level evaluation of the topological properties of the system. Our SMRN could also be instrumental in the understanding of the functional role of different small-molecule enzyme interactions, in combination with kinetic models. For example, an SMRN may prioritize metabolite-enzyme pairs to be included in a kinetic model based on the number of independent literature reports supporting their existence, or based on the elasticity of the interactions in different conditions. In addition, the SMRN and its associated inhibitor constants can be used as prior information to parameterize dynamic models of metabolism, an approach which has proven to be successful in E. coli and yeast (Hackett et al., 2016; Link et al., 2013).

A critical shortcoming of our approach is the inherent biases of the BRENDA and Ecocyc data, i.e. the tendency for well-studied enzymes, pathways, and organisms to be overrepresented in these databases. Indeed, one factor in selecting E. coli as the organism of choice for reconstruction was the breadth of studies conducted on its metabolism. One approach we took to resolving this issue was identifying putatively “high-confidence” edges in the SMRN, i.e those with at least 2 independent literature reports supporting the interaction (Table S2, Figure S7). This portion of the SMRN retains 325 (20%) of the total edges, a figure an order of magnitude larger than the number of edges included in typical kinetic models of metabolism. Furthermore, wherever possible, we perform our analyses on the exhaustively explored sub-network of central carbon metabolism, as well as on the full genome-scale network. For example, in the thermodynamic analysis, we indeed find a weak but statistically significant signal when testing for enrichment of small-molecule regulation in irreversible reactions. However, when the analysis is expanded to the full network, we no longer find a statistically significant difference in small molecule regulation between reversible and irreversible reactions. This might suggest that the thermodynamic principle is most relevant for reactions with high fluxes like those in CCM, and does not apply more generally to the entire metabolic network.

Our theoretical analysis of a wide class of inhibiting and activating small molecules shows that, in general, there is a direct trade-off between the elasticity of an effector, and the reduction in activity which is caused by its interaction with the enzyme. Mathematically, if θ is the relative activity of the enzyme (e.g. $\theta =1-\frac{x}{x+K_I}$ in the case of non-competitive inhibition), then the absolute scaled elasticity will be equal to |ε_x^v| = 1 – θ (see Supplementary Text S1). We show that this relationship between activity and elasticity holds for activators and inhibitors alike. Therefore, using a small molecule effector to regulate a flux always comes with the cost of effectively lowering the activity of the enzyme. This cost of regulation might be the reason why E. coli does not have end-product inhibition for 4 of its amino-acid biosynthesis pathways. Perhaps, the cost of regulation for these “metabolically cheap” amino-acids is larger than the energetic cost of overproduction.

In order to estimate the level of control imposed by a small molecule, we made several simplifications. First, we assumed that all substrates and inhibitors bind non-cooperatively and that inhibition is not competitive. Second, because a detailed and accurate representation of the kinetic form of each reaction rate law in E. coli was unavailable, we estimated elasticities assuming irreversible, mono-substrate kinetics. In the SI Text, we explore the consequences of these assumptions. In particular, we find that substrate elasticities assuming irreversibility are generically upper bounds on reversible substrate elasticities. Furthermore, we show that the elasticity of a substrate in a bi-substrate reaction is (assuming identical kinetic rate constants where applicable) generically a lower bound on the corresponding elasticity assuming a mono-substrate rate law. Relaxing these assumptions can both strengthen and weaken some of our conclusions, depending on the magnitude of their effect (which itself depends on detailed rate laws and parameters), such as those in Figure 4.

Perhaps more importantly, our results regarding elasticities must be treated carefully when making inferences on metabolic control. According to MCA, a high elasticity is a necessary but not sufficient condition for high control of a flux by a metabolite. We treat interactions with high elasticity as cases where high regulatory capacity is possible; in contrast, interactions with low elasticity are likely to have little regulatory capacity. A tradeoff between enzyme activity and elasticity will therefore translate to a tradeoff between activity and regulation. In order to be fully consistent with MCA, one would have to calculate all control coefficients for the inhibited reactions and apply MCA to calculate response coefficients, which quantify the level of flux control of a metabolite, something that is not in the scope of our work. A tractable path forward for decoding the control of flux by the SMRN is to integrate data on changes in in vivo metabolite abundance across conditions/perturbations. As we showed in Figure 5, doing so creates a map of the condition-dependent regulatory capacity (i.e. the elasticity) of small molecules, and prioritizes interactions which appear particularly relevant in a subset of conditions. For canonical interactions with available data on binding affinities, this kind of analysis can be used as a first step in understanding the importance of a regulatory interaction, perhaps by focusing on those interactions with a particularly large change in elasticity between two conditions. For instance, we found that certain metabolites (e.g. fructose bisphosphate) may have a substantially higher inhibition capacity in a subset of conditions. Doing so will likely add to the rich composition of transcriptional, post-translational, and small molecule regulatory interactions which we know to control metabolic flux.

Methods

Assembly of the SMRN

Raw data were obtained from BRENDA and BioCyc databases. Scripts for parsing the obtained data, filtering unwanted values (i.e. for mutants or negative results), and mapping between BRENDA ligand IDs, KEGG identifiers and BiGG metabolite IDs were written in Python and can all be found on GitHub (https://github.com/eladnoor/small-molecule-regulation, available under an MIT license). Likewise, all computations and analyses done for this paper can be found in the same repository.

Genome-scale metabolic model

All calculations involving the metabolic network of E. coli (i.e. distance calculations, thermodynamics of regulated and unregulated reactions, etc.) were done using the iJO1366 metabolic model downloaded from the BiGG website (http://bigg.ucsd.edu/models/iJO1366) (Orth and Palsson, 2012) and with the help of the cobrapy toolbox (https://opencobra.github.io/cobrapy/) (Ebrahim et al., 2013)

Distance calculations in the SMRN

First, we removed all the rows corresponding to co-factors from the genome-scale stoichiometric matrix of E. coli (the full list of co-factors is provided in the Supplementary Text). Then, the matrix was converted into an undirected bipartite graph where nodes were either metabolites or reactions. An edge was added between every reaction and all of its substrates and products. Then, the distance between each metabolite and enzyme was calculated by first finding the shortest path between the two on the bipartite graph, and counting the number of enzyme nodes along that path (i.e. excluding the metabolite nodes and the target enzyme itself). For example, the distance between an enzyme and one of its substrates is 0.

Cross-species analysis of small molecule regulation

All data regarding activation or inhibition was extracted from the BRENDA database. The R package taxize (Chamberlain and Szöcs, 2013) was used to recover taxonomic information using the species name provided in the BRENDA database. Activating/inhibiting interactions with the same ligand ID (regulating metabolite) and EC number (target enzyme) were aggregated, and the number of such unique entries for each taxonomic group was calculated. Additionally, the number of unique literature references supporting each interaction was recorded, in order to preclude cases where a single interaction reported across multiple species was supported by a small number of independent sources.

Supplementary Material

2

Table S1 - SMRN: The SMRN of E. coli, Related to Figure 3

3

Table S2 - Confidence: Confidence on different regulatory interactions, based on literature, Related to Figures 2 and 6

4

Table S3 - CCM: Conserved small molecule regulatory interactions across species, Related to Figure 6

5

Table S4 - Thermodynamics: Thermodynamics of regulated and unregulated reactions, Related to Figure 4

6

Table S5 - SubstrateElasticity: Elasticities of all substrate-enzyme pairs in 13 conditions, Related to Figures 4 and 5

7

Table S6 - SubstrateMedianElasticity: Median elasticities per substrate in 13 conditions, Related to Figures 4 and 5

8

Table S7 - InhibitorElasciticy: Elasticities of all inhibitor-enzyme pairs in 13 conditions, Related to Figures 4 and 5

9

Table S8 - InhibtorMedianElasticity: Median elasticities per inhibitor in 13 conditions, Related to Figures 4 and 5

Abbreviations

G6P

glucose-6-phosphate

6PGL

6-phosphogluconolactone

6PGC

6-phosphogluconate

Ru5P

ribulose-5- phosphate

KDG

2-keto-3-deoxygluconate

R5P

ribose-5-phosphate

S7P

sedoheptulose-7-phosphate

E4P

erythrose-4-phosphate

X5P

xylulose-5-phosphate

F6P

fructose-6-phosphate

FDP

fructose-1,6-bisphophate

F1P

fructose-1-phosphate

DHAP

dihydroxacetone-phosphate

G3P

glyceraldehyde-3-phosphate

BPG

1,3- bisphosphogylcerate

3PG

3-phosphoglycerate

2PG

2-phosphogylcerate

PEP

phosphoenolpyruvate

PYR

pyruvate

ACCOA

acetyl-CoA

OAA

oxaloacetate

CIT

citrate

ACON

aconitate

ICIT

isocitrate

GLX

glyoxylate

AKG

alpha-ketoglutarate

SUCCOA

succinyl-CoA

SUCC

succinate

FUM

fumarate

MAL

malate

ACTP

acetylphosphate

ACE

acetate

PI

phosphate

PPI

diphosphate

NAD

nicotinamide adenine dinucleotide

NADH

nicotinamide adenine dinucleotide

NADP

Nicotinamide adenine dinucleotide phosphate

NADPH

Nicotinamide adenine dinucleotide phosphate - reduced

2PGLYC

2-phosphoglycolate

GLYC

glycerol

GLYC3P

glycerol-3- phosphate

NH3

ammonia

GLU

glutamate

ASP

aspartate

OXA

oxalate

ARA5P

arabinose-5-phosphate

SPDM

spermidine

H2O2

hydrogen peroxide