Bayesian hierarchical modeling for subject-level response classification in peptide microarray immunoassays

Summary

The peptide microarray immunoassay simultaneously screens sample serum against thousands of peptides, determining the presence of antibodies bound to array probes. Peptide microarrays tiling immunogenic regions of pathogens (e.g. envelope proteins of a virus) are an important high throughput tool for querying and mapping antibody binding. Because of the assay’s many steps, from probe synthesis to incubation, peptide microarray data can be noisy with extreme outliers. In addition, subjects may produce different antibody profiles in response to an identical vaccine stimulus or infection, due to variability among subjects’ immune systems. We present a robust Bayesian hierarchical model for peptide microarray experiments, pepBayes, to estimate the probability of antibody response for each subject/peptide combination. Heavy-tailed error distributions accommodate outliers and extreme responses, and tailored random effect terms automatically incorporate technical effects prevalent in the assay. We apply our model to two vaccine trial datasets to demonstrate model performance. Our approach enjoys high sensitivity and specificity when detecting vaccine induced antibody responses. A simulation study shows an adaptive thresholding classification method has appropriate false discovery rate control with high sensitivity, and receiver operating characteristics generated on vaccine trial data suggest that pepBayes clearly separates responses from non-responses.

1. Introduction

The peptide microarray immunoassay simultaneously screens serum samples against thousands of peptides. Peptide microarrays have been applied to identify antibody epitopes, develop diagnostic tests, and determine antibody response to treatments. In a vaccine study, peptide microarrays can detect changes in antibody profiles and quantify the immunogenic properties of a vaccine regimen (Neuman de Vegvar et al., 2003). Lin et al. (2009) employ a peptide tiling array to map linear epitopes for milk allergens, and in a similar vein Shreffer et al. (2004) use a peptide tiling array to map linear peanut allergen epitopes.

Techniques for analyzing peptide microarray data vary among studies. For example Lin et al. (2009) use the median and median absolute deviation (MAD) of a large pool of control spots to form a z score for each observation, and the z scores are thresholded to determine positive calls. The rapmad method developed in Renard et al. (2011) normalizes probe responses with a set of control peptides, then applies a two component normal mixture model to classify peptides into null and response distributions. Nahtman et al. (2007) use a linear mixed model to estimate technical and biological effects and subsequently input normalized responses into Significance Analysis of Microarrays (Tusher et al., 2001). Gaseitsiwe et al. (2010) apply a linear model to remove technical effects and use the intensity distribution of control peptides to define a threshold to remove spots with no detectable response. Imholte et al. (2013) introduce the pepStat method, which models slide effects and secondary antibody binding in a linear model with heavy-tailed errors, and demonstrate the presence of replicable subject-specific binding effects associated with the fluorochrome-labeled secondary antibody.

Available methods for analyzing peptide microarrays suffer from unrealistic modeling assumptions, or do not perform subject-specific inference on a per-peptide basis. Careful protocol can reduce variability due to experimental procedures, but slide imperfections, non-specific secondary antibody reactivity, differences in sample concentration, and other factors can generate outliers and experimental noise that violate assumptions of normality. Furthermore, among a large library of peptides and a tremendous variety of possible antibodies, an assumption of constant error variance across a wide variety of peptide sequences is untenable. Within-slide technical replicates are often used to assess slide integrity, but replicates are typically summarized into a mean or median statistic discarding information about replicate variability. Moreover, normalization techniques based on linear mixed effects models such as in Nahtman et al. (2007) become computationally intractable with off-the-shelf software as the number of slides grows. Methods developed for cDNA microarrays seem promising, but are either not specialized to accommodate secondary antibody technical effects or are not suited for performing inference on a per-subject/peptide basis.

Variability among immune system responses raises further considerations when modeling peptide microarray responses. The human adaptive immune system relies on the random recombination of genes in order to produce an effective response against an unlimited variety of antigens (Market and Papavasiliou, 2003). As such, different subjects produce different antibody responses toward an identical stimulus (i.e. antigen exposure). An important goal of inference, then, is to determine whether each subject generated a response to the antigen and how these responses differ across subjects.

We introduce a robust Bayesian hierarchical model, pepBayes, to perform inference on a per-subject/peptide basis for two common peptide microarray experimental designs, which we refer to as paired and unpaired designs. The paired design draws samples from each subject before and after administering a treatment. An unpaired design compares samples drawn from a population of interest and a control population. Non-conjugate error and random effect distributions are specially suited to accommodate technical effects and extreme observations associated with peptide microarray data. Technical effects are explicitly modeled alongside biological effects, eliminating the typical separation between normalization and analysis. Section 2 explains the model and prior distribution of parameters. In Section 3 we apply pepBayes and pepStat to two vaccine trial data sets and compare their sensitivity and specificity with visual summaries and a receiver operating characteristic analysis. A simulation study demonstrates high sensitivity and appropriate false discovery rate (FDR) control with an adaptive thresholding technique. We conclude with a discussion of current limitations and possible extensions of the model.

2. PepBayes Models

A peptide microarray slide is a rectangular grid of probes, where each probe is a spot comprising numerous identical copies of a single peptide (Figure 1). A peptide is represented on several probe replicates to help verify slide integrity and improve estimation. Peptide sequences are typically drawn from the linear amino acid sequence of a protein of interest in an overlapping fashion, in what is known as a tiling array. Several proteins may be tiled, possibly including different subtypes of the same protein. Slides are incubated with sample solution, and primary antibodies in the sample bind to various peptides within probes. A solution of fluorescent-labeled secondary antibody is then applied, marking bound primary antibodies for scanning. The observed fluorescence intensity for a probe is a proxy for the amount of bound primary antibody from sample solution.

Figure 1.

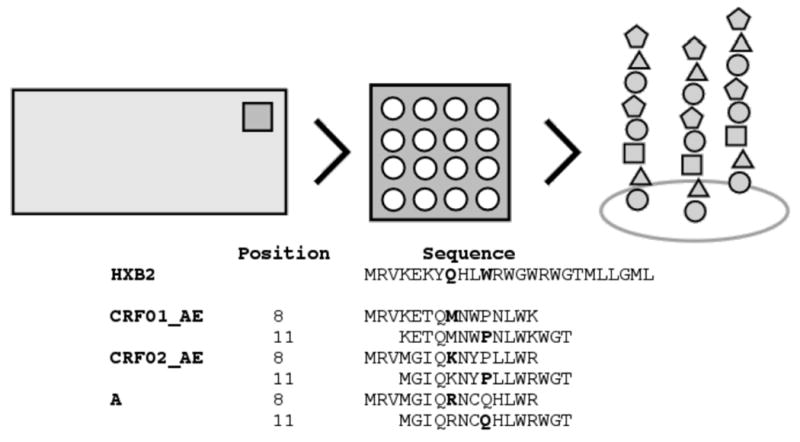
Representation of peptides on a slide probe. A probe comprises numerous identical copies of a single peptide. Peptide sequences on tiling arrays overlap and are drawn from the amino acid sequence of a protein of interest. Example sequences and positions for three clades of HIV are shown against the standard reference sequence HXB2.

Prior to modeling, probe measurements should be corrected for background fluorescence to reduce undesirable spatial heterogeneity. We chose the normexp method described in Ritchie et al. (2007), which models observed foreground intensity as a sum of observed background intensity, normal residual background, and an exponential signal S. The expected value of S given the observed intensities serves as a strictly positive estimate of a probe’s signal. The normexp method was found to have low bias recovering control quantities compared with other methods. Compared with other background correction methods, normexp with an additional offset parameter achieved lower false discovery rates when used prior to other algorithms detecting differential expression.

Estimated foreground intensity values were log₂-transformed to stabilize variance across the range of intensity values. The pepBayes method accommodates two experimental designs commonly applied in peptide microarray studies. We first describe the paired data method, where each subject has a pre and post-treatment measurement. We also develop an unpaired data method, where we compare antibody binding in a population of interest against a control population.

2.1 Paired data

We let N denote the number of subjects. With P we denote the number of unique peptide sequences among the measurement probes. For p = 1,…, P we let n_p denote the number of probe replicates for peptide p on each slide. The r-th probe measurement of peptide p from subject i at time t is y_iptr, for i = 1, … , N , p = 1, … , P , t = 0, 1, and r = 1, … , n_p. We model a probe response y_iptr as

$$y_{\mathit{ip}0r}={\beta }_{p0}+{\mu }_{i0}+{\alpha }_{\mathit{ip}0}+{\epsilon }_{\mathit{ip}0r}$$ (1)

$$y_{ip1r}=\{\begin{array}{cc}{\beta }_{p0}+{\mu }_{i1}+{\alpha }_{ip0}+{\epsilon }_{ip1r}\hfill & \mathrm{if}{\gamma }_{\mathit{ip}}=0\\ {\beta }_{p0}+{\mu }_{i1}+{\beta }_{p1}+{\alpha }_{\mathit{ip}1}+{\epsilon }_{\mathit{ip}1r}& \mathrm{if}{\gamma }_{\mathit{ip}}=1.\end{array}$$ (2)

A parameter ß_p0 represents the average baseline intensity of peptide p for a typical pre-treatment subject. The strictly positive effect ß_p1 captures the average intensity increase from treatment response. Subjects responding against peptide p generate new antibodies due to treatment, and thus have higher average post-treatment probe intensities. Random effects α_ip0 and α_ip1 represent a subject’s particular preexisting antibodies and antibody response to treatment.

Terms μ_it are slide level effects that represent aggregated influences of experimental batch effects (e.g. slide manufacture, laboratory environment, slide handling, and sample preparation) and subject effects (e.g. immune system response). Subject measurements are usually not replicated across slides, so that interactions between slide effects and peptide effects are confounded with subject-specific antibody reactions. Batch effects in microarray experiments have received wide acknowledgement (Leek et al., 2010; Nahtman et al., 2007; Chen et al., 2011). Because peptides are processed in parallel within the same plate, the additive structure of slide effects μ and peptide effects β assumes that peptides within a plate experience a similar effect due to the same batch perturbation. Examining replicated placebo subjects in RV144, we find that an additive slide effect structure (Web Appendix A) approximately holds and usefully explains variability in the data.

A latent binary indicator parameter γ_ip determines the location and covariance structure of probe responses. The parameters γ_ip have prior distribution Bernoulli(ω_p), with ω_p denoting the probability a subject responds against peptide p. When γ_ip = 0 or 1, subject i is called a non-responder or responder against peptide p, respectively. A non-responder for a peptide produces no new antibodies against that peptide, so secondary antibody effect α_ip0 is shared between pre and post-treatment responses. Sharing α_ip0 induces positive correlation between pre and post-treatment measurements among non-responders. When γ_ip equals one, the post-treatment intensity has a new random effect α_ip1. A responder produces new antibodies against that peptide, and α_ip1 models a new subject-specific deviation. The new term α_ip1 is independent of baseline effect α_ip0, diminishing pre and post-treatment correlation.

Outlying observations are common in microarray data, due to effects such as probe imperfections. Low levels of replication make outlier deletion dubious, so pepBayes uses t-distributed residual errors to accommodate extreme observations (Lange et al., 1989). We denote a p-dimensional multivariate t-distribution with location parameter a, positive definite covariance matrix Σ, and degrees of freedom ν > 2 as MVT(a, Σ, ν), having density function

$$\pi (\mathit{x};\mathit{a},\mathrm{\sum },\nu )=\frac{\mathrm{\Gamma }(\frac{\nu +p}{2}){\mid \mathrm{\sum }\mid }^{-.5}}{\mathrm{\Gamma }(\frac{\nu }{2}){\{\pi (\nu -2)\}}^{\frac{p}{2}}}{\{1+\frac{1}{\nu -2}{(\mathit{x}-\mathit{a})}^T{\mathrm{\sum }}^{-1}(\mathit{x}-\mathit{a})\}}^{-\frac{\nu +p}{2}}\mathrm{.}$$

Our parameterization standardizes the covariance to be Σ for all values of ν > 2. The vectorized residual errors ε_ip0, ε_ip1 have independent multivariate t-distributions ${\mathit{\epsilon }}_{\mathit{ip}0}\sim \mathrm{MVT}(\mathbf{0},{\upsilon }_{\mathit{\epsilon p}}^{-1}I,{\nu }_{\epsilon })$ and ${\mathit{\epsilon }}_{\mathit{ip}1}\sim \mathrm{MVT}(\mathbf{0},{\upsilon }_{\mathit{\epsilon p}}^{-1}I,{\nu }_{\epsilon })$. The degrees-of-freedom parameter ν_ε has a shifted Gamma prior distribution, ${\nu }_{\epsilon }\sim 2.0+\mathrm{Gamma}(1,\frac{1}{2})$.

2.1.1 Mixture indicator and random effect parameters for paired data

The joint prior distribution of (γ_ip, α_ip1) is a mixture of discrete and continuous distributions. First, π(γ_ip = 0, α_ip1 = 0) = 1 – ω_p. The parameter γ_ip = 1 with probability ω_p, and given γ_ip = 1 the responder random effect α_ip1 is t_να-distributed with location zero and scale parameter ${\upsilon }_{\mathit{\alpha p}1}^{-1}$. Secondary antibody binding effects α_ip0 are t_να-distributed as well, with location zero and a scale parameter ${\upsilon }_{\mathit{\alpha p}0}^{-1}$. A heavy tailed distribution on secondary and primary antibody binding effects accommodates strong responses occasionally observed in these data. The parameter ν_α also has a prior distribution shifted Gamma prior distribution ${\nu }_{\alpha }\sim 2.0+\mathrm{Gamma}(1,\frac{1}{2})$.

2.2 Unpaired data

A second method is developed to compare antibody profiles between a control population and a population of interest. Parameters and responses associated with the control population and population of interest are labeled with subscripts c, t respectively. For control subjects j = 1, …,N_c and subjects of interest i = 1, … ,N_t we model probe responses as

$$y_{\mathit{jpr},c}={\beta }_{p0}+{\mu }_{j,c}+{\alpha }_{\mathit{jp},c}+{\epsilon }_{\mathit{jpr},c}$$ (3)

$$y_{\mathit{ipr},t}={\beta }_{p0}+{\mu }_{i,t}+{\alpha }_{\mathit{ip},t}+{\gamma }_{\mathit{ip}}{\beta }_{p1}+{\epsilon }_{\mathit{ipr},t}.$$ (4)

In this setting, no direct contrast exists between samples for each subject. Instead, the control population helps estimate the average baseline binding effect β_p0 and precision parameters. As with paired data the residuals have multivariate t-distributions ${\mathit{\epsilon }}_{\mathit{jp},c}\sim \mathrm{MVT}(\mathbf{0},{\upsilon }_{\mathit{\epsilon p}}^{-1}\mathit{I},{\nu }_{\epsilon })$, ${\mathit{\epsilon }}_{\mathit{ip},t}\sim \mathrm{MVT}(\mathbf{0},{\upsilon }_{\mathit{\epsilon p}}^{-1}\mathit{I},{\nu }_{\epsilon })$. Again β_p1 is constrained to be strictly positive. The unpaired method detects whether a subject in the population of interest has a stronger antibody response against a given peptide than the control population.

A focus on stronger responses is based on antibody production in the humoral immune system. Antibodies are developed in B-cells as a response to antigen stimulation, leading to a specific antibody response to a given antigen (Thompson, 2015; Janeway et al., 2001). A suitable control population therefore depends on the population of interest. Generally, control subjects either have not encountered an antigen common to the population of interest (e.g. infectious diseases), or demonstrably have not developed antibodies known to define the population of interest (e.g. food allergies, autoimmune disorders). Framed as such, the unpaired method covers numerous biologically relevant cases. In the first case the control population will not have produced specific responses against the peptide library due to lack of antigen exposure. For example, the unpaired method is suitable for comparing antibody profiles of HIV infected subjects with a population of uninfected control subjects. An alternate example is the study of food allergy epitopes, where allergic subjects are compared with a non-allergic control population known to lack an antibody-induced inflammatory response. The unpaired pepBayes model would not be suitable to study populations of interest expected to have lower than average antibody responses.

2.2.1 Mixture indicator and random effect parameters for unpaired data

The parame-ter ω_p now denotes the proportion of subjects generating stronger antibody binding than the control population against peptide p. Subject-level antibody binding effects α_jp,c are t_vα-distributed with center zero and scale parameter ${\upsilon }_{\mathit{\alpha p}0}^{-1}$. The joint prior distribution of (γ_ip, α_ip,t) is a mixture of discrete and continuous distributions with π(γ_ip = 0) = 1 – ω_p. Given γ_ip, the random effect α_ip,t is t_vα-distributed with location zero, and scale parameter ${\upsilon }_{\mathit{\alpha p}0}^{-1}$ or ${\upsilon }_{\mathit{\alpha p}1}^{-1}$ when γ_ip equals zero or one, respectively.

2.3 Mixture proportion hierarchy

A hierarchical prior on the response probability ω_p allows peptides with similar sequences to share information about their response rates. In our application, the peptide library tiles seven amino acid sequences for human immunodeficiency virus (HIV) envelope protein glycoprotein-160 (gp160). The surface of an HIV virion is studded with gp160 molecules. Antibodies targeting gp160 have shown neutralization potential, and vaccines eliciting strong responses against gp160 could generate a protective response (Overbaugh and Morris, 2012).

HIV mutates rapidly, resulting in wide genetic diversity among viral variants. Variants of HIV are grouped into clades by genetic similarity, so that two strains within the same clade share more common sequence than two strains from different clades. The seven amino acid sequences in our peptide library are consensus sequences covering seven HIV clades, to measure antibody responses against a breadth of HIV strains. The seven sequences are aligned to the standard HIV sequence HXB2. The HXB2 sequence is a common reference sequence in HIV functional and structural studies. Each peptide is assigned a position value according to where the central amino acid aligns against the HXB2 sequence (Figure 1). We define u = pos(p), where pos is a function mapping a peptide’s index to its position value. For p such that pos(p) = u we let ω_p have a beta distribution with shape parameters (a_u, b_u). Parameters (a_u, b_u) have exponential prior distributions with fixed rates (λ_a, λ_b), respectively. Setting (λ_a, λ_b) to (10.0, 1.0) results in a prior favoring low response rates. In the event that a peptide library has no such grouping, (a_u, b_u) may be fixed. Fixed prior values such as (a_u, b_u) = (.125, 1.125) tend to favor low response rates ω_p.

2.4 Location and precision parameter hierarchy

Without constraints, the likelihood is not identified between β₀ and μ. To stabilize estimation slide effects μ are constrained to sum to zero. A degenerate normal prior on μ enforces this constraint. Further details regarding this prior may be found in Web Appendix B. We let ${\beta }_{p0}\stackrel{i.i.d}{\sim }\mathrm{Normal}(m_0,{\nu }_{{\beta }_0}^{-1})$, while m₀ ~ Normal $({\overline{m}}_0,{\nu }_{m_0}^{-1})$ and $v_{{\beta }_0}\sim \mathrm{Gamma}(\frac{1}{2},\frac{1}{2})$. The average treatment response β_p1 has a normal distribution, truncated to be strictly positive, ${\beta }_{p1}\stackrel{i.i.d}{\sim }\mathrm{TN}(m_1,v_{{\beta }_1}^{-1},0,\infty )$. A strictly positive effect reflects the belief that treatment response will only increase antibody binding. Hyperparameters for β_p1 have distributions m₁ ~ Normal $({\overline{m}}_1,v_{m_1}^{-1})$ and $v_{{\beta }_1}\sim \mathrm{Gamma}(\frac{1}{2},\frac{1}{2})$.

Residual precision υ_εp has a gamma prior distribution with shape S_ε and rate λ_ε, while υ_αp0 and υ_αp1 have gamma priors with shape S_α and λ_α. The hyperparameters S_α and S_ε have exponential distributions with rate r_s while λ_α and λ_ε have exponential distributions with rate r_λ . For estimation we fix r_s and r_λ to a large number such as 100, which sets a prior favoring very low precision.

2.5 Model fitting and response classification

The quantity of interest for pepBayes is the posterior probability of binding (PPB), which is the posterior probability that γ_ip equals one. We implement two algorithms for fitting the pepBayes models: an Expectation Conditional Maximization algorithm (Meng and Rubin, 1993) whose E-step is conducted with Monte Carlo methods (Wei and Tanner, 1990), and a Markov Chain Monte Carlo (MCMC) algorithm to sample the posterior distribution. Moves within the MCMC algorithm are a typical combination of variable-at-a-time Metropolis-Hastings updates and Gibbs samples. Further details regarding the ECM algorithm are available in Web Appendix C. The two methods generate slightly different PPB estimates, which we denote as

$${\widehat{\tau }}_{\mathit{ip}}=\pi (y_{\mathit{ip}}\mid \mathit{y})\mathrm{and}{\widehat{\tau }}_{\mathit{ip}}=\pi (y_{\mathit{ip}}\mid \mathit{y},\theta =\widehat{\theta }),$$

where θ̂ is a posterior maximum. After calculating response probabilities, we classify subjects’ response statuses against each peptide. The high throughput, exploratory nature of the peptide microarray assay lends itself to a classification method that controls the false discovery rate (FDR) q. Following the adaptive thresholding technique in Newton et al. (2004), we sort τ̂_ip in descending order (τ₍₁₎, τ₍₂₎, … , τ_(NP)) and find an index

$$K(q,\mathit{y})=\max \{K:\frac{1}{K}\sum _{k=1}^K{\widehat{\tau }}_{(k)}\ge (1-q)\}.$$

With a detection threshold c(q, y) = τ̂ (K(q,y)), we classify subject i as a responder against pep-tide p when τ̂_ip exceeds c(q, y). The two fitting methods complement each other’s strengths. The EM algorithm is much faster than MCMC for a large number of slides, but access to the full posterior distribution allows for a variety of posterior summaries. Our results also indicate that marginal PPBs τ̂_ip have slightly better classification properties.

3. Results

We run pepBayes on peptide microarray experiments conducted with plasma samples drawn from two HIV vaccine efficacy trials. Each was a placebo-controlled, randomized, double-blind trial. The first study, referred to as RV144, was a community-based trial testing a regimen of four priming injections of a recombinant canarypox vector vaccine containing env, gag, and pol genes (ALVAC-HIV) in addition to two booster injections of a recombinant glycoprotein 120 (gp120) subunit vaccine (AIDSVAX B/E) in Thailand (Rerks-Ngarm et al., 2009). The second study, referred to as Vax003, tested a vaccine regimen comprising seven injections of AIDSVAX B/E among intravenous drug users in Bangkok, Thailand (Pitisuttithum et al., 2006). Peptide microarray assays were conducted on 100 subjects sampled from RV144, 80 of whom received experimental vaccine and 20 of whom received placebo. The Vax003 data set contains 90 vaccinated subjects. Assays were conducted on samples drawn from each subject before and after treatment.

3.1 Assays

Peptides were chosen to cover consensus amino acid sequences of HIV-1 glycoprotein 160 (gp160) in group M and subtypes A, B, C, D, CRF 01AE, and CRF AG. Peptides were 15 amino acids in length, overlapping by 12, and a total of 1423 unique peptides covered the seven sequences. PepStar peptide microarrays were produced by JPT Peptide Technologies GmbH, and each peptide was printed in triplicate to verify slide integrity and data quality. Briefly, slides were incubated with diluted sample plasma and then incubated with a dilution of anti-Ig Cy5 secondary antibody, with washes between steps. Slides were scanned using an Axon Genepix 4300 Scanner. Further details regarding materials, slide manufacture, and assay protocol may be found in Gottardo et al. (2013).

3.2 HIV data set model output

The structure of the RV144 data set allows us study the performance of pepBayes. The surface protein gp160 is composed of two sub-proteins gp120 and gp41. Because the RV144 trial vaccine contained only a gp120 insert, no response is expected against peptides drawn from gp41. Placebo subjects also should not generate new specific antibody responses. With combined insert and placebo information, we can evaluate the false positive rate of our classification algorithm. Vax003 also did not contain a gp41 insert and we may similarly evaluate model output. We apply pepBayes to these data and evaluate the model output from MCMC posterior samples.

Figure 2 plots the proportion of placebo or treatment RV144 subjects classified as responders against each peptide’s position in HXB2 (FDR = .05). Among treatment subjects, we observe four regions of strong antibody response in variable loops V2 and V3, the C terminus of gp120, and a region prior to V1. Notably, very low levels of binding are observed among gp41 peptides and also among placebo subjects, indicating that pepBayes enjoys high specificity. Figure 3 shows results from applying the unpaired pepBayes method to the RV144 data set, instead using pre-treatment samples as a control population. The same four regions of strong binding are identified, but have slightly lower estimated response rates. Overall, the unpaired method also has lower levels of background calls across gp120 and gp41, but has a slightly elevated false positive rate among placebo subjects in regions of strong vaccine response.

Figure 2.

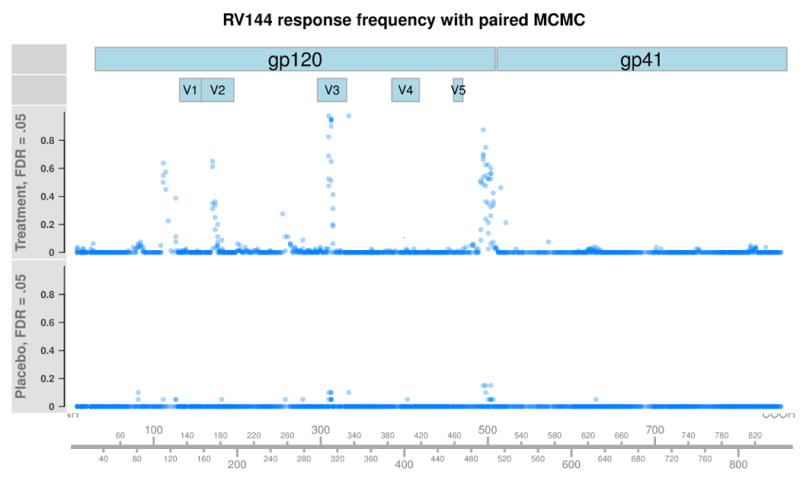
Each point represents the proportion of placebo or vaccinated RV144 subjects classified as responders against a peptide, using pepBayes paired MCMC fit at .05 FDR. The x-axis represents a peptide’s position when aligned against the standard HIV reference sequence HXB2. Very few placebo subjects are classified as responders, and response frequencies in gp41 are very low throughout, indicating high specificity.

Figure 3.

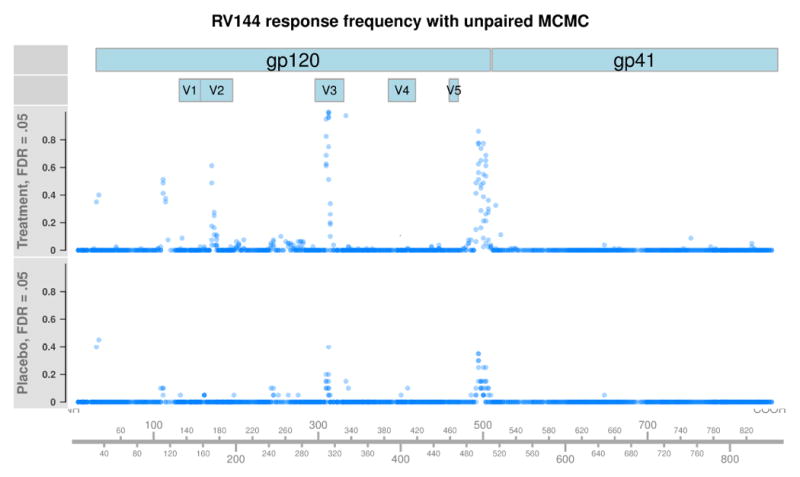
Each point represents the proportion of placebo or vaccinated RV144 subjects classified as responders against a peptide, using pepBayes unpaired MCMC fit at .05 FDR. The x-axis represents a peptide’s position when aligned against the standard HIV reference sequence HXB2. Very few placebo subjects are classified as responders, and response frequencies in gp41 are very low throughout, indicating high specificity. Placebo responses in areas of vaccine response are slightly elevated when compared with the paired algorithm, and treatment response rates in regions of high response are slightly lower than with the paired algorithm.

Figure 4 plots the proportion of Vax003 subjects classified as responders against each peptide’s position in HXB2. Vax003 shares the same four regions of strong response as seen in RV144, but responses against the V2 loop, the region prior to V1, and the C-terminus are more abundant. Very low levels of binding are called in gp41, indicating high specificity. We also observe elevated levels of binding throughout gp120. The nature of this binding is uncertain, but could be related to non-specific binding from antibodies generated in response to vaccine treatment.

Figure 4.

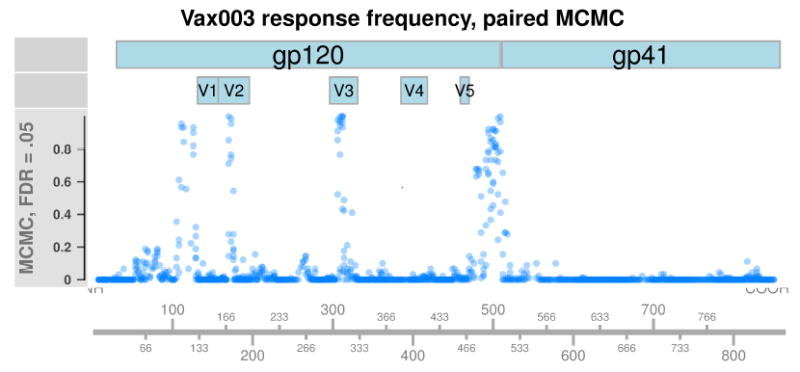
Each point represents the proportion of Vax003 subjects classified as responders against a peptide, using pepBayes paired MCMC fit at .05 FDR. The x-axis represents a peptide’s position when aligned against the standard HIV reference sequence HXB2. Response frequencies in gp41 are very low throughout, indicating good specificity. Higher response rates are estimated in the same regions as RV144 subjects.

3.3 Simulation results

We evaluate the characteristics of our classification method with a simulation study. Data were simulated from the paired model taking parameter values inspired by peptide microarray data. Ten percent of peptides had a non-zero probability of subject response. For such a peptide, subject responses were Bernoulli distributed with a probability drawn from a Beta (1.5, 1.5) distribution. The number of subjects was fixed to 30, for 500 peptides. Slide effects were drawn from a Gaussian distribution with σ 2 and then mean centered. Peptide baseline effects β_p0 had a Normal(4, 1) distribution while response effects β_p1 were drawn from a positively truncated Normal $(2,\frac{1}{4})$ distribution. Random effects α_ip0 and α_ip1 were drawn from a t-distribution with degrees of freedom ν = 4 and scale parameters drawn from an inverseGamma(4, scale = 4) distribution. Residuals ε_ip0 and ε_ip1 had multivariate-t distributions with degrees of freedom ν = 4 and scale matrix equal to the identity matrix times an inverseGamma(40, scale = 4) random variate. At such parameter values, responder and non-responder intensity distributions may share a moderate level of overlap. We fit the pepBayes model to 500 simulated data sets using MCMC and ECM methods.

For each replication, we examine the false discovery proportion (FDP) and the recall of the model output at various FDR values q, where

$$\mathrm{FDP}(q,\mathit{y})=\frac{\#\{{\widehat{\tau }}_{\mathit{ip}}>c(q,\mathit{y}):{\gamma }_{\mathit{ip}}=0\}}{\#\{{\widehat{\tau }}_{\mathit{ip}}>c(q,\mathit{y})\}},\mathrm{recall}(q,\mathit{y})=\frac{\#\{{\widehat{\tau }}_{\mathit{ip}}>c(q,\mathit{y}):{\gamma }_{\mathit{ip}}=1\}}{{\sum }_{i,p}{\gamma }_{\mathit{ip}}}.$$

Averaging across simulated data sets, the expectation of the FDP estimates the actual FDR at a nominal q-level, while the expectation of recall summarizes sensitivity. The variability of the FDP and recall also provide important information about the quality of inference from experiment to experiment. Table 1 summarizes the expectation and variability of FDP and recall for the EM and MCMC fitting algorithms. The actual FDR of both fitting methods is close to the nominal level, although the EM method appears slightly conservative across q values. The distribution of FDP has very low variability between simulations, indicating that the proportion of false positives tends to remain close to the desired FDR q value. Sensitivity is dependent on simulation parameters, but the procedure enjoys similar levels of sensitivity between EM and MCMC fitting algorithms.

Table 1.

The expected value of the FDP and recall quantities for EM and MCMC fitting algorithms at various FDR q values, from 250 replications of simulated data. Values in parentheses indicate the estimated standard deviation of FDP and recall. EM is slightly conservative at FDR values, while the MCMC algorithm is well calibrated. Both algorithms have low variability in the FDP, indicating that FDR control is tight. At modest FDR, both methods enjoy high sensitivity.

	EM		MCMC
q	E[FDP]	E[recall]	E[FDP]	E[recall]
.01	.006(sd .003)	.869 (sd .019)	.013 (sd .004)	.891 (sd .018)
.05	.036 (sd .007)	.923 (sd .014)	.052 (sd .008)	.935 (sd .014)
.1	.078 (sd .009)	.948 (sd .012)	.100 (sd .009)	.955 (sd .011)
.2	.172 (sd .010)	.973 (sd .008)	.197 (sd .010)	.976 (sd .008)

3.4 Receiver operating characteristic comparison

The receiver operating characteristic (ROC) compares classifier performance in terms of false and true positive rates as its threshold varies. We apply an ROC analysis with the RV144 and Vax003 data to compare our method with pepStat, which had previously been compared to other methods (Gottardo et al., 2013). Calculating an ROC requires knowledge of the true binding status of each subject-peptide combination. For these data we cannot know exactly which subjects were responders, but prior knowledge of common HIV-Env epitopes and basic summary statistics provide insight about regions where true binding effects likely occurred. Placebo subjects should not generate any new binding response, and the vaccines used in RV144 and Vax003 did not contain a gp41 insert. Any peptide corresponding to a placebo subject or a gp41 peptide is therefore classified as a negative peptide with very high confidence. A peptide from gp120 is designated as a positive peptide for vaccine subjects if the mean difference in intensity before and after treatment is significantly greater than zero. For Vax003 and RV144 data, we define z_ip = ȳ_ip1 – ȳ_ip0 and calculate for 1423 peptides t-test statistics

$$t_p=\sqrt{N}\frac{\frac{1}{N}{\sum }_{i=1}^N{z}_{\mathit{ip}}}{{\widehat{\sigma }}_p}$$

where σ̂_p is the sample standard deviation of z_ip across all subjects i = 1, …, N. Peptides with t_p statistics exceeding the $(1-\frac{.01}{1423})$ quantile of a t_N–1 distribution are considered positive peptides for vaccine subjects. This quantile is based on the Bonferroni correction to control family-wise error rate at level α = .01 for testing the null hypotheses that E{z_ip} = μ_p = 0 versus the alternatives μ_p > 0 across all p. Web Appendix D shows that the ROC results are insensitive to several choices of α. Positive peptides were selected separately for Vax003 and RV144. Using this procedure, peptides corresponding to known immunogenic regions in the V2/V3 loop are selected, as well as peptides just prior to the V1 loop and the gp120 C-terminus peptides. As expected, no peptides from gp41 are selected via this criterion. Figure 5 suggests that our model has increased sensitivity relative to pepStat for unpaired and paired methods, as the ROC for pepBayes dominates that of pepStat along the range of the curves.

Figure 5.

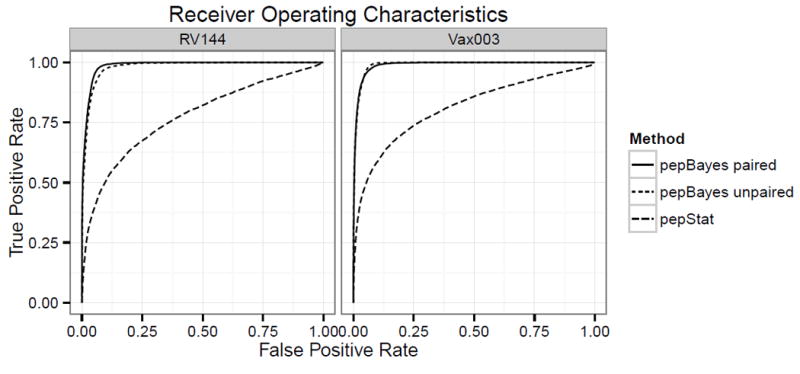
The receiver operating characteristic (ROC) of a classifier shows a method’s tradeoff between false positive rate and true positive rate as a decision threshold varies. A large area under the curve indicates good discrimination. Curves are displayed for pepBayes and pepStat methods, based on a set of control peptides and response peptides from RV144 and Vax003. Regardless of whether data are run as paired or treated as unpaired, pepBayes more clearly separates likely positives from negatives.

4. Discussion

PepBayes is a powerful, robust method for the analysis of peptide microarray data when subject-specific inference is required. Modeling probe replicates increases the information available in the model and, along with a robust error model, eliminates the dubious process of outlier deletion. Observations are implicitly up or down-weighted based on the relative precision of probe replicates. The t-distribution was chosen for its tractability, small number of tuning parameters, and heavy tails that accommodate extreme observations. Other robust error models such as contaminated normal might also be feasible, but results in Little (1988) suggest that the choice among robust error distributions is not crucial when estimating location parameters. Binding effects associated with secondary antibody are explicitly modeled, and the concurrent estimation of technical and biological effects incorporates the uncertainty of normalization into our estimation of responses. Prior to estimation, the normexp method corrects probes for background intensity and adds a fixed offset parameter to all values prior to log₂ transformation. Background correction relieves us from cumbersome modeling assumptions associated with foreground and background fluorescence channels. We have chosen an offset of one, but have found our results to be insensitive to the offset value (data not shown).

The pepBayes method identifies regions of high peptide response, while maintaining low estimated response rates in regions expected to generate no response. The RV144 and Vax003 trials elicited moderate or strong responses against the same four major regions of the gp120 peptide. Both trials’ vaccine regimens shared an identical AIDSVAX B/E recombinant gp120 insert, so this is not unexpected. The higher estimated response rates observed in Vax003 is plausible, as Vax003’s vaccine regimen provided more exposure to the gp120 insert. An ROC analysis leveraging experimental design suggests that pepBayes enjoys high specificity and sensitivity, and simulation results with a correctly specified model show that our FDR-based response classification is well calibrated.

The ROC analysis suffers from the limitation that the exact truth of peptide response is not known. Peptides within gp41 should experience no binding effects, and designating all such peptides as negative responses provides a large, reliable pool for estimating false positive rates. However, all vaccinated subjects for a positive peptide are designated as responders, which is unrealistic because of immune system heterogeneity. As such we expect most misclassification of true binding status to be from subjects designated as responders when they truly did not respond. For a given point on the ROC, we expect the true positive rate to be underestimated. Meanwhile, the ROC false positive rate should remain close to its true value because of the large pool of reliable true negative peptides from gp41. Another limitation is that positive peptides are selected by overall response strength. We have high confidence that our selected peptides correspond to regions with high response rates, but we possibly ignore other gp120 peptide where responses are more subtle. Subtle response are precisely where we aim to achieve higher power, but our ROC analysis cannot measure such improvements. Nonetheless, we see that pepBayes clearly separates placebo responses and gp41 peptides from high response peptides among vaccinated subjects.

Notably, pepBayes does not induce a higher correlation between random effects α_ip0 for peptides with neighboring positions. With tiled arrays, overlapping peptides sequences are drawn from a protein’s amino acid sequence. Overlapping peptides tend to experience similar levels of baseline antibody response, and can share similar response levels if they share a common antibody epitope. Sharing information between random effects α_ip0 based on sequence overlap could yield further power, but we find that our conditionally independent prior on random effects α_ip0 produces satisfactory results and is easily estimated.

Given an extensive peptide microarray assay protocol and a physicochemically diverse peptide library, it is unlikely that an entire peptide library interacts identically with the same batch factor level. In the case of true non-response, a relatively strong batch effect interaction could result in false positive detections for a peptide. Similarly, a set of responders could be missed in a similar fashion, giving a peptide the appearance of no effect between treatments. Careful experimental design is required to avoid complete confounding of batch effects with treatments of interest. In a paired design, we recommend processing pre-treatment and post-treatment slides from the same subject in tandem to minimize differences due to technical effects. In an unpaired experiment, slides from both populations should be as balanced as possible across batches. If severe batch effects are a concern, additional preprocessing such as surrogate variable analysis (Leek and Storey, 2007) or ComBat (Li and Rabinovic, 2007) can model and remove batch effects prior to pepBayes modeling. A possible extension to pepBayes could incorporate such effects.

Two fitting algorithms are available for the pepBayes model. An ECM fit is well suited for a quick understanding of the results, while MCMC posterior samples give marginalized estimates of posterior binding probabilities that account for uncertainty in parameter estimation. MCMC samples of the full posterior distribution also admit a broad variety of posterior summary statistics. An R package for fitting the pepBayes model is available on Github (http://www.github.com/RGLab/pepBayes).