Gao et al. propose several approaches to incorporate gene annotation into genomic prediction and evaluate these new methods on populations.....
Keywords: genomic selection, gene annotation, categorical model, haplotype, GenPred, Shared Data Resources
Abstract
Today, genomic prediction (GP) is an established technology in plant and animal breeding programs. Current standard methods are purely based on statistical considerations but do not make use of the abundant biological knowledge, which is easily available from public databases. Major questions that have to be answered before biological prior information can be used routinely in GP approaches are which types of information can be used, and at which points they can be incorporated into prediction methods. In this study, we propose a novel strategy to incorporate gene annotation into GP of complex phenotypes by defining haploblocks according to gene positions. Haplotype effects are then modeled as categorical or as numerical allele dosage variables. The underlying concept of this approach is to build the statistical model on variables representing the biologically functional units. We evaluate the new methods with data from a heterogeneous stock mouse population, the Drosophila Genetic Reference Panel (DGRP), and a rice breeding population from the Rice Diversity Panel. Our results show that using gene annotation to define haploblocks often leads to a comparable, but for some traits to a higher, predictive ability compared to SNP-based models or to haplotype models that do not use gene annotation information. Modeling gene interaction effects can further improve predictive ability. We also illustrate that the additional use of markers that have not been mapped to any gene in a second separate relatedness matrix does in many cases not lead to a relevant additional increase in predictive ability when the first matrix is based on haploblocks defined with gene annotation data, suggesting that intergenic markers only provide redundant information on the considered data sets. Therefore, gene annotation information seems to be appropriate to perceive the importance of DNA segments. Finally, we discuss the effects of gene annotation quality, marker density, and linkage disequilibrium on the performance of the new methods. To our knowledge, this is the first work that incorporates epistatic interaction or gene annotation into haplotype-based prediction approaches.
IN recent years, the superiority of genomic prediction (GP) (Meuwissen et al. 2001) over pedigree-based best linear unbiased prediction (Henderson 1984) and marker-assisted selection has been demonstrated (Crossa et al. 2010; Albrecht et al. 2011). GP has been applied to many different organisms, including humans (de los Campos et al. 2013), model species such as Drosophila melanogaster (Ober et al. 2012), plants (Jannink et al. 2010; Hayes et al. 2013), domestic animals (Hayes and Goddard 2010), and aquaculture species (Sonesson and Meuwissen 2009). Accompanied by the fast development of genotyping and sequencing technologies in the last decades, a huge number of different methods for GP have been established (Gianola 2013; de Vlaming and Groenen 2015; Misztal and Legarra 2017). Among these methods, the current standard method is ridge regression best linear unbiased prediction (), which uses single nucleotide polymorphisms (SNPs) as predictor variables. It has been shown that this marker effect ridge regression model can be translated into a relationship-matrix-based approach (GBLUP) (Habier et al. 2007), and this correspondence between marker effect and relationship matrix models allows us to use the classical methodology that has been developed for the pedigree BLUP for GP.
Most of the established GP methods are based on purely statistical considerations and disregard existing biological knowledge. A remarkable difference exists between the often mechanistically simplistic structure of statistical models describing the phenotype and the complexity of the biological processes underlying the phenotypic expression. Only recently, researchers started to work on bridging the gap between mathematical models and underlying biological mechanisms. Encouragingly, several recent studies have shown that integrating biological information in proper ways improves predictive ability under certain circumstances. For instance, it has been shown that GP accuracies can be improved by incorporating results from genome-wide association studies, either from databases (Zhang et al. 2014) or from the data set on hand (de los Campos et al. 2013; Gao et al. 2015; Ramstein et al. 2016). Other types of biological information, which are easily available from public databases, include gene annotation, information on biochemical interactions, and gene expression networks. In some of the latest publications, different types of biological knowledge were incorporated by partitioning markers into classes based on their functional annotation (Morota et al. 2014; Do et al. 2015; Abdollahi-Arpanahi et al. 2016; MacLeod et al. 2016) or gene ontology categories (Edwards et al. 2016). After the partitioning, one approach is to assign different prior distributions to the different classes of SNPs and then to use all markers for prediction (MacLeod et al. 2016). Another way is performing GP with each class separately and then selecting classes that give the best predictive ability for further predictions (Morota et al. 2014; Do et al. 2015; Abdollahi-Arpanahi et al. 2016; Edwards et al. 2016). It has been demonstrated that these approaches for incorporating biological knowledge improve the predictive ability in some cases.
At the same time, it is suggested to alter the structure of the standard models using alternative predictor variables, for instance haplotypes or interactions terms (Su et al. 2012; Jiang and Reif 2015; Martini et al. 2016). Whereas standard models are based on individual SNP markers, several new approaches are built on haplotypes (Calus et al. 2008; Cuyabano et al. 2014, 2015; Meuwissen et al. 2014; Yang 2015), that is, on tuples of SNPs. The basic underlying assumption for models based on individual markers is that, at a sufficiently high density, at least one marker is in linkage disequilibrium (LD) with each quantitative trait locus (QTL). However, if more than two alleles of a gene exist in a population, multi-allelic haplotypes are expected to capture the state of a QTL better than single markers (Calus et al. 2008; Meuwissen et al. 2014). For this reason, haplotypes instead of single markers were used as predictor variables in several recent publications (Cuyabano et al. 2014, 2015; Meuwissen et al. 2014; Yang 2015). In these studies, for each haploblock, pseudomarkers were created by counting the number of copies of the respective allele carried by a certain individual (Meuwissen et al. 2014). Thus, the pseudomarker matrix had the entries {0,1,2} and the haplotype-based relatedness matrix was constructed as the dot products of the rows of this pseudomarker matrix. The relatedness matrix was further scaled by the number of haploblocks.
Here we propose several new approaches of using gene annotation to define haplotypes in both numerical dosage and categorical effect models. To bridge the gap between the mathematical models and biology, the first step is to describe the biological system using a mathematical model on its biologically functioning units. As a first attempt, we consider the protein-coding genes (and thus the corresponding proteins) including their regulatory regions as biologically acting units, hoping to capture some characteristics of the biology of complex phenotypes. In addition, we extend the haplotype-based categorical effect models to epistasis models and show how all these approaches can be translated into relatedness matrices. We then test the prediction performance of our approaches with several data sets with different genetic background and discuss the similarities and relatedness of the different approaches.
Materials and Methods
To incorporate gene annotation into GP, we first mapped SNPs to genes according to their relative positions and defined haploblocks using the phased SNP data (detailed description below). Gene-based haplotypes were coded using both numerical and categorical approaches. Numeric coding refers to a dosage model in which the assumption of intralocus additive allele effects is made (Calus et al. 2008; Cuyabano et al. 2014, 2015; Meuwissen et al. 2014; Yang 2015). With A denoting the reference allele in a diploid population, intralocus additivity means, for instance, for the SNP-marker-based that the marker state AA () at locus i has twice the effect of AB (). The categorical coding does not assume this intralocus additivity, but models the effect of a haplotype allele being present twice, independent of the effect when being present once. For instance, the effect of configuration AA in Table 1 is assumed to be independent from AB. Thus, the categorical model can capture dominance (Martini et al. 2017). We then constructed relatedness matrices for both types of models. The following sections give a detailed description of these steps.
Table 1. Categorical and numerical codings of a haploblock with four alleles.
| Allele dosage | ||||||
|---|---|---|---|---|---|---|
| Allele 1 | Allele 2 | Haplotype categories | A | B | C | D |
| A | A | AA | 2 | 0 | 0 | 0 |
| A | B | AB | 1 | 1 | 0 | 0 |
| A | C | AC | 1 | 0 | 1 | 0 |
| A | D | AD | 1 | 0 | 0 | 1 |
| B | B | BB | 0 | 2 | 0 | 0 |
| B | C | BC | 0 | 1 | 1 | 0 |
| B | D | BD | 0 | 1 | 0 | 1 |
| C | C | CC | 0 | 0 | 2 | 0 |
| C | D | CD | 0 | 0 | 1 | 1 |
| D | D | DD | 0 | 0 | 0 | 2 |
A, B, C, and D are four alleles of the same haploblock.
SNP mapping and gene-based haploblock derivation
The latest version of the gene annotation of each considered species was downloaded from Ensemble (http://www.ensembl.org) using the biomaRt package (Durinck et al. 2005, 2009) of the statistical platform R (R Development Core Team 2016) (Table 3). Only genes indicated as “protein_coding” by the “gene_biotype” attribute were considered. Gene boundaries were extended by 5 kb in both upstream and downstream flanking regions to include possible regulatory elements. Then SNPs were mapped to these genic regions based on their corresponding genomic positions. After the SNP mapping step, SNP sets were formed for genes with at least one mapped marker. For genes with only one mapped SNP, the corresponding haploblock existed of only this marker. For genes with more than one mapped SNP, phased alleles of the corresponding SNPs were combined into haplotypes with the approach described by Meuwissen et al. (2014). Briefly, haplotypes were built via the following steps:
Table 3. Data sets description.
| Data sets | No. of individuals | No. of markers | Reference genome | No. of mapped SNPs | No. of represented genes | No. of haploblocks |
|---|---|---|---|---|---|---|
| Mice | 1940 | 9,266 | Mus musculus (GRCm38.p4) | 5,036 | 4,100 | 4,119 |
| DGRP | 205 | 2,863,909 | Drosophila melanogaster (assembly Release 6) | 2,467,249 | 12,586 | 725,520 |
| Rice | 315 | 58,227 | Oryza sativa Japonica Group (Build 4.0) | 44,831 | 22,509 | 25,453 |
Initialization: for each gene, start with the first SNP
Step 1: include SNP into the haploblock.
Step 2: determine the number of alleles of the haploblock defined by these markers across the whole population.
Step 3: repeat step 1 and step 2 if the number of alleles remains below a previously chosen threshold restricting the number of alleles of a haploblock [we used 10 as proposed by Meuwissen et al. (2014)]. Otherwise, if the number of alleles exceeds this threshold, the lastly added SNP is excluded from the current haploblock and is used as the starting position of the next haploblock. Return the alleles of the current haploblock and go to the initialization step with the lastly added SNP to define the next haploblock. Repeat this procedure until all SNPs of the currently considered gene are processed.
This approach produces one or more haploblocks with at least two haplotype alleles per block for each gene. The effects of haplotypes were then coded in two different ways:
Numerical (allele dosage) coding: For each haploblock, artificial SNPs are created for each haplotype allele, and these “SNPs” are coded as the number of copies ({0,1,2}) present in the respective individual. The sum over all alleles of a certain autosomal haploblock must be two for each individual when diploid species are considered.
Categorical coding: Haplotype variants are coded by the haplotype allele configurations (genotypes). Each allele combination has its own independent effect in the categorical coding strategy.
Table 1 contrasts the different codings of a haploblock with four alleles A, B, C, and D.
The genomic prediction models
We compared the predictive ability of the proposed approaches to the standard (VanRaden 2008). The genomic prediction model can be expressed as:
| (1) |
where y is the vector of precorrected phenotypes; is an vector with entries equal to one; μ is the overall mean; is a vector of genetic values and K is the relatedness matrix of the respective models (Table 2); is the genetic variance; is a vector of residuals and is the model residual variance.
Table 2. Relatedness matrices in corresponding models (see text for definition of the variables).
| Models | Relatedness matrices (K) | Description |
|---|---|---|
| Genomic best linear unbiased prediction | ||
| Extended (epistatic) | ||
| Haplotype-based | ||
| Haplotype-based given gene annotation | ||
| Categorical marker effect model | ||
| Categorical epistasis model | ||
| Haplotype-based | ||
| Haplotype-based | ||
| Haplotype-based given gene annotation | ||
| Haplotype-based given gene annotation |
means Hadamard product.
For the relatedness matrix was calculated according to VanRaden (2008). Briefly, let denote the minor allele frequency (MAF) of marker k, M denote the {0,1,2} coded genotypes, and Z denote the MAF adjusted marker matrix with entries (), (), and () for genotypes AA, AB, and BB, respectively. The relatedness matrix is calculated as The “extended ” () (Su et al. 2012; Jiang and Reif 2015; Martini et al. 2016), whose epistasis relatedness matrix is was also calculated for comparison. Here, # denotes the Hadamard product. In we only modeled the interaction effect and ignored the additive SNP effects, since additive effects can be expressed as the sum of their interactions. Moreover, we saw in previous studies that the predictive ability of the model including both matrices—the additive and the pairwise interaction matrix—will usually tend to the predictive ability of the model with only the matrix with higher predictive ability. Thus, a small potential gain faces the disadvantage of potentially causing numerical problems in the estimation of the variance components, due to the very similar structure of the matrices G and EG.
For the SNP-based categorical model ( Martini et al. 2017), the relatedness matrix S has the entries where is scored 1 if individual i and j share the same genotype at marker k, otherwise is scored 0, and m is the number of SNPs. For data sets of completely inbred lines without heterozygous markers, the model has been shown to be equivalent to (Martini et al. 2017). The first order epistasis among markers can be modeled by extending to the (categorical epistasis) model, where the genotype combinations of each pair of loci are treated as categorical variables and the relatedness of two individuals is measured by counting the number of pairs of markers in the same state. The relatedness matrix of can be expressed as (Martini et al. 2017).
Analogously, we also used these two types of models for gene-annotation-based variables (see above). In the numerical allele dosage coding, pseudomarkers are created and the haplotype-based, intralocus additive genetic relatedness matrix is constructed as the dot product of the haplotype allele matrix (). The intralocus additive relatedness matrix is expressed as where is a matrix of pseudomarkers with values 0, 1, and 2 representing the number of copies of each haplotype allele being present and where Q is the number of haploblocks. We call this model haplotype-based genomic best linear unbiased prediction given gene annotation (). For comparison, the haplotype-based model without gene annotation () was also calculated. Here the haplotype-based relatedness matrix is (Meuwissen et al. 2014). Haplotypes are built here for each chromosome separately (starting with the first marker and following their physical order).
In the categorical coding, we count the number of haploblocks that are in the same state between pairs of individuals, and the relatedness is measured as the ratio between the number of haploblocks with identical state and the total number of haploblocks. In an equation form, the relatedness matrix can be expressed as with entries representing the relatedness between individuals i and j. Moreover, is scored 1 if individual i and j have the same state on haploblock q, otherwise is scored 0. We call this model haplotype-based categorical model given gene annotation (). Similar to the SNP version of the categorical model, we can build a relatedness matrix for modeling the first order epistasis among haploblocks in the form We call this model the haplotype-based categorical epistasis model given gene annotation (). For comparison, a categorical haplotype model based on the haploblocks suggested by Meuwissen et al. (2014) (without the use of gene annotation) was constructed as well. We denote the categorical version of this haplotype model as A corresponding epistatic version that models the first order epistasis among haploblocks was developed and denoted as
In the and models, only SNPs that have been mapped to genes are included. Therefore, we evaluated a broadened model:
| (2) |
including unmapped markers as well. The model terms here are the same as those defined in model 1, except for the additional term , which models the effects captured by unmapped SNPs. Here, and denote the relatedness matrix calculated with unmapped SNPs and the corresponding variance component. We introduced the notation and for the broadened versions, respectively. In where is the matrix containing the MAF-adjusted genotypes of unmapped SNPs and where is the number of unmapped SNPs. In
In both models 1 and 2, variance components were estimated using average information restricted maximum likelihood (AI-REML) (Jensen et al. 1997) via the regress (Clifford and McCullagh 2014) package for the R statistical platform (R Development Core Team 2016). Given the dispersion matrices and the variance components, predictions of genetic values were obtained by solving the mixed model equations (Henderson 1975, 1984).
Data
For all data sets used for model evaluation, SNPs with a call rate of <95% or MAF smaller than 0.01 and individuals with a call rate of <95% were excluded. Missing genotypes were imputed and phased simultaneously using Beagle (version 4.1) (Browning and Browning 2008), which was embedded in the synbreed R package (version 0.11; Wimmer et al. 2012), using the default parameter settings. Important characteristics of the data sets after quality control are described in Table 3.
Mouse data:
The heterogeneous stock (HS) mice data were generated by the Wellcome Trust Centre for Human Genetics (Valdar et al. 2006a). Genotypes and phenotype records were available at http://mtweb.cs.ucl.ac.uk/mus/www/mouse/HS/index.shtml. In total, 9266 SNPs and 1940 individuals remained after quality control steps. For computational simplicity, we used the precorrected phenotypes provided by Valdar et al. (2006b). Physical positions of SNPs were mapped to the latest version of the mouse genome (Mus musculus, assembly GRCm38.p4) with the biomaRt (Durinck et al. 2005, 2009) R package. Only SNPs mapped to the GRCm38.p4 were used for further analysis. Gene boundaries were downloaded from Ensemble with the biomaRt (Durinck et al. 2005, 2009) R package. Sixteen phenotypic traits related to growth, obesity, and immunology were used in this study to compare the performance of our models.
D. melanogaster data:
The Drosophila Genetic Reference Panel (DGRP) is a population consisting of 205 inbred lines derived from the Raleigh, USA population (Mackay et al. 2012). Genetic variants called from whole genome sequencing data were downloaded from the DGRP2 website (http://dgrp2.gnets.ncsu.edu/). In total, 2,863,909 SNPs remained after quality control steps. The gene annotation information of the latest version of the D. melanogaster genome (Drosophila melanogaster, assembly Release 6) was downloaded from Ensemble via the biomaRt (Durinck et al. 2005, 2009) R package (Table 3). We used two adaptive traits (Mackay et al. 2012), one food intake trait (Garlapow et al. 2015), two alcohol sensitivity traits (Morozova et al. 2015), and twelve olfactory behavior traits (Arya et al. 2015) to evaluate the models. The line means (males and females independently) of all traits were adjusted for the effects of a Wolbachia infection and five major inversions [In(2L)t, In(2R)NS, In(3R)K, In(3R)P, and In(3R)Mo] using a mixed model is a vector of line means; X is a design matrix assigning the fixed effects b to the lines. The random line effects were modeled ), where G is the marker-derived genomic relationship matrix according to VanRaden (2008); is a vector of model residuals. Variance components were estimated using the regress (Clifford and McCullagh 2014) R package. The adjusted phenotypes , without any weight, were used for model evaluation.
Rice data:
The genotypes and phenotypes of the rice breeding population were downloaded from the Rice Diversity Panel (https://ricediversity.org; Begum et al. 2015; Spindel et al. 2015). In total, 315 elite rice breeding lines from the International Rice Research Institute irrigated rice breeding program were included in this data set. Several traits such as plant height (PH), flowering time (FLW), and grain yield (YLD) were recorded in both the dry (DS) and the wet season (WS) for the years 2009–2012. The means of the phenotypes across years for DS or WS for each line were used as response variable (provided by Spindel et al. 2015). In total, 58,227 SNPs passed the quality control steps and remained for further analysis. The gene annotation information of the latest version of the rice genome (Oryza sativa Japonica Group, Build 4.0) was downloaded from Ensemble via the biomaRt (Durinck et al. 2005, 2009) R package.
Predictive ability evaluation
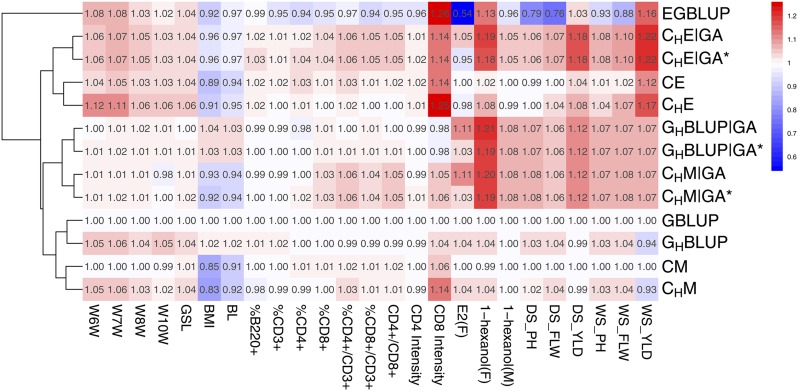
We used 20 replicates of a fivefold random cross-validation to assess the predictive ability of the different approaches. The variance components were estimated within the training set. Phenotypes of the validation set were treated as unknown and genetic values were predicted based on models 1 and 2, respectively. The predictive ability was calculated as Pearson’s correlation between the predicted genetic values and the (precorrected) phenotypes of the validation population. Predictive abilities of other models were compared to (allele dosage models) or (categorical models) via a two-sided t-test. Moreover, for Figure 1, the relative predictive abilities were calculated as the ratio between the mean predictive ability of the alternative models and that of The models were clustered based on these relative predictive abilities using the pheatmap R package, where the hierarchical clustering is performed according to the euclidean distance of the vectors of relative predictive abilities for all traits.
Figure 1.
Comparison of the predictive ability of different models. Rows are different models and columns are traits from three data sets. For each trait, relative predictive ability is calculated by setting as reference (mean accuracies divided by that of ). For the DGRP, only traits where gene-annotation-based models give extra predictive accuracy are presented. Trait “E2” of male lines in the DGRP data were also removed due to the extremely low predictive ability. W6W–W10W: body weight at 6 to 8 and 10 weeks; GSL: growth slope between 6 and 10 weeks of age; BMI, body mass index; BL, body length; %B220+, percentage of B220 cells; %CD3+, percentage of CD3 cells; %CD4+, percentage of CD4 cells; %CD8+, percentage of CD8 cells; %CD4+/CD3+, percentage of CD4 and CD3 cells; %CD8+/CD3+, percentage of CD8 and CD3 cells; CD4+/CD8+, ratio of CD4 to CD8 cells; CD4Intensity, CD4inCD3XGeoMean; CD8Intensity, CD8inCD3YGeoMean. F, female; M, male. DS, dry season; WS, wet season; PH, plant height; FLW, flower time; YLD, grain yield.
Data availability
The mouse data used in this study is available at http://mtweb.cs.ucl.ac.uk/mus/www/mouse/HS/index.shtml. The D. melanogaster data is available at http://dgrp2.gnets.ncsu.edu/. The rice breeding population data is available at https://ricediversity.org.
Results
Predictive abilities on the considered data sets
In this work, we considered marker-based and (gene annotation guided) haplotype-based models. We built the models on numerical allele dosage or on categorical variables, and incorporated epistasis. In the following, we will compare the predictive ability of the different models on three data sets. The results are summarized in Figure 1, Table 4, and Table 5. Additional results for the Drosophila data set, which are not included in these tables, can be found in Supplemental Material, Table S1.
Table 4. Predictive ability in allele dosage models (mean ± SE).
| Data sets | Traits | * | ||||
|---|---|---|---|---|---|---|
| Mouse | W6W | 0.494 ± 0.001 | 0.534 ± 0.002 | 0.521 ± 0.001 | 0.496 ± 0.002 | 0.498 ± 0.001 |
| W7W | 0.495 ± 0.002 | 0.537 ± 0.002 | 0.527 ± 0.002 | 0.502 ± 0.002 | 0.503 ± 0.002 | |
| W8W | 0.510 ± 0.001 | 0.523 ± 0.001 | 0.531 ± 0.001 | 0.518 ± 0.001 | 0.517 ± 0.001 | |
| W10W | 0.481 ± 0.001 | 0.491 ± 0.002 | 0.507 ± 0.001 | 0.487 ± 0.001 | 0.486 ± 0.001 | |
| GSL | 0.389 ± 0.001 | 0.405 ± 0.002 | 0.405 ± 0.001 | 0.388 ± 0.001 | 0.392 ± 0.001 | |
| BMI | 0.224 ± 0.002 | 0.206 ± 0.002 | 0.228 ± 0.002 | 0.234 ± 0.002 | 0.231 ± 0.002 | |
| BL | 0.264 ± 0.002 | 0.255 ± 0.002 | 0.268 ± 0.002 | 0.272 ± 0.002 | 0.273 ± 0.002 | |
| %B220+ | 0.546 ± 0.002 | 0.541 ± 0.001 | 0.549 ± 0.002 | 0.543 ± 0.002 | 0.547 ± 0.002 | |
| %CD3+ | 0.522 ± 0.002 | 0.495 ± 0.002 | 0.531 ± 0.002 | 0.517 ± 0.002 | 0.523 ± 0.002 | |
| %CD4+ | 0.481 ± 0.002 | 0.454 ± 0.001 | 0.481 ± 0.001 | 0.473 ± 0.002 | 0.482 ± 0.002 | |
| %CD8+ | 0.702 ± 0.001 | 0.668 ± 0.001 | 0.701 ± 0.001 | 0.706 ± 0.001 | 0.707 ± 0.001 | |
| %CD4+/CD3+ | 0.638 ± 0.001 | 0.617 ± 0.001 | 0.633 ± 0.001 | 0.641 ± 0.001 | 0.642 ± 0.001 | |
| %CD8+/CD3+ | 0.676 ± 0.001 | 0.636 ± 0.002 | 0.670 ± 0.002 | 0.680 ± 0.001 | 0.680 ± 0.001 | |
| CD4+/CD8+ | 0.671 ± 0.001 | 0.636 ± 0.001 | 0.665 ± 0.001 | 0.674 ± 0.001 | 0.675 ± 0.001 | |
| CD4Intensity | 0.573 ± 0.002 | 0.550 ± 0.002 | 0.569 ± 0.002 | 0.570 ± 0.002 | 0.574 ± 0.002 | |
| CD8Intensity | 0.388 ± 0.002 | 0.489 ± 0.002 | 0.404 ± 0.002 | 0.379 ± 0.002 | 0.382 ± 0.002 | |
| DGRP | E2 (F) | 0.202 ± 0.010 | 0.110 ± 0.012 | 0.210 ± 0.010 | 0.225 ± 0.010 | 0.208 ± 0.010 |
| E2 (M) | 0.026 ± 0.010 | 0.038 ± 0.008 | 0.039 ± 0.010 | 0.045 ± 0.009 | 0.041 ± 0.011 | |
| 1-hexanol (F) | 0.185 ± 0.010 | 0.209 ± 0.010 | 0.193 ± 0.009 | 0.223 ± 0.009 | 0.220 ± 0.010 | |
| 1-hexanol (M) | 0.235 ± 0.009 | 0.225 ± 0.009 | 0.236 ± 0.009 | 0.254 ± 0.008 | 0.254 ± 0.008 | |
| Rice | DS_PH | 0.486 ± 0.007 | 0.383 ± 0.006 | 0.499 ± 0.007 | 0.522 ± 0.007 | 0.522 ± 0.007 |
| DS_FLW | 0.534 ± 0.005 | 0.405 ± 0.006 | 0.556 ± 0.005 | 0.568 ± 0.005 | 0.568 ± 0.005 | |
| DS_YLD | 0.289 ± 0.006 | 0.298 ± 0.008 | 0.285 ± 0.006 | 0.323 ± 0.005 | 0.323 ± 0.005 | |
| WS_PH | 0.482 ± 0.006 | 0.448 ± 0.007 | 0.496 ± 0.005 | 0.516 ± 0.005 | 0.516 ± 0.005 | |
| WS_FLW | 0.467 ± 0.007 | 0.412 ± 0.008 | 0.487 ± 0.006 | 0.502 ± 0.006 | 0.501 ± 0.006 | |
| WS_YLD | 0.258 ± 0.007 | 0.299 ± 0.008 | 0.242 ± 0.007 | 0.276 ± 0.008 | 0.276 ± 0.008 | |
| Mean accuracy | 0.431 | 0.418 | 0.440 | 0.444 | 0.444 |
For the DGRP data set, two traits for which the gene-annotation-based models show improved predictive ability are presented. W6W–W10W, body weight at 6–8 and 10 weeks; GSL, growth slope between 6 and 10 weeks of age; BMI, body mass index; BL, body length; %B220+, percentage of B220 cells; %CD3+, percentage of CD3 cells; %CD4+, percentage of CD4 cells; %CD8+, percentage of CD8 cells; %CD4+/CD3+, percentage of CD4 and CD3 cells; %CD8+/CD3+, percentage of CD8 and CD3 cells; CD4+/CD8+, ratio of CD4 to CD8 cells; CD4Intensity, CD4inCD3XGeoMean; CD8Intensity, CD8inCD3YGeoMean. F, female; M, male. DS, dry season; WS, wet season; PH, plant height; FLW, flower time; YLD, grain yield. For each trait (row), the values in boldface indicate the best prediction among all models and values in italic are those significantly higher than (P < 0.05, pairwise t-test).
Indicates models including gene-based haplotypes and unmapped SNPs simultaneously.
Table 5. Predictive ability in categorical models (mean ± SE).
| Data sets | Traits | a | * | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mouse | W6W | 0.493 ± 0.002 | 0.516 ± 0.002 | 0.519 ± 0.002 | 0.551 ± 0.002 | 0.498 ± 0.002 | 0.524 ± 0.002 | 0.501 ± 0.002 | 0.525 ± 0.002 |
| W7W | 0.497 ± 0.002 | 0.519 ± 0.002 | 0.527 ± 0.002 | 0.550 ± 0.002 | 0.502 ± 0.002 | 0.528 ± 0.002 | 0.504 ± 0.002 | 0.528 ± 0.002 | |
| W8W | 0.512 ± 0.002 | 0.527 ± 0.002 | 0.525 ± 0.001 | 0.543 ± 0.001 | 0.515 ± 0.002 | 0.533 ± 0.002 | 0.517 ± 0.002 | 0.533 ± 0.002 | |
| W10W | 0.477 ± 0.002 | 0.494 ± 0.002 | 0.491 ± 0.002 | 0.511 ± 0.002 | 0.473 ± 0.002 | 0.494 ± 0.002 | 0.479 ± 0.002 | 0.497 ± 0.002 | |
| GSL | 0.394 ± 0.001 | 0.404 ± 0.001 | 0.403 ± 0.001 | 0.414 ± 0.001 | 0.394 ± 0.001 | 0.404 ± 0.001 | 0.396 ± 0.001 | 0.406 ± 0.001 | |
| BMI | 0.190 ± 0.003 | 0.199 ± 0.003 | 0.186 ± 0.003 | 0.203 ± 0.003 | 0.208 ± 0.002 | 0.216 ± 0.002 | 0.207 ± 0.002 | 0.215 ± 0.002 | |
| BL | 0.239 ± 0.002 | 0.248 ± 0.002 | 0.244 ± 0.002 | 0.252 ± 0.002 | 0.249 ± 0.002 | 0.257 ± 0.002 | 0.248 ± 0.002 | 0.255 ± 0.002 | |
| %B220+ | 0.544 ± 0.002 | 0.559 ± 0.002 | 0.534 ± 0.002 | 0.556 ± 0.001 | 0.541 ± 0.002 | 0.558 ± 0.002 | 0.545 ± 0.002 | 0.560 ± 0.002 | |
| %CD3+ | 0.523 ± 0.003 | 0.530 ± 0.003 | 0.518 ± 0.003 | 0.523 ± 0.003 | 0.518 ± 0.003 | 0.527 ± 0.003 | 0.523 ± 0.003 | 0.529 ± 0.003 | |
| %CD4+ | 0.486 ± 0.001 | 0.494 ± 0.001 | 0.478 ± 0.001 | 0.488 ± 0.001 | 0.482 ± 0.001 | 0.492 ± 0.001 | 0.491 ± 0.001 | 0.498 ± 0.001 | |
| %CD8+ | 0.707 ± 0.001 | 0.712 ± 0.001 | 0.700 ± 0.001 | 0.699 ± 0.001 | 0.722 ± 0.001 | 0.728 ± 0.001 | 0.721 ± 0.001 | 0.728 ± 0.001 | |
| %CD4+/CD3+ | 0.651 ± 0.001 | 0.655 ± 0.001 | 0.654 ± 0.001 | 0.650 ± 0.001 | 0.674 ± 0.001 | 0.678 ± 0.001 | 0.674 ± 0.001 | 0.678 ± 0.001 | |
| %CD8+/CD3+ | 0.684 ± 0.001 | 0.686 ± 0.001 | 0.680 ± 0.001 | 0.674 ± 0.001 | 0.706 ± 0.001 | 0.709 ± 0.001 | 0.706 ± 0.001 | 0.709 ± 0.001 | |
| CD4+/CD8+ | 0.682 ± 0.001 | 0.685 ± 0.001 | 0.678 ± 0.001 | 0.674 ± 0.001 | 0.703 ± 0.001 | 0.707 ± 0.001 | 0.703 ± 0.001 | 0.707 ± 0.001 | |
| CD4Intensity | 0.574 ± 0.002 | 0.582 ± 0.002 | 0.569 ± 0.002 | 0.580 ± 0.002 | 0.569 ± 0.002 | 0.579 ± 0.002 | 0.578 ± 0.002 | 0.586 ± 0.002 | |
| CD8Intensity | 0.413 ± 0.002 | 0.443 ± 0.002 | 0.442 ± 0.002 | 0.485 ± 0.002 | 0.409 ± 0.003 | 0.444 ± 0.002 | 0.412 ± 0.002 | 0.443 ± 0.002 | |
| DGRP | E2 (F) | 0.201 ± 0.010 | 0.201 ± 0.010 | 0.211 ± 0.010 | 0.198 ± 0.011 | 0.225 ± 0.010 | 0.212 ± 0.011 | 0.208 ± 0.010 | 0.192 ± 0.011 |
| E2 (M) | 0.026 ± 0.010 | 0.028 ± 0.010 | 0.040 ± 0.010 | 0.038 ± 0.009 | 0.045 ± 0.009 | 0.043 ± 0.009 | 0.039 ± 0.011 | 0.039 ± 0.012 | |
| 1-hexanol (F) | 0.184 ± 0.010 | 0.188 ± 0.010 | 0.193 ± 0.009 | 0.199 ± 0.009 | 0.222 ± 0.009 | 0.221 ± 0.009 | 0.220 ± 0.010 | 0.219 ± 0.010 | |
| 1-hexanol (M) | 0.234 ± 0.009 | 0.235 ± 0.009 | 0.235 ± 0.009 | 0.233 ± 0.009 | 0.254 ± 0.008 | 0.247 ± 0.008 | 0.254 ± 0.008 | 0.246 ± 0.009 | |
| Rice | DS_PH | 0.486 ± 0.007 | 0.483 ± 0.007 | 0.497 ± 0.007 | 0.484 ± 0.006 | 0.523 ± 0.007 | 0.517 ± 0.007 | 0.523 ± 0.007 | 0.517 ± 0.007 |
| DS_FLW | 0.534 ± 0.005 | 0.536 ± 0.005 | 0.556 ± 0.005 | 0.556 ± 0.005 | 0.567 ± 0.005 | 0.570 ± 0.005 | 0.567 ± 0.005 | 0.569 ± 0.005 | |
| DS_YLD | 0.289 ± 0.006 | 0.301 ± 0.006 | 0.285 ± 0.006 | 0.313 ± 0.006 | 0.325 ± 0.005 | 0.340 ± 0.005 | 0.324 ± 0.005 | 0.340 ± 0.005 | |
| WS_PH | 0.482 ± 0.006 | 0.487 ± 0.006 | 0.496 ± 0.005 | 0.500 ± 0.005 | 0.518 ± 0.005 | 0.521 ± 0.005 | 0.518 ± 0.005 | 0.521 ± 0.005 | |
| WS_FLW | 0.467 ± 0.007 | 0.476 ± 0.007 | 0.487 ± 0.006 | 0.500 ± 0.006 | 0.504 ± 0.006 | 0.513 ± 0.006 | 0.503 ± 0.006 | 0.513 ± 0.006 | |
| WS_YLD | 0.258 ± 0.007 | 0.288 ± 0.007 | 0.241 ± 0.007 | 0.302 ± 0.007 | 0.275 ± 0.008 | 0.314 ± 0.008 | 0.275 ± 0.008 | 0.314 ± 0.008 | |
| Mean accuracy | 0.432 | 0.441 | 0.438 | 0.449 | 0.447 | 0.457 | 0.448 | 0.456 |
For the DGRP data set, two traits for which the gene-annotation-based models show improved predictive ability are presented. W6W–W10W, body weight at 6–8 and 10 weeks; GSL, growth slope between 6 and 10 weeks of age; BMI, body mass index; BL, body length; %B220+, percentage of B220 cells; %CD3+, percentage of CD3 cells; %CD4+, percentage of CD4 cells; %CD8+, percentage of CD8 cells; %CD4+/CD3+, percentage of CD4 and CD3 cells; %CD8+/CD3+, percentage of CD8 and CD3 cells; CD4+/CD8+, ratio of CD4 to CD8 cells; CD4Intensity, CD4inCD3XGeoMean; CD8Intensity, CD8inCD3YGeoMean. F, female; M, male. DS, dry season; WS, wet season; PH, plant height; FLW, flower time; YLD, grain yield. For each trait (row), the values in boldface indicate the best prediction among all models and values in italic are those significantly higher than (P < 0.05, pairwise t-test).
Indicates models including gene-based haplotypes and unmapped SNPs simultaneously.
Mouse data:
Let us consider the predictive abilities of the different models for the growth-related traits body weight at 6–10 weeks (W6W, W7W, W8W, W10W) and the growth slope from 6 to 10 weeks (GSL). Here, we observe consistent patterns for certain changes of numerical dosage and categorical models (Figure 1). The step from to improves predictive ability by which can similarly be observed from to The improvement from marker-based models to the gene-annotation-guided haplotype-based models is less than from marker-based models to the ordinary haplotype models without the use of gene annotation. Moreover, the incorporation of epistasis improves the predictive ability consistently from to from to from to and from to Overall, shows the highest predictive ability for these traits, and the differences between models and those incorporating the unmapped markers in a second matrix () are small.
For the obesity-related traits, body mass index (BMI) and body length (BL), all categorical models and are outperformed by (Table 4 and Table 5). For the numerical dosage models, we see that the predictive ability of is increased by the step to which again is improved by using gene annotation in Analogously, the predictive ability of is similar to that of which is improved by incorporating gene annotation information in The same stepwise improvement is true for and Comparing the epistasis models to the additive effect models, we observe an increase in predictive ability for all categorical models. The predictive ability of is higher than that of which can analogously be observed comparing to and to The use of a second relatedness matrix constructed with unmapped markers does not lead to a relevant increase in predictive ability (Figure 1, Table 4, and Table 5). Overall, due to the relative low performance of the categorical models, and perform best for BMI and BL, respectively.
For the immunology traits except CD8Intensity, we observe a relatively homogeneous predictive ability across all models (Table 4 and Table 5). The performance of is constantly low on these traits. For the traits CD8+, CD4+/CD3+, CD8+/CD3+, and CD4+/CD8+, we see that the categorical gene-annotation-based haplotype models and perform notably better than the other models. The epistasis variant improves the predictive ability slightly, compared to
Drosophila data:
In the DGRP population, we analyzed 17 phenotypic traits (34 trait–sex combinations) related to adaptation, food intake, alcohol sensitivity, and olfactory behavior (Table S1). Overall, gene-annotation-based models improve or maintain the predictive ability in 13 out of 34 scenarios compared to SNP-based models (Table S1). performs best in 15 scenarios. Predictive ability of is omitted since it is similar to (identical in 21 scenarios) due to the extremely rare occurrence of heterozygotes (0.39%) in the DGRP population. Table 4 and Table 5 show the two traits for which gene-annotation-based models show a considerable improvement. In one of the alcohol sensitivity traits, which was measured as alcohol knockdown time (Mean Elution Time, MET) in an “inebriometer” after a second exposure (E2) following a 2-hr recovery period (Morozova et al. 2015), improves the predictive ability in females from 0.202 to 0.225 compared to However, the predictive ability for E2 in males is close to zero. In the olfactory behavior trait “1-hexanol,” predictive ability is improved by from 0.185 (0.235) in to 0.223 (0.254) for females (males). For both traits E2 and 1-hexanol, for which and have the same performance, neither modeling epistasis nor including unmapped SNPs in a second relatedness matrix leads to an additional improvement.
Rice data:
With the rice data, we observe a systematic improvement using models built on gene-annotation-based haplotypes. Whereas the performance of is on average very similar to that of across traits, systematically outperforms other numerical dosage models on five out of six traits (Table 4). The categorical models and (Table 5) perform very similarly to their numerical allele dosage counterparts, which meets our expectations on the similarity of and on data with a low heterozygosity rate. For the categorical epistasis models, we observe a systematic improvement of predictive ability from to and to For the incorporation of epistasis, we see a consistent tendency across traits. Thus, tends to perform better than better than and better than However, the transition from the additive to the epistasis model does not improve predictive ability of numerical allele dosage models on the traits plant height and flowering time (from to ). Overall, for plant height, flowering time, and grain yield, predictive abilities were improved by by 6.4% (8.1%), 6.7% (9.9%), and 17.6% (21.7%), respectively, in dry season (wet season) compared to An inclusion of unmapped SNPs in a second relatedness matrix did not improve predictive ability for any trait/model combination for the rice data.
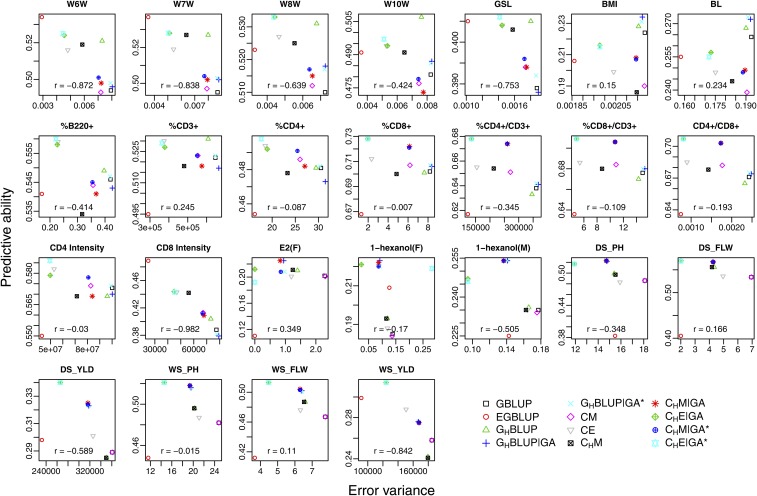
Predictive ability vs. unexplained variance
To highlight the difference between explained variance and predictive ability, we plotted the unexplained error variance for each model and trait against the predictive ability (Figure 2). Here, we excluded the model, because its relatedness matrix has very small off-diagonal elements for the mouse data set. This leads to a situation in which the covariance matrix is more similar to the identity matrix than usual. Consequently, a certain part of the variance can be assigned to either the error or to the relatedness matrix, which causes extreme estimates for the variance components for some traits on the mouse data. Considering Figure 2, we see that there is a negative correlation between the error variance and predictive ability for most of the traits, which indicates that a model explaining the variance better also gives a higher predictive ability. However, this correlation is not and has a high variation across traits. For some traits, it is even positive for the considered models. Moreover, we see also that has the tendency to be perceived as an “outlier” in several traits, which has already been seen with the results on predictive ability alone.
Figure 2.
Error variance vs. predictive ability. Description of traits and models: see text and Figure 1.
Discussion
The concept of gene-annotation-based haplotype models
The prediction methods used in this work are all built on the classical standard assumption of the genetic values (and the error terms) being multivariate Gaussian distributed. Different concepts of defining matrices reflecting genomic relatedness were applied and the well-known mixed model equations (Henderson 1984) were used for the prediction of genetic values. Implicitly, each protocol of constructing a relatedness matrix is based on prior assumptions on how the multivariate Gaussian distributed genetic values are generated. For instance, for the model these assumptions are that each marker has an intralocus additive dosage effect, and that all these marker effects are independent realizations from the same 1-dimensional Gaussian distribution. Clearly, in a situation in which the number of markers (predictor variables) is much higher than the number of individuals, and without penalization of effect sizes, any fit of the data that is generated by one of the presented models can also be obtained by an intralocus additive marker model. However, the regularization implemented by the shrinkage of effect sizes in the ridge regression approach pushes the estimated effects towards the framework defined by the prior assumptions. Thus, prior assumptions reflecting underlying biological processes may improve the estimation of the effects of the predictor variables. In this work, these prior assumptions were set by building the model on predictor variables defined by protein-coding genes. Not every marker has an effect, but rather the biological unit “gene.” More specific knowledge, for instance on the biology of the respective trait, has not been used. With this conceptually simple modification, the epistatic model had a higher predictive ability than for all traits of the rice and the mouse data, except for BMI and BL (Figure 1, Table 4, and Table 5). For the Drosophila data set, remained the best model on average (Table S1).
Predictive abilities and model clusters
The predictive abilities of the different models are shown relative to the predictive ability of in Figure 1. This relative performance gives four main clusters (based on the predictive abilities for the data presented in Figure 1; an extended pattern based on the data including all traits of the Drosophila data set can be found in Figure S1).
The first cluster consists of only, whose relative predictive ability varies substantially across traits. The reason for being distinct from all other models can be seen in the centering by allele frequencies, which had been applied to the additive matrix, before the Hadamard square was calculated. Since the epistatic effects are modeled as products of the centered matrix entries, this version is built on allele-frequency-dependent parametric models for the interaction effects, which means that each pair of marker has its own interaction model, which may lead to the strong variation of the performance across traits (Martini et al. 2017).
The second cluster consists of the four categorical epistasis models, of which shows the highest average predictive ability across traits. is more similar to than to which is in line with the conceptual structure of the models. In consecutive SNPs are combined into haploblocks but no external information is used to define them. uses the gene annotation information additionally. In the rice data in particular, these conceptual construction steps also translate into predictive ability, where is outperformed by whose predictive ability is further improved by for all traits.
The third cluster contains and both of which are built upon gene annotation–based haplotypes. Even though the underlying variables are more complex than single markers, their behavior relative to each other is very similar to the comparison of the marker-based numerical dosage model and the categorical marker model (Figure 1).
The fourth cluster consists of and Except for the traits BMI, BL, and CD8Intensity, the performance of is very similar to that of Indeed, both methods are also theoretically identical in the case that each predictor variable has only two possible states, for instance due to complete homozygosity (Martini et al. 2017). However, their performances on the mouse data set illustrate that the mean predictive ability of and can also be very similar for data in which the two homozygous and the heterozygous states are well represented (56.06, 34.40, and 9.53% of 0, 1, and 2, respectively). The two models perform very similarly for the majority of the considered traits, and their difference is only visible for BMI, BL, and CD8Intensity. The fact that is more similar to its haplotype analog than to the categorical marker model is most probably a result of the difference in predictive ability for these traits. Indeed, if the additional traits of the Drosophila data set are included, and are closest (Figure S1), which may be a result of the high frequency of homozygous markers in the DGRP data set (84.10, 0.39, and 15.51% of 0, 1, and 2, respectively) and of the two models consequently being almost identical for all additional traits that have not been included in Figure 1.
Overall, the clusters based on predictive abilities are in line with the conceptual construction of the models. Our results show that accounting for gene locations when defining haploblocks can improve the predictive ability, using intralocus additive or categorical models. Across the traits of Figure 1, the categorical epistasis model shows the highest predictive ability on average. For the rice data, has the highest predictive ability for five of six traits. The trait plant height in dry season is predicted best by Adding a second relatedness matrix defined by SNPs that have not been mapped to genes (indicated by an *) does not systematically improve the predictive ability for most of the considered traits, indicating that unmapped SNPs do not contain sufficient additional information.
Factors affecting the performance of the gene-annotation-based haplotype models
As previously argued, the approaches are based on the concept of defining biologically functional units as predictor variables and by this constructing a statistical framework that reflects the underlying biological processes. In addition to general factors affecting the performance of GP, such as the training set size, the number of markers, the genetic distance between training and test set, and the genetic architecture of the trait of interest (Shengqiang et al. 2009; Daetwyler et al. 2010), there are other important factors influencing the performance of gene-annotation-based prediction methods.
Evidently, a reference genome and the annotation information must be available for the target species. The quality of the annotation information will have an important impact on the number of predictor variables, on the set and the number of markers that are mapped to genes, and on how the markers are clustered. Generally, with a decreasing number of markers, the average predictive ability will decrease (Ober et al. 2012). However, in our results the addition of a second relatedness matrix based on unmapped markers did not overall relevantly improve predictive ability. Thus, the marker reduction does not seem to be a critical point for the data sets used in this work.
Addressing the percentage of genes represented by haploblocks, in the mouse data set only 18.4% (4100 out of 22,225) of all genes were represented by SNPs (Table 3). For the rice data set, for which the models improved the predictive ability strongly, 63.1% (22,509 out of 35,679) of the genes were modeled by at least one haploblock, whereas for the Drosophila data, 90.4% (12,586 out of 13,918) of the genes were included in the model. Even though the latter had the highest percentage of represented genes, the use of gene annotation did not lead to a systematic improvement, but outperformed the other models for the majority of the traits (Table S1). Besides other factors, this may in part be a result of the small population size and of the way that the phenotypes were corrected. The correction already included the G matrix and may have slightly adapted the remaining variance to this matrix. Nevertheless, we used this approach of correction since a correction for fixed effects was necessary and this type of correction has already been used previously (Edwards et al. 2016).
Concerning this genotype–phenotype mapping, the results on the mouse data, where all categorical models are outperformed by for the traits BMI and BL, illustrate again that a crucial point is the trait-specific architecture. The fact that the model, which has an advantage when dominance structures are present (Martini et al. 2017), is significantly outperformed by can be seen as an indicator for the absence of statistical dominance. However, the observation of a reduced predictive ability of categorical models, which incorporate dominance, should be interpreted with caution since such global quantities may not be directly linked to a biological genetic architecture of the trait (Huang and Mackay 2016).
Another important characteristic may be the average number of markers included in a haploblock, which is not only influenced by the number of markers mapped to a gene, but also by the LD pattern of the data. It is clear that in a data set for which each haploblock consists of only one marker, a haplotype model is identical to the corresponding marker model. For the mouse data with mapped SNPs and haploblocks (Table 3), the majority of the haploblocks consist of not more than two markers (on average 1.22 markers per haploblock). This explains partially why the increase in predictive ability with gene-annotation-based haplotypes is not on the same scale as for the rice data (1.76 markers per haploblock). However, our results also show that an increasing average number of markers per haploblock does not necessarily make a model more different from a marker-based model. This becomes clear by considering the fact that all haplotype models without the use of gene annotation have a higher average number of markers per haploblock than the models, but are still clustered closer to their respective marker model than the models. The average number of markers per haplotype was 7.28, 7.32, and 8.08 for the mouse, the DGRP, and rice data for the models without gene annotation, which was reduced to 1.22, 3.4, and 1.76, respectively, for the models. For data sets with a rapid LD decay, adding markers to a haplotype block will rapidly increase the number of haplotype alleles. With the “maximum number of alleles” method, which we used for the construction of haplotypes, a lower LD leads to fewer markers per haploblock, which may make the haplotype-based models more similar to the corresponding SNP-based models. The DGRP population exhibits a rapid LD decay (Mackay et al. 2012), which is also reflected by the fact that the haploblocks in models without gene annotation on average have a comparable number of markers for the three data sets, even though the marker density of the DGRP data is much higher. For the DGRP data, the average number of markers per haploblock is the highest of the three data sets (3.4) for the models, which is a consequence of the high number of markers mapped to genes. This illustrates again that the interplay of multiple factors makes pure and simple statements on the causes of differences in the predictive ability difficult.
Conclusions
In this study, we proposed different ways to incorporate gene annotation information into different haplotype-based genomic prediction approaches, including categorical and epistasis models. We used gene annotation information to point at the DNA segments that are more likely to play an important role in the biology of the trait and to define the model on the biologically functional unit “gene.” We validated the new methods with several data sets representing different data structures (with respect to marker density, extent of LD, and diversity) and a wide range of traits. Our results show that gene annotation can be beneficial in the construction of haplotype-based models if some prerequirements, such as the availability of a reference genome and sufficiently accurate gene annotation information, are fulfilled. The suggested strategy allows us to measure the pairwise individual similarity on the gene level and provides a novel option for incorporating gene annotation into GP.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300198/-/DC1.
Acknowledgments
N.G. thanks China Scholarship Council (CSC) for the financial support of his study in Germany. J.W.R. Martini thanks KWS SAAT SE for financial support. We thank the colleagues who have generated the data used in the present study for making them openly accessible. This work is partly founded by the earmarked fund for China Agriculture Research System (CARS-35), National Natural Science Foundation of China (31772556, 31371258), Basic Work of Science and Technology Project (2014FY120800), Guangdong Sailing Program (2014YT02H042), and Guangdong Natural Science Foundation (2014A030313453).
Author contributions: N.G., J.W.R.M., and H.S. conceived the study. N.G. and J.W.R.M. performed the analysis and wrote the manuscript. Z.Z., X.Y., H.Z., H.S., and J.L. contributed to the manuscript. All authors have read and approved the final manuscript. The authors declare that they have no competing interests.
Footnotes
Communicating editor: E. Stone
Literature Cited
- Abdollahi-Arpanahi R., Morota G., Valente B. D., Kranis A., Rosa G. J., et al. , 2016. Differential contribution of genomic regions to marked genetic variation and prediction of quantitative traits in broiler chickens. Genet. Sel. Evol. 48: 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albrecht T., Wimmer V., Auinger H.-J., Erbe M., Knaak C., et al. , 2011. Genome-based prediction of testcross values in maize. Theor. Appl. Genet. 123: 339–350. [DOI] [PubMed] [Google Scholar]
- Arya G. H., Magwire M. M., Huang W., Serrano-Negron Y. L., Mackay T. F. C., et al. , 2015. The genetic basis for variation in olfactory behavior in Drosophila melanogaster. Chem. Senses 40: 233–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begum H., Spindel J. E., Lalusin A., Borromeo T., Gregorio G., et al. , 2015. Genome-wide association mapping for yield and other agronomic traits in an elite breeding population of tropical rice (Oryza sativa). PLoS One 10: e0119873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning B. L., Browning S. R., 2008. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am. J. Hum. Genet. 84: 210–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calus M. P. L., Meuwissen T. H. E., De Roos A. P. W., Veerkamp R. F., 2008. Accuracy of genomic selection using different methods to define haplotypes. Genetics 178: 553–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clifford D., McCullagh P., 2014. The regress package R package version 1.3–14.
- Crossa J., Campos G. l., Pérez P., Gianola D., Burgueño J., et al. , 2010. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 186: 713–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuyabano B. C., Su G., Lund M. S., 2014. Genomic prediction of genetic merit using LD-based haplotypes in the Nordic Holstein population. BMC Genomics 15: 1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuyabano B. C., Su G., Lund M. S., 2015. Selection of haplotype variables from a high-density marker map for genomic prediction. Genet. Sel. Evol. 47: 61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daetwyler H. D., Pong-Wong R., Villanueva B., Woolliams J. A., 2010. The impact of genetic architecture on genome-wide evaluation methods. Genetics 185: 1021–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G., Vazquez A. I., Fernando R., Klimentidis Y. C., Sorensen D., 2013. Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet. 9: e1003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vlaming R., Groenen P. J. F., 2015. The current and future use of ridge regression for prediction in quantitative genetics. BioMed Res. Int. 2015: 143712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do D. N., Janss L. L. G., Jensen J., Kadarmideen H. N., 2015. SNP annotation-based whole genomic prediction and selection: an application to feed efficiency and its component traits in pigs. J. Anim. Sci. 93: 2056–2063. [DOI] [PubMed] [Google Scholar]
- Durinck S., Moreau Y., Kasprzyk A., Davis S., De Moor B., et al. , 2005. BioMart and bioconductor: a powerful link between biological databases and microarray data analysis. Bioinformatics 21: 3439–3440. [DOI] [PubMed] [Google Scholar]
- Durinck S., Spellman P. T., Birney E., Huber W., 2009. Mapping identifiers for the integration of genomic datasets with the R/Bioconductor package biomaRt. Nat. Protoc. 4: 1184–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S. M., Sørensen I. F., Sarup P., Mackay T. F. C., Sørensen P., 2016. Genomic prediction for quantitative traits is improved by mapping variants to gene ontology categories in Drosophila melanogaster. Genetics 203: 1871–1883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao N., Li J., He J., Xiao G., Luo Y., et al. , 2015. Improving accuracy of genomic prediction by genetic architecture based priors in a Bayesian model. BMC Genet. 16: 120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garlapow M. E., Huang W., Yarboro M. T., Peterson K. R., Mackay T. F. C., 2015. Quantitative genetics of food intake in Drosophila melanogaster. PLoS One 10: e0138129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianola D., 2013. Priors in whole-genome regression: the Bayesian alphabet returns. Genetics 194: 573–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R. L., Dekkers J. C. M., 2007. The impact of genetic relationship information on genome assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B., Goddard M., 2010. Genome-wide association and genomic selection in animal breeding. Genome 53: 876–883. [DOI] [PubMed] [Google Scholar]
- Hayes B. J., Cogan N. O. I., Pembleton L. W., Goddard M. E., Wang J., et al. , 2013. Prospects for genomic selection in forage plant species. Plant Breed. 132: 133–143. [Google Scholar]
- Henderson C. R., 1975. Best linear unbiased estimation and prediction under a selection model. Biometrics 31: 423–447. [PubMed] [Google Scholar]
- Henderson C. R., 1984. Applications of Linear Models in Animal Breeding. University of Guelph Press, Guelph, Canada. [Google Scholar]
- Huang W., Mackay T. F., 2016. The genetic architecture of quantitative traits cannot be inferred from variance component analysis. PLoS Genet. 12: e1006421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jannink J.-L., Lorenz A. J., Iwata H., 2010. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9: 166–177. [DOI] [PubMed] [Google Scholar]
- Jensen J., Mantysaari E. A., Madsen P., Thompson R., 1997. Residual maximum likelihood estimation of (Co) variance components in multivariate mixed linear models using average information. J. Indian Soc. Agric. Stat. 49: 215–236. [Google Scholar]
- Jiang Y., Reif J. C., 2015. Modeling epistasis in genomic selection. Genetics 201: 759–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay T. F. C., Richards S., Stone E. A., Barbadilla A., Ayroles J. F., et al. , 2012. The Drosophila melanogaster genetic reference panel. Nature 482: 173–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLeod I. M., Bowman P. J., Vander Jagt C. J., Haile-Mariam M., Kemper K. E., et al. , 2016. Exploiting biological priors and sequence variants enhances QTL discovery and genomic prediction of complex traits. BMC Genomics 17: 144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martini J. W. R., Wimmer V., Erbe M., Simianer H., 2016. Epistasis and covariance: how gene interaction translates into genomic relationship. Theor. Appl. Genet. 129: 963–976. [DOI] [PubMed] [Google Scholar]
- Martini J. W. R., Gao N., Cardoso D. F., Wimmer V., Erbe M., et al. , 2017. Genomic prediction with epistasis models: on the marker-coding-dependent performance of the extended gblup and properties of the categorical epistasis model (ce). BMC Bioinformatics 18: 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Odegard J., Andersen-Ranberg I., Grindflek E., 2014. On the distance of genetic relationships and the accuracy of genomic prediction in pig breeding. Genet. Sel. Evol. 46: 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misztal I., Legarra A., 2017. Invited review: efficient computation strategies in genomic selection. Animal 11: 731–736. [DOI] [PubMed] [Google Scholar]
- Morota G., Abdollahi-Arpanahi R., Kranis A., Gianola D., 2014. Genome-enabled prediction of quantitative traits in chickens using genomic annotation. BMC Genomics 15: 109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morozova T. V., Huang W., Pray V. A., Whitham T., Anholt R. R. H., et al. , 2015. Polymorphisms in early neurodevelopmental genes affect natural variation in alcohol sensitivity in adult Drosophila. BMC Genomics 16: 865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ober U., Ayroles J. F., Stone E. A., Richards S., Zhu D., et al. , 2012. Using whole-genome sequence data to predict quantitative trait phenotypes in Drosophila melanogaster. PLoS Genet. 8: e1002685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramstein G. P., Evans J., Kappler S. M., Mitchell R. B., Vogel K. P., et al. , 2016. Accuracy of genomic prediction in switchgrass (Panicum virgatum L.) improved by accounting for linkage disequilibrium. G3 6: 1049–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team , 2016. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Shengqiang Z., Dekkers J. C. M., Fernando R. L., Jannink J. L., 2009. Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study. Genetics 182: 355–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonesson A. K., Meuwissen T. H. E., 2009. Testing strategies for genomic selection in aquaculture breeding programs. Genet. Sel. Evol. 41: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spindel J., Begum H., Akdemir D., Virk P., Collard B., et al. , 2015. Genomic selection and association mapping in rice (Oryza sativa): effect of trait genetic architecture, training population composition, marker number and statistical model on accuracy of rice genomic selection in elite, tropical rice breeding lines. PLoS Genet. 11: e1004982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su G., Christensen O. F., Ostersen T., Henryon M., Lund M. S., 2012. Estimating additive and non-additive genetic variances and predicting genetic merits using genome-wide dense single nucleotide polymorphism markers. PLoS One 7: e45293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar W., Solberg L. C., Gauguier D., Burnett S., Klenerman P., et al. , 2006a Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat. Genet. 38: 879–887. [DOI] [PubMed] [Google Scholar]
- Valdar W., Solberg L. C., Gauguier D., Cookson W. O., Rawlins J. N. P., et al. , 2006b Genetic and environmental effects on complex traits in mice. Genetics 174: 959–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanRaden P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91: 4414–4423. [DOI] [PubMed] [Google Scholar]
- Wimmer V., Albrecht T., Auinger H.-J., Schön C.-C., 2012. Synbreed: a framework for the analysis of genomic prediction data using R. Bioinformatics 28: 2086–2087. [DOI] [PubMed] [Google Scholar]
- Yang D., 2015. Multi-allelic haplotype model based on genetic partition for genomic prediction and variance component estimation using SNP markers. BMC Genet. 16: 144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Ober U., Erbe M., Zhang H., Gao N., et al. , 2014. Improving the accuracy of whole genome prediction for complex traits using the results of genome wide association studies. PLoS One 9: e93017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The mouse data used in this study is available at http://mtweb.cs.ucl.ac.uk/mus/www/mouse/HS/index.shtml. The D. melanogaster data is available at http://dgrp2.gnets.ncsu.edu/. The rice breeding population data is available at https://ricediversity.org.