Between-Region Genetic Divergence Reflects the Mode and Tempo of Tumor Evolution

Abstract

Given the implications of tumor dynamics for precision medicine, there is a need to systematically characterize the mode of evolution across diverse solid tumor types. In particular, methods to infer the role of natural selection within established human tumors are lacking. By simulating spatial tumor growth under different evolutionary modes and examining patterns of between-region subclonal genetic divergence from multi-region sequencing (MRS) data, we demonstrate that it is feasible to distinguish tumors driven by strong positive subclonal selection from those evolving neutrally or under weak selection, as the latter fail to dramatically alter subclonal composition. We developed a classifier based on measures of between-region subclonal genetic divergence and projected patient data into model space, revealing different modes of evolution both within and between solid tumor types. Our findings have broad implications for how human tumors progress, accumulate intra-tumor heterogeneity, and ultimately how they may be more effectively treated.

Introduction

The multistage model of carcinogenesis described in the early 1950s ^1,2 and Nowell’s 1976 perspective piece on the clonal evolution of tumor cells ³ provided a conceptual framework for understanding tumor progression. These and other studies ^4,5 were foundational in defining the elements of somatic evolution. However, the evolutionary dynamics that govern tumor initiation and subsequent growth after transformation remain poorly understood. Moreover, the distinction between stages is often blurred since tumorigenesis is largely occult often taking place over decades ^6,7 where lesions are only detected once they achieve a certain size or cause symptoms.

Evolution is the product of three major underlying processes: mutation, selection and genetic drift ⁸. Mutations are readily measured in human tumors, and it is generally assumed that ongoing strong selection governs the growth of an established tumor after transformation, leaving a detectable signal on the genome, where the acquisition of additional ‘drivers’ results in multiple selective sweeps ^9,10. In this scenario, driver mutations accompanied by numerous hitchhiking passengers can attain high frequency and manifest as ‘subclonal clusters’ in bulk tumor sequencing data ¹⁰. This led to the development of a suite of methods aimed at inferring subclonal clusters. However, inference of the number of subclones and their proportions from bulk tumor sequencing is a non-trivial task with the solution non-identifiable under most conditions ^11–14. Drift can also cause extensive intra-tumor heterogeneity (ITH) that may be difficult to distinguish from selection without appropriate population genetics methods. For example, we proposed and tested several predictions of a Big Bang model of colorectal tumor growth, wherein after transformation, the tumor grows as a single terminal expansion populated by a large number of heterogeneous—and effectively equally fit—subclones ¹⁵. In this model, most detectable subclonal (private) alterations arise early during growth. While post-transformation selection could be detected in these colorectal tumors, it was often too weak to alter tumor subclonal architecture. Rather, patterns of ITH were suggestive of effectively-neutral evolution.

Other studies have since corroborated ‘Big Bang’ dynamics in colorectal tumors ^16–19. Additionally, neutral evolution was reported in hepatocellular carcinoma via in depth multi-region profiling ²⁰. Williams et al. further investigated evidence for neutral evolution in multiple solid tumors using bulk single sample sequencing data compared to a theoretical null neutral model ²¹. However, as we show, this task is better powered using MRS, which captures additional features of genetic diversity.

Progression modes and tempos differ between neutrally evolving tumors and those tumors with post-transformation selection. Hence, there remains a need for the systematic evaluation of different modes of evolution in diverse solid tumors within a population genetics framework. As selection is complex, it is instructive to initially focus on the commonly assumed scenario of strong positive selection after transformation and contrast this with a neutral model. We leverage the fact that spatiotemporal patterns of genetic variation among cancer cell populations and in particular their variant allele frequency (VAF) distributions (also known as the site frequency spectrum or SFS) ²² derived from next generation sequencing (NGS) can be used to test hypotheses about the underlying evolutionary processes, including the strength of selection and extent of genetic drift. To this end, we simulated spatial tumor growth under different modes of evolution and trained a classifier based on ITH metrics derived from the SFS to discriminate between these scenarios. By projecting MRS data from various solid tumors into model space, we categorize their patient-specific evolutionary dynamics.

Results

Spatial simulation of distinct modes of tumor evolution

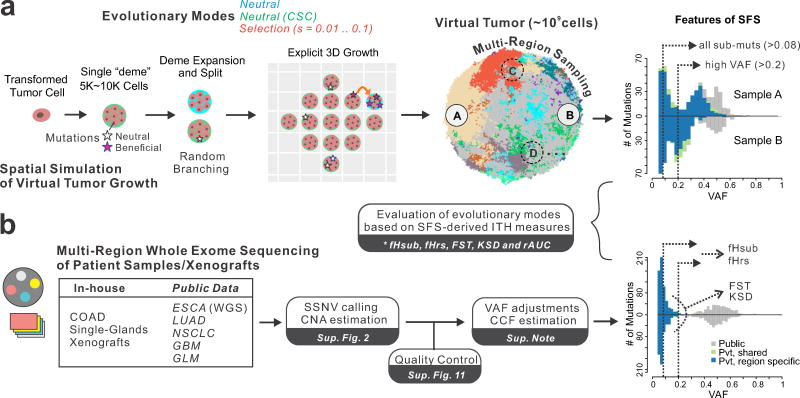
To investigate how different modes of tumor evolution influence the SFS from bulk sequencing data, as well as the power to detect signals of positive selection, we developed an agent-based model of spatial tumor growth (parameters reported in Supplementary Table 1). Within this framework, we simulated various modes of tumor evolution, including a neutral model and an alternate neutral model based on cancer stem cell (CSC) driven growth (neutral-CSC). We also simulated various levels of positive selection (s=0.01, 0.02, 0.03, 0.05, 0.1), such that the acquisition of advantageous mutations alters the cell birth-death rate according to the selection coefficient, s (Figure 1, Supplementary Figure 1, Methods). In all models random neutral point mutations arise via a Poisson process during each cell division. Virtual tumor growth is simulated via the expansion of deme ²³ subpopulations (i.e. neighborhoods of 5–10k cells) within a defined 3D lattice, and cells within each deme are well-mixed and replicate via a random branching process. By recording mutational lineages as the tumor expands and subsequently virtually sampling the ‘final’ tumor as is done experimentally after resection, we evaluate differences in the SFS arising under different levels of selection, and the utility of different tissue sampling strategies (Figure 1a). Thus, we model spatial tumor growth and the inherent stochasticity of this process while accounting for the truncated SFS derived from bulk sequencing due to the large number of rare subclones that are not sampled or below detection limits. This facilitates comparisons with data derived from patient tumors analyzed within a sensitive pipeline for calling somatic single nucleotide variants (SSNVs) from MRS (Figure 1b, Supplementary Figure 2, Methods). A summary of terminology is provided in Supplementary Table 2.

Figure 1. Overview of simulation framework and genomic data analysis pipeline.

(a) Schematic overview of our agent-based computational framework to simulate 3D tumor growth (after transformation) under various modes of evolution, including neutral evolution (null model) and different levels of positive selection, followed by spatial sampling and multi-region sequencing of the virtual tumor. Tumor growth is simulated via the expansion of deme subpopulations within a defined 3D cubic lattice according to explicit rules dictated by spatial constraints, where cells within each deme are well-mixed and grow via a stochastic branching (birth-death) process (Methods and Supplementary Figure 1). By simulating the acquisition of random mutations (neutral or beneficial), tracing the genealogy of each cell as the tumor expands and subsequently virtually sampling and sequencing the ‘final’ virtual tumor as is done experimentally after resection or biopsy, it is possible to evaluate differences in the site frequency spectrum (SFS) under different modes of selection and sampling strategies. Five intra-tumor heterogeneity (ITH) metrics derived from the SFS were employed to distinguish between different evolutionary modes. Sub muts, subclonal mutations. (b) A unified sequencing analysis pipeline based on SSNV calling, copy number estimation, as well as stringent quality control was employed to obtain variant allele frequency (VAF) estimates adjusted for purity and local copy number for seven multi-region sequencing (MRS) datasets derived from patient samples across diverse tissue types. The ITH metrics were similarly computed in patient tumor samples and compared to those observed in virtual tumors under different evolutionary modes.

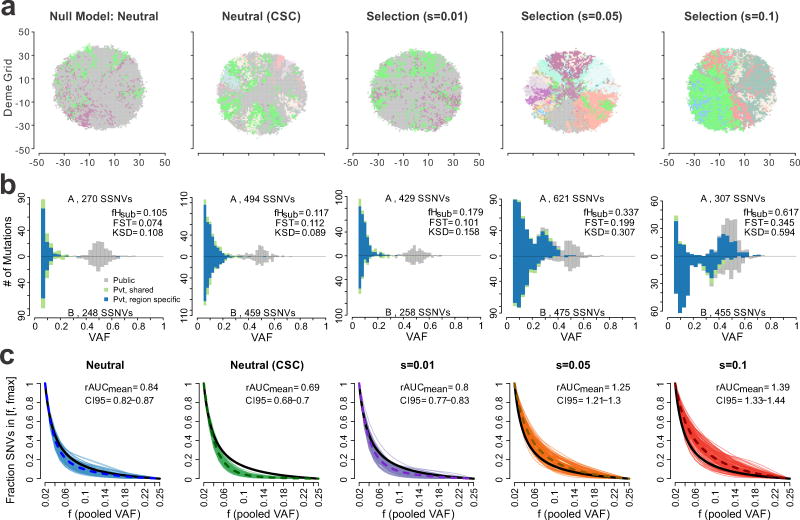
Spatial subclone composition and the distribution of subclonal VAFs derived from MRS (n=2, 4 and 8 regions) of ‘virtual’ tumors differed dramatically depending on the mode of evolution, as illustrated for representative virtual tumors (Figure 2ab, Supplementary Figure 3). In particular, under stronger selection (s≥0.02), multiple subclone expansions occur in different regions of the virtual tumor, as shown in the clone map (Figure 2a). Likewise, multiple peaks (mutational clusters) were observed in the SFS histograms due to the enrichment of high frequency (VAF>0.2) subclonal SSNVs under stronger selection (Figure 2b and shown schematically in Supplementary Figure 4), which were largely region-specific, reflecting elevated genetic divergence. Indeed, subclonal selection typically resulted in detectable differences in the SFS histograms from different tumor regions. In contrast, under neutral growth, a neutral CSC-like model where only a subset of cells have unlimited proliferative potential (equivalent to a smaller deme size), or weak selection (s=0.01), subclonal composition is preserved in the final tumor. The SFS for these three modes were generally similar between regions consisting of two ‘mutational clusters’, namely a public cluster centered at VAF=0.5 composed of mutations that occurred prior to transformation and present in all tumor cells (fixed) and a right skewed distribution of private (subclonal) mutations at low VAF (<0.25) (Figure 2b), where their detection depends on sequencing depth. Importantly, MRS but not single-sample sequencing enables the identification of private SSNVs present at high frequency in one or a few regions, but subclonal in the entire tumor (Supplementary Figure 4). Indeed, at least two spatially separated regions are needed to accurately distinguish public SSNVs in solid tumors, as mutations that are subclonal in the whole tumor can appear ‘clonal’ within some samples due to sampling bias ²⁴. In each of the modes, over 70% of subclonal SSNVs were region-specific due to spatial constraints during virtual tumor expansion. However, selection increased the fraction of high frequency (VAF>0.2) region-specific subclonal SSNVs out of all region-specific subclonal SSNVs (VAF>0.08) (fHrs) (Supplementary Table 4). Hence, MRS aids the identification of subclonal SSNVs that reflect the dynamics of clonal expansion after tumor transformation, whereas clonal SSNVs are not informative in this regard.

Figure 2. Characteristics of virtual tumors simulated under different modes of evolution.

(a) A 2D visualization of a clone map in virtual tumors simulated under different modes of evolution, including the null neutral model (selection coefficient, s=0), a neutral model with cancer stem cell driven growth (neutral-CSC), and varying levels of selection (s=0.01, 0.05 and 0.1). Colors correspond to distinct clones with high VAF (> 0.4) in each deme subpopulation. (b) Representative pairwise SFS histograms derived from two spatially separated regions (labeled A and B) within the same tumor are shown for tumors simulated under different evolutionary modes. SSNVs were classified as Public (gray), Private (Pvt)-shared (green), or Private-region specific (blue) based on their presence in the virtual MRS data (Methods). The total number of SSNVs detected in each region, as well as three ITH metrics are indicated, namely fHsub, FST, KSD. (c) The cumulative SFS derived from virtual tumors (100 shown for each mode) was computed based on the pooled VAF for subclonal SSNVs for four regions in the frequency (f) range 0.02–0.25. Curves are Bezier smoothed. The dashed curve corresponds to the average and the black curve to a theoretical cumulative SFS under neutral exponential growth in a well-mixed population. For each mode, the mean ratio of the area under the cumulative SFS from the virtual tumors compared to that of the theoretical cumulative SFS (denoted rAUC) based on 100 virtual tumors is indicated as are the 95% bootstrap confidence intervals.

To quantify the extent of ITH defined as between-region genetic divergence based on subclonal SSNVs (identified through MRS) under different levels of selection, we employed the following metrics (Methods) in addition to fHrs (defined above):

• fHsub – fraction of subclonal SSNVs (VAF>0.08) with high frequency (VAF>0.2).

• F_ST (Fixation index) – a measure of genetic divergence between regions ²⁵.

• KSD (Kolmogorov-Smirnov distance) – dissimilarity of the SFS between regions.

As expected, fHrs and fHsub were correlated, as were other features, albeit to a lesser extent (Supplementary Figure 5). All of the statistics increased in value under stronger selection (s≥0.02) relative to the neutral/neutral-CSC/weak selection (s=0.01) models. This suggests that selection causes characteristic and detectable genetic divergence between regions when it fails to result in complete sweeps (Figure 2b, Supplementary Table 4).

We further explored the relationship between different modes of evolution and genetic divergence captured by MRS (n=2,4,8 regions) and single sample sequencing at various depths (80–640x) (Figure 2c, Supplementary Figures 6–7, Methods). For reference, the theoretical cumulative SFS assuming neutral exponential growth in a well-mixed population ^21,26 (referred to as the theoretical neutral SFS) is also shown. Differences in the SFS were evident such that tumors simulated under higher selection (s≥0.02) typically fell above the theoretical neutral SFS, whereas the remaining modes generally traced or fell below this curve. The variability in the SFS within individual modes highlights the importance of stochastic simulations.

To compare the utility of single sample data versus MRS, we computed the ratio of the area under the cumulative SFS (based on the pooled VAF for MRS) to the area under the theoretical neutral SFS (rAUC) as this is applicable to both single sample and MRS. Comparison of the rAUC for virtual tumors simulated under different modes demonstrates the challenge of distinguishing between s>0.05 or s≤0.01 (including the neutral and neutral-CSC models) with a single sample, even at high depth, whereas better separation is achieved with even one additional region (Supplementary Figure 8). This is also reflected in comparisons of the sensitivity and specificity to distinguish alternative models from the simulated neutral model based on the rAUC (Supplementary Figure 9a). Whereas power increased with selection intensity (s=0.05–0.1) and the number of regions (n=2–8), this was not the case for increased depth alone due to sampling bias and the inability to capture regionally localized high frequency subclonal mutations that arose under strong selection (Supplementary Figure 9b, Methods). In contrast, metrics that capture between-region ITH such as fHsub are better able to distinguish a specific alternate model than rAUC. Of note, s=0.01 could not be distinguished from the simulated neutral model. The neutral-CSC model is also similar to the ‘vanilla’ neutral model, but generates localized diversity. Thus, we refer to these three modes as effectively-neutral, since the population dynamics of such nearly neutral mutations are virtually equivalent to those of neutral mutations ^27,28. Similarly, it was not feasible to distinguish the SFS under different levels of elevated selection (s≥0.02) (Supplementary Figure 5). Many factors can dampen signals of selection as in the case of strong, but less frequent ‘drivers’ that are very rare or occur late without sufficient time to expand (Supplementary Figure 10). As such, we focus on effective neutrality and strong selection (s≥0.02), but present results from all modes for completeness.

The site frequency spectrum reflects tumor growth dynamics

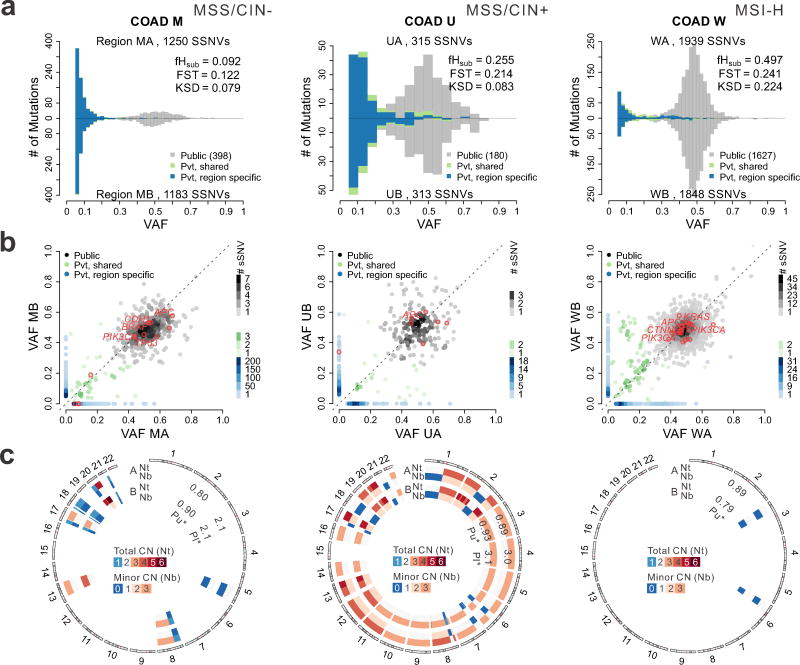
In order to evaluate the SFS in patient samples, we first analyzed MRS data from colorectal adenocarcinomas sampled from two regions (COAD, taken >3 cm apart) ¹⁵ with high purity (72–96%) and adequate coverage (80–120X median WES depth) (Supplementary Figures 11–12). We devised a MuTect-based Variant Assurance Pipeline (VAP) to enable the sensitive and accurate detection of subclonal SSNVs from MRS (Supplementary Figures 2, 13, Methods and Supplementary Note). The observed VAF estimates were adjusted for sample purity and local copy number, enabling pairwise comparisons between tumor regions, and throughout we refer to adjusted VAFs as VAFs (Supplementary Figures 14–15). As noted above, the SFS histograms appear bimodal for both regions, as shown for representative tumors spanning the major pathways of colorectal cancer pathogenesis, categorized according to microsatellite instability (MSI) versus microsatellite stability (MSS) status and chromosomal instability (CIN) status ²⁹ (Figure 3a). A peak centered at a VAF of 0.5 was observed in all tumors with constituent mutations that were present at similar frequencies in the left and right samples (Figure 3b). This VAF cluster primarily represents public mutations present in the founding tumor cell. Whereas private high-VAF (0.2–0.4) SSNVs were infrequent, low frequency subclonal SSNVs (VAF<0.2) were common and generally region-specific despite having similar VAF, suggesting that mutation frequency is not a reliable surrogate for subclone identity. Similar patterns were observed in additional cancers and an adenoma (Supplementary Figure 15). We computed the five ITH metrics, which exhibited low or intermediate values for COADs M, O, and U comparable to those noted in ‘virtual’ tumors under effectively-neutral growth. In contrast, tumors G, N, W, and adenoma S exhibited higher values, similar to those noted in ‘virtual’ tumors subject to selection (Figure 3, Supplementary Tables 4–5).

Figure 3. Colorectal tumors exhibit patterns of between-region genetic divergence consistent with effectively-neutral growth or selection.

(a) Pairwise comparison of SFS histograms from each of three bi-sampled colon adenocarcinomas (COADs) representing the major molecular subgroups, including MSI-H (carcinoma W, right), MSS/CIN+ (carcinoma U, middle) and MSS/CIN- (carcinoma M, left). The pairwise histograms illustrate the number of SSNVs detected at a given VAF for the two tumor regions shown above and below the x-axis. SSNVs were classified as Public (gray), Private (Pvt)-shared (green), or Private-region specific (blue). The total number of SSNVs detected in each region and the fHsub, FST, and KSD values are indicated. (b) Scatterplots comparing SSNVs detected in each tumor region at a given VAF. The color of individual SSNV points correspond to that in Panel A and hues reflect the number of SSNVs in a square (0.02 on a side) centered on each SSNV, as depicted in the legend. Nonsilent SSNVs in predicted COAD driver genes are denoted by red circles with known drivers labeled. (c) Circos plot illustrating the predicted absolute total CN (Nt) and minor allele CN (Nb) for each tumor sample. Diploid segments are indicated in white for Nt (two copies) and Nb (one copy), while segments with copy number gain and loss are shown in red and blue, respectively, according to the scale bar. Tumor cell purity (Pu) as well as ploidy (Pl) estimates for each region are indicated on the corresponding concentric rings.

We further evaluated the genetic divergence within a clonal in vivo tumor growth model by generating single cell expansions from mismatch repair (MMR) deficient COAD cell lines followed by xenotransplantation into opposite flanks of immune compromised mice and WES of the resultant tumors (Methods). In both technical replicates and independent cell line experiments, the data yielded SFS histograms that lacked enrichment for high-frequency private SSNVs (Supplementary Figures 16–17). Additionally, the corresponding ITH metrics were congruent with effectively-neutral growth, as might be expected for fully transformed cells that do not require further alterations to propagate tumor growth.

VAF clusters do not necessarily capture subclone identity

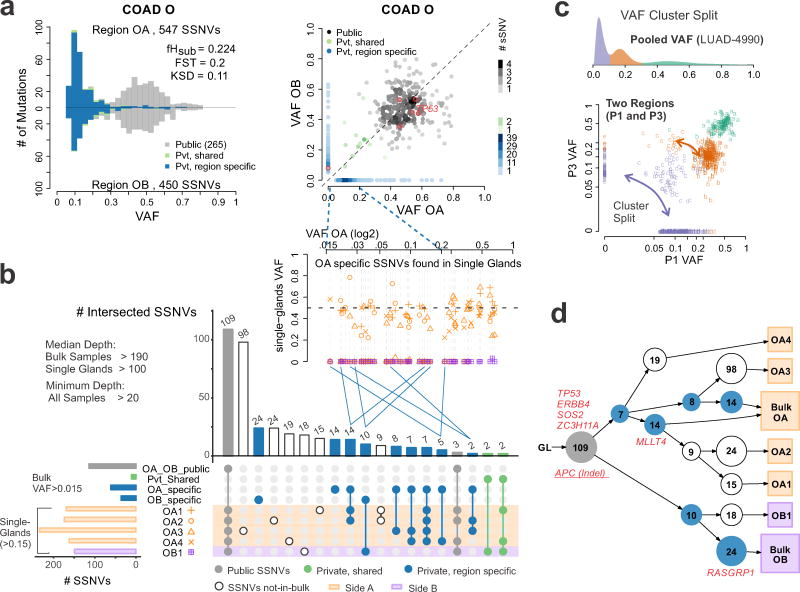
Existing computational methods to infer tumor subclonal architecture from bulk sequencing data exploit the observation that SSNVs cluster around several distinct VAF modes or ‘clonal clusters’ ^10–13,30. These methods aim to assign ‘subclone’ identity based on the assumption that mutations with similar frequencies are in the same cell and that a limited number of dominant subclones underwent clonal expansion ^9,11,31. However, mutational clusters do not guarantee unique lineages, and therefore do not necessarily capture clonal identity. In addition, subclone architecture is influenced by selection and spatial constraints. Indeed, visual inspection of the SFS histograms and scatterplots from the bi-sampled COAD dataset revealed that in all cases, the majority of subclonal SSNVs with VAF<0.2 were region-specific (Figures 3, Supplementary Figure 15). This suggests that mutations grouped based on their VAF do not correspond to unique clones. To evaluate subclonal architecture at higher resolution, we performed WES on five individual COAD glands and bulk samples from two distant tumor regions of a representative cancer (COAD O). The private mutations specific to either bulk sample (OA or OB, Figure 4a, b) were only detected in glands from the same tumor region (p=5E-11, Fisher’s exact test) and similar patterns were noted based on targeted sequencing of private SSNVs in multiple individual glands for each of the bi-sampled COADs (Supplementary Figure 18). In a subset of single glands from two spatially separated regions, the same SSNVs were detected despite being subclonal in the bulk tumor (Figure 4b, green dots), potentially reflecting early subclone mixing ^15,19 or sampling of a clone boundary. In contrast, later arising SSNVs were generally region-specific, consistent with spatial constraints during expansion. SSNVs specific to bulk sample OA (VAF < 0.2) were detected in different combinations of single glands with VAF > 0.2, suggesting that distinct lineages can have similar VAFs in the bulk tumor. Reconstruction of a possible phylogenetic tree using LICHeE ³² also revealed subclone spatial segregation, where essentially every gland within a bulk region is a subclone (Figure 4d), emphasizing the star-like phylogeny predicted for a neutrally growing population ²⁶ (Supplementary Figure 19). WES of single glands from COAD U yielded similar results (Supplementary Figure 20).

Figure 4. Single-gland WES reveals spatial constraints amongst subclonal mutations.

(a) Pairwise histogram of the SFS and SSNV scatterplots from two regions of COAD-O (OA vs. OB). (b) Intersection of SSNVs found in bulk regions and single-glands. In the inset, the VAFs for single-gland vs. bulk sample OA (side-A) specific SSNVs are shown. OA specific SSNVs present in different sets of single-glands collapse to similar VAF values (<0.2) in the bulk sample (blue lines connecting the insert), indicating that mutational clusters do not necessarily guarantee clonal identity. (c) The pooled VAF (derived from four regions) is shown for for LUAD-4990, indicating a clonal cluster (centered at 0.5) and two subclonal clusters. In pairwise comparisons of the VAF from two regions (P3 and P1) the clonal VAF cluster persists, consistent with the mutations in this cluster being present in all cells, whereas the subclonal clusters partition into distinct clusters according to the two tumor regions. (d) Phylogenetic tree based on SSNV presence/absence in single glands and bulk samples constructed using LICHeE. The bulk sample and corresponding single-glands from the same tumor region share a common lineage relationship, potentially reflecting spatial constraints during tumor expansion. SSNVs in known and candidate driver genes are labeled. A truncal APC indel was also detected, but not used for tree construction.

We further reasoned that a ‘true’ clone should form a cluster that persists (e.g. mutations remain grouped), irrespective of the inclusion of data from additional regions. We evaluated this in other solid tumors by analyzing published MRS datasets for esophageal carcinoma (ESCA) ³³, lung adenocarcinoma (LUAD) ³⁴, non-small cell lung cancer (NSCLC) ³⁵, glioma (GLM) ³⁶ and glioblastoma (GBM) ³⁷ (Supplementary Figure 2, 11, Supplementary Table 3, Methods). Application of SciClone ¹³ to MRS data from several representative tumors (COAD-O, ESCA-8, LUAD-4990 for which 2, 3 and 4 regions were available, respectively) consistently resulted in the dissolution of subclonal clusters when data from additional regions were included in the analysis (Figure 4c, Supplementary Figures 21–23). Whereas SSNVs in the subclonal clusters did not remain grouped, those in the clonal clusters did (p=0.0003, Fisher’s exact test), consistent with them being in the founding clone. A persistent mutational cluster in LUAD-4990 was detected through the analysis of 4 regions, potentially corresponding to a subclone that arose under selection (Supplementary Figure 22). Collectively, these results illustrate conceptual challenges in inferring subclonal architecture from bulk sequencing VAF data alone.

Distinguishing the mode and tempo of solid tumor evolution

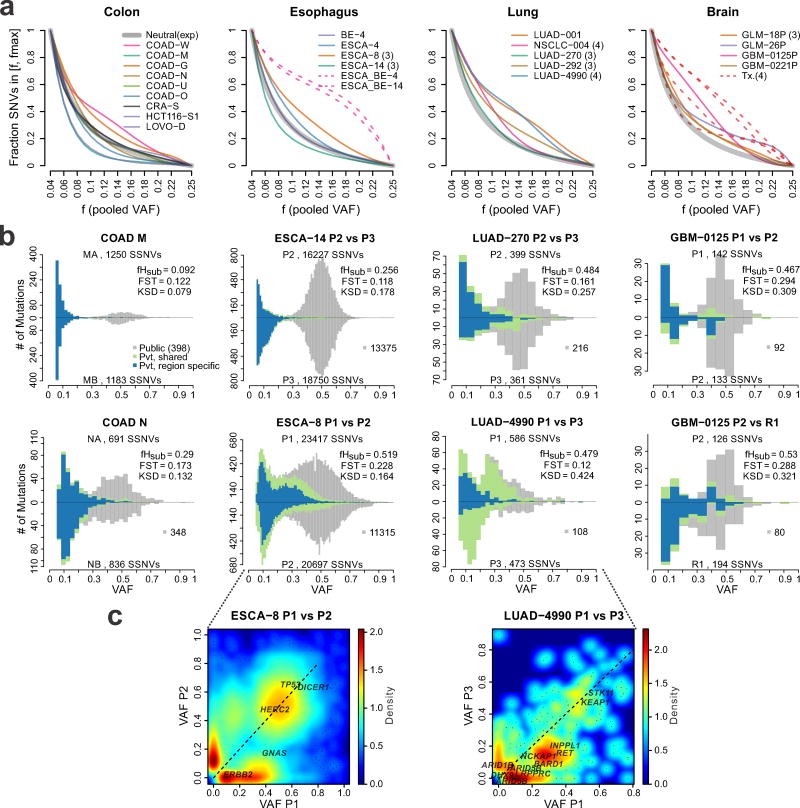
We next evaluated genetic divergence based on MRS of treatment naïve primary tumors, including COAD, ESCA, LUAD, LUSC, and GBM relative to those observed in virtual tumors under different modes. Non-hypermutated GBMs (n=2) and gliomas (n=2) obtained pre- and post-treatment with temazolamide, a mutagenic alkylating agent assumed to impose a positive selective pressure ³⁶, were included as positive controls. Additionally, matched Barrett’s esophageal (BE) lesions and adenocarcinomas from two patients (BE-ESCA-4 and BE-ESCA-14) were included as positive controls, since selection is expected during progression from a pre-malignant lesion. The degree of deviation of the pooled cumulative SFS above the theoretical neutral curve highlights differences in selection across tumor types (Figure 5a). As predicted, each of the positive controls exhibited cumulative SFSs above the neutral curve, consistent with strong selection. In contrast, deviation below the theoretical neutral curve is indicative of spatial constraints, as illustrated by simulating smaller deme sizes (0.5–1k vs. 5–10k), where the ability to distinguish selection from effective neutrality was reduced (Supplementary Figures 24–25). Such strong spatial constraints result in infrequent sharing of subclonal mutations between regions (fShr, Supplementary Table 4–5), a pattern inconsistent with most patient tumors (p < 2.2e-16, Wilcoxon rank sum test), suggesting that larger deme size better reflects the patient data.

Figure 5. The SFS reflects differential modes of evolution within and between tumors types.

(a) Cumulative SFS based on the merged VAF for tumors derived from four tissue types (colon, esophageal, lung, brain) analyzed using the VAP (Methods). All samples were subject to WES with the exception of the ESCA/BE cases for which WGS was available. Each line corresponds to a Bezier smoothed curve of the cumulative SFS. Thick gray curves correspond to the theoretical cumulative SFS under neutral exponential growth in a well-mixed population, shown for reference. Dashed lines correspond to comparisons of tumor regions sampled at distinct stages of tumor progression in the same patient, e.g., Barrett’s esophagus (BE) versus esophageal carcinoma (ESCA), or treatment naïve primary tumor versus post-treatment (Tx) recurrent brain tumors, both of which represent positive controls for selection. (b) Pairwise SFS histograms from representative tumors of different tissue type are shown and depict the number of SSNVs detected at a given VAF for two regions, where SSNVs are grouped according to Public (gray), Private (Pvt)-Shared (green) and Private-Region specific (blue) mutations (as in Figure 3). Histogram bin widths were optimized based on the number of SSNVs (Methods). (c) Two-way density plots of SSNVs present in each region at a given VAF are shown for two tumors. Non-silent SSNVs in known and candidate driver genes are labeled. The color scale reflects the relative density of mutations.

COAD-M and ESCA-14 exhibited bimodal SFS histograms with scant enrichment for high frequency private SSNVs, most consistent with patterns of effective neutrality (Figure 5b). In contrast, COAD-N and LUAD-270 exhibited modest enrichment for such SSNVs, whereas this was more striking in ESCA-8 and LUAD-4990 (Figure 5c). Despite the lower number of SSNVs in treatment-naïve primary GBMs, enrichment of high frequency private SSNVs was evident and similar to that noted in the primary versus post-treatment recurrence (Figure 5b).

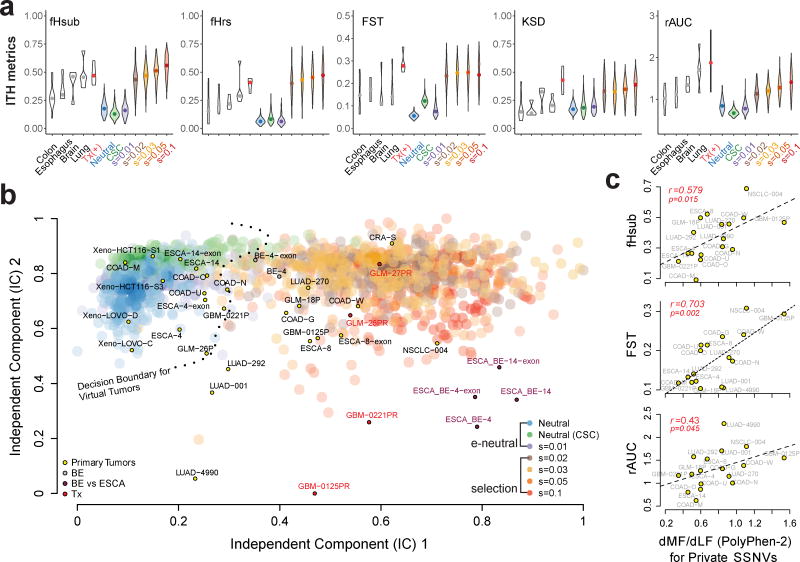
The five ITH metrics were calculated for primary solid tumors, paired pre- and post-temazolamide treated gliomas and GBMs (positive controls) and BE-ESCA pairs (positive controls), as well as virtual tumors simulated under various evolutionary modes (Figure 6a). Amongst the virtual tumors, all five metrics increased markedly under selection (s≥0.02) relative to effective neutrality. The primary COADs and ESCAs tended to exhibit lower detectable divergence than lung and brain cancers, which were lower than the temazolamide treated positive controls.

Figure 6. Projection of patient samples onto distinct evolutionary modes.

(a) Violin plots for each of five ITH metrics, namely, fHsub, fHrs, Fst, KSD, and rAUC. Colored violin plots show the virtual tumors simulated under different evolutionary modes, whereas the white plots correspond to patient tumor data. Paired pre-treatment primary and post-treatment recurrent brain tumors are denoted by “Tx” and serve as a positive control for selection. (b) Independent component analysis (ICA) of virtual and patient tumors based on the five ITH metrics. The independent components separate virtual tumors simulated under effectively (e) neutral growth (neutral, neutral-CSC and s=0.01) versus positive selection (s≥0.02) where the decision boundary for a SVM trained on two independent components (IC) based on the virtual tumors (e-neutral versus positive selection models) is indicated by the dashed line. Large transparent colored circles represent values from virtual tumors under different models (200 tumors from each of the seven modes are shown). Small circles indicate patient tumors labeled by their corresponding sample ID and color-coded according to the type of sample. COAD: colorectal adenocarcinoma; CRA: colorectal adenoma; ESCA: esophageal adenocarcinoma; BE: Barrett’s esophagus; LUAD: lung adenocarcinoma; NSCLC: non-small-cell lung cancer; GLM: glioma; GBM: glioblastoma; Xeno: COAD cell line xenografts. (c) The ratio of private SSNVs at more functional (MF) relative to less functional (LF) sites (dMF/dLF) based on PolyPhen2 was calculated for each of the primary tumors in order to evaluate the correlation with various ITH metrics.

The SFS is commonly used in population genetics ^22,38 and it is appreciated that tests of neutrality based on a single summary statistic can be difficult to establish, whereas composite metrics can aid the detection of selection ³⁹. Given the multi-faceted nature of ITH and the noise in real data, we reasoned that the major components of the ITH metrics would capture complementary aspects of subclonal genetic divergence. Independent component analysis (ICA) using the five ITH metrics revealed two distinct clusters, corresponding to selection with s≥0.02 and neutral/weak selection (s=0.01)/neutral-CSC (Figure 6b). A support vector machine (SVM) was trained on the two independent components (ICs) to discriminate between selection (4 modes with s≥0.02) and effectively-neutral evolution (3 modes with s≤0.01). The SVM based on the ICs performed better than individual ITH metrics and although models using two or more ITH metrics performed well (Supplementary Figures 26–27), we adopted the two ICs to survey genetic divergence in patient samples.

We then classified patient tumors and visualized them in model space (Figure 6b, Supplementary Figures 28–29, Supplementary Table 5), revealing trends with respect to the mode of evolution in a given tumor type, despite patient to patient variability. For example, COADs exhibited both effective neutrality as well as selection, as did ESCAs. In contrast, lung and brain tumors tended to show stronger signals of selection. In total, 5 primary tumors were categorized as being compatible with effective-neutrality and 12 with selection, whereas only 3 did not robustly fit either scenario. As expected, all four pre- versus post-temazolamide treated GBMs and gliomas were most compatible with strong positive selection and several appear as outliers on the ICA, potentially because the full impact of treatment is not modeled (Figure 6b). The paired BE-ESCA cases (ESCA_BE-14 and ESCA_BE-4) exhibited patterns consistent with selection during tumorigenesis, followed by effectively-neutral growth of the primary (ESCA-14 and ESCA-4). Patterns of genetic divergence in multiple BE lesions from patient 4 (BE-4) were similarly indicative of selection (Supplementary Figure 30). Importantly, irrespective of whether WGS or WES data was used, the classification was the same indicating that WES is adequate for this task given sufficient subclonal SSNVs (Figure 6b).

Positive selection for ‘drivers’ during tumor expansion is expected to be associated with an increase in the rate of private SSNVs at more functional (MF) relative to less functional (LF) sites ⁴⁰. Amongst primary tumors, the dMF/dLF ratio was positively correlated with several ITH metrics, e.g., fHsub, FST, and rAUC (Figure 6c). This suggests a general trend between selection and the levels of detectable between-region genetic divergence, although specific patterns could be model dependent (Supplementary Figure 31). Conversely, the fold enrichment for driver genes amongst non-silent public SSNVs was negatively correlated with fHsub, consistent with a greater number of public drivers in tumors characterized by effectively-neutral growth (Supplementary Figure 32). Hence, these results corroborate our finding that patterns of genetic divergence in MRS inform the mode and drivers of tumor growth.

Discussion

Here we show that tumors evolving near neutrally or through strong selection exhibit fundamentally different patterns of ITH and that these can be distinguished via MRS. Further, we developed a classification framework based on features of the SFS that capture between-region subclonal divergence and applied this to publicly available MRS data, revealing different modes of evolution within and between solid tumor types. We note that compatibility with effective neutrality does not necessarily imply the complete absence of selection. Rather, positive selection may have been weak, variable or abrogated by negative selection throughout tumor growth ⁴¹, but the overall patterns do not deviate significantly from those expected under a neutral model. The timing of a mutation is also critical since within a rapidly expanding adaptive population, only mutations that occur early are likely to be ‘fixed’ in relevant time frames and detectable by NGS, even if they are under strong positive selection, whereas partial sweeps are potentially common ⁴². The lack of evidence for ongoing stringent selection in some of the tumors examined here is congruent with a Big Bang model of effectively-neutral tumor growth where the tumor grows as a single expansion with selection uniformly conferred by common drivers in the first tumor cell ¹⁵.

The finding that human tumors can be categorized into different modes of evolution has implications for defining the ‘drivers’ of growth and treatment strategies. For example, near-neutrally evolving tumors show enrichment for drivers amongst public SSNVs, and it is potentially most efficacious to target these truncal mutations. While most detectable ITH occurs early during effectively-neutral growth, the large number of heterogeneous subclones that fall below detection limits increases the chance that pre-existing treatment resistant variants are present. In contrast, putatively functional private variants were enriched amongst tumors characterized by ongoing positive selection, suggesting these may represent relevant targets.

Our findings also inform practical guidelines for studies of tumor evolution. For example, we show that while at least two regions are required to robustly distinguish public versus private alterations, inclusion of sequencing data from additional regions yielded greater discrimination between different modes of evolution and was more informative than deeper sequencing of a single sample. Even under strong spatial constraints such as small (0.5–1k) deme size, where the efficacy of selection is impeded, sequencing additional regions should aid the detection of selection. Improved sensitivity to distinguish different modes of evolution may be achieved by modeling the distinct architecture and microenvironments in different tissues, although these are as of yet poorly understood ⁴³. It will also be important to understand the contribution of deleterious passenger alterations ⁴⁴ and clonal cooperation ^45,46 to tumor dynamics, as well as to evaluate more complex modes of selection in human tumors. Thus, although MRS does not fully resolve the SFS, it nonetheless captures global and local genetic divergence, enabling the detection of signals of selection in individual tumors under certain conditions.

Online Methods

Multi-region sequencing studies

We evaluated patterns of ITH in several publicly available MRS datasets spanning multiple tumor types, including colorectal adenoma/COAD (one adenoma, six patients with COAD) ¹⁵, ESCA/BE (three patients) ³³, LUAD (four patients) ³⁴, NSCLC (one patient) ³⁵, GLM (three patients) ³⁶, and GBM (two patients) ³⁷, numbers refer to cases with MRS data that passed QC. The study accession IDs and list of samples that met coverage and purity requirements are reported in Supplementary Table 3. Details on sequencing depth and purity are provided in Supplementary Figure 11. All samples were analysed using a custom pipeline (Supplementary Note) to enable the sensitive detection of private SSNVs and standardized comparisons across cohorts, as detailed below.

Single gland whole-exome sequencing

Building on our prior description of multi-region WES of colorectal tumors and targeted single gland sequencing, we performed WES of multiple single glands from two tumors in this study (Figures 4, Supplementary Figure 20) on the Illumina platform using the Agilent SureSelect 2.0 or Illumina NRCE kit. Samples were collected under an institutional review board (IRB)-approved protocol (University of Southern California Keck School of Medicine) as de-identified excess tissues not requiring patient specific consent, as previously described ¹⁵. The single gland WES data were analyzed using the same pipeline as was applied to bulk tumor regions. Intersection plots for SSNVs found in bulk regions and single-glands were generated based on mutations that were i) covered by at least 20 reads in each sample; ii) with a VAF above 1.5% in the bulk sample or above 15% in the single-glands; and iii) do not derive from regions with varying patterns of LOH amongst samples.

In vivo modeling of colorectal tumor growth

Cells were expanded in vitro and a single ‘founding’ cell from this population was cloned and expanded to ~6 million (M) cells prior to transplantation of ~1M cells into the right and left flanks of a NSG mouse (HCT116) or a Nude (Nu/Nu) mouse (LoVo), where tumors were allowed to develop to a size of ~1 billion cells (1 cm³) before being sampled and subject to WES (Figures 3, Supplementary Figure 16–17). The HCT116 and LoVo MMR-deficient COAD cell lines were obtained from the ATCC (authenticated using cytochrome C oxidase I assays and STR typing and tested for mycoplasma contamination) and cultured under standard conditions. Tissue was collected separately from the right and left tumors and DNA was extracted for WES using the Illumina TruSeq Exome kit, as was DNA from the first passage population (a polyclonal tissue culture for HCT116 and a polyclonal xenograft sample for LoVo), which were employed as a reference for detecting SSNVs and for copy number alteration (CNA) estimation. Procedures performed on the mice were approved by the Institutional Animal Care and Use Committee (IACUC) at the Oregon Health and Science University (OHSU; NSG mice) and the University of Southern California (USC; nude mice).

Somatic SNV calling, SCNA detection and VAF adjustment

To facilitate quantitative comparisons of the SFS, we devised a unified variant assurance (filtering and rescuing) pipeline (VAP) to achieve balance in sensitivity and specificity when MRS is available such that information can be borrowed across tumor regions. For each raw SNV call by MuTect (v1.1.4, unfiltered) ⁴⁷, the read alignment features from all samples was re-inspected in an automated fashion to assess the confidence (in detected samples) and evidence (in un-detected samples) for the alternative allele (Supplementary Figure 13). Somatic copy number alterations and tumor purity (p) were estimated with TitanCNA ⁴⁸ (version 1.8.0) in exome-seq mode (except for the ESCA dataset where WGS was available). The observed VAF for each detected somatic SNV was adjusted based on CCF (Cancer Cell Fraction) calculation by taking into account tumor purity, local copy numbers as well as the inferred time ordering between SCNA and SSNV as previously described ³¹ (Supplementary Figure 14–15), in order to enable comparisons of genetic divergence between regions. Additional details for this section, including benchmarking of VAP (Supplementary Figure 33–35), can be found in the Supplementary Note.

Spatial computational modeling of tumor growth dynamics

We extended our previously described spatial agent-based model ¹⁵ to simulate tumor growth and mutation accumulation under different scenarios ranging from neutral evolution to strong selection and compare the SFS of SSNVs arising from 1, 2, 4 and 8 regions sampled from spatially separated quadrants of individual virtual tumors. In this agent-based model, spatial tumor growth is simulated via the expansion of deme subpopulations (composed of 5–10k cells), which mimics the glandular structures often found in epithelial tumors (Supplementary Table 1). The deme model is well established for modeling spatially expanding populations ²³. Here, deme subpopulations expand within a defined 3D cubic lattice (Moore neighborhood, 26 neighbors), where demes expand by particular rules of spatial constraints (peripheral growth ⁴⁹ or alternatively shifting growth ¹⁵) while cells within each deme are well-mixed and grow via a random branching (birth-death) process. The panmixia of cells in the formation of the first deme from a single transformed cell allows for subclone mixing amongst early-arising mutations ^15,19, which can subsequently spread during tumor expansion. Random neutral mutations arise via a Poisson process at each cell division, assuming an infinite sites model.

More specifically, at each time step, we simulate deme division by selecting a deme at random and choosing a neighboring lattice site where the new deme will be placed. We employ a peripheral growth model ⁴⁹ (Supplementary Table 1), where only demes on the surface of the tumor can grow and divide such that a random empty neighbor site was chosen for each newly generated deme. The peripheral growth model is supported by recent studies indicating that cancer cells at the periphery of the tumor exhibit higher proliferative activity than those at the core ⁴³. We assume a maximum deme size of 10,000 cells in order to minimize the effect of deme structure, which hinders selection. While we focus on this conservative scenario, we also explored the impact of a smaller deme sizes (down to 1,000 cells) (Supplementary Figures 24–25). Within the model there is no spatial partition for tumor cells within demes which proliferate via a discrete stochastic birth-and-death process (division rate p and death rate q=1-p, the death/birth ratio h=q/p), where the first deme is generated by the same process beginning with a single transformed tumor cell. Simple birth-death processes give rise to exponential growth of each deme on average where the growth rate is r=ln(2p). Here we employ the following parameters: p=0.55, q=0.45 and thus r=ln(2×0.55)≈0.1 as the growth rate of deme expansion, where p and q were empirically chosen by assuming a relatively high death versus birth rate (h=q/p=0.82) in each cell generation in line with previous estimates in a rapidly growing colorectal cancer metastasis (h=0.72) ⁵⁰ and in early tumors (h=0.99) ⁵¹. Once the deme exceeds the maximum size, the deme will split into two offspring demes via sampling from a binomial distribution [Nc, p=0.5] where Nc is the current deme size. During each cell division, the number of neutral passenger mutations that arise in the coding portion of the genome follows a Poisson distribution with mean, u, where an infinite sites model and constant mutation rate was assumed. Under the null model, all somatic mutations are assumed to be neutral and do not confer a fitness advantage, whereas in the selection models, beneficial mutations (or advantageous mutations) occur stochastically via a Poisson process with mean u_b during each cell division. Thus, we consider the null neutral model (s=0), as well as varying degrees of selection: s=0.01, 0.02, 0.03, 0.05 and 0.1, where s is the selection coefficient defined by the increase in the cell division rate when a beneficial mutation occurs in the neutral cell lineage. The cell division rate and death rate of a selectively beneficial clone is p_b=p×(1+s) and q_b=1-p_b=1-p×(1+s), respectively. The growth rate of a selective lineage within a deme is r_b=ln(2*p_b). The parameters employed are reported in Supplementary Table 1 and include u=1.2 within the 60 Mb of coding sequence in a diploid genome corresponding to a mutation rate of 2×10⁻⁸ per cell division per site. For the selection models, we assume u_b=10⁻⁵ per cell division for driver mutations, on order with that previously suggested by Bozic et al. ⁵¹. We also investigated the impact of a lower selectively advantageous mutation rate (u_b=10⁻⁶) on the SFS, as this mimics late arising driver mutations (Supplementary Figure 10).

We also sought to explore how a naïve model of neutral cancer stem cell (neutral-CSC) driven tumor growth would influence the resultant SFS. Here, each deme comprises two subpopulations – stem cells (SCs) and non-SCs where the SC fraction is p(SC). In each cell generation, SCs divide symmetrically generating two SCs with probability α and asymmetrically generating one SC and one non-SC with probability β (where α+β=1 and thus the probability of symmetric SC differentiation is 0). Non-SCs can only divide with probability γ or die with probability δ (where γ+δ=1). We exploit a set of parameter values: namely α=0.15, β =0.85, γ=0.565 and δ=0.435 to ensure the maximum deme size is ~10,000 cells and the SC fraction p(SC)≈ 1–2%, consistent with estimates in solid tumors ⁵². While it is of potential interest to consider a CSC model in the context of selection, this is complicated by the need for additional parameters with little experimental support, and hence we do not investigate this here.

During virtual tumor growth, each mutation was assigned a unique index and is recorded with respect to its genealogy and host cells during the simulation, enabling analysis of its frequency in a subpopulation or the whole tumor at different stages of growth. Once the tumor reached a final size of ~10⁹ cells, approximately the size when it is detectable and routinely resected, we virtually sampled: 1, 2, 4, or 8 regions composed of ~10⁶ cells from an individual virtual tumor (200 tumors under each of the 7 evolutionary modes, totaling 1400 virtual tumors). The VAF of all SSNVs in the sampled bulk subpopulation were considered the true value, whereas observed VAF values were obtained via a statistical model that mimics the random sampling of alleles during sequencing. In particular, we applied a Binomial distribution (n, f) to generate the observed VAF of each site given its true frequency f and number of covered reads n. The number of covered reads in each site is assumed to follow a negative-binomial distribution. Here, we assume depth=80 representing 80x sequencing depth on average with a variation in parameter size of 2. A mutation is called when the number of variant reads is ≥ 3, thereby applying the same criteria as for the actual tumors. For each virtual tumor, 100 clonal SSNVs were assigned to represent public mutations, where VAF values were simulated using the statistical model described above with mean VAF of 0.5.

Identification of subclonal SSNVs in MRS

A SSNV m is defined as subclonal if all of the three following criterion are met,

1. A total probability $P_m={\mathrm{\Pi }}_{i=1}^k{P}_{mi}(X_{mi}\le S_{mi},N_{mi},f.{\mathit{pub}}_{mi})<0.05$, where P_mi is a binomial probability for region i of observing less than or equal to S_mi reads carrying mutant allele out of total reads N_mi, provided a lower bound of expected allele frequency if m is public, given that the tumor purity for region i equals to pu_i, the total, minor copy numbers and the cellular prevalence of the SCNA where m resides equal to nt_mi, nb_mi, and pa_mi within the tumor content,

   $$f.{\mathit{pub}}_{mi}=\{\begin{array}{ll}{pu}_i\times \frac{{nb}_{mi}}{{nc}_{mi}}\hfill & \hfill if{nb}_{mi}\ge 1,{nt}_{mi}\ge 2\\ ({pu}_i\times ({nt}_{mi}-{nb}_{mi}))/{nc}_{mi}\hfill & \hfill \mathit{otherwise}\end{array}$$

   where nc_mi = nt_mi × pa_mi × pu_i + 2 × (1 − pa_mi × pu_i). For sites devoid of SCNAs, nt_mi = 2, nb_mi = 1 and pa_mi = 0.

2. At least one region i with CCF_mi ± 95% CI_mi < 1

3. At least one region i with adjusted VAF VAF_ami < 0.25. Here 0.25 was chosen because of its good performance in defining subclonality based on simulated virtual tumors (Supplementary Figure 36).

A SSNV that does not meet one of the above criterion is considered public. SSNVs with varying patterns of loss of heterozygosity (LOH) amongst regions were not included for pairwise SFS comparisons. The pooled cumulative SFS was computed when multiple samples were available. Here we employ an f_max of 0.25 as the upper value for subclonal mutations, whereas f_min depends on the total sequencing depth (and hence number of regions sequenced) and is chosen conservatively, while maximizing the inclusion of high confidence low VAF SSNVs.

ITH metrics

For pairwise comparisons between regions, subclonal (private) SSNVs were assigned as being either private-shared or region-specific. Private-shared SSNVs are present in both regions, whereas region-specific SSNVs are unique to one region where we reject a null model of the same VAF in the variant-missing region (given the sequencing depth) with a 5% significance level. For each pairwise SFS histogram, the bin width was optimized for visualization purposes based on the number of SSNVs ⁵³. Metrics capturing between-region ITH were computed for k regions and $r=\left(\begin{array}{c}k\\ 2\end{array}\right)$ pairwise comparisons as follows:

1. $\mathit{fHsub}=\frac{1}{k}\times {\mathrm{\sum }}_{i=1}^k\frac{{SM}_i^{\mathit{high}}}{{SM}_i^{\mathit{all}}}$, where ${SM}_i^{\mathit{high}},{SM}_i^{\mathit{all}}$ are the number of high frequency subclonal SSNVs (adjusted VAF>0.2, hereafter referred to as VAF) and the number of all subclonal SSNVs with VAF>0.08 for region i. The cutoff was set to 0.2 since above this value fHsub tends to plateau in its sensitivity to distinguish the neutral and selection models (Supplementary Figure 36). A lower cutoff of 0.08 was chosen empirically to satisfy the tradeoff between the number of subclonal SSNVs and variant calling errors.

2. $\mathit{fHrs}=\frac{1}{r}\times {\mathrm{\sum }}_{j=1}^r\left(\frac{{\mathit{RSM}}_{ja}^{\mathit{high}}}{2\times {\mathit{RSM}}_{ja}^{\mathit{all}}}+\frac{{\mathit{RSM}}_{jb}^{\mathit{high}}}{2\times {\mathit{RSM}}_{jb}^{\mathit{all}}}\right)$, where ${\mathit{RSM}}_{ja}^{\mathit{high}},{\mathit{RSM}}_{ja}^{\mathit{all}}$ represent the number of high-frequency (VAF>0.2) region-specific SSNVs and the number of all region-specific SSNVs with VAF>0.08 for region a, in a pairwise comparison j between regions a and b.

3. $\mathit{FST}=\frac{1}{r}\times {\mathrm{\sum }}_{j=1}^r{\mathit{FST}}_j^{\mathit{hudson}}$, and ${\mathit{FST}}_j^{\mathit{hudson}}=\frac{{\mathrm{\sum }}_{m=1}^{m_t}{(f_a^m-f_b^m)}^2-\frac{f_a^m\times (1-f_a^m)}{d_a^m-1}-\frac{f_b^m\times (1-f_b^m)}{d_b^m-1}}{{\mathrm{\sum }}_{m=1}^{m_t}{f}_a^m\times \left(1-f_b^m\right)+f_b^m\times (1-f_a^m)}$, where $f_a^m$ is the VAF for SSNV m and $d_a^m$ is the sequencing depth for SSNV m in region a. The genetic variance components (nominator and denominator) are averaged separately to obtain a ratio combining the Hudson FST estimates across all m_t SSNVs ⁵⁴.

4. $\mathit{KSD}=\frac{1}{r}\times {\mathrm{\sum }}_{j=1}^r{\mathit{KSD}}_j$, and KSD_j = max|F_a − F_b|, where F_a is the cumulative SFS of region a, in a pairwise comparison j between regions a and b.

5. rAUC = ^AUC_merged/_AUCtheor, corresponding to the ratio of the area under the pooled cumulative SFS to the area under a theoretical cumulative SFS assuming neutral exponential growth of a well-mixed population ^21,26. For MRS, the pooled VAF is the total number of alternative alleles divided by total read depth. As this represents the alternative allele frequency pooled across tumor regions, it should capture overall tumor dynamics, but not between region diversity and complements other ITH metrics.

To evaluate the power (at a significance level of 0.10) or sensitivity of ITH metrics to distinguish a specific alternate model from the neutral model in the simulated data given varying numbers of samples (n=1, 2, 4 and 8) or variable sequencing depths of a single sample (80–640x), we employed rAUC as it is applicable to single sample data, as well as fHsub, one of the MRS specific statistics. The power was computed empirically as the percentage of virtual tumors under an alternative model for which the statistic (rAUC or fHsub) was greater than 95% or less than 5% of the corresponding statistic in the neutral model (taking the larger percentage).

Evolutionary mode classifier

A radial basis function (RBF) kernel SVM was built based on 1,400 simulated tumors derived from seven growth models (200 for each of neutral, neutral-CSC, s=0.01, 0.02, 0.03, 0.05 and 0.1). We grouped virtual tumors simulated under the neutral, neutral-CSC and s=0.01 models as “effectively-neutral” and those simulated under higher selection coefficients (s≥0.02) as “selection” based on the distribution of the five statistics (Figure 6a). The five ITH metrics derived from the SFS were Z-score centered and scaled to have mean 0 and SD equal to 1. The SVM was trained using 10 fold cross validation with the R package caret ⁵⁵. Two rounds of training were performed to optimize the two parameters for RBF (C: the “cost” of the radial kernel and sigma: the smoothing parameter). In the first round, tuning parameters were arbitrarily selected and the default settings were used for the remainder. The training function was employed to calculate estimates for the parameters. In a second round, sensitivity analysis was performed to refine the parameter choice. To evaluate the relative importance of different combinations of the five ITH metrics for classification, SVMs were run 20 times for each of 26 possible combinations of five statistics with the same seed used for random splitting, where 4/5 virtual tumors were used for training and 1/5 for testing, and the resulting ROC AUCs were compared (Supplementary Figure 27). A SVM was also built using the two major independent components (IC) obtained from independent component analysis (ICA) of the five ITH metrics where the decision boundaries are shown on the ICA scatter plots. ICA was performed on features derived from the virtual tumors and patient tumors for n=2 (Supplementary Figure 28), n=4 (Figure 6b) and n=8 (Supplementary Figure 29) virtual tumor regions. The performance of the SVM to distinguish each alternative model from the neutral model was evaluated by comparing 100 virtual tumors for training and 100 virtual tumors for testing (Supplementary Figure 26).

Functionality assessment of private and public SSNVs

The ratio of private SSNVs at more functional (MF) relative to less functional (LF) sites was determined as previously described ⁴⁰ in order to evaluate the correlation between dMF/dLF and various ITH metrics derived from the SFS. SSNVs were considered MF if classified by Polyphen-2 as “damaging” or “probably damaging” and LF if classified as “benign”. The dMF/dLF ratio was calculated by normalizing MF/LF for private SSNVs in each tumor to a background MF/LF ratio based on random substitutions in the mutated genes. We also determined the fold enrichment for driver genes (defined based on IntOGen v.2016.5) amongst non-silent public SSNVs and the correlation with various ITH metrics.

Code availability

Code for the simulation studies and the Variant Assurance Pipeline are available at:

https://github.com/cancersysbio/VirtualTumorEvolution

https://github.com/cancersysbio/VAP

Data availability

The single gland WES data and xenograft WES data are available at EMBL-EBI ArrayExpress under accession number E-MTAB-5547. Data from previously published studies are available at: European Genotype Phenotype Archive (EGA): EGAD00001001394, EGAD00001000714, EGAD00001000900, EGAD00001000984, EGAD00001001113.