Abstract
Complex mathematical models of interaction networks are routinely used for prediction in systems biology. However, it is difficult to reconcile network complexities with a formal understanding of their behavior. Here, we propose a simple procedure (called ) to reduce biological models to functional submodules, using statistical mechanics of complex systems combined with a fitness-based approach inspired by in silico evolution. The algorithm works by putting parameters or combination of parameters to some asymptotic limit, while keeping (or slightly improving) the model performance, and requires parameter symmetry breaking for more complex models. We illustrate on biochemical adaptation and on different models of immune recognition by T cells. An intractable model of immune recognition with close to a hundred individual transition rates is reduced to a simple two-parameter model. The algorithm extracts three different mechanisms for early immune recognition, and automatically discovers similar functional modules in different models of the same process, allowing for model classification and comparison. Our procedure can be applied to biological networks based on rate equations using a fitness function that quantifies phenotypic performance.
Introduction
As more and more systems-level data are becoming available, new modeling approaches have been developed to tackle biological complexity. A popular bottom-up route inspired by “-omics” aims at exhaustively describing and modeling parameters and interactions (1, 2). The underlying assumption is that the behavior of systems taken as a whole will naturally emerge from the modeling of its underlying parts, leading scholars to propose the “hairball” as the contemporary dominant image of biology (3). Although such approaches are rooted in biological realism, there are well-known modeling issues. By design, complex models are challenging to study and to use. More fundamentally, connectomics does not necessarily yield clear functional information of the ensemble, as recently exemplified in neuroscience (4). Big models are also prone to overfitting (5, 6), which undermines their predictive power. It is thus not clear how to tackle network complexity in a predictive way, or, to quote Gunawardena (7), “how the biological wood emerges from the molecular trees.”
More synthetic approaches have actually proved successful. Biological networks are known to be modular (8), suggesting that much of the biological complexity emerges from the combinatorics of simple functional modules. Specific examples from immunology to embryonic development have shown that small and well-designed phenotypic networks can recapitulate most important properties of complex networks (9, 10, 11). A fundamental argument in favor of such phenotypic modeling is that biochemical networks themselves are not necessarily conserved, whereas their function is. This is exemplified by the significant network differences in segmentation of different vertebrates despite very similar functional roles and dynamics (12). It suggests that the level of the phenotype is the most appropriate one and that a too-detailed (gene-centric) view might not be the best level to assess systems as a whole.
The predictive power of simple models has been theoretically studied by Sethna and co-workers (13, 14, 15, 16), who argued that even without complete knowledge of parameters, one is able to fit experimental data and predict new behavior. These ideas are inspired by recent progress in statistical physics, where parameter space compression naturally occurs, so that dynamics of complex systems can actually be well described with few effective parameters (17). Methods have further been developed to generate parsimonious models based on data fitting that are able to make new predictions (18, 19). However, such simplified models might not be easily connected to actual biological networks. An alternative strategy is to enumerate (20, 21) or evolve in silico networks that perform complex biological functions (22), using predefined biochemical grammar, and allowing for a more direct comparison with actual biology. Such approaches typically give many results. However, common network features can be identified in retrospect, and as such, are predictive of biology (22). Nevertheless, as soon as a microscopic network-based formalism is chosen, tedious labor is required to identify and study underlying principles and dynamics. If we had a systematic method to simplify/coarse-grain models of networks while preserving their functions, we could better understand, compare, and classify different models. This would allow us to extract dynamic principles underlying given phenotypes with maximum predictive power.
Inspired by a recently proposed boundary manifold approach (23), we propose a simple method to coarse-grain phenotypic models, focusing on their functional properties via the definition of a so-called fitness. Complex networks, described by rate equations, are then reduced to much simpler ones that perform the same biological function. We first reduce biochemical adaptation, then consider the more challenging problem of absolute discrimination, an important instance being the early immune recognition (24). In particular, we succeed in identifying functional and mathematical correspondence between different models of the same process. By categorizing and classifying them, we identify general principles and biological constraints for absolute discrimination. Our approach suggests that complex models can indeed be studied and compared using parameter reduction, and that minimal phenotypic models can be systematically generated from more complex ones. This may significantly enhance our understanding of biological dynamics from a complex network description.
Materials and Methods
An algorithm for fitness-based asymptotic reduction
Transtrum and Qiu (23, 25) studied the problem of data fitting using cellular regulatory networks modeled as coupled ordinary differential equations. They proposed that models can be reduced by following geodesics in parameter space, using error fitting as the basis for the metric. This defines the manifold boundary approximation method (MBAM) that extracts the minimum number of parameters compatible with data (23).
Although simplifying models to fit data is crucial, it would also be useful to have a more synthetic approach to isolate and identify functional parts of networks. This would be especially useful for model comparison of processes where abstract functional features of the models (e.g., the qualitative shape of a response) might not correspond to one another, or where the underlying networks are different although they perform the same overall function (12). We thus elaborate on the approach of (23) and describe in the following an algorithm for FItness Based Asymptotic parameter Reduction (FIBAR, abbreviated with ). The algorithm does not aim at fitting data, but focuses on extracting functional networks, associated to a given biological function. To define a biological function, we require a general fitness (symbolized by ϕ) to quantify performance. Fitness is broadly defined as a mathematical quantity encoding biological function in an almost parameter independent way, which allows for a much broader search in parameter space than traditional data fitting (examples are given in the next sections). The term “fitness” is inspired by its use in evolutionary algorithms to select for coarse-grained functional networks (22). We then define “model reduction” as the search for networks with as few parameters as possible optimizing a predefined fitness. There is no reason, a priori, that such a procedure would converge for arbitrary networks or fitness functions: it might simply not be possible to optimize a fitness without some preexisting network features. A more traditional route to optimization would rather be to increase the number of parameters to explore missing dimensions, rather than decrease them (see discussions in (18, 19)). We will show how reveals network features in known models that were explicitly designed to perform the fitness of interest.
Due to the absence of an explicit cost function to fit data, there is no equivalence in to the metric in parameter space in the MBAM allowing us to incrementally update parameters. However, upon further inspection, it appears that most limits in (23) correspond to simple transformations in parameter space: single parameters disappear by putting them to 0 or ∞, or by taking limits in which their product or ratio is constant, whereas individual parameters go to 0 or ∞. In retrospect, some of these transformations can be interpreted as well-known limits such as quasi-static assumptions or dimensionless reduction, but there are more subtle transformations, as will appear below.
Instead of computing geodesics in parameter space, we directly probe asymptotic limits for all parameters, either singly or in pairs. Practically, we generate a new parameter set by multiplying and dividing a parameter by a large enough rescaling factor f (which is a parameter of our algorithm; we have taken f = 10 for the simulations presented here), keeping all other parameters constant, or doing the same operation on a couple of parameters.
At each step of the algorithm, we compute the behavior of the network when changing single parameters, or any couple of parameters by factor f in both directions. We then compute the change of fitness for each of the new models with changed parameters. In most cases, there are parameter modifications that leave the fitness unchanged or even slightly improve network behavior. Among this ensemble, we follow a conservative approach and select (randomly or deterministically) one set of parameter modifications that minimizes the fitness change. We then implement parameter reduction by effectively pushing the corresponding parameters to 0 or ∞, and iterate the method until no further reduction enhances the fitness or leaves it unchanged, or until all parameters are reduced. The evaluation of these limits effectively removes parameters from the system while keeping the fitness unchanged or incrementally improving it. There are technical issues we have to consider: for instance, if two parameters go to ∞, some numerical choices have to be made about the best way to implement this. Our choice was to keep the reduction simple: in this example, instead of defining explicitly a new parameter, we increase both parameters to a very high value, freeze one of them, and allow variation of the other one for subsequent steps of the algorithm. Another issue with asymptotic limits for rates is that corresponding divergence of variables might occur. To ensure proper network behavior, we thus impose overall mass conservation for some predefined variables, e.g., total concentration of an enzyme (which effectively adds fluxes to the free form of the considered biochemical species). We also explicitly test for convergence of differential equations and discard parameter modifications leading to numerical divergences. Details on the implementation of the reduction rules for specific models are presented in the Supporting Material and can be automatically implemented for any model based on rate equations.
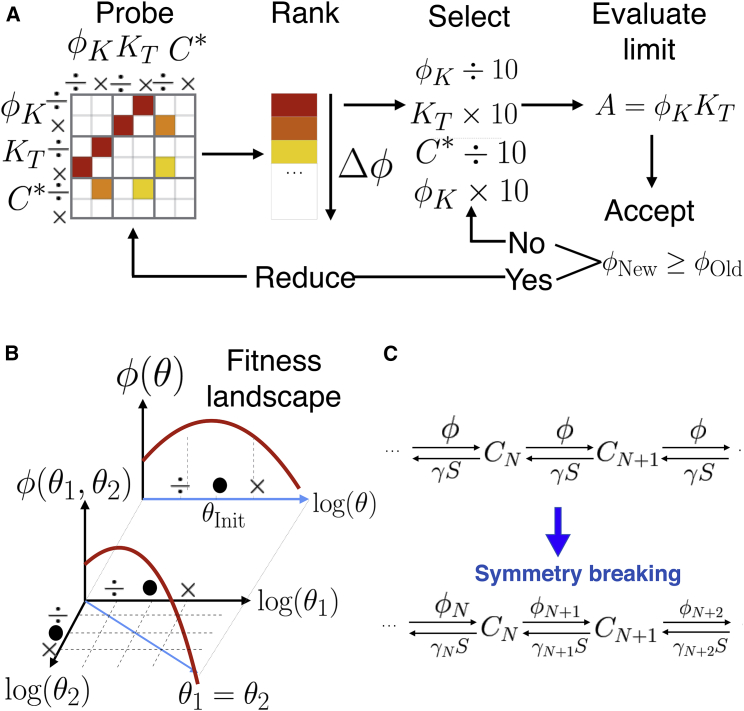
These iterations of parameter changes alone do not always lead to simpler networks. This is also observed in the MBAM when it is sometimes no longer possible to fit all data as well upon parameter reduction. However, with the goal to extract minimal functional networks, we can circumvent this problem by implementing what we call “symmetry breaking” of the parameters (Fig. 1, B and C): in most networks, different biochemical reactions are assumed to be controlled by the same parameter. An example is a kinase acting on different complexes in a proofreading cascade with the same reaction rate. However, an alternative hypothesis is that certain steps in the cascade are recognized to activate specific pathways, or targeted for removal (e.g., in limited signaling models, the signaling step is specifically tagged, thus having dual specificity (11)). So to further reduce parameters, we assume that those rates, which are initially equal, can now be varied independently by (Fig. 1 C). Symmetry breaking in parameter space allows us to reduce models to a few relevant parameters/equations, and as explained below is necessary to extract simple descriptions of network functions. Note that symmetry breaking transiently expands the number of parameters, allowing for a more global search for a reduced model in the complex space of networks. Fig. 1 A summarizes this asymptotic reduction.
Figure 1.
Summary of algorithm. (A) Given here is asymptotic fitness evaluation and reduction. For a given network, the values of the fitness ϕ are computed for asymptotic values of parameters or couples of parameters. If the fitness is improved (warmer colors), one subset of improving parameters is chosen and pushed to its corresponding limits, effectively reducing the number of parameters. This process is iterated. See main text for details. (B) Shown here is parameter symmetry breaking. A given parameter present in multiple rate equations (here θ) is turned into multiple parameters (θ1,θ2) that can be varied independently during asymptotic fitness evaluation. (C) Given here are examples of parameter symmetry breaking, considering a biochemical cascade similar to the model from (10). See main text for comments. To see this figure in color, go online.
We have implemented in the software MATLAB (The MathWorks, Natick, MA) for the specific cases described here, and samples of code used are available as Supporting Material.
Defining the fitness
To illustrate the algorithm, we apply it to two different biological problems: biochemical adaptation and absolute discrimination. In this section we briefly describe those problems and define the associated fitness functions.
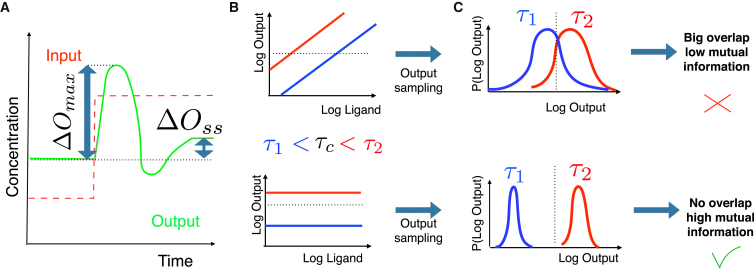
The first problem we study is “biochemical adaptation”, a classical, ubiquitous phenomenon in biology in which an output variable returns to a fixed homeostatic value after a change of input (see Fig. 2 A). We apply on models inspired by (20, 25), expanding Michaelis-Menten approximations into additional rate equations, which further allows us to account for some implicit constraints of the original models (see details in the Supporting Material). We use a fitness that was first detailed in (26): we measure the deviations from equilibrium at steady state ΔOss, and the maximum deviation ΔOmax after a change of input, and aim at minimizing the former while maximizing the latter. Combining both numbers into a single sum ΔOmax + ε/ΔOss gives the fitness we are maximizing (see more details in the Supporting Material). This simple case study illustrates how works and allows us to compare our findings to previous works such as (25).
Figure 2.
Fitness explanations. (A) Given here is the fitness used for biochemical adaptation. The step of an input variable is imposed (red dashed line) and behavior of an output variable is computed (green line). Maximum deviation ΔOmax and steady-state deviation ΔOss are measured and optimized for fitness computation. (B) Shown here are the schematics of a response line for absolute discrimination. We represent expected dose response curves for a bad (top) and a good (bottom) model. Response to different binding times τ are symbolized by different colors. For the bad monotonic model (e.g., kinetic proofreading (33)), by setting a threshold (horizontal dashed line), multiple intersections with different lines corresponding to different values of τ are found, which means it is not possible to measure τ based on the output. The bottom corresponds to absolute discrimination. Flat responses plateau at different output values that easily measure τ. Thus, the network can easily decide the position of τ with respect to a given threshold (horizontal dashed line). (C) For actual fitness computation, we sample the possible values of the output with respect to a predefined ligand distribution for different values of τ (we have indicated a threshold similar to (B) by a dashed line). If the distributions are not well separated, one cannot discriminate between values of τ based on outputs and mutual information between output and τ is low. If they are well separated, one can discriminate values of τ based on output and mutual information is high. See technical details in the Supporting Material. To see this figure in color, go online.
The second problem is “absolute discrimination”, defined as the sensitive and specific recognition of signaling ligands based on one biochemical parameter. Possible instances of this problem can be found in immune recognition between self and not self for T cells (24, 27) or mast cells (28), and recent work using chimeric DNA receptor confirm sharp thresholding based on binding times (29). More precisely, we consider models where a cell is exposed to an amount L of identical ligands, and their binding time τ defines their quality. Then the cell should discriminate only on τ, i.e., it should decide if τ is higher or lower than a critical value τc independently of ligand concentration L. This is a nontrivial problem, because many ligands with binding time slightly lower than τc should not trigger a response, whereas few ligands with binding time slightly higher than τc should. Absolute discrimination has direct biomedical relevance, which explains why there are models of various complexities, encompassing several interesting and generic features of biochemical networks (biochemical adaptation, proofreading, positive and negative feedback loops, combinatorics, etc.). Such models serve as ideal tests for the generality of .
The performance of a network performing absolute discrimination is illustrated in Fig. 2. We can plot the values of the network output O as a function of ligand concentration L, for different values of τ (Fig. 2 B). Absolute discrimination between ligands is possible only if one (or more realistically few) values of τ correspond to a given output value O(L, τ) (as detailed in (24)). Intuitively, this is not possible if the dose response curves O(L, τ) are monotonic: the reason is that for any value of output O, one can find many associated couples of (L, τ) (see Fig. 2 B). Thus, ideal performance corresponds to separated horizontal lines, encoding different values of O for different τ independently of L (Fig. 2 B). For suboptimal cases and optimization purposes, a probabilistic framework is useful. Our fitness is the mutual information between the distribution of outputs O with τ for a predefined sampling of L, as proposed in (30). If those distributions are not well separated (meaning that we can frequently observe the same output value for different values of τ and L; Fig. 2 C, top), the mutual information is low and the network performance is bad. Conversely, if those distributions are well separated (Fig. 2 C, bottom), this means that a given output value is statistically very often associated to a given value of τ. Then the mutual information is high and network performance is good. More details on this computation can be found in Fig. S2.
We have run on three different models of this process: adaptive sorting with one proofreading step (30), a simple model based on feedback by phosphatase SHP-1 from (10) (SHP-1 model), and a complex realistic model accounting for multiple feedbacks from (31) (Lipniacki model). Initial models are described in more detail in the following sections. We have taken published parameters as initial conditions. Those three models were all explicitly designed to describe absolute discrimination, modeled as sensitive and specific sensing of ligands of a given binding time τ (24), so ideally those networks would have perfect fitness. However, due to various biochemical constraints, these three models have very good initial (but not necessarily perfect) performance for absolute discrimination. We see that after some initial fitness improvement, reaches an optimum fitness within a few steps and thus merely simplifies models while keeping constant fitness (see fitness values in the Supporting Material). We have tested with several parameters of the fitness functions, and we give in the following for each model the most simplified networks obtained with the help of those fitness functions. Complementary details and other reductions are given in the Supporting Material.
For both problems, succeeds in fully reducing the system to a single equation with essentially two effective parameters at steady state (see the Supporting Material; the final model is given in the FINAL OUTPUT formula, and discussion of the effective parameters is given in Comparison and Categorization of Models). However, to help in understanding the mathematical structure of the models, it is helpful to deconvolve this final reduced expression to exhibit the underlying differential equations for the most relevant variables. In particular, this helps to identify functional submodules of the network that perform independent computations. Thus for each example below, we give a small set of differential equations capturing the functional mechanisms of the reduced model. In the figures, we show in the “FINAL” panel the behavior of the full system of ordinary differential equations including all parameters (but potentially very big or very small values after reduction, and thus including local flux conservation).
Results
for biochemical adaptation: feedforward and feedback models
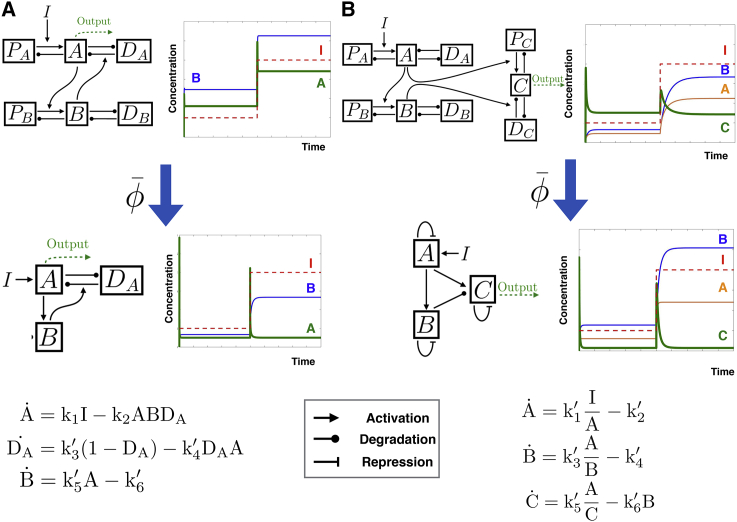
The problem of biochemical adaptation allows us to simply illustrate and compare the algorithm on problems described and well-studied elsewhere. We consider two models based on feedforward and feedback loops, with corresponding interactions between the nodes. These models are adapted from (20), and have network topologies known to be compatible with biochemical adaptation. The algorithm is designed to work with rate equations, so to keep mathematical expressions compatible with the ones in (20) we have to introduce new nodes corresponding to enzymes and regulations for production and degradation. For instance, a nonlinear degradation flux for protein A of the form −A/(A + A0) in (20) implicitly means that A deactivates its own degrading enzyme, that we include and call DA (see equations in the Supporting Material). This gives networks with 6 differential equations/12 parameters for the negative feedback network, and 9 differential equations/18 parameters for the incoherent feedforward network. For this problem, we have not tried to optimize initial parameters for the networks; instead, we start with arbitrary parameters (and thus arbitrary nonadaptive behavior), and we simply let reduce the system using the fitness function defined above. The goal is to test the efficiency of , and to see if it finds a subset of nodes/parameters compatible with biochemical adaptation by pure parameter reduction (we know from analytical studies similar to what is done in (20) that such solutions exist, but it is not clear that they can be found directly by asymptotic parameter reduction). Fig. 3 summarizes the initial network topologies considered, including the associated enzymes and the final reduced models, with equations. Steps of the reductions are given in the Supporting Material.
Figure 3.
Adaptation networks considered and their reduction by . We explicitly include production and degradation nodes (Ps and Ds) that are directly reduced into Michaelis-Menten kinetics in other works. From top to bottom, we show the original network, the reduced network, and the equations for the reduced network. Dynamics of the networks under control of a step input (I) is also shown. Notice that the initial networks are not adaptive whereas the final reduced networks are. (A) Shown here is the negative feedback network, including enzymes responsible for Michaelis-Menten kinetics for production and degradation. A is the adaptive variable. (B) Shown here are the incoherent feedforward networks. C is the adaptive variable. To see this figure in color, go online.
Both networks converge toward adaptation by working in a very similar way to networks previously described in (20, 25). For the negative feedback network of Fig. 3 A, at steady state, A is pinned to a value independent of I ensuring its adaptation by stationarity of protein B . Stationarity of A imposes that B essentially buffers the input variation and that A transiently feels I (see equations and corresponding behavior on Fig. 3 A). This is a classical implementation of integral feedback (32) with a minimum number of two nodes, automatically rediscovered by .
We see similar behavior for reduction of the incoherent feedforward networks (Fig. 3 B). At steady state, stationarity of B pins the ratio A/B to a value independent of I, whereas stationarity of C imposes that C is proportional to A/B and thus adaptive (see equations and corresponding behavior in Fig. 3 B). This is a classical implementation of another feedforward adaptive system (20, 26), rediscovered by . When varying simulation parameters for , we can see some variability in the results, where steady-state relations among A, B, and C are formally identical but with another logic (see details of such a reduction in the Supporting Material).
During parameter reduction, ratios of parameters are systematically eliminated, corresponding to classical limits such as saturation or dimensionless reductions, as detailed in the Supporting Material. Similar limits were observed in (25) when applying the MBAM to fit simulated data for biochemical adaptation. The systems reduce in both cases to a minimum number of differential equations, allowing for transient dynamics of the adaptive variable. Interestingly, in this case we have not attempted to optimize parameters a priori, but nevertheless is able to converge toward adaptive behavior only by removing parameters. In the end, we recover known reduced models for biochemical adaptation, very similar to what is obtained with artificial data fitting in (25), confirming the efficiency and robustness of fitness-based asymptotic reduction.
for adaptive sorting
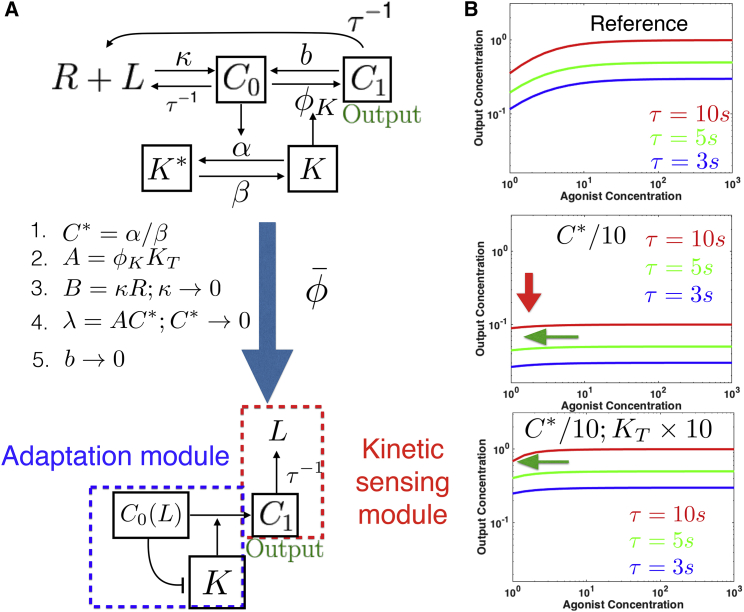
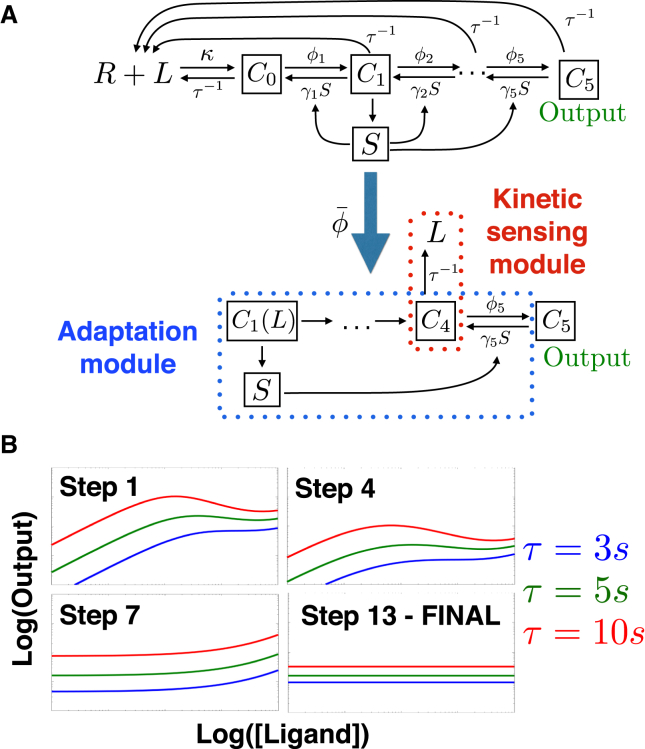
We now proceed with applications of to the more challenging problem of absolute discrimination. Adaptive sorting (30) is one of the simplest models of absolute discrimination. It consists of a one-step kinetic proofreading cascade (33) (converting complex C0 into C1) combined with a negative feedforward interaction mediated by a kinase K (see Fig. 4 A for an illustration). A biological realization of adaptive sorting exists for FCR receptors (28).
Figure 4.
Reduction of adaptive sorting. (A) Given here is a sketch of the network, with five steps of reductions by . Adaptation and kinetic sensing modules are indicated for comparison with reduction of other models. (B) Given here is an illustration of the specificity/response tradeoff solved by Step 4 of . Compared to the reference behavior (top panel), decreasing C∗ (middle panel) increases specificity with less L dependency (horizontal green arrow) but globally reduces signal (vertical red arrow). If KT is simultaneously increased (bottom panel), specificity alone is increased without detrimental effect on overall response, which is the path found by To see this figure in color, go online.
This model has a complete analytic description in the limit where the backward rate from C1 to C0 cancels out (30). The dynamics of C1 is then given by
| (1) |
K is the activity of a kinase regulated by complex C0(L), itself proportional to ligand concentration L. The K activity is repressed by C0 (Fig. 4; Eq. 1), implementing an incoherent feedforward loop in the network (the full system of equations is given in the Supporting Material).
Absolute discrimination is possible when C1 is a pure function of τ irrespective of L (so that C1 encodes τ directly) as discussed in (24, 30). Theoretically, both C0 and C1 depend on the input ligand concentration L. If we require C1 to be independent of L, the product KC0 has to become a constant irrespective of L. This is possible because K is repressed by C0, so there is a tug-of-war on C1 production between the substrate concentration C0, and its negative effect on K. In the limit of large enough C0, K indeed becomes inversely proportional to C0, giving a production rate of C1 independent of L. The τ-dependency is then encoded in the dissociation rate of C1, so that in the end C1 is a pure function of τ.
The steps of for adaptive sorting are summarized in Fig. 4 A. The first steps correspond to standard operations: step 1 is a quasi-static assumption on kinase concentration, step 2 brings together parameters having similar influence on the behavior, and step 3 is equivalent to assuming receptors are never saturated. Those steps are already taken in (30), and are automatically rediscovered by . Notably, we see that during reduction several effective parameters emerge, e.g., the parameter A = KTϕK can be identified in retrospect as the maximum possible activity of kinase K.
Step 4 is the most interesting step and corresponds to a nontrivial parameter modification specific to , which simultaneously reinforces the two tug-of-war terms described above, so that they balance more efficiently. This transformation solves a trade-off between sensitivity of the network and magnitude in response, illustrated in Fig. 4 B. If one decreases only parameter C∗, the dose response curves for different values of τ become flatter, allowing for better separation of values of τ (i.e., specificity; Fig. 4 B, middle panel). However, the magnitude of the dose response curves is proportional to C∗ so that if we were to take C∗ = 0, all dose response curves would go to zero as well and the network would lose its ability to respond. It is only when both C∗ and the parameter A = KTϕK are changed in concert that we can increase specificity without losing response (Fig. 4 B, bottom panel). This ensures that K(L) becomes always proportional to L without changing the maximum production rate AC∗ of C1. The algorithm finalizes the reduction by putting other parameters to limits that do not significantly change in the value of C1. There is no need to perform symmetry breaking for this model to reach optimal behavior and one-parameter reduction.
This simple example illustrates that not only is able to rediscover automatically classical reduction of nonlinear equations, but also, as illustrated by step 4 above, it is able to find a nontrivial regime of parameters where the behavior of the network can be significantly improved. Here this is done by reinforcing simultaneously the weight of two branches of the network implicated in a crucial incoherent feedforward loop, implementing perfect adaptation, and allowing us to define a simple adaptation submodule. The τ-dependency is encoded downstream of this adaptation module in C1, defining a kinetic sensing submodule. A general feature of is its ability to identify and reinforce crucial functional parts in the networks, as will be further illustrated below.
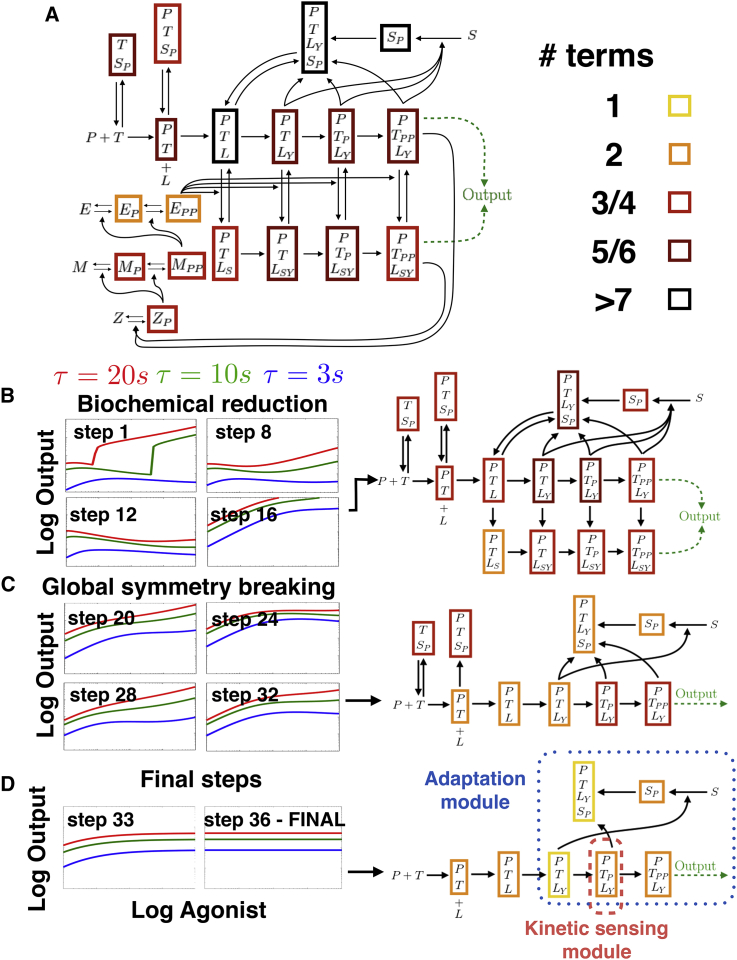
for SHP-1 model
This model aims at modeling early immune recognition by T cells (10) and combines a classical proofreading cascade (33) with a negative feedback loop (Fig. 5 A, top). The proofreading cascade with N steps amplifies the τ-dependency of the output variable, whereas the variable S in the negative feedback encodes the ligand concentration L in a nontrivial way. The full network presents dose response-curves plateauing at different values for different values of τ, allowing for approximate discrimination as detailed in (10) (Fig. 5 B, step 1). Full understanding of the steady state requires solving a N × N linear system in combination with a polynomial equation of order N − 1, which is analytically possible if N is small enough (see the Supporting Material). Behavior of the system can only be intuitively grasped in limits of strong negative feedback and infinite ligand concentration (10). The logic of the network appears superficially similar to the previously described adaptive sorting network, with a competition between proofreading and feedback effects compensating for L, thus allowing for approximated kinetic discrimination based on parameter τ. Other differences include the sensitivity to ligand antagonism because of the different number of proofreading steps, discussed in (24).
Figure 5.
Reduction of SHP-1 model. (A) Given here is the initial model considered and the final reduced model (bottom). Step 1 shows the initial dynamics. Equations can be found in the Supporting Material. The algorithm (with parameter symmetry breaking) eliminates most of the feedback interactions by S, separating the full network into an adaptation module and a kinetic sensing module. See main text for discussion. (B) Dose response curves for τ = 3, 5, 10 s and different steps of reduction are given, showing how the curves become more and more horizontal for different τ, corresponding to better absolute discrimination. Corresponding parameter modifications are given in the Supporting Material. FINAL panel shows behavior of Eqs. 9–15 in the Supporting Material (full system including local mass conservation). To see this figure in color, go online.
When performing on this model, the algorithm quickly gets stuck without further reduction in the number of parameters and corresponding network complexity. By inspection of the results, it appears that the network is too symmetrical: variable S acts in exactly the same way on all proofreading steps at the same time. This creates a strong nonlinear feedback term that explains why the nonmonotonic dose-response curves are approximately flat as L varies as described in (10), as well as other features, such as loss of response at high ligand concentration that is sometimes observed experimentally. This also means the output can never be made fully independent of L (see details in the Supporting Material). But it could also be interesting biologically to explore limits where dephosphorylations are more specific, corresponding to breaking symmetry in parameters.
We thus perform symmetry breaking, so that converges in <15 steps, as shown in one example presented in Fig. 5. The dose-response curves as functions of τ become flatter while the algorithm proceeds, until perfect absolute discrimination is reached (flat lines in Fig. 5 B, step 13).
A summary of the core network extracted by is presented in Fig. 5 A (in the Supporting Material, we explicitly list the equations of the core network, illustrating how all reaction terms are initially present in the original model; this ensures that we obtain an existing limit on the original model manifold). In brief, symmetry breaking in parameter space concentrates the functional contribution of S in one single network interaction. This actually reduces the strength of the feedback, making it exactly proportional to the concentration of the first complex in the cascade C1, allowing for a better balance between the negative feedback and the input signal in the network.
After the reduction, the dynamics of the last two complexes in the cascade can be simply extracted analytically and are given by
| (2) |
| (3) |
Now at steady state, we get ϕ5C4 = γ5SC5 from Eq. 3 so that those terms cancel out in Eq. 2; and we get that at steady state, C4 = ϕ4τC3. Due to the removal by of the reaction backward terms with S in the cascade C1 → C2 → C3, C3 is exactly proportional to C1 in the reduced model. Looking back at Eq. 3, it means that at steady state both the production and the degradation rates of C5 are proportional to C1 (respectively via C3 for production and S for degradation). This is another tug-of-war effect, so that at steady-state C5 concentration is independent of C1 and thus from L. However, there is an extra τ-dependency coming from C4 at steady state (Eq. 2), so that C5 concentration is simply proportional to a power of τ (see full equations in the Supporting Material).
Again, identifies and focuses on different parts of the network to perform perfect absolute discrimination. Symmetry breaking in the parameter spaces allows us to decouple identical proofreading steps and effectively makes the behavior of the network more modular, so that only one complex in the cascade is responsible for the τ-dependency (see kinetic sensing module in Fig. 5) whereas another one carries the negative interaction of S (see adaptation module in Fig. 5).
When varying initial parameters for reduction, we see different possibilities for the reduction of the network (see examples in the Supporting Material). Although different branches for degradation by S can be reinforced by , eventually only one of them performs perfect adaptation. Similar variability is observed for τ-sensing. Another reduction of this network is presented in the Supporting Material.
for Lipniacki model
Although the algorithm works nicely on the previous examples, the models are simple enough that in retrospect the reduction steps might appear as natural (modulo nontrivial effects such as mass conservation or symmetry breaking). It is thus important to validate the approach on a more complex model, which can be understood intuitively but is too complex mathematically to assess without simulations, a situation typical in systems biology. It is also important to apply to a published model that is not designed by ourselves.
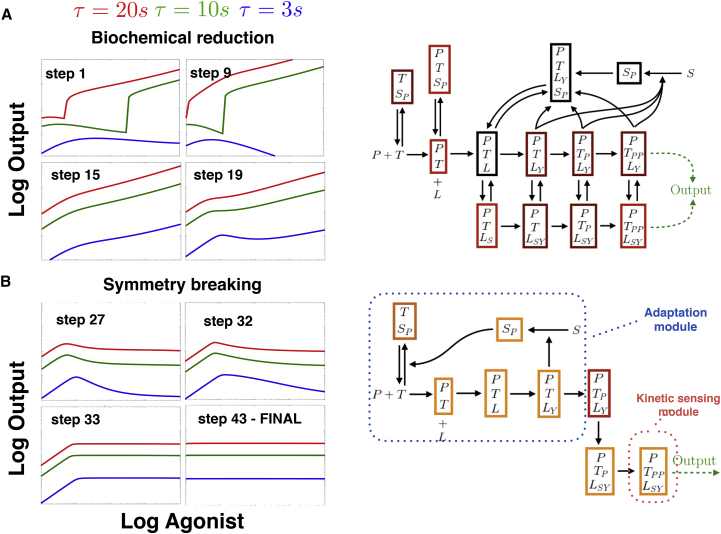
We thus consider a much more elaborate model for T cell recognition proposed in (31) and inspired by (34). This models aims at describing many known interactions of receptors in a realistic way, and accounts for several kinases such as Lck, ZAP70, ERK, and phosphatases such as SHP-1—multiple phosphorylation states of the internal ITAMs. Furthermore, this model accounts for multimerization of receptors with the enzymes. As a consequence, there is an explosion of the number of cross-interactions and variables in the system, as well as associated parameters (because all enzymes modulate variables differently), which renders its intractable without numerical simulations. It is nevertheless remarkable that this model is able to predict a realistic response line (e.g., Fig. 3 in (31)), but its precise quantitative origin is unclear. The model is specified in the Supporting Material by its 21 equations that include a hundred-odd terms corresponding to different biochemical interactions. With multiple runs of we found two variants of reduction. Figs. 6 and 7 illustrate examples of those two variants, summarizing the behavior of the network at several reduction steps. Due to the complexity of this network, we first proceed with biochemical reduction. Then we use the reduced network and perform symmetry breaking.
Figure 6.
Reduction of Lipniacki model. (A) Given here is the initial model considered. We indicate complexity with colored squared boxes that correspond to the number of individual reaction rates in each of the corresponding differential equations for a given variable. (B–D) Dose response curves for different reduction steps are given. Step 1 shows the initial dynamics. From top to bottom, graphs on the right column display the (reduced) networks at the end of steps 16 (biochemical reduction), 32 (symmetry breaking), and 36 (final model). The corresponding parameter reduction steps are given in the Supporting Material. FINAL panel shows behavior of Eqs. 28–34 in the Supporting Material (full system is given, including local mass conservation). To see this figure in color, go online.
Figure 7.
Another reduction of the Lipniacki model starting from the same network as in Fig. 6A leading to a different adaptive mechanism. The corresponding parameter reduction steps are given in the Supporting Material. (A) Initial biochemical reduction suppresses the positive feedback loop in a similar way (compare with Fig. 6B). (B) Symmetry breaking breaks proofreading cascades and isolates different adaptive and kinetic modules (compare with Fig. 6D). FINAL panel shows behavior of Eqs. 35–43 in the Supporting Material (full system is given, including local mass conservation). To see this figure in color, go online.
The network topology at the end of both reductions is shown in Figs. 6 and 7 with examples of the network for various steps. Interestingly, the steps of the algorithm correspond to successive simplifications of clear biological modules that appear in retrospect unnecessary for absolute discrimination (multiple runs yield qualitatively similar steps of reduction). In both cases, we observe that biochemical optimization first prunes out the ERK positive feedback module (which in the full system amplifies response), but keeps many proofreading steps and cross regulations. The optimization eventually gets stuck because of the symmetry of the system, just like we observed in the SHP-1 model from the previous section (Figs. 6 B and 7 A).
Symmetry breaking is then performed, and allows us to considerably reduce the combinatorial aspects of the system, reducing the number of biochemical species and fully eliminating one parallel proofreading cascade (Fig. 6 C) or combining two cascades (Fig. 7 B). In both variants, the final steps of optimization allow for further reduction of the number of variables keeping only one proofreading cascade in combination with a single loop feedback via the same variable (corresponding to phosphorylated SHP-1 in the complete model).
Further study of this feedback loop reveals that it is responsible for biochemical adaptation, similarly to what we observed in the case of the SHP-1 model. However, the mechanism for adaptation is different for the two different variants and corresponds to two different parameter regimes.
For the variant of Fig. 6, the algorithm converges to a local optimum for the fitness. However upon inspection, the structure appears very close to the SHP-1 model reduction, and can be optimized by putting three additional parameters to zero. Again, the dynamics at the end of reduction is simple enough that it can be comprehended analytically. The output of the system of Fig. 6 is then governed by three variables out of the initial 21 and is summarized by
| (4) |
| (5) |
| (6) |
Here C5(L) is one of the complex concentrations midway of the proofreading cascade (we indicate here L dependency that can be computed by mass conservation but is irrelevant for the understanding of the mechanism). S is the variable accounting for phosphatase SHP-1 in the Lipniacki model, and Rtot is the total number of unsaturated receptors (the reduced system with the name of the original variables is given in the Supporting Material).
At steady state, S is proportional to C5(L) from Eq. 5. We see from Eq. 4 that the production rate of C7 is also proportional to C5(L). Its degradation rate ϕ2 + γS is proportional to S if ϕ2 ≪ γS (which is the case). So both the production and degradation rates of C7 are proportional (similar to what happens in the SHP-1 model, Eq. 3), and the overall contribution of L cancels out. This corresponds to an adaptation module.
One τ-dependency remains downstream of C7 through Eq. 6 (realizing a kinetic sensing module) so that the steady-state concentration of CN is a pure function of τ, thus realizing absolute discrimination. Notably, this model corresponds to a parameter regime where most receptors are free from phosphatase SHP-1, which actually allows for the linear relationship between S and C5.
For the second variant, when the system has reached optimal fitness, the same feedback loop in the model performs perfect adaptation, and the full system of equations in both reductions has similar structure (compare Eqs. 28–34 to Eqs. 35–43 in the Supporting Material). But the mechanism for adaptation is different: this second reduction corresponds to a regime where receptors are essentially all titrated by SHP-1. More precisely, we have (calling Rf the free receptors, and Rp the receptors titrated by SHP-1):
| (7) |
| (8) |
| (9) |
| (10) |
Now at steady state, ϵ is small so that almost all receptors are titrated in the form Rp, and thus Rp Rtot. This fixes the product Rf(L)S ∝ Rtot to a value independent of L in Eq. 7, so that at steady state of S in Eq. 8, C5 = ϵRtot/λ is itself fixed at a value independent of L. This implements an integral feedback adaptation scheme (32). Down C5, there is a simple linear cascade so that one τ-dependency survives (Eq. 10), ensuring kinetic sensing and absolute discrimination by the final complex of the cascade CN.
Comparison and categorization of models
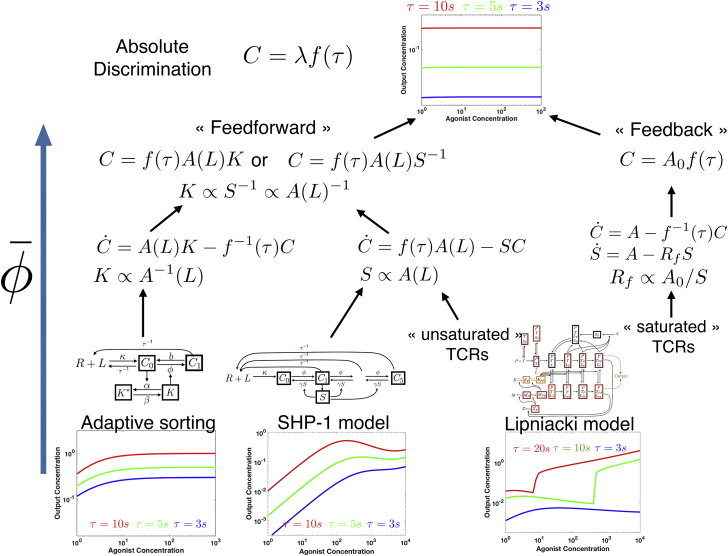
An interesting feature of is that reduction allows us to formally classify and connect models of different complexities. We focus here on absolute discrimination only. Our approach allows us to distinguish at least four levels of coarse-graining for absolute discrimination, as illustrated in Fig. 8.
Figure 8.
Categorization of networks based on reduction. Absolute discrimination models considered here (bottom of the tree) can all be coarse-grained into the same functional forms (top of the tree). Intermediate levels in reduction correspond to two different mechanisms—feedforward-based and feedback-based. See main text for discussion. To see this figure in color, go online.
At the upper level, with maximal coarse-graining and minimal complexity, we observe that all reduced absolute discrimination models considered can be broken down into two parts of similar functional relevance. In all reduced models, we can clearly identify an adaptation module realizing perfect adaptation (defining an effective parameter λ in Fig. 8), and a kinetic sensing module performing the sensing of τ (function f(τ) in Fig. 8). If f(τ) = τ, we get a two-parameter model, where each parameter relates to a submodule.
The models can then be divided in the nature of the adaptation module, which gives a functional level of coarse-graining at the second level of complexity. With , we automatically recover a dichotomy previously observed for biochemical adaptation between feedforward and feedback models (20, 26). The second variant of Lipniacki relies on an integral feedback mechanism, where adaptation of one variable (C5) is due to the buffering of a negative feedback variable (S(L)) ((7), (8), (9); Fig. 8). Adaptive sorting, the SHP-1 model and the first variant of Lipniacki model instead rely on a feedforward adaptation module where a tug-of-war between two terms (an activation term A(L) and feedforward terms K/S in Fig. 8) exactly compensates.
The tug-of-war necessary for adaptation is realized in two different ways, which is an implementation level of coarse-graining at the third level of complexity. In adaptive sorting, this tug-of-war is realized at the level of the production rate of the output, which is made ligand independent by a competition between a direct positive contribution and an indirect negative one (Eq. 1; Fig. 8). In the reduced SHP-1 model, the concentration of the complex C upstream of the output is made L independent via a tug-of-war between its production and degradation rates. The exact same effect is observed in the first variant of the Lipniacki model: at steady state, from Eqs. 4 and 5, the production and degradation rates of C7 are seen as proportional (Fig. 8), which ensures adaptation. So allows us to rigorously confirm the intuition that the SHP-1 model and the Lipniacki model indeed work in a similar way and belong to the same category in the unsaturated receptor regime. We also notice that suggests a new coarse-grained model for absolute discrimination based on modulation of degradation rates, with fewer parameters and simpler behavior than the existing ones, by assuming specific dephosphorylation in the cascades (we notice that some other models have suggested specificity for the last step of the cascade, e.g., in limited signaling models (11)).
Importantly, the variable S, encoding for the same negative feedback in both the SHP-1 and the first reduction of Lipniacki model, plays a similar role in the reduced models, suggesting that two models of the same process, although designed with different assumptions and biochemical details, nevertheless converge to the same class of models. This variable S also is the buffering variable in the integral feedback branch of the reduction of the Lipniacki model, yet adaptation works in a different way for this reduction. This shows that even though the two reductions of the Lipniacki model work in different parameter regimes and rely on different adaptive mechanisms, the same components in the network play the crucial functional roles, suggesting that the approach is general. As a negative control of both the role of SHP-1 and more generally of the algorithm, we show in the Supporting Material for the SHP-1 model that reduction does not converge in the absence of the S variable (Fig. S3).
Coarse-graining further allows us to draw connections between network components and parameters for those different models. For instance, the output is a function of K(L)A(L) for adaptive sorting and A(L)S(L)−1 for SHP-1/Lipniacki models. In both cases, A(L) is a smooth function of ligand concentrations (corresponding to an upstream complex) exactly compensated by K and S. So we can formally identify K(L) with S(L)−1. The immediate interpretation is that deactivating a kinase is similar to activating a phosphatase, which is intuitive but only formalized here by model reduction.
At lower levels of coarse graining, complexity is increased, so that many more models are expected to be connected to the same functional absolute discrimination model. For instance, when we run several times, the kinetic discrimination module on the SHP-1 model is realized on different complexes (see several other examples in the Supporting Material). Also, the precise nature and position of kinetic discriminations in the network might influence properties that we have not accounted for in the fitness. In the Supporting Material, we illustrate this on ligand antagonism (35): depending on the complex regulated by S in the different reduced models, and adding back kinetic discrimination (in the form of τ−1 terms) in the remaining cascade on the reduced models, we can observe different antagonistic behavior, comparable with the experimentally measured antagonism hierarchy (Fig. S4). Finally, a more realistic model might account for nonspecific interactions (relieved here by parameter symmetry breaking), which might only give approximate biochemical adaptation (as in (10)) although still keeping the same core principles (adaptation + kinetic discrimination) that are uncovered by
Discussion
When we take into account all possible reactions and proteins in a biological network, a potentially infinite number of different models can be generated. But it is not clear how the level of complexity relates to the behavior of a system, nor how models of different complexities can be grasped or compared. For instance, it is far from obvious whether a network as complex as the one from (31) (Fig. 6 A) can be simply understood in any way, or if any clear design principle can be extracted from it. We propose , a simple procedure to reduce complex networks, which is based on a fitness function that defines network phenotype, and on simple coordinated parameter changes.
The algorithm relies on the optimization of a predefined fitness that is required to encode coarse-grained phenotypes. It performs a direct exploration of the asymptotic limit on boundary manifolds in parameter space. In silico evolution of networks teaches us that the choice of fitness is crucial for successful exploration in parameter spaces and to allow for the identification of design principles (22). Fitness should capture qualitative features of networks that can be improved incrementally. An example is mutual information, and simulations optimizing it have recently led to new insights on the design and evolution of biological systems for development (36) and immune recognition (30), as further illustrated here. Although adjusting existing parameters or even adding new ones (potentially leading to overfitting) could help in optimizing this fitness, it is not obvious a priori that systematic removal of parameters is possible without decreasing the fitness, even for networks with initial good fitness. For both cases of biochemical adaptation and absolute discrimination, is nevertheless efficient at pruning and reinforcing different network interactions in a coordinated way while keeping an optimum fitness, finding simple limits in network space, with submodules that are easy to interpret. Reproducibility in the simplifications of the networks suggests that the method is robust.
In the examples of SHP-1 and Lipniacki models, we notice that disentangles the behavior of a complex network into two submodules with well-identified functions, one in charge of adaptation and the other of kinetic discrimination. To do so, is able to identify and reinforce tug-of-war terms, with direct biological interpretation. This allows for a formal comparison of models. The reduced SHP-1 model and the first reduction of the Lipniacki model have a similar feedforward structure, controlled by a variable corresponding to phosphatase SHP-1 defining the same biological interaction. This is reassuring because both models aim to describe early immune recognition; this was not obvious a priori from the complete system of equations or the considered network topology (compare Fig. 5 with Fig. 6 A). These feedforward dynamics discovered by contrast with the original feedback interpretation of the role of SHP-1 from the network topology only (10, 31, 34). Adaptive sorting, although performing the same biochemical function, works differently by adapting the production rate of the output, and thus belongs to another category of networks (Fig. 8).
The algorithm is also able to identify different parameter regimes for a network performing the same function, thereby uncovering an unexpected network plasticity. The two reductions of the Lipniacki model work in a different way (one is feedforward-based, the other one is feedback-based), but importantly, the crucial adaptation mechanism relies on the same node, again corresponding to phosphatase SHP-1, suggesting the predictive power of this approach irrespective of the details of the model. From a biological standpoint, because the same network can yield two different adaptive mechanisms depending on the parameter regime (receptors titrated or not by SHP-1), it could be that both situations are observed. In mouse, T cell receptors do not bind to phosphatase SHP-1 without engagement of ligands (37), which would be in line with the reduction of the SHP-1 model and the first variant of the Lipniacki model reduction. But we cannot exclude that a titrated regime for receptors exists, e.g., due to phenotypic plasticity (38), or that the very same network works in this regime in another organism. More generally, one may wonder if the parameters found by are realistic in any way. In the cases studied here, the values of parameters are not as important as the regime in which the networks behave. For instance, we saw for the feedforward models that some specific variables have to be proportional, which requires nonsaturating enzymatic reactions. Conversely, the second reduction of the Lipniacki model requires titration of receptors by SHP-1. These are direct predictions on the dynamics of the networks, not specifically tied to the original models.
Because works by sequential modifications of parameters, we get a continuous mapping between all the models at different steps of the reduction process, via the most simplified one-parameter version of the model. By analogy with physics, thus renormalizes different networks by coarse-graining (17), possibly identifying universal classes for a given biochemical computation, and defining subclasses (39). This allows us to draw correspondences between networks with very different topologies, formalizing ideas such as the equivalence between activation of a phosphatase and repression of a kinase (as exemplified here by the comparison of influences of K(L) and S(L) in reduced models from Fig. 8). In systems biology, models are neither traditionally simplified, nor are there systematic comparisons between models, in part because there is no obvious strategy to do so. The approach proposed here offers a solution for both comparison and reduction, which complements other strategies such as the evolution of phenotypic models (22) or direct geometric modeling in phase space (9).
To fully reduce complex biochemical models, we have to perform symmetry breaking on parameters. Similar to parameter modifications, the main role of symmetry breaking is to reinforce and adjust dynamical regimes in different branches of the network, e.g., imposing proportionality to tug-of-war terms. Intuitively, symmetry breaking embeds complex networks into a higher dimensional parameter space allowing for better optimization. Much simpler networks can be obtained with this procedure, which shows in retrospect how the assumed nonspecificity of interactions strongly constrains the allowed behavior. Of course, in biology, some of this complexity might also have evolutionary adaptive values. More detailed models are valuable and needed to model behaviors that we do not consider here, such as amplification or bistability (31, 40). A tool like allows for a reductionist study by specifically focusing on one phenotype of interest to extract its core working principles. Once the core principles are identified, it should be easier to complexify a model by accounting for other potential adaptive phenotypes (e.g., as is done to reduce antagonism in (30) or in Fig. S4).
Finally, there is a natural evolutionary interpretation of . In both evolutionary computations and evolution, random parameter modifications in evolution can push single parameters to zero or potentially very big values (corresponding to the ∞ limit). However, it is clear from our simulations that concerted modifications of parameters are needed, e.g., for adaptive sorting, the simultaneous modifications of the kinetics and the efficiency of a kinase regulation is required in step 4 of the reduction. Evolution might select for networks explicitly coupling parameters that need to be modified in concert. Conversely, there might be other constraints preventing efficient optimizations in two directions in parameter space at the same time, due to epistatic effects. Gene duplications provide an evolutionary solution to relieve such tradeoffs, after which previously identical genes can diverge and specialize (41). This clearly bears resemblance to the symmetry breaking proposed here. For instance, having two duplicated kinases instead of one would allow us to have different phosphorylation rates in the same proofreading cascades. We also see, in the examples of Figure 5, Figure 6, Figure 7, that complex networks that cannot be simplified by pure parameter changes can be improved by parameter symmetry breaking via decomposition into independent submodules. Similar evolutionary forces might be at play to explain the observed modularity of gene networks (8). More practically, could be useful as a complementary tool for artificial or simulated evolution (22) to simplify complex simulated dynamics (42).
Author Contributions
P.F., conceptualization. T.J.R., methodology. P.F. and T.J.R., software, validation, and formal analysis. F.P.-G., T.J.R., and P.F., investigation. P.F., writing. F.P.-G. and P.F., funding acquisition. P.F., project administration and supervision.
Acknowledgments
We thank the members of the François group for their comments on the manuscript. We also thank anonymous referees for useful comments.
This work was supported by a Simons Investigator in Mathematical Modelling of Biological Systems award to P.F. F.P.G. is supported by a Fonds de Recherche du Québec Nature et Technologies (FRQNT) Master fellowship.
Editor: Stanislav Shvartsman.
Footnotes
Félix Proulx-Giraldeau and Thomas J. Rademaker contributed equally to this work.
Supporting Materials and Methods, four figures, eighteen tables, and one data file are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30931-1.
Supporting Material
This package contains MATLAB code used for the FIBAR reductions presenter in the main text.
References
- 1.Karr J.R., Sanghvi J.C., Covert M.W. A whole-cell computational model predicts phenotype from genotype. Cell. 2012;150:389–401. doi: 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Markram H., Muller E., Schürmann F. Reconstruction and simulation of neocortical microcircuitry. Cell. 2015;163:456–492. doi: 10.1016/j.cell.2015.09.029. [DOI] [PubMed] [Google Scholar]
- 3.Lander A.D. The edges of understanding. BMC Biol. 2010;8:40. doi: 10.1186/1741-7007-8-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jonas E., Kording K.P. Could a neuroscientist understand a microprocessor? PLoS Comput. Biol. 2017;13:e1005268. doi: 10.1371/journal.pcbi.1005268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mayer J., Khairy K., Howard J. Drawing an elephant with four complex parameters. Am. J. Phys. 2010;78:648–649. [Google Scholar]
- 6.Lever J., Krzywinski M., Altman N. Points of significance: model selection and overfitting. Nat. Methods. 2016;13:703–704. [Google Scholar]
- 7.Gunawardena J. Models in biology: “accurate descriptions of our pathetic thinking”. BMC Biol. 2014;12:29. doi: 10.1186/1741-7007-12-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Milo R., Shen-Orr S., Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- 9.Corson F., Siggia E.D. Geometry, epistasis, and developmental patterning. Proc. Natl. Acad. Sci. USA. 2012;109:5568–5575. doi: 10.1073/pnas.1201505109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.François P., Voisinne G., Vergassola M. Phenotypic model for early T-cell activation displaying sensitivity, specificity, and antagonism. Proc. Natl. Acad. Sci. USA. 2013;110:E888–E897. doi: 10.1073/pnas.1300752110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lever M., Maini P.K., Dushek O. Phenotypic models of T cell activation. Nat. Rev. Immunol. 2014;14:619–629. doi: 10.1038/nri3728. [DOI] [PubMed] [Google Scholar]
- 12.Krol A.J., Roellig D., Pourquié O. Evolutionary plasticity of segmentation clock networks. Development. 2011;138:2783–2792. doi: 10.1242/dev.063834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brown K.S., Sethna J.P. Statistical mechanical approaches to models with many poorly known parameters. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:021904. doi: 10.1103/PhysRevE.68.021904. [DOI] [PubMed] [Google Scholar]
- 14.Brown K.S., Hill C.C., Cerione R.A. The statistical mechanics of complex signaling networks: nerve growth factor signaling. Phys. Biol. 2004;1:184–195. doi: 10.1088/1478-3967/1/3/006. [DOI] [PubMed] [Google Scholar]
- 15.Gutenkunst R.N., Waterfall J.J., Sethna J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Transtrum M.K., Machta B.B., Sethna J.P. Perspective: sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 2015;143:010901. doi: 10.1063/1.4923066. [DOI] [PubMed] [Google Scholar]
- 17.Machta B.B., Chachra R., Sethna J.P. Parameter space compression underlies emergent theories and predictive models. Science. 2013;342:604–607. doi: 10.1126/science.1238723. [DOI] [PubMed] [Google Scholar]
- 18.Daniels B.C., Nemenman I. Automated adaptive inference of phenomenological dynamical models. Nat. Commun. 2015;6:8133. doi: 10.1038/ncomms9133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Daniels B.C., Nemenman I. Efficient inference of parsimonious phenomenological models of cellular dynamics using S-systems and alternating regression. PLoS One. 2015;10:e0119821. doi: 10.1371/journal.pone.0119821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ma W., Trusina A., Tang C. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cotterell J., Sharpe J. An atlas of gene regulatory networks reveals multiple three-gene mechanisms for interpreting morphogen gradients. Mol. Syst. Biol. 2010;6:425. doi: 10.1038/msb.2010.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.François P. Evolving phenotypic networks in silico. Semin. Cell Dev. Biol. 2014;35:90–97. doi: 10.1016/j.semcdb.2014.06.012. [DOI] [PubMed] [Google Scholar]
- 23.Transtrum M.K., Qiu P. Model reduction by manifold boundaries. Phys. Rev. Lett. 2014;113:098701. doi: 10.1103/PhysRevLett.113.098701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.François P., Altan-Bonnet G. The case for absolute ligand discrimination: modeling information processing and decision by immune T cells. J. Stat. Phys. 2016;162:1130–1152. [Google Scholar]
- 25.Transtrum M.K., Qiu P. Bridging mechanistic and phenomenological models of complex biological systems. PLoS Comput. Biol. 2016;12:e1004915. doi: 10.1371/journal.pcbi.1004915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.François P., Siggia E.D. A case study of evolutionary computation of biochemical adaptation. Phys. Biol. 2008;5:026009. doi: 10.1088/1478-3975/5/2/026009. [DOI] [PubMed] [Google Scholar]
- 27.Feinerman O., Germain R.N., Altan-Bonnet G. Quantitative challenges in understanding ligand discrimination by αβ T cells. Mol. Immunol. 2008;45:619–631. doi: 10.1016/j.molimm.2007.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Torigoe C., Inman J.K., Metzger H. An unusual mechanism for ligand antagonism. Science. 1998;281:568–572. doi: 10.1126/science.281.5376.568. [DOI] [PubMed] [Google Scholar]
- 29.Taylor M.J., Husain K., Vale R.D.A. A DNA-based T cell receptor reveals a role for receptor clustering in ligand discrimination. Cell. 2017;169:108–119.e20. doi: 10.1016/j.cell.2017.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lalanne J.B., François P. Principles of adaptive sorting revealed by in silico evolution. Phys. Rev. Lett. 2013;110:218102. doi: 10.1103/PhysRevLett.110.218102. [DOI] [PubMed] [Google Scholar]
- 31.Lipniacki T., Hat B., Hlavacek W.S. Stochastic effects and bistability in T cell receptor signaling. J. Theor. Biol. 2008;254:110–122. doi: 10.1016/j.jtbi.2008.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yi T.M., Huang Y., Doyle J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McKeithan T.W. Kinetic proofreading in T-cell receptor signal transduction. Proc. Natl. Acad. Sci. USA. 1995;92:5042–5046. doi: 10.1073/pnas.92.11.5042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Altan-Bonnet G., Germain R.N. Modeling T cell antigen discrimination based on feedback control of digital ERK responses. PLoS Biol. 2005;3:e356. doi: 10.1371/journal.pbio.0030356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.François P., Hemery M., Saunders L.N. Phenotypic spandrel: absolute discrimination and ligand antagonism. Phys. Biol. 2016;13:066011. doi: 10.1088/1478-3975/13/6/066011. [DOI] [PubMed] [Google Scholar]
- 36.François P., Siggia E.D. Predicting embryonic patterning using mutual entropy fitness and in silico evolution. Development. 2010;137:2385–2395. doi: 10.1242/dev.048033. [DOI] [PubMed] [Google Scholar]
- 37.Dittel B.N., Stefanova I., Janeway C.A., Jr. Cross-antagonism of a T cell clone expressing two distinct T cell receptors. Immunity. 1999;11:289–298. doi: 10.1016/s1074-7613(00)80104-1. [DOI] [PubMed] [Google Scholar]
- 38.Feinerman O., Veiga J., Altan-Bonnet G. Variability and robustness in T cell activation from regulated heterogeneity in protein levels. Science. 2008;321:1081–1084. doi: 10.1126/science.1158013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Transtrum M. K., Hart G, and Qiu P. 2014. Information topology identifies emergent model classes. arXiv.org. arXiv:1409.6203.
- 40.Rendall A. D., and Sontag E. D. 2017. Multiple steady states and the form of response functions to antigen in a model for the initiation of T cell activation. arXiv.org. arXiv:1705.00149. [DOI] [PMC free article] [PubMed]
- 41.Innan H., Kondrashov F. The evolution of gene duplications: classifying and distinguishing between models. Nat. Rev. Genet. 2010;11:97–108. doi: 10.1038/nrg2689. [DOI] [PubMed] [Google Scholar]
- 42.Sussillo D., Abbott L.F. Generating coherent patterns of activity from chaotic neural networks. Neuron. 2009;63:544–557. doi: 10.1016/j.neuron.2009.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
This package contains MATLAB code used for the FIBAR reductions presenter in the main text.