Abstract
Quantifying the relationship between protein sequence and structure is key to understanding the protein universe. A fundamental measure of this relationship is the total number of amino acid sequences that can fold to a target protein structure, known as the “sequence capacity,” which has been suggested as a proxy for how designable a given protein fold is. Although sequence capacity has been extensively studied using lattice models and theory, numerical estimates for real protein structures are currently lacking. In this work, we have quantitatively estimated the sequence capacity of 10 proteins with a variety of different structures using a statistical model based on residue-residue co-evolution to capture the variation of sequences from the same protein family. Remarkably, we find that even for the smallest protein folds, such as the WW domain, the number of foldable sequences is extremely large, exceeding the Avogadro constant. In agreement with earlier theoretical work, the calculated sequence capacity is positively correlated with the size of the protein, or better, the density of contacts. This allows the absolute sequence capacity of a given protein to be approximately predicted from its structure. On the other hand, the relative sequence capacity, i.e., normalized by the total number of possible sequences, is an extremely tiny number and is strongly anti-correlated with the protein length. Thus, although there may be more foldable sequences for larger proteins, it will be much harder to find them. Lastly, we have correlated the evolutionary age of proteins in the CATH database with their sequence capacity as predicted by our model. The results suggest a trade-off between the opposing requirements of high designability and the likelihood of a novel fold emerging by chance.
Introduction
The database of protein sequences contains a wealth of evolutionary information. In particular, since for folded proteins their structure is critical to their biological function, the requirement of native-state stability alone places a strong evolutionary constraint on the set of sequences allowed for a given structure, in addition to functional constraints such as binding or enzymatic function (1, 2, 3). How many sequences are there that satisfy this requirement of stability for a given protein fold (4)? The answer to this question is a fundamental property of the fold known as the sequence capacity (SC), and it is often used as a measure of protein “designability” (5, 6). This designability has been shown to be highly correlated with the actual sizes of gene families (7). From the perspective of evolution, if the SC of a protein system is large, its structure or function is likely to be robust to mutation (8). Higher SC has also been associated with a higher rate of protein evolution (9) and with thermophilic adaptation (10). The snapshot of the protein universe contained in the UniProt database (11) includes 70 million protein sequences, a number that is still growing rapidly owing to the recent efforts in genomic sequencing. However, even if the current genomic databases were complete, they could not be used directly to count the number of sequences belonging to a given fold, for the simple reason that sequence space is vast and likely only a tiny fraction has been explored. Indeed, recent work has shown that the sequence universe is still expanding (12). Similarly, even though natural protein sequences are optimized for their native structures (13), there are still many artificial sequences that can be designed to fold to the same structure (14).
Since counting the number of sequences that fold to a given structure implies knowing which structure each sequence folds to, the problem of protein designability is closely related to the folding problem—already a challenge for computational models. Therefore, pioneering works on protein designability and its relation to protein structure have been carried out using simplified physical models (5, 15, 16, 17) in which the energy of a protein conformation is given by the summation of pairwise contact potentials. A key conclusion of these theoretical works was that the SC is primarily determined by the contact density, i.e., the total number of contacts, normalized by the sequence length. Theoretical arguments and analytic theory further supported this conclusion (6, 18). However, because these studies used lattice models and highly coarse-grained energy functions, they could not quantitatively address the SC of real protein folds. Atomistic redesign methods have been used to address the designability of certain folds (13, 19), although the sampling problem for these is much more challenging. Alternatively, computationally cheap threading methods (14, 20, 21, 22), in which sequences are scored in the context of a structure using a simple contact potential, have also been used to estimate the SC of the proteins that are registered in the Protein Data Bank (PDB) (23, 24).
Given the challenges associated with structure-based modeling, an alternative may be to exploit directly the evolutionary information contained in the large database of protein sequences now available. An important aspect of this information is coevolution of residues at different positions in a protein (25, 26). Because the structure of folded proteins is critical for their function, it imposes a strong constraint on the mutational history: during evolution, if one residue is mutated to a different amino acid, the proximal residue is also likely to mutate to maintain compatible interactions. This residue-residue coevolution signal can be detected from covariance analysis of the sequences of homologs, which is usually done by fitting a likelihood model including residue-residue couplings to observed sequence data. Such models have been successfully exploited to predict residue pairs that are in contact in the native state (i.e., those with significant couplings between them) (25, 27, 28, 29, 30, 31, 32). These predicted contacts have provided a new tool for protein structure determination.
Inspired by these results, in this article, we take a complementary approach to estimating SC. We use the observed sequences from the same protein family to infer a fitness model for sequences that can fold into a given structure, using a likelihood function similar to those used for contact prediction. Our approach avoids the problem of determining protein folds ab initio; instead, we exploit the known information about which sequences fold to a given structure. We show that the model can capture the pattern of sequence variation of natural sequences in terms of single-site propensity and residue-residue covariation inferred from evolutionary information. Furthermore, the associated energy function is a good predictor of native-state stability, as would be expected. By combining these two insights, we are able to estimate the total number of sequences folding to a given structure by simple integration of the density of states. We apply the model to 10 different protein folds, chosen for the availability of both sequence information and experimentally measured stabilities; the latter allow the threshold energy values for foldable sequences to be determined. We have verified the robustness of our approach by applying it to a simple lattice model, which can be directly enumerated. We can generalize our estimates to other folds by establishing an empirical relation, justified by theory, between the contact density of a fold and its SC. This relation allows us to estimate the SC of each protein fold in the CATH database. Analysis of the CATH sequence capacities supports our finding that there is a minimal contact density for a folded protein. It also suggests a tension in evolution between optimizing SC and maximizing the probability of finding a new fold by chance, which we term “discoverability.”
Materials and Methods
Choice of proteins
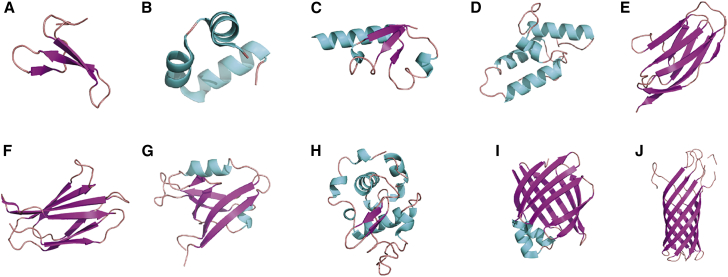
We have chosen for our study 10 different single-domain proteins (Fig. 1) whose folds are common in nature, i.e., there are many sequences which fold to these structures. The set includes all-β proteins: WW domains (33), the outer membrane protein OmpA (90), the immunoglobulin-like β-sandwich domain titin I27 (35), and the fibronectin type III domain from tenascin (TNfn3) (36); all-α proteins: villin (37) and the bacterial immunity protein Im7 (38); and α/β proteins: the ribosomal domain NTL9 (39), a PDZ domain (40), α-lactabumin (α-LA) (41), and fatty acid binding protein-like protein (IFABP) (34). An additional criterion for selection was that stability data should be available for a large number of mutants of each protein (most frequently, from ϕ-value analysis). In earlier ϕ-value studies, thermodynamic information for multiple mutants was obtained for villin (42), the titin I27 domain (43), the PDZ domain (44), OmpA (45), Im7 (46), IFABP (47), α-LA (48), TNfn3 (49), NTL9 (50), and the WW domain (51). These rich experimental data allow us to evaluate our evolutionary model by predicting the folding stability of different mutants.
Figure 1.
Representative structures of the proteins we studied here: (A) WW domain (PDB: 1I5H (33)), (B) villin (PDB: 1QQV (37)), (C) NTL9 (PDB: 1DIV (39)), (D) Im7 (PDB: 1AYI (38)), (E) titin I27 (PDB: 1TIT (35)), (F) TNfn3 (PDB: 1TEN (36)), (G) PDZ domain (PDB: 1GM1 (40)), (H) α-lactalblumin (PDB: 1HFY (41)), (I) IFABP (PDB: 1IFC (34)), and (J) OmpA (PDB: 1QJP (90)). To see this figure in color, go online.
Multiple sequence alignment and reweighting
For each protein family in Fig. 1, we have built a likelihood function for foldable sequences based on multiple sequence alignments (MSAs). The input MSAs were generated using the Jackhammer method (52) with an E-value of ( for titin I27 considering its high abundance in nature) and eight iterations, using the Uniref90 database (53). Sequences that have >25% gaps were removed. The sequences obtained in the MSA usually have a phylogenetic bias. A sequence re-weighting algorithm is therefore used here to mitigate the effects of uneven sampling of sequences. The algorithm has previously been very successful in improving the accuracy of protein structure prediction (54). Specifically, the weight given to a sequence, , is set to , where is the number of sequences in the MSA similar to : , where is the fraction sequence identity between two sequences and , and N is the total number of sequences in the MSA. x is a threshold whose optimal value was found to be 0.8. The same reweighting scheme is also used on the sequences from the hydrophobic-polar (HP) model, described below.
Statistical model of protein sequences
To find protein sequences that can fold to a given structure, the amino acid composition should follow the pattern of the natural sequences that fold into the same structure, represented by an MSA for the fold in question. We describe this pattern using a statistical model that includes parameters for single-site amino acid propensity as well as residue-residue co-evolution. Specifically, we describe the likelihood of an amino acid sequence to fold into a given protein structure, using the function
| (1) |
In this Potts-type model, the parameters represent the propensity for amino acid to occur at position i in a sequence. In addition to this conventional sequence propensity, the parameters measure the coupling propensity of amino acids and to be at aligned positions i and j. Z is the partition function, defined such that the likelihood is normalized over all possible sequences. With the MSA as input (Supporting Material), our aim is to maximize the log-likelihood of the observed sequences , . Because optimizing the likelihood directly is very expensive owing to the size of the sequence space, we instead use an established pseudolikelihood optimization method (54) to estimate the parameters of h and J with appropriate regularization to prevent overfitting.
Specifically, a regularization term is added to the negative pseudo-log-likelihood to keep unimportant parameters close to zero and thus avoid overfitting:
| (2) |
where and are two regularization parameters for single-site and coupling parameters. The empirically determined optimal is 0.05 (54).
By defining a corresponding evolutionary Hamiltonian energy, , for a given sequence A as
| (3) |
it is possible to sample sequences from the likelihood function using algorithms sampling the canonical distribution, such as the Metropolis Monte Carlo (55) used here. Note that although this energy is formally dimensionless, we report it in units of by analogy with statistical mechanics. This provides the means, in principle, to compute the SC, provided we can also determine which sequences are stable. In this way, we would not rely on existing databases to sample sequence space exhaustively (since in reality only a tiny (and biased) fraction of possible sequences is likely to be sampled).
Computational sampling in protein sequence space
To fully explore the mutational landscape and find the absolute sequence entropy as a function of , simulated annealing Monte Carlo simulations (Eq. 4) are carried out. In each Monte Carlo iteration, the amino acid of one random chosen residue is perturbed by a flip from one type of amino acid to another, taking the system from one sequence, x, of energy to a new sequence, , with energy . The move is accepted/rejected with acceptance probability
| (4) |
where , with being the Boltzmann constant and T the temperature. The simulations are started at a very high temperature to permit many sequence rearrangements. Then, the system is cooled down slowly with the temperature decreased in steps, with the time between temperature steps long enough for it to reach equilibrium at each new temperature level. Each simulation is terminated when the sequence is frozen. All the trial mutations are chosen from existing amino acid types in the same aligned position of the MSA. Besides the 20 natural amino acids, we also allow gaps to be sampled (as captured by the model (Eq. 1)), since the sequence length of the same protein family fluctuates slightly.
For every protein system we studied here, 100 independent simulated annealing simulations are carried out from random sequences; each simulation contains 10 billion Monte Carlo steps, and β starts at 0.1 and increases 0.04 every 100 million steps. Histograms of at different temperatures are extracted from the simulations. The overall density of states (sequence entropy) is obtained by combining the histograms using WHAM (56).
HP model
The model is a 27-mer HP model that contains two types of beads to represent polar and hydrophobic amino acids (5, 57, 58, 59) (Fig. 4), and that can be exhaustively enumerated owing to the reduced amino acid alphabet. The energy of the HP sequence in a target structure is based on the contact interactions:
| (5) |
where if residues and are adjacent on the lattice but not adjacent in sequence, and otherwise. The energy contribution, , depends on the residue types of and . = −2.3, = 0.0, and = −1.0 (5).
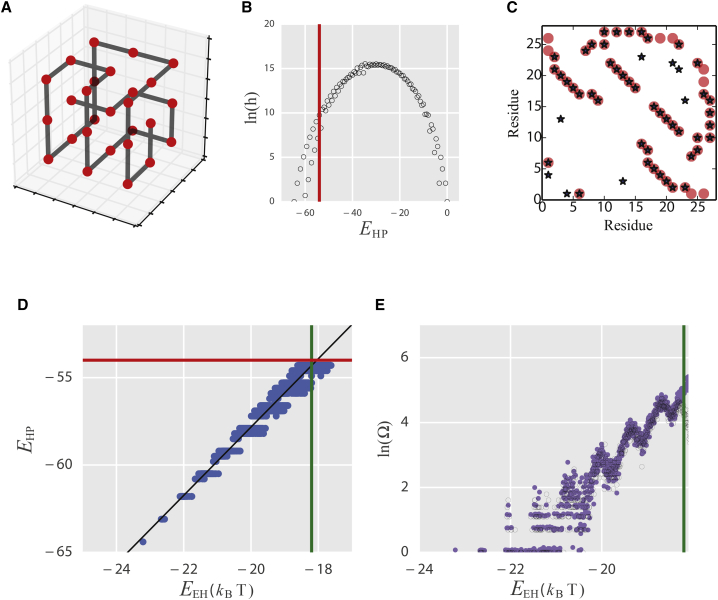
Figure 4.
Lattice-model test of robustness of the coevolutionary model for determining SC. (A) The most designable 27-mer structure for the HP model. (B) The logarithm of the density of sequences on the HP energy. (C) Native contact predictions from the fitness model. Native contacts are shown as red circles and the (top 27) predicted contacts based on the sequences as blue crosses. (D) Correlation of the energy in the HP model, , with the evolutionary energy, , for all the sequences . The green line is , which is obtained by fitting the correlation between and with a black line at position (red line). (E) The logarithms of the exact density of sequences on from enumeration of the HP model are shown in black; corresponding results from Monte Carlo simulations using the energy are shown in purple. To see this figure in color, go online.
In fitting the statistical potential to the sequences from the HP model, we have slightly modified the regularization term: owing to the reduced alphabet of the HP model, we found that = 0.5 is a more optimal value in that case with respect to native contact prediction accuracy. Similar to proteins, the residue coupling score can be obtained by the norm of Ji,j,
| (6) |
where the amino acid types of a and b are only “H” or “P.” The final ranking score, , is adjusted by an average-product correction term to reduce the background effect (60). A large value of means the mutations at residues i and j are highly correlated and the two residues are likely to be in contact in the 3D structure.
Alternative scaling of density of states
As an alternative procedure to obtain the absolute scaling of the density of states, , we use the concept of the median energy , which is the energy value, , at which 50% of the amino acid sequence energies are below it and 50% are above. It can be estimated easily by unbiased sampling of random sequences. If a protein is composed of L residues, and the total number of existing amino acid types at residue position i is , the total number of different possible sequences (with gaps allowed) is , so that the number of sequences below the median energy is simply (23). The parameter γ is introduced to scale the estimation of obtained from simulated annealing simulations. Given the and the median energies , γ can be estimated by requiring
| (7) |
Then, the adjusted SC is given by
| (8) |
The adjusted SC estimated by the median energy method is shown in Fig. S4. As is evident, the adjusted estimations are in general consistent with the direct estimations in Fig. 3 in the main text.
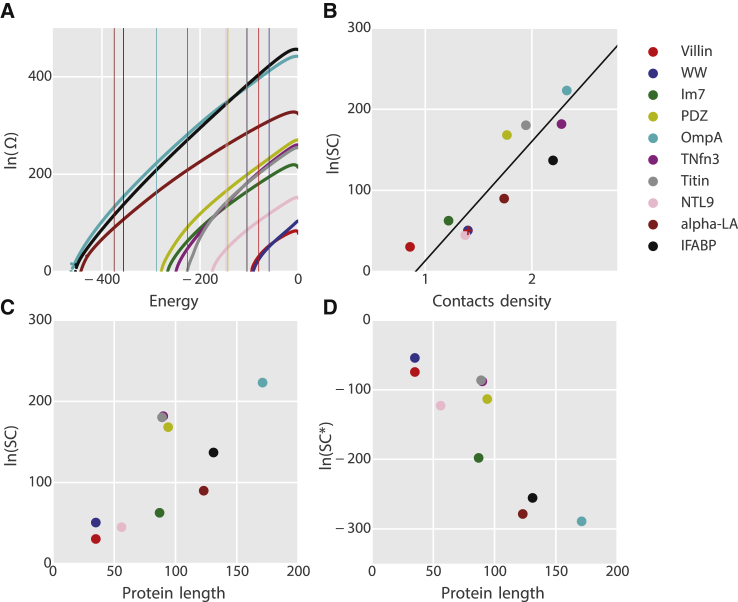
Figure 3.
Densities of sequences and SCs. (A) Entropy of sequences on the coordinate for each of the 10 proteins. The vertical lines are the boundaries of foldability () obtained for each protein (Fig. S1). (B and C) Correlations of the SC with CD (B) and protein length (C). The red plus sign in (B) is the SC of the WW domain calculated using = −59.2 . The black line in (B) is a linear fit to the dependence of ln(SC) on CD. (D) SC∗ plotted against the protein length. To see this figure in color, go online.
Results and Discussion
Fitness of protein sequences correlates with thermodynamic stability
We have chosen for our study 10 protein folds (Fig. 1) that are common in the structural and sequence databases, and therefore amenable to statistical sequence analysis. The proteins were also selected to be representative of different structural classes (such as all-α, all-β, or α/β), and to have extensive mutational data, for reasons which will become clear. For each of these folds, we have inferred a fitness model and corresponding statistical energy. Theoretical models have reasonably assumed that the fitness of protein sequences is correlated with the thermodynamic stability of their folded states (15, 61, 62). Consistent with this hypothesis, several recent studies have shown that there is indeed a correlation between the statistical energy, , from such evolutionary models and protein stability (3, 63).
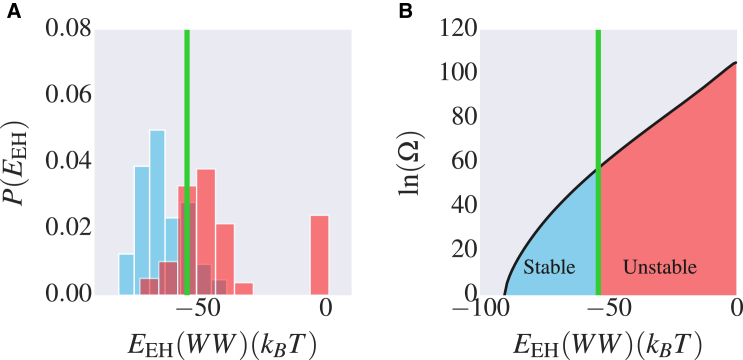
Therefore, we can in principle identify stable sequences by establishing a critical value, , below which most sequences are expected to be stable. To demonstrate this for the 10 proteins we consider, we have built an evolutionary model of the form of Eq. 1 for each protein family. For example, for the 35-residue WW domain (Fig. 1 A), 42 natural sequences and 105 artificial sequences have been characterized systematically by experiment (1). Among all the sequences, 28 of the natural sequences and 12 of the artificial sequences can adopt a WW-domain fold (1). In addition, the PDB contains a further 68 wild-type and mutated WW-domain sequences with solved structures, which we also consider to be stable proteins. Taken together, there are in total 108 protein sequences that are known to adopt the WW-domain fold and 107 sequences that do not. We have calculated the of each sequence, and the distributions of these two groups of sequences are shown in Fig. 2 A. As anticipated, separates the two groups fairly well, the approximate border being ∼ , which we define as the folding energy, . There is some overlap of the folded and unfolded sequences on the coordinate . At least some of this must be due to the limitations of our energy function. In addition, factors besides stability will play an auxiliary role in determining the fitness of a sequence.
Figure 2.
Correlation of evolutionary Hamiltonian energy, , with protein stability. (A) Distribution of of experimentally characterized stable (blue) and unstable (red) sequences of the WW domain. (B) Estimated entropy of sequences (on a log scale) along , obtained by Monte Carlo simulation. The green line is the approximate threshold of separating the stable and unstable sequences of the WW domain. To see this figure in color, go online.
For the other nine protein families, we have fewer mutant sequences to determine than for the WW domain, and in particular few unstable sequences. Therefore, we adopt an alternative approach based on the correlation between and experimental folding stability for different mutations (Fig. S1), as has been observed for other proteins (3, 63). By extrapolating a linear fit of these data to a stability of zero, we can determine the critical . We have tested the robustness of estimating the using this method on the WW domain. The folded state stability of a wild-type WW domain and 64 mutants, which are different from the sequences used in Fig. 2 A, are reported in an experimental ϕ-value study of the WW domain (51). To be consistent with the temperature at which the stability of the mutants in Fig. 2 A was determined, the folded-state stability was calculated at 298 K from the reported thermodynamic data (51). The estimated (Fig. S1) is −59.2 , very close to the value obtained from Fig. 2 A, −54.0 . The same approach was used to estimate the critical folding energy, , for the other domains we studied. An important consequence of this correlation is that it should be possible to design sequences that are more stable than the wild-type based on the sequence energy. Indeed, we find for titin I27, TNfn3, and NTL9 that the several variants that are more stable also have lower statistical energy, supporting this conclusion (Fig. S1). It should also be possible to use this method to design foldable sequences, a goal we are currently pursuing.
Since the simple cutoff on does not exactly separate folded and unfolded sequences, there will be some fraction of sequences predicted to fold that do not (false positive fraction (FPF)) and vice versa (false negative fraction (FNF)). Given the density of sequences (Fig. 2 B) and the fraction of sequences predicted to be folded that are in fact unstable according to experiment (Fig. 2 A), we can estimate the false positives from the WW-domain data for the SC estimation. By assuming that the fraction of foldable sequences at a given energy is correctly estimated, we computed the fraction of non-foldable sequences as
| (9) |
where = −59.2 . We describe as a sigmoidal function fitted to the observed fraction of folded sequences at each energy value from the experimental data.
Although we include non-foldable sequences, we also miss some foldable sequences that have energy larger than our simple cutoff. The number of false negatives as a fraction of our prediction of non-foldable sequence space can be computed from
| (10) |
The FPF and FNF values we obtained for the WW domain are 31.0% and 0.3%, respectively. Considering that we are making order-of-magnitude estimates of the SC, these errors are acceptable.
Density of sequences on
Since is a good indicator of foldability, we set out to calculate the SC starting with the density of states (i.e., sequences) in , (i.e., the total number of possible sequences per unit of ); an analogous approach has previously been applied in lattice-model studies (16). We estimate using simulated annealing Monte Carlo simulations in sequence space (Eq. 4). For the WW domain, for example, all the sequences whose value falls below −59.2 are considered to adopt the native fold.
However, to estimate the total SC, it is critical to determine an absolute scale for the density of sequences, . We did this in two ways that gave comparable results. In the first, we located, where possible, the unique sequence with the global minimum energy and used this to scale the overall density of states. Since 100 simulated annealing simulations of the WW domain (starting from different, random initial sequences) converge to the same final amino acid sequence, we assign that sequence the lowest energy. The resulting estimated for the WW domain is shown in Fig. 2 B. This procedure also consistently yielded the same lowest-energy sequence in independent simulated annealing simulations for each of the other proteins considered, with the exception of OmpA. This protein may be unusual due to inherent differences in the sequence energy landscape between membrane proteins (such as OmpA) and globular proteins (all of the others considered). For OmpA, the global minimal energy was approximated by the lowest energy of 100 independent annealing simulations. We also used an independent approach for scaling the sequence entropy by determining the median energy (23), as described in the Materials and Methods; very similar final results were obtained, as shown in Fig. S4.
Quantitative estimates of SC
Having obtained both the density of states on and an estimated cutoff , we can now obtain the sequence capacity by simple integration of the density of states. It is clear that the SC is an enormous number. For example, in the case of the WW domain, the SC is estimated to be , larger even than Avogadro’s number! However, the relative SC, SC∗, i.e., the fraction of the total number of possible sequences ( for the WW domain) that fold is extremely tiny, with SC∗ for the WW domain. We note that considering the small variations of length in sequences that fold to a given structure (accommodated by gaps in our model) changes the number of possible sequences by a negligible amount (<5%). In addition, using the alternative of also yields a very similar SC for the WW domain (Fig. 3 B, red plus sign).
The SC and SC∗ of each of the 10 protein structures are listed in Table 1. The densities of sequences as a function of are plotted in Fig. 3 A.
Table 1.
Estimates of SC
| Protein | L | Fold | SC | SC∗ | M |
|---|---|---|---|---|---|
| WW | 35 | all-β | 9.9 | 2.9 | 5800 |
| Villin | 35 | all-α | 1.6 | 4.7 | 759 |
| NTL9 | 56 | α/β | 3.2 | 4.4 | 4828 |
| IM7 | 87 | all-α | 1.6 | 1.1 | 536 |
| Titin I27 | 89 | all-β | 2.0 | 3.2 | 55,422 |
| TNfn3 | 90 | all-β | 8.5 | 6.9 | 66,289 |
| PDZ | 94 | α/β | 1.2 | 5.8 | 30,176 |
| α-LA | 123 | α/β | 1.1 | 1.0 | 934 |
| IFABP | 131 | α/β | 3.0 | 1.1 | 1691 |
| OmpA | 171 | all-β | 7.9 | 2.6 | 31,397 |
L refers to the protein length, SC∗ is the absolute SC normalized by the total number of possible sequences (), and M is the number of sequences in the MSA for each protein family.
This calculation of the SC makes an important assumption: if a sequence is predicted to be stable for a given fold, it should not be more stable (or even similarly stable) in some other fold. We do not think this is a significant effect in our calculation for two reasons. First, if we treat the probabilities of a sequence folding to each of two different folds as being independent, it is clear from the low probability of being stable in even a single fold that the probability of being stable in two folds is negligible. Second, it is well known that it is extremely rare for a protein to be stable in alternative folds. Even in those cases, usually one fold is most stable, and some energetic factor, e.g., dimer formation, ligand binding, or change of solution conditions is needed to cause a switch to a different fold (64).
Robustness test of SC estimation
A key issue for our model is that it has been parameterized using a limited set of sequences compared with the total number of sequences that can fold. The obvious question that arises is how dependent our knowledge-based model is on the number of sequences for a protein that are available in the database. To mitigate this dependence, we have deliberately chosen proteins for which a large number of sequences are already known. We have also determined, for all the proteins studied here, that using only half of the sequences (Fig. S2, gray) to build the energy function still results in a prediction of comparably low energies (high propensities) for the omitted sequences (Fig. S2, red). Moreover, as shown in Fig. S3, the SC estimated using half of the sequence of MSA is highly consistent with the value estimated using the full MSA (Fig. 3). This suggests that the accuracy of the model does not depend critically on the size of the database.
To further validate whether a small subset of sequences can be used to recapitulate the properties of the full set of foldable sequences, we have employed a highly simplified 27-mer lattice model in which the chain is confined to lie on a cubic lattice (i.e., considering only compact conformations such as that shown in Fig. 4 A). Similar models have been used previously to study protein designability (16, 65, 66), as well as to benchmark inferred Potts Hamiltonians (Eq. 1) (67). Although highly simplified, it has been found that the trends of designability obtained with the HP model agree qualitatively with those using the Miyazawa-Jernigan model (68), which uses all 20 amino acids (69). The restriction to a 3 3 3 cubic lattice allows the such conformations to be enumerated for each sequence, versus the conformations on an unrestricted cubic lattice (70). This restriction is somewhat unrealistic for protein folding, as unfolded conformations will not, in general, be compact (70, 71); furthermore, it has been shown that in many cases the true lowest-energy (native) configuration is not even a compact structure (71). However, since our aim is to count foldable sequences within the context of a simplified model, rather than to have a more realistic model, we can include the restriction to compact structures in our model definition. We could alternatively have used a two-dimensional HP model, the only type of lattice model for which all conformations can be practically enumerated (72, 73). We have chosen not to do this here, because the SCs tend to be much smaller (e.g., the SC of the most designable structure of a 24-mer is 228 (74), and only 24 sequences are left if sequences with >90% sequence identity are removed).
We chose the most designable structure of the 27-mer three-dimensional HP lattice model, shown in Fig. 4 A (5), and we enumerated the energy of all possible HP sequences threaded onto this structure (density of states shown in Fig. 4 B). We assume that the relative folded-state stability of the sequences is given by (i.e., that the energy and entropy of the unfolded states of all sequences are similar). We initially defined the foldable sequences as those with , where is chosen as −54.0, so that only sequences in the low-energy tail of the distribution are included, yielding a total of 22,185 sequences. We then constructed a subset of the foldable sequences by filtering the full set of foldable sequences so that the maximum pairwise sequence identity is 90% to yield a subset, , which contains 994 sequences. We used the MSA of these 994 sequences as input to build the Hamiltonian energy, , as Eq. 1. The structure contacts predicted (Fig. 4 C) using the covariance parameters obtained in Eq. 1, are highly consistent with the “native contacts” of the lattice structure (Fig. 4 A), showing that the sequence model can accurately describe the foldable sequences that can fold to the target structure. Similar results were also obtained for a randomly chosen subset of 1% of the foldable sequences.
As for the real proteins (Fig. S1), we found that the of the HP model sequences is highly correlated with the stability, , so that the boundary of foldability defined by the evolutionary model can be determined from the stability, , using this correlation (Fig. 4 D). Following the same procedures as for the real proteins, we estimate the absolute sequence entropy of the HP model as a function of by carrying out simulated annealing Monte Carlo simulations (Eq. 4). As one can see, the estimated sequence entropy agrees very well with the exact sequence entropy on (Fig. 4 E). The estimated SC from Fig. 4 E (purple) is 21,398, which is very close to the exact SC of 22,185. In summary, the SC estimation of a lattice model, which can be enumerated (75), indicates that our method is robust.
In the above example we have successfully recovered the HP-model SC, in which folded sequences are defined purely by the physical energy. However, the folded state is normally taken as the unique, lowest-energy structure for a given sequence. We have therefore checked the energy of each of our foldable sequences (as defined by ) when it is threaded onto a set of 10,000 representative compact folds (67). This comparison revealed that the model is in fact quite degenerate, with many sequences having other folds of equal or slightly lower energy, likely due to the limited sequence alphabet. Moreover, the lowest-energy sequences also have a high fraction of hydrophobic residues and hence the most potential for degeneracy. We therefore defined the foldable sequences as those for which the target structure (Fig. 4 A) is below = −54.0 and also a ground state for that sequence, i.e., there are no other structures with lower energy for that sequence (69). A total of 2880 sequences fulfill these two requirements; we constructed a subset, , of 207 sequences, after filtering with maximum pairwise sequence identity of 90%. The MSA of these 207 sequences sequences was used to build the Hamiltonian energy (Eq. 1). As shown in Fig. S5 A, the of the HP-model sequences still correlated very well with the stability and the estimated SC of 8409 (density of sequences is shown in Fig. S5 B) remains close to the true sequence capacity of 2880, considering the order of magnitude nature of our estimate. The predicted 8409 sequences show a good overlap with the true stable sequences, with 89% of the learning set and 84% of the full set of foldable sequences being included in the predictions.
Long-range native contacts are important for protein designability
The SC and SC∗ values of all the 10 protein structures are listed in Table 1. The densities of sequences as a function of are plotted in Fig. 3 A. Previous theoretical studies had suggested that SC is determined by contact density (CD), which is the total number of native contacts of the protein structure divided by the sequence length (6, 18). A simplified explanation for this is that structures with higher CD can be designed to be more stable (with the right choice of sequence) because of the higher number of total interactions, and that more stable proteins are more designable, because they allow more unfavorable interactions to be accommodated without making the folded state unstable. Very short-range contacts, although numerous, would not contribute much to stability, as they are also likely to be formed in the unfolded state.
To test the relation of SC to CD, we define two residues as being in contact as long as any pair of heavy atoms, one from each residue, are closer than 4.5 Å. We observed that the correlation between SC and CD varies depending on the chosen minimal residue distance for the CD calculation. We do not find significant correlations between SC and CD for a minimal sequence separation of native contacts between residues i and j of for , similar to what has been found using sequence threading (24). On the other hand, there is a strong correlation between SC and CD for for , where local contacts are excluded in the CD calculation. This is consistent with previous studies suggesting that long-range contacts are more important in determining the designability of proteins (17, 76, 77). In Fig. 3 B, SC is plotted against CD with , giving a Spearman rank correlation of 0.93. The SC also increases with protein length (Fig. 3 C), as expected from the general trend of increasing CD with length (due to the reduced contribution from surface residues in larger proteins). We note anecdotally that for proteins of similar length in our data set, the SC appears to be more discriminating than protein size alone. For example, both villin and the WW domain have 35 residues, but the WW domain has many more long-range contacts and it has higher SC. Similarly, Im7, titin I27, TNfn3, and the PDZ domain all contain around 90 residues, and the SC is clearly distinguished by the CD with .
Although absolute SC increases with CD or protein size, the SC∗ decreases (Fig. 3 D) with sequence length, indicating that although larger proteins may have more sequences available to design, the task of finding those sequences from the many possible sequences may be harder. Thus, if the absolute SC is associated with the “designability” of a sequence, the SC∗ could be assigned to its “discoverability.”
How big is the sequence universe of natural protein folds?
There are ∼70 million protein sequences registered in the UniProt database so far (11). According to either the CATH (78) or SCOPe (79) databases, all of these sequences can be classified into only ∼2000 superfamilies. The number of registered sequences is increasing rapidly owing to the advances of genomic sequencing techniques. However, the number of distinct protein superfamilies appears to be saturating (80). Protein sequences with the same superfamily share highly similar protein structure. Given the good correlation between CD and SC, we sought to use CD to predict the SC of each protein superfamily based on the CD of a representative PDB structure. Assuming a negligible sequence overlap between different superfamilies (81), we can estimate the total number of possible stable sequences of all the natural folds by summing up the SCs of all the superfamilies.
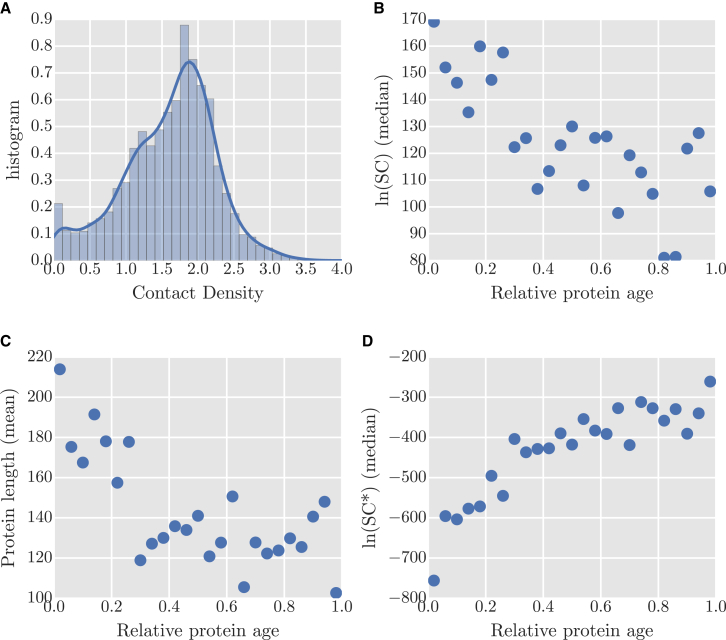
A straight-line fit to the data in Fig. 3 B yields a simple approximation for the SC of a given structure, with with best-fit parameters of and . This expression suggests a minimal designable , below which it will be hard to find foldable sequences. With this empirical function, we can estimate the SC of a given structure from the CD. The histogram of CDs of 2737 representative structures (one structure from each superfamily) from the CATH database are shown in Fig. 5 A. Indeed, there are very few superfamilies whose CD lies below 0.9. The structures in most of those superfamilies have very few, if any, tertiary contacts, such as single α-helices (CATH: 1.20.5) and the “irregular” architecture in CATH (CATH: 4.10). These are mainly protein subunits, e.g., ribosomal protein S8 (CATH: 1.20.5.1150) and Foot-And-Mouth Disease Virus subunit (CATH: 4.10.90.10), which derive their stability from assembly with other proteins or biomolecules. Considering the SC of these proteins without their partner domains makes little sense, so here we consider only the SC of the domains whose CD is >0.9. By adding together the SCs of all those superfamilies, the number of all the foldable sequences of the current (natural) fold universe is estimated to be 7.4 . Considering that there is evidence that the naturally occurring folds are just a small fraction of the possible folds (82, 83), the total number of foldable protein sequences over all folds would be even larger.
Figure 5.
(A) Histogram of CDs for all the representative protein structures (2737) from each CATH superfamily. (B–D) The relative age of all the superfamilies from the CATH database are plotted against the median of SC (B), mean protein length (C), and median of SC∗ (D). To see this figure in color, go online.
Older proteins have larger SC
Protein evolutionary history might be influenced by many structural properties (9). Here, we have investigated the relation between the evolutionary age of proteins and their SC. The relative evolutionary ages of different CATH superfamilies have been previously estimated using phylogenetic analysis (84, 85, 86, 87). Here, we compare the ages of CATH superfamilies determined by Alva et al. (87) with our estimates of SC. As shown in Fig. 5 B, we find that there is a clear trend for ancient folds to have higher SC than the folds that have arisen more recently (Spearman rank correlation = −0.86; note that the relative protein ages of 1.0 and 0.0 represent the most recent and ancient proteins, respectively). This may be because the higher designability enabled by the more complex (larger) folds with higher CD is ultimately more desirable; protein folds can become increasingly complex over the course of evolution by fusion, repetition, and recombination (Fig. 5 C) (86, 88). High designability is desirable, because it results in folds that are more robust to mutation and allows more functional diversity (89). Therefore, highly designable proteins are more likely to emerge though adaptive evolution.
However, considering the relationship between the SC∗ and protein age reveals the opposite result: SC∗ is highly anti-correlated with protein age (Fig. 5 D). Although a larger absolute SC may emerge in more highly evolved folds as a result of selective pressure, there may also be advantages to a higher SC∗ for more recent folds. A higher SC∗ means that these novel structures would then have a higher probability of emerging by chance, rather than evolving from something else. There is thus some tension between the competing advantages conferred by high absolute or relative SC, which may lead to the correlations observed with protein age.
Conclusions
Using a protein fitness model based on sequence variation inferred from evolutionary information, our study has provided a quantitative estimate of the SC for 10 different protein families by computational sampling of sequence space. We find that the SC of even the simplest folds is enormous, exceeding even the Avogadro constant, suggesting a lot of room for redesign of existing structures. Our SC estimates appear to be robust, as they are not sensitive to the size of the protein sequence database used; furthermore, our method successfully predicts the SC of a lattice protein model, which can be exactly enumerated, based on a small subset of the foldable sequences. We find that larger proteins, or those with higher CD, are more designable, in accord with theoretical predictions. On the other hand, the SC∗ is strongly anti-correlated with protein length. Therefore, accessing the larger SC of larger proteins places more demanding requirements on rational design protocols, such that the search problem in sequence space can be overcome. Based on our results, we have obtained a simple empirical formula to predict SC from CD. The formula predicts that structures with a CD of <0.9 (using our definition) would be hard to design. Indeed, analysis of the CATH database of protein structures reveals that those with a CD of <0.9 are generally part of a larger complex, and unstable in isolation. Our SC estimates for the CATH database enable us to estimate the total SC of the known universe of protein structures, and to correlate the SC of a fold with its evolutionary age. We find that more recently evolved proteins have higher SC∗, which may be an advantage for initial discovery of a folded structure, but that more ancient proteins have a higher absolute SC, suggesting that evolution guides proteins toward more designable structures.
Author Contributions
P.T. and R.B. designed research; P.T. performed research; P.T. analyzed data; P.T. and R.B. wrote the article.
Acknowledgments
We thank Prof. Gustavo Caetano-Anollés for sharing the data of protein ages for the CATH superfamilies. P.T. and R.B. were supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health. This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).
Editor: Michele Vendruscolo.
Footnotes
Five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30934-7.
Supporting Material
References
- 1.Socolich M., Lockless S.W., Ranganathan R. Evolutionary information for specifying a protein fold. Nature. 2005;437:512–518. doi: 10.1038/nature03991. [DOI] [PubMed] [Google Scholar]
- 2.Bloom J.D., Labthavikul S.T., Arnold F.H. Protein stability promotes evolvability. Proc. Natl. Acad. Sci. USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Morcos F., Schafer N.P., Wolynes P.G. Coevolutionary information, protein folding landscapes, and the thermodynamics of natural selection. Proc. Natl. Acad. Sci. USA. 2014;111:12408–12413. doi: 10.1073/pnas.1413575111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Finkelstein A.V., Gutun A.M., Badretdinov AYa Why are the same protein folds used to perform different functions? FEBS Lett. 1993;325:23–28. doi: 10.1016/0014-5793(93)81407-q. [DOI] [PubMed] [Google Scholar]
- 5.Li H., Helling R., Wingreen N. Emergence of preferred structures in a simple model of protein folding. Science. 1996;273:666–669. doi: 10.1126/science.273.5275.666. [DOI] [PubMed] [Google Scholar]
- 6.England J.L., Shakhnovich E.I. Structural determinant of protein designability. Phys. Rev. Lett. 2003;90:218101. doi: 10.1103/PhysRevLett.90.218101. [DOI] [PubMed] [Google Scholar]
- 7.Shakhnovich B.E., Deeds E., Shakhnovich E. Protein structure and evolutionary history determine sequence space topology. Genome Res. 2005;15:385–392. doi: 10.1101/gr.3133605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wagner A. Robustness and evolvability: a paradox resolved. Proc. Biol. Sci. 2008;275:91–100. doi: 10.1098/rspb.2007.1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bloom J.D., Drummond D.A., Wilke C.O. Structural determinants of the rate of protein evolution in yeast. Mol. Biol. Evol. 2006;23:1751–1761. doi: 10.1093/molbev/msl040. [DOI] [PubMed] [Google Scholar]
- 10.England J.L., Shakhnovich B.E., Shakhnovich E.I. Natural selection of more designable folds: a mechanism for thermophilic adaptation. Proc. Natl. Acad. Sci. USA. 2003;100:8727–8731. doi: 10.1073/pnas.1530713100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bateman A., Martin M.J., Zaru R., The UniProt Consortium UniProt: the universal protein knowledgebase. Nucleic Acids Res. 2017;45(D1):D158–D169. doi: 10.1093/nar/gkw1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Povolotskaya I.S., Kondrashov F.A. Sequence space and the ongoing expansion of the protein universe. Nature. 2010;465:922–926. doi: 10.1038/nature09105. [DOI] [PubMed] [Google Scholar]
- 13.Kuhlman B., Baker D. Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dahiyat B.I., Mayo S.L. De novo protein design: fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
- 15.Shakhnovich E.I., Gutin A.M. Engineering of stable and fast-folding sequences of model proteins. Proc. Natl. Acad. Sci. USA. 1993;90:7195–7199. doi: 10.1073/pnas.90.15.7195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shakhnovich E.I. Protein design: a perspective from simple tractable models. Fold. Des. 1998;3:R45–R58. [PubMed] [Google Scholar]
- 17.Govindarajan S., Goldstein R.A. Why are some proteins structures so common? Proc. Natl. Acad. Sci. USA. 1996;93:3341–3345. doi: 10.1073/pnas.93.8.3341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wolynes P.G. Symmetry and the energy landscapes of biomolecules. Proc. Natl. Acad. Sci. USA. 1996;93:14249–14255. doi: 10.1073/pnas.93.25.14249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koehl P., Levitt M. Protein topology and stability define the space of allowed sequences. Proc. Natl. Acad. Sci. USA. 2002;99:1280–1285. doi: 10.1073/pnas.032405199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jones D.T., Taylor W.R., Thornton J.M. A new approach to protein fold recognition. Nature. 1992;358:86–89. doi: 10.1038/358086a0. [DOI] [PubMed] [Google Scholar]
- 21.Meller J., Elber R. Linear programming optimization and a double statistical filter for protein threading protocols. Proteins. 2001;45:241–261. doi: 10.1002/prot.1145. [DOI] [PubMed] [Google Scholar]
- 22.Panchenko A.R., Marchler-Bauer A., Bryant S.H. Combination of threading potentials and sequence profiles improves fold recognition. J. Mol. Biol. 2000;296:1319–1331. doi: 10.1006/jmbi.2000.3541. [DOI] [PubMed] [Google Scholar]
- 23.Meyerguz L., Kleinberg J., Elber R. The network of sequence flow between protein structures. Proc. Natl. Acad. Sci. USA. 2007;104:11627–11632. doi: 10.1073/pnas.0701393104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cao B., Elber R. Computational exploration of the network of sequence flow between protein structures. Proteins. 2010;78:985–1003. doi: 10.1002/prot.22622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marks D.S., Hopf T.A., Sander C. Protein structure prediction from sequence variation. Nat. Biotechnol. 2012;30:1072–1080. doi: 10.1038/nbt.2419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Harms M.J., Thornton J.W. Evolutionary biochemistry: revealing the historical and physical causes of protein properties. Nat. Rev. Genet. 2013;14:559–571. doi: 10.1038/nrg3540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schug A., Weigt M., Szurmant H. High-resolution protein complexes from integrating genomic information with molecular simulation. Proc. Natl. Acad. Sci. USA. 2009;106:22124–22129. doi: 10.1073/pnas.0912100106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marks D.S., Colwell L.J., Sander C. Protein 3D structure computed from evolutionary sequence variation. PLoS One. 2011;6:e28766. doi: 10.1371/journal.pone.0028766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Morcos F., Pagnani A., Weigt M. Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. USA. 2011;108:E1293–E1301. doi: 10.1073/pnas.1111471108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kamisetty H., Ovchinnikov S., Baker D. Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. USA. 2013;110:15674–15679. doi: 10.1073/pnas.1314045110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tian P., Boomsma W., Lindorff-Larsen K. Structure of a functional amyloid protein subunit computed using sequence variation. J. Am. Chem. Soc. 2015;137:22–25. doi: 10.1021/ja5093634. [DOI] [PubMed] [Google Scholar]
- 32.Wang S., Sun S., Xu J. Accurate de novo prediction of protein contact map by ultra-deep learning model. PLOS Comput. Biol. 2017;13:e1005324. doi: 10.1371/journal.pcbi.1005324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kanelis V., Rotin D., Forman-Kay J.D. Solution structure of a Nedd4 WW domain-ENaC peptide complex. Nat. Struct. Biol. 2001;8:407–412. doi: 10.1038/87562. [DOI] [PubMed] [Google Scholar]
- 34.Scapin G., Gordon J.I., Sacchettini J.C. Refinement of the structure of recombinant rat intestinal fatty acid-binding apoprotein at 1.2-Å resolution. J. Biol. Chem. 1992;267:4253–4269. doi: 10.2210/pdb1ifc/pdb. [DOI] [PubMed] [Google Scholar]
- 35.Improta S., Politou A.S., Pastore A. Immunoglobulin-like modules from titin I-band: extensible components of muscle elasticity. Structure. 1996;4:323–337. doi: 10.1016/s0969-2126(96)00036-6. [DOI] [PubMed] [Google Scholar]
- 36.Leahy D.J., Hendrickson W.A., Erickson H.P. Structure of a fibronectin type III domain from tenascin phased by MAD analysis of the selenomethionyl protein. Science. 1992;258:987–991. doi: 10.1126/science.1279805. [DOI] [PubMed] [Google Scholar]
- 37.Vardar D., Buckley D.A., McKnight C.J. NMR structure of an F-actin-binding “headpiece” motif from villin. J. Mol. Biol. 1999;294:1299–1310. doi: 10.1006/jmbi.1999.3321. [DOI] [PubMed] [Google Scholar]
- 38.Dennis C.A., Videler H., Kleanthous C. A structural comparison of the colicin immunity proteins Im7 and Im9 gives new insights into the molecular determinants of immunity-protein specificity. Biochem. J. 1998;333:183–191. doi: 10.1042/bj3330183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hoffman D.W., Davies C., Ramakrishnan V. Crystal structure of prokaryotic ribosomal protein L9: a bi-lobed RNA-binding protein. EMBO J. 1994;13:205–212. doi: 10.1002/j.1460-2075.1994.tb06250.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Walma T., Spronk C.A., Vuister G.W. Structure, dynamics and binding characteristics of the second PDZ domain of PTP-BL. J. Mol. Biol. 2002;316:1101–1110. doi: 10.1006/jmbi.2002.5402. [DOI] [PubMed] [Google Scholar]
- 41.Pike A.C., Brew K., Acharya K.R. Crystal structures of guinea-pig, goat and bovine α-lactalbumin highlight the enhanced conformational flexibility of regions that are significant for its action in lactose synthase. Structure. 1996;4:691–703. doi: 10.1016/s0969-2126(96)00075-5. [DOI] [PubMed] [Google Scholar]
- 42.Kubelka J., Henry E.R., Eaton W.A. Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc. Natl. Acad. Sci. USA. 2008;105:18655–18662. doi: 10.1073/pnas.0808600105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fowler S.B., Clarke J. Mapping the folding pathway of an immunoglobulin domain: structural detail from ϕ value analysis and movement of the transition state. Structure. 2001;9:355–366. doi: 10.1016/s0969-2126(01)00596-2. [DOI] [PubMed] [Google Scholar]
- 44.Gianni S., Geierhaas C.D., Brunori M. A PDZ domain recapitulates a unifying mechanism for protein folding. Proc. Natl. Acad. Sci. USA. 2007;104:128–133. doi: 10.1073/pnas.0602770104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hong H., Park S., Tamm L.K. Role of aromatic side chains in the folding and thermodynamic stability of integral membrane proteins. J. Am. Chem. Soc. 2007;129:8320–8327. doi: 10.1021/ja068849o. [DOI] [PubMed] [Google Scholar]
- 46.Capaldi A.P., Kleanthous C., Radford S.E. Im7 folding mechanism: misfolding on a path to the native state. Nat. Struct. Biol. 2002;9:209–216. doi: 10.1038/nsb757. [DOI] [PubMed] [Google Scholar]
- 47.Kim K., Ramanathan R., Frieden C. Intestinal fatty acid binding protein: a specific residue in one turn appears to stabilize the native structure and be responsible for slow refolding. Protein Sci. 1997;6:364–372. doi: 10.1002/pro.5560060212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Saeki K., Arai M., Kuwajima K. Localized nature of the transition-state structure in goat α-lactalbumin folding. J. Mol. Biol. 2004;341:589–604. doi: 10.1016/j.jmb.2004.06.010. [DOI] [PubMed] [Google Scholar]
- 49.Hamill S.J., Steward A., Clarke J. The folding of an immunoglobulin-like Greek key protein is defined by a common-core nucleus and regions constrained by topology. J. Mol. Biol. 2000;297:165–178. doi: 10.1006/jmbi.2000.3517. [DOI] [PubMed] [Google Scholar]
- 50.Lim W.A., Farruggio D.C., Sauer R.T. Structural and energetic consequences of disruptive mutations in a protein core. Biochemistry. 1992;31:4324–4333. doi: 10.1021/bi00132a025. [DOI] [PubMed] [Google Scholar]
- 51.Jäger M., Dendle M., Kelly J.W. Sequence determinants of thermodynamic stability in a WW domain—an all-β-sheet protein. Protein Sci. 2009;18:1806–1813. doi: 10.1002/pro.172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Eddy S.R. A new generation of homology search tools based on probabilistic inference. Genome Inform. 2009;23:205–211. [PubMed] [Google Scholar]
- 53.Suzek B.E., Huang H., Wu C.H. UniRef: comprehensive and non-redundant UniProt reference clusters. Bioinformatics. 2007;23:1282–1288. doi: 10.1093/bioinformatics/btm098. [DOI] [PubMed] [Google Scholar]
- 54.Ekeberg M., Lövkvist C., Aurell E. Improved contact prediction in proteins: using pseudolikelihoods to infer Potts models. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;87:012707. doi: 10.1103/PhysRevE.87.012707. [DOI] [PubMed] [Google Scholar]
- 55.Metropolis N., Metropolis A.W., Teller E. Equation of state calculation by fast computing machines. J. Chem. Phys. 1953;21:1087. [Google Scholar]
- 56.Kumar S., Rosenberg J.M., Kollman P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 57.Chan H.S., Dill K.A. Sequence space soup of proteins and copolymers. J. Chem. Phys. 1991;95:3775–3787. [Google Scholar]
- 58.Yue K., Dill K.A. Inverse protein folding problem: designing polymer sequences. Proc. Natl. Acad. Sci. USA. 1992;89:4163–4167. doi: 10.1073/pnas.89.9.4163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Irbäck A., Peterson C., Sandelin E. Design of sequences with good folding properties in coarse-grained protein models. Structure. 1999;7:347–360. doi: 10.1016/s0969-2126(99)80044-6. [DOI] [PubMed] [Google Scholar]
- 60.Dunn S.D., Wahl L.M., Gloor G.B. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics. 2008;24:333–340. doi: 10.1093/bioinformatics/btm604. [DOI] [PubMed] [Google Scholar]
- 61.Shakhnovich E.I., Gutin A.M. A new approach to the design of stable proteins. Protein Eng. 1993;6:793–800. doi: 10.1093/protein/6.8.793. [DOI] [PubMed] [Google Scholar]
- 62.Ramanathan S., Shakhnovich E. Statistical mechanics of proteins with “evolutionary selected” sequences. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;50:1303–1312. doi: 10.1103/physreve.50.1303. [DOI] [PubMed] [Google Scholar]
- 63.Figliuzzi M., Jacquier H., Weigt M. Coevolutionary landscape inference and the context-dependence of mutations in beta-lactamase TEM-1. Mol. Biol. Evol. 2016;33:268–280. doi: 10.1093/molbev/msv211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bryan P.N., Orban J. Proteins that switch folds. Curr. Opin. Struct. Biol. 2010;20:482–488. doi: 10.1016/j.sbi.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Micheletti C., Seno F., Banavar J.R. Protein design in a lattice model of hydrophobic and polar amino acids. Phys. Rev. Lett. 1998;80:2237–2240. [PubMed] [Google Scholar]
- 66.Micheletti C., Maritan A., Banavar J.R. A comparative study of existing and new design techniques for protein models. J. Chem. Phys. 1999;110:9730–9738. [Google Scholar]
- 67.Jacquin H., Gilson A., Monasson R. Benchmarking inverse statistical approaches for protein structure and design with exactly solvable models. PLOS Comput. Biol. 2016;12:e1004889. doi: 10.1371/journal.pcbi.1004889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Miyazawa S., Jernigan R.L. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 69.Li H., Tang C., Wingreen N.S. Designability of protein structures: a lattice-model study using the Miyazawa-Jernigan matrix. Proteins. 2002;49:403–412. doi: 10.1002/prot.10239. [DOI] [PubMed] [Google Scholar]
- 70.Sikosek T., Chan H.S. Biophysics of protein evolution and evolutionary protein biophysics. J. R. Soc. Interface. 2014;11:20140419. doi: 10.1098/rsif.2014.0419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Yue K., Fiebig K.M., Dill K.A. A test of lattice protein folding algorithms. Proc. Natl. Acad. Sci. USA. 1995;92:325–329. doi: 10.1073/pnas.92.1.325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Bornberg-Bauer E. How are model protein structures distributed in sequence space? Biophys. J. 1997;73:2393–2403. doi: 10.1016/S0006-3495(97)78268-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Bornberg-Bauer E., Chan H.S. Modeling evolutionary landscapes: mutational stability, topology, and superfunnels in sequence space. Proc. Natl. Acad. Sci. USA. 1999;96:10689–10694. doi: 10.1073/pnas.96.19.10689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Irbäck A., Troein C. Enumerating designing sequences in the HP model. J. Biol. Phys. 2002;28:1–15. doi: 10.1023/A:1016225010659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Heo M., Maslov S., Shakhnovich E. Topology of protein interaction network shapes protein abundances and strengths of their functional and nonspecific interactions. Proc. Natl. Acad. Sci. USA. 2011;108:4258–4263. doi: 10.1073/pnas.1009392108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Govindarajan S., Goldstein R.A. Searching for foldable protein structures using optimized energy functions. Biopolymers. 1995;36:43–51. [Google Scholar]
- 77.Buchler N.E., Goldstein R.A. Effect of alphabet size and foldability requirements on protein structure designability. Proteins: Struct., Funct. 1999;34:113–124. [PubMed] [Google Scholar]
- 78.Greene L.H., Lewis T.E., Orengo C.A. The CATH domain structure database: new protocols and classification levels give a more comprehensive resource for exploring evolution. Nucleic Acids Res. 2007;35:D291–D297. doi: 10.1093/nar/gkl959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Chaiken R., Jenkins B., Zhou J. SCOPE: easy and efficient parallel processing of massive data sets. Proceedings VLDB Endowment. 2008;1:1265–1276. [Google Scholar]
- 80.Levitt M. Growth of novel protein structural data. Proc. Natl. Acad. Sci. USA. 2007;104:3183–3188. doi: 10.1073/pnas.0611678104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Rost B. Twilight zone of protein sequence alignments. Protein Eng. 1999;12:85–94. doi: 10.1093/protein/12.2.85. [DOI] [PubMed] [Google Scholar]
- 82.Taylor W.R., Chelliah V., Jonassen I. Probing the “dark matter” of protein fold space. Structure. 2009;17:1244–1252. doi: 10.1016/j.str.2009.07.012. [DOI] [PubMed] [Google Scholar]
- 83.Cossio P., Trovato A., Laio A. Exploring the universe of protein structures beyond the Protein Data Bank. PLOS Comput. Biol. 2010;6:e1000957. doi: 10.1371/journal.pcbi.1000957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Winstanley H.F., Abeln S., Deane C.M. How old is your fold? Bioinformatics. 2005;21(Suppl 1):i449–i458. doi: 10.1093/bioinformatics/bti1008. [DOI] [PubMed] [Google Scholar]
- 85.Wang M., Boca S.M., Caetano-Anollés G. A phylogenomic reconstruction of the protein world based on a genomic census of protein fold architecture. Complexity. 2006;12:27–40. [Google Scholar]
- 86.Choi I.-G., Kim S.-H. Evolution of protein structural classes and protein sequence families. Proc. Natl. Acad. Sci. USA. 2006;103:14056–14061. doi: 10.1073/pnas.0606239103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Bukhari S.A., Caetano-Anollés G. Origin and evolution of protein fold designs inferred from phylogenomic analysis of CATH domain structures in proteomes. PLOS Comput. Biol. 2013;9:e1003009. doi: 10.1371/journal.pcbi.1003009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Alva V., Söding J., Lupas A.N. A vocabulary of ancient peptides at the origin of folded proteins. eLife. 2015;4:e09410. doi: 10.7554/eLife.09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Ferrada E., Wagner A. Protein robustness promotes evolutionary innovations on large evolutionary time-scales. Proc. Biol. Sci. 2008;275:1595–1602. doi: 10.1098/rspb.2007.1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Pautsch A., Schulz G.E. High-resolution structure of the OmpA membrane domain. J. Mol. Biol. 2000;298:273–282. doi: 10.1006/jmbi.2000.3671. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.