Abstract
The role that epistasis plays during adaptation remains an outstanding problem, which has received considerable attention in recent years. Most of the recent empirical studies are based on ensembles of replicate populations that adapt in a fixed, laboratory controlled condition. Researchers often seek to infer the presence and form of epistasis in the fitness landscape from the time-evolution of various statistics averaged across the ensemble of populations. Here we provide a rigorous analysis of what quantities, drawn from time-series of such ensembles, can be used to infer epistasis for populations evolving under weak mutation on finite-site fitness landscapes. First we analyze the mean fitness trajectory—that is, the time course of the ensemble average fitness. We show that for any epistatic fitness landscape and starting genotype, there always exists a non-epistatic fitness landscape that produces the exact same mean fitness trajectory. Thus, the presence of epistasis is not identifiable from the mean fitness trajectory. By contrast, we show that two other ensemble statistics—the time evolution of the fitness variance across populations, and the time evolution of the mean number of substitutions—can detect certain forms of epistasis in the underlying fitness landscape.
Keywords: adaptation, weak mutation, fitness trajectory, molecular clock, reversible Markov chains
1 Introduction
A basic problem in evolutionary biology is to understand the relationship between the structure of the fitness landscape and the dynamics of adaptation (Wright, 1932; Maynard Smith, 1970; Kauffman, 1993; Whitlock et al., 1995; Fontana and Schuster, 1998; Weinreich et al., 2005; Jain and Krug, 2007; Kryazhimskiy et al., 2009; de Visser and Krug, 2014; Hartl, 2014). One simple classification distinguishes non-epistatic fitness landscapes, where the fitness effects of mutations are independent of genetic background, from epistatic landscapes, where some mutations have background-dependent effects (Fisher, 1918; Weinberger, 1990; Phillips, 2008; de Visser et al., 2011; Szendro et al., 2013; Weinreich et al., 2013; de Visser and Krug, 2014). Because the class of epistatic fitness landscapes is far more diverse than the class of non-epistatic fitness landscapes, it seems intuitive that the dynamics of adaptation possible on epistatic fitness landscapes should be more diverse than the dynamics possible on non-epistatic landscapes.
In the field of experimental evolution, this intuition has led researchers to study the role of epistasis in shaping the dynamics observed across an ensemble of replicate populations that evolve independently from the same starting genotype (Lenski et al., 1991; Lenski and Travisano, 1994; Kryazhimskiy et al., 2009; Wiser et al., 2013; Good and Desai, 2014). Such studies often focus on the time-evolution of some quantity averaged across the ensemble, and ask if the observed dynamics are consistent with the hypothesis of a non-epistatic fitness landscape. Typical examples of such quantities include the average fitness across populations (Lenski et al., 1991; Lenski and Travisano, 1994; Kryazhimskiy et al., 2009; Wiser et al., 2013), the average number of substitutions across populations (Kryazhimskiy et al., 2009; Good and Desai, 2014) and the variance in fitness across populations (Lenski et al., 1991). The time-evolution of these quantities are known, respectively, as the “mean fitness trajectory”, “mean substitution trajectory” and “variance trajectory”.
Here, we provide a rigorous investigation into whether the presence of epistasis can be inferred from such trajectories. We consider this question in the setting of finite-site fitness landscapes, with both forward and backward mutations at each site. We define a fitness landscape to be non-epistatic if each site makes an additive contribution to a genotype’s fitness. While this is the classical definition of epistasis (Phillips, 2008; de Visser et al., 2011; Szendro et al., 2013; Weinreich et al., 2013; de Visser and Krug, 2014) and the one most commonly used in empirical studies of fitness landscapes (e.g. Chou et al., 2011; Khan et al., 2011; Szendro et al., 2013; Weinreich et al., 2013), other definitions of epistasis are also worthy of investigation (see, e.g. Kryazhimskiy et al., 2009; Good and Desai, 2014, for related work that assumes infinite sites and defines epistasis as the non-constancy of the distribution of mutational effects on fitness). Our analysis assumes that mutation is weak, so that each new mutation is lost or goes to fixation before the next new mutation enters the population (see McCandlish and Stoltzfus, 2014, for a review). Although our main interest is in adaptation, our framework accommodates both advantageous and deleterious substitutions, allowing us to study both the adaptive transient and the longer-term approach to mutation-selection-drift balance.
Under these assumptions we characterize the possible shapes of various trajectories on non-epistatic fitness landscapes. We then ask, for each type of trajectory, whether epistatic landscapes can produce ensemble dynamics that are impossible in the absence of epistasis.
Our most important result concerns how the expected fitness of an ensemble of replicate populations changes over time, i.e. the mean fitness trajectory. Surprisingly, we prove that, for any finite epistatic fitness landscape and choice of starting genotype, one can always construct a non-epistatic fitness landscape that produces the exact same mean fitness trajectory as the epistatic landscape produces. Thus, it is impossible to infer the presence of epistasis from observation of the mean fitness trajectory alone.
To illustrate this general result in a specific case, Figure 1A shows an epistatic and a non-epistatic fitness landscape that produce the exact same mean fitness trajectory (Figure 1B) for an ensemble of populations that starts at the left-most genotype (ab or abc). Note that the first fitness landscape in Figure 1A is not merely epistatic, but exhibits reciprocal sign epistasis (Weinreich et al., 2005). Furthermore, while all finite fitness landscapes must produce saturating fitness trajectories that asymptotically approach the expected fitness at mutation-selection-drift balance, the shape of the mean fitness trajectory in this example is complex, decreasing initially (due to deleterious fixations into the fitness valley) before increasing as more populations cross the fitness valley. It may seem surprising that one can construct a non-epistatic landscape that produces the same, complex dynamics. And, yet, our main result says that constructing such a landscape is always possible.
Figure 1.
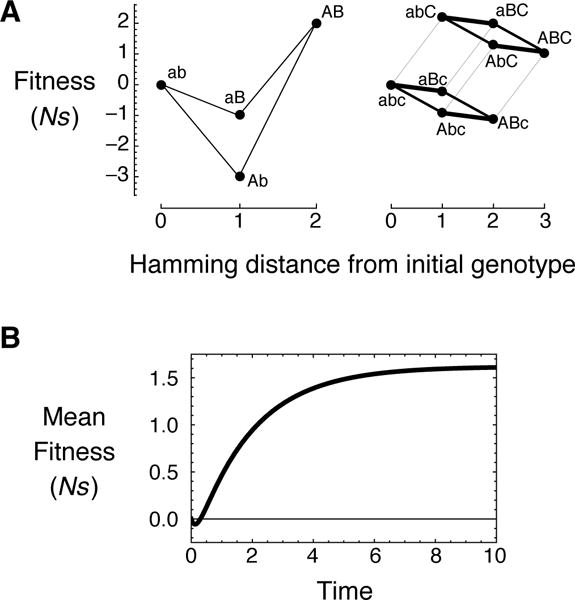
(A) A fitness landscape with reciprocal sign epistasis and a non-epistatic fitness landscape that both produce the exact same mean fitness trajectory (B) when the population begins at the left-most genotype (ab or abc). Edges are mutations and points are genotypes. The height of a genotype indicates its scaled selection coefficient (Ns) relative to the initial (left-most) genotype. Edge thickness is proportional to mutation rate. The bottom panel shows expected fitness as a function of time (the mean fitness trajectory), where time is measured in terms of expected substitutions at a neutral locus with a unit mutation rate. Notice that the trajectory is quite complex; in particular, it decreases slightly at short times before increasing to its asymptotic value at long times.
Our main result shows that the set of realizable mean fitness trajectories for epistatic landscapes is no more diverse than the set of mean fitness trajectories for non-epistatic landscapes, despite the fact that, e.g. epistatic fitness landscapes can have multiple fitness peaks while non-epistatic landscapes are always single-peaked. However, the presence of epistasis does increase the diversity of possible dynamics for several more subtle descriptors of the adaptive process. For instance, if we again consider an ensemble of replicate populations evolving from the same starting genotype, we can study the variance in fitness across these populations as a function of time. We will show that there exist epistatic fitness landscapes whose variance trajectories cannot be produced on any non-epistatic landscape. In particular, a variance trajectory that is accelerating at short times can occur only on an epistatic fitness landscape. A similar result holds for the expected number of substitutions that accrue over time, i.e. the mean substitution trajectory (Kryazhimskiy et al., 2009): for any non-epistatic fitness landscape the expected substitution rate can never be less than half the equilibrium substitution rate, whereas some epistatic fitness landscapes violate this condition and produce a broader range of expected substitution rates.
2 Results
2.1 Population-genetic model
We consider the space of all possible haploid fitness landscapes with a finite number of bi-allelic sites. A genotype is defined by the state at all of its sites, and the fitness of the i-th genotype is denoted F(i). We will work in scaled Malthusian fitness (i.e. the fitness of a genotype is equal to the logarithm of the standard, Wrightean fitness times the population size) so that the scaled selection coefficient of genotype j relative to genotype i is given by F(j) − F(i).
Our main population-genetic assumption is that mutation is weak, i.e. that each new mutation is either fixed or lost before the next mutation enters the population. Because the time during which a mutation segregates in such a population is much shorter than the waiting time between new mutations, we neglect the time that a mutation segregates and simply model the population as monomorphic, jumping from genotype to genotype at the birth of each new mutation destined for fixation (Iwasa, 1988; Berg et al., 2004; Sella and Hirsh, 2005; McCandlish and Stoltzfus, 2014).
We use the standard model for a population evolving under weak mutation in continuous time. More formally, we model evolution as a continuous time Markov chain with rate matrix Q, where
| (1) |
and QM is the mutational rate matrix. We assume that forward mutations arise at site l as a Poisson process with rate μl and back mutations arise as at site l as a Poisson process with rate νl. Thus, QM(i, j) for i ≠ j is equal to μl > 0 if genotype j can arise from genotype i by a forward mutation at site l, νl > 0 if genotype j can arise from genotype i by a back mutation at site l, and 0 otherwise; the QM(i, i) are chosen so that the row sums are zero. While for convenience the above expression is based on the classical approximation to the probability of fixation of a new mutation in the diffusion limit (Fisher, 1930; Wright, 1931), our results can easily be extended to hold exactly in the limit of weak mutation for a population of finite size N evolving under a Moran process by using the appropriate exact expression for the probability of fixation (Moran, 1959).
We define a non-epistatic fitness landscape (Phillips, 2008; de Visser et al., 2011; Szendro et al., 2013; Weinreich et al., 2013; de Visser and Krug, 2014) as one in which each site makes an additive contribution to fitness (recall that we are working in Malthusian fitness, so that this corresponds to a multiplicative landscape in Wrightean fitness). More formally, for a non-epistatic fitness landscape each site l is associated with a value Sl such that, for any ordered pair of genotypes i and j differing by a forward mutation at site l, we have F(j) − F(i) = Sl. Under this definition, the non-epistatic fitness landscapes are precisely those landscapes for which sites evolve independently of each other. This is because the forward substitution rate at site l is always
| (2) |
and the corresponding backwards substitution rate is
| (3) |
Thus, for a non-epistatic fitness landscape the evolutionary dynamics at site l depend only the state of site l and not on the states of the other sites.
Our emphasis here is on detecting epistasis from the time-evolution of some quantity, averaged across many independent replicate populations founded from the same genotype. Nevertheless, we note in passing that it may also be possible to detect epistasis from a detailed analysis of the evolution in a single population observed for a long period of time. In particular, the analysis above shows that in the absence of epistasis the evolution of each site will be independent of all others and that (for bi-allelic sites) the waiting time until reversion events will be exponential. Deviations from either of these expectations would provide evidence for epistasis from a single population, however we will not consider this type of inference here.
2.2 Mean fitness trajectories
2.2.1 Formal results
Suppose a population is initially fixed for some genotype i, with fitness F (i), at time 0. At any time t in the future, the population has some probability of being fixed for each other genotype j, with fitness F (j). We can therefore ask: What is the expected fitness of the population at time t? The course of the expected fitness over time is called the mean fitness trajectory, which we write as f(t). In the Supporting Information, we show that the mean fitness trajectory can always be written in the form:
| (4) |
for some constants c2,…, cn, with λ2,…, λn > 0 and n denoting the number of genotypes in the fitness landscape. In other words, for an arbitrary fitness landscape, including all epistatic landscapes, the mean fitness trajectory can always be expressed as a sum of exponentially decaying deviations from the equilibrium mean fitness, f(∞). Figure 2 illustrates this decomposition for the fitness trajectory shared by the two fitness landscapes in Figure 1A.
Figure 2.
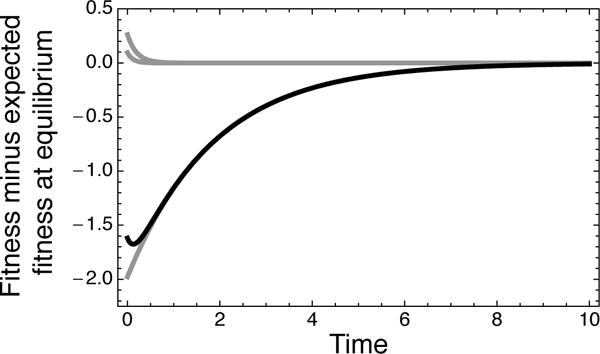
The mean fitness trajectory shared by the two fitness landscapes in Figure 1 (black) together with each of the corresponding exponentially decaying deviations from the equilibrium expected fitness (gray) that can be combined together to compose the trajectory. There are two positive deviations from the equilibrium expected fitness that decay very rapidly, producing the small dip in fitness at short times, and a much more slowly decaying negative deviation from the equilibrium distribution that corresponds to crossing the fitness valley in the epistatic landscape or to having a substitution at the third site in the non-epistatic landscape.
Now, let us restrict our attention to non-epistatic landscapes, and consider what types of fitness trajectories can arise. Because fitness is additive over sites in such a landscape, we can write the fitness trajectory as a sum over sites. In particular, using the standard solution for a two-state Markov chain, the fitness trajectory for a non-epistatic landscape is given by:
| (5) |
where f(0) is the initial fitness and we assume (without loss of generality) that the population begins fixed for the first of the two states for each site at t = 0. Rewriting Equation 5 in the same form as Equation 4, we have:
| (6) |
We now arrive at our main result. Comparing Equations 4 and 6, we see that given an arbitrary epistatic fitness landscape we can always construct a non-epistatic fitness landscape that will produce a fitness trajectory of the same shape, provided we can choose values Sl, μl and νl for each k such that
| (7) |
and
| (8) |
Indeed, such choices can always be made. For instance, one solution is αl = βl = λk/2, Sl = −2ck and , , but there are an infinite number of such solutions (in the Supporting Information we also provide a generalization of the above analysis that allows the non-epistatic landscape to have equal forward and backward mutation rates at each site).
Thus far we have shown that given a fitness trajectory from an epistatic fitness landscape, we can construct a non-epistatic fitness landscape whose fitness trajectory has the same shape, i.e. one that differs from the target fitness trajectory by an additive constant. In order to match the fitness trajectory exactly, we need to be able to choose the term in parentheses in Equation 6 to be equal to f(∞). But this, too, is always possible to do, because we can freely choose the initial fitness f(0) and the sum over sites has some definite value fixed by our previous choice of Sl, μl and νl, i.e. we can always use the solution
| (9) |
To summarize, we have shown that given an arbitrary epistatic fitness landscape and choice of initial genotype, we can always construct a non-epistatic fitness landscape that will produce the exact same mean fitness trajectory. In other words, the presence of epistasis does not expand the range of possible dynamics of expected fitness gains over time. As a result, one cannot infer whether epistasis is present or absent from the mean fitness trajectory alone.
2.2.2 Practical analysis
The preceding formal analysis demonstrates the existence of non-epistatic fitness landscapes that can produce the same mean fitness trajectory as an arbitrary epistatic landscape. However, this formal analysis provides no guarantee that such non-epistatic fitness landscapes have reasonable biological properties.
For instance, the non-epistatic fitness landscapes constructed above will typically be much larger than the focal epistatic landscape. If the focal landscape has L sites and 2L genotypes, the corresponding non-epistatic fitness landscape with the same fitness trajectory produced by the method described above will generically have 2L − 1 sites and therefore 22L−1 genotypes (see the Supporting Information for a bound on the error when attempting to match a fitness trajectory using fewer than 2L− 1 sites). There is also no guarantee that the selection coefficients and mutation rates required by the above formal analysis will take reasonable values.
In order to address these practical concerns, we considered a large set of epistatic fitness landscapes and fit the resulting mean fitness trajectories by constructing non-epistatic fitness landscapes with the same number of sites as the original epistatic landscapes. We also constrained the mutation rates and selection coefficients to fall within a reasonable range, and forced the forward and backward mutation rates to be equal at each site. The results of these constrained fits show that reasonable non-epistatic landscapes can often provide a very close approximation to the mean fitness trajectories of epistatic fitness landscapes.
In particular, we considered the class of LK landscapes (Kauffman and Weinberger, 1989; Kauffman, 1993) with L = 10. The parameter L controls the number of sites, whereas K controls the ruggedness of the landscape, so that K = 0 produces a non-epistatic landscape and K = L −1 produces an uncorrelated (i.e. house of cards) landscape. We constructed these landscapes as described in the original publications (Kauffman and Weinberger, 1989; Kauffman, 1993), but multiplied all fitnesses by a constant chosen so that for the non-epistatic case (K = 0) the expected value of |Sl| equals 5; and we set the forward- and back-mutation rates at each site equal to unity. For each LK landscape we constructed, we picked an initial genotype and calculated the resulting mean fitness trajectory at intervals of 0.01 time units, until reaching the final time of 10 units. So as to focus on cases of adaptive evolution, we retained only those landscapes for which the increase in mean fitness over this time period was at least 10 in units of scaled fitness, and we continued to generate landscapes until we had 1000 such landscapes for each value of K = 1, K = 2 and K = 9. We then fit these mean fitness trajectories to a non-epistatic model of the form given in Equation 5, using non-linear least squares with the constraints that −20 ≤ Sl ≤ 20, .01 ≤ μl ≤ 10 and νl = μl.
Figure 3 (top) shows the complete distribution of R2 values for the resulting fits. Most of the observed R2 values are very close to 1 (median R2 of .999999, .999997, and .999986 for K = 1, 2, and 9 respectively), indicating that the non-epistatic fitness landscapes provide very close approximations to the shape of the epistatic mean fitness trajectories. Figure 3 (bottom) shows the distribution of absolute maximal errors for each fit, defined as the maximum absolute value difference between the epistatic mean fitness trajectory and the best-fit non-epistatic trajectory, with the maximum taken over all time points. Most of these maximal errors are very small (median absolute maximal error of |Ns| = .014, .030 and .044 for K = 1, 2, and 9 respectively). Thus, besides matching the overall shape of the epistatic trajectories, the corresponding non-epistatic mean fitness trajectories typically approximate the epistatic trajectories very closely at all time points. These results suggest that, as a practical matter, the mean fitness trajectories of epistatic fitness landscapes can often be closely matched by the mean fitness trajectories of non-epistatic landscapes with the same number of sites and with comparable mutation rates and selection coefficients.
Figure 3.
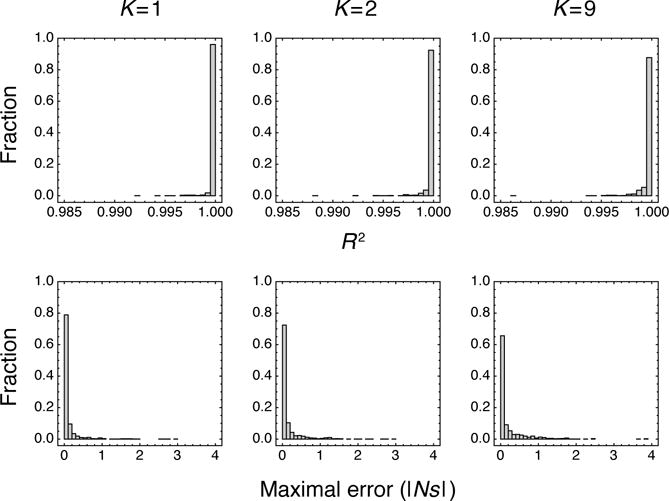
Fitting epistatic mean fitness trajectories using non-epistatic fitness landscapes of the same size. Histograms show coefficient of determination (R2, top) and the absolute value of the maximal error at any time point (bottom) for 1,000 constrained fits to LK landscapes for L = 10 and, from left to right, K = 1, K = 2 and K = 9.
While the above results show that one can achieve good fits with a relatively limited range of symmetric mutation rates, some amount of variation in mutation rates between sites plays an essential role in achieving a good fit. At a mathematical level, this is necessary to allow the initial deviation from the equilibrium fitness contribution of a site and the rate at which that site approaches equilibrium to be varied independently. At an intuitive level, small mutation rates are being used to mimic the effects on expected fitness of complex epistatic evolutionary dynamics, such as the waiting time to cross fitness valleys.
2.3 Variance trajectories
We have seen that any mean fitness trajectory produced by an epistatic fitness landscape can also be produced by a non-epistatic fitness landscape. However, the mean fitness trajectory captures only the central tendency of population fitness through time. If we initiate many replicate populations fixed for the same genotype, then it is likely that some populations will adapt more quickly than others, so that there will typically be variation in fitness across populations at any given time t > 0. Aside from the mean, discussed above, it is natural to ask whether the presence of epistasis increases the diversity of the possible dynamics of the inter-population variation in fitness.
To make this idea more precise, let us consider the fitness of a population at time t as a random variable. The variance of this random variable viewed as a function of time is called the “variance trajectory”, v(t). In other words, the variance trajectory is the time evolution of the second central moment of the fitness distribution, across an ensemble of replicate populations.
We would like to know whether the set of variance trajectories that can be achieved by epistatic fitness landscapes is more diverse than the set that can be achieved by non-epistatic fitness landscapes. To answer this question, we will first use the standard solution for a two-state Markov chain to write down the variance trajectory for a single site:
| (10) |
assuming without loss of generality that the population starts in the first state. It is easy to show that the first derivative of v(t) with respect to time is maximized at t = 0, since the derivatives of both 1 − e−t and e−t − e−2t are maximized at t = 0. Thus, the rate that variance in fitness increases takes its maximum at t = 0, which makes sense, because at t = 0 the fitness of the alternative state is maximally different from the current mean fitness, and the increase in the frequency of the alternative state is also maximized (because back-substitutions cannot occur at time t = 0).
The variance trajectory of a non-epistatic fitness landscape is simply the sum of the variance trajectories across all sites (because variances can be summed when random variable are independent). Now, because the slope of the variance trajectory is maximized for each site at t = 0, it follows that the slope of the variance trajectory is maximized at t = 0 for any finite, non-epistatic fitness landscape. Furthermore, because the slope is maximized at t = 0, it follows that the second derivative of the fitness trajectory must be negative at t = 0. In other words, all non-epistatic fitness landscapes share a fundamental qualitative feature: their variance trajectories are concave at short times.
Are variance trajectories for all epistatic fitness landscapes also concave at short times? The answer is no. For instance, consider a two-site fitness landscape with genotypes ab, Ab, aB, and AB, and μl = νl = 1 for both sites, with a population initially fixed for genotype ab. Suppose the fitnesses of ab, Ab and aB are all equal but genotype AB has fitness advantage S over the other three genotypes. The first derivative of the resulting variance trajectory at t = 0 (i.e., v′(0)) is zero, and the second derivative at t = 0 (i.e. v″(0)) is S3/1 − e−S, which is positive for S ≠ 0. Thus, for any such landscape with S ≠ 0, the variance trajectory is convex at short times—a feature that cannot be achieved by any non-epistatic landscape.
As illustrated by the example above, the range of possible dynamics for the variance trajectory is larger for epistatic landscapes than for non-epistatic landscapes. And so it may be possible to infer epistasis from the pattern of variance in fitness across populations, even though it is impossible to do so from the pattern of mean fitness alone.
To explore the range of epistatic landscapes that produce variance trajectories that are convex at short times, we considered the two-site landscapes described above, but allowed Ab and aB to have some selection coefficient relative ab, and also allowed AB to have some other selection coefficient relative to Ab and aB (i.e. genotypes with equal hamming distances from ab are assigned equal fitnesses). The dark gray region in Figure 4 shows the subset of landscapes whose the variance trajectories are convex at short times. Although this region is primarily composed of landscapes with positive epistasis (above the line y=x), it is also possible to have convex variance trajectories for landscapes with negative epistasis (below the line y=x) when the selection coefficient of the first mutation is small.
Figure 4.
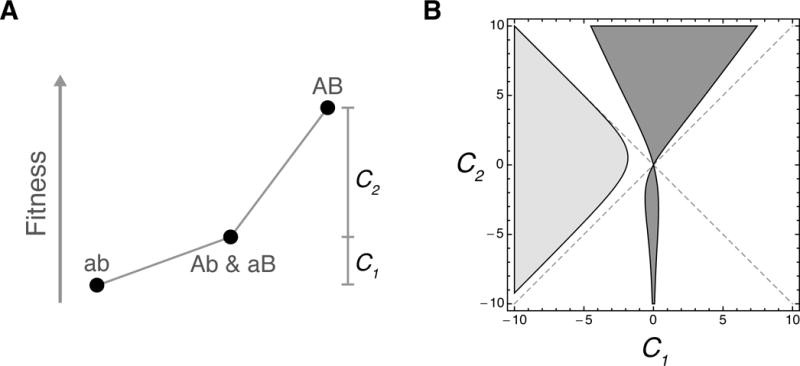
Epistatic fitness landscapes can produce dynamics that differ from all non-epistatic landscapes. (A) We consider two-site landscapes with genotypes ab, Ab, aB, and AB, with the population initially fixed for ab. Assigning Ab and aB equal fitnesses, we let C1 be the selection coefficient of Ab and aB relative to ab and let C2 be the selection coefficient of AB relative to Ab and aB. We set the mutation rates to be μl = νl = 1 for both sites. (B) Properties of two-site fitness landscapes using the parameterization described in the previous panel. The dark gray region shows the set of landscapes whose variance trajectories are convex at t = 0. The light gray region shows the set of landscapes whose equilibrium substitution rates are greater than twice their initial substitution rates. The diagonal dashed line with positive slope shows the set of non-epistatic fitness landscapes, whereas the diagonal dashed line with negative slope shows the set of epistatic landscapes whose fitness dynamics cannot be distinguished from the non-epistatic case.
We have seen that some epistatic fitness landscapes produce variance trajectories that cannot be achieved by any non-epistatic fitness landscapes. Thus, we have shown that one can sometimes tell that a fitness landscape is epistatic by observing its time-dependent fitness distribution. However, one might wonder whether given the time-dependent fitness distribution it is always possible to distinguish epistatic from non-epistatic fitness landscapes. The answer is no. As a counter-example, consider again the two-site case in which Ab and aB have equal fitness. If the selection coefficient of ab relative to Ab and aB is equal to the selection coefficient of AB relative to Ab and aB, then the entire fitness distribution can be matched by a single-site fitness landscape. These landscapes are illustrated by the dashed line with negative slope in Figure 4. Thus, there is no characteristic of the time-dependent fitness distribution that can be used to distinguish all epistatic landscapes from all non-epistatic fitness landscapes.
Another natural question, in light of our earlier results on fitness trajectories, concerns the relationship between the mean fitness trajectory and the variance trajectory, for a given landscape. Within the class of non-epistatic landscapes, it is easy to show that the variance and mean fitness trajectories can be modified essentially independently of each other. This is because the variance in fitness can be made arbitrarily small while preserving the fitness trajectory by replacing single sites of large fitness effect with many sites of small effects; on the other hand, the variance in fitness can be made arbitrarily large without altering the fitness trajectory by constructing pairs of sites whose site-specific fitness trajectories cancel each other out, but which still contribute to the time-evolution of the variance. As a result, considering the fitness and variance trajectories jointly is likely to provide little more information about the presence of epistasis than considering the variance trajectory alone.
2.4 Substitution trajectories
Changes in fitness during adaptation are the result of substitutions – that is, mutations at individual sites that eventually reach fixation in the population. Therefore, aside from studying the expected fitness of a population, it is also interesting to consider the the number of substitutions that accumulate in a population over time. For instance, consider the time-evolution of the expected number of substitutions that have accumulated in the population by time t, what we call the “substitution trajectory”, s(t) (Kryazhimskiy et al., 2009). Just as we did for mean fitness trajectories, we want to ask whether the set of possible substitution trajectories for epistatic fitness landscapes is more diverse than the set of possible substitution trajectories in the absence of epistasis.
To study the substitution trajectory, it is helpful to note that the derivative of the substitution trajectory is equal to the expected substitution rate at time t, which we will write as q(t). That is, s′ (t) = q(t). Because no substitutions have accumulated at time 0, this relation means that the substitution trajectory is fully specified by the time-dependent expected rates of substitution.
Consider the time-dependent rate of substitution at a single site. Assuming without loss of generality that the population begins in the first state, and using the standard solution for a two-state Markov chain, the expected substitution rate is given by:
| (11) |
where the first term on the right-hand side is the equilibrium rate of substitution, q(∞). The initial substitution rate is α, and so the ratio between the equilibrium substitution rate and the initial substitution rate is q(∞)/q(0) = 2β/(α + β) – a ratio than can never exceed 2, which is the value achieved in the limit as β/α → ∞. Indeed, because the expected substitution rate approaches its equilibrium value monotonically, we also have a stronger result: the expected substitution rate can never be less than half of its equilibrium rate, i.e. q(∞)/q(t) ≤ 2.
For a non-epistatic landscape, the expected substitution rate is simply a sum of rates at each of its constituent sites. Using the inequality developed above, we thus have:
| (12) |
| (13) |
| (14) |
where ql(t) is the expected substitution rate at the l-th site at time t. In words, for any finite-state non-epistatic fitness landscape, the ratio between the equilibrium rate and the expected rate at any time can never exceed two.
For epistatic landscapes, by contrast, it is easy to see that this condition on the substitution rate can be violated. For instance, consider a fitness landscape with three or more sites in which all genotypes have the same fitness. Then, pick an initial genotype, and alter the fitnesses of its mutational neighbors such that these neighbors now have selection coefficient S relative to the initial genotypes, where we choose S to be negative. That is, consider a neutral plateau and modify it by constructing a fitness valley around the initial genotype. As the depth of this valley increases (i.e. as S approaches −∞), the initial substitution rate converges to 0, while the equilibrium substitution rate approaches some non-zero constant. This means that by choosing S to be sufficiently large and negative the ratio between the equilibrium substitution rate and the initial substitution rate can be made arbitrarily large and, in particular, larger than two. (While no adaptation occurs in this example – the mean equilibrium fitness is lower than the initial fitness – this defect is easy to correct by giving a fitness advantage to genotypes of distance two or more from the initial genotype). Thus, we conclude that the set of possible substitution trajectories is indeed enlarged by the presence of epistasis.
The light gray region in Figure 4 illustrates this fact, by indicating the set of two-site fitness landscapes whose ratios of equilibrium to initial expected substitution rates exceeds 2. Roughly speaking, this region corresponds to landscapes with a fitness valley, with population initialized on the fitter of the two peaks. Note that the light gray region does not extend all the way to the landscapes in which the two peaks have equal heights: these landscapes (dashed diagonal line with negative slope) have substitution trajectories of precisely the same form as a single site, and therefore the ratio of rates must be less than or equal to 2 along this line. More generally, the adaptive situation most likely to produce initial substitution rates that are less than half the equilibrium substitution rate is a population that is currently at an isolated local fitness maximum, but which, after crossing a fitness valley, will spend most of its time on a broad, high fitness plateau.
Why is the range of dynamics of mean fitness identical for epistatic and non-epistatic landscape, but not the range of dynamics of the mean number of substitutions? One way to understand these results is to notice that, because mutation can oppose or augment selection, two non-epistatic landscapes with different fitness functions and different mutation rates might still have the same evolutionary dynamics in genotype space (i.e. the same rate matrix, Q). As a consequence, for each non-epistatic matrix Q and choice of starting genotype, there is a large class of possible fitness trajectories, determined by the choices of the site-specific selection coefficients Sl. In contrast, having specified the matrix Q and the initial genotype completely determines the substitution trajectory. The extra flexibility produced by choosing Q and the Sl independently allows non-epistatic fitness landscapes to produce fitness trajectories whose dynamics are as general as the time-evolution of the expectation of an arbitrary function defined on an arbitrary finite-state reversible Markov chain.
For completeness, we can also consider the ensemble variance in substitution rate as a function of time. The derivative of this trajectory is maximized at t = 0, just as the derivative of the variance in fitness is as well. While this criterion can be used to identify some fitness landscapes as epistatic, the time evolution of the variance in substitution rate is much more difficult to observe than the time evolution of the mean substitution rate or the time evolution of the fitness distribution, and so we will not discuss the matter further here.
2.5 Equilibrial dynamics
Although our main focus has been adaptation, it is also interesting to consider whether epistatic and non-epistatic landscapes differ in the range of dynamics they can produce at equilibrium, i.e. in the limit of long times when all influence of the choice of initial genotype has been lost. We study the equilibrial dynamics by again considering an ensemble of replicate populations. However, instead of assuming that all of these populations are initially fixed at a single genotype, we assume that the initial genotype for each population is drawn from the equilibrium distribution, that is, the distribution that gives the probability of a population being fixed for any given genotype in the limit of long times.
An ensemble of populations that is initially distributed according to the equilibrium distribution will continue to be described by the equilibrium distribution at all future times. Hence the expected fitness, the variance for fitness, and indeed all moments of the fitness distribution are constant in time. Indeed, the equilibrium fitness distribution is determined solely by the fitnesses of the individual genotypes together with their equilibrium frequencies, and it is therefore independent of the structure of the fitness landscape in the sense that the structure of mutational adjacency is irrelevant (see McCandlish, 2011, pg. 1547). Because the equilibrium distribution remains constant in time and each genotype has its own substitution rate, substitutions likewise accumulate at a constant rate across the ensemble as a whole.
However, while the fitness distribution across the ensemble remains constant in time, individual populations in the ensemble will still experience changes in fitness. We can study the structure of these changes by studying the correlations between the fitness of a population at one time and its fitness at another. In particular, we consider the covariance in fitness between time t′ and some later time t′ + t, where again the genotype at time 0 is drawn from the equilibrium distribution. Viewed as a function of the difference, t between these two times, this covariance is known as the equilibrium autocovariance for fitness, denoted a(t). In the Supporting Information, we show that the equilibrium autocovariance for an arbitrary epistatic fitness landscape has the form:
| (15) |
where d2, d3, ⋯ ≥ 0 and λ2, λ3,… > 0.
For comparison, let us know consider the autocovariance for non-epistatic landscapes, considering first a landscape with a single site with selection coefficient S. In this case the equilibrium autocovariance for fitness is given by
| (16) |
The autocovariance of a sum of independent processes is the sum of the corresponding autocovariances, and the term S2αβ/(α + β)2 can assume any non-negative value even with a fixed value of λk = α + β. This implies that, given the equilibrium autocovariance function for an epistatic fitness landscape, one can always construct a non-epistatic landscape with an identical equilibrium autocovariance function by assigning one site to correspond to each term in Equation 15. Thus, while the presence of epistasis increases the possible dynamics for the second moment of fitness for an adapting population, epistatic and non-epistatic fitness landscapes have the same range of possible dynamics for the equilibrium autocovariance in fitness.
2.6 Multi-allelic models
One potential limitation of our analysis is that we have considered fitness landscapes composed of only bi-allelic sites. This assumption does not, in fact, influence our results on the space of dynamics possible under epistatic landscapes. This is because, as shown in the Supporting Information, our results for epistatic fitness landscapes hold for any time-independent, finite-state fitness landscape whose neutral mutational dynamics take the form of a reversible Markov chain (see, e.g. Sella and Hirsh, 2005; McCandlish, 2011). Thus, our results on epistatic dynamics apply also to models with more than two alleles per site (so long as the mutational dynamics within a site form a reversible Markov chain); and, indeed, they even apply when the genotypic space cannot be decomposed into individual sites. But our assumption of bi-allelic sites does influence our analysis of non-epistatic models, because our strategy for determining the behavior of such models has been to sum over the dynamics of independently evolving sites. The dynamics at a single site can be more complex when there are more than two alleles, and so the dynamics that are possible under multi-allelic finite-site non-epistatic fitness landscapes are more diverse than those described here for non-epistatic models with bi-allelic sites. Thus, all our negative results concerning whether epistatic models have more diverse dynamics than non-epistatic models (such as our main result on the mean fitness trajectory) continue to hold for multi-allelic models, but our positive results (such as our results on the variance trajectory) may no longer apply.
3 Discussion
Can the presence of epistasis be inferred from the dynamics observed across an ensemble of replicate populations? Here we have studied this question by examining the time-evolution of various ensemble averages (e.g. the mean fitness or number of substitutions accrued over time) under the assumptions that mutation is weak and that evolution occurs on a time-invariant fitness landscape defined on a finite number of bi-allelic sites. Although other definitions for epistasis—and even epistatic null hypotheses such as Fisher’s geometric model (e.g. Martin et al., 2007; Trindade et al., 2012; Bank et al., 2014)—are also worthy of investigation (e.g. Kryazhimskiy et al., 2009; Good and Desai, 2014), here we consider the classical definition of epistasis as a deviation from additivity in the fitness effects of individual sites (Phillips, 2008; de Visser et al., 2011; Szendro et al., 2013; Weinreich et al., 2013; de Visser and Krug, 2014). We find epistasis can be inferred from some types of ensemble statistics, but not from others.
The most basic and essential descriptor of adaptation is the mean fitness trajectory—that is, the mean pattern of fitness gains over time, where this mean is taken across an ensemble of replicate populations. In contrast to the received wisdom that the presence or specific form of epistasis can be deduced from this mean pattern of adaptation (e.g. epistasis “accelerating” or “de-accelerating” adaptation, Chou et al., 2011; Khan et al., 2011; Kryazhimskiy et al., 2011), we have shown that any mean fitness trajectory that can be achieved on an epistatic fitness landscape can also be acheived by an infinite number of non-epistatic fitness landscapes. This means that the shape of the mean fitness trajectory alone is insufficient to infer whether epistasis is present, let alone to infer its specific form. Furthermore, while our analytical results show that the number of sites needed to exactly match the mean fitness trajectory with a non-epistatic fitness landscape is typically much larger than the number of sites in the original fitness landscape, our numerical results on LK landscapes (Kauffman and Levin, 1987; Kauffman and Weinberger, 1989; Kauffman, 1993) suggest that the mean fitness trajectories of even highly rugged fitness landscapes may often be closely approximated by the mean fitness trajectories of non-epistatic landscapes with the same number of sites.
In contrast to the mean fitness trajectory, we have shown that the time-evolution of the variance in fitness across replicate populations can display qualitatively different behavior on some epistatic landscapes than can be achieved in the absence of epistasis. Likewise, the pattern of the expected number of substitutions accrued over time can also be qualitatively different on epistatic fitness landscapes than is possible on non-epistatic landscapes.
While most of our results have focused on adaptive evolution, we also studied the nearly-neutral dynamics of a population evolving at equilibrium on a time-invariant fitness landscape. In particular, we showed that the autocovariance function for fitness of such a population cannot be used to determine whether a fitness landscape is epistatic or not. This result is in contrast to the autocovariance function of a completely random walk on the space of genotypes, whose characteristics have long been used to quantify the “ruggedness” of fitness landscapes (Weinberger, 1990, 1991; Stadler, 2003).
These results have implications for efforts to infer the prevailing form of epistasis by experimentally observing the evolutionary dynamics in an ensemble of replicate populations (Lenski et al., 1991; Lenski and Travisano, 1994; Kryazhimskiy et al., 2009; Wiser et al., 2013; Good and Desai, 2014). Such an approach is appealing because while epistasis is easy to detect by considering combinations of mutations directly (e.g. Chou et al., 2011; Khan et al., 2011), inferences about the prevailing form of epistasis based on small samples of mutations can be strongly misleading (Blanquart et al., 2014), particularly when the mutations chosen are those that fixed during adaptation (Draghi and Plotkin, 2013). Efforts to infer the global form of epistasis using random mutagenesis (e.g. Olson et al., 2014; Bank et al., 2015) suffer from other difficulties, such as only giving information about epistasis in a local region of sequence space or between mutations that are too deleterious to ever fix (Otwinowski and Plotkin, 2014). Inferring the form of epistasis from the trajectories observed during experimental evolution overcomes these difficulties because the trajectory data contains information about both those mutations that do fix and also those that do not fix (e.g. through the waiting times between substitutions) and because the mutations sampled by evolving populations are precisely the mutations most relevant to the evolutionary process.
Existing approaches to infer the form of epistasis from experimental trajectories typically consist of fitting a handful of simple epistatic and non-epistatic models to the observed data (e.g. Kryazhimskiy et al., 2009; Wiser et al., 2013; Good and Desai, 2014). However, as emphasized by Frank (2014), all we can really infer from such an approach is the set of models consistent with the observed dynamics. Our results show that, for populations under weak mutation, the shape of the mean fitness trajectory alone can never be used to infer the presence or form of epistasis, even with an unlimited number of replicate experimental populations. Epistasis is not identifiable by these type of data because any mean fitness trajectory that can occur on an epistatic landscape is consistent with some non-epistatic landscape as well. On the other hand, the variance and substitution trajectories can in principle sometimes allow us to conclude that epistasis must be present. Indeed, our results on the variance trajectory confirm the conjecture by Lenski et al. (1991) that the time-evolution of the variance in fitness across replicate populations can be used to detect epistasis. The simple intuition underlying our analysis is that positive epistasis can cause the slope of the variance trajectory to increase as time elapses, whereas when epistasis is absent the slope of the variance trajectory is always maximized at t = 0.
While our results on variance and substitution trajectories suggest possibilities for empirical tests of epistasis, there still remain several obstacles to developing rigorous and practical tests for the presence and form of epistasis from these types of data. First, the results presented here are based on the assumption that we have access to an infinite ensemble of individual populations, whereas in practice we only have a finite sample of populations. Such a finite sample produces a number of technical complications, such as the fact that errors in the estimation of the expected trajectories will be correlated across time points (Good and Desai, 2014). Another complication is that, strictly speaking, under our model the sample means will be piecewise constant, and therefore the derivatives that we have studied here cannot be calculated directly from the sample means. Second, there is the issue of measurement error, which we have neglected in our treatment. Third, there are questions of power. While Figure 4 shows that many simple fitness landscapes would produce substitution and variance trajectories incompatible with a non-epistatic model, we suspect our compatibility criterion for the substitution trajectory may be less informative in more realistic landscapes, both because of neutral substitutions (which will make the initial and equilibrium substitution rates more similar) and because of the general intuition that substitution rates should be decreasing during adaptation as the supply of beneficial mutations is exhausted. Tests of epistasis based on the variance trajectory or a combination of the substitution and fitness trajectories (c.f. Good and Desai, 2014) may provide better avenues for future research. Indeed, the variance trajectory may be particularly well-suited for detecting situations where neutral potentiating mutations are required before substantial adaptation is possible (Wagner, 2008, 2011; Draghi et al., 2010; Bloom et al., 2010). Finally, while our results here assume that mutation is weak, most experimental evolution involves large microbial populations in the regime of clonal interference (Gerrish and Lenski, 1998). Thus, it is possible that existing experimental mean fitness trajectories (e.g. Wiser et al., 2013) may contain information about the presence of epistasis. However, without a comparable demonstration that epistasis is indeed identifiable from the mean fitness trajectory for such populations, our negative results under weak mutation suggest extreme caution in using empirical mean fitness trajectories to argue for or against the hypothesis that epistasis is present or to estimate the prevailing form of epistasis.
Two recent theoretical studies have also analyzed the relationship between the presence or absence of epistasis and the dynamics of adaptation under weak mutation. Kryazhimskiy et al. (2009) considered the space of fitness landscapes in which the distribution of mutational effects on fitness (DFE) is solely a function of the current fitness of the population, and they concluded that it is possible to identify epistasis from the mean fitness trajectory. On the whole, the class of models studied by Kryazhimskiy et al. (2009) is much broader than the one considered here (since any finite-state fitness landscape can be arbitrarily well approximated in their framework so long as each genotype has a unique fitness), and it includes many models that are inconsistent with finite-site landscapes. In particular, Kryazhimskiy et al. (2009) considered a fitness landscape to be non-epistatic if its DFE is independent of the population’s fitness. Such a situation can never arise on a non-trivial finite-site landscape, because the DFE must be entirely negative at the fittest genotype and entirely positive at the least-fit genotype. Our results are thus complementary to those of Kryazhimskiy et al. (2009), and we conclude that while the shape of the fitness trajectory may be informative in distinguishing between various models in their broader class, it is not informative for the narrower set of models corresponding to finite-site fitness landscapes. It is also worth noting that the analytical results presented by Kryazhimskiy et al. (2009) are approximations that hold only for a relatively limited subset of models within this broader class (see van Kampen, 2007, pp. 124–127), whereas the analytical results presented here are exact and apply to arbitrary fitness landscapes with a finite number of biallelic sites.
Good and Desai (2014) also present results on the diversity of mean fitness and substitution trajectories that can be produced by non-epistatic fitness landscapes, but they assume that selection is strong so that deleterious mutations cannot fix. Under strong selection and weak mutation Good and Desai (2014) found that non-epistatic landscapes can produce only a subset of possible mean fitness trajectories (these trajectories correspond to the case with all ck ≤ 0 in our Equation 4). In contrast, here we have allowed for the possibility of deleterious substitutions and we have shown that any mean fitness trajectory that can be produced by an epistatic landscape can also be produced by a non-epistatic landscape.
This difference arises from the assumption of strong selection, which changes the basic character of the evolutionary dynamics (see also McCandlish et al., 2014). Under our model, each site in a non-epistatic fitness landscape independently approaches a mutation-selection-drift equilibrium (Bulmer, 1991). At this equilibrium, the expected fitness and substitution rate can be either lower or higher than the initial fitness and substitution rate. In contrast, under strong-selection weak-mutation, each site in a non-epistatic fitness landscape results in exactly one beneficial substitution, and all evolution comes to a halt when the population reaches the fittest genotype. Thus, the rate of adaptation must be decreasing in time as the finite supply of beneficial mutations becomes exhausted; the same is true of the substitution rate. This greatly constrains the set of mean fitness and substitution trajectories that can be produced by non-epistatic fitness landscapes under strong-selection weak-mutation. Good and Desai (2014) also derive a necessary relation between the substitution and mean fitness trajectories for non-epistatic landscapes when mutation rates are uniform across sites, but show in their supplementary material that this relationship breaks down if different sites are permitted to have different mutation rates.
Supplementary Material
Acknowledgments
4 Acknowledgements
We thank Richard Lenski, Noah Ribeck, Bjørn Østman, Benjamin Good and Michael Desai for helpful discussion, and Thomas Lenormand, Sylvain Glémin and two anonymous reviewers for their comments on the manuscript. We acknowledge funding from the Burroughs Wellcome Fund, the David and Lucile Packard Foundation, the James S. McDonnell Foundation, the Alfred P. Sloan Foundation, the U.S. Department of the Interior (D12AP00025), the U.S. Army Research Office (W911NF-12-1-0552), and the National Institutes of Health (2T32AI055400).
References
- Bank C, Hietpas RT, Jensen JD, Bolon DN. A systematic survey of an intragenic epistatic landscape. Molecular biology and evolution. 2015;32:229–238. doi: 10.1093/molbev/msu301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bank C, Hietpas RT, Wong A, Bolon DN, Jensen JD. A bayesian mcmc approach to assess the complete distribution of fitness effects of new mutations: Uncovering the potential for adaptive walks in challenging environments. Genetics. 2014;196:841–852. doi: 10.1534/genetics.113.156190. URL http://www.genetics.org/content/196/3/841.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg J, Willmann S, Lassig M. Adaptive evolution of transcription factor binding sites. BMC Evol Biol. 2004;4:42. doi: 10.1186/1471-2148-4-42. URL http://www.ncbi.nlm.nih.gov/pubmed/15511291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanquart F, Achaz G, Bataillon T, Tenaillon O. Properties of selected mutations and genotypic landscapes under fisher’s geometric model. Evolution. 2014;68:3537–3554. doi: 10.1111/evo.12545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom JD, Gong LI, Baltimore D. Permissive secondary mutations enable the evolution of influenza oseltamivir resistance. Science. 2010;328:1272–1275. doi: 10.1126/science.1187816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer M. The selection-mutation-drift theory of synonymous codon usage. Genetics. 1991;129:897–907. doi: 10.1093/genetics/129.3.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou HH, Chiu HC, Delaney NF, Segrè D, Marx CJ. Diminishing returns epistasis among beneficial mutations decelerates adaptation. Science. 2011;332:1190–1192. doi: 10.1126/science.1203799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draghi JA, Parsons TL, Wagner GP, Plotkin JB. Mutational robustness can facilitate adaptation. Nature. 2010;463:353–355. doi: 10.1038/nature08694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Draghi JA, Plotkin JB. Selection biases the prevalence and type of epistasis along adaptive trajectories. Evolution. 2013;67:3120–3131. doi: 10.1111/evo.12192. URL http://dx.doi.org/10.1111/evo.12192. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of mendelian inheritance. Transactions of the royal society of Edinburgh. 1918;52:399–433. [Google Scholar]
- Fisher RA. The Genetical Theory of Natural Selection. Clarendon Press; London: 1930. [Google Scholar]
- Fontana W, Schuster P. Continuity in evolution: on the nature of transitions. Science. 1998;280:1451–1455. doi: 10.1126/science.280.5368.1451. [DOI] [PubMed] [Google Scholar]
- Frank SA. Generative models versus underlying symmetries to explain biological pattern. Journal of evolutionary biology. 2014;27:1172–1178. doi: 10.1111/Jeb.12388. [DOI] [PubMed] [Google Scholar]
- Gerrish P, Lenski R. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. doi: 10.1023/A:1017067816551. URL http://dx.doi.org/10.1023/A:1017067816551. [DOI] [PubMed] [Google Scholar]
- Good BH, Desai MM. The impact of macroscopic epistasis on long-term evolutionary dynamics. Genetics. 2014 doi: 10.1534/genetics.114.172460. URL http://www.genetics.org/content/early/2014/11/12/genetics.114.172460.abstract. [DOI] [PMC free article] [PubMed]
- Hartl DL. What can we learn from fitness landscapes? Current opinion in microbiology. 2014;21:51–57. doi: 10.1016/j.mib.2014.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa Y. Free fitness that always increases in evolution. J Theor Biol. 1988;135:265–281. doi: 10.1016/s0022-5193(88)80243-1. URL http://www.sciencedirect.com/science/article/pii/S0022519388802431. [DOI] [PubMed] [Google Scholar]
- Jain K, Krug J. Deterministic and stochastic regimes of asexual evolution on rugged fitness landscapes. Genetics. 2007;175:1275–1288. doi: 10.1534/genetics.106.067165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kammler DW. Chebyshev approximation of completely monotonic functions by sums of exponentials. SIAM Journal on Numerical Analysis. 1976;13:761–774. [Google Scholar]
- van Kampen NG. Stochastic Processes in Physics and Chemistry. Third. Elsevier; Amsterdam: 2007. [Google Scholar]
- Kauffman S, Levin S. Towards a general theory of adaptive walks on rugged landscapes. J Theor Biol. 1987;128:11–45. doi: 10.1016/s0022-5193(87)80029-2. [DOI] [PubMed] [Google Scholar]
- Kauffman SA. The Origins of Order: Self Organization and Selection in Evolution. Oxford Univ. Press; New York: 1993. [Google Scholar]
- Kauffman SA, Weinberger ED. The NK model of rugged fitness landscapes and its application to maturation of the immune response. Journal of theoretical biology. 1989;141:211–245. doi: 10.1016/s0022-5193(89)80019-0. [DOI] [PubMed] [Google Scholar]
- Khan AI, Dinh DM, Schneider D, Lenski RE, Cooper TF. Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011;332:1193–1196. doi: 10.1126/science.1203801. [DOI] [PubMed] [Google Scholar]
- Kryazhimskiy S, Draghi JA, Plotkin JB. In evolution, the sum is less than its parts. science. 2011;332:1160–1161. doi: 10.1126/science.1208072. [DOI] [PubMed] [Google Scholar]
- Kryazhimskiy S, Tkaçik G, Plotkin JB. The dynamics of adaptation on correlated fitness landscapes. Proc Natl Acad Sci U S A. 2009;106:18638–18643. doi: 10.1073/pnas.0905497106. URL http://www.pnas.org/content/106/44/18638.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski RE, Rose MR, Simpson SC, Tadler SC. Long-term experimental evolution in Escherichia coli. I. adaptation and divergence during 2,000 generations. The American Naturalist. 1991;138:1315–1341. URL http://www.jstor.org/stable/2462549. [Google Scholar]
- Lenski RE, Travisano M. Dynamics of adaptation and diversification: a 10,000-generation experiment with bacterial populations. Proceedings of the National Academy of Sciences. 1994;91:6808–6814. doi: 10.1073/pnas.91.15.6808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G, Elena SF, Lenormand T. Distributions of epistasis in microbes fit predictions from a fitness landscape model. Nat Genet. 2007;39:555–560. doi: 10.1038/ng1998. URL http://dx.doi.org/10.1038/ng1998. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J. Natural selection and the concept of a protein space. Nature. 1970;225:563–564. doi: 10.1038/225563a0. [DOI] [PubMed] [Google Scholar]
- McCandlish DM. Visualizing fitness landscapes. Evolution. 2011;65:1544–1558. doi: 10.1111/j.1558-5646.2011.01236.x. URL http://dx.doi.org/10.1111/j.1558-5646.2011.01236.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCandlish DM, Epstein CL, Plotkin JB. The inevitability of unconditionally deleterious substitutions during adaptation. Evolution. 2014;68:1351–1364. doi: 10.1111/evo.12350. URL http://arxiv.org/abs/1309.1152. [DOI] [PubMed] [Google Scholar]
- McCandlish DM, Stoltzfus A. Modeling evolution using the probability of fixation: History and implications. The Quarterly Review of Biology. 2014;89:225–252. doi: 10.1086/677571. URL http://www.jstor.org/stable/10.1086/677571. [DOI] [PubMed] [Google Scholar]
- Moran PAP. The survival of a mutant gene under selection. Journal of the Australian Mathematical Society. 1959;1:121–126. [Google Scholar]
- Olson CA, Wu NC, Sun R. A comprehensive biophysical description of pairwise epistasis throughout an entire protein domain. Current Biology. 2014;24:2643–2651. doi: 10.1016/j.cub.2014.09.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otwinowski J, Plotkin JB. Inferring fitness landscapes by regression produces biased estimates of epistasis. Proceedings of the National Academy of Sciences. 2014;111:E2301–E2309. doi: 10.1073/pnas.1400849111. URL http://www.pnas.org/content/111/22/E2301.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips PC. Epistasis—the essential role of gene interactions in the structure and evolution of genetic systems. Nat Rev Genet. 2008;9:855–867. doi: 10.1038/nrg2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella G, Hirsh AE. The application of statistical physics to evolutionary biology. Proc Natl Acad Sci U S A. 2005;102:9541–9546. doi: 10.1073/pnas.0501865102. URL http://www.pnas.org/content/102/27/9541.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler PF. Spectral landscape theory. In: Crutchfield J, Schuster P, editors. Evolutionary Dynamics: Exploring the Interplay of Selection, Accident, Neutrality and Function. Oxford Univ. Press; Oxford: 2003. pp. 231–271. [Google Scholar]
- Szendro IG, Schenk MF, Franke J, Krug J, de Visser JAG. Quantitative analyses of empirical fitness landscapes. Journal of Statistical Mechanics: Theory and Experiment. 2013;2013:P01005. [Google Scholar]
- Trindade S, Sousa A, Gordo I. Antibiotic resistance and stress in the light of fisher’s model. Evolution. 2012;66:3815–3824. doi: 10.1111/j.1558-5646.2012.01722.x. URL http://dx.doi.org/10.1111/j.1558-5646.2012.01722.x. [DOI] [PubMed] [Google Scholar]
- de Visser JAG, Cooper TF, Elena SF. The causes of epistasis. Proceedings of the Royal Society B. Biological Sciences. 2011;278:3617–3624. doi: 10.1098/rspb.2011.1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser JAG, Krug J. Empirical fitness landscapes and the predictability of evolution. Nature Reviews Genetics. 2014 doi: 10.1038/nrg3744. [DOI] [PubMed] [Google Scholar]
- Wagner A. Neutralism and selectionism: a network-based reconciliation. Nat Rev Genet. 2008;9:965–974. doi: 10.1038/nrg2473. URL http://dx.doi.org/10.1038/nrg2473. [DOI] [PubMed] [Google Scholar]
- Wagner A. The Origins of Evolutionary Innovations: A Theory of Transformative Change in Living Systems. Oxford Univ Pr 2011 [Google Scholar]
- Weinberger E. Correlated and uncorrelated fitness landscapes and how to tell the difference. Biol Cybern. 1990;63:325–336. doi: 10.1007/BF00202749. URL http://dx.doi.org/10.1007/BF00202749. [DOI] [Google Scholar]
- Weinberger E. Fourier and Taylor series on fitness landscapes. Biol Cybern. 1991;65:321–330. doi: 10.1007/BF00216965. URL http://dx.doi.org/10.1007/BF00216965. [DOI] [Google Scholar]
- Weinreich DM, Lan Y, Wylie CS, Heckendorn RB. Should evolutionary geneticists worry about higher-order epistasis? Current opinion in genetics & development. 2013;23:700–707. doi: 10.1016/j.gde.2013.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreich DM, Watson RA, Chao L. Perspective: sign epistasis and genetic costraint on evolutionary trajectories. Evolution. 2005;59:1165–1174. [PubMed] [Google Scholar]
- Whitlock MC, Phillips PC, Moore FBG, Tonsor SJ. Multiple fitness peaks and epistasis. Annual Review of Ecology and Systematics. 1995:601–629. [Google Scholar]
- Wiser MJ, Ribeck N, Lenski RE. Long-term dynamics of adaptation in asexual populations. Science. 2013;342:1364–1367. doi: 10.1126/science.1243357. [DOI] [PubMed] [Google Scholar]
- Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proceedings of the Sixth International Congress of Genetics. 1932:356–366. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


