Abstract
Inference on data with missingness can be challenging, particularly if the knowledge that a measurement was unobserved provides information about its distribution. Our work is motivated by the Commit to Quit II study, a smoking cessation trial that measured smoking status and weight change as weekly outcomes. It is expected that dropout in this study was informative and that patients with missed measurements are more likely to be smoking, even after conditioning on their observed smoking and weight history. We jointly model the categorical smoking status and continuous weight change outcomes by assuming normal latent variables for cessation and by extending the usual pattern mixture model to the bivariate case. The model includes a novel approach to sharing information across patterns through a Bayesian shrinkage framework to improve estimation stability for sparsely observed patterns. To accommodate the presumed informativeness of the missing data in a parsimonious manner, we model the unidentified components of the model under a non-future dependence assumption and specify departures from missing at random through sensitivity parameters, whose distributions are elicited from a subject-matter expert.
Keywords: Informative missingness, Longitudinal data, Mixed data, Non-future dependence, Pattern mixture model, Sensitivity, Shrinkage
1. Introduction
One of the more challenging aspects in analyzing repeatedly measured data on human subjects is handling missing observations. This is particularly true when the knowledge that an observation is missing may itself provide information about the distribution of the unobserved data. Methodology to deal with this informative missingness is both challenging and potentially controversial, as any analysis will require the statistician to make untestable assumptions about the unobserved data. Despite this difficulty missingness in experimental data is ubiquitous, and the analyst risks mischaracterizing the results or drawing faulty conclusions by failing to deal with it appropriately.
We recall some key results from the missing data literature (e.g., Little and Rubin, 2002). Let Yi = (Yi1, …, YiT) denote the vector of (potentially observed) responses, and let Rit be an indicator that response Yit is observed, i.e., Rit = I(Yit is observed). Define the (full) data response model as the probability model for Y, p(y|θ1), parametrized by θ1. We then define the missing data mechanism (MDM) as p(r|y, θ2) with parameter θ2. Finally, yobs (respectively, ymis) is the set of Yits that are observed (missing). The missing data mechanism is ignorable if the following three conditions hold: 1) p(r|y, θ2) = p(r|yobs, θ2), i.e., the missingness only depends on the observed responses, so it is missing at random (MAR); 2) the parameter θ of the full model p(y, r|θ) can be decomposed as (θ1, θ2) with p(y|θ1) and p(r|y, θ2); 3) the parameters of the response model and the missing data mechanism are a priori independent, i.e. p(θ) = p(θ1)p(θ2). Models with ignorable missingness comprise a wide and commonly used class of techniques. In particular, standard Bayesian analysis using the observed data likelihood for the responses implicitly makes the assumption that missingness is ignorable (Schafer, 1997; Little and Rubin, 2002).
When any of the three conditions above are not satisfied, the missingness is referred to as non-ignorable. Often, this is due to the first condition failing, i.e., p(r|y, θ2) ≠ p(r|yobs, θ2), known as missing not at random (MNAR). It is then necessary to specify the MDM as a function of both yobs and ymis. The joint model for (y, r) will require untestable assumptions about the missing data, as can be seen from the factorization
| (1) |
While the parameters of the observed data model θO are identifiable, it is clear that the observed data provide no information about θE. We call the leading term on the right the extrapolation distribution (Daniels and Hogan, 2008).
There are three main classes of models based on different factorizations of the full data distribution p(y, r|θ): selection models, shared parameter models, and pattern mixture models. Selection models involve the factorization p(y, r|θ) = p(y|θ1)p(r|y, θ2) (Diggle and Kenward, 1994). If data are MNAR, structural assumptions about the MDM lead to a fully identified model, including the extrapolation distribution for which the observed data give no information. Shared parameter models assume a latent variable βi, and typically set yi and ri to be independent given βi by modeling p(yi|βi) and p(ri|βi) (Wu and Carroll, 1988; Cowles et al., 1996; Dunson and Perreault, 2001). A drawback of shared parameter models is that formulas for the MDM are generally difficult to obtain (β must be integrated out), making it challenging to specify MAR models.
Alternatively, pattern mixture models (PMM) factor p(y, r|θ) as p(r|π)p(y|r, ψ), first drawing the missingness indicators R, referred to as the missingness pattern, then the responses conditional on the pattern (Little, 1993, 1994). The data response model is recovered by marginalizing over R, p(y|θ1) = Σr p(r|π)p(y|r, ψ). A key advantage to PMMs with missingness due to dropout is that the extrapolation distribution appears explicitly in the model specification. Hence, PMMs often lead to a straightforward understanding of the role the missing data assumptions play and provide easier specification of θE through sensitivity parameters, as opposed to selection and shared parameter models (Daniels and Hogan, 2000).
While many of these methods are well understood when the response Yit is univariate, additional considerations arise if a bivariate (or more generally, multivariate) response is repeatedly observed and subject to non-ignorable missingness. Our work is partially motivated by the analysis of a smoking cessation trial (Marcus et al., 2005). In this study patients were measured weekly for whether they had smoked during the previous week and for the percentage weight change from baseline. In addition to study dropout, the analysis is further complicated by the joint modeling of the discrete and continuous longitudinal outcomes.
In the next section we provide details on the motivating data. Section 3 introduces our proposed bivariate pattern mixture model and the role of the extrapolation distribution. In particular, we propose new methodology to share information across patterns to gain stability in the parameter estimates for patterns with few patients. Section 4 contains a simulation study to evaluate the performance of our proposed model, and we then apply the methods to the smoking cessation data in Section 5. Next, we discuss issues arising from non-ignorability including the role of sensitivity parameters, elicitation of their distribution, and the estimation of treatment effects. We provide some concluding remarks in Section 7.
2. The Commit to Quit II smoking cessation trial
The Commit to Quit II study (CTQ2; Marcus et al., 2003, 2005) was a 4-year randomized trial undertaken to test the efficacy of moderate-intensity physical activity as an aid for smoking cessation in women. Study enrollees were healthy women aged 18–65 who had regularly smoked five or more cigarettes per day for at least a year and who routinely exercise for less than 90 minutes a week. Patients were randomized into one of two treatments, a moderate-intensity exercise condition (denoted as exercise) and a contact condition (denoted as wellness). The outcomes of interest, measured weekly, were quit status (a longitudinal binary outcome) and weight change (a longitudinal continuous outcome). As it is believed that many cessation attempts fail due to weight gain, the goal of the study was to test whether an exercise treatment may lead to higher quit rates by better managing weight changes.
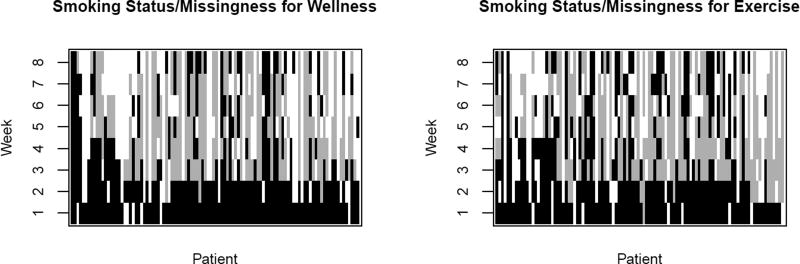
Two hundred, seventeen women were enrolled into the study, and measurements were intended to be taken for each of T = 8 weeks. For our analysis we exclude patients who were missing a baseline weight or who missed all eight measurement times. This left 208 patients with 104 in each treatment arm. As is common in studies of this type, there was substantial missingness with only a third of patients having an observed smoking status for all time points. Figure 1 displays smoking and missingness statuses for each patient by treatment; black, gray, and white represent smoking, not smoking, and missing for a given week. Patients are not asked to quit until week 3 (bottom two rows are mostly black), and the amount of missingness (white) increases by week. It is believed that patients who miss an appointment are more likely to be smoking than those who are observed, so a careful handling of the missingness is necessary to make appropriate conclusions from this study. In addition to comparing cessation success and weight change between the two treatments, we also wish to determine the sensitivity of these conclusions to our assumptions about the role of the missingness.
Figure 1.
Depiction of smoking status and missingness values by treatment group. Each column represents a patient’s status at each of the T = 8 measurement occasions. Black represents an observed value with smoking in the given week, gray represents an observed value of no smoking in the given week, and white represents the patient was missing for the week.
We let Qit denote weekly smoking quit status, equal to 1 (0) if patient i abstains (smokes) during week t. The percentage weight change from baseline is Wit, and ai denotes the indicator of whether subject i was randomized to the exercise treatment. The corresponding vectors of the binary and continuous outcomes are Qi = (Qi1, ⋯, QiT)⊤ and Wi = (Wi1, ⋯, WiT)⊤, with Qi,obs and Wi,obs representing the observed parts of Qi and Wi respectively. We assume a normally-distributed, latent variable Zit whose sign determines the weekly cessation status through Qit = I(Zit ≥ 0), and let Zi = (Zi1, ⋯, ZiT)⊤.
Liu et al. (2009) analyze the CTQ2 data by modeling the joint distribution of the binary and continuous variables by a multivariate normal specification on the latent quit propensity and weight change through . An important complication is that the T × T block of Σai corresponding to Zi must be a correlation matrix for identifiability (Chib and Greenberg, 1998; Gueorguieva and Agresti, 2001). However, their analysis is made under the assumption of ignorable missingness, whereas the goal of this work to develop models appropriate for analysis under MNAR. To that end we introduce a pattern mixture model for this data.
There are alternatives to using normal latent variables for the binary responses to specify a joint distribution of categorical and continuous outcomes. One could potentially use the general location model (Olkin and Tate, 1961; Liu and Rubin, 1998) or Gaussian copulas (Nelsen, 1999). An overview of Bayesian methods for mixed data can be found in the chapter Daniels and Gaskins (2013). As the latent variable choice yields a model that can more easily be extended to non-ignorability, we do not explore other choices here. In the next section we introduce a bivariate pattern mixture model for this type of data.
3. Bivariate pattern mixture model
3.1. Partial ignorability and the model for the missingness
The pattern mixture model is specified as p(y, r|θ) = p(r|π)p(y|r, ψ), where r is the missingness pattern. The CTQ2 data has 2T − 1 = 255 potential patterns, far too many to handle efficiently. Hence, we model this missingness through a dropout process. We say patient i drops out at time t if their final observed value occurs at t (Rit = 1 and Rij = 0 for all j > t). We denote this by Di = d(Ri) = t, and Di = T indicates that patient i completed the study. (Note that sometimes dropout is defined by Di + 1 and ranges from 2 to T + 1.) We assume that any missed values before dropout (called intermittent missingness) are MAR conditional on Di, while those after dropout may be MNAR. This is called partial ignorability (Harel and Schafer, 2009) and requires an MDM of the form p(r|y, θ2) = p(d|y, θ2A)p(r|yobs, d(r), θ2B) with θ2 = (θ2A, θ2B). Note R depends only on the observed data and the dropout time D, whereas D may depend on both the observed and missing data. If p(d|y, θ2A) = p(d|yobs, θ2A), then the model is (fully) ignorable and MAR.
Under the partially ignorable mechanism described above, we base inference on the joint distribution p(y, d) instead of p(y, r) as partial ignorability implies that the only relevant information about Y from R is found in D = d(R) (Harel and Schafer, 2009, Proposition 2). See Section A.1 of the Web Appendix for details. We model p(y|θ1)p(d|y, θ2A) using the PMM factorization p(d|π)p(y|d, ψ) where p(d|π) is the model for dropout and p(y|d, ψ) is the model for the response. The distribution of dropout Di is multinomial on {1, …, T} with probabilities πai,d = P (Di = d) depending on the treatment assignment ai. A convenient conjugate prior for πa = (πa,1, …, πa,T) is Dirichlet(1,…,1) for a = 0, 1. The complexity lies in specifying the response model p(y|d, ψ) as a function of the pattern d. We assume different sets of model parameters (πa, ψa) for the two treatments, but to simplify notation we suppress the dependence on a in the following.
At each measurement time we have a pair of observations, and in all but a few instances, smoking status and weight change are either both observed or both missing at a particular week. When only one is observed, we treat this as observed to assign pattern membership and assume the missing measurement is partially ignorable since it occurs before dropout. Table 1 provides the number of patients in each pattern by treatment. As stated previously, our model is defined through the weight change Wit and the cessation latent variable Zit not the actual smoking status Qit. Likewise, partial ignorability assumes R depends on dropout time, the observed weight changes, and the “observed” Zits (Zit corresponding to an observed Qit). We return to the role of partial ignorability in the discussion of Section 7.
Table 1.
Dropout time di by treatment group.
| Treatment | Number of patients with drop out at week d | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Exercise | 7 | 2 | 7 | 7 | 1 | 5 | 5 | 70 |
| Wellness | 9 | 6 | 8 | 4 | 5 | 3 | 3 | 66 |
3.2. Model for the observed data response
We now introduce the response model conditional on the dropout time. To that end, let Yit = (Zit, Wit)⊤ be the quit status latent variable and weight change pair at time t, and the time-ordered arrangement of the full response is Yi = (Zi1, Wi1, Zi2, Wi2, …, ZiT, WiT)⊤. The history at week t (t > 1) is denoted by . We construct the distribution for each pattern d sequentially through the factorization
where fd;t(yit|ȳit) is the density of the pair of measurements Yit at time t for subjects who leave the study at time d, conditional on the history Ȳit. Only those distributions fd;t(yit|ȳit) with d ≥ t are identified by the observed data. The remaining distributions, which taken together form the extrapolation distribution in equation (1), need to be specified through a combination of modeling choices and sensitivity parameters.
The identifiable distributions are modeled as follows. The week one distributions fd;1(yi1) have the form N2(ζd;1, Ωd;1) (d = 1, …, T), where ζd;1 is a 2-vector and Ωd;1 is 2 × 2 positive definite. Recall that the first component of Yi1 is Zi1, the latent quit propensity. As its scale is unidentified, the variance is constrained to be 1. For the identified distributions at time t > 1, fd;t(yit|ȳit) (d ≥ t), we choose N2 (ζd;t + (Φd;1t, …, Φd;t−1,t)ȳit, Ωd;t); ζd;t is a 2-vector, each Φd;jt is a 2 × 2 matrix, and Ωd;t is 2 × 2 positive definite. The Φd;jt matrix contains regression coefficients for the patient’s history at time j, controlling the longitudinal dependence on the earlier observations. ζd;t is called the conditional intercept, the intercept for the condition regression of Ȳit onto Yit. Ωd;t is the covariance matrix for this conditional regression, and as with t = 1 the leading variance is constrained to 1. We parametrize this matrix as and Ωd;t[2, 2] = ωd;t. Positive definiteness is guaranteed by ρd;t ∈ (−1, 1) and ωd;t > 0. We refer to the elements of the Φd;jt matrices as generalized auto-regressive parameters (GARPs) and Ωd;t as the innovation covariance matrix, treating our model as a multivariate extension of the modified Cholesky parametrization of the covariance matrix (Pourahmadi, 1999). This model is also related to the vector autoregressive model (VAR) from time series analysis (Lütkepohl, 1991), but we do not require stationarity. Allowing Ωd;t to be constant across t, ζd;t to be zero for t > 1, and Φd;jt to be constant in t − j would lead to the stationary VAR model.
For a particular pattern d, let be the vector of identified conditional intercepts and Ωd be the block diagonal matrix of Ωd;1, …, Ωd;d. Further define Φd to be the 2d × 2d block lower triangular matrix with (t, t) block as the 2 × 2 identity matrix, I2, and the (t, j) block −Φd;jt for j < t. The joint distribution of the observed data given the pattern Di = d is (see the Web Appendix for derivation).
Under partial ignorability the distribution p(ȳi,d+1|Di = d) is the identifiable piece of the response model p(yi|Di = d) from factorization (1), and if d ≠ T the distribution of the unobserved variables p(yi,d+1, …, yiT|ȳi,d+1, Di = d) is the unidentified extrapolation distribution. As mentioned previously, this transparency of the extrapolation is an important benefit to using PMMs. Furthermore, it provides intuitive choices for specifying the unidentifiable distributions, which we explore in Section 6. For now we consider the bivariate PMM in the context of the MAR assumption, so that we have a fully defined model. The MAR restriction uniquely specifies the unidentified distributions (d < t) to be
| (2) |
(Molenberghs et al., 1998), which is a mixture over the distributions at time t for the identified patterns s = t, …, T. The terms in braces are the mixing coefficients, which are equal to P (D = s|ȳit, D ≥ t). Note that this distribution fd;t(yit|ȳit) is constant in d (d < t), and hence, fd;t(yit|ȳit) = fd′;t(yit|ȳit) for all d, d′ < t at each time t.
We remind the reader that we have specified our model in terms of the full data Y which contains both Zobs, the unobserved latent variables corresponding to the observed smoking statuses Qobs, and (Qmis, Wmis), the values that are missing either intermittently or due to dropout. We obtain the observed data likelihood by integrating the identified model p(d, ȳd+1) with respect to the latent variables and the intermittently missed responses:
| (3) |
where z has length di, wint = {wit : t ≤ di, rit = 0} denotes the intermittently missed weight changes, and 𝒵(qi,obs) represents the set of latent variables consistent with the sign restrictions of the observed smoking statuses. We obtain parameter samples from our model using MCMC with data augmentation that draws (zi, wi,int) given (di, qi,obs, wi,obs) during each iteration.
The identified distributions from p(yi|Di = d) are which contain a large number of parameters. In the next two sections, we formulate the prior distributions in such a way as to effectively reduce the number of parameters that must be estimated from the data.
3.2.1. Priors to induce sharing information across patterns
A common issue when using a PMM is that some of the patterns contain relatively few observations, leading to instability in the parameter estimates of the pattern-specific distributions. Our model as presented thus far estimates 2 conditional intercepts, 4(t − 1) GARPs, and 2 covariance parameters for each d and t with d ≥ t. In the CTQ2 data only the completer pattern (d = T) has more than ten patients (Table 1), so we must develop methodology to handle these sparsely observed patterns.
An obvious solution is to set the parameters equal across patterns, yielding fd;t(yit|ȳit) = fd′;t(yit|ȳit) for all d, d′ ≥ t. However, together with (2) this will imply p(y|d, ψ) = p(y|ψ), which is the missing completely at random (MCAR) assumption. While requiring fewer parameters, assuming y and d are independent seems unlikely to hold in most practical settings, particularly in the context of smoking cessation. Other parameter reduction choices include grouping the dropout times into a smaller number of patterns (Hogan et al., 2004) or assuming the distribution of Yi differs across a small number of latent classes Ci whose distribution depends on dropout Di (Roy, 2003; Roy and Daniels, 2008).
Rather than reducing the number of patterns, Wang and Daniels (2011) consider equality constraints on subsets of model parameters across patterns. They show that for the full response distribution p(yi|Di = d) under MAR (2) to be multivariate normal for each pattern, the distribution of Yit given Ȳit must be the same across all patterns d for t > 1, that is, for t > 1, fd;t(yit|ȳit) = ft(yit|ȳit) for all d. Hence, the conditional intercepts, GARPs, and innovation covariances are equal across d for t > 1. The t = 1 means ζd;1 differ across patterns, and the covariances Ωd;1 may also differ across d but are generally assumed equal. This constraint results in a MDM that depends only on Yi1 (Wang and Daniels, 2011, Corollary 1).
A somewhat more flexible model would be to assume the dependence parameters are equal across identifiable patterns, and and to allow the conditional intercepts ζd;t to differ. Unlike the previous model where the extrapolation distributions fd;t(yit|ȳit) (d > t) are multivariate normal, the extrapolation distributions here will be a mixture of T − t + 1 normals as defined in (2).
While these types of equality assumptions can provide stable estimation, the resulting models may be a poor representations of the true response distribution. Hence, a middle ground between equality and independence through sharing information across patterns would be welcome. There is a growing literature on Bayesian estimation for multiple, potentially similar covariance matrices (e.g., Daniels, 2006; Pourahmadi et al., 2007; Hoff, 2009; Gaskins and Daniels, 2013, 2015), but due to the constraint in the (1, 1) component of each Ωd;t and the unidentifiability of the extrapolation parameters, these methods cannot be directly implemented. Hence, we introduce a method that borrows strength in estimating the identifiable parameters across patterns.
To that end, we propose shrinking the pattern-specific parameters toward a global value for the distributions identified by the observed data. Let be these global parameters, which are the shrinkage targets of the identified parameters ζd;t, Φd;jt, ρd;t, ωd;t (d ≥ t). While we suppress the notation, we use a distinct set of for each treatment. These are connected through the following distributions for d ≥ t:
| (4) |
| (5) |
| (6) |
| (7) |
Here, vec(·) is the standard vector operator that stacks the columns of a matrix. This model assumes the identifiable parameters in each pattern are exchangeable and makes no use of the temporal ordering of the patterns. Extensions along these lines are possible but not pursued here.
For each of the four sets of parameters, the shrinkage variance τ2 governs the amount of information shared across patterns. Large values of τ2 allow large differences between the parameters of different patterns, while the identified fd;t(yit|ȳit) (d ≥ t) will be similar under small τ2. Note that in the special case where , this shrinkage model goes to MCAR (assuming MAR for the extrapolation terms). Further with and not too small, this will be equivalent to the model that sets the dependence parameters equal and leaves the mean parameters flexible. Hence, our model allows the data to inform the appropriate level of information sharing.
To fully define our Bayesian model, we must choose prior distributions for the remaining parameters. For the (treatment-specific) shrinkage targets, we use
| (8) |
| (9) |
| (10) |
| (11) |
where pΦ(·) will be defined in the following section and 0k represents the k-vector of zeros. We use a half-Cauchy prior for the shrinkage standard deviations τζ, τϕ, τρ, τω. That is, for k ∈ {ζ, ϕ, ρ, ω}, , τk > 0. This is the Cauchy distribution with location zero and scale γk, restricted to positive half-line. Under the support restriction γk is both the scale and median of τk. The half-Cauchy distribution has found an important role in Bayesian variable shrinkage since it has non-zero density at 0 and heavy tails (Carvalho et al., 2010). Here, we choose γζ = γω = 0.1 and γϕ = γρ = 0.05 as the hyperparameter values to represent reasonable guesses at the prior median of the τ s. For the other hyperparameters the prior choices are and λ1, λ2 ~ Gamma(1, 1). With the exception of the shrinkage targets, the other hyperparameters ( , λ1, λ2) are common across the two treatments.
3.2.2. Sparse prior models for GARP matrices
A well known issue in the modeling of a covariance matrix is the quadratic number of parameters. In our model this is manifested in the 2(d − 1)(d − 2) GARPs defining Φd. One Bayesian solution is to use as the prior for the GARP shrinkage target in (9) a mixture of a point mass at zero and a normal distribution, known as the “spike-and-slab” prior (Smith and Kohn, 2002). A computationally faster alternative uses a prior that shrinks the GARPs toward zero. We explore this using a longitudinal extension of the normal-gamma model of Griffin and Brown (2010).
We define the prior pΦ(·) for in (9) through the following hierarchical model, where is the kth component of (k = 1, …, 4),
| (12) |
| (13) |
for λ, γ0 > 0 and ξ ∈ (0, 1). Here, represents a GARP-specific shrinkage factor, showing that this model falls in the global-local shrinkage framework (Polson and Scott, 2010). Marginally, has mean zero, variance 2λγ0ξt−j, and excess kurtosis 3/λ (Griffin and Brown, 2010). The constraint on ξ implies the variance of decreases in the lag t − j, that is, the regression coefficient of the responses at time j onto the time t measurement is more aggressively shrunk for j further back in time. This is consistent with the longitudinal nature of the history, as less recent responses will generally be less relevant for predicting the current measurement. Smaller values of λ give the distribution heavier tails, providing protection from over-shrinking large GARPs. As a special case, setting λ = 1 implies that (13) is an exponential distribution as in the Bayesian Lasso (Park and Casella, 2008) and a GARP-shrinkage model proposed in Gaskins and Daniels (2015). For hyperpriors we choose λ ~ Exp(1), γ0 ~ InvGamma(1, 1), and ξ ~ Unif(0, 1). The GARP shrinkage target and its variance are treatment specific, while the hyperparameters λ, γ0, ξ are common across treatments.
4. Simulation study to evaluate model performance
To assess the performance of our proposed methodology, we consider a simulation study based on the Commit to Quit II study. We compare our model to frequently-used choices. For the model on the conditional intercepts, let mvn-mar denote the constraint for d ≥ t and t ≠ 1, which provides a multivariate normal distribution for the full response p(yi|Di = d) under MAR (assuming equality of GARPs and innovation covariance matrix) (Wang and Daniels, 2011). For modeling the intercepts distinctly across patterns, each ζd;t (d ≥ t) is drawn independently from the distribution in (8), and we call this model pattern. Our proposed model that shrinks ζd;t toward given by (4) and (8) is shrink.
With each of the three intercept models, we assume equality in the dependence structure across patterns ( and for d ≥ t). With this equal structure, the GARPs have the sparse prior in (12)–(13). We also consider the shrink dependence model from equations (5)–(7) and (9)–(11) with the sparse GARP model and the shrink intercept choice. Finally, we pair the pattern mean model with a pattern dependence model with no information sharing across dependence parameters and a non-sparse (normal) prior for the GARPs. As a shorthand, we denote these five models by the triple that defines the mean structure, the dependence structure, and the prior on the GARPs.
We consider four data generating mechanism. Model (A) draws the data using the parameter estimates from shrink/equal/sparse model fit to the CTQ2 data. Data generating model (B) is consistent with mvn-mar assumption for the intercepts, and in model (C) the ζd;t differ more substantially across patterns than model (A). Model (C) should favor the pattern mean model or shrink with a large value of τζ. While choices (A)–(C) all assume common (equal) dependence structures across patterns, model (D) allows the intercepts, GARPs, correlation, and innovation variances to each vary across patterns. Model (D) is consistent with shrink/shrink and pattern/pattern mean/dependence models. Details about selection of parameter values can be found in the Section A.3 of the Web Appendix.
For each model specification considered, we run a Markov chain Monte Carlo (MCMC) algorithm to obtain a sample of the parameters from the posterior distribution. We run the chain for 75,000 iterations after a burn-in of 15,000 and retain every 50th iteration for inference. We use the data augmentation algorithm in Liu et al. (2009, Proposition 1) to sample the constrained latent variables Z, which is more efficient that one-at-a-time conditioning (Robert, 1995). Many of the model parameters are updated conjugately (πa, Zit for t ≤ di, any missing Wit for t ≤ di, ζd;t, , Φd;jt, , λ2, , γ0). For those parameters whose distributions are non-conjugate (ρd;t, , ωd;t, , λ1, λ, ξ), we update using the slice sampler (Neal, 2003). See the Web Appendix, Section A.2 for the form of the full conditional (sampling) distributions. Depending on the complexity of the model involved, the MCMC algorithm takes between 10 and 18 hours to run on a desktop computer per data set. R code is available at the website of the second author, *****.
For each of the true models, we generate 100 data sets, maintaining the same dropout and intermittent missingness patterns from the original CTQ2 data. For each of data sets, we run MCMC chains to compare five model specifications. To evaluate the estimation accuracy, we compute the risk for estimating the conditional intercepts, the mean functions, and the covariance matrices using the following loss functions: , where is the marginal mean vector and is the (2d) × (2d) marginal covariance matrix. Results are in Table 2.
Table 2.
Estimated risk for each parameter set (conditional intercepts, marginal mean, covariance matrix) by estimation model under each of the four data generating mechanisms.
| Loss Function | Estimation Model | |||||
|---|---|---|---|---|---|---|
|
|
||||||
| Mean: Dependence: GARP: |
mvn-mar equal sparse |
pattern equal sparse |
shrink equal sparse |
shrink shrink sparse |
pattern pattern non-sparse |
|
| Data Generating Model (A) | ||||||
| Zeta | 33.9 | 68.6 | 8.2 | 34.9 | 56.7 | |
| Mu | 53.5 | 130.6 | 9.2 | 54.4 | 120.7 | |
| Sigma | 22.8 | 33.6 | 16.7 | 49.8 | 54.2 | |
| Data Generating Model (B) | ||||||
| Zeta | 29.8 | 65.5 | 16.8 | 46.9 | 56.9 | |
| Mu | 47.3 | 120.3 | 32.1 | 57.3 | 110.4 | |
| Sigma | 17.6 | 30.8 | 15.0 | 49.8 | 53.2 | |
| Data Generating Model (C) | ||||||
| Zeta | 310.8 | 67.9 | 61.9 | 140.9 | 95.1 | |
| Mu | 191.7 | 111.8 | 90.8 | 97.2 | 123.2 | |
| Sigma | 30.3 | 32.8 | 20.6 | 51.1 | 52.9 | |
| Data Generating Model (D) | ||||||
| Zeta | 243.6 | 245.7 | 190.5 | 31.8 | 85.1 | |
| Mu | 250.7 | 120.5 | 106.9 | 92.3 | 119.2 | |
| Sigma | 388.4 | 377.7 | 367.6 | 29.9 | 45.6 | |
Generating models (A)–(C) have the same dependence structure for each pattern, and we find that the shrink/equal/sparse is found to be the best in each case. It is perhaps surprising that using the shrinkage framework produces better estimation than the correct mvn-mar choice in model (B). This is, in part, a consequence of the unbalanced pattern memberships. All of the non-completer patterns have fewer than 10 subjects, implying that there is very little information from the data about ζd;1 for d < T. This leads to large sampling variability (and higher risk) in these intercept estimates and the resulting marginal means. Even though the shrink models are biased toward the population—not pattern—mean, the stability it imposes yields better estimation. For data generating model (C), there are large differences in the conditional intercept across patterns that should favor the pattern or shrink with large τζ, but by introducing a small amount of shrinkage, shrink/equal/sparse has slightly lower risk. In the shrink-mean model the average value of τ̂ζ is 1.18 (80% of τ̂ζ ’s are between 1.10 and 1.26) compared to 0.09 (0.06, 0.15) and 0.13 (0.07, 0.24) in scenarios (A) and (B), respectively. Clearly, our shrinkage framework is flexible enough to adapt to the situation when there is little similarity across patterns. In scenario (C), the mvn-mar assumption produces highly biased mean estimates as expected.
Simulation (D) has distinct covariance structures across the patterns, and we find that shrinkage on both the mean and dependence parameters produces the minimum risk. Estimation using a pattern-specific dependence structure also leads to low risk for Σ but poorer performance for the mean parameters. The risk in estimation of the covariance matrices and the conditional intercepts is much higher when common dependence is imposed, although estimation of mean structure (and hence, treatment effects) is impacted less.
Typically, one would fit the data to multiple models, and choose the best model using a selection method such as deviance information criterion (dic; Spiegelhalter et al., 2002). However, evaluation of the dic statistic demonstrated mixed performance in data such as ours. dic tends to systematically favor simpler models: shrink mean to mvn-mar and pattern mean structures and equal dependence to the shrink and pattern choices. Further simulation experiments also indicate poor performance with other model selection criteria: log psuedo-marginal likelihood (Geisser and Eddy, 1979) and posterior predictive loss based criteria (Ibrahim and Laud, 1994; Daniels et al., 2012). Details about dic simulation studies can be found in Section A.3 of the Web Appendix.
Based on the results from risk simulations and the unsatisfactory performance of several model selection criteria, we recommend using the shrinkage framework for the mean structure and either the equal or shrink model for the dependence, with the sparse GARP prior. The choice between equal and shrink dependence will be guided by the level of balance between dropout patterns. When patterns are unbalanced or sample sizes are small, the equal model should be favored to stabilize estimation of the covariance matrix; shrink can be used with large sample sizes and more balanced dropout times. Consequently, we base our analysis of the CTQ2 data in Sections 5 and 6 on the model formed by using the shrink framework for the conditional intercepts, equal for the dependence, and sparse for the GARPs.
5. CTQ2 data analysis under non-ignorable MAR
We now turn to the analysis of the CTQ2 data using the shrink/equal/sparse model under the MAR assumption. As in the simulation, our MCMC chain runs for 90,000 iterations, and we throw out the first 15,000 and retain every 50th sample.
The main targets of inference are the probability of abstaining at the final time point T = 8 for each treatment (marginally over patterns) and the expected weight change over the course of the study, as well as significance tests for a treatment effect due to exercise. As a key concern of this study is the interaction between smoking and weight change, we also consider the correlation between QiT and WiT. To obtain estimates of these quantities, we draw 5000 fully-observed responses from p(di, yi) at each parameter value in the posterior sample and compute sample means. Details of the algorithm are found in the Web Appendix, Section A.4.
The estimated probability that a patient abstains in the final week, P(QiT = 1), is 0.47 for the exercise treatment and 0.53 for the control with a posterior probability of 0.25 that the exercise treatment is superior. For the weight measurements, we find an expected weight change of 3.0% from baseline for both the wellness and exercise treatments, and the posterior probability that patients gain less under exercise is 0.51. For the exercise treatment the correlation between QiT and WiT is 0.13, and it is 0.18 for the control group. These positive values support the study motivation that women who successfully abstain tend to gain weight and that the exercise treatment may reduce this interaction as seen by the smaller correlation, although the 95% credible interval covers zero (see Table 4). Overall, under MAR we fail to find evidence that the exercise treatment produces better results than wellness in terms of quit rates, weight changes, or their relationship. Credible intervals for these quantities can be found in Table 4.
Table 4.
Posterior mean and 95% credible interval for the quantities of interest under each missingness assumption. The posterior probability row gives the probability that the exercise treatment is superior: higher cessation rate, lower weight change, lower correlation.
| Missing data assumption | |||||
|---|---|---|---|---|---|
|
|
|||||
| Quantity of interest |
Treatment |
Zit MAR Wit MAR |
Zit MNAR Wit MNAR |
Zit MNAR Wit MAR |
Qit = 0 if missing Wit MAR |
| Wellness | 0.53 (0.40, 0.65) | 0.50 (0.37, 0.63) | 0.50 (0.37, 0.63) | 0.30 (0.21, 0.39) | |
| P (QiT = 1) | Exercise | 0.47 (0.35, 0.59) | 0.44 (0.32, 0.56) | 0.43 (0.32, 0.56) | 0.28 (0.20, 0.37) |
| Post. prob. | 0.25 | 0.24 | 0.23 | 0.42 | |
| Wellness | 3.0% (2.3, 3.8) | 2.9% (2.2, 3.6) | 3.0% (2.2, 3.7) | 2.6% (1.8, 3.3) | |
| E(WiT) | Exercise | 3.0% (2.3, 3.7) | 2.8% (2.0, 3.4) | 3.0% (2.3, 3.6) | 2.7% (2.1, 3.4) |
| Post. prob. | 0.51 | 0.61 | 0.51 | 0.38 | |
| Wellness | 0.18 (− 0.08, 0.42) | 0.18 (− 0.08, 0.42) | 0.18 (− 0.07, 0.42) | 0.21 (0.02, 0.39) | |
| corr(QiT, WiT) | Exercise | 0.13 (− 0.14, 0.36) | 0.13 (− 0.13, 0.36) | 0.13 (− 0.14, 0.36) | 0.17 (− 0.04, 0.35) |
| Post. prob. | 0.61 | 0.59 | 0.61 | 0.62 | |
Comparing our results under non-ignorable MAR to the previous analysis under ignorable MAR in Liu et al. (2009), we note that our estimates of the quit probabilities are 7 to 9 percentage points higher, although their estimates are contained within our credible intervals. By allowing the response distribution to vary across dropout times, our model is more flexible whereas their model implicitly assumes a common distribution across Di. However, this increased flexibility does come at a cost of wider credible intervals.
We additionally run MCMC chains using the CTQ2 data with changes to hyperparameter values in the priors to test the sensitivity of our prior choices. The models with pattern dependence are somewhat sensitive to the priors, but this is expected as inference for the sparsely observed patterns will be more influenced by the prior. The parameter estimates and conclusions are relatively unchanged for the equal and shrink dependence structures, including the selected model.
6. Missing not at random PMM
6.1. Specifying the extrapolation distribution
To this point we have considered missingness to be MAR by using (2) to define the extrapolation distribution. As stated earlier, this is a questionable assumption, if not wholly unreasonable, as we expect patients who leave the study are more likely to smoke than those that continue on, even after conditioning on their history. Hence, we need to extend the model of Section 3 to allow informative missingness by considering alternative specifications of the extrapolation distributions fd;t(yit|ȳit) (d < t) through sensitivity parameters.
To do this, we consider non-future dependent missing data mechanisms. An MDM is said to satisfy non-future dependence (NFD) if P(D = d|y) = P(D = d|y1, …, yd+1), that is, the probability a patient’s last observation occurs at time d depends on her observed measurements Y1, …, Yd and the first missed observation Yd+1 but is independent of all future missed measurements (Kenward et al., 2003). Clearly, if the extrapolation distributions are chosen through MAR, it will satisfy NFD (MDM is also independent of Yd+1), but other choices of the extrapolation distributions generally will not. NFD only impacts the form of p(ymis|yobs, θE) and thus, cannot be tested from the data. However, it provides a realistic and intuitive starting point for defining the extrapolation distribution under MNAR. Kenward et al. (2003) show that for a PMM with NFD the distributions for patterns d < t − 1 have the form
| (14) |
In comparison with MAR (2), we are now conditioning on the observed patterns as well as the d = t − 1 first missed observation pattern. In particular, (14) depends on the unidentified ft−1;t(yit|ȳit), the model for the first missed observation. A further benefit to the NFD assumption is that the number of extrapolation distributions to define decreases from (T − 1)(T − 2)/2 to T − 1.
To specify these first post-dropout distributions ft−1;t(yit|ȳit), we apply a location shift to the MAR mixture distribution which will allow a sensitivity parameter specification. This idea was previously considered in the univariate context by Wang and Daniels (2011, with correction). To that end we rewrite the MAR distribution (2) as , letting α(s, ȳit) be the mixing weight P(D = s|ȳit, D ≥ t). The location shift on the MAR distribution implies
that is, the mean of the mixture is shifted by Δt = (Δt1, Δt2)⊤. This is accomplished by choosing , where f̃d;t(yit|ȳit) is multivariate normal with mean ζd;t + Δt + (Φd;1t, …, Φd;t−1,t)⊤ȳit and covariance matrix Ωd;t. The choice Δt = 02 produces ft−1;t(yit|ȳit) as the MAR distribution (2), and plugging that into (14) gives the MAR distribution (2) for all terms in the extrapolation (d < t − 1). It is also possible to introduce sensitivity parameters for the GARP coefficients Φ and/or the variance Ω, but in the interest of model parsimony, we do not pursue such models here. Also, note incorporating a location shift for missing data is closely related to the exponential tilting model (e.g., Birmingham et al., 2003; Kim and Yu, 2011).
As we are only making adjustments to the extrapolation term, the observed data distribution remain the same as under MAR. In fact, running a new MCMC chain for the MNAR analysis is not even needed. Letting π(Δ|θO) be a prior distribution for the sensitivity parameters potentially depending on the observed data distribution parameter θO, we can draw the MNAR posterior sample by first drawing θO from the observed data posterior (as sampled using non-ignorable MAR) and drawing Δ from π(Δ|θO); we provide details in the Web Appendix, Section A.4. In contrast, selection and shared parameter models typically do not exhibit a sensitivity parametrization; this implies that the observed data likelihood will depend on the assumptions made about the missing data mechanism. In such cases it will be necessary to refit the data and repeat any model selection procedure for each new MNAR assumption.
Using NFD and sensitivity parameters, we have reduced the problem of specifying (T − 1)(T − 2)/2 extrapolation distributions to that of choosing a distribution for T − 1 Δts. We further assume the distribution of the sensitivity parameters is independent of t, leaving specification of a single Δ for each treatment. Next, we introduce a strategy to elicit expert opinion about their distribution.
6.2. Elicitation of distribution for sensitivity parameters
Elicitation of prior distributions from (non-statistician) subject-matter experts can be a challenging task. The best strategy is typically to ask for expected values or quantiles of observable measurements, and for the statistician to translate this into a distribution for the parameter (Bedrick et al., 1996; Chaloner, 1996). In the context of this smoking cessation trial, we do not explicitly ask about a distribution for Δ, but instead we inquire about the anticipated behavior of a dropout patient relative to a non-dropout patient (similar to Daniels and Hogan (2008), Section 10.2). To that end, our collaborator Dr. Marcus filled in the form in Table 3 with her beliefs about the status of the unobserved patients. Her answers are depicted in bold, and we use them to form our distribution for Δ as follows.
Table 3.
Elicitation of distributions for the sensitivity parameter ∆. Our subject-matter expert was asked to fill out this form to elicit the values for the sensitivity parameters. Her responses are shown in bold.
| Consider two women who have the same history of smoking and weight change and are receiving the same intervention (exercise or wellness). Patient A is observed at time t − 1 but drops out of the study and is not seen at time t, while patient B remains in the study and is observed at time t. | ||||
|
| ||||
| If the probability that patient B smoked during week t is p, what is your best guess (median) for the probability that patient A (who dropped out) smoked during week t? Also provide a lower bound and upper bound on reasonable values. | ||||
| Treatment | Prob. observed patient B smokes (p) | Best guess | Lower bound | Upper bound |
| for the probability that the unobserved Patient A smokes | ||||
| Wellness | 25 % | 50 % | 40 % | 60 % |
| Wellness | 50 % | 70 % | 60 % | 80 % |
| Wellness | 75 % | 95 % | 90 % | 100 % |
| Exercise | 25 % | 50 % | 40 % | 60 % |
| Exercise | 50 % | 70 % | 60 % | 80 % |
| Exercise | 75 % | 95 % | 90 % | 100 % |
|
| ||||
| If the observed patient B has an expected percentage weight change from baseline of w at week t, what is your best guess (median) for the expected percentage weight change from baseline at week t for patient A who dropped out? Also provide a lower bound and upper bound on reasonable values. | ||||
| For reference, the average weight change was 2.4% and the standard deviation was 2.6%. Also, negative values are allowed if it is believed that the patient will have lost weight since baseline. | ||||
| Treatment | Weight change for observed patient B (w) |
Best guess | Lower bound | Upper bound |
| for the expected weight change of the unobserved Patient A | ||||
| Wellness | 2.5 % | 2 % | 0 % | 5 % |
| Exercise | 2.5 % | 1.5 % | 0 % | 4 % |
Translating the information in Table 3 into a prior for the sensitivity parameter Δ2 = E [Wit|ȳit, D = t − 1] − E [Wit|ȳit, D ≥ t] is relatively straightforward as Δ2 represents the difference in the expected weight change between patient A in pattern D = t − 1 and patient B with pattern D ≥ t. For each treatment we let δk (k = med, LB, UB) be the difference between the elicited value for patient A and the provided value for patient B at percentile k (median, lower bound/minimum, upper bound/maximum). The assumed prior for Δ2 is a 50-50 mixture of Unif(δLB, δmed) and Unif(δmed, δUB) which will match the elicited percentiles (Wang et al., 2010). For example, for the exercise treatment.
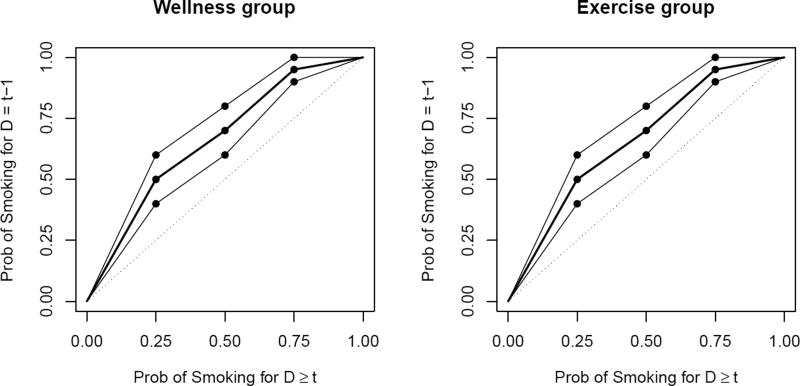
Dealing with Δ1 = E [Zit|ȳit, D = t − 1] − E [Zit|ȳit, D ≥ t] is more challenging because we elicit the expert opinion not in terms of the (fictional) latent variables Z on which the sensitivity parameter is defined, but in terms of the smoking status Q. This choice is consistent with our previous observation that we obtain higher quality information when we elicit in terms of potential measurements. From Table 3, let ψLB(p), ψmed(p), ψUB(p) denote the lower bound, median, and upper bound for p̃ = P (Qit = 0|ȳit, D = t − 1) (patient A’s smoking probability) given p = P (Qit = 0|ȳit, D ≥ t − 1) (patient B’s smoking probability) at the elicited values p = 0.25, 0.50, 0.75. We obtain the functions ψLB(p), ψmed(p), ψUB(p) that cover the full range of p ∈ [0, 1] by linear interpolation as in Figure 2. Similarly to Δ2 the implied distribution for p̃, the probability of smoking for a dropout patient with history ȳit, is the mixture , where p̂ = P (Qit = 0|ȳit, D ≥ t − 1) is the smoking probability for the observed counterpart. From our choice , this distribution on p̃ implies a distribution on Δ1 through
| (15) |
where F{·} is the standard normal cumulative distribution function. This model can be viewed in a similar spirit to the marginalized models of Heagerty (1999). In practice to obtain a sample value of Δ1, we calculate p̂, draw p̃ from the mixture distribution, and numerically solve (15) for Δ1. In the special case where the MAR distribution is a single component (not a mixture), as in the MCAR and mvn-mar models, a simpler log-odds approximation exists that avoids to the need to numerically solve (15); see Section A.5 of the Web Appendix for details.
Figure 2.
Prior distribution of P (Qit = 0|Ȳit, D = t − 1) given P (Qit = 0|Ȳit, D ≥ t) for each treatment. The bold line represents the median value, the solid lines the lower and upper bounds, and the dotted line is P (Qit = 0|Ȳit, D ≥ t). The points marked with the dot are elicited from Table 3, and the remainder of the prior is linearly interpolated.
Also note that we have assumed that the distribution of Δ2 = E [Wit|ȳit, D = t − 1] − E [Wit|ȳit, D ≥ t] is constant in the expected weight change of the observed patient w = E [Wit|ȳit, D ≥ t]. This assumption could be easily relaxed by eliciting δk for a few values of w and interpolating functions δk(w). Given ŵ = E [Wit|ȳit, D ≥ t], Δ2 would be drawn from the mixture defined by δk(ŵ).
6.3. Estimation of treatment effects under MNAR
Having specified a prior distribution for the sensitivity parameters, we may now estimate the main quantities of interest under MNAR. Recall that our inferential focus is the probability of smoking, the percentage weight change from baseline, and the correlation between smoking and weight change at the final week for each treatment. With only about 60% of patients completing the study, we also want to consider how the MAR/MNAR assumptions and the choice of priors on Δ affect our conclusions about these quantities.
To that end, we consider three MNAR missing data assumptions in addition to the MAR analysis of Section 5. First, we apply the elicited prior on the sensitivity parameters. Next, we consider a prior for Δ that uses the elicited prior for Δ1 but sets Δ2 = 0. This choice is motivated by the fact that the expert has strong intuition about the probability of smoking for the dropouts but may be less clear about how their weight will behave due to the competing factors that the patient is no longer attending exercise sessions (if ai = 1) and has likely relapsed to smoking. Hence, we use the MNAR assumption on Z but treat the weight measurements as partially ignorable. Finally, we make the assumption that all unobserved smoking statuses are 0 (smoke) as has been previously used in the smoking cessation literature (Marcus et al., 2005). This extreme assumption falls outside of the framework of PMMs, partial ignorability, and sensitivity parameters, and it requires a new MCMC chain to fit a single pattern model to this augmented data with the sparse prior on the GARPs, assuming the missing weight changes are ignorable.
As in the MAR case, we estimate treatment effects by drawing full data for 5000 patients at each parameter value in the posterior sample. For the MNAR-PMMs this is the same MCMC sample used in Section 5 for the MAR analysis. Pseudo-code for the algorithm may be found in the Web Appendix, Section A.4. Table 4 contains the estimated quantities and 95% credible intervals.
When accounting for the informativeness of the study dropout on cessation in the PMM, we observe slightly lower quit probabilities whether we assume the post-dropout weight changes to be informative or not. The posterior probability of improved cessation rates under exercise is relatively unchanged, which is not surprising as our elicited prior assumes an equal change in smoking rates for both arms relative to the patients that remain under observation (Table 3 and Figure 2). When we consider the strong assumption that all missing Qits are smoking, we see a more dramatic change in the estimated cessation rates. However, this assumption sets all missing cessation values to zero and will necessarily be biased low for the true cessation probability. For the expected weight change during the study period, estimates are stable across our three PMMs, and somewhat lower under the Qit = 0 assumption due to the positive correlation between Q and W and the additional zeros in Q. The substantive conclusions for the relationship between smoking status and weight change do not differ from the MAR results. This is not surprising since our sensitivity prior assumes dropouts are less likely to abstain and have lower weight changes, agreeing with our MAR results. Overall, all conclusions are unchanged as there continues to be no evidence of a treatment difference. Further, our cessation rate and weight change estimates differ from the MAR results relatively little across the PMMs, indicating that the results are insensitive to small-to-moderate departures from MAR.
In Section A.6 of the Web Appendix, we consider the estimation error and efficiency of using our framework in a simulation study designed to mimic the CTQ2 data. When the missingness is MNAR in the true model, we find reduced bias and mean squared error in the quit rate and mean weight change estimates when using our modeling framework versus the MAR assumption or complete case analysis. In Section A.7, we also explore additional analyses of the CTQ2 data to better understand the sensitivity of our conclusions to the assumptions of non-future dependence and partial ignorability of the intermittent missingness. Additionally, we consider alternative choices of the distribution on the sensitivity parameters Δ including a dispersed version of our expert-elicited choice and a more extreme prior. We conclude that partial ignorability has the least impact on inference, followed by the choice of distribution on Δ, and the NFD assumption has the largest impact of the three.
7. Discussion
In this work we have proposed methodology to analyze mixed longitudinal data with informative dropout, which was motivated by a smoking cessation study. We consider pattern mixture models to allow the MNAR distributions to be defined through sensitivity parameters. As many patterns contain few observations, Bayesian shrinkage on the mean and dependence parameters is incorporated to share information across potentially similar patterns. Distributions for the sensitivity parameters are elicited from a subject-matter expert. Based on careful analysis of the CTQ2 data, we conclude that the exercise intervention has no effect on cessation rates or weight changes and that the conclusions are robust to post-dropout departures from missing at random.
One issue deserving additional consideration is that the sensitivity parameters for the MNAR model is defined in terms of the history Ȳit, which include not the smoking statuses Qobs but the latent variables Zobs. While it may be reasonable to compare the unobserved and observed patients with common weight changes and inclinations to smoke each week (richer information than just whether or not she smoked), this is a distinction likely to be lost on the clinician from whom the sensitivity parameter distribution is elicited. It is unclear how to avoid this issue when using a model with latent variables for the discrete process nor is it apparent what modeling scheme without latent variables would be appropriate for a longitudinal, mixed binary-continuous process with dropout. Defining the assumptions through Z leads to more accessible models and can be viewed as reasonably close to the assumptions in terms of Q, but further exploration of this issue is warranted. Similar issues arise with the definition of partial ignorability through Z instead of Q.
As noted in Section 4, model selection in this context proved particularly challenging. None of the usual methods (deviance information criteria, log psuedo-marginal likelihood, posterior predictive loss criteria) were able to discriminate between models in our simulation study. More research in this area is needed but beyond the scope of this paper.
While our model has considered the case of a single binary and continuous response at each time point, this methodology can easily be extended beyond the bivariate case and to allow alternative data types such as ordinal responses. Important considerations will include the necessary identifiability constraints in Ωd;t for the latent variables corresponding to binary and ordinal responses, elicitation of sensitivity parameters or their distribution, and the potential need for sparsity in Ωd;t or its inverse if many responses are observed at each time point.
Although exploratory analysis of covariates indicated little predictive value for the CTQ2 data, it is also possible to extend our model to adjust for covariates. The model for dropout time can easily be adapted by specifying π as a function of covariates. To allow the response model to depend on predictors, we add a β′xit term to the mean of fd;t(yit|ȳit), although the interpretation of these regression parameters may be challenging due to the sequential nature of the distribution.
Supplementary Material
Acknowledgments
This work was supported by NIH grants CA-85295, CA-183854, and CA-77249. The authors also wish to thank Dr. Shira Dunsiger for her helpful comments.
Footnotes
An online Web Appendix contains further information describing the joint distribution of the response with the observed data and data-augmented likelihoods, the sampling distributions for MCMC, simulation studies on model comparison and estimation efficiency, the estimation scheme for quantities of interest under MNAR, and further data analyses using alternative missingness assumptions.
References
- Bedrick EJ, Christensen R, Johnson W. A new perspective on priors for generalized linear models. Journal of the American Statistical Association. 1996;91(436):1450–1460. [Google Scholar]
- Birmingham J, Rotnitzky A, Fitzmaurice GM. Pattern-mixture and selection models for analysing longitudinal data with monotone missing patterns. Journal of the Royal Statistical Society, Series B: Statistical Methodology. 2003;65(1):275–297. [Google Scholar]
- Carvalho CM, Polson NG, Scott J. The horseshoe prior for sparse signals. Biometrika. 2010;97(2):465–480. [Google Scholar]
- Chaloner K. Elicitation of prior distributions. In: Berry DA, Stangl DK, editors. Bayesian Biostatistics. Marcel Dekker Inc; 1996. pp. 141–156. [Google Scholar]
- Chib S, Greenberg E. Analysis of multivariate probit models. Biometrika. 1998;85(2):347–361. [Google Scholar]
- Cowles MK, Carlin BP, Connett JE. Bayesian tobit modeling of longitudinal ordinal clinical trial compliance data with nonignorable missingness. Journal of the American Statistical Association. 1996;91(433):86–98. [Google Scholar]
- Daniels MJ. Bayesian modelling of several covariance matrices and some results on the propriety of the posterior for linear regression with correlated and/or heterogeneous errors. Journal of Multivariate Analysis. 2006;97(5):1185–1207. [Google Scholar]
- Daniels MJ, Chatterjee A, Wang C. Bayesian model selection for incomplete data using the posterior predictive distribution. Biometrics. 2012;68:1055–1063. doi: 10.1111/j.1541-0420.2012.01766.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels MJ, Gaskins JT. Bayesian methods for the analysis of mixed categorical and continuous (incomplete) data. In: de Leon AR, Carriére Chough K, editors. Analysis of Mixed Data. 2013. [Google Scholar]
- Daniels MJ, Hogan JW. Reparameterizing the pattern mixture model for sensitivity analyses under informative dropout. Biometrics. 2000;56(4):1241–1248. doi: 10.1111/j.0006-341x.2000.01241.x. [DOI] [PubMed] [Google Scholar]
- Daniels MJ, Hogan JW. Missing Data in Longitudinal Studies: Strategies for Bayesian Modeling and Sensitivity Analysis. Chapman & Hall; 2008. [Google Scholar]
- Diggle P, Kenward MG. Informative drop-out in longitudinal data analysis (with discussion) Applied Statistics. 1994;43:49–93. [Google Scholar]
- Dunson DB, Perreault SD. Factor analytic models of clustered multivariate data with informative censoring. Biometrics. 2001;57(1):302–308. doi: 10.1111/j.0006-341x.2001.00302.x. [DOI] [PubMed] [Google Scholar]
- Gaskins JT, Daniels MJ. A nonparametric prior for simultaneous covariance estimation. Biometrika. 2013;100(1):125–138. doi: 10.1093/biomet/ass060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaskins JT, Daniels MJ. Covariance partition prior: A Bayesian approach to simultaneous covariance estimation for longitudinal data. Journal of Computation and Graphical Statistics. 2015 doi: 10.1080/10618600.2015.1028549. page Accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisser S, Eddy WF. A predictive approach to model selection. Journal of the American Statistical Association. 1979;74(365):153–160. [Google Scholar]
- Griffin JE, Brown PJ. Inference with normal-gamma prior distributions in regression problems. Bayesian Analysis. 2010;5(1):171–188. [Google Scholar]
- Gueorguieva RV, Agresti A. A correlated probit model for joint modeling of clustered binary and continuous responses. Journal of the American Statistical Association. 2001;96(455):1102–1112. [Google Scholar]
- Harel O, Schafer JL. Partial and latent ignorability in missing-data problems. Biometrika. 2009;96(1):37–50. [Google Scholar]
- Heagerty PJ. Marginally specified logistic-normal models for longitudinal binary data. Biometrics. 1999;55(3):688–698. doi: 10.1111/j.0006-341x.1999.00688.x. [DOI] [PubMed] [Google Scholar]
- Hoff PD. A hierarchical eigenmodel for pooled covariance estimation. Journal of the Royal Statistical Society, Series B. 2009;71(5):971–992. [Google Scholar]
- Hogan JW, Roy J, Korkontzelou C. Handling dropout in longitudinal studies. Statistics in Medicine. 2004;23(9):1455–1497. doi: 10.1002/sim.1728. [DOI] [PubMed] [Google Scholar]
- Ibrahim JG, Laud PW. A predictive approach to the analysis of designed experiments. Journal of the American Statistical Association. 1994;89(425):309–319. [Google Scholar]
- Kenward M, Molenberghs G, Thijs H. Pattern-mixture models with proper time dependence. Biometrika. 2003;90(1):53–71. [Google Scholar]
- Kim JK, Yu CL. A semiparametric estimation of mean functionals with nonignorable missing data. Journal of the American Statistical Association. 2011;106(493):157–165. [Google Scholar]
- Little RJA. Pattern-mixture models for multivariate incomplete data. Journal of the American Statistical Association. 1993;88(421):125–134. [Google Scholar]
- Little RJA. A class of pattern-mixture models for normal incomplete data. Biometrika. 1994;81(3):471–483. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. John Wiley & Sons; New York; 2002. [Google Scholar]
- Liu C, Rubin DB. Ellipsoidally symmetric extensions of the general location model for mixed categorical and continuous data. Biometrika. 1998;85(3):673–688. [Google Scholar]
- Liu X, Daniels MJ, Marcus B. Joint models for the association of longitudinal binary and continuous processes with application to a smoking cessation trial. Journal of the American Statistical Association. 2009;104(486):429–438. doi: 10.1198/016214508000000904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lütkepohl H. Introduction to Multiple Time Series Analysis. Springer-Verlag; 1991. [Google Scholar]
- Marcus B, Lewis B, King T, Albrecht A, Hogan J, Bock B, Parisi A, Abrams D. Rationale, design, and baseline data for Commit to Quit II: An evaluation of the efficacy of moderate-intensity physical activity as an aid to smoking cessation in women. Preventive Medicine. 2003;36(4):479–492. doi: 10.1016/s0091-7435(02)00051-8. [DOI] [PubMed] [Google Scholar]
- Marcus BH, Lewis B, Hogan J, King TK, Albrecht A, Bock B, Parisi A. The efficacy of moderate-intensity exercise as an aid for smoking cessation in women: A randomized controlled trial. Nicotine and Tobacco Research. 2005;7(6):871–880. doi: 10.1080/14622200500266056. [DOI] [PubMed] [Google Scholar]
- Molenberghs G, Michiels B, Kenward MG, Diggle PJ. Monotone missing data and pattern-mixture models. Statistica Neerlandica. 1998;52:153–161. [Google Scholar]
- Neal RM. Slice sampling. The Annals of Statistics. 2003;31(3):705–767. [Google Scholar]
- Nelsen RB. An Introduction to Copulas. Springer-Verlag Inc; 1999. [Google Scholar]
- Olkin I, Tate RF. Multivariate correlation models with mixed discrete and continuous variables. The Annals of Mathematical Statistics. 1961;32(2):448–465. [Google Scholar]
- Park T, Casella G. The Bayesian lasso. Journal of the American Statitistical Association. 2008;103(482):681–686. [Google Scholar]
- Polson NG, Scott J. Shrinkg globally, act locally: Sparse Bayesian regularization and prediction. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, West M, editors. Bayesian Statistics. Vol. 9. 2010. pp. 501–538. [Google Scholar]
- Pourahmadi M. Joint mean-covariance models with applications to longitudinal data: Unconstrained parameterisation. Biometrika. 1999;86(3):677–690. [Google Scholar]
- Pourahmadi M, Daniels MJ, Park T. Simultaneous modelling of the Cholesky decomposition of several covariance matrices. Journal of Multivariate Analysis. 2007;98(3):568–587. [Google Scholar]
- Robert CP. Simulation of truncated normal variables. Statistics and Computing. 1995;5(2):121–125. [Google Scholar]
- Roy J. Modeling longitudinal data with nonignorable dropouts using a latent dropout class model. Biometrics. 2003;59(4):829–836. doi: 10.1111/j.0006-341x.2003.00097.x. [DOI] [PubMed] [Google Scholar]
- Roy J, Daniels MJ. A general class of pattern mixture models for nonignorable dropout with many possible dropout times. Biometrics. 2008;64(2):538–545. doi: 10.1111/j.1541-0420.2007.00884.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer JL. Analysis of Incomplete Multivariate Data. Chapman & Hall Ltd; 1997. [Google Scholar]
- Smith M, Kohn R. Parsimonious covariance matrix estimation for longitudinal data. Journal of the American Statistical Association. 2002;97(460):1141–1153. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society, Series B. 2002;64(4):583–639. [Google Scholar]
- Wang C, Daniels MJ. A note on MAR, identifying restrictions, model comparison, and sensitivity analysis in pattern mixture models with and without covariates for incomplete data (with correction) Biometrics. 2011;67(3):810–818. doi: 10.1111/j.1541-0420.2011.01565.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Daniels MJ, Scharfstein DO, Land S. A Bayesian shrinkage model for incomplete longitudinal binary data with application to the breast cancer prevention trial. Journal of the American Statistical Association. 2010;105(492):1333–1346. doi: 10.1198/jasa.2010.ap09321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu MC, Carroll RJ. Estimation and comparison of changes in the presence of informative right censoring by modeling the censoring process. Biometrics. 1988;44(1):175–188. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.