Pressure effects on collective density fluctuations in water and protein solutions

Significance

This is a combined study, which employs neutron scattering experiments and molecular dynamics simulations to compare high pressure-induced effects on collective properties of protein solutions and bulk water, to observe changes in the HB network structure of protein hydration water upon compression. Our experimental results reflect distinct properties of water at the protein–water interface, while at the same time atomistic molecular dynamics simulations allow us to analyze its pressure-dependent structural changes. This study therefore provides insights that allow establishing measurements of pressure-induced variations in collective dynamics as a probe to characterize biomolecular systems as complex as entire cells.

Abstract

Neutron Brillouin scattering and molecular dynamics simulations have been used to investigate protein hydration water density fluctuations as a function of pressure. Our results show significant differences between the pressure and density dependence of collective dynamics in bulk water and in concentrated protein solutions. Pressure-induced changes in the tetrahedral order of the water HB network have direct consequences for the high-frequency sound velocity and damping coefficients, which we find to be a sensitive probe for changes in the HB network structure as well as the wetting of biomolecular surfaces.

High-pressure effects on protein structure and dynamics are of significant interest in biology, not only to account for the adaptation of life to extreme environments but also to understand how macromolecules behave under normal conditions (1, 2). Pressure can modulate protein activity (3), and it may lead to dissociation of oligomeric proteins (4) and other supermolecular structures (5), induce (6) or inhibit (7, 8) the formation of aggregates and amyloid fibrils, induce denatured states (9), and modify their solvation (10). High pressure makes it possible to explore different conformational substates and to study folding and unfolding (11) and affects the kinetics of enzymatic reactions (9, 12). In some cases, high pressure increases the local roughness of the free energy landscape, thus increasing the depth of local minima and stabilizing intermediate states (13–15). A general feature of pressure-induced effects on protein dynamics is the slowing down of motions and a consequent stiffening and an increase of relaxation times (13–15).

Moderate, nondenaturing pressures induce an elastic response of solvated proteins. The applied pressure modifies the packing and order of the solvent at the protein surface, increases the protein hydration, and promotes the penetration of water in hydrophobic cavities (16, 17). This induces swelling and eventually unfolding at pressures sufficient for denaturation (18). Detailed changes in protein hydration at elevated pressures have been observed in molecular dynamics simulations of isolated proteins in solution, i.e., distortion of tetrahedral structure and stiffening of vibrational modes (19).

Detailed comparisons of pressure-induced effects (at moderate nondenaturing pressures ≤3 kbar) in protein solutions and the bulk solvent can provide insights into the hydration of proteins. Small-angle X-ray scattering (SAXS) and neutron scattering experiments have been recently combined by Russo and coworkers (20–22) to investigate high pressure-induced changes on particle–particle interactions, low-resolution structure, and global and local dynamics of lysozyme in aqueous solutions. The results showed that lysozyme maintains its globular structure up to at least 1,500 bar, while the density of the hydration shell slightly increases as a function of pressure. This causes a moderate nonlinear change in the effective protein–protein interaction potential observed by SAXS measurements (20, 23). At the same time, local dynamics described by mean square displacements of the protein protons [measured by quasi-elastic neutron scattering (QENS)] decreases as pressure increases, suggesting a loss in mobility following an increase of the hydration shell density. Both global and local protein dynamics change at the same threshold pressure, and for timescales accessible in a QENS experiment (ps), a transition from diffusive internal protein dynamics to localized motions within a local potential energy well has been observed (20, 21). This behavior has been attributed to denser structural packing of the first protein hydration layer at elevated pressure.

A similar behavior can be also found for other examples of biomolecular interfaces (24). However, we note that in protein hydration water pressure-induced disruption of the tetrahedral water structure can speed up local dynamics, such as translational and rotational diffusion and HB rearrangements (19, 25–28). In the context of the present study, it is important to note that collective and local single-particle dynamics describe fundamentally different processes. Single-particle dynamics as reported by QENS report on atomic mobilities of the nondeuterated fraction of a system, while coherent scattering experiments are sensitive to the propagation of density fluctuations in the entire system due to dynamic correlations in time and space.

To shed light on pressure effects on the structure of the protein hydration water hydrogen bond (HB) network and its correlation to a general slowdown of protein dynamics, we investigate here the collective dynamics of water in the presence of solvated proteins, combining coherent neutron scattering with computer simulations. Collective dynamics of water on an energy scale of 5–30 meV provide direct insights into correlated intermolecular vibrations (29, 30), i.e., propagating density fluctuations in the HB network of an aqueous solution. These modes are sensitive to HB network properties and therefore provide an excellent tool to study solute- and pressure-induced changes in water and aqueous solutions. Coherent scattering experiments and molecular dynamics simulations have therefore been used frequently to study collective dynamics in biomolecular solutions and even in living cells or the influence of temperature and/or pressure on the HB network of bulk water (30–37).

Methods

Here we study room temperature neutron Brillouin measurements of lysozyme solutions combined with molecular dynamics simulations as a function of pressure. The analysis of experimental results provides a description of dispersion curves, defining the active collective modes that propagate within the sample, and the damping factor, related to the propagation lifetimes. The measurements were performed on concentrated solutions of lysozyme (10% wt/wt) dissolved in D₂O buffer (10 mM Tris, pD = 6.0) using the time of flight neutron Brillouin spectrometer (BRISP) and a titanium alloy large-volume, high-pressure sample holder (see SI Appendix for experimental details). To obtain information on the protein interface and the contribution of the hydration water layer, both lysozyme solution and neat D₂O were measured at pressures of 1 bar, 2kbar, and 3 kbar. The stability of the protein solutions under the experimentally studied conditions has been established by pressure denaturation studies in the literature using various experimental probes, including Raman spectroscopy, NMR (38), and tryptophane fluorescence (39, 40) (see SI Appendix for more detailed discussion). Molecular dynamics simulations were carried out for bulk water and for solvated lysozyme proteins, in dilute and high-concentration conditions (10% wt/wt), at pressures of 1 bar, 500 bar, 1 kbar, 2 kbar, 3 kbar, and 5 kbar, allowing microscopic insights into structural changes in water and the protein hydration shell as a response to pressure (see SI Appendix for simulation details).

At the experimentally studied protein concentration, approximately two thirds of all water molecules are found at distances greater than 10 Å from the protein surface based on our simulation models, suggesting a significant amount of bulk-like water.

Results and Discussion

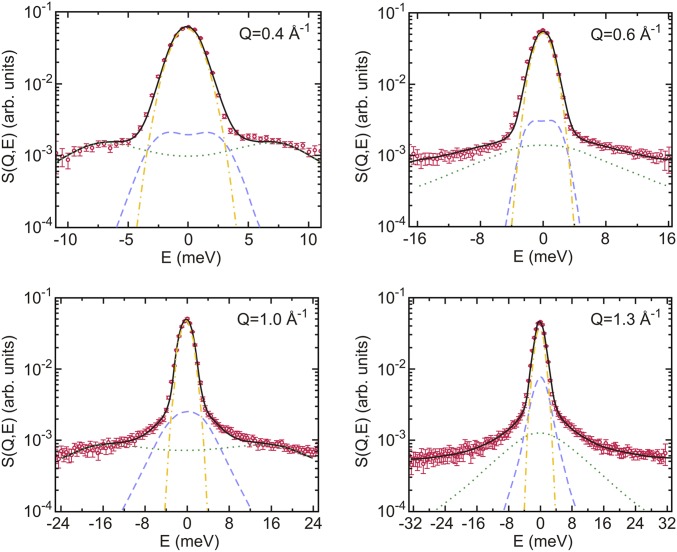
Fig. 1 shows experimental data at four selected wave vectors obtained for the lysozyme solution at 2 kbar, together with the best fit using a two-component damped harmonic oscillator model (DHO; see SI Appendix for details).

Fig. 1.

Coherent inelastic spectra of lysozyme solution at 2 kbar at selected Q values. The thick black line shows fits of the two-component DHO model (see SI Appendix for details). The dashed blue and dotted green lines represent the resulting low- and high-frequency DHO, respectively. The dashed–dotted yellow line shows the experimental resolution function.

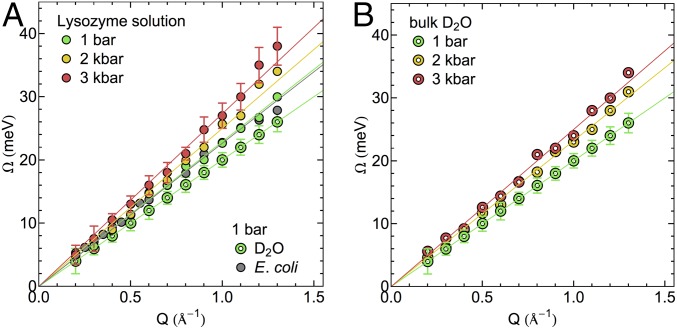
The dependence of the fitted DHO frequencies on the momentum transfer Q defines the dispersion curves shown in Fig. 2. Only the high-frequency mode is of dispersive nature and will be discussed in the following paragraphs. Fig. 2 shows a comparison of the experimental dispersion curves of lysozyme solution (Fig. 2A) and neat D₂O (Fig. 2B) as a function of pressure. Fig. 2A further shows a dispersion curve corresponding to measurements on Escherichia coli cells at ambient pressure from a previous study (32). The pronounced similarity to the concentrated protein solution at the same pressure shows that collective properties in both samples are comparable. Differences between collective dynamics in protein solutions, living cells, and bulk water at ambient pressure are statistically significant but small compared with pressure-induced changes. Considering high water concentrations of up to 80% within cells (41), this observation would be consistent with largely bulk-like collective properties of water within cells as probed via coherent neutron scattering. From the slope of the linear regime (between Q = 0.2 and 1.1 Å⁻¹), we obtain a propagation velocity of density fluctuations, i.e., the high frequency or fast sound velocity, of 3,460 ± 160 m/s for the collective excitation in the protein solution at ambient pressure. The corresponding slope of the dispersion curve for neat D₂O is equal to 3,040 ± 50 m/s. Both the pure water samples and the concentrated protein solutions show a statistically significant increase of the propagation velocity with increasing pressure. For the protein solution, the propagation velocity of the high-frequency mode increases to 3,730 ± 180 and 3,920 ± 210 m/s at 2 and 3 kbar, respectively. The corresponding propagation velocities in the neat water sample are observed as 3,530 ± 175 and 3,770 ± 188 m/s at 2 and 3 kbar.

Fig. 2.

Experimental dispersion curves of THz collective modes in hydration water of (A) lysozyme solution water network and (B) neat D₂O as a function of pressure (D₂O data for 1 bar from ref. 55). The dispersion curve of E. coli is reported in A for comparison (data from ref. 32). Error bars are equivalent for measurements at different pressures. For clarity, they are shown only for one respective data set for the protein solution and bulk water.

The comparison between neat water and protein solutions allows us to study differences in pressure-induced changes of collective dynamics in both samples, which are attributed to the presence of the proteins and their interactions with the surrounding hydration water.

At equivalent pressures, the sound propagation velocity in the protein solution is higher compared to bulk water in the studied pressure range (SI Appendix, Fig. S2), suggesting an increased rigidity of the water HB network in the presence of the protein. This interpretation agrees with experimental observations and simulations that observe a slowdown of dynamical processes in the protein hydration shell. This applies, for example, to translational and rotational motions of water molecules as probed by magnetic relaxation dispersion (42), nuclear Overhauser effects in reverse micelles (43), Overhauser dynamic nuclear polarization (44), and ultrafast fluorescence (45, 46), to name but a few. Numerous molecular dynamics simulations reproduce these observations (47–50). The consensus is an up to twofold dynamical retardation for the majority of water molecules in a protein hydration shell, while only a small number of water molecules might be strongly bound and therefore further immobilized.

In our present study, we find that for both samples bulk water and the protein solution propagation velocities further increase with pressure. We note that the increase in the propagation velocity is not the result of an increased rigidity of the water HB network as one would define it based on noncollective, single-particle dynamics, for example, via lifetimes of individual HBs. The pressure-induced distortion of the water HB network structure weakens water–water HBs, hence decreasing the average lifetime (19, 25, 27, 28).

From previous simulations and experiments, it is known that the increase in pressure results in a slowdown of picosecond-timescale protein dynamics (14, 21), which might be intimately related to pressure-induced changes in the hydration environment. We highlight that the pressure dependence of the propagation velocity is more pronounced in bulk water than in the protein solution. Consequently, the difference in sound propagation velocities between both systems decreases at high pressure (linear extrapolation of the pressure-dependent experimental data yields equal sound propagation velocities in both systems at ∼4.4 kbar; see SI Appendix, Fig. S2 for details). Further, the sound propagation velocity in bulk water at 2 kbar (3,530 ± 175 m/s) is approximately equivalent to the sound propagation velocity in the protein solution at ambient pressure (3,460 ± 160 m/s). This indicates potential similarities of protein-induced and pressure-induced effects on the HB network structure of water, which largely determines the collective properties in both samples. An increased density of water in protein hydration shells, which would qualitatively mimic the effect of increased pressure, has been observed experimentally in combined X-ray and neutron scattering experiments (51).

For protein solutions, it has been shown that particularly the densities of the hydration layer are strongly pressure dependent (20, 21). In Fig. 3, we therefore analyze pressure-induced changes of the propagation velocity as a function of the sample density. Due to the lack of experimental densities for pressurized protein solutions, we obtained the density data from our molecular dynamics simulations of deuterated protein solutions and bulk D₂O. We also plot the sound velocity probed for water solvating hydrophilic and hydrophobic protein model interfaces at ambient pressure (52). Single-particle vibrations in these solutions at frequencies comparable to the ones studied here in the context of collective dynamics were previously shown to correlate with those of high-density amorphous (HDA) ice and low-density amorphous (LDA) ice, respectively (53). Therefore, we combined the sound velocities of both samples with the densities of HDA and LDA ice in Fig. 3, observing that they follow the overall observed trend. We note that the high-density data point (water solvating a hydrophilic surface) is found in close proximity to bulk D₂O at ∼2 kbar. Interactions with the hydrophilic model interface at ambient pressure therefore also give rise to qualitatively similar changes in the water HB network as found for the protein solution; that is, they resemble densities and collective dynamics of pressurized water. The high-density region, represented in Fig. 3, shows an approximate linear density dependence of the sound velocity. The plotted data points provide a weak indication that this trend may not hold for densities lower than 1.1 g/cm³. We note that Krisch et al. (54) observed an anomalous feature in X-ray scattering experiments of H₂O between 1.1 and 1.17 g/cm³, i.e., a shoulder in the density-dependent sound velocity. The data shown in Fig. 3 exhibit a similar behavior; however, the small number of data points and the statistical error bars of the sound velocities inhibit a direct comparison. Arguably, the feature observed by Krisch et al. (54) might be expected at higher densities in our sample due to the use of D₂O in neutron scattering experiments. Krisch et al. (54) also show that the dependence of the low-frequency, hydrodynamic sound velocity on the increasingly distorted HB network structure for increasing pressure is more pronounced compared with the high-frequency sound velocity analyzed here. However, our results show that the high-frequency sound velocity is suitable to observe distinct pressure-induced changes in bulk water and protein hydration water due to differences in the structural response upon compression.

Fig. 3.

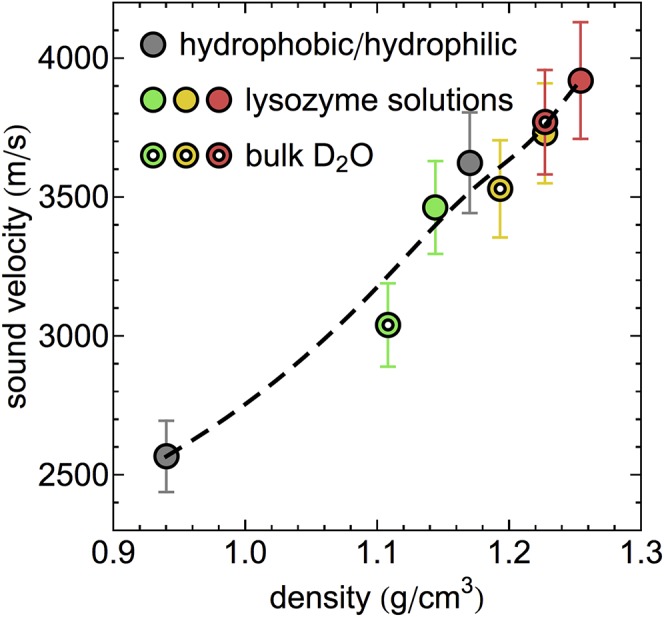
Density dependence of the sound velocity of D₂O and lysozyme solution at various pressures. Data obtained for solutions containing large concentrations of hydrophilic and hydrophobic biointerface are shown according to ref. 52. Colors indicate the distinct pressures equivalent to Fig. 2. The dashed line serves as a guide to the eye.

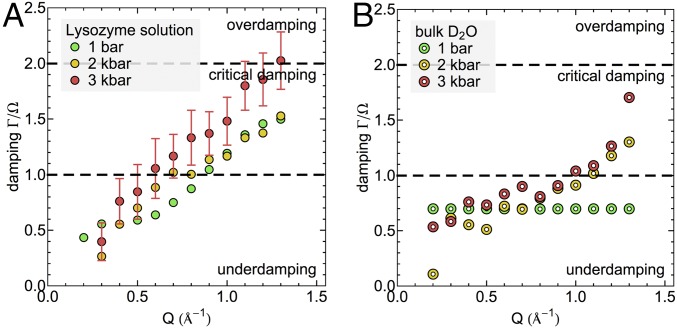
Further analysis of the related damping factors gives access to the lifetimes of the collective modes (see SI Appendix for details). Fig. 4 reports the damping factors of lysozyme solution (Fig. 4A) and neat D₂O (Fig. 4B) as a function of pressure. The results show underdamping (0.5 < Γ/Ω < 1) for bulk water at ambient pressure over the entire Q range within the DHO model. We note that a constant damping ratio has been imposed in the underlying fit of this data set, which was obtained from ref. 55, while no such constraint has been used for the remaining datasets reported here. However, in pressurized D₂O this trend is unchanged in the low-Q range, and the damping ratio remains <1. At Q > 1.0 Å⁻¹ a transition toward high, close-to-critical damping ratios occurs (Γ/Ω > 1), which approaches critical damping (Γ/Ω = 2) at pressures of 3 kbar. Within the simple DHO picture, this means that short-wavelength pressure fluctuations (2π/Q on the order of intermolecular distances) in compressed water (2–3 kbar) decay in an increasingly nonoscillatory fashion with lifetimes on the same order of magnitude as the period of underlying intermolecular vibrations. Equivalently to the increase of propagation velocities, the increased dampening of short-wavelength fluctuations indicates pressure-induced structural changes in the HB network. In the concentrated protein solution, close-to-critical damping (Γ/Ω > 1) of short-wavelength pressure fluctuations occurs already at ambient pressure. The ratio Γ/Ω at high Q values (Q > 1.0 Å⁻¹) experiences only a small change between 1 bar and 2 kbar. However, at 3 kbar the critically damped regime is reached, resulting in fast exponential decays of pressure fluctuations described by the fitted DHO model. We note that also in case of dampening of short-wavelength fluctuations, protein-induced effects at ambient pressure resemble the properties of bulk water at elevated pressure. In addition, with increasing pressure the differences between bulk water and the protein solutions in terms of short-wavelength dampening at Q ∼ 1.3 Å⁻¹ decrease, equivalently to increasingly similar propagation velocities. However, the onset of critical damping for the highest pressure remains a distinct characteristic feature of the protein solutions.

Fig. 4.

Damping factors relative to mode frequency for (A) concentrated lysozyme solution and (B) neat D₂O with increasing pressure. The results for bulk water at 1 bar are reproduced from ref. 55. For clarity, error bars, equivalent for all measurements, are represented only for one dataset.

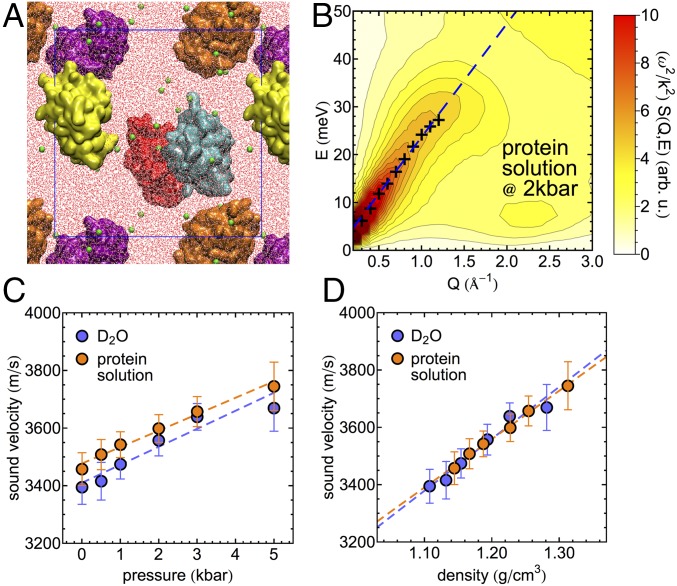
To investigate in more detail the structural changes in the water HB network with increasing pressure, we employ molecular dynamics simulations. First, we validate the simulation model by analyzing the pressure dependence of its collective properties as a function of pressure and compare it to the experimental observations. For this purpose, we utilize simulations of a deuterated multiprotein system resembling the experimental concentration of 10% wt/wt, which contains five lysozyme proteins, ∼30,000 water molecules, and 40 chloride ions for charge neutralization (illustrated in Fig. 5A). A bulk D₂O simulation of approximately the same size is used as reference. The collective dynamics are analyzed directly via the longitudinal current spectrum $I^{\parallel }\left(Q,\mathit{\omega }\right)$ obtained from space–time Fourier transformations of density currents computed from atomic velocities (SI Appendix). The longitudinal current spectrum is related to the dynamic structure factor via $I^{\parallel }\left(Q,E=\hslash \omega \right)=\left({\omega }^2/Q^2\right)S\left(Q,E\right)$. The propagation velocities of density fluctuations are obtained equivalently to the processing of the experimental data via (i) fitting of a two-component DHO model for $S\left(Q,E\right)$ and (ii) extracting the linear Q dependence of the dispersive high-frequency mode. We note that we limit the quantitative analysis to the determination of the frequency and propagation velocity of the dispersive high-frequency mode. As an example, the longitudinal current spectrum, the frequencies of the high-frequency mode obtained from the DHO fit, and the corresponding linear fit of its Q dependence are shown for the protein solution at a pressure of 2 kbar in Fig. 5B. Propagation velocities observed for bulk water, and the protein solutions are shown as a function of pressure and the corresponding density in Fig. 5 C and D, respectively. In qualitative agreement with the experimental results, we find increased propagation velocities in the protein solutions compared with bulk D₂O, when compared at equivalent pressures. When propagation velocities are compared as a function of the system density, the collective properties of bulk water and the protein solution describe essentially the same linear trend, which agrees with the experimental observations in the high-density regime in Fig. 3.

Fig. 5.

Molecular dynamics simulations of concentrated protein solutions. (A) Snapshot of the simulated system containing five individual proteins (colored individually) in water (red and white) with chloride ions for charge neutralization (green spheres). The blue box indicates the periodically replicated simulation cell. (B) Simulated longitudinal current spectrum of the protein solution at 2 kbar. Crosses indicate the Q-dependent frequency of the high-frequency mode obtained from the fit between 0.3 and 1.2 Å⁻¹. The blue dashed line shows a linear fit of the mode position. (C) High-frequency sound velocity obtained from simulations of the protein solution and bulk D₂O as a function of pressure between 1 bar and 5 kbar. (D) Same as C shown as a function of the density observed in the respective simulation. Dashed lines in C and D indicate linear trends in the pressure- and density-dependent sound velocity data.

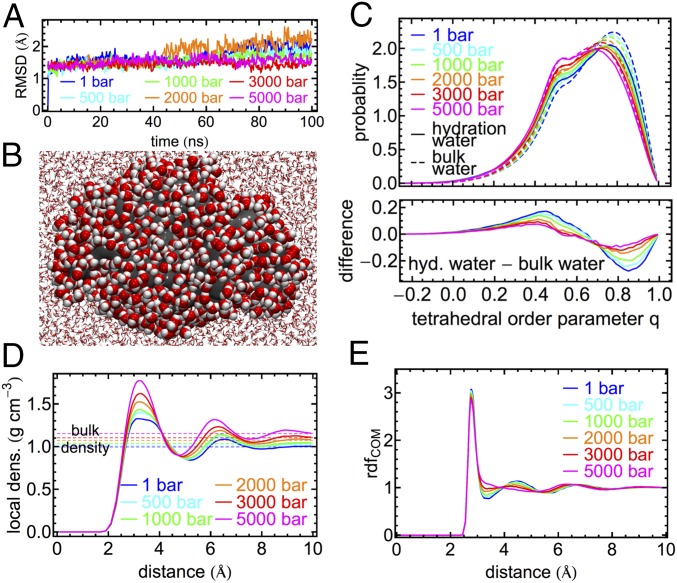
While we observe some quantitative differences between simulations and experiments, the qualitative trends observed experimentally for the pressure-dependent propagation velocity are reproduced. To analyze pressure-induced structural changes in the hydration water of the protein, we refer to a second set of simulations of a single solvated protein to simplify the analysis. Our structural analysis can be compared with previous work by Lerbret et al. (19). Our simulations show that the structure of the lysozyme protein is essentially constant within simulations on the 100-ns timescale for all pressures studied here, as indicated by root mean squared deviations of nonhydrogen protein atoms between 1.6 and 2.4 Å in Fig. 6A. This confirms previous observations in experimental studies up to 1.5 kbar (20, 21) and an analysis of the stability of secondary structure elements up to pressures of 6 kbar in simulations on a shorter 10-ns timescale (19). To analyze structural changes in the protein hydration shell in comparison with bulk water, we analyzed water within 5 Å from the protein surface as illustrated in Fig. 6B. This included an analysis of tetrahedral order parameters q (Fig. 6C), which yields 1 for a perfectly tetrahedral environment and 0 for an ideal gas (56) (SI Appendix). We note that distributions of the q parameter indicate two distinct subpopulations of water molecules: one with a relatively high tetrahedral order (q = 0.8) and one with a lower tetrahedral order (q = 0.5). Indications for both populations are observed for bulk water and protein hydration water. At ambient pressure the fraction of water molecules with low tetrahedral order is increased in protein hydration water compared to bulk water. With increasing pressure the population of water molecules with high tetrahedral order decreases, while the fraction of water molecules with low tetrahedral order increases. This is observed in the protein hydration shell and in bulk water. However, pressure-induced changes in the protein hydration shell are less pronounced compared with the bulk, resulting in increasingly similar distributions of the tetrahedral order parameter with increasing pressure. This is highlighted by the difference plot in Fig. 6C, Bottom. Consequently, we find that with increasing pressure differences between hydration shell water and bulk water structure become less pronounced. The pressure-induced structural changes in bulk water observed in our simulations reproduce previous work based on numerous empirical potentials (57). Likewise, the increased similarity of bulk and protein hydration water at high pressure in terms of the orientational order quantified by q seems to be independent of the underlying water model (19).

Fig. 6.

Molecular dynamics simulations of solvated lysozyme protein and bulk water at pressures ranging from 1 bar to 5 kbar. (A) Root-mean-square deviation (RMSD) of all nonhydrogen atoms of the protein from the crystal structure in 100-ns simulations. (B) Snapshot from the simulation of a single lysozyme molecule (gray) illustrating water molecules within 5 Å of the protein (1 bar). (C) Distribution of the tetrahedral order parameter q in bulk water (dashed lines) and protein hydration water (solid lines; defined as water within 5 Å of the closest nonhydrogen protein atom). (D) Water density profiles measured as a function of distance to the protein surface (defined by distance to closest nonhydrogen protein atom). (E) Radial distribution functions (rdf) of water molecule centers of mass (COM) in bulk water.

To understand this observation, we analyzed the structural changes in the protein hydration shell via density profiles measured as a function of distance from the protein surface (Fig. 6D). We compare our observations with radial distribution functions (rdfs) between water molecule centers of mass (COM) in bulk water simulations (Fig. 6E). With increasing pressure, we find a deformation of the first peak in the protein hydration water density profile. At ambient pressure the first peak between 2.5 and 4.0 Å is broad and shows indications of additional substructure, which we assign to the chemical heterogeneity of the protein surface, i.e., the distinct hydration of hydrophilic and hydrophobic groups. With increasing pressure, the peak narrows, and its intensity increases disproportionally compared with the accompanying increase in bulk water density. This indicates a more uniform hydration of the protein surface, independent of its chemical properties. Generally, this observation agrees with the pressure-induced increased hydration of hydrophobic pockets observed previously in T4-lysozyme mutants (17). A pressure-induced increase in the hydration of nonpolar atoms has also been observed in extensive simulations of the folding/unfolding equilibrium of the Trp-cage miniprotein, whereas the hydration of polar atoms was found insensitive to pressure (58). Changes in the relative hydration of polar and nonpolar surface groups quantified by solvent accessible surface areas at pressures of 3 kbar were also reported for simulations of apomyoglobin and lysozyme (59). In addition, Fig. 6D indicates an increased layering in the protein hydration shell, due to a more pronounced second peak, which increases in amplitude and changes its position from ∼6.5 Å at 1 bar to ∼6.0 Å at 5 kbar. Pressure-induced changes in the bulk water structure as described by the rdfs in Fig. 6E show qualitatively distinct characteristics, which are in accord with experimental data (60). The narrow first peak, describing the first shell of neighboring water molecules, is essentially unchanged with increasing pressure. Hence, the oxygen–oxygen distance of water–water HBs is roughly pressure-independent. The structural response to increasing pressure mainly affects the first minimum and the second peak of the rdf, representing interstitial water and the second hydration shell, respectively. Both features are clearly resolved at ambient pressure. However, with increasing pressure water molecules from the second hydration shell penetrate into the interstitial region as a primary elastic response to compression, hence increasing the packing density (60, 61). The observations in Fig. 6 D and E explain the distinct behavior of the tetrahedral order parameters as a function of pressure in the protein environment and in pure water. In case of the protein hydration shell, the main elastic response to pressure-induced compression is the increased hydration of the protein surface, which requires a less pronounced change in the water HB network structure. In bulk water this predetermined breaking point is absent, and high pressures result in more pronounced changes in the tetrahedral HB network structure, mainly affecting HB angles and not HB lengths.

Generally, we recognize that the water structure and collective dynamics are distinct in the protein hydration shell and bulk water, which is reflected here by the difference in pressure-induced changes in collective dynamics. Our findings indicate that the tetrahedral order of the water HB network may be tightly linked to the high-frequency collective properties of water and protein solutions. Both experimentally observed propagation velocities and short wavelength damping coefficients are increased in protein solutions compared with bulk water of equivalent pressure, in qualitative agreement with the decreased tetrahedral order of the water HB network in the protein hydration shell. Likewise, differences between the collective properties of protein solutions and bulk water decrease with increasing pressure, akin to the increased similarity of the tetrahedral order parameter distributions in Fig. 6C. In experiments and simulations alike, the propagation velocities are roughly proportional to the total density of the system and seem relatively independent of the system composition (Figs. 3 and 5D). Protein solutions at ambient pressure, with an increased overall density and a protein-induced decrease of the tetrahedral order in the water HB network, exhibit collective dynamics that can be qualitatively compared with bulk water at increased pressures with an equivalent overall density. With increasing pressure, the overall densities and fast sound propagation velocities become increasingly similar between protein solutions and pure water, due to distinct pressure-induced changes in the water HB network structure.

However, we also note a qualitative difference in the pressure response of collective properties with and without solvated proteins. The onset of high dampening coefficients Γ, i.e., the occurrence of damping ratios Γ/Ω > 1 at intermediate wavelengths, i.e., Q < 1.0 Å⁻¹ (Fig. 4A), indicating increasingly nonoscillatory dynamics, is only observed for the protein solutions and occurs simultaneously with an increased hydration of the protein surface (Fig. 6D). Likewise, the damping of short-wavelength fluctuations (Q > 1.0 Å⁻¹) remains significantly more pronounced in protein solutions compared with bulk water, also at high pressures or equivalent densities. While it is difficult to provide a detailed microscopic interpretation of the damping of collective modes obtained in the fit of the DHO model, we recall the occurrence of a slowdown of protein dynamics as a response to increased pressure (20). Pressure induces an increase in hydration of the protein surface and therefore results in altered properties of the average protein–water interface in the solution. We may speculate that the observation of enhanced damping of collective modes in protein solutions and a slowdown of protein dynamics are related to each other because the dynamics of system components are coupled via the altered protein–water interface. Interactions between the protein and water at the biomolecular interface play an important role for the coupling of vibrational modes between both components. In previous simulations of hydrated protein crystals, it could be shown that collective modes, characteristic of the protein, propagate into the surrounding hydration water (62). Likewise, correlated protein–water vibrations and resulting collective modes were shown to depend on the chemical properties of the protein–water interface (63, 64).

Promising future extensions or our studies involve simultaneous variations in temperature and pressure. Raman spectroscopy studies of lysozyme solutions suggest that increased, nondenaturating pressures are able to reverse structural changes involved in early stages of thermal denaturation (65). Such pressure-induced suppressions of conformational fluctuations are likely to also affect picosecond-timescale, collective dynamics in the protein and its dynamical coupling to the surrounding water HB network.

Conclusion

In summary, this study investigates the pressure dependence of structural properties and collective dynamics in water and protein solutions for moderate, nondenaturing pressures between 1 bar and 3 kbar (up to 5 kbar in simulations). We find that protein hydration water exhibits some features of pressurized water and that with increasing pressure and density, differences in the water HB network structure and collective dynamics decrease, apart from critical damping of collective modes, which only occurs in protein solutions.

Previous experimental studies have shown that high-frequency sound propagation velocities between various biomolecular systems (protein or peptide solutions, living cells) are roughly comparable at ambient pressures, while fitted damping factors of the collective modes often exhibit distinct Q-dependent behavior (52). Here we add external pressure as an additional variable and observe distinct pressure-induced changes of high-frequency sound velocities and damping factors in absence or presence of solvated proteins. However, the overall density seems to remain the main factor influencing collective mode propagation on the experimental timescale, while the specific interactions between the solvated protein surface and the hydration shell, as well as the collective properties of the proteins themselves, seem to affect the damping.

In total, we find that pressure-induced changes of collective dynamics provide a promising probe to study the hydration of biomolecules, providing information also relevant for ambient conditions, i.e., via the pressure-dependent hydration of the heterogeneous protein surface. Ambient pressure collective dynamics of various biological samples are currently an active field of research. In this context, it is essential to be able to provide microscopic interpretations for the available experimental observables, such as sound propagation velocities and damping. This combined experimental and theoretical study provides a crucial step along those lines because the pressure dependence allows us to analyze the influence of structural changes in the water HB network, either due to interaction with a solvated biomolecule or pressure, on the experimentally accessible properties.