Abstract
Admixed populations result from recent admixture of two or more ancestral populations with divergent allele frequencies. The genome of each admixed individual is a mosaic of haplotypes inherited from the ancestral populations. Despite the substantial work to assess power and sample size requirements for association mapping in genetically homogeneous populations of European ancestry, power and sample size estimation methods for mapping genes in genetically heterogeneous admixed populations such as African Americans are lacking. Admixture mapping is a method that traces the ancestral origin of disease-susceptibility genetic loci in the admixed population. We developed AdmixPower, a freely available tool set based on the open-source R software, to perform power and sample size analysis for genetically heterogeneous admixed populations considering continuous or dichotomous outcomes with a case-only or case-control study design. AdmixPower can be used to compute the sample size required to achieve investigator-specified statistical power under several key parameters including ancestry odds ratio, genotype risk ratio, parental risk ratio, an underlying genetic risk model, trait type, and admixture model (hybrid-isolation or continuous gene flow model). We demonstrate that differences in the key parameters in the admixed population results in substantial differences in the sample size required to achieve adequate power in admixture mapping studies. Our tool provides a resource for researchers to develop a strategy to minimize cost and maximize the success of identifying disease-susceptibility loci in an admixed population. R code used in the sample size and power analysis is freely available from https://research.cchmc.org/mershalab/Tools.html.
Keywords: admixed population, admixture mapping, statistical power, sample size, AdmixPower
ADMIXED populations are the result of gene flow between distinct, historically divergent, parental populations, such as those from different continents like Africa and Europe. The rate, extent, and timing of gene flow between genetically distinct populations have resulted in unique genetic complexity in almost all populations in the United States (Li et al. 2008; Baye and Wilke 2010). Understanding the genetic structure of admixed populations is not only important to reconstruct human evolutionary history, but also has implications for the study of disease risk (Hellenthal et al. 2014). However, research into the link between ancestry and disease risk in an admixed population is sparse and lacks rigorous statistical methods. For example, sample size and statistical power analysis in gene mapping studies are well developed and successfully applied for genetically homogeneous samples of European ancestry (Purcell et al. 2003; Skol et al. 2006; Feng et al. 2011). However, these methods are not applicable for mapping susceptibility loci in admixed populations such as African Americans and Latinos. Admixed populations are not ancestrally homogeneous but rather ancestrally heterogeneous with ancestry from more than one parental population (Rosenberg et al. 2002; Mersha 2015). In European ancestry populations, the underlying hypothesis is homogeneity in ancestry background. However, the general hypothesis to map susceptibility loci for samples of admixed individuals is that the disease-causing genetic variants are transmitted to the admixed population in higher proportion from the ancestral population with the higher rate of disease prevalence. The genetics underlying human disease phenotype variation in admixed populations has been underresearched. Understanding the role of ancestry in disease risk in an admixed sample could help to identify novel “ancestry-related disease risk” in the most vulnerable populations.
Admixture mapping methods are used to investigate the association between a phenotype and the ancestry of alleles at a marker locus by comparing the observed proportion of alleles at a marker locus from the high-risk population to the expected proportion in the admixed population. A significant difference in the observed and expected proportion of ancestry would suggest an association between the phenotype and the ancestry origin (Mersha 2015). Calculating statistical power in an admixed population for admixture mapping studies is a complicated process that requires the researcher to specify several factors including (a) risk allele frequency differences between ancestral populations, (b) disease prevalence (penetrance) differences between ancestral populations, (c) parental risk ratio, (d) admixture proportion, (e) mode of inheritance, (f) number of generations since the admixture, (g) recombination rate between the disease locus and the candidate marker, (h) study design (case-only or case-control design), and (i) admixture process [hybrid isolation (HI) or continuous gene flow (CGF)]. In this article, we describe a freely available tool set, AdmixPower, for power and sample size analysis of admixed populations to conduct admixture mapping. AdmixPower computes (a) the power of an admixture mapping study given the population parameters and study sample size, and (b) the sample size required for a study design to achieve investigator-specified power to map risk loci using admixture mapping.
In implementing AdmixPower, the trait under study can be either dichotomous or quantitative. For a dichotomous trait, there could be a case-only or case-control study design with additive, multiplicative, recessive, or dominant genetic models. Also, the admixture process can be described as a HI model or a CGF model (Pfaff et al. 2001; Rosenberg and Nordborg 2006). For the HI model, AdmixPower performs the power and sample size analysis based on the analytical approach proposed by both Montana and Pritchard (2004) and Zhu et al. (2004). For a CGF model, a similar analysis is conducted using the Zhu et al. (2004) approach. Under the model of Montana and Pritchard (2004), the power analysis is performed for both case-only and case-control designs using the multiplicative mode of inheritance. The power analysis using the Zhu et al. (2004) approach is also carried out under additive, multiplicative, recessive, and dominant genetic models for both case-only and case-control study designs. For quantitative traits, we developed a linear regression framework modeling the genetic effect as additive and the nonadditive effects as covariates. Even though power and sample size analysis to test associations using multiple regression is well established in genetically homogeneous populations, to our best knowledge, this is the first tool set developed for estimating power and sample size for quantitative traits in admixed populations.
In the Analytical Theory section, we first define study designs for dichotomous and quantitative traits followed by the mathematical derivation of power and sample size analysis for AdmixPower. AdmixPower is implemented in the R program. In the Program availability and implementation section, we describe different functions developed in AdmixPower and investigate the relationship between power, sample size, and various population-specific parameters and risk factors. Our goal is to provide a resource tool for the analysis of power and sample size for both dichotomous and quantitative traits under various genetic model assumptions and disease prevalence in the parental populations, admixture proportion, as well as for the presence of polymorphic markers between ancestral populations.
Analytical Theory
Admixed population: dichotomous phenotype
Suppose we have an admixed population resulting from an admixture of two ancestral populations X and Y, where the proportion of genome from population X in the admixed population is Suppose there are M markers genotyped in cases and controls in the study samples. The objective here is to find markers with a significantly higher-than-average proportion of risk alleles from ancestral population X with higher disease risk. This can be done through one of two study designs: (i) case-only study design, and (ii) case-control study design.
Case-only design:
In a case-only study design, the observed ancestry proportion at a marker locus is compared with the genome-wide average ancestry across the genome. The unit of observation is a single gamete. Let be the proportion of the alleles from the ancestral population X among cases at marker locus j. If is the average ancestry across the genome in cases, then the null hypothesis is
If is the estimate of the test statistic for the case-only design is:
| (1) |
Under the null hypothesis, has a central t-distribution, which can be approximated by the normal distribution N(0, 1), when the sample size is large.
Case-control design:
In a case-control study design, the ancestry proportions at a marker locus in cases and controls are compared. The unit of observation is a single individual. Let and be the proportion of the alleles from the ancestral population X among cases and controls at a marker locus j, respectively. Let and be the average ancestry across genome in cases and control, then the null hypothesis is
| (2) |
Let and be the estimates of and the test statistics for a case-control study design based on (2) is
Similar to the situation of the case-only design, can be approximated with the standard normal distribution N(0, 1) when the sample size is large.
In practice, we compute the estimates of admixture from the sample data (Zhu 2012). Let and be the proportion of alleles from the ancestral X for the i-th individual at marker j in cases and controls, respectively, then
and
where and are the estimate of the genome-wide average ancestry for cases and controls, respectively.
We have defined the test statistics for the case-only and case-control study design and provided a general approach of computing the test statistics based on sample data under the assumption of constant genome-wide average ancestry for cases and controls.
Admixed population: quantitative phenotype
For mapping quantitative traits in admixed population via an admixture mapping framework, investigators map the association of quantitative traits with the excess ancestry from a high-risk population at a putative locus in the admixed genome. Let be the phenotype measurement and be the proportion of alleles from population X of the i-th individual at the marker locus. Also, let be the admixture proportion of population X in the admixed population. The difference measures the excess ancestry at the locus for the i-th individual. A linear regression model can be used for finding the association between and as follows:
| (3) |
where is a vector of the covariates, is the intercept, is the coefficient of ancestry effect, is a vector of covariates effect, and is the residual. Such covariates may include age, gender, age of disease onset, medication status, average ancestry of the individual, and other clinical genotypes and environmental exposure factors. A significant indicates a possible association between the phenotype and the ancestry. To assess the association between the phenotype and the excess ancestry, we will conduct a hypothesis test of vs.
Power and sample size analysis for admixed population: dichotomous phenotype
For a two-way admixed population with a dichotomous phenotype, the ancestry proportion of alleles at genomic loci can be modeled as a binomial distribution. The power analysis to localize loci in an admixed population via a case-only study or a case-control study can be done following the one-sample or two-sample proportion tests for binomially distributed random variables, respectively.
Let and be the estimate of the proportion of alleles at marker j from the ancestry population X in cases and controls. Also, we assume that all individuals (cases and controls) have the average ancestry across the genome from the ancestry population X with constant Also, we assume that the true ancestry information at each marker locus is known. Under these assumptions, we derive the power and sample sizes for the case-only and case-control study designs as described below. As noted in Montana and Pritchard (2004), these theoretical assumptions do not meet in practice and the calculation results in the upper limit of the power achieved in practice.
Case-only study design: test statistics:
The case-only design compares the locus-specific ancestry proportion, at a marker j to the average ancestry proportion Then, the null and alternate hypotheses are:
The test statistics for the case-only design is
Under the null hypothesis, the test statistics follows a central t-distribution, which can be approximated as N(0, 1) for a large
If is the ancestry from the population X in cases under a disease model at the marker j, then under the alternate hypothesis:
Let be the type-I error rate after the adjustment for multiple testing. For example, using a Bonferroni adjustment to maintain the nominal level of a 5% type-I error rate for testing M independent markers (such as ancestry informative markers),
Let be the type-II error rate of the test. Then, the power is the probability of flagging a true effect as statistically significant (i.e., probability of correctly rejecting the null hypothesis). These analyses are usually performed by fixing power at a desired level (usually 80–90%) and estimating the sample size required for a given effect size and significance level with the test to be used.
If is the percentile from the standard normal variable, the power for a one-sided test is given by:
| (4a) |
The sample size, to achieve this power can be calculated by solving for which, after some algebra, is
| (4b) |
For a two-sided test, the power or the sample size to achieve the power can be obtained by replacing with in (4a) or (4b), respectively.
Case-control study design: test statistics:
In a case-control study design, we compare the locus-specific excess ancestry in cases and control. The case-control test statistics is based on the assumption that, at a disease-susceptibility locus, there is excess transmission of alleles from the risk population in the case, but not in the control. Under the assumption of constant average ancestry across all individuals in the cases and controls, the null and alternate hypotheses of the case-control study design are:
The test statistics is given as:
where
Under the null hypothesis, can be approximated as N(0, 1) when the sample sizes are large.
If is the ancestry from the population X in cases under a disease model at the marker j, then under the alternate hypothesis:
Let be the type-I and be the type-II error rate. For a one-sided test, the power is given by
| (5a) |
For sample size computation, we assume Then, by solving for n, we have:
| (5b) |
For a two-sided test, the power and sample sizes are computed by replacing with in (5a) and (5b), respectively.
Power and sample size analysis for admixed population: quantitative phenotype
The test statistics for quantitative trait mapping is based on the linear regression model (3), i.e., with or without covariates. In either case, we will be testing H0: against H1:
Let be an estimate of the slope () of the model (3). Under the null hypothesis, the distribution of is the central t-distribution with the degree of freedom = n - k, where n is the sample size and k is the number of parameters estimated in the regression model. It is not unrealistic in current times to consider that the sample size of a typical quantitative trait study will be a few hundreds and the number of covariates will be very low relative to n. As we collect more samples and generate more genomic information from the admixed population, we will have the sample size (n) large enough that we can approximate the t-distribution with the standard normal distribution N(0, 1). That is, under the null hypothesis,
where is the SE of which is approximately
For the type-I error rate (adjusted for the multiple testing) and the type-II error rate the power of the test for the one-sided test is:
So, we have
| (6) |
Here, will be estimated as
where = SE of model, = SD of the variable and = multiple R2 from the linear model regressing against the rest of the covariates in the model. The sample size required to achieve the power can be derived as:
| (7) |
For a simple linear model, we also have the relation If is the proportion of the variation of phenotype explained by the ancestry at the marker locus, then Using these relations, the power and sample size calculation for a simple linear model can be written as:
| (8) |
| (9) |
For a two-sided test, will be used instead of in the Equations 6–9.
To estimate the power and sample size in quantitative trait mapping, we must have the prior knowledge of and the value of under the alternate hypothesis. This information may be obtained from similar published studies or by analyzing preliminary data. If there is no covariate in the model, then we will have in (6) and (7).
For dichotomous traits, the power and sample size calculations in (4a, b) and (5a, b) depends on the parameters and the proportion of ancestry from the population X under the null and alternate model, respectively. The estimation of and depend on several parameters such as the risk allele frequencies in both populations X and Y, number of generations since admixture, population admixture rate, admixture process, mode of disease inheritance, ancestry odds ratio, genotype risk ratio, and the parental risk ratio. In AdmixPower, we implement different approaches of estimating and for a two-way admixture of ancestry population X and Y, with being the ancestry proportion from the population X.
In the next section, we describe three different approaches of estimating and (i) using the genotype risk ratio as proposed by Montana and Pritchard (2004), (ii) using the parental risk ratio as described by Zhu et al. (2004), and (iii) using the ancestry odds ratio. Investigators can choose the approach that is best suited for their own research specific parameters (see Supplemental Material, File S1 II: Practical examples).
Estimation of the parental allele frequency proportion ( and ) from the admixed population
Methods by Montana and Pritchard:
The “ancestry association” methods of Montana and Pritchard (2004) compare the observed locus-specific ancestry proportion to the population admixture rate The proportion of alleles from population X at disease locus in cases is
Let and be the allele frequencies of the risk allele, say allele “1,” in the ancestry population X and Y, respectively. For a multiplicative mode of inheritance with the genotype risk ratio the alternate is computed as follows:
where is the combined frequency of the risk allele.
We can perform the power and sample size analysis for case-only and case-control study designs for the multiplicative mode under the HI model based on the ancestry association methods of Montana and Pritchard (2004) by using the estimates and in Equations 4a and 4b for case-only, and 5a and 5b for case-control designs.
These formulas assume that the ancestry of individuals is known with certainty. In real practice, we need to infer the ancestry origin of the individuals, so the power computed using the formulas are the upper bound, and the sample size required to achieve a specified power represents the lower bound.
Methods by Zhu et al.:
Zhu et al. (2004) analytically established the admixture proportion at a marker locus in an admixed population as a function of the recombination fraction between the marker locus, the disease locus, and the number of generations since admixture g under two different admixture mapping processes (HI and CGF) and four different modes of inheritance (multiplicative, additive, recessive, and dominant). However, the authors only describe the case-only design. We extend the approach to a case-control study by assuming the control population is equivalent to the null population with no linkage. We only report the formulas for the multiplicative mode for both HI and CGF models. For more details of the mathematical computation, we refer to Zhu et al. (2004).
Let and be the allele frequencies of allele 1 at a disease locus in the population X and Y, respectively. Also, let be the penetrances of the disease genotype 00, 01, and 11 (0 = nonrisk allele and 1 = disease risk allele). Then, the parental risk ratio of the parental population X to Y is
In practice, the penetrance functions may not be accessible. However, we can easily find the disease prevalence rate in the ancestry population X and Y. Then, the parental risk ratio can be alternately defined as Note that and represent the disease prevalence in populations X and Y, respectively.
For the HI process with the multiplicative mode where is the genotype risk ratio (constant for both populations), the proportion of the ancestry from the population X after g generation of admixture is
where and “mul” indicates the multiplicative mode.
For the case-only design, under the null hypothesis and under the alternate hypothesis. So, the power and the sample size for the case-only design for the multiplicative mode under the HI process of admixture can be obtained by using and for some nonzero in the Equations 4a and 4b.
Extending the case-only approach of Zhu et al. (2004) to a case-control study design, we consider the control population as an equivalent of a no linkage model. We extend the case-only design to the case-control design by considering for the control sample under both null and alternate hypotheses. Then, we perform the power and sample size analysis of the case-control study design for the multiplicative mode under the HI process by using and for some nonzero in Equations 5a and 5b.
In the CGF model, there will be a continuous contribution from the population Y in the admixed population. If the proportion of alleles contributed per generation by the population Y is in the admixed population, then in the g generation, the contribution from the population X is given as or For the multiplicative mode of inheritance, the proportion of the allele from the population X after g generation of admixture is
where
Hence, we can perform the power and sample size analysis for the case-only and case-control study designs for the multiplicative mode under the CGF process by using and for some nonzero in the Equations 4a and 4b or 5a and 5b.
Estimation of ancestry proportion based on ancestry odds ratio:
For a two-way admixture between the populations X and Y, with θ being the admixture proportion from the high-risk population X, the ancestral odds ratio per one copy of the allele from X is defined as
where ancestry proportion in cases, and = ancestry proportion in control. So, for a given ancestral odds ratio () and the admixture proportion (), we can estimate as below:
| (10) |
The ancestry proportion in the control is equivalent to the admixture proportion under the null. We can perform the power and sample size analysis for the case-control study design for the multiplicative mode under the HI process by using and in (5a, b) with computed for some in (10).
Program availability and implementation
AdmixPower is implemented in the R programming language. The program source code and some examples are available at https://research.cchmc.org/mershalab/Tools.html. For a dichotomous (or discrete) phenotype, three pairs of functions (within each pair one function to compute the power and the other function to compute sample size) are developed: (i) PowerDiscreteGRR() and SampleDiscreteGRR() based on Montana and Pritchard (2004), (ii) PowerDiscretePRR() and SampleDiscretePRR() based on Zhu et al. (2004), and (iii) SampleDiscreteAOR() and SampleDiscreteAOR() bases on the ancestry odds ratio-based approach (for details see the Analytical Theory section). These methods use a slightly different set of population-specific parameters in the estimation of the ancestry proportion under the null and alternate hypothesis. The output from functions SampleDiscreteGRR(), SampleDiscretePRR(), and SampleDiscreteAOR() are the minimum number of cases required to achieve the desired power of the test in the case-only study design. For the case-control study design, the output is the total of cases and controls required to achieve the desired power, assuming an equal number of cases and controls.
For a quantitative trait, two pair of functions are developed for the power and sample size analysis: (i) PowerQTraitCoeff() and SampleQTraitCoeff(), based on the Wald test for a regression coefficient in the linear regression framework as defined by Equations 6 and 7, respectively; and (ii) PowerQTraitRSquare() and SampleQTraitRSquare(), based on the percentage of the explained variation of the phenotype () as defined by Equations 8 and 9, respectively.
Details of the AdmixPower functions and their arguments are provided in File S1 (I: AdmixPower functions and arguments). Based on the available set of parameters, we can choose different AdmixPower functions to carry out the power and sample size analysis for dichotomous and quantitative traits. Examples of power and sample size analysis for admixed populations using AdmixPower are provided in File S1 (II: Practical examples). The R code used to graphically describe the relationship of power, sample size, different population-specific risk factors, and model parameters by applying appropriate functions implemented in AdmixPower are provided in File S1 (III: R code for figures).
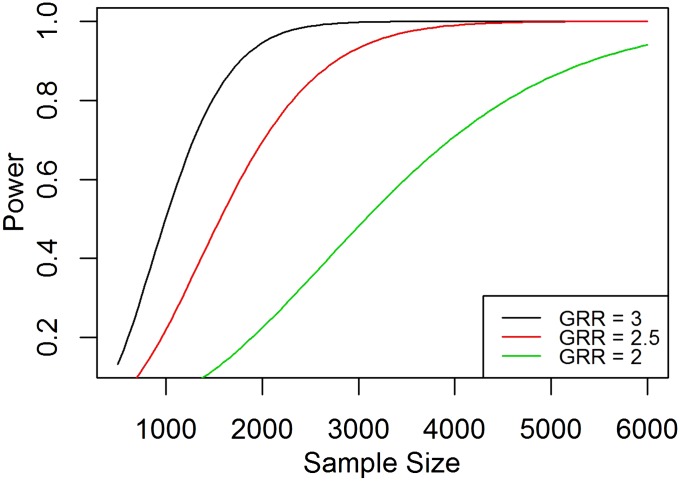
Effect of sample size on power for different genotype risk ratios
In planning a genetic association study, it is critical to determine the sample size required to detect susceptibility loci with sufficient power. Figure 1 shows the power as a function of sample size in a case-control admixed sample study design for different genotype risk ratios (), assuming equal case and control samples. A larger sample size is required to have adequate power if the genotype risk ratio in the admixed population is low.
Figure 1.
Power as a function of sample size for different genotype risk ratios. The graphs show the power as a function of sample size for case-control study design assuming multiplicative mode of inheritance with genotype risk ratio (λ) = 3, 2.5, and 2, respectively. Power is computed using the function PowerDiscreteGRR() with the admixture proportion = 0.8, risk allele frequencies and for a one-sided test, and adjusted type-I error rate = 0.000025. GRR, genotype risk ratio.
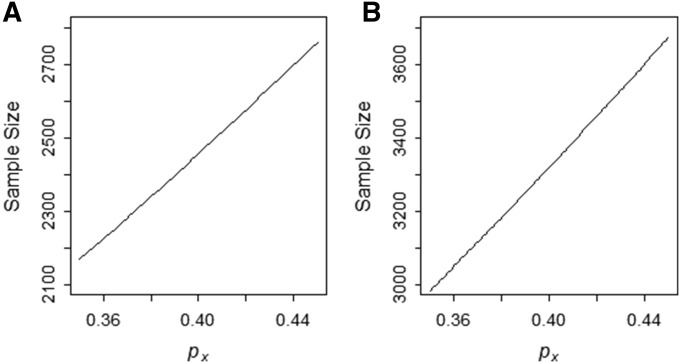
Sample size as a function of allele frequency of the risk allele in admixed population
Figure 2 shows the total number of samples required to detect an allele frequency difference of 0.3 between ancestral populations and with power 0.8, assuming equal sizes for the case and control in the case-control study design. We consider a two-way admixture of two ancestral populations X and Y with θ = 0.8 as the average contribution from the population X. When population X is the high-risk population, we will then have (Figure 2A, disease locus is mapped to the higher proportion of admixed ancestry). On the other hand, if the population Y is the high-risk population, we will have (Figure 2B, disease locus is mapped to the lower admixture proportion in the admixed sample). To map the disease locus that occurs in the ancestral population of the lowest admixture proportion, we need to ascertain large numbers of samples (Figure 2).
Figure 2.
Sample size as a function of allele frequency of the risk allele in population X. The graph shows the number of individuals in case sample to detect the allele frequency difference of 0.3 between the ancestry populations for different value of (A) The graph with (that is, population X is the high-risk population) with varying from 0.35 to 0.45. (B) The graph with (that is, the population Y is the high-risk population). Sample size is computed using the function SampleDiscreteGRR() with the admixture proportion admixture proportion = 0.8, the genotype risk ratio (λ) = 2, multiplicative mode of inheritance, and the two-sided test with adjusted type-I error rate = 0.000025 and type-II error rate = 0.2.
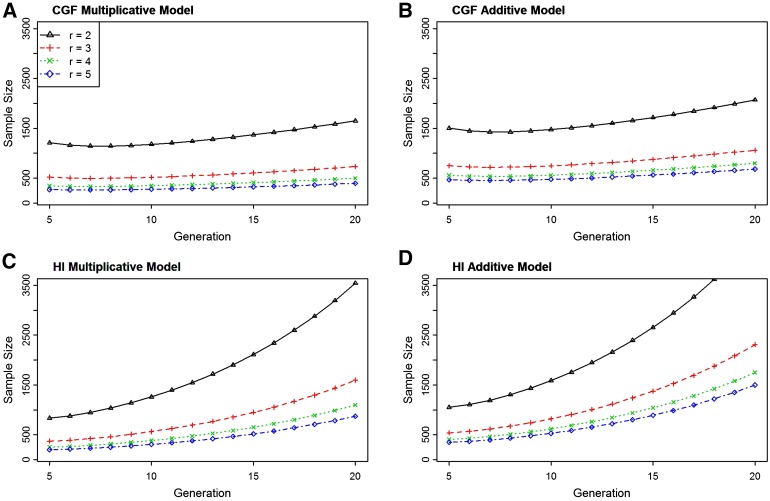
Sample size as a function of number of generations since admixture and parental risk ratio
Recently admixed populations have larger chromosomal regions, due to the shorter period of time for breaking up the linkage disequilibrium created as a result of admixture, than populations which are admixed for longer generations. We expect admixture mapping to have a lower power for detecting the ancestry–phenotype association from populations with a relatively longer time since admixture, due to shorter linkage disequilibrium, than recently admixed populations (Smith and O’Brien 2005).
Figure 3 shows the sample size as a function of the numbers of generations since admixture to achieve a power of 80% for the case-only study design with different parental risk ratios. The graph suggests that the sample size required for detecting the ancestry-linked marker increases with an increased number of generations since admixture. As the generations of admixture increases, recombination events break down the region of linkage disequilibrium (due to admixture), causing decay in the linkage between the marker locus and the disease locus and, hence, reducing the power of admixture mapping. For the HI model, the sample size increases at a much faster rate than that for the CGF model. This is because, under the CGF admixture process, steady inflow of recently admixed genome slows down the breakdown of linkage disequilibrium due to admixture, whereas in the HI process no such event occurs.
Figure 3.
Sample size as a function of number of generations since the admixture for CGF (A and B) and HI (C and D) processes of admixture. Sample size is computed for the different parental risk ratios (r = 2, 3, 4, and 5) to achieve 80% power with genome-wide level of significance 0.001 under the multiplicative (A and C) and additive (B and D) mode of inheritance. The computation is done using the function SampleDiscretePRR() with the recombination rate of 0.05 and the admixture proportion 0.80.
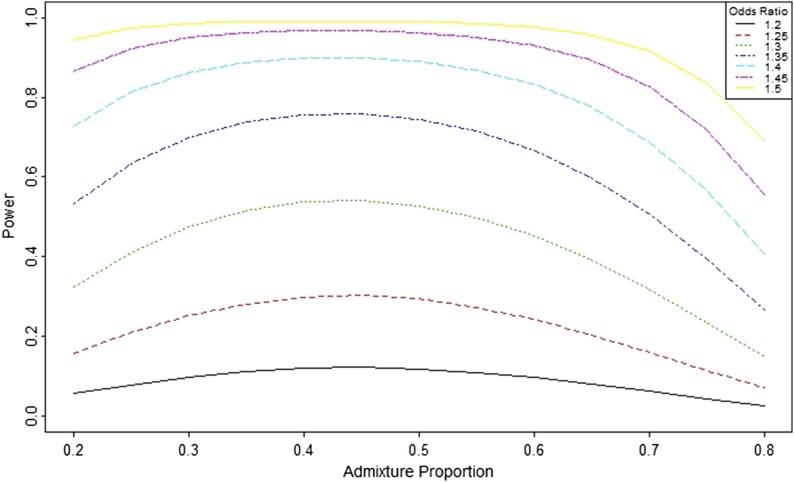
Power as a function of the odds ratio and admixture proportion
The ancestry odds ratio is a commonly used parameter in the study of the admixed population. Figure 4 shows the power as the function of the admixture proportion for different ancestry odds ratios. The power is higher for the admixed population when the ancestry proportion is in the interval 0.4–0.5. This result suggests that the highest power achieved for the admixture proportion (θ) will be slightly <0.5. A higher ancestry odds ratio yields higher power. When the ancestry odds ratio is 1.5, the power of admixture mapping is close to 1 for the ancestry proportion in the range of 0.3–0.7.
Figure 4.
Power as a function of admixture proportion and ancestry odds ratio. Power is calculated for different ancestry odds ratio (η = 1.2–1.5 by 0.05) for case-control study design with 1000 cases and 1000 controls. Computation is done using the function PowerDiscreteAOR() with adjusted type-I error rate 0.00025.
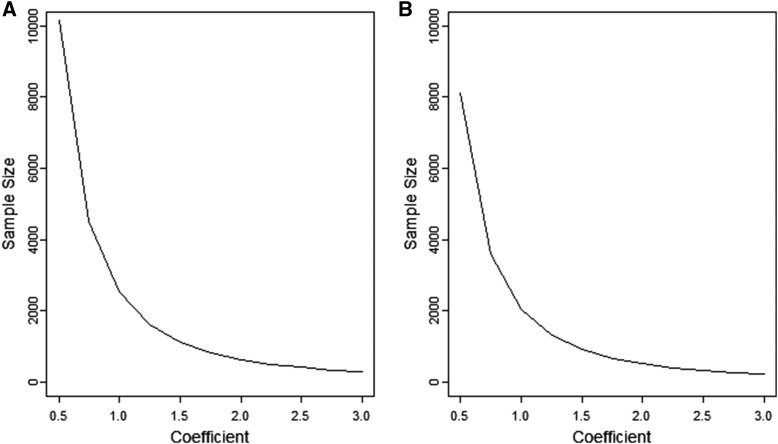
Sample size as a function of the slope of the linear regression model for the quantitative trait
For mapping quantitative traits in an admixed population, we are interested in estimating the regression coefficient from the model (3). Figure 5 shows the sample size required for detecting the phenotype–ancestry association with 80% power for with and without a correlation () between the ancestry and covariates. A larger sample size is required when the ancestry is correlated with the covariates rather than when the ancestry and covariates are independent. This is because the covariates explain some parts of the association and hence reduce the explanatory power of the ancestry. For a simple regression model without covariates, the power can be calculated by assuming
Figure 5.
Sample size as a function of Sample size is computed for with 80% power and type-I error rate 0.00025. (A) The sample size when there is a small correlation between the ancestry and other covariates (). (B) The sample size when the ancestry is independent of the covariates ().
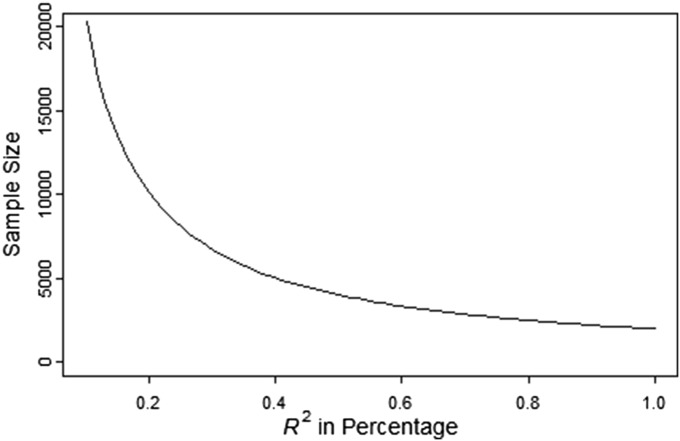
Sample size as a function of the percentage of explained variation of phenotype
For a simple linear model without covariates, testing for is equivalent to testing for correlation r between the phenotype and the ancestry, or testing for (the proportion of variance of phenotype explained by the ancestry). Figure 6 shows the sample size as a function of In this figure, assuming for a single marker, a small is expected.
Figure 6.
Sample size a function of the percentage of variation explained. Sample size is computed with 80% power and 0.00025 type-I error rate. The x-axis represents in percentage.
Data availability
AdmixPower is implemented in the R programming language and the program source code and some examples are available at https://research.cchmc.org/mershalab/Tools.html. Supplemental materials include the text in File S1 which describes functions, the arguments, practical examples, and R code for Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, and Figure 6.
Discussion
Over the past decade, genome-wide association studies using single nucleotide polymorphism markers have been highly successful in the study of complex diseases, with power analysis aided by software packages such as Genetic Power Calculator (Purcell et al. 2003) and CaTS (Skol et al. 2006). Currently, there is growing interest in detecting complex trait-associated variants in admixed populations using admixture mapping. Due to disease prevalence and genome variation among ancestral populations, admixed populations offer distinctive advantages over homogeneous populations in localizing ancestry-specific genetic risk variants. This is because admixture analysis efficiently tests regions that exhibit different risk allele frequencies among ancestral populations (within admixed samples) and allows for the efficient detection of genomic regions with an exponentially smaller sample size and increased power compared to genome-wide association studies (Mersha 2015). In presenting sample size and power analysis for the research community, we first consider power and sample size calculations for case-only and case-control studies, and then extend the approach for quantitative traits using a linear regression model for additive effects with or without covariates. To our knowledge, this is the first tool set for determining power and sample size for admixture mapping using admixed populations.
Sample size and power analysis are the most crucial steps in designing complex genetic trait association studies. Several investigators have presented power and sample size guidelines for association studies of genetically homogeneous populations. In contrast, the genetic complexity arising from an admixed population makes power and sample size estimations challenging. As a result, information on power and sample size analysis for admixed population studies is lacking. The purpose of the present article is to provide sample size and power analysis guidelines for admixture studies to map dichotomous (or qualitative) and quantitative (or continuous) traits under a variety of genetic and disease phenotype models. Specifically, we consider the effects of (1) study design, including case-only and case-control designs; (2) genetic models, including dominant, recessive, additive, and multiplicative models; (3) odds ratio; (4) admixture models, including HI and CGF models; and (5) allele frequency and disease prevalence differences between ancestral populations.
Theoretically, a larger sample size leads to higher confidence in detecting significant effects in a given clinical study. However, in reality, clinical samples are often limited and/or the cost of sampling is high. With a smaller sample size, a study may not be able to detect the small or moderate effects. On the other hand, a larger sample size results in wastage of precious resources and the researchers’ time. Ensuring adequate sample sizes for detecting expected power is an essential part of study design to approve/reject the stated hypothesis. This article presents sample size and power calculation methods for determining ancestry–phenotype associations for a specified sample size or for estimating the sample size for a given (prespecified) power for a variety of genetic models and statistical methods.
Conclusion
Acting as a natural experiment, admixed populations provide insight into unique genomic recombination and segmental reshuffling of their parental chromosomal ancestry. One of the major opportunities in these populations is the potential to apply an admixture mapping method, which evaluates the association of local ancestry with phenotypic traits, especially with regard to diseases with different frequencies across parental populations. In this study, we addressed the two most common questions researchers have to answer before undertaking an admixture mapping project: (1) “How large a sample size do I need?” (2) “How do I decide the sample size of a given study to ensure adequate power for observing a given effect size?” In this study, we provided an easily accessible and easy-to-use R-based application that provides power and sample size estimates for investigators planning genetic studies in admixed populations. Even though the true underlying genetic model may be unknown, using a range of genetic models, odds ratio, effect sizes, and admixture processes extrapolated from the literature, an investigator can determine whether a study has adequate power to detect ancestry–phenotype associations.
There are several areas where AdmixPower will be expanded. First, we will expand to determine sample size and power analysis for multiple ancestral populations in an admixed population. Second, we plan to expand the command-line use and develop a Web application for interactive use via a simple “point-and-click-of-a-button” function that enables researchers to calculate power with user-friendly queries through a single Web interface. We hope that this tool will prove of value for investigators planning admixture mapping studies for publication and for determining the sample size required in grant applications.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300312/-/DC1.
Acknowledgments
This work was supported by National Institutes of Health grants R01 HL-132344 and R03 HL-133713, Clinical and Translational Science Award program grant 5UL1TR001425-02, and the Diversity and Health Disparities Award of the Cincinnati Children’s Research Foundation.
Footnotes
Communicating editor: N. Yi
Literature Cited
- Baye T. M., Wilke R. A., 2010. Mapping genes that predict treatment outcome in admixed populations. Pharmacogenomics J. 10: 465–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng S., Wang S., Chen C. C., Lan L., 2011. GWAPower: a statistical power calculation software for genome-wide association studies with quantitative traits. BMC Genet. 12: 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellenthal G., Busby G. B., Band G., Wilson J. F., Capelli C., et al. , 2014. A genetic atlas of human admixture history. Science 343: 747–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J. Z., Absher D. M., Tang H., Southwick A. M., Casto A. M., et al. , 2008. Worldwide human relationships inferred from genome-wide patterns of variation. Science 319: 1100–1104. [DOI] [PubMed] [Google Scholar]
- Mersha T. B., 2015. Mapping asthma-associated variants in admixed populations. Front. Genet. 6: 292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montana G., Pritchard J. K., 2004. Statistical tests for admixture mapping with case-control and cases-only data. Am. J. Hum. Genet. 75: 771–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaff C. L., Parra E. J., Bonilla C., Hiester K., McKeigue P. M., et al. , 2001. Population structure in admixed populations: effect of admixture dynamics on the pattern of linkage disequilibrium. Am. J. Hum. Genet. 68: 198–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., Cherny S. S., Sham P. C., 2003. Genetic power calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics 19: 149–150. [DOI] [PubMed] [Google Scholar]
- Rosenberg N. A., Nordborg M., 2006. A general population-genetic model for the production by population structure of spurious genotype-phenotype associations in discrete, admixed or spatially distributed populations. Genetics 173: 1665–1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg N. A., Pritchard J. K., Weber J. L., Cann H. M., Kidd K. K., et al. , 2002. Genetic structure of human populations. Science 298: 2381–2385. [DOI] [PubMed] [Google Scholar]
- Skol A. D., Scott L. J., Abecasis G. R., Boehnke M., 2006. Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nat. Genet. 38: 209–213. [DOI] [PubMed] [Google Scholar]
- Smith M. W., O’Brien S. J., 2005. Mapping by admixture linkage disequilibrium: advances, limitations and guidelines. Nat. Rev. Genet. 6: 623–632. [DOI] [PubMed] [Google Scholar]
- Zhu X., 2012. The analysis of ethnic mixtures. Methods Mol. Biol. 850: 465–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X., Cooper R. S., Elston R. C., 2004. Linkage analysis of a complex disease through use of admixed populations. Am. J. Hum. Genet. 74: 1136–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
AdmixPower is implemented in the R programming language and the program source code and some examples are available at https://research.cchmc.org/mershalab/Tools.html. Supplemental materials include the text in File S1 which describes functions, the arguments, practical examples, and R code for Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, and Figure 6.